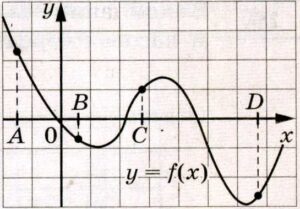
На рисунке изображён график функции y = f( x) и отмечены точки A, B, C и D на оси x.
Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ
1) значение функции в точке положительно и значение производной функции в точке положительно
2) значение функции в точке отрицательно и значение производной функции в точке отрицательно
3) значение функции в точке положительно, а значение производной функции в точке отрицательно
4) значение функции в точке отрицательно, а значение производной функции в точке положительно
В таблице под каждой буквой укажите соответствующий номер.
Спрятать решение
Решение.
В точке A значение функции в точке положительно, а значение производной функции в точке отрицательно.
В точке B значение функции в точке отрицательно и значение производной функции в точке отрицательно функции в точке отрицательно
В точке C значение функции в точке положительно и значение производной функции в точке положительно.
В точке D значение функции в точке отрицательно, а значение производной функции в точке положительно
Таким образом, получаем соответствие A — 3, B — 2, C — 1 и D — 4.
Ответ: 3214.
Источник: Пробный экзамен Санкт-Петербург 04.04.2018. Вариант 1.

на базовом ЕГЭ по математике отведено немного места, но всё же она присутствует.
В данной статье рассмотрим серию задач из открытого банка заданий ФИПИ по
математике (базовый уровень).
Задание 1. На рисунке изображён график функции
y=f(x) и отмечены точки A, B, C и D на оси
Ox. Пользуясь графиком, поставьте в соответствие каждой точке
характеристики функции и её производной.
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ ФУНКЦИИ И ПРОИЗВОДНОЙ |
|
А |
1. |
|
В |
2. |
|
С |
3. |
|
D |
4. |
В таблице под каждой буквой укажите соответствующий
номер.
Решение. Для выполнения этого задания
необходимо вспомнить свойства производной функции. Если на некотором числовом
промежутке производная функции положительна, то функция на этом числовом
промежутке возрастает, если же производная отрицательна, то функция убывает.
В точке А значение функции отрицательно и функция на
числовом промежутке, в который входит точка А, возрастает, значит производная
положительна. Это соответствует характеристике 4.
В точке В значение функции положительно, а функция на
числовом промежутке, в который входит точка В, убывает, значит производная
отрицательна. Это соответствует характеристике 1.
В точке С значение функции отрицательно, а функция на
числовом промежутке, в который входит точка С, убывает, значит производная
отрицательна. Это соответствует характеристике 2.
В точке D значение функции положительно, и
функция на числовом промежутке, в который входит точка D, возрастает, значит, производная
положительна. Это соответствует характеристике 3.
Указываем в таблице под каждой буквой соответствующий
номер характеристики.
Ответ 4123.
Задание 2. На рисунке изображён график функции
y=f(x). Точки a, b, c, d и e задают
на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому
интервалу характеристику функции или её производной.
|
ИНТЕРВАЛЫ |
ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ |
|
А) (a; b) |
1. Значения функции положительны |
|
Б) (b; c) |
2. Значения производной функции |
|
В) (c; d) |
3. Значения производной функции |
|
Г) (d; e) |
4. Значения функции отрицательны |
В таблице ниже под каждой буквой укажите
соответствующий номер.
Решение. На
отрезке (a; b) функция убывает, значит, значения производной
функции отрицательны в каждой точке интервала, характеристика 2.
На отрезке (b; c)
значения функции отрицательны
в каждой точке интервала, характеристика 4.
На отрезке (c; d)
функция возрастает, значит, значения производной функции положительны в каждой
точке интервала, характеристика 3.
На отрезке (d; е)
значения функции положительны
в каждой точке интервала, характеристика 1.
Указываем в таблице
под каждой буквой соответствующий номер.
Ответ
2431.
Задание 3. На рисунке изображены график
функции и касательные, проведённые к нему в точках с абсциссами A, B,
C и D.
В правом столбце указаны значения производной функции
в точках A, B, C и D. Пользуясь графиком, поставьте
в соответствие каждой точке значение производной функции в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
А |
1) – 1,5 |
|
В |
2) 0,5 |
|
С |
3) 2 |
|
D |
4) – 0,3 |
В таблице под каждой буквой укажите соответствующий
номер.
Решение. В
точке А касательная резко возрастающая, значит угловой коэффициент её
положителен и большой. Это соответствует значению производной 3.
В точке В касательная
медленно убывает, значит угловой коэффициент её отрицателен и небольшой по
модулю. Это соответствует значению производной 4.
В точке С касательная
быстро убывает, значит угловой коэффициент её отрицателен и достаточно большой
по модулю. Это соответствует значению производной 1.
В точке D касательная
медленно возрастающая, значит угловой коэффициент её положителен и небольшой.
Это соответствует значению производной 2.
Указываем в таблице
под каждой буквой соответствующий номер.
Ответ
3412.
Задания для самостоятельной работы.
Задание 1. На рисунке изображены график
функции и касательные, проведённые к нему в точках с абсциссами A, B,
C и D.
В правом столбце указаны значения производной функции
в точках A, B, C и D. Пользуясь графиком, поставьте
в соответствие каждой точке значение производной функции в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ |
|
А |
1) |
|
В |
2) |
|
С |
3) |
|
D |
4) |
В таблице под каждой буквой укажите соответствующий номер.
Задание 2. На рисунке изображены график
функции и касательные, проведённые к нему в точках с абсциссами A, B,
C и D.
В правом столбце указаны значения производной функции
в точках A, B, C и D. Пользуясь графиком, поставьте
в соответствие каждой точке значение производной функции в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ |
|
А |
1) |
|
В |
2) |
|
С |
3) |
|
D |
4) |
В таблице под каждой буквой укажите соответствующий
номер.
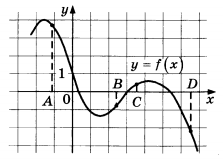
На рисунке изображён график функции у = f(x) и отмечены точки А, В, С и D на оси Ох. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
| ТОЧКИ | ХАРАКТЕРИСТИКИ |
|
А |
1) значение функции в точке положительно, и значение производной функции в точке положительно 2) значение функции в точке отрицательно, и значение производной функции в точке отрицательно 3) значение функции в точке положительно, а значение производной функции в точке отрицательно 4) значение функции в точке отрицательно, а значение производной функции в точке положительно |
В таблице для каждой точки укажите номер соответствующий характеристике.
Источник: Ященко ЕГЭ 2022 (30 вар).
Решение:
Дан график функции.
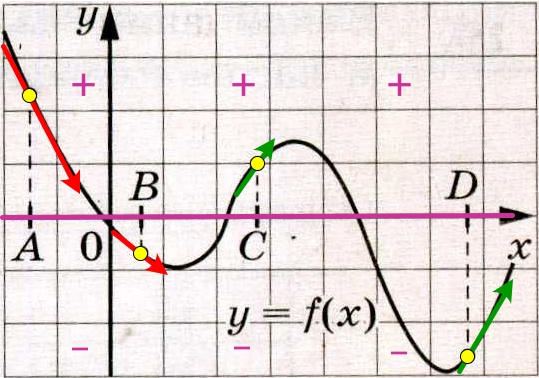
Точка А выше оси Ох, значит значение функции положительно, расположена на промежутке убывания, значит значение производной отрицательно – это 3).
Точка В ниже оси Ох, значит значение функции отрицательно, расположена на промежутке убывания, значит значение производной отрицательно – это 2).
Точка С выше оси Ох, значит значение функции положительно, расположена на промежутке возрастания, значит значение производной положительно – это 1).
Точка D ниже оси Ох, значит значение функции отрицательно, расположена на промежутке возрастания, значит значение производной положительно – это 4).
Ответ: 3214.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Условие
На рисунке изображён график функции у = f(x) и отмечены точки А, В, С и D на оси Ох. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
ТОЧКИ
А) А
Б) В
В) С
Г) D
ХАРАКТЕРИСТИКИ ФУНКЦИИ И ПРОИЗВОДНОЙ
1) значение функции в точке положительно, а значение производной функции в точке отрицательно
2) значение функции в точке отрицательно, а значение производной функции в точке положительно
3) значение функции в точке положительно и значение производной функции в точке положительно
4) значение функции в точке отрицательно и значение производной функции в точке отрицательно
В таблице под каждой буквой укажите соответствующий номер.
математика 10-11 класс
34225
Решение
Дальше по аналогии
Б — 2
В — 3
Г — 4
Ответ: 1234
Написать комментарий
На этой странице вы узнаете
- Где проходит граница между теплом и холодом?
- Почему успех фильма не всегда зависит от наличия экшн-сцен?
- Чем кофе похож на функцию, ее первообразную и производную?
Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.
Связь графика функции и производной
Подготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.
Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.
Возьмем график произвольной функции.
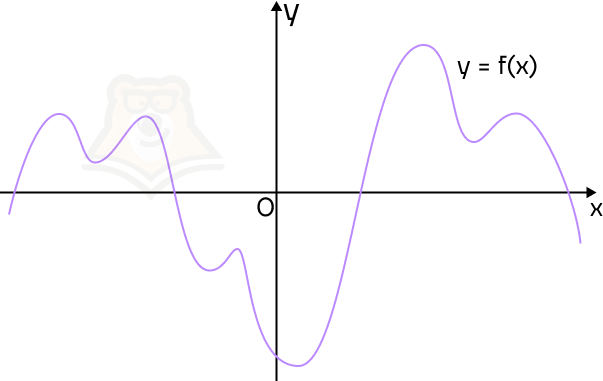
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».
Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.
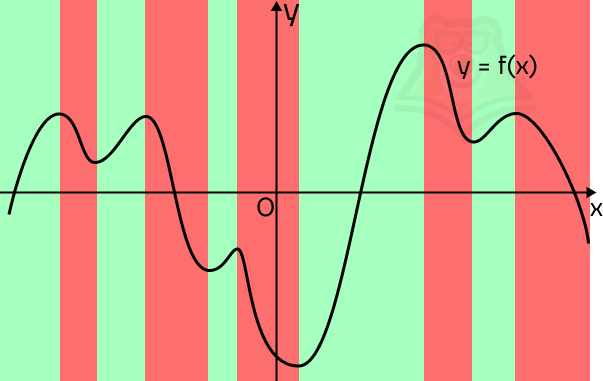
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.
Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
В точках экстремума производная равна 0.
Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.
Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан
y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.
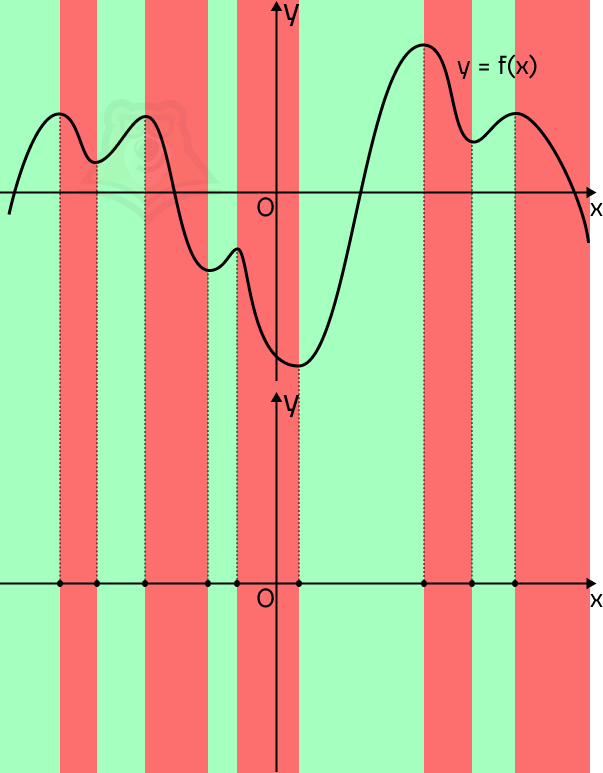
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.
Вспомним, что:
- производная положительна на промежутках возрастания функции;
- производная отрицательна на промежутках убывания функции.
Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.
Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.
Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной.
Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах.
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.
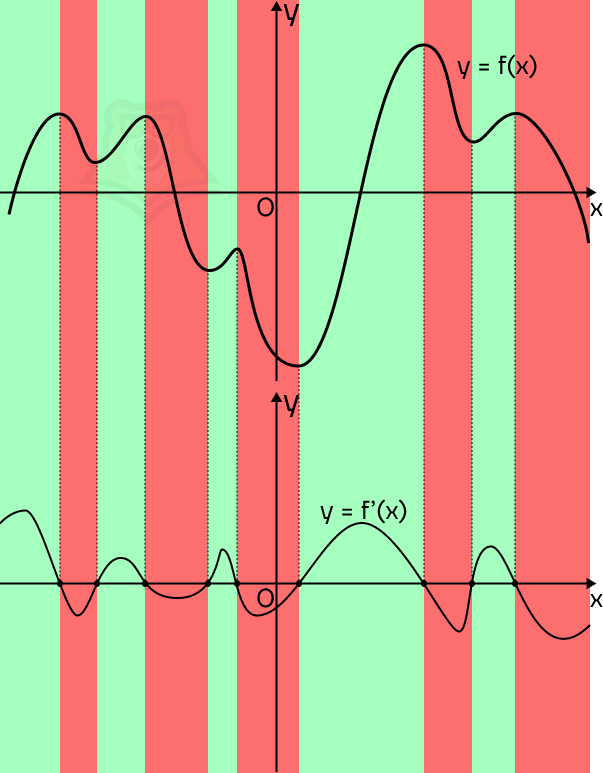
Подведем итоги:
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
Эти зависимости можно отследить на любых графиках функции и ее производной.
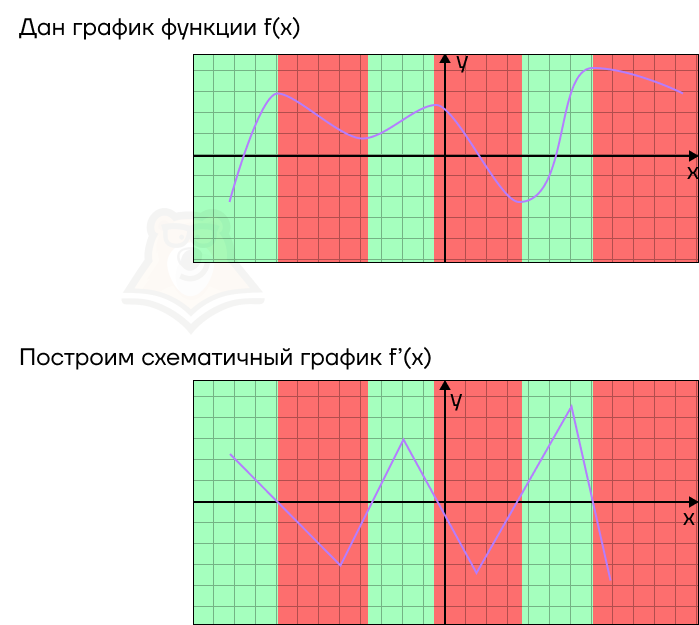
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:
- В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
- На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
- На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.
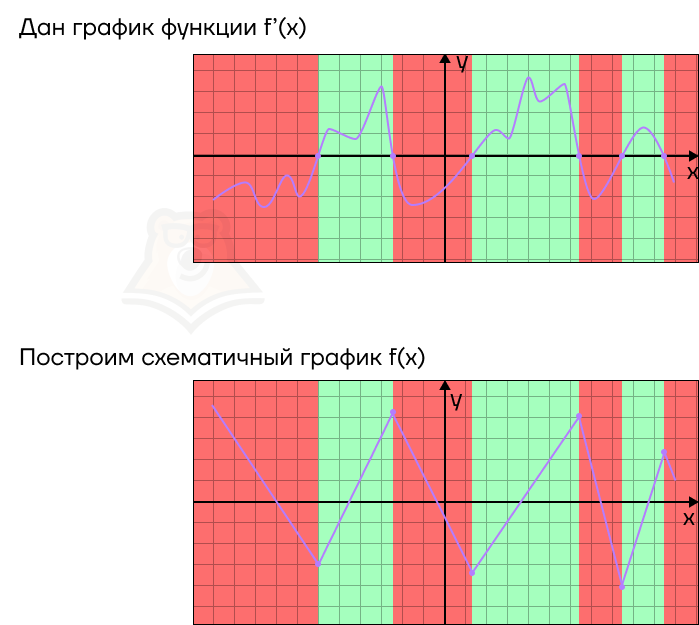
Разберем несколько примеров, где можно применить эти знания.
Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x1, x2, x3, x4, x5. В скольких из этих точек производная функции отрицательна?
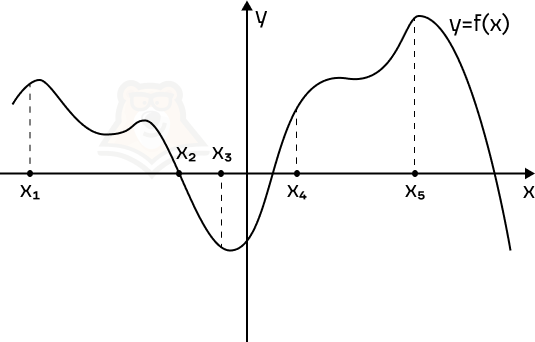
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.
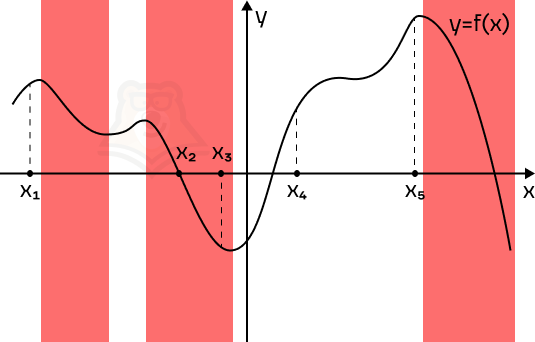
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.
Ответ: 2
Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).
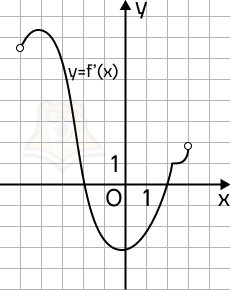
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.
Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.
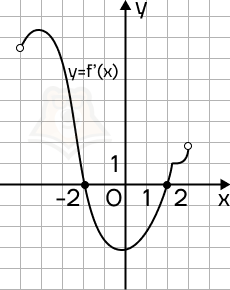
Ответ: -2
Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Совпадут ли эти графики? Скорее всего, нет.
Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой.
Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются.
Связь графика функции и первообразной
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?
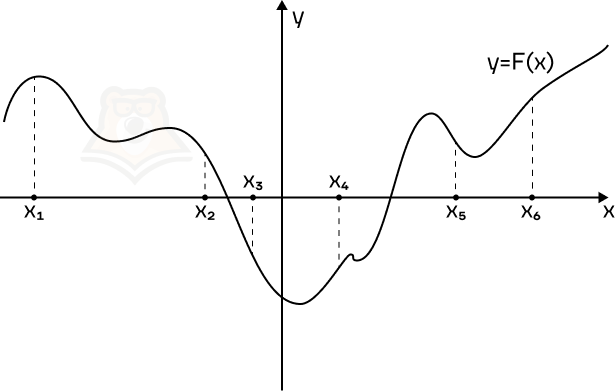
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
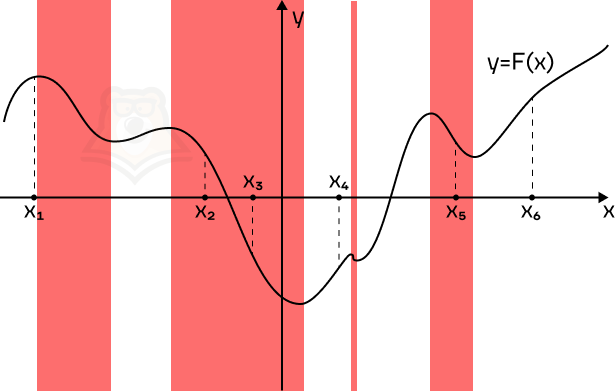
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].
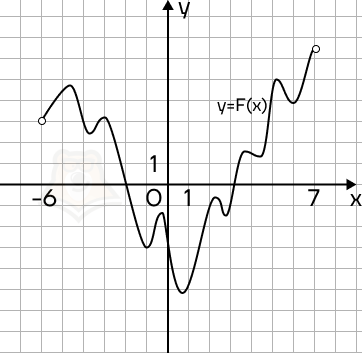
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
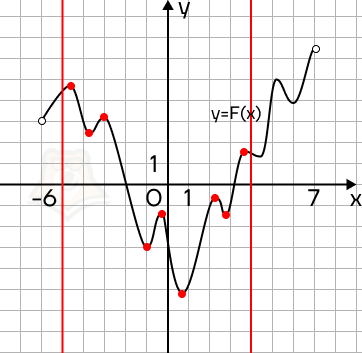
Ответ: 9
Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток.
Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная.
Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной.
Фактчек
- Графики функции, производной и первообразной связаны между собой.
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
- Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.
Проверь себя
Задание 1.
На каких промежутках будет производная функции будет положительна?
- На промежутках убывания функции.
- На промежутках возрастания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 2.
На каких промежутках производная функции будет отрицательна?
- На промежутках возрастания функции.
- На промежутках убывания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?
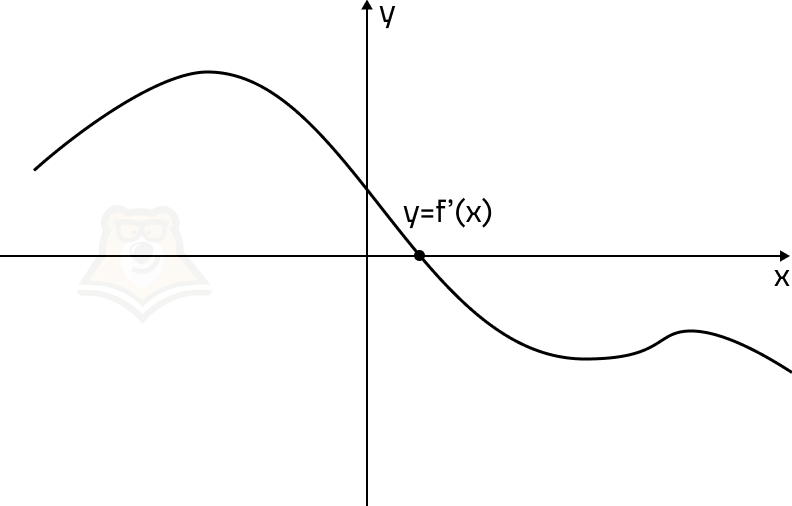
- Точка максимума функции.
- Точка минимума функции.
- Любая произвольная точка на функции.
- Невозможно определить по графику.
Задание 4.
Выберите верный вариант:
- F(x) = f'(x)
- F(x) = f(x)
- F'(x) = f'(x)
- F'(x) = f(x)
Ответы: 1. — 2 2. — 2 3. — 1 4. — 4
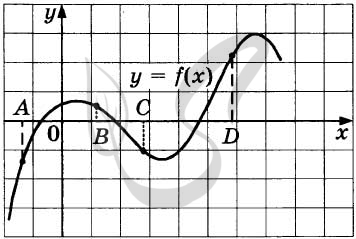
9490. На рисунке изображён график функции y = f(x) и отмечены точки A, B, C и D на оси Ox. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
ТОЧКИ
А) C
Б) D
В) B
Г) A
ХАРАКТЕРИСТИКИ
1) значение функции в точке положительно, а значение производной функции в точке отрицательно
2) значение функции в точке отрицательно и значение производной функции в точке отрицательно
3) значение функции в точке положительно и значение производной функции в точке положительно
4) значение функции в точке отрицательно, а значение производной функции в точке положительно

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 
При обращении указывайте id этого вопроса — 9490.
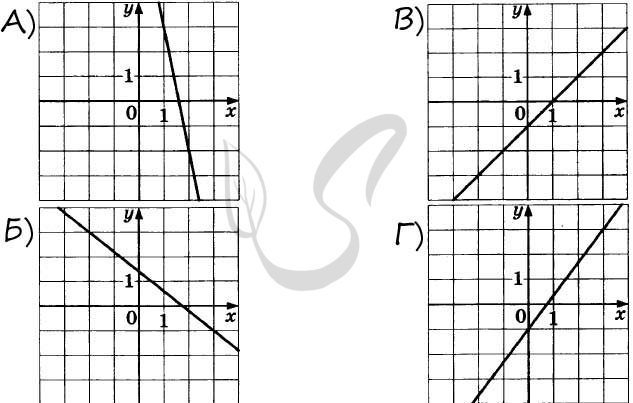
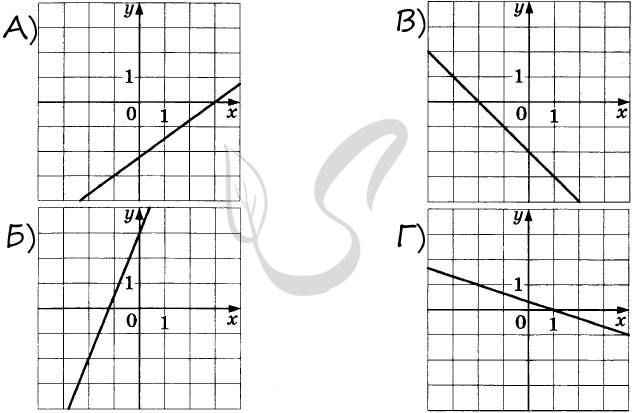
9470. На рисунках изображены графики функций вида ( y = kx + b ). Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ ФУНКЦИЙ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) 0,5
2) 2
3) -0,2
4) ( — frac{4}{3} )

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 
При обращении указывайте id этого вопроса — 9470.
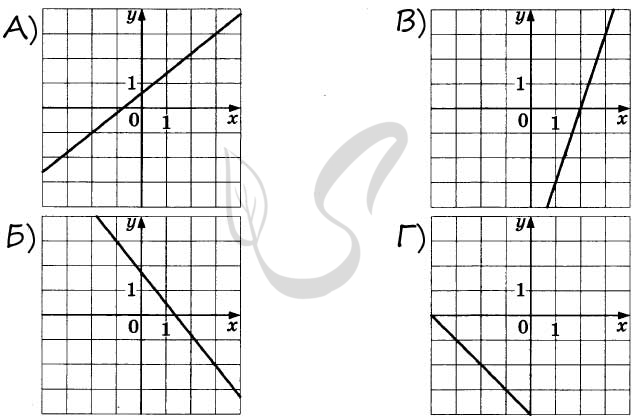
9450. На рисунках изображены графики функций вида ( y = kx + b ). Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ ФУНКЦИЙ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) -0,8
2) 1
3) ( frac{4}{3} )
4) -5

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 
При обращении указывайте id этого вопроса — 9450.
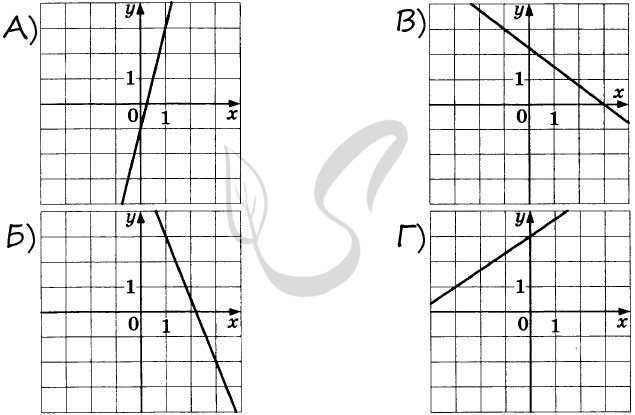
9430. На рисунках изображены графики функций вида ( y = kx + b ). Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ ФУНКЦИЙ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) -1
2) 2,5
3) 0,75
4) ( — frac{1}{3} )

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 
При обращении указывайте id этого вопроса — 9430.
9410. На рисунках изображены графики функций вида ( y = kx + b ). Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ ФУНКЦИЙ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 
При обращении указывайте id этого вопроса — 9410.
9390. На рисунках изображены графики функций вида ( y = kx + b ). Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ ФУНКЦИЙ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) 4
2) -2,5
3) ( frac{2}{3} )
4) -0,75

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 
При обращении указывайте id этого вопроса — 9390.
Для вас приятно генерировать тесты, создавайте их почаще