Отличался от других идиотов тем, что считал себя продолговатым
|
Вступительный тест по математикеПредлагаемый Вашему вниманию тест «Вступительный тест по математике» создан на основе одноименной базы знаний, состоящей из 80 вопросов. В данном тесте будет задано 30 вопросов. Для успешного прохождения теста необходимо правильно ответить на 27 вопросов. После ответа на каждый вопрос сразу будет отображаться правильный ответ, поэтому в этом режиме сделанный ответ исправить будет нельзя. идет загрузка вопросов теста, пожалуйста подождите… Просьба от разработчиков поделиться ссылкой. Спасибо!Хотите встроить тест «Вступительный тест по математике» в свой сайт?Или провести тестирование?ИндексСписок вопросов базы знаний |
Copyright testserver.pro 2013-2021
Пример вступительного испытания по математике
№1. Решите уравнение
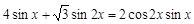
№2. Решите систему уравнений
№3. Найдите уравнение прямой, проходящей через точку с координатами (1; 3), касающейся графика функции 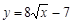
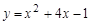
№4. Хорда окружности, удалённая от центра на расстояние 15, разбивает окружность на два сегмента, в каждый из которых вписан квадрат. Найдите разность сторон этих квадратов.
№5. Решите неравенство
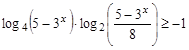
№6. В две бочки были налиты растворы соли, причём в первую бочку было налито 16 кг, а во вторую – 25 кг. Оба раствора разбавили водой так, что процентное содержание соли уменьшилось в k раз в первом бочке и в m раз во второй. О числах k и m известно, что km = k+m+3. Найдите наименьшее количество воды, которое могло быть долито в обе бочки вместе.
№7. Вершина прямого угла C прямоугольного треугольника ABC расположена на диаметре окружности, параллельном хорде AB. Найдите площадь треугольника ABC, если 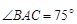
№8. Найдите все значения параметра a, для каждого из которых неравенство
выполняется для всех значений x.
Пройди тесты по математике онлайн – проверь уровень своих знаний
Одна из древнейших наук в мире, которая сложилась исторически, на основе описания форм предметов,
операций подсчета и измерения – это математика. Мы изучаем ее с самого раннего детства,
знакомясь с цифрами и их обозначениями, геометрическими фигурами и их размерами. Без математики
у нас не было очень многих вещей, которые стали привычными – даже домов, не говоря уже о сложных
электронных приборах.
Поэтому знания в области математики нужны не только для того, чтобы хорошо сдать тесты
ЕГЭ математика, но и пригодятся каждому в жизни.
Проверить, насколько хорошо ты разбираешься в математических понятиях, тебе помогут математика
тесты, размещенные в этом разделе нашего сайта.
Тесты по математике, как простые, так и сложные, могут использоваться для
самоконтроля, периодической проверки знаний по предмету, или же в комплексной подготовке к ЕГЭ.
Попробуй сам – увидишь, это просто!
| 3446 | Биссектриса AL треугольника ABC перпендикулярна его медиане BM. Найдите площадь этого треугольника, если известно, что иAB=sqrt3 и ML=1 |
Биссектриса AL треугольника ABC перпендикулярна его медиане BM ! ДВИ в МГУ 2022 — резервный день Задание 5 | |
| 3445 | Решите неравенство log_{x-3/4}(x-3/2) >= 1/2 |
Решите неравенство log x-3/4 (x-3/2) >= 1/2 ! ДВИ в МГУ 2022 — резервный день Задание 4 | |
| 3444 | Решите уравнение 5+cos(4x)=6(sin(x))^2 |
Решите уравнение 5+cos4x=6sin^2 x ! ДВИ в МГУ 2022 — резервный день Задание 3 | |
| 3443 | Произведение седьмого и восьмого членов непостоянной арифметической прогрессии равно произведению пятого и девятого её членов. Найдите одиннадцатый член данной прогрессии |
Произведение седьмого и восьмого членов непостоянной арифметической прогрессии равно произведению пятого и девятого её членов ! ДВИ в МГУ 2022 — резервный день Задание 2 | |
| 3442 | Определите, какое из двух чисел больше: sqrt(3)+sqrt(7)+sqrt(21) или 9 |
Определите, какое из двух чисел больше: sqrt3 + sqrt7 +sqrt21 или 9 ! ДВИ в МГУ 2022 — резервный день Задание 1 | |
| 3441 | Основание ABCD прямоугольного параллелепипеда ABCDA1B1C1D1 с боковыми рёбрами AA1, BB1, CC1, DD1 является квадратом со стороной sqrt2. Известно, что AE ⟂ D1F, где E — центр грани BCC1B1. F — центр квадрата ABCD. Найдите расстояние между серединами отрезков AE и D1F |
Основание ABCD прямоугольного параллелепипеда ABCDA1B1C1D1 с боковыми рёбрами AA1, BB1, CC1, DD1 является квадратом со стороной корень из 2 ! ДВИ в МГУ 2022 — 6 поток, Вариант 6 Задание 7 | |
| 3440 | Окружность, проходящая через вершину A треугольника ABC, касается его стороны BC в точке D и пересекает стороны AC и AB в точках E и F соответственно. Известно, что AF=3BF, BD=CD, AE=2CE и что ED=sqrt10. Найдите BC |
Окружность, проходящая через вершину A треугольника ABC, касается его стороны BC в точке D и пересекает стороны AC и AB в точках E и F соответственно! ДВИ в МГУ 2022 — 6 поток, Вариант 6 Задание 5 | |
| 3439 | Решите неравенство log_{x}(x^2+3/2) <= 4log_{x^2+3/2}(x) |
Решите неравенство log_x x^2+3/2 <= 4log_x^2+3/2 x ! ДВИ в МГУ 2022 — 6 поток, Вариант 6 Задание 4 | |
| 3438 | Решите уравнение tan(x)=4sin(x)-sqrt(3) |
Решите уравнение tgx =4sinx -sqrt3 ! ДВИ в МГУ 2022 — 6 поток, Вариант 6 Задание 3 | |
| 3437 | Числа a_1, a_2, a_3,…,a_30 образуют арифметическую прогрессию. Известно, что a_2+a_4+a_6+…+a_30=45 и что a_3+a_6+a_9+…+a_30=100. Найдите разность этой прогрессии |
Числа a1, a2, a3,…,a30 образуют арифметическую прогрессию ! ДВИ в МГУ 2022 — 6 поток, Вариант 6 Задание 2 | |

Показана страница 1 из 16
Высшее Учебное Заведение. Россия. ВИ. ЕГЭ. 2019, 2020, 2021, 2022 год
Если вы в этом году решили поступить в ВУЗ на очное обучение или заочное отделение, тогда вам придется сдавать Вступительные испытания ВИ. Если вы не сдавали ЕГЭ в школе, тогда вам пригодится эта информация для поступления в ВУЗ
На этой страницу вы можете бесплатно скачать тесты, задания и примеры вступительных экзаменов в ВУЗ, а так же подробное решение и ответы на задания.
Вступительные испытания в ВУЗ по математике. Примеры с ответами
Процедура проведения вступительного испытания
1. Вступительное испытание проводится в соответствии с действующими Правилами приема в бакалавриат и специалитет и Положением о порядке проведения вступительных испытаний МФТИ.
2. Вступительное испытание по математике проводится с совмещением письменной и устной форм.
3. Вступительное испытание состоит из четырех частей.
4. Первые три части вступительного испытания – решение задач с численным ответом. Длительность каждой части – 45 минут.
5. Первая часть вступительного испытания вступительного испытания, проводимого с использованием дистанционных технологий, проверяется программно-аппаратным способом.
6. Допуск ко второй письменной части и последующим частям вступительного испытания проводится по результатам проверки первой письменной части. Недопущенным ко второй и последующим частям вступительного испытания выставляется балл на основании проверки первой части вступительного испытания.
7. Четвертая часть вступительного испытания – устный опрос по задачам и программе вступительного испытания. Длительность устной части – до 30 минут.
Программа вступительного испытания
1. Натуральные числа. Делимость. Простые и составные числа. Признаки делимости. Наибольший общий делитель и наименьшее общее кратное.
2. Целые, рациональные, действительные числа и операции с ними.
3. Преобразование арифметических и алгебраических выражений. Формулы сокращённого умножения.
4. Числовые неравенства и их свойства.
5. Функция. Область определения и множество значений. График функции. Чётность, нечётность, периодичность функций. Линейная, квадратичная, степенная, дробно-рациональная функции и их свойства.
6. Линейные уравнения. Квадратные уравнения. Рациональные уравнения. Уравнения с модулем. Уравнения высших степеней. Разложение многочленов на множители.
7. Линейные неравенства. Квадратные неравенства. Рациональные неравенства. Неравенства с модулем.
8. Корень из числа и его свойства. Арифметический корень. Иррациональные уравнения. Иррациональные неравенства.
9. Арифметическая и геометрическая прогрессии и их свойства.
10. Комбинаторика. Правила суммы и произведения. Перестановки, размещения, сочетания.
11. Задачи на составление уравнений (задачи на движение, на проценты, на совместную работу, на смеси и пр.).
12. Тригонометрические формулы. Тригонометрические и обратные тригонометрические функции и их свойства. Преобразование тригонометрических выражений. Тригонометрические уравнения и неравенства.
13. Свойства степеней. Логарифмы и их свойства. Показательная и логарифмическая функции и их свойства. Показательные и логарифмические уравнения и неравенства.
14. Производная. Исследование функций с помощью производных.
15. Задачи с параметром.
16. Системы уравнений и неравенств.
17. Множества точек на координатной плоскости.
18. Планиметрия:
— смежные и вертикальные углы,
— признаки и свойства равнобедренного треугольника, признаки равенства треугольников,
— теоремы о параллельных прямых, сумма углов треугольника, сумма углов выпуклого многоугольника,
— геометрические места точек (множество внутренних точек угла, равноудалённых от его сторон, множество точек, равноудалённых от концов отрезка),
— медианы, биссектрисы, высоты треугольника и их свойства,
— подобие треугольников, теорема Фалеса, теорема о пропорциональных отрезках,
— четырёхугольники; параллелограмм, прямоугольник, ромб, квадрат, трапеция и их свойства,
— пропорциональные отрезки в прямоугольном треугольнике, теорема Пифагора,
— площадь и её свойства,
— формулы площади треугольника, параллелограмма, трапеции,
— точки пересечения высот, медиан, биссектрис, серединных перпендикуляров треугольника,
— теоремы синусов, косинусов и Менелая для треугольника,
— окружность и её свойства,
— касательная к окружности и её свойства,
— теоремы о пропорциональных отрезках в окружности,
— теоремы об углах, связанных с окружностью (вписанный угол, центральный угол, угол между касательной и хордой),
— окружность, описанная около треугольника; окружность, вписанная в треугольник,
— окружность, описанная около четырёхугольника; окружность, вписанная в четырёхугольник,
— правильные многоугольники и их свойства,
— длина окружности, площадь круга и его частей,
— векторы, скалярное произведение векторов,
— метод координат на плоскости.
19. Стереометрия. Параллельность прямых и плоскостей, перпендикулярность прямых и плоскостей. Объём фигуры; площадь поверхности фигуры. Куб, параллелепипед, призма, пирамида, шар, цилиндр, конус и их свойства. Векторы и координаты в пространстве. Сечения многогранников. Углы и расстояния в пространстве.
.