Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
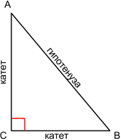
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
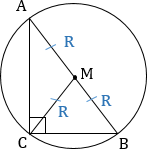
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = — 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
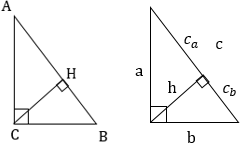
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
Свойства:
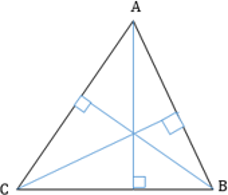
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
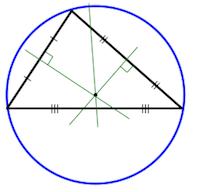
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
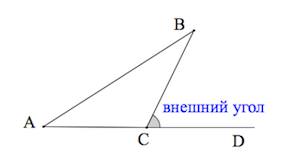
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
$∠BCD$ — внешний угол треугольника $АВС$.
$∠BCD=∠A+∠B$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$.
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Пример:
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tg B={AC}/{BC};$
$ctg B={BC}/{AC}$.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA= — cos BOC;$
$tg BOA= — tg BOC;$
$ctg BOA= — ctg BOC.$
Пример:
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.
Решение:
Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)
Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$
Рассмотрим прямоугольный треугольник $АНС$.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:
$cos∠НСА={НС}/{АС}={НС}/{34}=0.15$
Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:
${НС}/{34}={15}/{100}$
$НС={34·15}/{100}=5.1$
Ответ: $5.1$
Теорема Менелая:
Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то
${АС_1}/{С_1 В}·{ВА_1}/{А_1 С}·{СВ_1}/{В_1 А}=1$
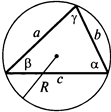
Теорема синусов.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС$ $ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA}=2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
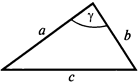
Теорема косинусов.
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
Треугольники общего вида.
Основные свойства треугольников:
- Сумма всех углов в треугольнике равна $180°$.
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
- В равностороннем треугольнике все углы по $60°$.
- Внешний угол треугольника равен сумме двух углов, не смежных с ним.
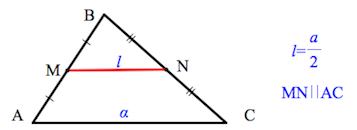
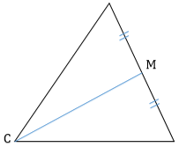
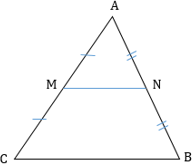
- Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
$MN$ // $AC$, $MN = {AC}/{2}$
Биссектриса — это линия, которая делит угол пополам.
Свойства биссектрисы:
- В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
- Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
- Биссектрисы смежных углов перпендикулярны.
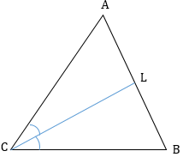
- В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
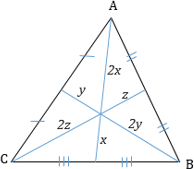
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
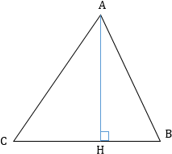
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
3. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна 90 градусов.
2. Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
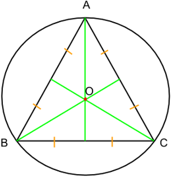
3. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)
4. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.
$CD=AC=CB=R$
5. В прямоугольном треугольнике радиус вписанной окружности равен: $r={a+b-c}/{2}$ , где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Тригонометрические тождества:
1. Основное тригонометрическое тождество:
$sin^2x+cos^2x=1$
2. Связь между тангенсом и косинусом одного и того же угла:
$1+tg^2x={1}/{cos^{2}x}$
3. Связь между котангенсом и синусом одного и того же угла:
$1+ctg^{2} x={1}/{sin^{2} x}$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
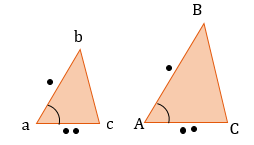
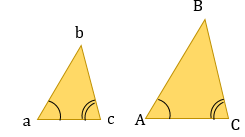
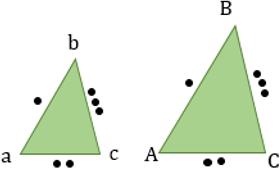
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
Формулы площадей треугольника:
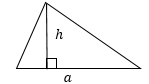
- ${a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
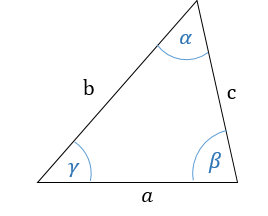
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
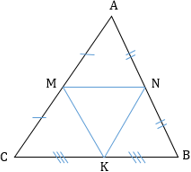
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
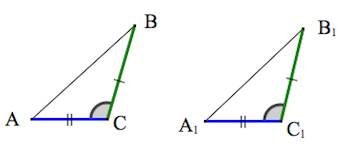
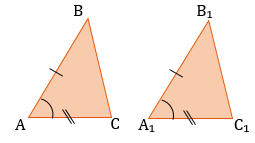
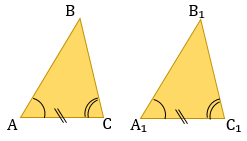
Первый признак равенства треугольников — по двум сторонам и углу между ними
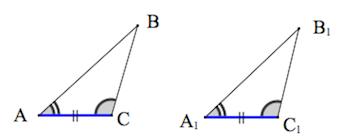
Второй признак равенства треугольников — по стороне и двум прилежащим углам
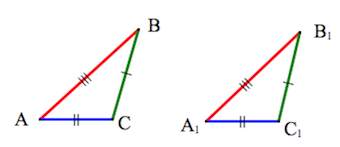
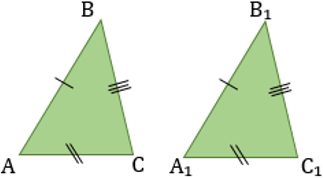
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
ЕГЭ формулы, шпаргалки — Элементарная геометрия. Треугольники.
— формула Герона .
где a, b, c — стороны треугольника, ha, hb, hc — высоты, опущенные на стороны a, b, c, 

Теорема тангенсов:
Формулы Мольвейде:
Линии в треугольнике.
Равносторонни треугольник (со стороной a).
Радиус описанной окружности:
Радиус вписанной окружности:
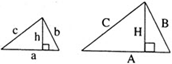
Прямоугольный треугольник (с катетами a и b и гипотенузой c).
Радиус описанной окружности:
Свойства прямоугольного треугольника:
Полный список всех формул, шпаргалок для ЕГЭ по математике тут: ЕГЭ математика — формулы, шпаргалки.
Треугольник
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
Виды треугольников :+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
Признаки равенства треугольников
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно
источники:
http://www.calc.ru/Yege-Formuly-Shpargalki-Elementarnaya-Geometriya-Treugolniki.html
http://egemaximum.ru/treugolnik/
Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
-
Остроугольный треугольник — все углы треугольника острые.
-
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
-
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
-
Разносторонний треугольник — все три стороны не равны.
-
Равнобедренный треугольник — две стороны равны.
-
Равносторонним треугольник или правильный треугольник — все три стороны равны.
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
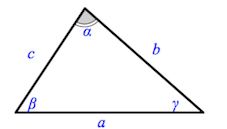
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2 + mc2) — mb2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
-
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)
-
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
-
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
-
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
-
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2—a2
mb = 12√2a2+2c2—b2
mc = 12√2a2+2b2—c2
Биссектрисы треугольника
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
-
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
-
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
-
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
-
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p — a)b + c
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc =
1a
:
1b
:
1c
= (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:
ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:
ha = bc2R
hb = ac2R
hc = ab2R
Окружность вписанная в треугольник
Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру:
r = Sp
Радиус вписанной в треугольник окружности через три стороны:
r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:
1r = 1ha + 1hb + 1hc
Окружность описанная вокруг треугольника
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь:
R = abc4S
Радиус описанной окружности через площадь и три угла:
R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):
R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.
d2 = R2 — 2Rr
= 4 sin
α2
sin
β2
sin
γ2
= cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2.
Средняя линия треугольника параллельна основанию и равна его половине.
MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника
S∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника
-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS =
12
a · ha
S =12
b · hb
S =12
c · hc
-
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p =
a + b + c2
— полупериметр треугльника.
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S =
12
a · b · sin γ
S =12
b · c · sin α
S =12
a · c · sin β
-
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их
соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK = k2
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
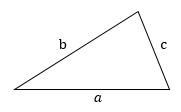
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

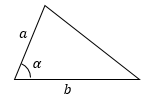
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
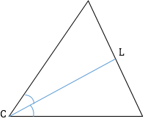
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
СВОЙСТВА ТРЕУГОЛЬНИКА:
1. Сумма углов в треугольнике равна α + β + γ = 180°.
2. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:
a < b < c, то α < β < γ и наоборот.
3. Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны:
a + b > c.
Если это правило не выполняется — треугольник не существует.
4. Формулы площади треугольника:
|
1 (через высоту) |
2 (через две стороны и синус угла между ними) |
3 (формула Герона) |
|
|
|
|
|
|
|
|
|
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. |
Площадь треугольника равна половине произведения его сторон на синус угла между ними. |
Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон. |
5. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
с² = а² + b² – 2ab · cosγ
6. Теорема синусов: Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.
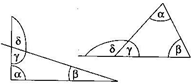
7. Внешний угол треугольника — δ, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ).
ВИДЫ ТРЕУГОЛЬНИКОВ:
Треугольники бывают:
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется:
- равнобедренным, если две его стороны равны;
- равносторонним, если все три стороны равны;
- разносторонним, если все его стороны разные.
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА:
БИССЕКТРИСА
Биссектриса ― луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.
Свойства биссектрисы треугольника:
1. Все три биссектрисы треугольника пересекаются в одной точке. Эта точка — центр вписанной в треугольник окружности.
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.
3. Формулы для биссектрисы треугольника. Если а и b — стороны треугольника, γ — угол между ними, l — биссектриса треугольника, проведённая из вершины этого угла, а а’ и b’ — отрезки, на которые биссектриса делит третью сторону треугольника, то
МЕДИАНА
Медиана ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
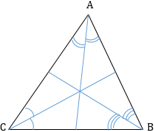
Свойства медианы треугольника:
1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Формула для медианы треугольника. Если стороны треугольника a и b, mc — медиана треугольника, проведённая к стороне c, то
ВЫСОТА
Высота — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника (для остроугольного треугольника),
- совпадать с его стороной (являться катетом прямоугольного треугольника),
- проходить вне треугольника (для тупоугольного треугольника).
Свойства высоты треугольника:
1. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
3. Если в треугольнике две высоты равны, то треугольник — равнобедренный.
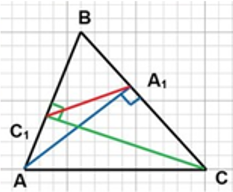
4. Если CC₁ и АА₁ — высоты треугольника АВС, то треугольник ВА₁С₁ подобен треугольнику АВС, причём коэффициент подобия равен cos B.
Сложные теоремы:
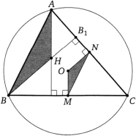
5. Если Н — точка пересечения высот треугольника AВС, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. То есть AH = 2OM.
6. Если Н — точка пересечения высот треугольника AВС, М — точка пересечения медиан треугольника AВС, а О — центр его описанной окружности, то точки О, H и М лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ : МН = 1 : 2.
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Срединный перпендикуляр треугольника — прямая, перпендикулярная стороне треугольника и проходящая через его середину.
Все три срединных перпендикуляра треугольника пересекаются в одной точке, которая является центром описанной около треугольника окружности.
СРЕДНЯЯ ЛИНИЯ
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника
Свойства средней линии треугольника:
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
MN||BC,MN = 1/2 BC
- В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
ПОДОБИЕ И РАВЕНСТВО ТРЕУГОЛЬНИКОВ
|
Подобные треугольники |
Равные треугольники |
|
Треугольники подобны, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами и другими линейными величинами (высоты, медианы, биссектрисы и периметры): Также сохраняется внутреннее отношение длин: |
Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны (треугольники равны, если их можно совместить наложением). |
|
Признаки подобия треугольников: 1. По двум пропорциональным сторонам и углу между ними: 2. 3. По двум равным углам (тогда и третьи тоже будут равны) 4. 5. По трем пропорциональным сторонам: |
Признаки равенства треугольников: 1. По двум сторонам и углу между ними: 2. По стороне и двум прилежащим к ней углам. 3. По трем сторонам. |
ОСОБЫЕ ТРЕУГОЛЬНИКИ И ИХ СВОЙСТВА:
«Особенными», то есть обладающими какими — то дополнительными свойствами, считаются:
- равнобедренный,
- равносторонний
- прямоугольный треугольники.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Равнобедренный треугольник ― это треугольник, у которого две стороны равны (АВ = АС).
Равные стороны (АВ и АС) в таком треугольнике называются боковыми, а оставшаяся третья сторона (ВС) ― основанием.
Свойства равнобедренного треугольника:
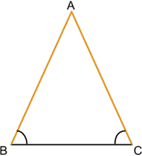
1. Углы при основании равны (∠АВС = ∠АСВ).
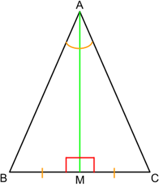
2. Медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (∠ВАМ = ∠МАС).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонний треугольник ― треугольник, у которого все три стороны равны
Свойства равностороннего треугольника:
1. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°/3 = 60°).
2. Медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
1. Центры вписанной и описанной окружностей совпадают.
2. Формулы 2 и 3 для площади треугольника превращаются в одну формулу:
— Через синус (так как все стороны равны и каждый угол равен 60°):
— Формула Герона (так как все стороны равны):
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Прямоугольный треугольник ― треугольник, у которого один угол равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).
Свойства прямоугольного треугольника:
1. В любом прямоугольном треугольнике гипотенуза всегда больше катета (против большего угла лежит большая сторона, и наоборот).
2. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
АВ2 = АС2 + ВС2
Теорема, обратная теореме Пифагора: Если для сторон произвольного треугольника выполняется отношение АВ2= АС2 + ВС2, то треугольник является прямоугольным.
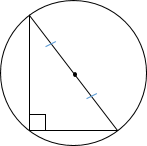
3. Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на середине гипотенузы (доказательство: прямой ∠С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром).
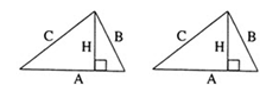
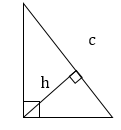
Высота, проведенная к гипотенузе, разбивает треугольник на два подобных прямоугольных треугольника, каждый из которых подобен исходному треугольнику
4. Высота, проведенная к гипотенузе, равна:
- Произведению катетов, деленному на гипотенузу
- Среднему геометрическому из произведений отрезков, на которые гипотенуза делится высотой
5. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть радиусу описанной около треугольника окружности.
6. Формулы площади прямоугольного треугольника:
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
Площадь прямоугольного треугольника равна половине произведения его катетов. |
Площадь прямоугольного треугольника равна половине произведения гипотенузы на опущенную к ней высоту. |
Площадь прямоугольного треугольника равна половине произведения его катета, гипотенузы и синуса угла между ними. |
ЗОЛОТОЙ И СЕРЕБРЯНЫЙ ТРЕУГОЛЬНИКИ:
|
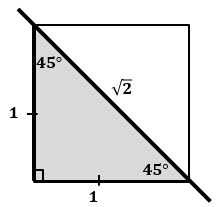
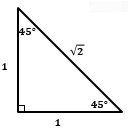
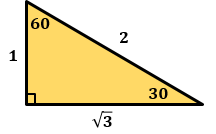
Серебряный треугольник — треугольник с углами 45°, 45° и 90° (разрубленный по диагонали квадрат) Отношение сторон в серебряном треугольнике: |
— треугольник с углами 30°, 60° и 90°. Отношение сторон в золотом треугольнике: |
29
Июл 2013
Категория: Справочные материалы
Треугольник
2013-07-29
2014-01-07
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
Виды треугольников:+ показать
Свойства
+ показать
Признаки равенства треугольников
+ показать
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника

Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
Формула Герона
, где
– полупериметр
Смотрите также площадь треугольника здесь.
И, думаю, будет полезна таблица формул для треугольника.
Автор: egeMax |
комментариев 12
| Метки: шпаргалки-таблицы
-
Треугольники
Треугольник— это геометрическая фигура, состоящая из трех точек плоскости, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.
Теорема об углах треугольника: Сумма углов треугольника равна 1800
Внешний угол треугольника: это угол смежный с любым углом треугольника Свойство: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
Неравенство треугольника: Любая сторона треугольника меньше суммы двух других сторон и больше их разности
Периметр треугольника: PABC = AB + BC + AC (сумма дин все сторон)
Площадь треугольника: 


Теорема синусов

Теорема косинусов
Признаки равенства треугольников
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны (по двум сторонам и углу между ними)
- Если сторона и два, прилежащих к ней угла одного треугольника соответственно равны стороне и и двум, прилежащим к ней углам другого треугольника, то треугольники равны (по стороне и двум углам, прилежащим к ней)
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны ( по трем сторонам)
Основные элементы треугольника
- Высота — перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.
- Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Основные свойства медианы:
а) Медиана разбивает треугольник на два треугольника одинаковой площади.
б) Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.
- Биссектриса — отрезок биссектрисы угла треугольника, соединяющий вершину с точкой, находящейся на противолежащей стороне. Свойства:
а) Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам
б) Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник.
в) Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
г) От любой точки, лежащей на биссектрисе угла, расстояния до сторон угла равны.
- Серединный перпендикуляр — прямая проходящая через середину стороны и перпендикулярна ей.
- Средняя линия — отрезок, соединяющий середины двух сторон. Свойства:
а) равна половине длины стороны треугольника и параллельна ей;
б) средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника
Виды треугольников:
1. равнобедренный — треугольник, у которого две стороны равны (стороны, которые равны называются боковыми, третья называется основанием) Свойства: 1) углы при основании равны; 2) биссектриса(медиана,высота), проведенная к основанию является медианой (биссектрисой, высотой);
2. равносторонний — треугольник, у которого все стороны равны. Свойства: 1) все углы равны 600.
3. разносторонний — треугольник, у которого все стороны разные
4. остроугольные — треугольник, у которого все углы острые (меньше 900)
5. тупоугольные — треугольник, у которого один из углов тупой (больше 900)
6. прямоугольные — треугольник, у которого один из углов прямой (равен 900).
Свойства прямоугольного треугольника
1) сумма острых углов равна 900;
2) катет, лежащий против угла в 300, равен половине гипотенузы;
3) если катет равен половине гипотенузы, то он лежит напротив угла в 300)
4) медиана проведенная к гипотенузе равна ее половине
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (с2=a2+b2)
Соотношения, связывающие пропорциональные отрезки в прямоугольном треугольнике
1. 
2. 
3. 
4
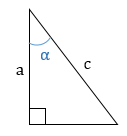
Отношение сторон прямоугольного треугольника (синус, косинус, тангенс)
Синус — отношение противолежащего катета к гипотенузе
Косинус — отношение прилежащего катета к гипотенузе
Тангенс -отношение противолежащего катета к прилежащему
Основное тригонометрическое тождество
Подобные треугольники
Треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны.
Коэффициентом подобия называют число k, равное отношению соответственных сторон подобных треугольников.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Признаки подобия треугольников
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.( по двум сторонам и углу между ними)
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. (по двум углам)
- Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны ( по трем сторонам)
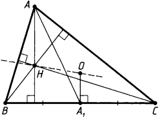
Теорема Менелая
Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C (рис.1), то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство







































































































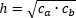




 Золотой треугольник
Золотой треугольник














