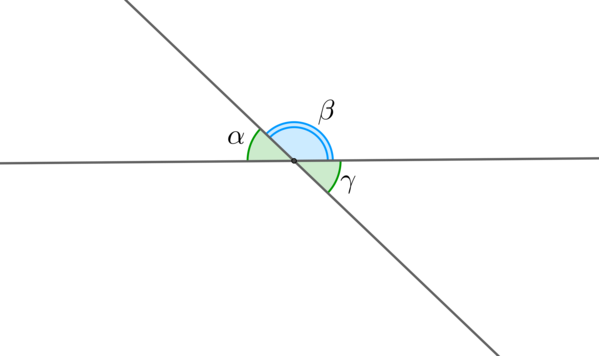
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
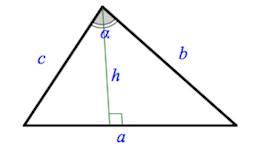
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = — 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
Свойства:
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
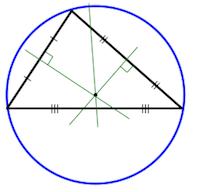
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
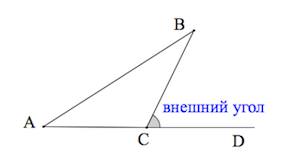
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
$∠BCD$ — внешний угол треугольника $АВС$.
$∠BCD=∠A+∠B$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$.
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Пример:
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tg B={AC}/{BC};$
$ctg B={BC}/{AC}$.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA= — cos BOC;$
$tg BOA= — tg BOC;$
$ctg BOA= — ctg BOC.$
Пример:
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.
Решение:
Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)
Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$
Рассмотрим прямоугольный треугольник $АНС$.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:
$cos∠НСА={НС}/{АС}={НС}/{34}=0.15$
Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:
${НС}/{34}={15}/{100}$
$НС={34·15}/{100}=5.1$
Ответ: $5.1$
Теорема Менелая:
Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то
${АС_1}/{С_1 В}·{ВА_1}/{А_1 С}·{СВ_1}/{В_1 А}=1$
Теорема синусов.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС$ $ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA}=2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов.
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
Треугольники общего вида.
Основные свойства треугольников:
- Сумма всех углов в треугольнике равна $180°$.
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
- В равностороннем треугольнике все углы по $60°$.
- Внешний угол треугольника равен сумме двух углов, не смежных с ним.
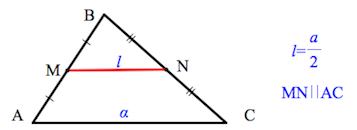
- Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
$MN$ // $AC$, $MN = {AC}/{2}$
Биссектриса — это линия, которая делит угол пополам.
Свойства биссектрисы:
- В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
- Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
- Биссектрисы смежных углов перпендикулярны.
- В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
3. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна 90 градусов.
2. Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
3. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)
4. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.
$CD=AC=CB=R$
5. В прямоугольном треугольнике радиус вписанной окружности равен: $r={a+b-c}/{2}$ , где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Тригонометрические тождества:
1. Основное тригонометрическое тождество:
$sin^2x+cos^2x=1$
2. Связь между тангенсом и косинусом одного и того же угла:
$1+tg^2x={1}/{cos^{2}x}$
3. Связь между котангенсом и синусом одного и того же угла:
$1+ctg^{2} x={1}/{sin^{2} x}$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
Формулы площадей треугольника:
- ${a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Треугольник
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
Виды треугольников :+ показать
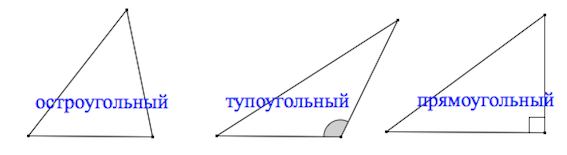
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
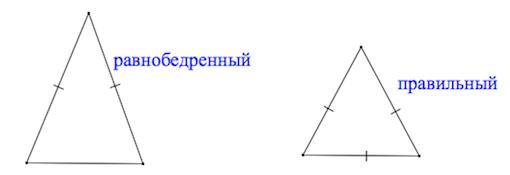
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
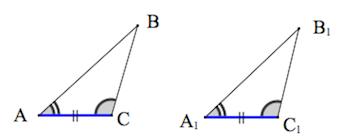
Признаки равенства треугольников
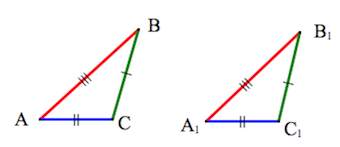
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно
ЕГЭ формулы, шпаргалки — Элементарная геометрия. Треугольники.
— формула Герона .
где a, b, c — стороны треугольника, ha, hb, hc — высоты, опущенные на стороны a, b, c, 

Теорема тангенсов:
Формулы Мольвейде:
Линии в треугольнике.
Равносторонни треугольник (со стороной a).
Радиус описанной окружности:
Радиус вписанной окружности:
Прямоугольный треугольник (с катетами a и b и гипотенузой c).
Радиус описанной окружности:
Свойства прямоугольного треугольника:
Полный список всех формул, шпаргалок для ЕГЭ по математике тут: ЕГЭ математика — формулы, шпаргалки.
источники:
http://egemaximum.ru/treugolnik/
http://www.calc.ru/Yege-Formuly-Shpargalki-Elementarnaya-Geometriya-Treugolniki.html
29
Июл 2013
Категория: Справочные материалы
Треугольник
2013-07-29
2014-01-07
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
Виды треугольников:+ показать
Свойства
+ показать
Признаки равенства треугольников
+ показать
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника

Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
Формула Герона
, где
– полупериметр
Смотрите также площадь треугольника здесь.
И, думаю, будет полезна таблица формул для треугольника.
Автор: egeMax |
комментариев 12
| Метки: шпаргалки-таблицы
Все формулы по геометрии. Площади фигур
Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Начнем с квадрата.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его длины и ширины.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.
Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
2) Она также равна половине произведения его сторон на синус угла между ними:
3) По формуле Герона, где
полупериметр.
4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.
5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности,
Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.
Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:
Площадь правильного треугольника равна квадрату его стороны, умноженному на и деленному на 4:
Площадь трапеции равна произведению полусуммы оснований на высоту,
Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,
Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними,
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:
Площадь круга равна произведению числа и квадрата радиуса круга.
Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:
Вспомним важные свойства площадей фигур.
- Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими. - Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.
Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см1см.
Решение:
Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.
На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.
Ответ: 18.
3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Треугольники АВС и на рисунке называются подобными.
У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника
в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника
в
раз больше, чем площадь треугольника АВС.
4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:
5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.
Отношение площадей этих треугольников равно отношению их высот:
6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.
На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.
7. Три медианы треугольника делят его на шесть равных по площади треугольников.
На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.
Задачи ЕГЭ и ОГЭ по теме: Площади фигур.
Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен
Решение:
Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому
Ответ: 24.
Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Решение:
Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Ответ: 1.
Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Решение:
Выразим площадь двумя способами:
Тогда
Ответ: 6.
Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Решение:
Треугольник CDE подобен треугольнику CAB с коэффициентом Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, 
Ответ: 7,5.
Задача 5. В параллелограмме ABCD AB = 3, AD = 21, . Найдите большую высоту параллелограмма.
Решение:
Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:
Ответ: 18.
Задача 6. Найдите площадь квадрата, если его диагональ равна 1.
Решение:
Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.
Ответ: 0,5.
Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Решение:
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.
Ответ: 18.
Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение:
Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна
а острый угол параллелограмма равен
Тогда площадь параллелограмма равна
а площадь прямоугольника равна
По условию площадь прямоугольника вдвое больше:
Следовательно,
Ответ: 30.
Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Решение:
Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.
Ответ: 8.
Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30
Решение:
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна
Получим уравнение:
Корень уравнения a = 4, поэтому
Ответ: 8.
Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.
Решение:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 24.
Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Решение:
Трапеция равнобедренная, значит,
Тогда по теореме Пифагора из треугольника ADH:
Ответ: 160.
Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45
Решение:
Проведем высоту CH. Треугольник CHB — прямоугольный, в нем
значит, он также равнобедренный, CH = HB = 4.
Ответ: 16.
Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
Ответ: 15.
Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда
Из этого уравнения получим: h = 4.
Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла
Ответ: 30.
Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Задача 16. Найдем площадь четырехугольника на рисунке.
Решение:
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
Ответ: 12,5.
В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
Ответ: 10,5.
Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.
Задача 18.
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Решение:
На этом рисунке мы видим часть круга. Площадь всего круга равна так как
Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна
(так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в
раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в
раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в
раз меньше, чем площадь всего круга.
Ответ: 1.
Формула Пика
Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.
Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.
Первый способ:
Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.
Имеем:
Второй способ — применить формулу Пика.
Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
Площадь многоугольника с целочисленными вершинами равна

Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.
Главное — аккуратно посчитать. На нашем рисунке
В = 24 (показаны зеленым),
Г = 8 (показаны красным),
S = 24 + — 1 = 27.
Ответ: 27.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Все формулы по геометрии. Площади фигур» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
[{Large{text{Основные сведения}}}]
Определения
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.
Угол (alpha) называется острым, если (0^circ<alpha<90^circ), прямым – если (alpha=90^circ), тупым – если (90^circ<alpha<180^circ), и развернутым – если (alpha=180^circ).
Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.
Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.
Теорема
Смежные углы (alpha) и (beta) в сумме дают (180^circ).
Вертикальные углы равны: (alpha=gamma).
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.
Теоремы: признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Определение
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Две прямые называются перпендикулярными, если угол между ними равен (90^circ).
Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ).
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
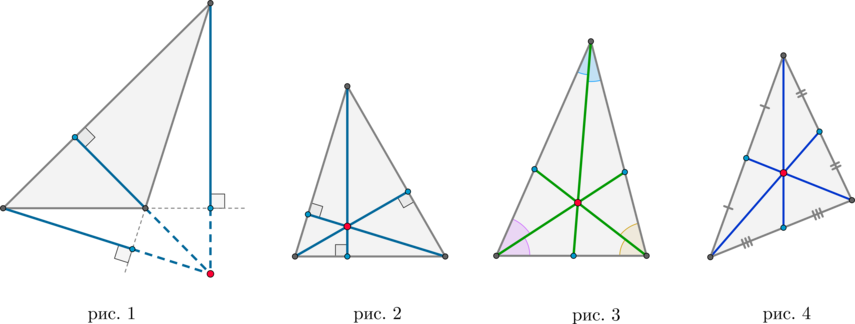
Замечание
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
[{Large{text{Параллельные прямые}}}]
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия из аксиомы
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
2. Две прямые, параллельные третьей прямой, параллельны.
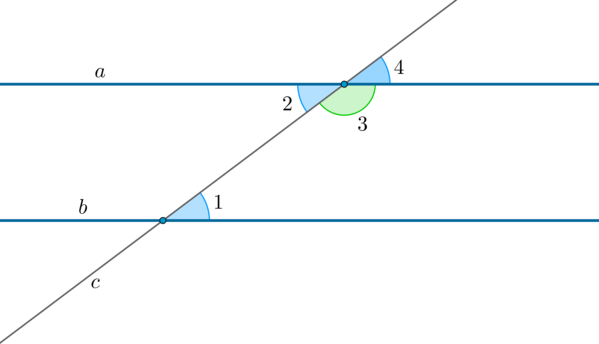
Теоремы: признаки параллельности прямых
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2), то такие прямые параллельны.
2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ), то такие прямые параллельны.
3. Если при пересечении двух прямых (a) и (b) секущей (c) соответственные углы равны: (angle 1=angle 4), то такие прямые параллельны.
Теоремы: свойства параллельных прямых
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ).
3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
[{Large{text{Углы треугольника}}}]
Определения
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).
Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).
Теорема
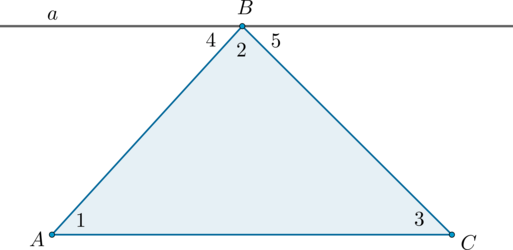
Сумма внутренних углов треугольника равна (180^circ).
Доказательство
Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A +
angle B + angle C = 180^circ).
Проведём через вершину (B) прямую (a), параллельную стороне (AC).
Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB), а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC). Поэтому [begin{aligned}
&angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad
(1)
end{aligned}]
Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B), то есть (angle 4 + angle 2 + angle 5 = 180^circ). Отсюда, учитывая равенства ((1)), получаем: (angle 1 + angle 2 + angle 3 = 180^circ).
Определение
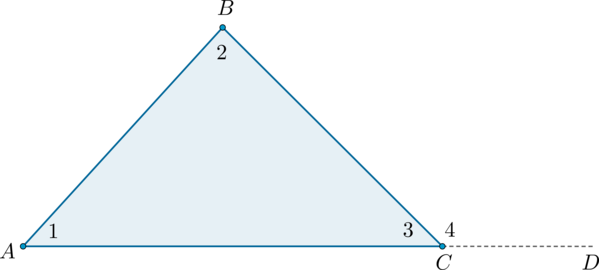
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC).
Доказательство
Рассмотрим рисунок.
Угол (4) – внешний угол треугольника, смежный с углом (3). Так как (angle 4 + angle 3 = 180^circ), а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ), то (angle 4 = angle 1 + angle 2), что и требовалось доказать.
[{Large{text{Равнобедренный треугольник}}}]
Определения
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
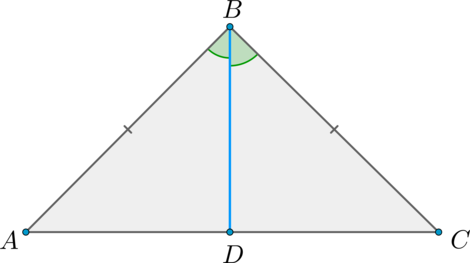
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
Пусть (ABC) – равнобедренный треугольник, (AB = BC), (BD) – биссектриса (проведённая к основанию).
Рассмотрим треугольники (ABD) и (BCD): (AB = BC), (angle ABD =
angle CBD), (BD) – общая. Таким образом, (triangle ABD =
triangle BCD) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что (AD = DC), следовательно, (BD) – медиана.
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC), следовательно, [begin{aligned}
&angle ADB = angle CDB, qquad qquad qquad (2)
end{aligned}] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ), откуда при учёте ((2)): (angle ADB = 90^circ = angle CDB), то есть (BD) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C).
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Теорема: неравенство треугольника
В треугольнике сумма любых двух сторон больше третьей стороны.
Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
[{Large{text{Прямоугольный треугольник}}}]
Определения
В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.
Теоремы: свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна (90^circ).
2. В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла (30^circ).
Треугольник, подготовка к ЕГЭ по математике
- 22.12.2017
Таблицы с теорией на тему: «Треугольник» для подготовки к ЕГЭ по математике. В кратком содержании изложена вся необходимая теория для этой темы.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить

- Сделать чертеж. Чертеж должен максимально соответствовать условию задачи, так его основная задача помочь найти ход решения
- Нанести все данные из условия задачи на чертеж
- Выписать все геометрические понятия, которые встречаются в задаче
- Вспомнить все теоремы, которые относятся к этим понятию
- Нанести на чертеж все соотношения между элементами геометрической фигуры, которые следуют из этих теорем
Например, если в задаче встречается слова биссектриса угла треугольника, нужно вспомнить определение и свойства биссектрисы и обозначить на чертеже равные или пропорциональные отрезки и углы.
В этой статье вы найдете основные свойства треугольника, которые необходимо знать для успешного решения задач.
Итак.
ТРЕУГОЛЬНИК.
Площадь треугольника.
1. 
здесь 

2. 
здесь 

3. Формула Герона:
— здесь 

4. 
здесь 

Пусть — длины отрезков касательных.
Тогда формулу Герона можно записать в таком виде:
5.
6. 
здесь 

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Медиана треугольника
— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.
Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.

Длина медианы произвольного треугольника вычисляется по формуле:

здесь 


Биссектриса треугольника
— это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:
Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.
Все точки биссектрисы угла равноудалены от сторон угла.
Высота треугольника
— это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Чтобы найти высоту треугольника, проведенную к стороне 
Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.
Радиус описанной окружности треугольника можно найти по таким формулам:
— здесь 


где 

Неравенство треугольника
Каждая сторона треугольника меньше суммы и больше разности двух других.
Сумма длин любых двух сторон всегда больше длины третьей стороны:

Напротив большей стороны лежит больший угол; напротив большего угла лежит большая сторона:
Если 



Теорема синусов:
стороны треугольника пропорциональны синусам противолежащих углов:
Теорема косинусов:
квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
Прямоугольный треугольник
— это треугольник, один из углов которого равен 90°.
Сумма острых углов прямоугольного треугольника равна 90°.
Гипотенуза — это сторона, которая лежит против угла 90°. Гипотенуза является наибольшей стороной.
Теорема Пифагора:
квадрат гипотенузы равен сумме квадратов катетов:
Радиус окружности, вписанной в прямоугольный треугольник, равен

здесь 

Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Определение синуса, косинуса , тангенса и котангенса прямоугольного треугольника смотрите здесь.
Соотношение элементов в прямоугольном треугольнике:
Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу:
Квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу:

Катет, лежащий против угла 
Равнобедренный треугольник.
Биссектриса равнобедренного треугольника, проведенная к основанию является медианой и высотой.
В равнобедренном треугольнике углы при основании равны.






Внимание! Высота, биссектриса и медиана, проведенные к боковой стороне не совпадают.
Правильный треугольник
(или равносторонний треугольник) — это треугольник, все стороны и углы которого равны между собой.
Площадь правильного треугольника равна

где 
Центр окружности, вписанной в правильный треугольник, совпадает с центром окружности, описанной около правильного треугольника и лежит в точке пересечения медиан.
Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.
Если один из углов равнобедренного треугольника равен 60°, то этот треугольник правильный.
Средняя линия треугольника
— это отрезок, соединяющий середины двух сторон.
На рисунке DE — средняя линия треугольника ABC.
Средняя линия треугольника параллельна третьей стороне и равна ее половине: DE||AC, AC=2DE
Внешний угол треугольника
— это угол, смежный какому либо углу треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
Тригонометрические функции внешнего угла:
Признаки равенства треугольников:
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Важно: поскольку в прямоугольном треугольнике два угла заведомо равны, то для равенства двух прямоугольных треугольников требуется равенство всего двух элементов: двух сторон, или стороны и острого угла.
Признаки подобия треугольников:
1. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами равны, то эти треугольники подобны.
2. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.
3. Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.
Важно: в подобных треугольниках сходственные стороны лежат против равных углов.
Теорема Менелая
Пусть прямая пересекает треугольник 



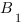

И.В. Фельдман, репетитор по математике.
[{Large{text{Основные сведения}}}]
Определения
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.
Угол (alpha) называется острым, если (0^circ<alpha<90^circ), прямым – если (alpha=90^circ), тупым – если (90^circ<alpha<180^circ), и развернутым – если (alpha=180^circ).
Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.
Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.
Теорема
Смежные углы (alpha) и (beta) в сумме дают (180^circ).
Вертикальные углы равны: (alpha=gamma).
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.
Теоремы: признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Определение
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Две прямые называются перпендикулярными, если угол между ними равен (90^circ).
Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ).
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Замечание
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
[{Large{text{Параллельные прямые}}}]
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия из аксиомы
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
2. Две прямые, параллельные третьей прямой, параллельны.
Теоремы: признаки параллельности прямых
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2), то такие прямые параллельны.
2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ), то такие прямые параллельны.
3. Если при пересечении двух прямых (a) и (b) секущей (c) соответственные углы равны: (angle 1=angle 4), то такие прямые параллельны.
Теоремы: свойства параллельных прямых
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ).
3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
[{Large{text{Углы треугольника}}}]
Определения
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).
Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).
Теорема
Сумма внутренних углов треугольника равна (180^circ).
Доказательство
Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A +
angle B + angle C = 180^circ).
Проведём через вершину (B) прямую (a), параллельную стороне (AC).
Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB), а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC). Поэтому [begin{aligned}
&angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad
(1)
end{aligned}]
Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B), то есть (angle 4 + angle 2 + angle 5 = 180^circ). Отсюда, учитывая равенства ((1)), получаем: (angle 1 + angle 2 + angle 3 = 180^circ).
Определение
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC).
Доказательство
Рассмотрим рисунок.
Угол (4) – внешний угол треугольника, смежный с углом (3). Так как (angle 4 + angle 3 = 180^circ), а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ), то (angle 4 = angle 1 + angle 2), что и требовалось доказать.
[{Large{text{Равнобедренный треугольник}}}]
Определения
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
Пусть (ABC) – равнобедренный треугольник, (AB = BC), (BD) – биссектриса (проведённая к основанию).
Рассмотрим треугольники (ABD) и (BCD): (AB = BC), (angle ABD =
angle CBD), (BD) – общая. Таким образом, (triangle ABD =
triangle BCD) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что (AD = DC), следовательно, (BD) – медиана.
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC), следовательно, [begin{aligned}
&angle ADB = angle CDB, qquad qquad qquad (2)
end{aligned}] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ), откуда при учёте ((2)): (angle ADB = 90^circ = angle CDB), то есть (BD) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C).
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Теорема: неравенство треугольника
В треугольнике сумма любых двух сторон больше третьей стороны.
Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
[{Large{text{Прямоугольный треугольник}}}]
Определения
В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.
Теоремы: свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна (90^circ).
2. В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла (30^circ).
Смотрите также
Определение треугольника
В любом треугольнике три угла и три стороны.
Против большего угла треугольника лежит большая сторона.
Виды треугольников
Треугольники бывают
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется
- равнобедренным, если две его стороны равны.
- равносторонним, если все три стороны равны,
- разносторонним, если все его стороны разные.
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
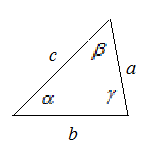
I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
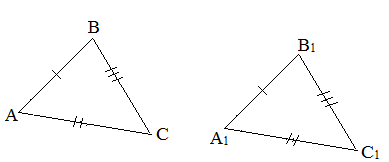
Подробнее про признаки равенства треугольников читайте по ссылке.
Признаки подобия треугольников
Треугольники называются подобными, если их стороны пропорциональны.
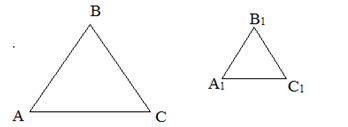
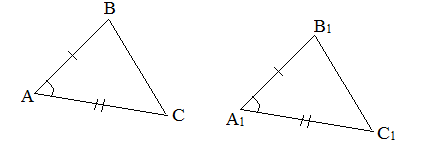
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Подробнее про признаки подобия треугольников читайте по ссылке.
Теоремы треугольников
Для любого треугольника справедливы следующие теоремы.
Подробнее про теорему косинусов читайте по ссылке.
Подробнее про теорему синусов читайте по ссылке.