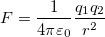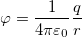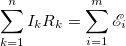Основные формулы по физике — ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
При изучении темы «Постоянный ток» необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении «Магнетизма» необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
Электрические и магнитные явления связаны особой формой существования материи — электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
Смотрите также основные формулы оптики
Таблица основных формул электричества и магнетизма
|
Физические законы, формулы, переменные |
Формулы электричество и магнетизм |
||||
|
Закон Кулона: |
|
||||
|
Напряженность электрического поля: где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля. |
|
||||
|
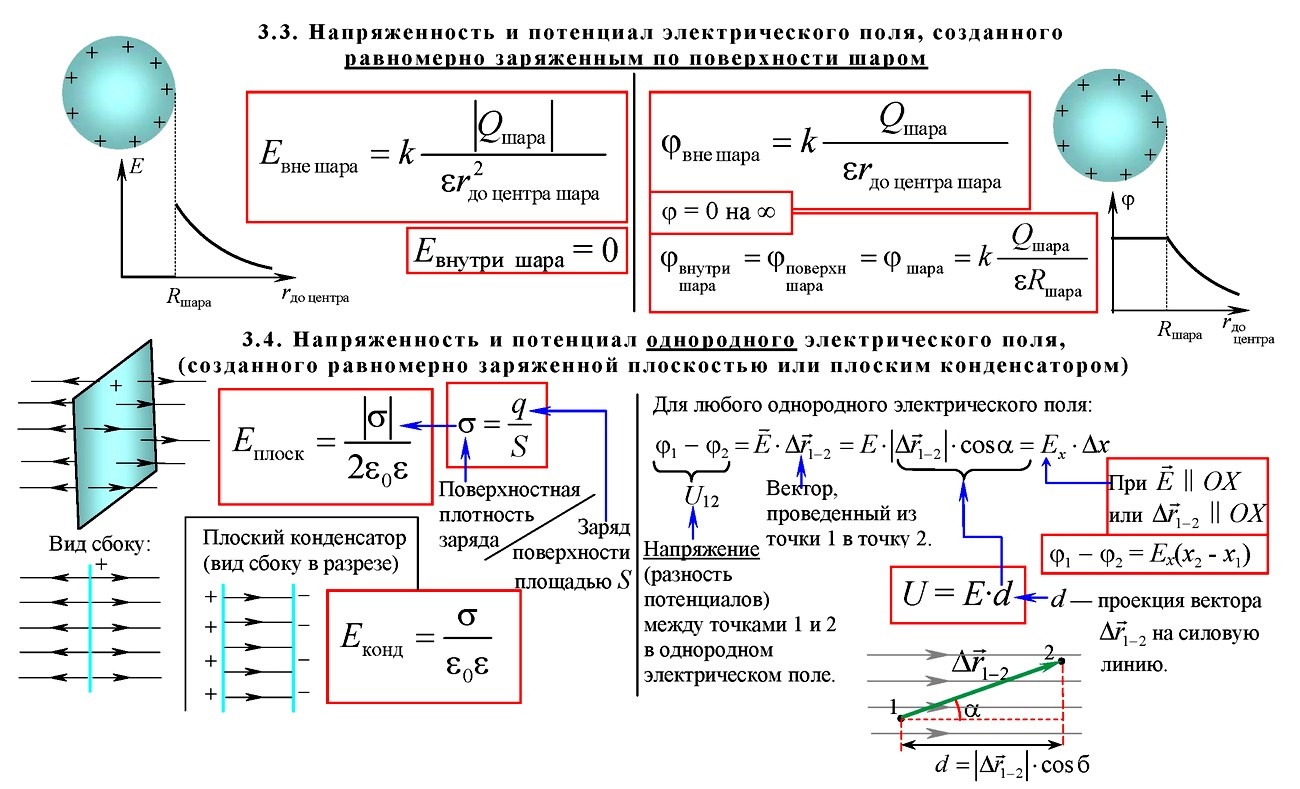
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями |
|||||
|
Потенциал электрического поля: где W — потенциальная энергия заряда q0 . |
|
||||
|
Потенциал поля точечного заряда на расстоянии r от заряда: |
|
||||
|
По принципу суперпозиции полей, напряженность: |
|
||||
|
Потенциал: где Ēi и ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. |
|
||||
|
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 : |
|
||||
|
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля: |
|
||||
|
Электроемкость уединенного проводника: |
|
||||
|
Электроемкость конденсатора: где U = ϕ1 — ϕ2 — напряжение. |
|
||||
|
Электроемкость плоского конденсатора: где S — площадь пластины (одной) конденсатора, d — расстояние между пластинами. |
|
||||
|
Энергия заряженного конденсатора: |
|
||||
|
Сила тока: |
|
||||
|
Плотность тока: где S — площадь поперечного сечения проводника. |
|
||||
|
Сопротивление проводника: ρ — удельное сопротивление; l — длина проводника; S — площадь поперечного сечения. |
|
||||
|
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: где ε — ЭДС источника тока, R и r — внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи: |
|||||
|
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: 2) для участка цепи с изменяющимся со временем током: |
|
||||
|
Мощность тока: |
|
||||
|
Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, |
|
||||
|
Магнитная индукция (индукция магнитного поля): 2) поля бесконечно длинного прямого тока 3) поля, созданного отрезком проводника с током ɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля; |
|||||
|
Сила Лоренца: по модулю |
|
||||
|
Поток вектора магнитной индукции (магнитный поток через площадку S): |
|
||||
|
Потокосцепление (полный поток): |
|
||||
|
Закон Фарадея-Ленца: |
|
||||
|
ЭДС самоиндукции: |
|
||||
|
Индуктивность соленоида: где n — число витков на единицу длины соленоида, |
|
||||
|
Энергия магнитного поля: |
|
||||
|
Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура. |
|
||||
|
Работа по перемещению замкнутого контура с током I в магнитном поле: |
|
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
Электричество Основные формулы
1. Электростатика
1.1 Закон Кулона
q1, q2 — величины точечных зарядов,
r — расстояние между зарядами.
1.2 Напряженность поля уединенного точечного заряда
q — величина уединенного точечного заряда,
r — расстояние от заряда.
1.3 Потенциал точки в поле точечного заряда
q — величина уединенного точечного заряда,
r — расстояние от заряда.
1.4 Потенциальная энергия заряда в электростатическом поле
φ — потенциал,
q1 — величина заряда.
1.5 Потенциальная энергия заряда q1 в поле точечного заряда
q — величина уединенного точечного заряда, который создает поле,
r — расстояние между зарядами.
1.6 Теорема Гаусса
N — поток вектора напряженности электрического поля через замкнутую поверхность,
q — полный заряд, находящийся внутри замкнутой поверхности.
1.7 Напряженность электрического поля вблизи от поверхности проводника
σ — поверхностная плотность заряда.
1.8 Емкость плоского кондесатора
q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.
1.9 Энергия плоского кондесатора
q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.
2. Постоянный электрический ток
2.1 Закон Ома для участка однородной цепи
U — напряжение на концах участка,
R — сопротивление участка цепи.
2.2 Закон Ома для замкнутой цепи с источником тока
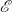
r — внутреннее сопротивление источника ЭДС.
2.3 Работа постоянного тока
U — напряжение на концах участка цепи,
t — время, за которое совершается работа.
2.4 Закон Джоуля-Ленца
Q — теплота,
R — сопротивление проводника,
t — время, за которое выделяется теплота.
2.5 Полная мощность, развиваемая источником тока
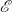
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.
2.6 Полезная мощность
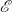
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.
2.7 Коэффициент полезного действия источника тока
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.
2.8 Первое правило Кирхгофа
n — число проводников, сходящихся в узле;
Ik — сила тока в k-м проводнике.
2.9 Второе правило Кирхгофа
n — число неразветвленных участков в контуре;
m — число ЭДС в контуре.
ЭЛЕКТРОСТАТИКА
Теория и формулы (кратко и сжато)
Электростатика – раздел электродинамики, изучающий покоящиеся электрически заряженные тела. Существует два вида электрических зарядов: положительные (стекло о шелк) и отрицательные (эбонит о шерсть).
Элементарный заряд – минимальный заряд (е = 1,6∙10-19 Кл)
Заряд любого тела кратен целому числу элементарных зарядов: q = N∙е
Электризация тел – перераспределение заряда между телами. Способы электризации: трение, касание, влияние.
Закон сохранения электрического заряда – в замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. q1 + q 2 + q 3 + …..+ qn = const
Пробный заряд – точечный положительный заряд.
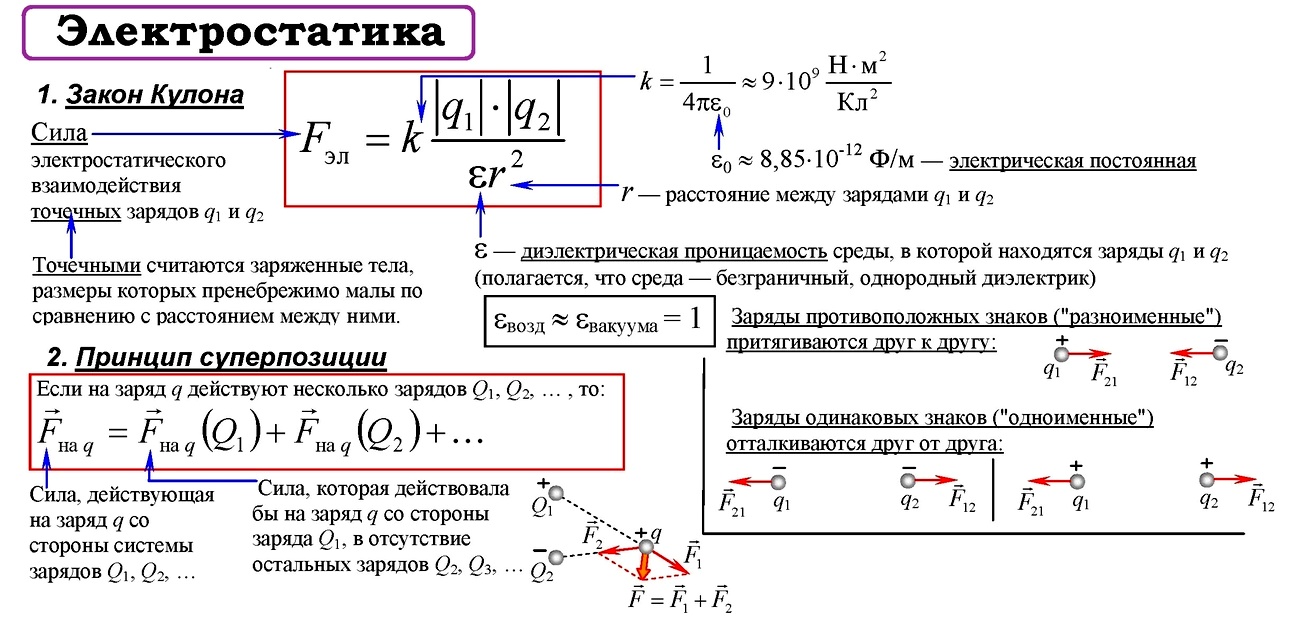
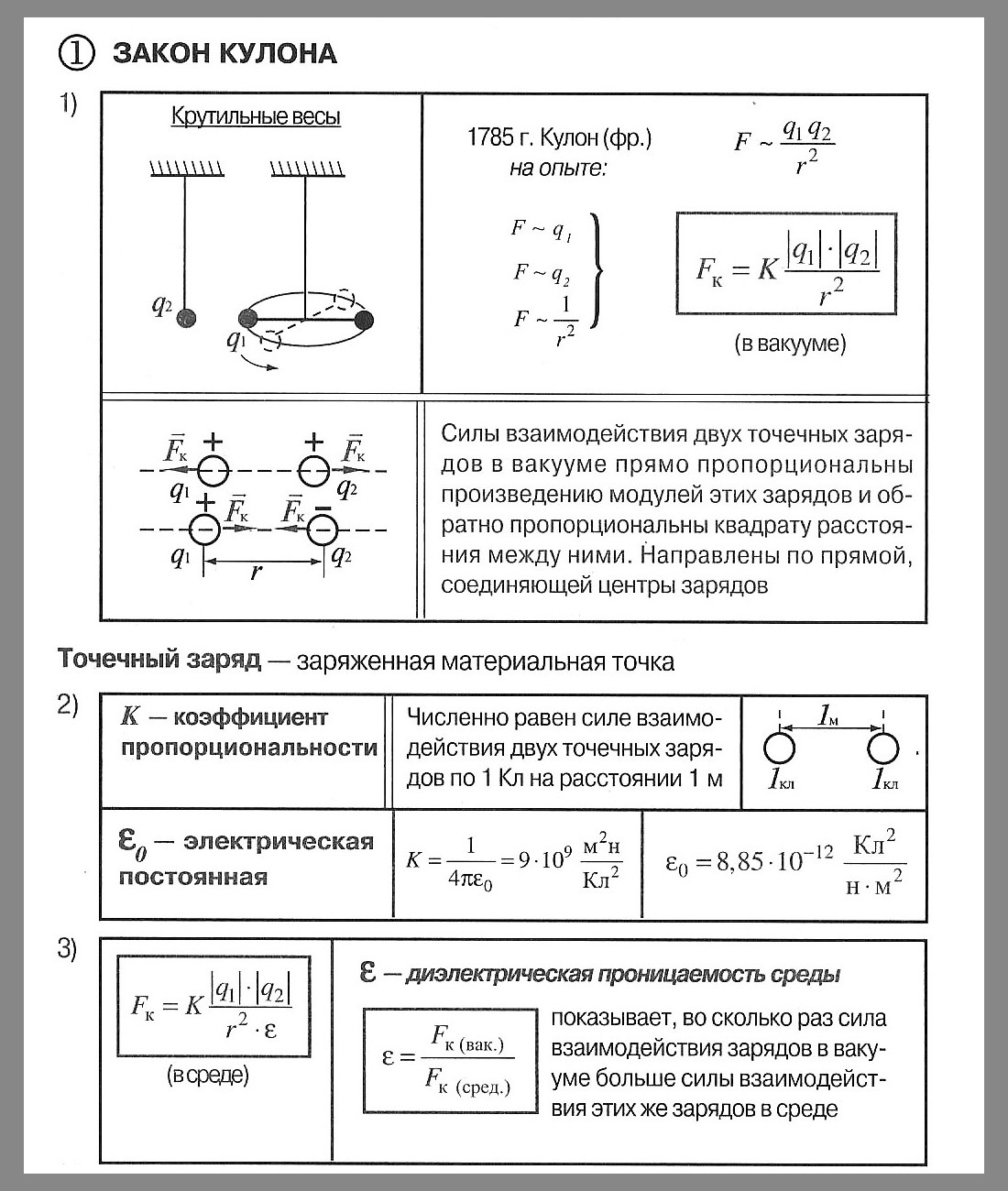
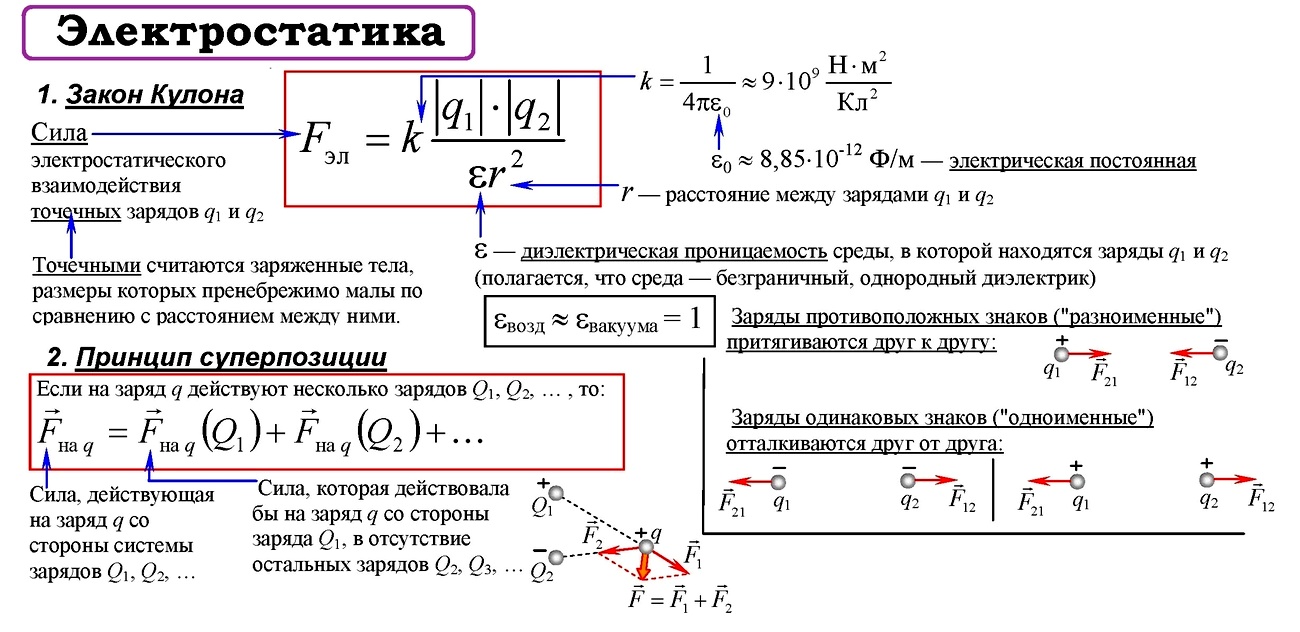
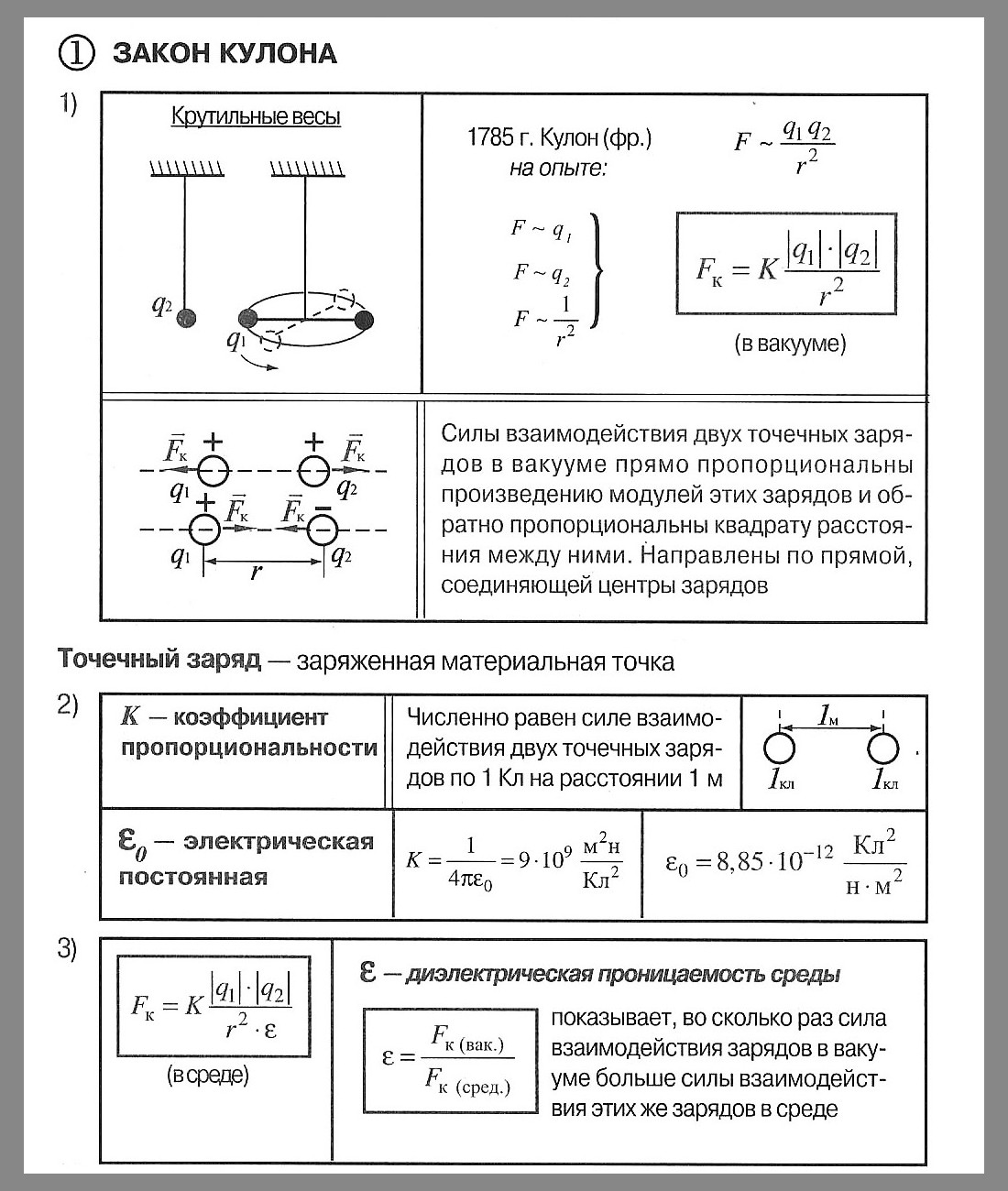
Закон Кулона
Закон Кулона (установлен опытным путем в 1785 году) Сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорционально квадрату расстояния между ними.
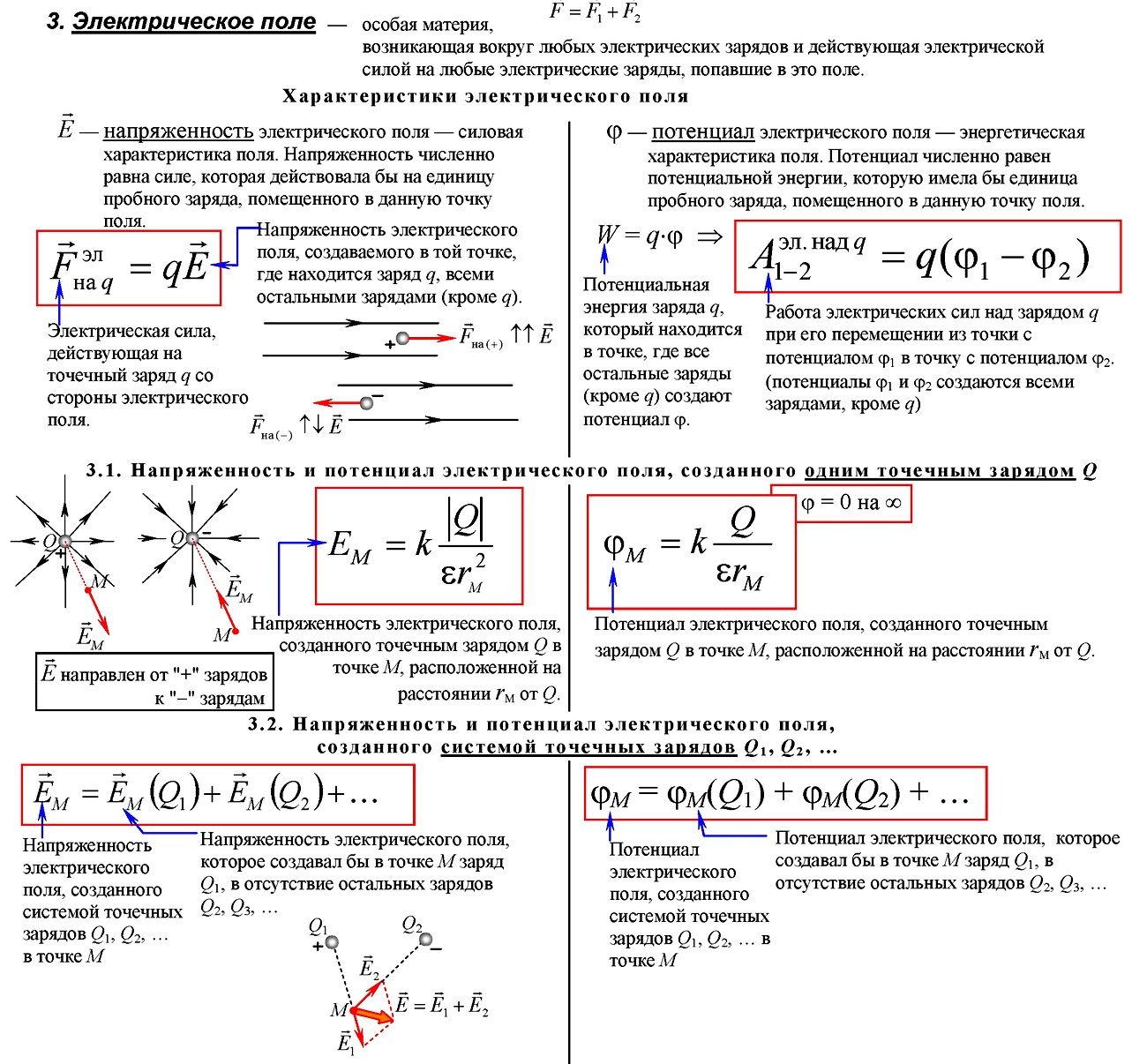
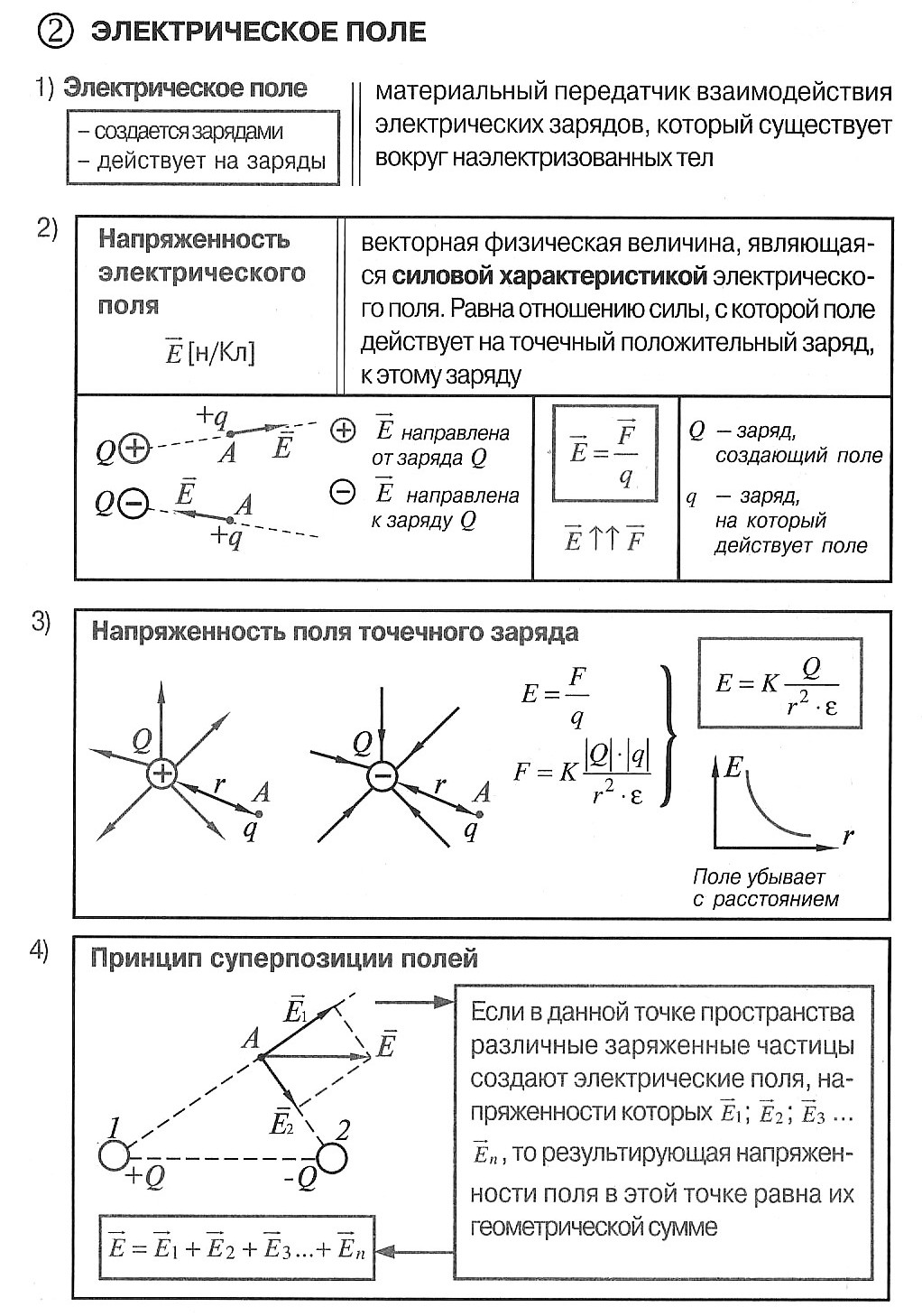
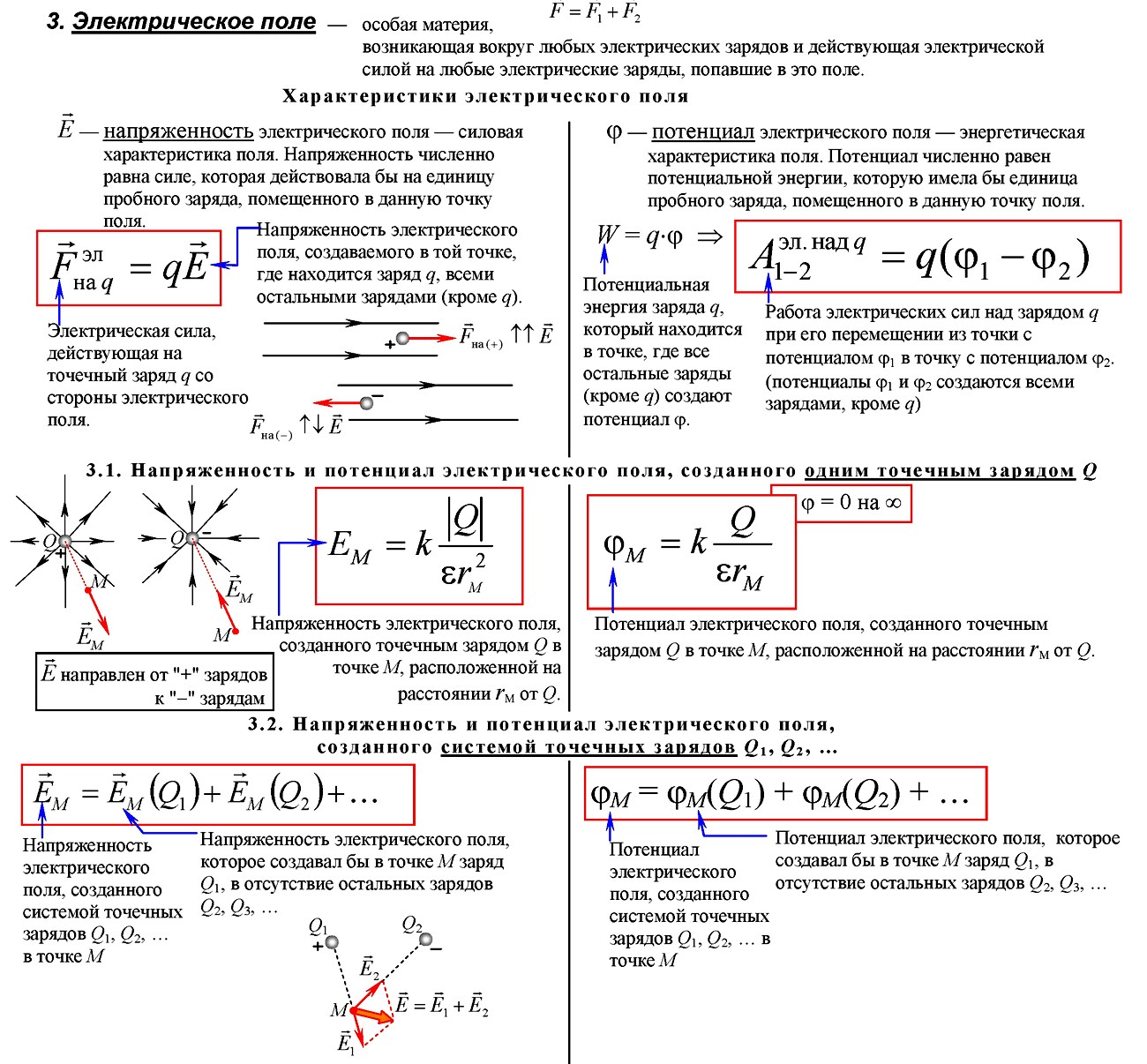
Электрическое поле
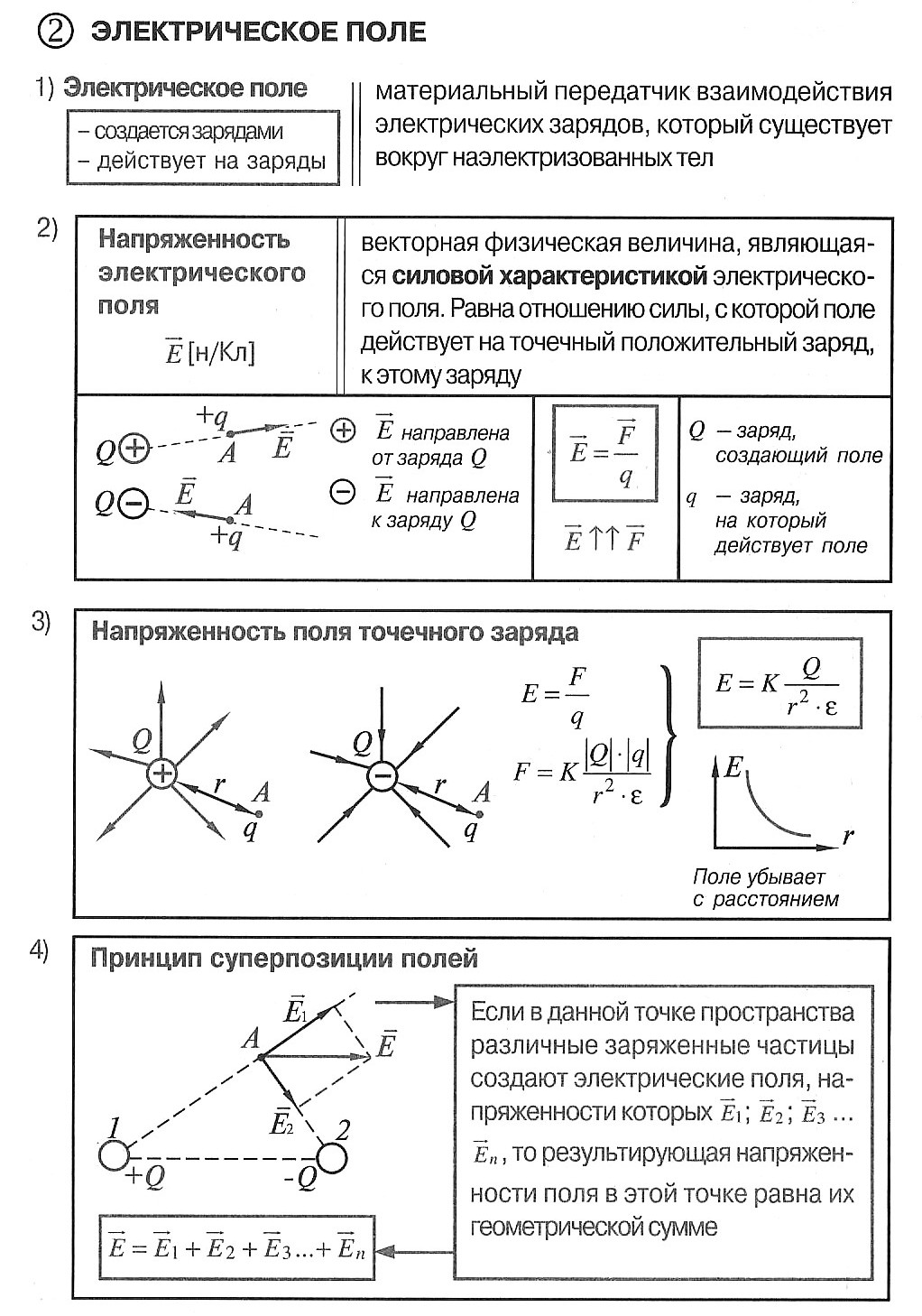
Электрическое поле – вид материи, осуществляющий взаимодействие между электрическими зарядами, возникает вокруг зарядов, действует только на заряды
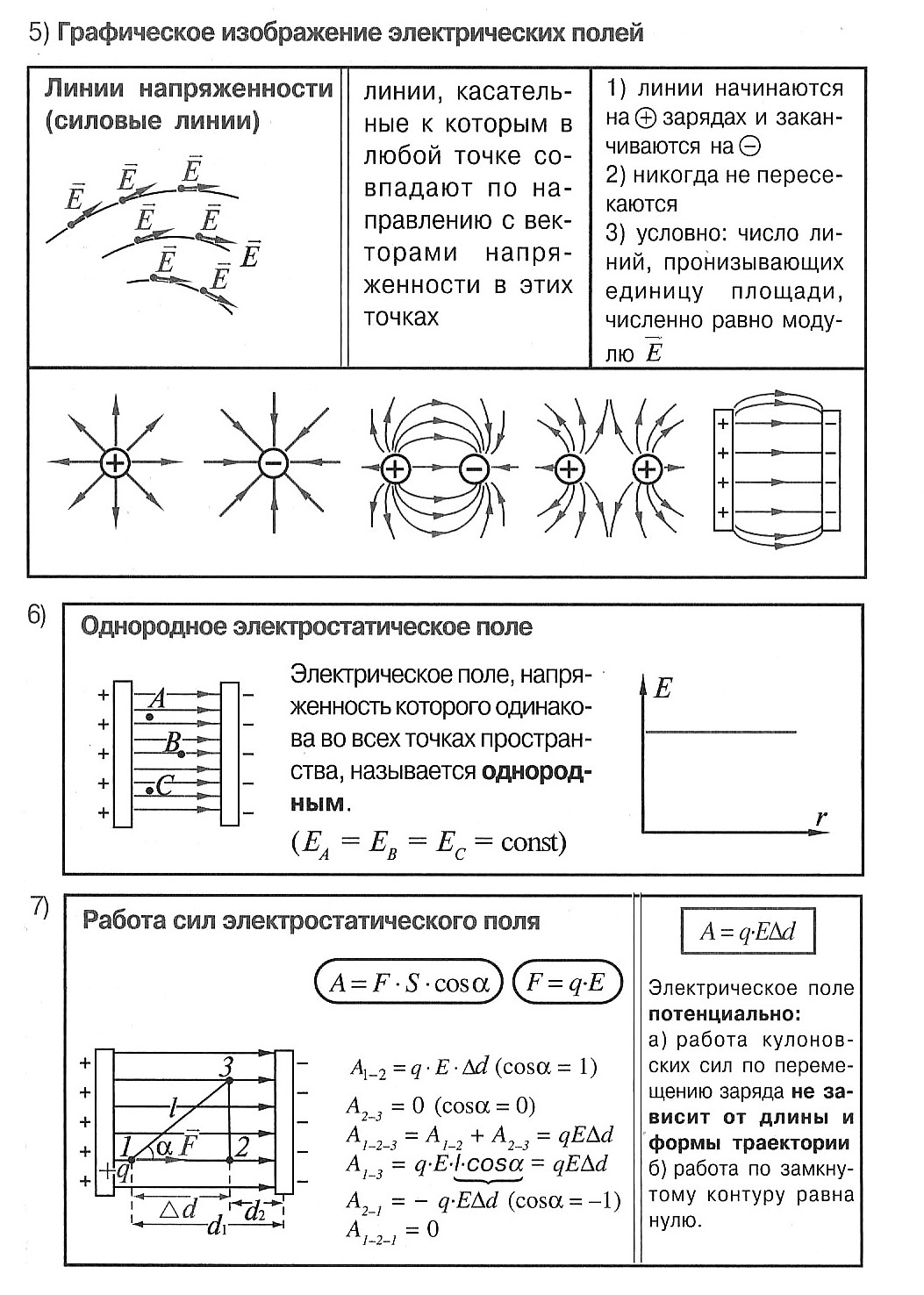
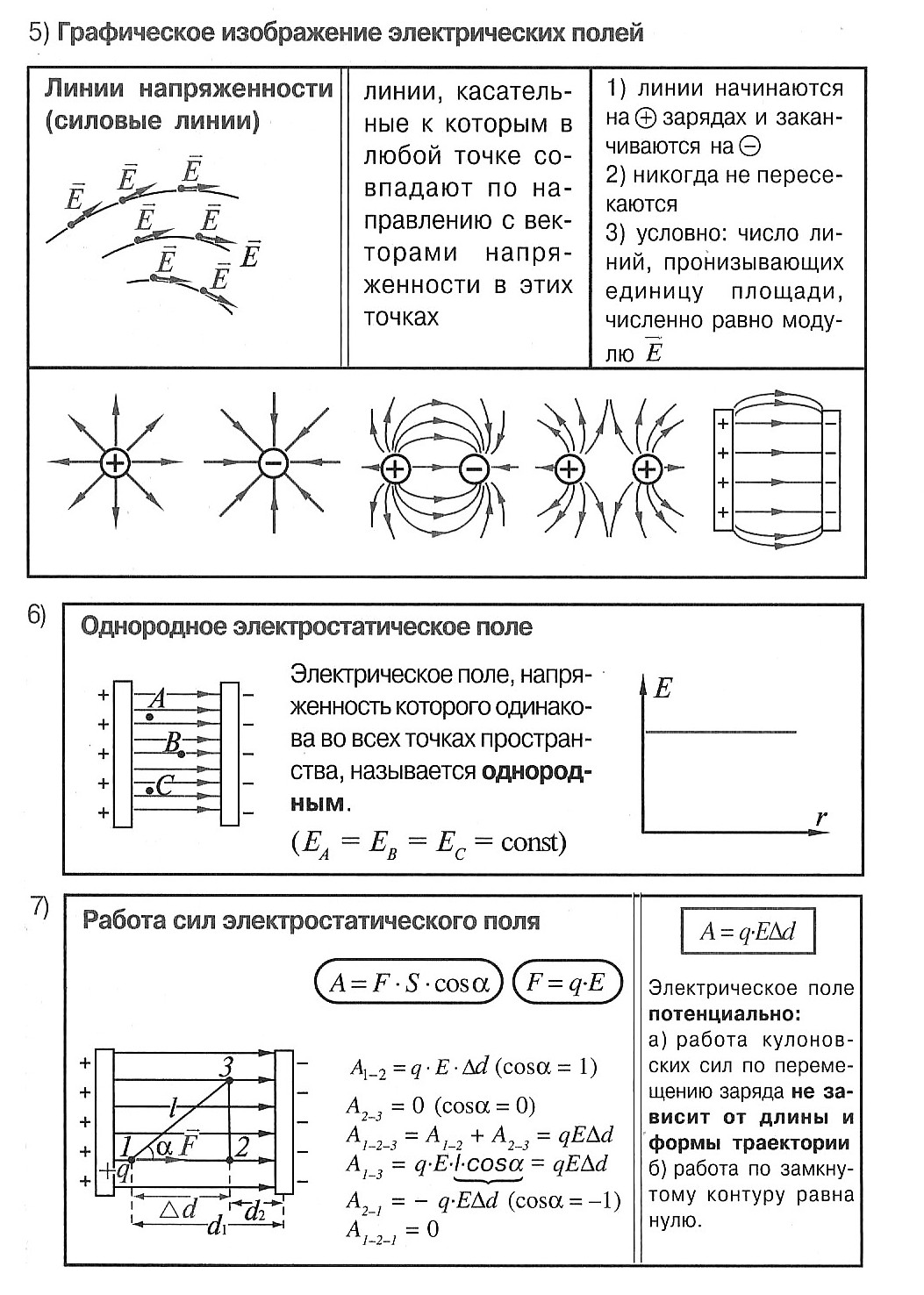
Силовые линии напряженности электрического поля – непрерывные линии, касательные к которым в каждой точке, через которые они проходят, совпадают с вектором напряженности.
Свойства силовых линий:
- не замкнуты;
- не пересекаются;
- непрерывны;
- направление совпадает с направлением вектора напряжённости;
- начало на + q или в бесконечности, конец на – q или в бесконечности;
- гуще вблизи зарядов (где больше напряжённость).
- перпендикулярны поверхности проводника
Разность потенциалов или напряжение (Δφ или U) — это разность потенциалов в начальной и конечной точках траектории заряда Δφ = φ1 – φ2
Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.
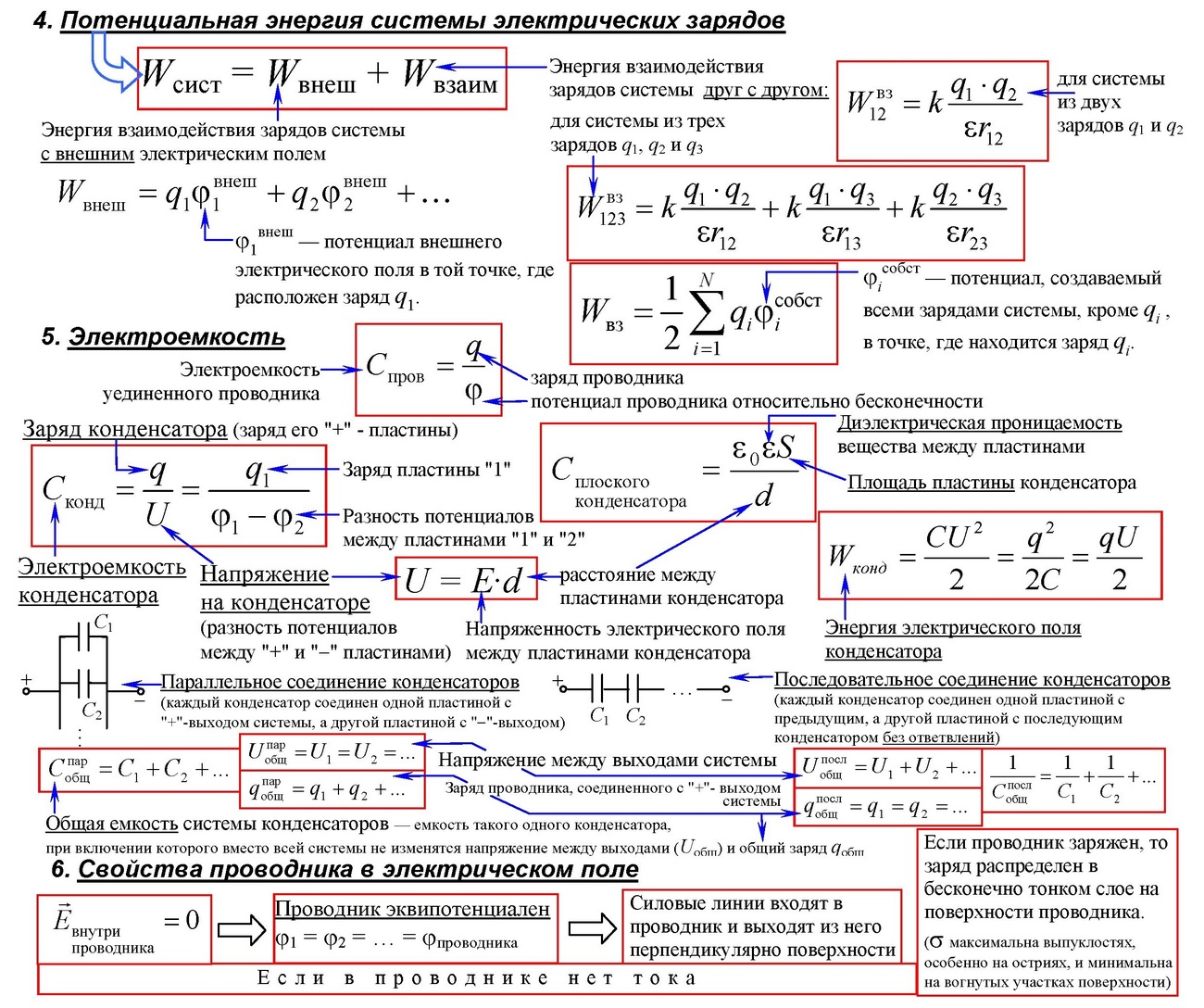
Электроемкость
Электроемкость С — характеризует способность проводника накапливать электрический заряд на своей поверхности.
- — не зависит от электрического заряда и напряжения.
- — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.
Проводники и диэлектрики
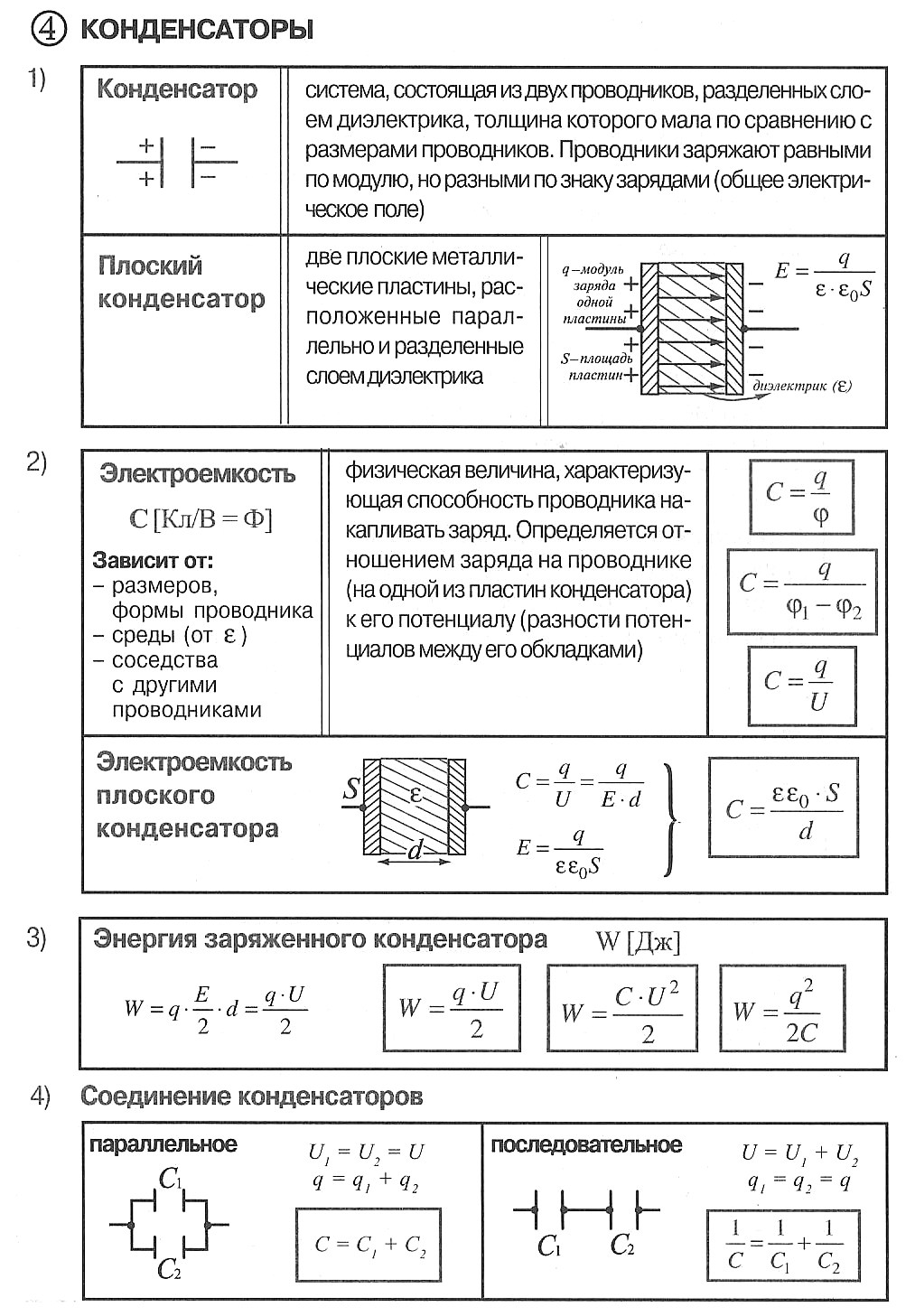
Конденсаторы
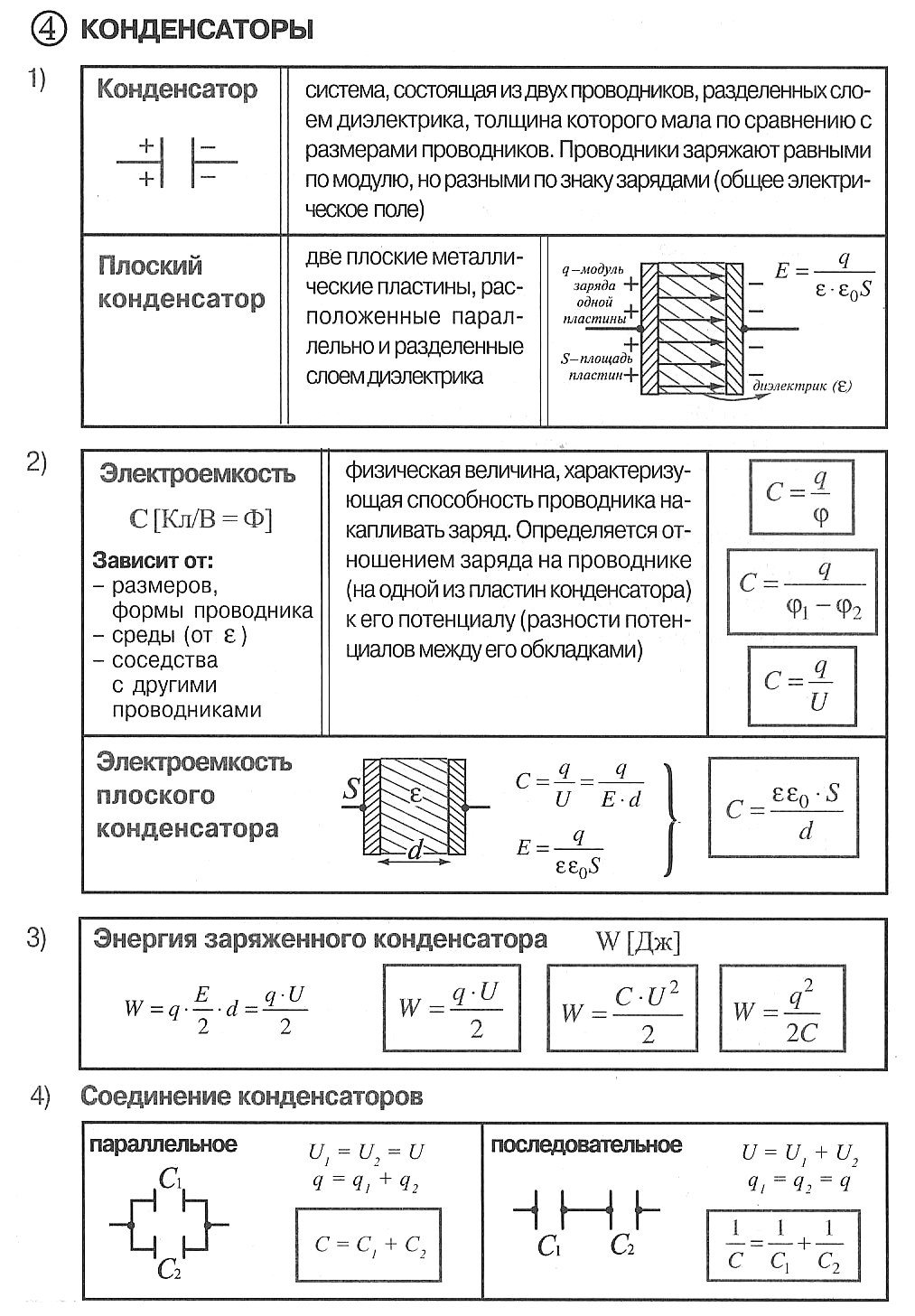
Конденсатор — электротехническое устройство, служащее для быстрого накопления электрического заряда и быстрой отдачи его в цепь (два проводника, разделенных слоем диэлектрика ).
Скачать таблицы по теме «Электростатика»
Конспект уроков по теме «Электростатика. Теория и формулы» + шпаргалка.
Еще конспекты для 10-11 классов:
Все формулы взяты в строгом соответствии с Федеральным институтом педагогических измерений (ФИПИ)
3.1 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
3.1.1 Электризация тел и её проявления. Электрический заряд. Два вида заряда. Элементарный электрический заряд. Закон сохранения электрического заряда
1. Существуют заряды двух видов: положительные (+) и отрицательные (-). Положительный заряд возникает при трении стекла о кожу или шелк, а отрицательный — при трении янтаря (или эбонита) о шерсть.
2. Заряды (или заряженные тела) взаимодействуют друг с другом. Одноименные заряды отталкиваются, а разноименные заряды притягиваются.
3. Состояние электризации можно передать от одного тела к другому, что связано с переносом электрического заряда. При этом телу можно передать больший или меньший заряд, т. е. заряд имеет величину. При электризации трением заряд приобретают оба тела, причем одно — положительный, а другое — отрицательный. Следует подчеркнуть, что абсолютные величины зарядов наэлектризованных трением тел равны, что подтверждается многочисленными измерениями зарядов с помощью электрометров.
Объяснить, почему тела электризуются (т. е. заряжаются) при трении, стало возможным после открытия электрона и изучения строения атома. Как известно, все вещества состоят из атомов; атомы, в свою очередь, состоят из элементарных частиц — отрицательно заряженных электронов, положительно заряженных протонов и нейтральных частиц —нейтронов. Электроны и протоны являются носителями элементарных (минимальных) электрических зарядов.
Элементарный электрический заряд (е) — это наименьший электрический заряд, положительный или отрицательный, равный величине заряда электрона:
Закон сохранения электрического заряда — алгебраическая сумма электрических зарядов всех частиц изолированной системы не меняется при происходящих в ней процессах.
3.1.2 Взаимодействие зарядов. Точечные заряды. Закон Кулона:
Электрический заряд (Кл) — это физическая величина, являющаяся источником электрического поля, посредством которого осуществляется взаимодействие частиц, обладающих зарядом.
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Кулон (Кл) — единица СИ количества электричества (электрического заряда).Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.
[1 Кл = 1 А ·Bс]
Точечный заряд — заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
3.1.3 Электрическое поле. Его действие на электрические заряды
Электрическое поле — это особая форма материи, посредством которой осуществляется взаимодействие электрически заряженных частиц.
Главным свойством электрического поля является действие его на электрические заряды с некоторой силой. По этому действию устанавливается факт его существования. Действие поля на единичный заряд — напряженность поля — является одной из его основных характеристик, по которой изучается распределение поля в пространстве.
3.1.4 Напряжённость электрического поля (Н/м) — векторная характеристика поля, сила, действующая на единичный покоящийся в данной системе отсчета электрический заряд:
Поле точечного заряда:
Однородное поле:
Картины линий полей
3.1.5 Потенциальность электростатического поля
Потенциал (потенциальная функция) (от лат. potentia — сила) является энергетической характеристикой векторных полей, к числу которых относятся гравитационное, электромагнитное и электростатическое поля.
Потенциал электростатического поля в данной точке численно равен работе, которую совершают силы поля при перемещении единичного положительного заряда из данной точки в бесконечность.
Разность потенциалов и напряжение
Работа по перемещению заряда (Дж) в однородном электростатическом поле зависит только от начального и конечного положений движущегося заряда и не зависит от формы траектории. При перемещении заряда по замкнутой траектории работа равна нулю.
Потенциальная энергия заряда в электростатическом поле(Дж):
Потенциал электростатического поля(Дж/Кл):
Связь напряжённости поля и разности потенциалов для однородного электростатического поля: U = Ed
3.1.6 Принцип суперпозиции электрических полей:
3.1.7 Проводники в электростатическом поле. Условие равновесия зарядов: внутри проводника
Внутри и на поверхности проводника
3.1.8 Диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества ε.
Диэлектрики (или изоляторы) — вещества, относительно плохо проводящие электрический ток (по сравнению с проводниками).
Полярные диэлектрики состоят из молекул, в которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы можно представить в виде двух одинаковых по модулю разноименных точечных зарядов, находящихся на некотором расстоянии друг от друга, называемых диполем.
Неполярные диэлектрики состоят из атомов и молекул, у которых центры распределения положительных и отрицательных зарядов совпадают.
Относительная диэлектрическая проницаемость среды ε — это физическая величина, показывающая, во сколько раз модуль напряженности электростатического поля Е внутри однородного диэлектрика меньше модуля напряженности поля Е0 в вакууме:
3.1.9 Конденсатор. Электроёмкость конденсатора(Ф):
Электроёмкость плоского конденсатора — величина заряда, которую нужно сообщить конденсатору, чтобы изменить его потенциал на единицу:
3.1.10 Параллельное соединение конденсаторов:
Последовательное соединение конденсаторов:
3.1.11 Энергия заряженного конденсатора (Дж):
Электрический заряд
q — заряд
n — число частиц
e — заряд электрона
Найти
- q
- n
- e
Известно, что:
=
Вычислить ‘q‘
Закон Кулона
F — сила
k — коэффициент пропорциональности
q1, q2 — заряды
r — расстояние
Найти
- F
- k
- q1
- q2
- r
Известно, что:
=
Вычислить ‘F‘
Постоянная Кулона
k — коэффициент пропорциональности
ε_0 — электрическая постоянная
Найти
- k
- π
- ε_0
Известно, что:
=
Вычислить ‘k‘
Относительная диэлектрическая проницаемость
ε — диэлектрическая постоянная (проницаемость)
F_вак — сила в вакууме
F_окр — сила в окружающей среде
Найти
- ε
- F_вак
- F_окр
Известно, что:
=
Вычислить ‘ε‘
Электрическое поле
E — электрическое поле
F — сила
q — заряд
Найти
- E
- F
- q
Известно, что:
=
Вычислить ‘E‘
Электрическое поле точечного заряда в вакууме
E — электрическое поле
k — коэффициент пропорциональности
q_0 — заряд
r — расстояние
Найти
- E
- k
- q_0
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле точечного заряда в окружающей среде
E — электрическое поле
k — коэффициент пропорциональности
q — заряд
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- E_окр
- k
- q_0
- ε
- r
Известно, что:
=
Вычислить ‘E_окр‘
Электрическое поле вне заряженной сферы
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
R — радиус
r — расстояние
Найти
- E
- k
- σ4
- π
- R
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле вне заряженной сферы
E — электрическое поле
k — коэффициент пропорциональности
q — заряд
r — расстояние
Найти
- E
- k
- q
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле бесконечной заряженной плоскости
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
Найти
- E
- k2
- π
- σ
Известно, что:
=
Вычислить ‘E‘
Электрическое поле бесконечной заряженной плоскости
E — электрическое поле
σ — плотность поверхностного заряда
ε_0 — электрическая постоянная
Найти
- E
- σ
- ε_0
Известно, что:
=
Вычислить ‘E‘
Электрическое поле конденсатора
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
Найти
- E
- k
- π
- σ
Известно, что:
=
Вычислить ‘E‘
Работа в электрическом поле
A — работа
F — сила
Δd — расстояние
Найти
- A
- F
- Δ_d
Известно, что:
=
Вычислить ‘A‘
Потенциальная энергия системы двух точечных зарядов
W — потенциальная энергия
k — коэффициент пропорциональности
q0, q — заряды
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- W
- k
- q0
- q
- ε
- r
Известно, что:
=
Вычислить ‘W‘
Работа в электрическом поле — разность потенциальных энергий
A — работа
W1 — начальная потенциальная энергия
W2 — конечная потенциальная энергия
Найти
- A
- W1
- W2
Известно, что:
=
Вычислить ‘A‘
Потенциал электростатического поля
φ — потенциал
W — потенциальная энергия
q — заряд
Найти
- φ
- W
- q
Известно, что:
=
Вычислить ‘φ‘
Напряжение — разность потенциалов
U — напряжение
φ1 — начальный потенциал
φ2 — конечный потенциал
Найти
- U
- φ1
- φ2
Известно, что:
=
Вычислить ‘U‘
Работа переноса заряда
A — работа
q — заряд
U — напряжение
Найти
- A
- q
- U
Известно, что:
=
Вычислить ‘A‘
Потенциал электростатического поля вокруг точечного заряда
φ — потенциал
k — коэффициент пропорциональности
q_0 — заряд
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- φ
- k
- q0
- ε
- r
Известно, что:
=
Вычислить ‘φ‘
Напряжённость электростатического поля
E — электрическое поле
U — напряжение
Δd — расстояние
Найти
- E
- U
- Δ_d
Известно, что:
=
Вычислить ‘E‘
Результирующее электрическое поле
E — результирующее электрическое поле
E0 — внешнее электрическое поле
E1 — внутреннее электрическое поле
Найти
- E
- E0
- E1
Известно, что:
=
Вычислить ‘E‘
Электрический момент
p — электрический момент
q — заряд
l — расстояние
Найти
- p
- q
- l
Известно, что:
=
Вычислить ‘p‘
Электрическая ёмкость
C — электрическая ёмкость
q — заряд
φ — потенциал
Найти
- C
- q
- φ
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость шара
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
R — радиус
k — коэффициент пропорциональности
Найти
- C
- ε
- R
- k
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость двух проводников
C — электрическая ёмкость
q — заряд
U — напряжение
Найти
- C
- q
- U
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость плоского конденсатора
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
S — площадь
d — расстояние между плас
Найти
- C
- ε
- ε0
- S
- d
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость сферического конденсатора
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
R1 — радиус внутренней сферы
R2 — радиу
Найти
- C
- π
- ε
- ε0
- R1
- R2
Известно, что:
=
Вычислить ‘C‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
E1 — напряженность электрического поля, создаваемого пластиной конденсатора
d — расстояние между пластин
Найти
- W
- q
- E1
- d
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
E — электрическое поле
d — расстояние между пластинами
Найти
- W
- q
- E
- d
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
U — напряжение
Найти
- W
- q
- U
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
C — электрическая ёмкость
U — напряжение
Найти
- W
- C
- U
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
C — электрическая ёмкость
Найти
- W
- q
- C
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
E — электрическое поле
V — объём
Найти
- W
- ε
- ε0
- E
- V
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
E — электрическое поле
S — площадь
d —
Найти
- W
- ε
- ε0
- E
- S
- d
Известно, что:
=
Вычислить ‘W‘
Плотность энергии электрического поля
ω_p — плотность энергии электрического поля
W — потенциальная энергия
V — объём
Найти
- ω_p
- W
- V
Известно, что:
=
Вычислить ‘ω_p‘
Плотность энергии электрического поля
ω_p — плотность энергии электрического поля
ε0 — электрическая постоянная
ε — диэлектрическая постоянная (проницаемость)
E — электрическое п
Найти
- ω_p
- ε0
- ε
- E
Известно, что:
=
Вычислить ‘ω_p‘
Оглавление:
- Основные теоретические сведения
- Электрический ток. Сила тока. Сопротивление
- Закон Ома. Последовательное и параллельное соединение проводников
- ЭДС. Закон Ома для полной цепи
- Работа и мощность тока. Закон Джоуля-Ленца
- Энергобаланс замкнутой цепи
- Электролиз
- Электрический ток в газах и в вакууме
Основные теоретические сведения
Электрический ток. Сила тока. Сопротивление
К оглавлению…
В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:
Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.
Средняя сила тока находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):
Если же ток равномерно меняется с течением времени от значения I1 до значения I2, то можно значение среднего тока можно найти как среднеарифметическое крайних значений:
Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:
При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:
где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.
Сопротивление проводника зависит и от его температуры:
где: R0 – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.
Диод в цепи постоянного тока
Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:
Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.
Закон Ома. Последовательное и параллельное соединение проводников
К оглавлению…
Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.
1. Закономерности последовательного соединения:
Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:
2. Закономерности параллельного соединения:
Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:
Электроизмерительные приборы
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.
ЭДС. Закон Ома для полной цепи
К оглавлению…
Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:
Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.
Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания:
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
Несколько источников ЭДС в цепи
Если в цепи присутствует несколько ЭДС подключенных последовательно, то:
1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:
Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.
2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:
В обоих случаях общее сопротивление источников увеличивается.
При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:
В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.
Работа и мощность тока. Закон Джоуля-Ленца
К оглавлению…
Работа A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в теплоту Q, выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока A к интервалу времени Δt, за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:
Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).
Энергобаланс замкнутой цепи
К оглавлению…
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. В этом случае полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
К оглавлению…
Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.
Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза.
Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией.
Закон электролиза был экспериментально установлен английским физиком М.Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Электрический ток в газах и в вакууме
К оглавлению…
Электрический ток в газах
В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов — электроны и положительные ионы. Этот процесс называется ионизацией газов.
Ионизировать молекулы газа можно внешним воздействием — ионизатором. Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α-частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов — электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).
Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.
Электрический ток в вакууме
Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.
Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.
ЭЛЕКТРОСТАТИКА
Теория и формулы (кратко и сжато)
[button title=»Электростатика – раздел электродинамики, изучающий покоящиеся электрически заряженные тела. Существует два вида электрических зарядов: положительные (стекло о шелк) и отрицательные (эбонит о шерсть).» color=»blue» size=»2″ full_width=»1″]
Элементарный заряд – минимальный заряд (е = 1,6∙10-19 Кл)
Заряд любого тела кратен целому числу элементарных зарядов: q = N∙е
Электризация тел – перераспределение заряда между телами. Способы электризации: трение, касание, влияние.
Закон сохранения электрического заряда – в замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. q1 + q 2 + q 3 + …..+ qn = const
Пробный заряд – точечный положительный заряд.
[hr height=»15″ style=»zigzag» line=»default» themecolor=»1″]
Закон Кулона
Закон Кулона (установлен опытным путем в 1785 году) Сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорционально квадрату расстояния между ними.
[hr height=»15″ style=»zigzag» line=»default» themecolor=»1″]
Электрическое поле
Электрическое поле – вид материи, осуществляющий взаимодействие между электрическими зарядами, возникает вокруг зарядов, действует только на заряды
Силовые линии напряженности электрического поля – непрерывные линии, касательные к которым в каждой точке, через которые они проходят, совпадают с вектором напряженности.
Свойства силовых линий:
- не замкнуты;
- не пересекаются;
- непрерывны;
- направление совпадает с направлением вектора напряжённости;
- начало на + q или в бесконечности, конец на – q или в бесконечности;
- гуще вблизи зарядов (где больше напряжённость).
- перпендикулярны поверхности проводника
Разность потенциалов или напряжение (Δφ или U) — это разность потенциалов в начальной и конечной точках траектории заряда Δφ = φ1 – φ2
Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.
[hr height=»15″ style=»zigzag» line=»default» themecolor=»1″]
Электроемкость
Электроемкость С — характеризует способность проводника накапливать электрический заряд на своей поверхности.
- — не зависит от электрического заряда и напряжения.
- — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.
[hr height=»15″ style=»zigzag» line=»default» themecolor=»1″]
Проводники и диэлектрики
[hr height=»15″ style=»zigzag» line=»default» themecolor=»1″]
Конденсаторы
Конденсатор — электротехническое устройство, служащее для быстрого накопления электрического заряда и быстрой отдачи его в цепь (два проводника, разделенных слоем диэлектрика ).
[hr height=»15″ style=»zigzag» line=»default» themecolor=»1″]
Скачать таблицы по теме «Электростатика»
Конспект уроков по теме «Электростатика. Теория и формулы» + шпаргалка.
Еще конспекты для 10-11 классов: