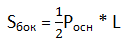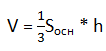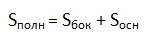Пирамида. Формулы и свойства пирамиды
Определение.
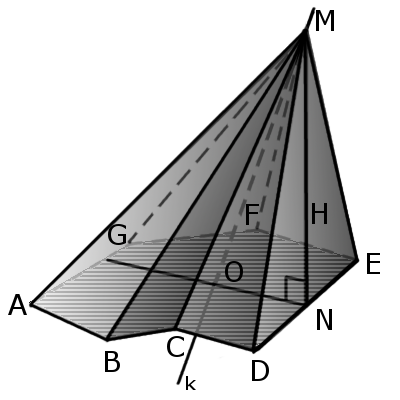
Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.
 |
| Рис.1 |
Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
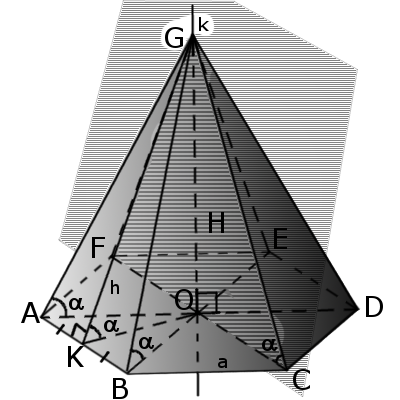
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Определение. Боковая поверхность пирамиды — это совокупная площадь всех боковых граней пирамиды.
Определение. Полная поверхность пирамиды — это совокупность площадей боковой поверхности и площади основания пирамиды.
Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:
Свойства пирамиды
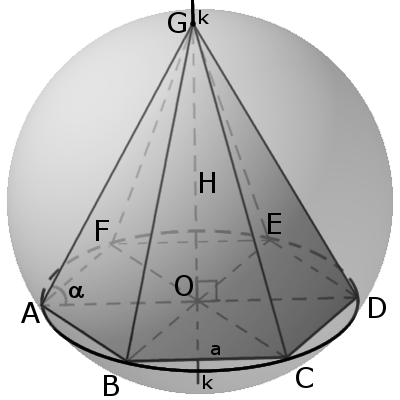
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
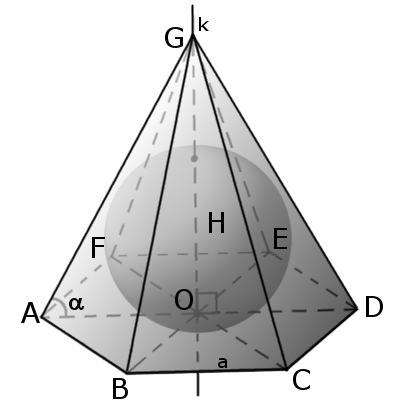
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
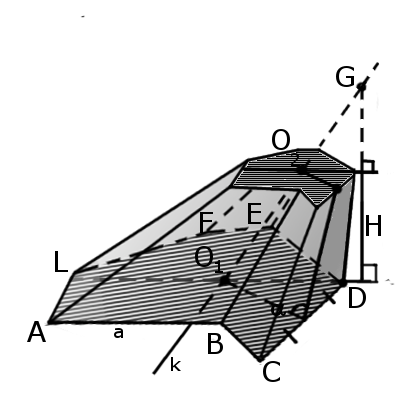
Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
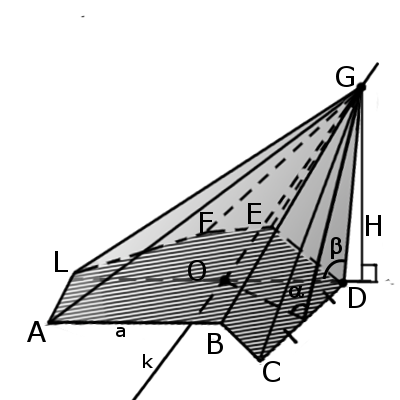
Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.
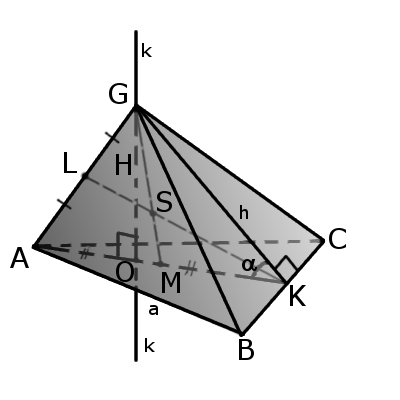
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
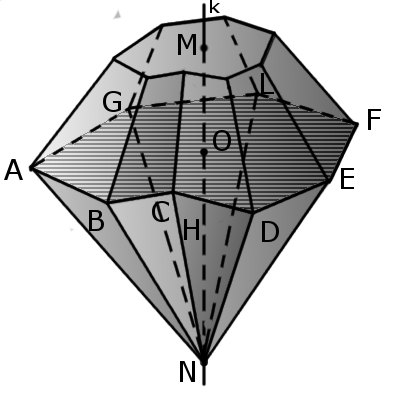
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.
Объем правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).
( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).
Вспомним, как искать эту площадь.
Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma )
У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2})
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle H).
По теореме Пифагора для ( displaystyle Delta SOC)
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}})
Чему же равно ( displaystyle OC)?
Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамида правильная и, значит, ( displaystyle O) – центр ( displaystyle Delta ABC)
Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).
( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) – точка пересечения и медиан тоже.
( displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}) (теорема Пифагора для ( displaystyle Delta ACK))
( displaystyle C{{K}^{2}}-{{a}^{2}}-frac{{{a}^{2}}}{4}=frac{3{{a}^{2}}}{4}); ( displaystyle CK=frac{asqrt{3}}{2})
Значит, ( displaystyle OC=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})
Подставим ( displaystyle OC) в формулу для ( displaystyle H).
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{left( frac{asqrt{3}}{3} right)}^{2}}={{b}^{2}}-frac{{{a}^{2}}}{3})
И подставим все в формулу объема:
( displaystyle V=frac{1}{3}{{S}_{ABC}}cdot H=frac{1}{3}cdot frac{{{a}^{2}}sqrt{3}}{4}cdot sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}})
( displaystyle V=frac{{{a}^{2}}sqrt{3}}{12}sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}}).
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).
Правильная пирамида.. Формулы.. ЕГЭ
Основные формулы правильной пирамиды, которые могут пригодиться на ЕГЭ. Пирамида называется правильной, если в основании правильный n-угольник, боковые грани — равные равнобедренные треугольники.
Формулы правильной пирамиды:
| Чертеж: | Обозначения: |
Формулы: |
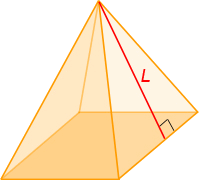 |
Sбок — площадь боковой поверхности. Sполн — площадь полной поверхности. Pосн — периметр основания. L — апофема(высота боковой грани). h — высота пирамиды. |
|
Определение
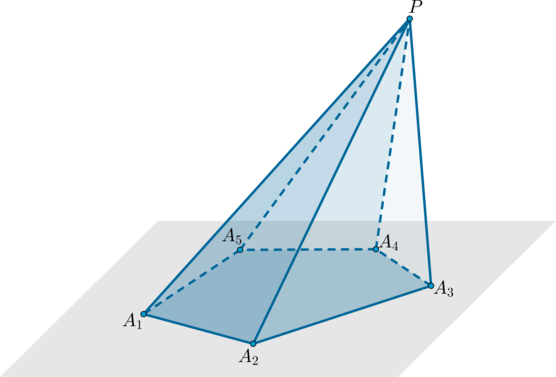
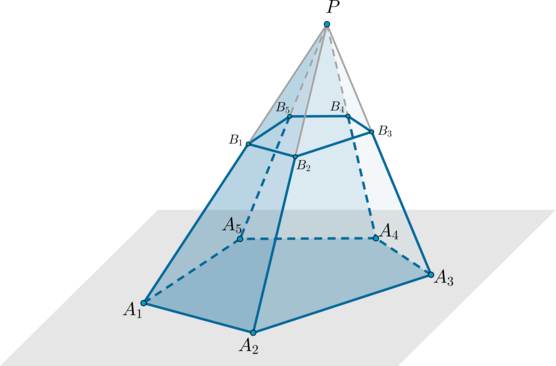
Пирамида – это многогранник, составленный из многоугольника (A_1A_2…A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2…A_n).
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5).
Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.
Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида, в основании которой лежит треугольник, называется тетраэдром.
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:
((a)) боковые ребра пирамиды равны;
((b)) высота пирамиды проходит через центр описанной около основания окружности;
((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.
((d)) боковые грани наклонены к плоскости основания под одинаковым углом.
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.
Теорема
Условия ((a), (b), (c), (d)) эквивалентны.
Доказательство
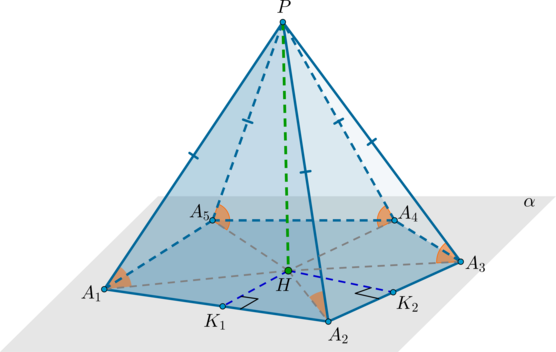
Проведем высоту пирамиды (PH). Пусть (alpha) – плоскость основания пирамиды.
1) Докажем, что из ((a)) следует ((b)). Пусть (PA_1=PA_2=PA_3=…=PA_n).
Т.к. (PHperp alpha), то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=…=PA_n). Значит, (A_1H=A_2H=…=A_nH). Значит, точки (A_1, A_2, …, A_n) находятся на одинаковом расстоянии от точки (H), следовательно, лежат на одной окружности с радиусом (A_1H). Эта окружность по определению и есть описанная около многоугольника (A_1A_2…A_n).
2) Докажем, что из ((b)) следует ((c)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=…=angle PA_nH).
3) Докажем, что из ((c)) следует ((a)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=…=PA_n).
4) Докажем, что из ((b)) следует ((d)).
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1,
HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ((PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, …) равны.
5) Докажем, что из ((d)) следует ((b)).
Аналогично четвертому пункту треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=…=HK_n). Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.
Следствие
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Определение
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
Важные замечания
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).
2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).
4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
Определение
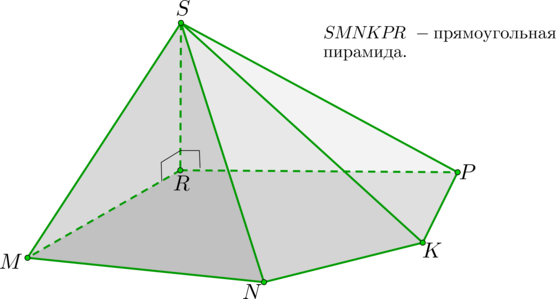
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.
Важные замечания
1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.
2. Т.к. (SR) перпендикулярно любой прямой из основания, то (triangle SRM, triangle SRP) – прямоугольные треугольники.
3. Треугольники (triangle SRN, triangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.
[{Large{text{Объем и площадь поверхности пирамиды}}}]
Теорема
Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_{text{пирамиды}}=dfrac13 S_{text{осн}}cdot h]
Следствия
Пусть (a) – сторона основания, (h) – высота пирамиды.
1. Объем правильной треугольной пирамиды равен (V_{text{прав.треуг.пир.}}=dfrac{sqrt3}{12}a^2h),
2. Объем правильной четырехугольной пирамиды равен (V_{text{прав.четыр.пир.}}=dfrac13a^2h).
3. Объем правильной шестиугольной пирамиды равен (V_{text{прав.шест.пир.}}=dfrac{sqrt3}{2}a^2h).
4. Объем правильного тетраэдра равен (V_{text{прав.тетр.}}=dfrac{sqrt3}{12}a^3).
Теорема
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.
[{Large{text{Усеченная пирамида}}}]
Определение
Рассмотрим произвольную пирамиду (PA_1A_2A_3…A_n). Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ((PB_1B_2…B_n)), а другой называется усеченная пирамида ((A_1A_2…A_nB_1B_2…B_n)).
Усеченная пирамида имеет два основания – многоугольники (A_1A_2…A_n) и (B_1B_2…B_n), которые подобны друг другу.
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.
Важные замечания
1. Все боковые грани усеченной пирамиды – трапеции.
2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.
Видео по теме
Задача 1. В правильной четырехугольной пирамиде точка
– центр основания,
– вершина,
Найдите длину отрезка
.
Решение: + показать
Задача 2. В правильной четырехугольной пирамиде точка
– центр основания,
– вершина,
Найдите боковое ребро
Решение: + показать
Задача 3. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны
Найдите площадь поверхности этой пирамиды.
Решение: + показать
Задача 4. В правильной четырёхугольной пирамиде точка
— центр основания,
— вершина,
Найдите длину отрезка
Решение: + показать
Задача 5. Основанием пирамиды является прямоугольник со сторонами и
Ее объем равен
Найдите высоту этой пирамиды.
Решение: + показать
Задача 6. В правильной четырёхугольной пирамиде с основанием
боковое ребро
равно
сторона основания равна
Найдите объём пирамиды.
Решение: + показать
Задача 7. В правильной четырёхугольной пирамиде все рёбра равны Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
Решение: + показать
Задача 8. Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен У второй пирамиды высота в
раза больше, а сторона основания в
раза больше, чем у первой. Найдите объём второй пирамиды.
Решение: + показать
Задача 9. В правильной четырёхугольной пирамиде боковое ребро равно а тангенс угла между боковой гранью и плоскостью основания равен
Найти сторону основания пирамиды.
Решение: + показать
Задача 10. Основанием пирамиды является прямоугольник со сторонами и
Ее объем равен
Найдите высоту этой пирамиды.
Решение: + показать
Задача 11. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны
Найдите площадь поверхности этой пирамиды.
Решение: + показать
Задача 12. В правильной треугольной пирамиде медианы основания
пересекаются в точке
. Площадь треугольника
равна
объем пирамиды равен
Найдите длину отрезка
.
Решение: + показать
Задача 13. В правильной треугольной пирамиде точка
— середина ребра
— вершина. Известно, что
а
. Найдите площадь боковой поверхности пирамиды.
Решение: + показать
Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны а высота равна
Решение: + показать
Задача 15. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны а объем равен
Решение: + показать
Задача 16. Стороны основания правильной шестиугольной пирамиды равны боковые ребра равны
Найдите площадь боковой поверхности этой пирамиды.
Решение: + показать
Задача 17. Объем правильной шестиугольной пирамиды Сторона основания равна
Найдите боковое ребро.
Решение: + показать
Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?
Решение: + показать
Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в раз?
Решение: + показать
Задача 20. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?
Решение: + показать
Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом °. Высота пирамиды равна
Найдите объем пирамиды.
Решение: + показать
Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно Найдите объем пирамиды.
Решение: + показать
Задача 23. От треугольной призмы, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Решение: + показать
Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен Найдите объем шестиугольной пирамиды. Видео по теме 1 2
Решение: + показать
Задача 25. Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.
Решение: + показать
Задача 26. Сторона основания правильной шестиугольной пирамиды равна а угол между боковой гранью и основанием равен
Найдите объем пирамиды.
Решение: + показать
Задача 27. Найдите объём правильной шестиугольной пирамиды если объём треугольной пирамиды
равен
Решение: + показать
Задача 28. Объем параллелепипеда равен
Найдите объем треугольной пирамиды
Решение: + показать
Задача 29. Объем куба равен Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение: + показать
Задача 30. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно
Решение: + показать
Задача 31. Объем правильной четырехугольной пирамиды равен
Точка
— середина ребра
. Найдите объем треугольной пирамиды
.
Решение: + показать
Задача 32. От треугольной пирамиды, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Решение: + показать
Задача 33. Ребра тетраэдра равны Найдите площадь сечения, проходящего через середины четырех его ребер.
Решение: + показать

Многогранник, одна грань которого является (n)-угольником, а остальные грани — треугольники с общей вершиной, называется пирамидой, (n)-угольник называется основанием пирамиды, а треугольники — боковыми гранями.
Общая вершина боковых граней называется вершиной пирамиды.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются рёбрами пирамиды.
В зависимости от количества сторон основания пирамиды могут быть треугольными, четырёхугольными, пятиугольными и т. д.
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Важно знать, где на плоскости основания находится проекция вершины пирамиды, она может быть в центре основания, на стороне основания, за пределами многоугольника основания. Решение задачи в большей степени зависит от расположения этой точки.
Чтобы нарисовать пирамиду, нужно соблюдать определённый порядок:
1. первым рисуется основание,
2. по условию задачи находится проекция вершины на плоскости основания,
3. вертикально проводится высота,
4. проводятся рёбра.
На рисунке изображена четырёхугольная пирамида (SABCD)
(первой пишут букву вершины).
Основание — четырёхугольник (ABCD).
Вершина проецируется в точку пересечения диагоналей (O) — основание высоты или проекция вершины.
(SA), (SB), (SC), (SD) — рёбра пирамиды,
(AB), (BC), (CD), (DA) — стороны основания.
В курсе средней школы в основном есть задачи, в которых даны:
— правильная пирамида (вершина проецируется в центр основания);
— пирамида, вершина которой проецируется в центр описанной окружности;
— пирамида, вершина которой проецируется в центр вписанной окружности;
— пирамида, высота которой совпадает с боковым ребром;
— пирамида, высота которой также является высотой боковой грани.
Углы, которые образованы боковой гранью и основанием пирамиды, называются двугранными углами при основании пирамиды.
Двугранный угол между боковой гранью (SCD) и гранью основания равен линейному углу
∠
(OES). Этот угол образован отрезками (OE) и (SE), лежащими в этих гранях и перпендикулярных их общей прямой (CD). То есть (OE)
⊥CD
и (SE)
⊥CD
.
Чтобы определить этот угол, часто нужно использовать теорему о трёх перпендикулярах.
Углы, которые образованы боковым ребром и его проекцией на плоскость основания, называются углами между боковым ребром и плоскостью основания.
На рисунке
∠
(OCS).
Угол, который образован двумя боковыми гранями, называется двугранным углом при боковом ребре пирамиды.
Угол, который образован двумя боковыми рёбрами одной грани пирамиды, называется углом при вершине пирамиды.
Основные формулы пирамиды
Площадь боковой поверхности равна сумме площадей всех боковых граней пирамиды:
S=S1+S2+S3+…
(Некоторые формулы годятся только для определённых видов пирамиды.)
Площадь полной поверхности
Sп.п.=S+Sоснования
.
Объём пирамиды (V =)
13Sоснования
(H), где (H) — высота пирамиды.
Формула объёма используется для пирамид любого вида.
Источники:
Рис. 1. Пирамида, © ЯКласс.