Задание 1
На автозаправке клиент купил стакан кофе за 99 руб. и попросил залить 25 л бензина по цене 36 руб. за литр. Какую сдачу (в рублях) получил клиент, если он расплатился за все 1000‐й купюрой?
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
За бензин заплатит: 25-36=900 руб
Итого покупка: 900+99=999 руб
Сдача равна: 1000-999=1 руб
Задание 2
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
580 мм.рт. ст. соответствует высота в два километра, это видно на графике
Задание 3
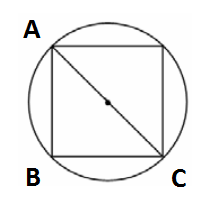
В окружность с диаметром $$3sqrt{2}$$ вписан квадрат. Найдите сторону квадрата.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Диаметр окружности является диагональю квадрата. Пусть x — сторона квадрата. Тогда из треугольника ABC:
$$x^{2}+x^{2}=(3sqrt{2})^{2}$$
Отсюда x=3
Задание 4
При каждом выстреле стрелок поражает мишень с вероятностью 0,8. В случае промаха стрелок делает повторный выстрел. Выстрелы повторяются до тех пор, пока мишень не будет поражена. Какое наименьшее количество выстрелов по мишени должен совершить стрелок, чтобы вероятность попадания в мишень составила более 0,995?
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Так как вероятность попадания 0,8, то вероятность промаха равна 1-0,8=0,2. Рассмотрим ситуацию обратную поражению мишени — что ниразу не попадет. Если надо найти вероятность попадания более 0,995, значит можно рассматривать ситуацию промахов с вероятностью 1-0,995, то есть менее 0,005. Пусть совершено n выстрелов:
$$0.2^{n} leq 0.005$$
Отсюда n⩾4. То есть необходимо не менее 4 выстрелов, чтобы вероятность всех промахов была менее 0,005, а значит и вероятность попадания более 0,995
Задание 5
В прямоугольном треугольнике гипотенуза равна $$6sqrt{5}$$ , а тангенс одного из углов равен 2. Найдите меньший катет.
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Тангенс угла, это отношение длин противолежащего катета к прилежащему, следовательно, мы можем взять один катет как x, а второй будет 2x(так как тангенс равен 2). Распишем теорему Пифагора с полученными значениями: $$x^{2}+(2x)^{2}=(6sqrt{5})^{2}$$ $$5x^{2}=36*5$$ $$x^{2}=36$$ $$x=6 ; x=-6$$ Длина не может быть отрицательной, поэтому ответ 6.
Задание 6
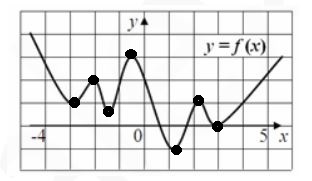
По графику функции у = f (x) определите количество точек на интервале (4;5), в которых касательная к графику параллельна оси абсцисс или совпадает с ней.
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Если касательная параллельна оси ОХ, то производная равна 0. Производная равна нулю на данном графике функции в точках максимума и минимума ( они отмечены жирной точкой ). Их всего 7
Задание 7
Площадь поверхности шара равна $$24sqrt[3]{frac{pi }{6}}$$. Найдите объем шара.
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь поверхности сферы вычисляется по формуле: $$S=4pi R^{2}$$ Объем шара вычисляется по формуле: $$V=frac{4}{3}pi R^{3}$$ Найдем сначала радиус сферы, зная площадь ее поверхности: $$4pi R^{2} =24sqrt[3]{frac{pi }{6}} $$ $$R^{2} =6frac{sqrt[3]{frac{pi }{6}}}{pi} $$ $$R=sqrt[3]{frac{6}{pi}} $$ Тогда объем шара будет равен: $$V=frac{4}{3}pi (sqrt[3]{frac{6}{pi}})^{3}=8$$
Задание 8
Известно, что $$frac{cos x-sin x}{cos x+sin x}=-0.8$$. Найдите $$ tg x $$
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{cos x-sin x}{cos x+sin x}=-0.8=frac{-4}{5}$$ $$(cos x-sin x)*5=-4*(cos x+sin x)$$ $$5cos x-5sin x=-4*cos x-4sin x$$ $$9cos x = sin x $$ Поделим обе части на cos x $$9 = tg x $$
Задание 9
Добираясь из села в город, Виктор сначала 4 часа ехал на велосипеде со скоростью 12 км/ч, после чего велосипед сломался, и Виктору пришлось идти пешком еще 2 часа со скоростью 6 км/ч. С какой средней скоростью добирался от села до города Виктор? Ответ дайте в км/ч.
Ответ: 10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
За 4 часа Виктор проехал 4*12=48 км
За 2 часа он прошел 2*6=12 км
Следовательно, средняя скорость его будет равна : $$ v=frac{48+12}{4*2}=10$$
Задание 10
Имеется два сосуда равного объёма. Первый наполнен раствором соли с концентрацией 44%, второй –раствором соли с концентрацией 66%. Из каждого сосуда взяли по 5,5 л раствора; взятое из первого сосуда вылили во второй,а взятое из второго – в первый, после чего концентрации растворов в сосудах стали равны. Сколько литров раствора было в первом сосуде?
Ответ: 11
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть V — одинаковый объем. Тогда соли в первом сосуде будет: V * 44 / 100 = 0.44V литра. Во втором сосуде: V * 66 / 100 = 0.66V литра
В 5,5 литрах первого раствора содержалось соли: 5.5 * 44 / 100 = 2.42 литра. Значит в первом растворе осталось 0.44V — 2.42 литров соли
В 5,5 литрах второго раствора содержалось соли: 5.5 * 66 / 100 = 3.63 литра. Значит во втором осталось 0,66V — 3,63 литров соли.
Но потом долили полученные значения в растворы, тогда в первом соли стало: 0.44V-2.42+3.63 литров соли, а во втором: 0.66V-3.63+2.42 литров.
Объемы остались одинаковые, а концентрации сравнялись, значит количество соли тоже одинаковое:
0.44V-2.42+3.63=0.66
V-3.63+2.42 0.22V=2.42
V=11
Задание 11
Найдите наибольшее значение функции $$f(x)=2^{x}(x+1)$$ , на отрезке [-1;2]
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную этой функции и приравняем ее к нулю:
$$f'(x)=2^{x}ln 2(x+1)+2^{x}$$
$$2^{x}(ln 2(x+1)+1)=0$$
$$ln 2 * x+ ln 2 + 1 = 0$$
$$x = -1 — frac{1}{ln 2}$$
Данное значение меньше -1, значит точка экстремума левее нашего промежутка, а это означает, в свою очередь, что на заданном промежутке функция монотонна. Если мы подставим ноль в производную, то получим, что на промежутке, где расположен ноль, производная больше нуля, значит функция возрастает. Поэтому наибольшее значение функции будет в конце промежутка.
$$f(2)=2^{2}(2+1)=4*3=12$$
Задание 12
Дано уравнение $$frac{2sqrt 3cos^2 x+sin x}{2cos x-1}=0$$.
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку $$[3pi;frac{9pi}{2}]$$.
Ответ: а) $$-frac{2pi}{3}+2pi n,nin Z$$; б) $$frac{10pi}{3}$$.
Задание 13
В конусе с вершиной в точке $$P$$ высота равна 1, а образующая равна 2. В основании конуса провели диаметр $$CD$$ и перпендикулярную ему хорду $$AB$$. Известно, что хорда $$AB$$ удалена от центра основания на расстояние, равное 1.
а) Докажите, что треугольник $$PAB$$ прямоугольный.
б) Найдите сумму объемов пирамид $$CAPB$$ и $$DAPB$$.
Ответ: $$frac{2sqrt6}{3}$$.
Задание 14
Решите неравенство $$frac{4^{sqrt{x-1}}-5cdot 2^{sqrt{x-1}}+4}{log^2_2(7-x)}geq 0.$$
Ответ: $${1}cup [5;6)cup (6;7)$$.
Задание 15
Диагонали прямоугольника $$ABCD$$ пересекаются в точке $$O$$. Окружности $$omega_1$$ и $$omega_2$$ описаны около треугольников $$AOB$$ и $$BOC$$ соответственно. Пусть $$O_1$$ – центр окружности $$omega_1$$, а $$O_2$$ – центр окружности $$omega_2$$.
а) Докажите, что прямая $$BO_1$$ касается окружности $$omega_2$$, а прямая $$BO_2$$ касается окружности $$omega_1$$.
б) Найдите длину отрезка $$O_1O_2$$, если известно, что $$AB=6$$, $$BC=8$$.
Ответ: $$frac{125}{24}$$.
Задание 16
Гражданка Васильева вложила 44 млрд. рублей в два оффшорных банка на 3 года: часть денег в банк А, остальное в банк Б. Известно, что банк А ежегодно начисляет 10% годовых; банк Б в первый год начисляет 5% годовых, во второй – 10%, а в третий – 15%. Сколько рублей было вложено в каждый из банков, если через три года доход гражданки Васильевой от вложения денег составил 14520 млн. рублей.
Ответ: 28;16 млрд.
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых уравнение $$sqrt{4x-x^2}cdot log_2(x^2-2ax+a^2)=0$$ имеет ровно три различных корня.
Ответ:
Задание 18
а) Найдите значение выражения $$tg1^{circ}cdot tg2^{circ}cdot tg3^{circ}cdot …cdot tg88^{circ}cdot tg89^{circ}$$.
б) Докажите, что $$tg40^{circ}+tg55^{circ}+tg85^{circ}=tg40^{circ}cdot tg55^{circ}cdot tg85^{circ}$$.
в) Найдите значение выражения $$(1+tg1^{circ})cdot (1+tg2^{circ})cdot …cdot (1+tg44^{circ})$$.
Ответ: а) 1; б) $$2^{22}$$.
Скрыть
a) $$tg1^{circ}cdot tg2^{circ}cdot tg3^{circ}cdot …cdot tg88^{circ}cdot tg89^{circ}=$$
$$=tg1^{circ}cdot tg2^{circ}cdot tg3^{circ}cdot …cdot tg44^{circ}cdot tg45^{circ}cdot tg(90^{circ}-44^{circ})cdot…cdot tg(90^{circ}-2^{circ})cdot tg(90^{circ}-1^{circ})=$$
$$=tg1^{circ}cdot tg2^{circ}cdot tg3^{circ}cdot …cdot tg44^{circ}cdot 1cdot ctg44^{circ}cdot…cdot ctg2^{circ}cdot ctg1^{circ}=$$
$$=(tg1^{circ}cdot ctg1^{circ})cdot (tg2^{circ}cdot ctg2^{circ})cdot …cdot (tg44^{circ}cdot ctg44^{circ})=1.$$
б) Покажем, что
$$tg40^{circ}+tg55^{circ}+tg85^{circ}-tg40^{circ}cdot tg55^{circ}cdot tg85^{circ}=0.$$
$$tg40^{circ}(1-tg55^{circ}cdot tg85^{circ})+tg55^{circ}+tg85^{circ}=$$
$$=(1-tg 55^{circ}cdot tg 85^{circ})(tg 40^{circ}+frac{tg 55^{circ}+tg 85^{circ}}{1-tg 55^{circ}cdot tg 85^{circ}})=$$
$$=(1-tg55^{circ}cdot tg85^{circ})(tg40^{circ}+tg140^{circ})=$$
$$=(1-tg55^{circ}cdot tg85^{circ})(tg40^{circ}+tg(180^{circ}-40^{circ}))=$$
$$=(1-tg55^{circ}cdot tg85^{circ})(tg40^{circ}-tg40^{circ})=0.$$
Что и требовалось доказать.
в) $$(1+tg1^{circ})cdot (1+tg2^{circ})cdot …cdot (1+tg44^{circ})=$$
$$=(frac{cos1^{circ}}{cos1^{circ}}+frac{sin1^{circ}}{cos1^{circ}})(frac{cos2^{circ}}{cos2^{circ}}+frac{sin2^{circ}}{cos2^{circ}})cdot …cdot (frac{cos44^{circ}}{cos44^{circ}}+frac{sin44^{circ}}{cos44^{circ}})=$$
$$=frac{cos1^{circ}+sin1^{circ}}{cos1^{circ}}cdot frac{cos2^{circ}+sin2^{circ}}{cos2^{circ}}cdot …cdotfrac{cos44^{circ}+sin44^{circ}}{cos44^{circ}}=$$
$$=frac{frac{sqrt2}{2}cos1^{circ}+frac{sqrt2}{2}sin1^{circ}}{frac{sqrt2}{2}cos1^{circ}}cdot frac{frac{sqrt2}{2}cos2^{circ}+frac{sqrt2}{2}sin2^{circ}}{frac{sqrt2}{2}cos2^{circ}}cdot …cdot frac{frac{sqrt2}{2}cos44^{circ}+frac{sqrt2}{2}sin44^{circ}}{frac{sqrt2}{2}cos44^{circ}}=$$
$$=frac{cos(1^{circ}-45^{circ})}{frac{sqrt2}{2}cos1^{circ}}cdot frac{cos(2^{circ}-45^{circ})}{frac{sqrt2}{2}cos2^{circ}}cdot …cdot frac{cos(44^{circ}-45^{circ})}{frac{sqrt2}{2}cos44^{circ}}=$$
$$=frac{sqrt2cdot cos44^{circ}}{cos1^{circ}}cdot frac{sqrt2cdot cos43^{circ}}{cos2^{circ}}cdot …cdot frac{sqrt2cdot cos1^{circ}}{cos44^{circ}}=(sqrt2)^{44}=2^{22}.$$
А. Ларин: Тренировочный вариант № 197.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В конусе с вершиной в точке Р высота равна 1, а образующая равна 2. В основании конуса провели диаметр CD и перпендикулярную ему хорду АВ. Известно, что хорда АВ удалена от центра основания на расстояние, равное 1.
а) Докажите, что треугольник РАВ прямоугольный.
б) Найдите сумму объемов пирамид САРВ и DАРВ.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
На следующей странице вам будет предложено проверить их самостоятельно.
5
Гражданка Васильева вложила 44 млрд рублей в два оффшорных банка на 3 года: часть денег в банк А, остальное в банк Б. Известно, что банк А ежегодно начисляет 10% годовых; банк Б в первый год начисляет 5% годовых, во второй — 10%, а в третий — 15%. Сколько рублей было вложено в каждый из банков, если через три года доход гражданки Васильевой от вложения денег составил 14 520 млн рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых уравнение
имеет ровно три различных корня.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
а) Найдите значение выражения
б) Докажите, что
в) Найдите значение выражения
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
- Cайты учителей
- Все блоги
- Все файлы
- Все тесты
-
1 - Войти
- Зарегистрироваться / Создать сайт


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 10.03.2023 05:32

Затеева Валентина Павловна
учитель математики
68 лет
426 899
19
19.08.2019 09:24
Тренировочный вариант № 197 математика ЕГЭ Ларин А.
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
14 мая 2017
В закладки
Обсудить
Жалоба
Решение тренировочного варианта по математике
Вариант 197 от Александра Ларина.
trvar197.pdf
Contents
- 1 Задание №1
- 1.1 Решение
- 2 Задание №2. Решение варианта №197 ОГЭ по математике Ларин
- 2.1 Решение
- 3 Задание №3
- 3.1 Решение
- 4 Задание №4. Решение варианта №197 ОГЭ по математике Ларин
- 4.1 Решение
- 5 Задание №5
- 5.1 Решение
- 6 Задание №6. Решение варианта №197 ОГЭ по математике Ларин
- 6.1 Решение
- 7 Задание №7. Решение варианта №197 ОГЭ по математике Ларин
- 7.1 Решение
- 8 Задание №8
- 8.1 Решение
- 9 Задание №9. Решение варианта №197 ОГЭ по математике Ларин
- 9.1 Решение
- 10 Задание №10
- 10.1 Решение
- 11 Задание №11
- 11.1 Решение
- 12 Задание №12
- 12.1 Решение
- 13 Задание №13. Решение варианта №197 ОГЭ по математике Ларин
- 13.1 Решение
- 14 Задание №14. Решение варианта №197 ОГЭ по математике. Ларин
- 14.1 Решение
- 15 Задание №15
- 15.1 Решение
- 16 Задание №16
- 16.1 Решение
- 17 Задание №17
- 17.1 Решение
- 18 Задание №18
- 18.1 Решение
- 19 Задание №19
- 19.1 Решение
- 20 Задание №20. Решение варианта №197 ОГЭ по математике Ларин
- 20.1 Решение
- 21 Задание №21
- 21.1 Решение
- 22 Задание №22
- 22.1 Решение
- 23 Задание №23
- 23.1 Решение
- 24 Задание №24
- 24.1 Решение
- 25 Задание №25
- 25.1 Решение
- 26 Задание №26
- 26.1 Решение
- 27 Видео: Разбор Варианта ОГЭ Ларина №197 (№1-20)
- 28 Видео: Разбор Варианта ОГЭ Ларина №197 (№21-26)
Задание №1
Найдите значение выражения:
Решение
Ответ: 1,6.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40–97 | 70–154 | 60–102 |
| Белки | 36–87 | 65–117 | 58–87 |
| Углеводы | 170–420 | 257–586 | 257–586 |
- Потребление жиров в норме.
- Потребление белков в норме.
- Потребление углеводов в норме.
Решение
- неверно, так как 50 меньше 60.
- верно.
- неверно, так как 250 меньше 257.
Ответ: 2.
Задание №3
Одно из чисел, √ отмечено на прямой, точкой А. Какое это число?
Варианты ответа
Решение
Число A A .
Число ближе к 2 , что соответствует 3 варианту ответа.
Ответ: 3.
Задание №4. Решение варианта №197 ОГЭ по математике Ларин
Решение
5√2∗√22∗3√11 = 15√(22∗22) = 15∗22=330.
Ответ: 330.
Задание №5
На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в км/ч), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъёмная сила (в тоннах силы) при скорости 400 км/ч
Решение
Исходя из графика при скорости в 400 км/ч сила составит 4 тс.
Ответ: 4.
Задание №6. Решение варианта №197 ОГЭ по математике Ларин

Решение
Ответ: -5
Задание №7. Решение варианта №197 ОГЭ по математике Ларин
Решение
Стоимость 2 футболки с учетом скидки:
300*0,3 = 90.
Итоговая стоимость двух футболок:
300 + 90 = 390.
Ответ: 390.
Задание №8
- 1. Индонезия входит в семёрку крупнейших по площади территории стран мира.
- Площадь территории США составляет 8,5 млн км².
- Площадь Австралии больше площади Индии.
- Площадь Канады больше площади Индии более чем в три раза.
Решение
- неверно, Индонезии нет среди стран.
- неверно, 9,5 млн км².
- верно.
- верно.
Ответ: 3, 4.
Задание №9. Решение варианта №197 ОГЭ по математике Ларин
Решение
всего возможных вариантов расстановки учебников 6:
- фхм
- фмх
- хмф
- хфм
- мфх
- мхф.
Из них всего в 4 вариантах выполняется условие. значит вероятность = 4/6 = 0,67.
Ответ: 0,67.
Задание №10
Решение
Ветви вниз . Пресекает Oy при y=4 следовательно c=4.
, то есть 4 вариант ответа.
Ответ: 4.
Задание №11
Решение
Ответ: 1365.
Задание №12

Решение
Ответ: 1,125.
Задание №13. Решение варианта №197 ОГЭ по математике Ларин
Решение
= (
Задание №14. Решение варианта №197 ОГЭ по математике. Ларин
Решение
, что соответствует 4 варианту ответа.
Ответ: 4.
Задание №15

Решение
ABCD -трапеция, MN-средняя линия:
50+x = 140 x = 90.
Ответ: 90.
Задание №16
Решение
:
Ответ: 30.
Задание №17
Решение
BC=10+18=28.
(AK-биссектриса).
(накрест лежащие)
P=(10+28)*2 = 76.
Ответ: 76.
Задание №18

Решение
Сторона :
Периметр треугольника:
Ответ: 12.
Задание №19

Решение
().
Ответ: 0,8.
Задание №20. Решение варианта №197 ОГЭ по математике Ларин
- Если угол острый, то вертикальный ему угол также является острым.
- Диагонали ромба взаимно перпендикулярны.
- В плоскости все точки, равноудалённые от заданной точки, лежат на одной прямой.
Решение
- верно.
- верно.
- неверно, лежат на окружности.
Ответ: 1, 2.
Задание №21

Решение
Ответ: (-3;-10);(10;3).
Задание №22
Решение
x-производительность первого, y-второго, V-объем ⇒:
Ответ: 1600.
Задание №23
Решение
Две точки пересечения будут в том случае, если прямая лежит в первой четверти при (от момента, когда она будет параллельна оси Ох, до момента, когда она будет параллельна прямой ).
Если прямая лежит во второй четверти при (от момента, когда она будет параллельна , до момента, когда она будет параллельна оси Ох):
Ответ:
Задание №24
Найдите высоту, опущенную на основание
Решение
Ответ: 8.
Задание №25
Докажите, что М – середина ВС.
Решение
- (AM-биссектриса ); (накрест лежащие) — равнобедренный треугольник.
- — равнобедренный AB = BM; MC=CD, но
Ответ: доказано.
Задание №26
Решение
Ответ: 56.