Задание 1
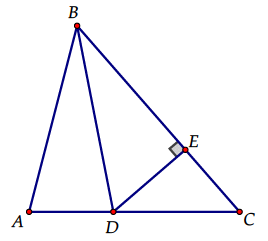
Площадь треугольника АВС равна 30. На стороне АС взята точка D так, что AD : DC = 2 : 3. Длина перпендикуляра DE, проведенного к стороне ВС, равна 9. Найдите ВС.
Ответ: 4
Скрыть
Проведенная из вершины В высота — общая для треугольников АВС, АВD и DBC, поэтому отношение их площадей равно отношению соответствующих оснований. По условию AD : DC = 2 : 3, значит DC : AC = 3 : 5 и площадь треугольника DBC равна трем пятым от площади треугольника АВС:
$$3cdotfrac{30}{5}=18$$.
Так как площадь треугольника DBC равна половине произведения длины высоты DE на длину стороны ВС, получаем, что
$$ВС=2cdotfrac{18}{9}=4$$.
Задание 2
Найдите объем правильной шестиугольной пирамиды, если ее боковое ребро равно 13, а радиус окружности, описанной около основания, равен 11.
Ответ: 726
Скрыть
Основанием данной пирамиды является правильный шестиугольник, и радиус окружности, описанной около этого шестиугольника, равен 11. Значит, длина стороны основания равна 11, и основание можно представить в виде объединения шести равносторонних треугольников со стороной 11. Соответственно, площадь S основания пирамиды равна умноженной на 6 площади равностороннего треугольника со стороной 11:
$$S = 6cdot11^2cdotfrac{3^{frac{1}{2}}}{4} = 181,5cdot3^{frac{1}{2}}$$.
Высоту h пирамиды найдем по теореме Пифагора из прямоугольного треугольника, в котором h — катет, боковое ребро пирамиды — гипотенуза, равная 13, и радиус описанной окружности — другой катет, равный 11:
$$h = (13^2-11^2)^{frac{1}{2}} = 48^{frac{1}{2}} = 4cdot3^{frac{1}{2}}$$.
Объем V данной пирамиды:
$$V = frac{Sh}{3} = 181,5cdot3^{frac{1}{2}}cdot4cdotfrac{3^{frac{1}{2}}}{3} = 181,5cdot4 = 726$$.
Задание 3
Вероятность того, что в будний день число посетителей торгового центра превысит 2000 человек, равна 0,34. Вероятность того, что число посетителей торгового центра превысит 2500 человек, равна 0,18. Найдите вероятность того, что в случайно выбранный будний день число посетителей окажется от 2001 до 2500 человек.
Ответ: 0,16
Скрыть
Вероятность того, что число посетителей превысит 2000 складывается из сумм вероятностей двух независимых событий:
Первое событие что это число будет от 2001 до 2500
Второе событие, что число посетителей будет больше 2500,а вероятность этого уже известна 0,18.
Значит, вероятность того что посетителей будет от 2001 до 2500 равна:
$$0,34-0,18=0,16$$
Задание 4
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,6. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет только одну партию из двух.
Ответ: 0,52
Скрыть
Итак, нам подходят результаты, когда А выигрывает только одну партию из двух. Варианты выигрыша двух партий или проигрыша обеих партий нам как раз не подходят. И мы точно знаем, что один раз А будет играть белыми и один раз чёрными. Очерёдность, по-моему, неважна.
Выигрыш двух партий $$= 0,6cdot0,4=0,24$$.
Проигрыш в двух партиях $$= (1-0,6)cdot(1-0,4)=0,24$$.
Все остальные исходы — это выигрыш в любой одной партии $$= 1- 0,24-0,24=0,52$$.
Задание 5
Решите уравнение $$9^{sqrt{x-5}}-27=6cdot3^{sqrt{x-5}}$$.
Ответ: 9
Скрыть
$$9^{sqrt{x-5}}-27=6cdot3^{sqrt{x-5}}$$
Пусть $$3^{sqrt{x-5}}=y>0$$. Тогда $$y^2-27=6yRightarrow y^2-6y-27=0Rightarrowleft[begin{matrix} y=9\ y=-3<0 end{matrix}right.$$
Получим $$3^{sqrt{x-5}}=9Rightarrow sqrt{x-5}=2Rightarrow x-5=4Rightarrow x=9$$
Задание 6
Найдите значение выражения $$4cos260^{circ}sin130^{circ}cos160^{circ}$$.
Ответ: 0,5
Скрыть
$$4cos260^{circ}sin130^{circ}cos160^{circ}=4cos(180+80)sin(90+40)cos(2cdot80)=$$
$$=-4cos80cos40cos160=frac{-4sin40cos40cos80cos160}{sin40}=$$
$$=frac{-frac{4}{2}sin80cos80cos160}{sin40}=frac{-frac{2}{2}sin160cos160}{sin40}=frac{-frac{1}{2}sin320}{sin40}=frac{frac{1}{2}sin(360-40)}{sin40}=$$
$$=frac{frac{1}{2}sin40}{sin40}=frac{1}{2}=0,5$$
Задание 7
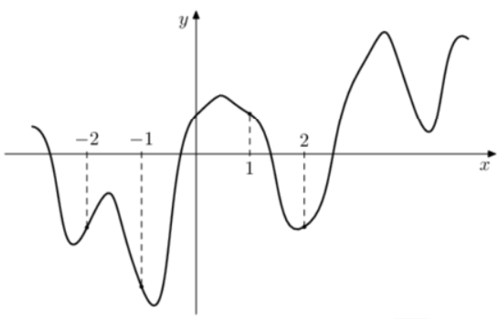
На рисунке изображен график функции $$y=f(x)$$. На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: -2
Скрыть
Производная положительная, если функция возрастает $$Rightarrow -2$$ и $$2$$. Там больше, где угол между касательной, проведённой в точку, и Ox ближе к $$90^{circ}Rightarrow -2$$.
Задание 8
При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,6cdot10^5$$ $$Паcdot м^2$$, где $$p$$ — давление газа (в Па), $$V$$ — объем газа (в $$м^3$$), $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в $$м^3$$) будет занимать газ при давлении $$p$$, равном $$6,25cdot10^6$$ Па.
Ответ: 0,064
Скрыть
Подставим данные в задании величины в формулу давления и объема, получим:
$$6,25cdot10^6cdot V^{frac{4}{3}}=1,6cdot10^5$$
$$V^{frac{4}{3}}=frac{1,6}{62,5}=frac{16}{625}$$
$$V=frac{(16)^{frac{3}{4}}}{(625)^{frac{3}{4}}}=frac{2^3}{5^3}=frac{8}{125}=0,064$$
Задание 9
Пункт С расположен в 12 км от пункта В вниз по течению. Рыбак отправился на лодке в пункт С из пункта А, расположенного выше пункта В. Через 4 часа он прибыл в С, а на обратный путь затратил 6 часов. В другой раз рыбак воспользовался моторной лодкой, увеличив тем самым собственную скорость передвижения относительно воды втрое, и дошел от А до В за 45 минут. Найдите скорость течения (в км/ч), считая ее постоянной.
Ответ: 1
Скрыть
Пусть $$v_т$$ км/ч — скорость течения; $$v_л$$ км/ч — скорость лодки; $$a$$ км/ч — расстояние между A и B. Тогда по условию:
$$left{begin{matrix} (v_л+v_т)cdot4=12+a\ (v_л-v_т)cdot6=12+a\ a=(3v_л+v_т)cdot0,75 end{matrix}right.$$
откуда $$v_т=1$$ км/ч
Задание 10
На рисунке изображен график функции $$f(x)=ksqrt{x}$$. Найдите $$f(7,84)$$.
Ответ: 9,8
Скрыть
График проходит через (4;7):
$$7=kcdotsqrt{4}Rightarrow k=3,5$$
$$f(7,84)=3,5sqrt{7,84}=3,5cdot2,8=9,8$$
Задание 11
Найдите наибольшее значение функции $$f(x)=e^{-x}-e^{-2x}$$ на отрезке [0;2].
Ответ: 0,25
Скрыть
Пусть $$e^{-x}=y$$. Получим $$f(y)=y-y^2$$.
Тогда $$f'(y)=1-2y=0Rightarrow y=frac{1}{2}$$
При этом $$y=frac{1}{2}$$ — точка максимума $$Rightarrow f_{max}(y)=frac{1}{2}-frac{1}{2}cdotfrac{1}{2}=0,25$$.
Задание 12
А) Решите уравнение $$log_{0,5sin2x}(sin x)cdotlog_{0,5sin2x}(cos x)=0,25$$
Б) Найдите все корни уравнения, принадлежащие промежутку $$(2,25pi;4,5pi]$$
Ответ: А)$$frac{pi}{4}+2pi n,nin Z$$ Б)$$frac{17pi}{4}$$
Задание 13
Точка F — середина бокового ребра SA правильной четырехугольной пирамиды SABCD, точка М лежит на стороне основания АВ. Плоскость $$beta$$ проходит через точки F и М параллельно боковому ребру SC.
А) Плоскость $$beta$$ пересекает ребро SD в точке К. Докажите, что ВМ : МА = DK : KS.
Б) Пусть ВМ : МА = 3 : 1. Найдите отношение объемов многогранников, на которые плоскость $$beta$$ разбивает пирамиду.
Ответ: $$frac{25}{39}$$
Задание 14
Решите неравенство: $$log_5 x+log_xfrac{x}{3}<frac{log_5 xcdot(2-log_3 x)}{log_3 x}$$
Ответ: $$(0;frac{sqrt{5}}{5}),(1;3)$$
Задание 15
У инвестора есть 50 млн рублей. Часть денег он планирует вложить в проект. Если он вложит в проект $$frac{5x^2}{144}$$ млн рублей, то по завершении проекта он получит $$x$$ млн рублей. Невложенные в проект деньги инвестор планирует разместить на банковском счете. По завершении проекта инвестор получит из банка сумму, увеличенную на 20%.
Инвестор собирается распределить деньги так, чтобы общая сумма полученных им денег от вложения в проект и размещения в банке оказалась наибольшей. Прибыль от проекта — это разность между полученной от проекта и вложенной в проект суммами денег.
Найдите сколько процентов составит прибыль от проекта от вложенной в него суммы денег.
Ответ: 140
Задание 16
В остроугольном треугольнике АВС на высоте AD взята точка М, а на высоте ВР — точка N так, что углы ВМС и ANC — прямые. Известно, что $$angle MCN = 30^{circ}, MN = 4 + 2sqrt{3}$$.
А) Докажите, что $$frac{MD^2}{BDcdot CD}=1$$.
Б) Найдите длину биссектрисы CL треугольника MCN.
Ответ: $$7+4sqrt{3}$$
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых уравнение:
$$3cdotsqrt[5]{x+2}=16a^2cdotsqrt[5]{32x+32}+sqrt[10]{x^2+3x+2}$$
имеет единственное решение.
Ответ: $$(-infty;-frac{1}{2sqrt{2}}],[-frac{1}{4};frac{1}{4}],[frac{1}{2sqrt{2}};infty)$$
Задание 18
На доске написано $$N$$ различных натуральных чисел, каждое из которых не превосходит 33. Для каждых двух написанных чисел $$a$$ и $$b$$ таких, что $$a < b$$, ни одно из написанных чисел не делится на $$b — a$$ и ни одно из написанных чисел не является делителем числа $$b — a$$.
А) Могли ли на доске быть написаны числа 11, 12, 13?
Б) Среди написанных на доске чисел есть число 15. Может ли $$N$$ быть равным 18?
В) Найдите наибольшее значение $$N$$?
Ответ: А) нет, Б) нет, В) 11
А. Ларин. Тренировочный вариант № 407.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Точка F — середина бокового ребра SA правильной четырехугольной пирамиды SABCD, точка М лежит на стороне основания AB. Плоскость β проходит через точки F и М параллельно боковому ребру SC.
а) Плоскость β пересекает ребро SD в точке К. Докажите, что
б) Пусть Найдите отношение объемов многогранников, на которые плоскость β разбивает пирамиду.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
У инвестора есть 50 миллионов рублей. Часть денег он планирует вложить в проект. Если он вложит в проект млн руб., то по завершении проекта он получит x млн руб. Невложенные в проект деньги инвестор планирует разместить на банковском счете. По завершении проекта инвестор получит из банка сумму, увеличенную на 20%.
Инвестор собирается распределить деньги так, чтобы общая сумма полученных им денег от вложения в проект и размещения в банке оказалась наибольшей. Прибыль от проекта — это разность между полученной от проекта и вложенной в проект суммами денег. Найдите, сколько процентов составит прибыль от проекта от вложенной в него суммы денег.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В остроугольном треугольнике ABC на высоте AD взята точка M, а на высоте BP точка N так, что углы BMC и ANC — прямые. Известно, что и
а) Докажите, что
б) Найдите длину биссектрисы CL треугольника MCN.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых уравнение:
имеет единственное решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
На доске написано N различных натуральных чисел, каждое из которых не превосходит 33. Для каждых двух написанных чисел a и b таких, что ни одно из написанных чисел не делится на
и ни одно из написанных чисел не является делителем числа
а) Могли ли на доске быть написаны числа 11, 12, 13?
б) Среди написанных на доске чисел есть число 15. Может ли N быть равным 18?
в) Найдите наибольшее значение N.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Вариант №407 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, а также полным видео разбором, который опубликован на сайте 19 ноября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
вариант-407-ларин-егэ2023
Видео решение заданий вариант 407 Ларин ЕГЭ 2023
1. Площадь треугольника АВС равна 30. На стороне АС взята точка D так, что AD : DC = 2 : 3. Длина перпендикуляра DE, проведенного к стороне ВС, равна 9. Найдите ВС.
2. Найдите объем правильной шестиугольной пирамиды, если ее боковое ребро равно 13, а радиус окружности, описанной около основания, равен 11.
3. Вероятность того, что в будний день число посетителей торгового центра превысит 2000 человек, равна 0,34. Вероятность того, что число посетителей торгового центра превысит 2500 человек, равна 0,18. Найдите вероятность того, что в случайно выбранный будний день число посетителей окажется от 2001 до 2500 человек.
4. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,6. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет только одну партию из двух.
9. Пункт С расположен в 12 км от пункта В вниз по течению. Рыбак отправился на лодке в пункт С из пункта А, расположенного выше пункта В. Через 4 часа он прибыл в С, а на обратный путь затратил 6 часов. В другой раз рыбак воспользовался моторной лодкой, увеличив тем самым собственную скорость передвижения относительно воды втрое, и дошел от А до В за 45 минут. Найдите скорость течения (в км/ч), считая ее постоянной.
13. Точка F – середина бокового ребра SA правильной четырехугольной пирамиды SABCD, точка М лежит на стороне основания АВ. Плоскость β проходит через точки F и М параллельно боковому ребру SC. А) Плоскость β пересекает ребро SD в точке К. Докажите, что ВМ : МА = DK : KS. Б) Пусть ВМ : МА = 3 : 1. Найдите отношение объемов многогранников, на которые плоскость β разбивает пирамиду.
18. На доске написано N различных натуральных чисел, каждое из которых не превосходит 33. Для каждых двух написанных чисел а и b таких, что а < b, ни одно из написанных чисел не делится на b – a и ни одно из написанных чисел не является делителем числа b – a. А) Могли ли на доске быть написаны числа 11, 12, 13? Б) Среди написанных на доске чисел есть число 15. Может ли N быть равным 18? В) Найдите наибольшее значение N?
Ответы для варианта
Сборник ЕГЭ 2023 Ященко математика 11 класс профиль
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Регистрация Форум Текущее время: 10 мар 2023, 16:19 Сообщения без ответов | Активные темы Страница 1 из 2 [ Сообщений: 16 ] На страницу 1, 2 След. Начать новую тему»> Ответить Тренировочный вариант №407
Тренировочный вариант №407
Страница 1 из 2 [ Сообщений: 16 ] На страницу 1, 2 След. Текущее время: 10 мар 2023, 16:19 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.
| 3471 | а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. |
а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12 | |
| 3470 | В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней |
В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13 | |
| 3469 | Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x). |
Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14 |
|
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN |
На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ |
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3466 | Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) |
Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6 | |
| 3465 | Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? |
Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9 | |
| 3464 | а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. |
а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12 | |
| 3463 | SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 |
SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13 | |
| 3462 | Решите неравенство 2^(x/(x+1))-2^((5x+3)/(x+1))+8<=2^((2x)/(x+1)) |
Решите неравенство 2 x/x+1 -2 5x+3 / x+1 +8 <= 2 2x/x+1 ! Тренировочный вариант 398 от Ларина Задание 14 |
|

Показана страница 1 из 89
Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |






 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 


