Задание 1
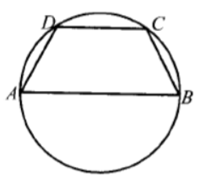
Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании трапеции равен 60°, большее основание равно 18. Найдите радиус описанной окружности этой трапеции
Ответ: 9
Скрыть
Рассмотрим треугольник ADC, в котором AD=DC по условию задания, а угол D равен:
$$angle D=frac{360^{circ}-angle A-angle B}{2}=frac{360^{circ}-60^{circ}-60^{circ}}{2}=120^{circ}.$$
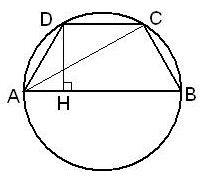
Найдем сторону AD=DC из треугольника ADH:
$$AD=frac{AH}{cos60^{circ}}=frac{(AB-DC):2}{0,5}=AB-DC$$
$$2AD=AB=18$$
$$AD=frac{18}{2}=9$$
Радиус описанной окружности можно найти по теореме синусов для треугольника ADC, имеем:
$$R=frac{AD}{2sinangle DCA}=frac{9}{2cdotsin30^{circ}}=9.$$
Задание 2
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен $$sqrt{3},$$ а высота равна 2. Найдите площадь боковой поверхности призмы.
Ответ: 24
Скрыть
В основании правильной четырёхугольной призмы лежит правильный шестиугольник:
Найдем сторону этого шестиугольника из треугольника, у которого известен угол 120 градусов между сторонами и противолежащая сторона $$D = 2sqrt{3}.$$ По теореме косинусов можно записать:
$$D^2=a^2+a^2-2cdot acdot acdotcos120$$
$$(2sqrt{3})^2=2a^2-2a^2cdot(-frac{1}{2})$$
$$12=3a^2$$
$$a=2$$
Площадь боковой поверхности правильной шестиугольной призмы со стороной a = 2 и высотой h = 3, равна:
Площадь боковой поверхности правильной призмы со стороной a = 6 и высотой h = 2, равна:
$$S=6cdot acdot h=6cdot2cdot2=24$$
Задание 3
Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
Ответ: 0,01
Скрыть
Цифры меняются от 0 до 9, значит, совпадение трех последних цифр – это одно из $$m = 10$$ событий:
$$000, 111, 222, …, 999.$$
Всего возможных комбинаций из трех цифр $$n=10^3=1000.$$ Получаем значение искомой вероятности:
$$P=frac{m}{n}=frac{10}{1000}=0,01$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Пусть первое число — результат первого броска, второе — второго, третье — третьего. Тогда возможные варианты превысить число 9 в сумме за три броска:
1 3…6 6 — четыре исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot4=frac{4}{216}$$
1 4…6 5 — три исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot3=frac{3}{216}$$
1 5…6 4 — два исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot2=frac{2}{216}$$
1 6 3 — один исход: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}=frac{1}{216}$$
Аналогично рассматривается с первой двойкой (15 исходов всего $$frac{15}{216}$$), тройкой — 21 исход $$frac{21}{216}$$
4 1…5 6 — 5 исходов: $$frac{5}{216}$$
4 1…5 5 — 5 исходов: $$frac{5}{216}$$
4 2…5 4 — 4 исхода: $$frac{4}{216}$$
4 3…5 3 — 3 исхода: $$frac{3}{216}$$
4 4…5 2 — 2 исхода: $$frac{2}{216}$$
4 5 1 — 1 исход: $$frac{1}{216}$$
Заметьте, что 4 6 не рассматриваем уже, т.к. тогда на втором броске уже будет больше 9.
Аналогично с пятеркой: 18 исходов: $$frac{18}{216}$$ и шестеркой: 15 исходов: $$frac{15}{216}$$
В итоге получили: $$10+15+21+20+18+15=99$$ исходов с вероятность $$frac{1}{216}$$
$$P(A)=frac{99}{216}=0,458(3)approx0,46$$
Задание 5
Решите уравнение $$sqrt{2log_8(-x)}-log_8sqrt{x^2}=0.$$ Если уравнение имеет несколько корней, в ответе укажите их сумму.
Ответ: -65
Скрыть
Учтём, что $$log_8sqrt{x^2}=log_8|x|.$$ Так как есть $$log_8(-x),$$ то $$-x>0Rightarrow x<0.$$ Тогда $$log_8|x|=log_8(-x)$$
Пусть $$log_8(-x)=y.$$ Получим: $$sqrt{2y}=yRightarrowleft{begin{matrix} 2y=y^2\ ygeq0 end{matrix}right.Leftrightarrowleft[begin{matrix} y=0\ y=2 end{matrix}right.$$
Обратная замена:
$$left[begin{matrix} log_8(-x)=0\ log_8(-x)=2 end{matrix}right.Leftrightarrowleft[begin{matrix} -x=1\ -x=64 end{matrix}right.Leftrightarrowleft[begin{matrix} x=-1\ x=-64 end{matrix}right.$$
Сумма корней $$(-1)+(-64)=-65.$$
Задание 6
Найдите значение выражения $$frac{p(b)}{p(frac{1}{b})},$$ если $$p(b)=(b+frac{3}{b})(3b+frac{1}{b})$$ при $$bneq0$$
Ответ: 1
Скрыть
$$frac{p(b)}{p(frac{1}{b})}=frac{(b+frac{3}{b})(3b+frac{1}{b})}{(frac{1}{b}+3b)(frac{3}{b}+b)}=1$$
Задание 7
Прямая $$y=x+7$$ является касательной к графику функции $$y=ax^2-15x+15.$$ Найдите $$a.$$
Ответ: 8
Скрыть
Приравниваем производные и функции:
$$left{begin{matrix} (x+7)’=(ax^2-15x+15)’\ x+7=ax^2-15x+15 end{matrix}right.Leftrightarrowleft{begin{matrix} 1=2ax-15\ ax^2-16x+8 end{matrix}right.Leftrightarrowleft{begin{matrix} x=frac{8}{a}\ acdotfrac{64}{a^2}-frac{16cdot8}{a}+8=0 end{matrix}right.$$
$$frac{64}{a}-frac{128}{a}=-8Rightarrow -frac{64}{a}=-8Rightarrow a=8$$
Задание 8
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории, кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна $$P=m(frac{v^2}{L}-g),$$ где $$m$$ — масса воды в килограммах, $$v$$ — скорость движения ведёрка в м/с, $$L$$ — длина верёвки в метрах, $$g$$ — ускорение свободного падения (считайте, что $$g = 10$$ м/с2). С какой минимальной скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 0,625 м? Ответ выразите в м/с.
Ответ: 2,5
Скрыть
Чем выше скорость вращения, тем больше давление воды ⇒ нужно найти минимальную скорость, давление должно быть равно 0.
$$m(frac{v_2}{0,625}-10)=0$$
Произведение равно 0, когда один из множителей равен 0. m ≠ 0
$$frac{v_2}{0,625}-10=0$$
$$frac{v_2}{0,625}=10$$
$$v_2 = 10cdot0,625$$
$$v_2 = 6,25$$
$$v = 2,5$$
Задание 9
Трем рабочим поручили изготовить одинаковые партии деталей. Производительность первого рабочего была на 10% меньше, чем у второго, и на 20% больше, чем у третьего. Первым приступил к работе третий рабочий, спустя 6 минут начал свою работу первый рабочий и они закончили свои задания одновременно. На сколько минут позже третьего рабочего начал работать второй, если он свое задание выполнил на 2 минуты раньше, чем первый и третий рабочий?
Ответ: 7
Скрыть
Пусть производительность третьего рабочего $$x$$ раб/мин, тогда производительность первого рабочего — $$(x+0,2x)=1,2x$$ раб/мин, а производительность третьего считаем по пропорции
1,2x — 90%
пр.тр. — 100%
пр.тр. $$=frac{1,2xcdot100}{90}=frac{4x}{3}$$ — производительность третьего рабочего.
Всю работу примем за 1. Тогда время на выполнение работы первым рабочим $$frac{1}{1,2x}$$ минут, третьим — $$frac{1}{x}$$ минут. Первый рабочий выполнил работу на 6 минут быстрее третьего. Составим и решим уравнение:
$$frac{1}{x}-frac{1}{1,2x}=6$$
$$frac{6-5}{6x}=6$$
$$frac{1}{6x}=6$$
$$36x=1$$
$$x=frac{1}{36}$$ раб/мин — производительность третьего рабочего, значит, всю работу он выполнит за 36 минут.
$$frac{4}{3}cdotfrac{1}{36}=frac{1}{27}$$ раб/мин — производительность второго рабочего, значит, всю работу он выполнит за 27 минут.
$$36-27=9$$ минут — на столько дольше работу выполняет третий рабочий, чем второй.
Если второй выполнил работу на 2 минуты раньше третьего, то
$$9-2=7$$ минут — на столько позже третьего второй начал работу.
Задание 10
На рисунке изображен график функции $$f(x)=b+log_a(-frac{1}{x}),$$ где $$a, b$$ — целые числа. Найдите значение $$x,$$ при котором $$f(x)=5.$$
Ответ: -0,25
Скрыть
График проходит через (-4;1) и (-1;3). Получим:
$$left{begin{matrix} 1=b+log_afrac{1}{4}\ 3=b+log_a 1 end{matrix}right.Leftrightarrowleft{begin{matrix} log_afrac{1}{4}=-2\ b=3 end{matrix}right.Leftrightarrowleft{begin{matrix} a=2\ b=3 end{matrix}right.$$
Получили $$f(x)=3+log_2(-frac{1}{x})=5Rightarrow log_2(-frac{1}{x})=2Rightarrow -frac{1}{x}=4Rightarrow x=-0,25$$
Задание 11
Найдите наименьшее значение функции $$f(x)=3x^4+4x^3-12x^2-12$$ на отрезке $$[-0,5;2].$$
Ответ: -17
Скрыть
Найдем производную и приравняем ее к нулю
$$12x^3+12x^2−24x=0$$
$$x(12x^2+12x−24)=0$$
$$x=0$$
$$x=1$$
$$x=−2$$ – не попадет в промежуток
Проверяем методом интервалов точка 1 – точка минимума
$$f(1)=−17$$
Задание 12
А) Решите уравнение $$(-2cos^2x+sin x+1)cdotlog_{0,5}(-0,8cos x)=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-6pi;-4pi]$$
Ответ: А)$$frac{5pi}{6}+2pi n,nin Z$$ Б)$$-frac{31pi}{6}$$
Задание 13
Конус и полусфера имеют общее основание, радиус которого относится к высоте конуса как 1:3.
А) Докажите, что поверхность полусферы делит образующую конуса в отношении 4:1, считая от вершины конуса.
Б) Найдите площадь поверхности полусферы, находящейся внутри конуса, если радиус их общего основания равен 5.
Ответ: $$20pi$$
Задание 14
Решите неравенство: $$sqrt{2-log_{frac{1}{2}}x}cdotfrac{(x-1)(x+7)}{x+2}geq0$$
Ответ: $$left{frac{1}{4}right},[1;infty)$$
Задание 15
Строительство нового цеха по производству роботов-пылесосов стоит 300 млн рублей. Затраты на производство $$x$$ тыс. единиц продукции на такой линии равны $$0,1x^2+3x+100$$ млн рублей в год. Если продукцию продавать по цене $$р$$ тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит $$px-(0,1x^2+3x+100).$$ Когда цех будет построен, каждый год фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки цеха цена продукции $$p = 12$$ тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство цеха?
Ответ: 3
Задание 16
Дана равнобедренная трапеция ABCD. На боковой стороне АВ и большем основании AD взяты соответственно точки К и L так, что KL||CD и CK=DL.
А) Докажите, что $$angle BCK = angle AKL$$
Б) Найдите площадь трапеции ABCD, если $$KL = 12,DL = 2,5BK, S_{CDLK} = 26sqrt{6}$$
Ответ: $$frac{196sqrt{6}}{5}$$
Задание 17
Найдите все положительные значения параметра $$a,$$ при каждом из которых любое значение $$x$$ из отрезка $$[-1;1]$$ будет являться решением неравенства
$$3a^{2x}-16^x+2cdot(4a)^xgeq0$$
Ответ: $$[frac{4}{3};12]$$
Задание 18
В натуральном числе $$n$$ между всеми парами соседних цифр вставили одну и ту же цифру $$c.$$ Получилось число $$m,$$ которое делится на $$n.$$ Их частное равно $$k.$$
А) Может ли быть $$k = 10$$?
Б) Может ли быть $$k = 2$$?
В) Чему может быть равно наименьшее значение числа $$k$$?
Ответ: А) да, Б) нет, В) 6
А. Ларин. Тренировочный вариант № 404.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Конус и полусфера имеют общее основание, радиус которого относится к высоте конуса как 1 : 3.
а) Докажите, что поверхность полусферы делит образующую конуса в отношении 4 : 1, считая от вершины конуса.
б) Найдите площадь поверхности полусферы, находящейся внутри конуса, если радиус их общего основания равен 5.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Строительство нового цеха по производству роботов-пылесосов стоит 300 миллионов рублей. Затраты на производство x тысяч единиц продукции на такой линии равны млн руб. в год. Если продукцию продавать по цене p тыс. руб. за единицу, то прибыль фирмы (в млн руб.) за один год составит
млн руб. Когда цех будет построен, каждый год фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки цеха цена продукции p = 12 тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство цеха?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Дана равнобедренная трапеция ABCD. На боковой стороне AB и большем основании AD взяты соответственно точки K и L так, что прямые KL и CD параллельны и CK = DL.
а) Докажите, что
б) Найдите площадь трапеции АВСD, если
и
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все положительные значения параметра a, при каждом из которых любое значение x из отрезка [−1; 1] является решением неравенства
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
В натуральном числе n между всеми парами соседних цифр вставили одну и ту же цифру c. Получилось число m, которое делится на n. Их частное равно k.
а) Может ли быть k = 10?
б) Может ли быть k = 2?
в) Чему может быть равно наименьшее значение числа k?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.

Вариант №404 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, а также полным видео разбором, который опубликован на сайте 29 октября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать вариант с ответами
Тренировочный вариант 404 Ларина ЕГЭ 2023 по математике профиль
вариант404-ларин-егэ2023-ответ
1. Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании трапеции равен 60°, большее основание равно 18. Найдите радиус описанной окружности этой трапеции.
2. Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен корень из 3, а высота равна 2. Найдите площадь боковой поверхности призмы.
3. Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
4. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
9. Трем рабочим поручили изготовить одинаковые партии деталей. Производительность первого рабочего была на 10% меньше, чем у второго, и на 20% больше, чем у третьего. Первым приступил к работе третий рабочий, спустя 6 минут начал свою работу первый рабочий и они закончили свои задания одновременно. На сколько минут позже третьего рабочего начал работать второй, если он свое задание выполнил на 2 минуты раньше, чем первый и третий рабочий?
13. Конус и полусфера имеют общее основание, радиус которого относится к высоте конуса как 1:3. А) Докажите, что поверхность полусферы делит образующую конуса в отношении 4:1, считая от вершины конуса. Б) Найдите площадь поверхности полусферы, находящейся внутри конуса, если радиус их общего основания равен 5.
Видео решение заданий варианта 404 Ларин ЕГЭ 2023
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Материалы и статьи
Тренировочный вариант №404 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, а также полным видео разбором, который опубликован на сайте 29 октября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать вариант с ответами
Тренировочный вариант 404 Ларина ЕГЭ 2023 по математике профиль
1. Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании трапеции равен 60°, большее основание равно 18. Найдите радиус описанной окружности этой трапеции.
2. Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен корень из 3, а высота равна 2. Найдите площадь боковой поверхности призмы.
3. Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
4. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
9. Трем рабочим поручили изготовить одинаковые партии деталей. Производительность первого рабочего была на 10% меньше, чем у второго, и на 20% больше, чем у третьего. Первым приступил к работе третий рабочий, спустя 6 минут начал свою работу первый рабочий и они закончили свои задания одновременно. На сколько минут позже третьего рабочего начал работать второй, если он свое задание выполнил на 2 минуты раньше, чем первый и третий рабочий?
13. Конус и полусфера имеют общее основание, радиус которого относится к высоте конуса как 1:3. А) Докажите, что поверхность полусферы делит образующую конуса в отношении 4:1, считая от вершины конуса. Б) Найдите площадь поверхности полусферы, находящейся внутри конуса, если радиус их общего основания равен 5.
Видео решение заданий варианта 404 Ларин ЕГЭ 2023
Вам будет интересно:
Вариант Ларина 403 ЕГЭ 2023 по математике профиль решение с ответами
Метки: 2022-2023 учебный год варианты и ответы математика
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №404
|
||||
|
https://alexlarin.net/ege/2023/trvar404.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
404.17 Подробности: 404.16 Подробности: исправлено, спасибо уважаемому hpbhpb. Последний раз редактировалось OlegTheMath 29 окт 2022, 21:11, всего редактировалось 1 раз. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
OlegTheMath писал(а): 404.17 Подробности: 404.16 Подробности: У меня в 16-м: Подробности: |
|||
  |
||||
|
Ирина Васина |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
№18 Подробности: |
|||
  |
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
hpbhpb писал(а): OlegTheMath писал(а): 404.16 Подробности: У меня в 16-м: Подробности: Вы правы, уважаемый hpbhpb. |
|||
  |
||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
Ирина Васина писал(а): №18 Подробности: В пункте в) k должно быть целым. |
|||
  |
||||
|
woodyp3cker |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
404.12 Подробности: 404.13 Подробности: 404.14 Подробности: 404.17 Подробности: 404.18 Подробности: 404.16 Подробности: |
|||
  |
||||
|
rgg |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
12 б) 31π/6 |
|||
  |
||||
|
Ирина Васина |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
Владимiръ писал(а): Ирина Васина писал(а): №18 Подробности: В пункте в) k должно быть целым. Тогда 108/18? |
|||
  |
||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №404
|
|||
|
Ирина Васина писал(а): Владимiръ писал(а): Ирина Васина писал(а): №18 Подробности: В пункте в) k должно быть целым. Тогда 108/18? Верно, т.е. 6. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 8 |
|
Вы не можете начинать темы |
|
|
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.