Вариант 402 егэ математика профиль

Задание 1

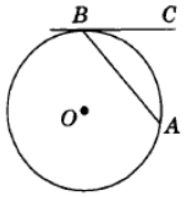
Хорда АВ стягивает дугу окружности в 40°. Найдите угол АВС между этой хордой и касательной к окружности, проведённой через точку В. Ответ дайте в градусах.

Ответ: 20

Скрыть
Угол между касательной и хордой равен половине дуги, заключённой между ними. Поэтому он равен 20.

Задание 2

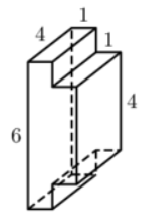
Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

Ответ: 84

Скрыть

Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь квадрата стороной 4:

$$S=2(4cdot1+6cdot1+4cdot6)+2(4cdot1+4cdot1+4cdot4)-2(4cdot4)=84$$

Задание 3

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 35% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 60% яиц высшей категории. Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Ответ: 0,2

Скрыть

Сначала определим вероятность того, что было куплено яйцо высшего сорта у первого или второго хозяйства. Пусть событие $$A$$ означает яйцо высшей категории, а события $$B_1$$ и $$B_2$$ определяют то, что яйцо высшей категории было произведено 1-м и 2-м хозяйством соответственно. Тогда условные вероятности $$P(A|B_1)$$ и $$P(A|B_2)$$ будут означать, вероятности закупки яйца первой категории у 1-го и 2-го хозяйства соответственно. По формуле полной вероятности найдем вероятность того, что будет куплено яйцо высшей категории, имеем:

$$P(AB_1)+B(AB_2)=P(A|B_1)cdot P(B_1)+P(A|B_2)cdot P(B_2)=$$

$$=0,35cdot P(B_1)+0,6cdot(1-P(B_1))=-0,25cdot P(B_1)+0,6$$

По условию задачи эта вероятность равна 0,55, следовательно, вероятность того, что купленное яйцо произведено в первом хозяйстве, равна:

$$P(B_1)=(0,55-0,6):(-0,25)=0,2$$.

Задание 4

Первый игральный кубик обычный, а на гранях второго кубика нет нечётных чисел, а чётные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали первый кубик?

Ответ: 0,2

Скрыть

Предположим, что бросали первый кубик. Тогда вероятность того, что в каком-то порядке выпали 4 и 6 очков, равна $$frac{1}{6}cdotfrac{1}{6}+frac{1}{6}cdotfrac{1}{6}=frac{1}{18}.$$

Теперь предположим, что бросали второй кубик. Поскольку на втором кубике числа 4 и 6 встречаются по два раза, вероятность того, что в каком-то порядке выпали 4 и 6 очков, равна $$frac{2}{6}cdotfrac{2}{6}+frac{2}{6}cdotfrac{2}{6}=frac{2}{9}.$$

Таким образом, искомая вероятность равна $$frac{frac{1}{18}}{frac{1}{18}+frac{2}{9}}=frac{1}{1+4}=0,2.$$

Задание 5

Решите уравнение $$sqrt[x]{64}-sqrt[x]{2^{3x+3}}+12=0.$$

Ответ: 3

Скрыть

$$sqrt[x]{64}-sqrt[x]{2^{3x+3}}+12=0$$

$$sqrt[x]{2^6}-sqrt[x]{2^{3x+3}}+12=0$$

$$(sqrt[x]{2^3})^2-2^{3}cdotsqrt[x]{2^3}+12=0$$

Замена: $$sqrt[x]{2^3}=y>0$$

$$y^2-8y+12=0Rightarrow (y-2)(y-6)=0Rightarrowleft[begin{matrix} y=2\ y=6 end{matrix}right.Leftrightarrowleft[begin{matrix} sqrt[x]{2^3}=2\ sqrt[x]{8}=6 end{matrix}right.Leftrightarrow x=3$$

Предполагается, что $$xin N,$$ поэтому $$sqrt[x]{8}=6$$ не имеет решений.

Задание 6

Найдите $$tg a,$$ если $$frac{5sin a-4cos a-2}{5sin a+cos a-3}=frac{2}{3}.$$

Ответ: 2,8

Скрыть

$$frac{5sin a-4cos a-2}{5sin a+cos a-3}=frac{2}{3}Leftrightarrow 15sin a-12cos a-6=10sin a+2cos a-6Rightarrow$$

$$Rightarrow5sin a=14cos a; |:cos aRightarrow 5tg a=14Rightarrow tg a=2,8$$

Задание 7

На рисунке изображен график производной $$y=f'(x)$$ функции $$f(x),$$ определенной на интервале $$(-4;8).$$ В какой точке отрезка $$[-3;1]$$ функция $$f(x)$$ принимает наименьшее значение?

Ответ: 1

Скрыть

На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наименьшее значение функции достигается на правой границе отрезка, т. е. в точке $$1.$$

Задание 8

При температуре $$0^{circ}$$ С рельс имеет длину $$l_0=10$$ м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t^{circ})=l_0(1+acdot t^{circ}),$$ где $$a=1,2cdot10^{-5}(^{circ} C)^{-1}$$ — коэффициент теплового расширения, $$t^{circ}$$ — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.

Ответ: 25

Скрыть

Необходимо рассчитать значение $$t,$$ при котором $$l(t)=l_0+3cdot10^{-3}$$ метров. Воспользуемся законом изменения длины рельс от температуры и выразим температуру, получим:

$$l_0+3cdot10^{-3}=l_0+l_0at$$

$$l_0at=3cdot10^{-3}$$

$$t=frac{3cdot10^{-3}}{l_0a}$$

$$t=frac{3cdot10^{-3}}{10cdot1,2cdot10^{-5}}=frac{3cdot10^{-3}}{12cdot10^{-5}}=25$$

Задание 9

По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 300 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 300 метрам.

На сколько километров в час скорость первого сухогруза меньше скорости второго?

Ответ: 4

Скрыть

Необходимо понять, как протекает данный процесс.

За точку, которая передвигается, принимается нос второго сухогруза. В таком случае он проходит сначала расстояние 300 метров, потом длину первого 120 метров, потом свою длину 80 метров, и только с этого момента начинает его опережать, то есть проходит еще 300 метров. В таком случае общий путь S=800 метров = 0,8 км.

Далее можно рассмотреть эту задачу немного иначе.

Раз один догоняет другого, мы можем представить, что первый стоит, а второй двигается к нему со скоростью, равной разности их скоростей, то есть то, что мы ищем.

Время представляем в часах: 0,2 часа и далее применяем стандартную формулу нахождения скорости через расстояние и время.

Получаем: $$v=frac{0,8}{0,2}=4$$

Задание 10

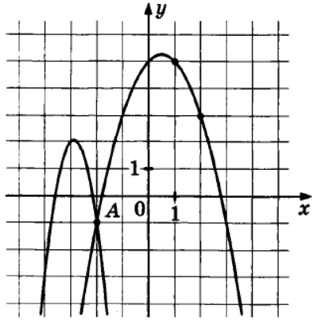
На рисунке изображены графики функций $$f(x)=-4x^2-23x-31$$ и $$g(x)=ax^2+bx+c,$$ которые пересекаются в точках А и В. Найдите абсциссу точки В.

Ответ: -6

Скрыть

Очевидно, что это правый график (у $$f(x)$$: $$a=-4$$ — сужение как у левого). $$g(x)$$ проходит через $$(2;3)$$ и $$(1;5).$$ Получим:

$$left{begin{matrix} 3=acdot2^2+bcdot2+5\ 5=acdot1^2+bcdot1+5 end{matrix}right.Leftrightarrowleft{begin{matrix} 4a+2b=-2\ a+b=0 end{matrix}right.Leftrightarrowleft{begin{matrix} 4a+2b=-2\ 4a+4b=0 end{matrix}right.Leftrightarrowleft{begin{matrix} 2b=2\ 4a+4=0 end{matrix}right.Leftrightarrow$$

$$Leftrightarrowleft{begin{matrix} b=1\ a=-1 end{matrix}right.$$

Получим $$g(x)=-x^2+x+5.$$ Тогда:

$$-4x^2-23x-31=-x^2+x+5Leftrightarrow 3x^2+24x+36=0Rightarrow x^2+8x+12=0Rightarrow$$

$$Rightarrowleft[begin{matrix} x=-2\ x=-6 end{matrix}right.$$

Тогда $$B_x=-6$$

Задание 11

Найдите наибольшее значение функции $$y=sqrt{2lg x-1}-lg x$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$${y}’=frac{1}{2sqrt{2lg x-1}}*frac{2}{xln 10}-frac{1}{xln10}=0$$

$$frac{1}{xln 10}(frac{1}{2sqrt{2lg x-1}})=0$$

$$left{begin{matrix}xneq 0 \sqrt{2lg x-1}=1(1)end{matrix}right.$$

$$(1): sqrt{2lg x-1}=1Leftrightarrow$$ $$2lg x-1leq 1Leftrightarrow$$ $$2lg x=2Leftrightarrow$$ $$lg x=1Leftrightarrow x=10$$

$$y(10)=y=sqrt{2lg 10-1}-lg 10=1-1=0$$

Задание 12

А) Решите уравнение $$cos x+sqrt{frac{2-sqrt{2}}{2}cdot(sin x+1)}=0$$

Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{11pi}{2};-4pi]$$

Ответ: А)$$-frac{pi}{2}+2pi n;frac{3pi}{4}+2pi n,nin Z$$ Б)$$-frac{9pi}{2};-frac{21pi}{4}$$

Задание 13

В правильной четырехугольной пирамиде SABCD точка L — середина бокового ребра SB. На ребре SA взята точка К так, что SK:KA=1:2.

А) Докажите, что плоскость DKL параллельна боковому ребру SC.

Б) Найдите площадь сечения пирамиды плоскостью DKL, если все ребра пирамиды равны 24.

Ответ: $$60sqrt{19}$$

Задание 14

Решите неравенство: $$log_5^2(x-8)-6log_5(sqrt{x-8})geq4-25cdot(x-8)cdot(log_5(x-8)-4)$$

Ответ: $$(8;frac{201}{25}],[633;infty)$$

Задание 15

Андрей планирует 19 декабря взять в банке кредит на 3 года в размере 2 029 000 рублей. Сотрудник банка предложил Андрею два различных плана погашения кредита, описание которых приведено в таблице.

План 1

— каждый январь долг возрастает на 8% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— кредит должен быть полностью погашен за три года тремя равными платежами.

План 2

— 1-го числа каждого месяца долг возрастает на 0,8% по сравнению с концом предыдущего месяца;
— со 2-го по 18-е число каждого месяца необходимо выплатить часть долга;
— 19-го числа каждого месяца со 2-го по 36-й долг должен быть меньше долга на 19-е число предыдущего месяца на одну и ту же сумму;
— к 19-му числу 36-го месяца кредит должен быть полностью погашен.

На сколько рублей меньше окажется общая сумма выплат Андрея банку по более выгодному плану погашения кредита?

Ответ: 32 668

Задание 16

В трапеции ABCD известно, что $$BC || AD, angle ABC=90^{circ}.$$ Прямая, перпендикулярная стороне CD, пересекает сторону АВ в точке М, а сторону CD — в точке N, DH — перпендикуляр, опущенный из точки D на прямую МС.

А) Докажите, что расстояние от точки А до прямой BN равно $$frac{BNcdot DH}{MC}$$

Б) Найдите отношение боковых сторон трапеции, если $$MC = 4, BN = 2$$

Ответ: $$1:2$$

Задание 17

Найдите все значения параметра $$a,$$ при каждом из которых уравнение

$$cossqrt{2pi ax-4x^2}+cos2sqrt{2pi ax-4x^2}=0$$

имеет ровно два решения.

Ответ: $$(-2;-frac{2}{3}),(frac{2}{3};2)$$

Задание 18

А) Уравнения $$ax^2+bx+c=0$$ и $$cx^2+bx+a=0$$ имеют корни, которые являются целыми числами. Коэффициенты уравнений являются натуральными числами (необязательно различными). Причем корни первого уравнения равны корням второго. Решите эти уравнения.

Б) Найдите квадратные уравнения $$ax^2+bx+c=0,$$ для которых коэффициенты $$a,b,c$$ являются корнями.

В) Три числа $$a,b,c$$ отличны от нуля. Квадратные уравнения

$$ax^2+bx+c=0$$

$$bx^2+cx+a=0$$

$$cx^2+ax+b=0$$

имеют общий корень. Решите эти уравнения.

Ответ: $$А)-1,$$ $$Б)-x^2-x=0,x^2+x-2=0,x^2-frac{1}{2}x-frac{1}{2}=0,ax^2+frac{1}{a}x+a=0,a^3+a+1=0,$$ $$В)left{1,frac{c}{a}right},left{1,frac{a}{b}right}left{1,frac{b}{c}right}$$

Источник

ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 402

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ на диагонали BD₁ отмечена точка N так, что Точка O  — середина отрезка CB₁.

а)  Докажите, что прямая NO проходит через точку A.

б)  Найдите объём параллелепипеда ABCDA₁B₁C₁D₁, если длина отрезка NO равна расстоянию между прямыми BD₁ и CB₁ и равна

Решите неравенство:

В июле 2026 года планируется взять кредит на три года в размере 500 тыс. руб. Условия его возврата таковы:

— каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

— платежи в 2027 и в 2028 годах должны быть по 100 тыс. руб.;

— к июлю 2029 года долг должен быть выплачен полностью.

Найдите сумму всех платежей после полного погашения кредита.

На стороне острого угла с вершиной A отмечена точка B. Из точки B на биссектрису и другую сторону угла опущены перпендикуляры BC и BD соответственно.

а)  Докажите, что

б)  Прямые AC и BD пересекаются в точке T найдите отношение AT:TC, если

Найдите все значения a, при каждом из которых уравнение

имеет ровно два различных корня.

На доске написано N различных натуральных чисел, каждое из которых не превосходит 159. Для любых двух написанных на доске чисел a и b, таких, что a < b, ни одно из написанных чисел не делится на b – a, и ни одно из написанных чисел не является делителем числа b – a.

а)  Могли ли на доске быть написаны какие-то два числа из чисел 28, 29 и 30?

б)  Среди написанных на доске чисел есть 13. Может ли N быть равно 20?

в)  Найдите наибольшее значение N.

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

ларин егэ 2023 математика профильный уровень

Новый тренировочный вариант №402 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, а также полным видео разбором, который опубликован на сайте 15 октября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.

Скачать этот вариант с ответами

Скачать предыдущий вариант Ларина

Тренировочный вариант 402 Ларина ЕГЭ 2023 по математике профиль

вариант-402-ларин-егэ2023

Полный разбор варианта

1.Хорда АВ стягивает дугу окружности в 40°. Найдите угол АВС между этой хордой и касательной к окружности, проведённой через точку В. Ответ дайте в градусах.

Ответ: 20

2.Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

Ответ: 84

3.Агрофирма закупает куриные яйца в двух домашних хозяйствах. 35% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 60% яиц высшей категории, Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Ответ: 0,2

4.Первый игральный кубик обычный, а на гранях второго кубика нет нечётных чисел, а чётные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком‐то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали первый кубик?

Ответ: 0,2

9.По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 300 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 300 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Ответ: 4

13.В правильной четырехугольной пирамиде SABCD точка L – середина бокового ребра SB. На ребре SA взята точка К так, что SK:KА=1:2. А) Докажите, что плоскость DKL параллельна боковому ребру SC. Б) Найдите площадь сечения пирамиды плоскостью DKL, если все ребра пирамиды равны 24.

15.Андрей планирует 19 декабря взять в банке кредит на 3 года в размере 2 029 000 рублей. Сотрудник банка предложил Андрею два различных плана погашения кредита, описание которых приведено в таблице.

Ответы для варианта:

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Регистрация
Вход

Форум
Поиск
FAQ   alexlarin.net

Текущее время: 10 мар 2023, 16:19
Часовой пояс: UTC + 3 часа

Сообщения без ответов | Активные темы

Страница 1 из 3 [ Сообщений: 27 ] На страницу 1, 2, 3 След.

Начать новую тему»>

Ответить

Тренировочный вариант №402

Для печати

Предыдущая тема | Следующая тема

Тренировочный вариант №402

Автор

Сообщение

Заголовок сообщения: Тренировочный вариант №402

Добавлено: 15 окт 2022, 10:14

Администратор

Центр пользователя

Зарегистрирован: 10 июн 2010, 15:00
Сообщений: 6118

https://alexlarin.net/ege/2023/trvar402.html

Владимiръ

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 15 окт 2022, 22:19

Центр пользователя

Зарегистрирован: 08 мар 2017, 23:11
Сообщений: 545
Откуда: Пущино

Задача 18
Надеюсь, я правильно понял условие.

Подробности:

Вложения:

Ответ 402-18.pdf [45.75 KIB]

Скачиваний: 6182

jav

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 16 окт 2022, 08:21

Центр пользователя

Зарегистрирован: 12 сен 2018, 18:09
Сообщений: 26

№402-17 2/3<|a|<2
№402-18 в) х=1 общий корень, с/а, а/в, в/с корни при условии а+в+с =0.

rgg

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 16 окт 2022, 21:33

Центр пользователя

Зарегистрирован: 29 окт 2014, 22:13
Сообщений: 3763

Завидую я тем, кто решает задания 18.
Это — удивительные люди!

lavrik

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 16 окт 2022, 22:13

Центр пользователя
Сайт

Зарегистрирован: 18 апр 2012, 17:33
Сообщений: 30
Откуда: Санкт-Петербург

12 a) -pi/2+2pik, 3pi/4+2pik.
б) -21pi/4, -9pi/2.
13.60sqrt{19}.

rgg

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 17 окт 2022, 08:00

Центр пользователя

Зарегистрирован: 29 окт 2014, 22:13
Сообщений: 3763

lavrik писал(а):

12 a) -pi/2+2pik, 3pi/4+2pik.
б) -21pi/4, -9pi/2.
13.60sqrt{19}.

Ответы по номеру 12 у меня такие же. А 13-ю задачу пока не рассматривал.

OlegTheMath

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 17 окт 2022, 22:30

Центр пользователя

Зарегистрирован: 06 май 2012, 21:09
Сообщений: 66

lavrik писал(а):

12 a) -pi/2+2pik, 3pi/4+2pik.
б) -21pi/4, -9pi/2.
13.60sqrt{19}.

12 совпадает, а в 13 по первому вычислению 30sqrt{19}
14.

Подробности:

dts

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 18 окт 2022, 15:47

Центр пользователя

Зарегистрирован: 18 окт 2022, 15:43
Сообщений: 1

16 б) 1/2

Последний раз редактировалось dts 18 окт 2022, 21:25, всего редактировалось 1 раз.

netka

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 18 окт 2022, 16:04

Центр пользователя

Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань

OlegTheMath писал(а):

12 совпадает, а в 13 по первому вычислению 30sqrt{19}
14.

Подробности:

в 14 ответ такой же, а в 13 согласна с lavrik

lavrik

Заголовок сообщения: Re: Тренировочный вариант №402

Добавлено: 19 окт 2022, 00:38

Центр пользователя
Сайт

Зарегистрирован: 18 апр 2012, 17:33
Сообщений: 30
Откуда: Санкт-Петербург

rgg писал(а):

Завидую я тем, кто решает задания 18.
Это — удивительные люди!

Спасибо, так гораздо лучше, чем изначально.

Показать сообщения за: Сортировать по:

Страница 1 из 3 [ Сообщений: 27 ] На страницу 1, 2, 3 След.

Текущее время: 10 мар 2023, 16:19 | Часовой пояс: UTC + 3 часа

Удалить cookies форума | Наша команда | Вернуться наверх

Кто сейчас на форуме

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 8

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Найти:

Перейти:

Источник

№ 08499
Скачать
Формулы
Ответы
Решения
Критерии
Демо
Обсуждения

Просмотр

Образцы заданий ПОЛУЧЕНЫ ИЗ ОТКРЫТЫХ ИСТОЧНИКОВ в Интернете и

ПУБЛИКУЮТСЯ ПОСЛЕ окончания ЭКЗАМЕНА в ознакомительных целях!

Решения

Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

ВХОД	РЕГИСТРАЦИЯ
*бесплатно, в один клик!

Источник

: ЕГЭ по математике профиль

Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2021 из различных источников.

Тренировочные варианты ЕГЭ 2021 по математике (профиль)

Связанные страницы:

Незнайка → ЕГЭ → Математика

Математика Базовый уровень

Варианты профильного уровня ЕГЭ по математике адаптированы под новую демоверсию ЕГЭ 2016. Базовый уровень остался без изменения по сравнению с прошлым годом.

Пока у нас нет готовых решений к каждому из заданий к ЕГЭ по математике базового и профильного уровней, зато сайт позволяет удобно проверить тестовую часть. Никаких диснейлендов, все просто и понятно. Ничего лишнего. Свои решения заданий пишите в комментариях, обсуждайте их друг с другом.

Мы ведем статистку по пройденным тестам, храним каждый бит информации на сервере, так что советуем вам зарегистрироваться, чтобы следить за своим прогрессом.

Старательным Незнайка обязательно поможет!)

Тренировочные варианты профильного ЕГЭ 2022 по математике с ответами.admin2022-04-17T20:59:36+03:00

Тренировочный вариант №172 профильного ЕГЭ (новый формат).
Тренировочный вариант №171 профильного ЕГЭ (новый формат).
Тренировочный вариант №170 профильного ЕГЭ (новый формат).
Тренировочный вариант №169 профильного ЕГЭ (новый формат).
Тренировочный вариант №168 профильного ЕГЭ (новый формат).
Тренировочный вариант №167 профильного ЕГЭ (новый формат).
Тренировочный вариант №166 профильного ЕГЭ (новый формат).
Тренировочный вариант №165 профильного ЕГЭ (новый формат).
Тренировочный вариант №164 профильного ЕГЭ (новый формат).
Тренировочный вариант №163 профильного ЕГЭ (новый формат).
Тренировочный вариант №162 профильного ЕГЭ (новый формат).
Тренировочный вариант №161 профильного ЕГЭ (новый формат).
Тренировочный вариант №160 профильного ЕГЭ (новый формат).
Тренировочный вариант №159 профильного ЕГЭ (новый формат).
Тренировочный вариант №158 профильного ЕГЭ (новый формат).
Тренировочный вариант №157 профильного ЕГЭ (новый формат).
Тренировочный вариант №156 профильного ЕГЭ (новый формат).
Тренировочный вариант №155 профильного ЕГЭ (новый формат).
Тренировочный вариант №154 профильного ЕГЭ (новый формат).
Тренировочный вариант №153 профильного ЕГЭ (новый формат).
Тренировочный вариант №152 профильного ЕГЭ (новый формат).
Тренировочный вариант №151 профильного ЕГЭ (новый формат).
Тренировочный вариант №150 профильного ЕГЭ (новый формат).
Тренировочный вариант №149 профильного ЕГЭ (новый формат).
Тренировочный вариант №148 профильного ЕГЭ (новый формат).
Тренировочный вариант №147 профильного ЕГЭ (новый формат).
Тренировочный вариант №146 профильного ЕГЭ (новый формат).
Тренировочный вариант №145 профильного ЕГЭ (новый формат).
Тренировочный вариант №144 профильного ЕГЭ (новый формат).
Тренировочный вариант №143 профильного ЕГЭ (новый формат).
Тренировочный вариант №142 профильного ЕГЭ (новый формат).
Тренировочный вариант №141 профильного ЕГЭ (новый формат).
Тренировочный вариант №140 профильного ЕГЭ (новый формат) (с видео-разбором).

Тренировочный вариант №139 профильного ЕГЭ.
Тренировочный вариант №138 профильного ЕГЭ.
Тренировочный вариант №137 профильного ЕГЭ.
Тренировочный вариант №136 профильного ЕГЭ.
Тренировочный вариант №135 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №134 профильного ЕГЭ.
Тренировочный вариант №133 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №132 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №131 профильного ЕГЭ.
Тренировочный вариант №130 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №129 профильного ЕГЭ.
Тренировочный вариант №128 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №127 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №126 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №125 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №124 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №123 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №122 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №121 профильного ЕГЭ.
Тренировочный вариант №120 профильного ЕГЭ.
Тренировочный вариант №119 профильного ЕГЭ.
Тренировочный вариант №118 профильного ЕГЭ.
Тренировочный вариант №117 профильного ЕГЭ.
Тренировочный вариант №116 профильного ЕГЭ.
Тренировочный вариант №115 профильного ЕГЭ.
Тренировочный вариант №114 профильного ЕГЭ.
Тренировочный вариант №113 профильного ЕГЭ.
Тренировочный вариант №112 профильного ЕГЭ.
Тренировочный вариант №111 профильного ЕГЭ.
Тренировочный вариант №110 профильного ЕГЭ.
Тренировочный вариант №109 профильного ЕГЭ.
Тренировочный вариант №108 профильного ЕГЭ.
Тренировочный вариант №107 профильного ЕГЭ.
Тренировочный вариант №106 профильного ЕГЭ.
Тренировочный вариант №105 профильного ЕГЭ.
Тренировочный вариант №104 профильного ЕГЭ.
Тренировочный вариант №103 профильного ЕГЭ.
Тренировочный вариант №102 профильного ЕГЭ.
Тренировочный вариант №101 профильного ЕГЭ.
Тренировочный вариант №100 профильного ЕГЭ.
Тренировочный вариант №99 профильного ЕГЭ.
Тренировочный вариант №98 профильного ЕГЭ.
Тренировочный вариант №97 профильного ЕГЭ.
Тренировочный вариант №96 профильного ЕГЭ.
Тренировочный вариант №95 профильного ЕГЭ.
Тренировочный вариант №94 профильного ЕГЭ.
Тренировочный вариант №93 профильного ЕГЭ.
Тренировочный вариант №92 профильного ЕГЭ.
Тренировочный вариант №91 профильного ЕГЭ.

Тренировочный вариант №90 профильного ЕГЭ.
Тренировочный вариант №89 профильного ЕГЭ.
Тренировочный вариант №88 профильного ЕГЭ.
Тренировочный вариант №87 профильного ЕГЭ.
Тренировочный вариант №86 профильного ЕГЭ.
Тренировочный вариант №85 профильного ЕГЭ.
Тренировочный вариант №84 профильного ЕГЭ.
Тренировочный вариант №83 профильного ЕГЭ.
Тренировочный вариант №82 профильного ЕГЭ.
Тренировочный вариант №81 профильного ЕГЭ.
Тренировочный вариант №80 профильного ЕГЭ.
Тренировочный вариант №79 профильного ЕГЭ.
Тренировочный вариант №78 профильного ЕГЭ.
Тренировочный вариант №77 профильного ЕГЭ.
Тренировочный вариант №76 профильного ЕГЭ.
Тренировочный вариант №75 профильного ЕГЭ.
Тренировочный вариант №74 профильного ЕГЭ.
Тренировочный вариант №73 профильного ЕГЭ.
Тренировочный вариант №72 профильного ЕГЭ.
Тренировочный вариант №71 профильного ЕГЭ.
Тренировочный вариант №70 профильного ЕГЭ.
Тренировочный вариант №69 профильного ЕГЭ.
Тренировочный вариант №68 профильного ЕГЭ.
Тренировочный вариант №67 профильного ЕГЭ.
Тренировочный вариант №66 профильного ЕГЭ.
Тренировочный вариант №65 профильного ЕГЭ.
Тренировочный вариант №64 профильного ЕГЭ.
Тренировочный вариант №63 профильного ЕГЭ.
Тренировочный вариант №62 профильного ЕГЭ.
Тренировочный вариант №61 профильного ЕГЭ.
Тренировочный вариант №60 профильного ЕГЭ.
Тренировочный вариант №59 профильного ЕГЭ.
Тренировочный вариант №58 профильного ЕГЭ.
Тренировочный вариант №57 профильного ЕГЭ.
Тренировочный вариант №56 профильного ЕГЭ.
Тренировочный вариант №55 профильного ЕГЭ.
Тренировочный вариант №54 профильного ЕГЭ.
Тренировочный вариант №53 профильного ЕГЭ.
Тренировочный вариант №52 профильного ЕГЭ.
Тренировочный вариант №51 профильного ЕГЭ.
Тренировочный вариант №50 профильного ЕГЭ.
Тренировочный вариант №49 профильного ЕГЭ.
Тренировочный вариант №48 профильного ЕГЭ.
Тренировочный вариант №47 профильного ЕГЭ.
Тренировочный вариант №46 профильного ЕГЭ.
Тренировочный вариант №45 профильного ЕГЭ.
Тренировочный вариант №44 профильного ЕГЭ.
Тренировочный вариант №43 профильного ЕГЭ.
Тренировочный вариант №42 профильного ЕГЭ.
Тренировочный вариант №41 профильного ЕГЭ.
Тренировочный вариант №40 профильного ЕГЭ.
Тренировочный вариант №39 профильного ЕГЭ.
Тренировочный вариант №38 профильного ЕГЭ.
Тренировочный вариант №37 профильного ЕГЭ.
Тренировочный вариант №36 профильного ЕГЭ.
Тренировочный вариант №35 профильного ЕГЭ.
Тренировочный вариант №34 профильного ЕГЭ.
Тренировочный вариант №33 профильного ЕГЭ.
Тренировочный вариант №32 профильного ЕГЭ.
Тренировочный вариант №31 профильного ЕГЭ.
Тренировочный вариант №30 профильного ЕГЭ.
Тренировочный вариант №29 профильного ЕГЭ.
Тренировочный вариант №28 профильного ЕГЭ.
Тренировочный вариант №27 профильного ЕГЭ.
Тренировочный вариант №26 профильного ЕГЭ.
Тренировочный вариант №25 профильного ЕГЭ.
Тренировочный вариант №24 профильного ЕГЭ.
Тренировочный вариант №23 профильного ЕГЭ.
Тренировочный вариант №22 профильного ЕГЭ.
Тренировочный вариант №21 профильного ЕГЭ.
Тренировочный вариант №20 профильного ЕГЭ.
Тренировочный вариант №19 профильного ЕГЭ.
Тренировочный вариант №18 профильного ЕГЭ.
Тренировочный вариант №17 профильного ЕГЭ.
Тренировочный вариант №16 профильного ЕГЭ.
Тренировочный вариант №15 профильного ЕГЭ.
Тренировочный вариант №14 профильного ЕГЭ.
Тренировочный вариант №13 профильного ЕГЭ.
Тренировочный вариант №12 профильного ЕГЭ.
Тренировочный вариант №11 профильного ЕГЭ.
Тренировочный вариант №10 профильного ЕГЭ.
Тренировочный вариант №9 профильного ЕГЭ.
Тренировочный вариант №8 профильного ЕГЭ.
Тренировочный вариант №7 профильного ЕГЭ.
Тренировочный вариант №6 профильного ЕГЭ.
Тренировочный вариант №5 профильного ЕГЭ.
Тренировочный вариант №4 профильного ЕГЭ.
Тренировочный вариант №3 профильного ЕГЭ.
Тренировочный вариант №2 профильного ЕГЭ.
Тренировочный вариант №1 профильного ЕГЭ.

Чтобы сдать профильное ЕГЭ по математике больше чем на 27 баллов, придётся усердно поработать. Важно не просто прорешать все возможные варианты с ФИПИ и Решу ЕГЭ, важно иметь полное системное представление о математике. Данные тренировочные варианты помогут вам проверить свои знания на практике, получить представление о трудностях на экзамене. Тренировочные варианты содержат задания разных уровней сложности:
1) 12 номеров с кратким вариантов ответа;
2) 7 номеров с развернутым вариантом ответа, из которых 2 последних задачи олимпиадного уровня.
На сайте math100.ru вы можете подготовиться к каждой теме, представленной в кодификаторе. Главное идти к цели — сдать не менее, чем на 100 баллов. И помни: «Математикой можно не заниматься только 2 дня в году: вчера и завтра».

Была в сети 19.04.2022 12:48

Коптева Лайсан Мунавировна

учитель математики

58 лет

313 697
21

24.12.2020 14:49

Приведен вариант ЕГЭ по профильной математике с ответами и решениями.

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задание 7

Задание 8

Задание 9

Задание 10

Задание 11

Задание 12

Задание 13

Задание 14

Задание 15

Задание 16

Задание 17

Задание 18

ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 402

Ответы для варианта:

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Тренировочный вариант №402

Тренировочный вариант №402

Кто сейчас на форуме

Просмотр

Решения

Математика Базовый уровень

Рекомендуем курсы ПК и ППК для учителей

Новое и интересное на сайте:

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задание 7

Задание 8

Задание 9

Задание 10

Задание 11

Задание 12

Задание 13

Задание 14

Задание 15

Задание 16

Задание 17

Задание 18

ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 402

Ответы для варианта:

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://alexlarin.com/egetren4.png" />

Тренировочный вариант №402

Тренировочный вариант №402

Кто сейчас на форуме

Просмотр

Решения

Математика Базовый уровень

Рекомендуем курсы ПК и ППК для учителей

Новое и интересное на сайте: