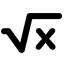Задание 1
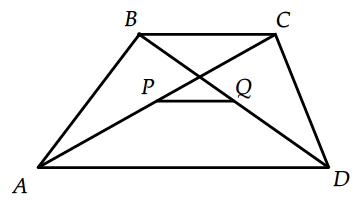
Основания трапеции равны 7 и 14. Найдите отрезок, соединяющий середины диагоналей трапеции.
Ответ: 3,5
Скрыть
Отрезок, соединяющий середины диагоналей трапеции равен полуразности большего и меньшего оснований. Поэтому он равен
$$frac{14-7}{2}=3,5$$
Задание 2
Длины двух ребер прямоугольного параллелепипеда равны 4 и 10, а площадь поверхности параллелепипеда равна 304. Найдите объем параллелепипеда.
Ответ: 320
Скрыть
Рассчитаем скольким условным единицам будет равняться третье измерение (обозначив его за $$c$$) заданной фигуры, если нам известно, согласно условиям этого задания, что первые два измерения равняются 4 и 10, в то время как площадь поверхности составляет 304:
$$2(4cdot c + 4cdot10 + 10cdot c) = 304$$
$$80+28c=304$$
$$28c=224$$
$$c=8$$
Рассчитаем скольким кубическим условным единицам будет равняться объем заданного параллелепипеда:
$$4cdot10cdot8 = 320$$
Задание 3
Из пруда, в котором плавают 40 щук, выловили 5 щук, пометили их и пустили обратно в пруд. Во второй раз выловили 9 щук. Какова вероятность того, что среди них окажутся только две помеченные щуки? Ответ округлите до тысячных.
Ответ: 0,246
Скрыть
После того как выловили и пометили 5 щук в пруде оказалось 5 помеченных щук и 35 без метки.
Количество исходов при выборе 2 щук из 5 помеченных: $$C^2_5 = frac{5!}{2!cdot(5-2)!} = 10$$
Количество исходов при вылове 7 щук из 35 без метки: $$C^{7}_{35}=frac{35!}{7!cdot(35-7)!)}=29cdot30cdot…cdotfrac{35}{1cdot2cdot…cdot7)} = 6724520$$
Общее количество исходов при вылове 9 щук из 40: $$C^9_{40}=frac{40!}{9!cdot(40 — 9)!}=32cdot33cdot…cdotfrac{40}{1cdot2cdot…cdot9} = 273438880$$
Вероятность выловить 2 помеченные щуки: $$P(2) = C^2_5cdotfrac{C_{35}^7}{C_{40}^9} = 10cdotfrac{6724520}{273438880} = 0,246.$$
Задание 4
На участке кросса для мотоциклиста-гонщика имеется три препятствия. Вероятность успешного прохождения первого препятствия равна 0,4, второго — 0,5, третьего — 0,6. Найдите вероятность успешного преодоления не менее двух препятствий.
Ответ: 0,5
Скрыть
$$p=p_1cdot p_2cdot q_3+p_1cdot q_2cdot p_3+q_1cdot p_2cdot p_3+p_1cdot p_2cdot p_3=$$
$$=0,4cdot0,5cdot0,4+0,4cdot0,5cdot0,6+0,6cdot0,5cdot0,6+0,4cdot0,5cdot0,6=$$
$$=0,08+0,12+0,18+0,12=0,5$$
Задание 5
Решите уравнение $$log_4(1,6-6x)=log_4(16x-0,6)-1.$$
Ответ: 0,175
Скрыть
ОДЗ:
$$1,6-6x>0$$
$$-6x>-1,6$$
$$x<frac{-1,6}{-6}$$
$$x<frac{4}{15}$$
$$16x-0,6>0$$
$$16>0,6$$
$$x>frac{3}{80}$$
$$xin(frac{3}{80};frac{4}{15})$$
Решение:
$$log_4(1,6-6x)=log_4(16x-0,6)-1$$
$$log_4(1,6-6x)=log_4(16x-0,6)-log_4 4$$
$$log_4(1,6-6x)=log_4((16x-0,6):4)$$
$$log_4(1,6-6x)=log_4(4x-0,15)$$
$$1,6-6x=4x-0,15$$
$$-4x-6x=-1,6-0,15$$
$$-10x=-1,75$$
$$x=0,175$$
$$frac{3}{80}<0,175<frac{4}{15}$$
Задание 6
Найдите значение выражения $$log_{0,8}log_{144}(288sqrt{3}).$$
Ответ: -1
Скрыть
$$log_{0,8}log_{144}288sqrt{3}=log_{0,8}log_{12^2}144cdot2sqrt{3}=log_{0,8}log_{12^2}12^2cdot(4cdot3)^{frac{1}{2}}=$$
$$=log_{0,8}log_{12^2}12^2cdot12^{frac{1}{2}}=log_{0,8}log_{12^2}12^{2,5}=log_{0,8}frac{2,5}{2}=log_{frac{4}{5}}frac{5}{4}=-1$$
Задание 7
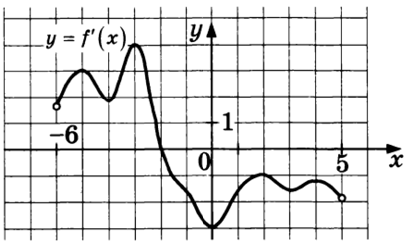
На рисунке изображен график $$y=f'(x)$$ производной функции $$f(x),$$ определенной на интервале $$(-6;5).$$ Найдите точку экстремума функции $$f(x),$$ принадлежащую отрезку $$[-3; 4].$$
Ответ: -2
Скрыть
Точка экстремума на графике производной – точка пересечения с осью Ox: -2.
Задание 8
Уравнение процесса, в котором участвовал газ, записывается в виде $$Рcdot V^a=const,$$ где $$P$$ — давление в газе (в Па), $$V$$ — объем газа (в м3), а $$const$$ и $$a$$ — постоянные величины. Найдите минимальное значение $$a$$ при котором уменьшение объема газа в 16 раз приводит к увеличению давления не менее, чем в 32 раза.
Ответ: 1,25
Скрыть
Согласно понятиям термодинамики, в каждом состоянии газ характеризуется определенными параметрами – давлением, объемом, температурой.
По условию задачи, газ переходит из одного состояния в другое так, что $$pV^a=const$$
Это значит, что
$$p_1V_1^a=p_2V_2^a$$
$$frac{p_1}{p_2}=(frac{V_2}{V_1})^2$$
Давление уменьшилось не менее чем в 32 раза, то есть
$$frac{p_1}{p_2}geq32$$
Значит,
$$(frac{V_2}{V_1})^2geq32$$
$$16^ageq32,$$ отсюда $$аgeq1,25$$
Наименьшее значение для а записываем в ответ.
Задание 9
Бассейн можно наполнить через четыре трубы. Если открыты вторая, третья и четвертая трубы, то бассейн наполняется за 1 час, если открыты первая, третья и четвертая трубы — за 1 час 15 минут, а если только первая и вторая — за 1 час 40 минут. За сколько минут наполнится бассейн, если открыть все четыре трубы?
Ответ: 50
Скрыть
Пусть производительность труб $$а,в,с,х$$ литров в час соответственно. Примем объем всего бассейна за 1.
Тогда $$в+с+х=1$$
$$(а+с+х)cdotfrac{1}{4} = 1$$
$$(а+в)cdotfrac{2}{3} = 1$$
Получили систему:
$$в+с+х=1$$
$$а+с+х= frac{4}{5}$$
$$а+в=frac{3}{5}$$
Сложим все уравнения:
$$2(а+в+с+х)= 1+frac{3}{5}+frac{4}{5}$$
$$2(а+в+с+х) = frac{12}{5}$$
$$а+в+с+х = frac{6}{5}$$ литров в час — совместная производительность
$$1:frac{6}{5}=frac{5}{6} ч=frac{5}{6}cdot60=50$$ минут
Задание 10
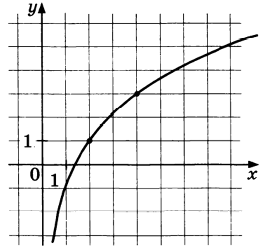
На рисунке изображен график функции $$f(x)=b+log_a x.$$ Найдите $$f(0,5).$$
Ответ: -3
Скрыть
График проходит через $$(2;1)$$ и $$(4;3).$$ Тогда:
$$left{begin{matrix} 1=b+log_a 2\ 3=b+log_a 4 end{matrix}right.Leftrightarrowleft{begin{matrix} 1=b+log_a 2\ 2=log_a 4-log_a 2 end{matrix}right.Leftrightarrowleft{begin{matrix} 1=b+2\ log_a 2=2 end{matrix}right.Leftrightarrowleft{begin{matrix} b=-1\ a=sqrt{2} end{matrix}right.$$
Получим:
$$f(x)=-1+log_{sqrt{2}} xRightarrow f(0,5)=-1+log_{sqrt{2}}frac{1}{2}=-1-2=-3$$
Задание 11
Найдите наибольшее значение функции $$y=x^3-frac{48}{x^2}$$ на отрезке $$[-3;2].$$
Ответ: -4
Скрыть
$$(x^3-frac{48}{x^2})’ = frac{3(x^5+32)}{x^3}$$
Точки экстремума:
$$frac{3(x^5+32)}{x^3} = 0$$
$$x^5+32 = 0$$
$$x^5= -32$$
$$x= — 2$$ входит в отрезок $$[-3;2]$$
Значение функции в точке экстремума $$y(-2)=(-2)^3-frac{48}{(-2)^2} = -20$$
Значение функции на концах отрезка $$[-3;2]:$$
$$y(-3)=(-2)^3-frac{48}{(-2)^2} = -frac{97}{3} =-32frac{1}{3}$$
$$y(2)=2^3-frac{48}{2^2}= -4$$
Наибольшее значение функции в точке $$x=2 ; y= -4$$
Задание 12
А) Решите уравнение $$sin^4x+(sin x-2)^4=2$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[4pi;5pi]$$
Ответ: А)$$frac{pi}{2}+2pi n,nin Z$$ Б)$$frac{9pi}{2}$$
Задание 13
В правильной треугольной пирамиде $$МАВС$$ двугранный угол при основании равен $$arctg3.$$ Через точку $$К$$ ребра $$МС$$ и вершины $$А$$ и $$В$$ проходит плоскость $$alpha$$ так, что площадь сечения пирамиды плоскостью $$alpha$$ относится к площади основания как $$3:sqrt{13}.$$
А) Докажите, что прямая $$МС$$ перпендикулярна плоскости $$alpha.$$
Б) Найдите объем пирамиды $$МАВК,$$ если объем пирамиды $$МАВС$$ равен $$52sqrt{5}.$$
Ответ: $$28sqrt{5}$$
Задание 14
Решите неравенство: $$frac{2x^3-11x^2+12x+9}{3^{2x+1}-7cdot3^x+2}leq0$$
Ответ: $$(-infty;-1),[-frac{1}{2};log_3 2),left{3right}$$
Задание 15
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение первого года кредитования нужно вернуть банку 2466 тыс. рублей. Какую сумму (в тыс. рублей) нужно выплатить банку за последние 12 месяцев?
Ответ: 2034
Задание 16
Внутри окружности с центром О построен правильный шестиугольник KOFPDL так, что его вершина D лежит на окружности. Из точки В, диаметрально противоположной точке D, проведены две хорды АВ и ВС, проходящие через вершины К и F шестиугольника соответственно.
А) Докажите, что АК : КВ = 3 : 7.
Б) Найдите площадь треугольника АВС, если радиус окружности равен 14.
Ответ: $$125sqrt{3}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых система:
$$left{begin{matrix} sqrt{x}(x^2-x+2)-yx^3=yx(2-x),\ y^2+(2a-7)y+(a+2)(5-3a)=0 end{matrix}right.$$
имеет ровно 2 решения.
Ответ: $$left{frac{3}{4}right}$$
Задание 18
Первый член геометрической прогрессии, состоящей из трехзначных натуральных чисел, равен 368. Известно, что в прогрессии не меньше трех чисел.
A) Может ли число 575 являться членом такой прогрессии?
Б) Может ли число 920 являться членом такой прогрессии?
В) Какое наибольшее число может являться членом такой прогрессии?
Ответ: А) да, Б) нет, В) 828
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 401
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В прямоугольном параллелепипеде ABCDA1B1C1D1 на диагонали BD1 отмечена точка N так, что Точка O — середина отрезка CB1.
а) Докажите, что прямая NO проходит через точку A.
б) Найдите объём параллелепипеда ABCDA1B1C1D1, если длина отрезка NO равна расстоянию между прямыми BD1 и CB1 и равна
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В июле 2026 года планируется взять кредит на три года в размере 700 тысяч рублей. Условия его возврата таковы:
— каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— платёж в 2027 и 2028 годах должен быть по 400 тыс. рублей
— к июлю 2029 года долг должен быть выплачен полностью.
Найдите сумму всех платежей после полного погашения кредита.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
На стороне острого угла с вершиной A отмечена точка B. Из точки B на биссектрису и другую сторону угла опущены перпендикуляры BC и BD соответственно.
а) Докажите, что
б) Прямые AC и BD пересекаются в точке T найдите отношение если
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
На доске написано N различных натуральных чисел, каждое из которых не превосходит 99. Для любых двух написанных на доске чисел a и b, таких, что a < b, ни одно из написанных чисел не делится на b – a, и ни одно из написанных чисел не является делителем числа b – a.
а) Могли ли на доске быть написаны какие-то два числа из чисел 18, 19 и 20?
б) Среди написанных на доске чисел есть 17. Может ли N быть равно 25?
в) Найдите наибольшее значение N.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Новый тренировочный вариант №401 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, а также полным видео разбором, который опубликован на сайте 8 октября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать этот вариант с ответами
Скачать предыдущий вариант Ларина
Тренировочный вариант 401 Ларина ЕГЭ 2023 по математике профиль
вариант-401-ларин-егэ2023-профиль
Полный разбор варианта
1.Основания трапеции равны 7 и 14. Найдите отрезок, соединяющий середины диагоналей трапеции.
Ответ: 3,5
2.Длины двух ребер прямоугольного параллелепипеда равны 4 и 10, а площадь поверхности параллелепипеда равна 304. Найдите объем параллелепипеда.
Ответ: 320
3.Из пруда, в котором плавают 40 щук, выловили 5 щук, пометили их и пустили обратно в пруд. Во второй раз выловили 9 щук. Какова вероятность того, что среди них окажутся только две помеченные щуки? Ответ округлите до тысячных.
Ответ: 0,246
6.На участке кросса для мотоциклиста‐гонщика имеется три препятствия. Вероятность успешного прохождения первого препятствия равна 0,4, второго – 0,5, третьего – 0,6. Найдите вероятность успешного преодоления не менее двух препятствий.
Ответ: -1
9.Бассейн можно наполнить через четыре трубы. Если открыты вторая, третья и четвертая трубы, то бассейн наполняется за 1 час, если открыты первая, третья и четвертая трубы – за 1 час 15 минут, а если только первая и вторая – за 1 час 40 минут. За сколько минут наполнится бассейн, если открыть все четыре трубы?
Ответ: 50
15.15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы: – 1‐го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; – со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга; – 15‐го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15‐е число предыдущего месяца. Известно, что в течение первого года кредитования нужно вернуть банку 2466 тыс. рублей. Какую сумму (в тыс. рублей) нужно выплатить банку за последние 12 месяцев?
Ответ: 2034
16.Внутри окружности с центром О построен правильный шестиугольник КОFPDL так, что его вершина D лежит на окружности. Из точки В, диаметрально противоположной точке D, проведены две хорды АВ и ВС, проходящие через вершины К и F шестиугольника соответственно. А) Докажите, что АК : КВ = 3 : 7. Б) Найдите площадь треугольника АВС, если радиус окружности равен 14.
18.Первый член геометрической прогрессии, состоящей из трехзначных натуральных чисел, равен 368. Известно, что в прогрессии не меньше трех чисел. A) Может ли число 575 являться членом такой прогрессии? Б) Может ли число 920 являться членом такой прогрессии? В) Какое наибольшее число может являться членом такой прогрессии?
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Диагностический вариант СтатГрад ЕГЭ База по математике 2110401-15.03.2022 с ответами
Регистрация Форум Текущее время: 10 мар 2023, 16:19 Сообщения без ответов | Активные темы Страница 3 из 4 [ Сообщений: 31 ] На страницу Пред. 1, 2, 3, 4 След. Начать новую тему»> Ответить Тренировочный вариант №401
Тренировочный вариант №401
Страница 3 из 4 [ Сообщений: 31 ] На страницу Пред. 1, 2, 3, 4 След. Текущее время: 10 мар 2023, 16:19 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
- № 08496
- Скачать
- Формулы
- Ответы
- Решения
- Критерии
- Демо
- Обсуждения


Просмотр
Образцы заданий ПОЛУЧЕНЫ ИЗ ОТКРЫТЫХ ИСТОЧНИКОВ в Интернете и
ПУБЛИКУЮТСЯ ПОСЛЕ окончания ЭКЗАМЕНА в ознакомительных целях!
Решения
Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
| ВХОД | РЕГИСТРАЦИЯ |
| *бесплатно, в один клик! |
ЕГЭ 2014, Математика, Тренировочная работа с ответами, Варианты 401-404, 28.01.2014.
Примеры заданий вариантов 401, 402, 403, 404.
Установка двух счётчиков воды (холодной и горячей) стоит 2500 руб. До установки счётчиков Александр платил за воду (холодную и горячую) ежемесячно 1700 руб. После установки счётчиков оказалось, что в среднем за месяц он расходует воды на 1000 руб. при тех же тарифах на воду. За какое наименьшее количество месяцев при тех же тарифах на воду установка счётчиков окупится?
Вопросы и задачи.
В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?
На бензоколонке один литр бензина стоит 30 руб. 20 коп. Водитель залил в бак 10 литров бензина и купил бутылку воды за 49 рублей. Сколько рублей сдачи он получит с 1000 рублей?
В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о Великой Отечественной войне.
Для приготовления вишнёвого варенья на 1 кг вишни нужно 1.5 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 16 кг вишни?
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ 2014, Математика, Тренировочная работа с ответами, Варианты 401-404, 28.01.2014 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ 2014, Математика, Тренировочная работа с ответами, Варианты 401-404, 28.01.2014
— pdf — Яндекс.Диск.
Дата публикации: 21.05.2014 08:10 UTC
Теги:
ЕГЭ по математике :: тренировочная работа по математике :: математика
Следующие учебники и книги:
- ЕГЭ 2014, Математика, Пробный экзамен, Брянск, Варианты 1-2, Корянов А.Г., 23.04.2014
- ЕГЭ 2014, Математика, Пробный экзамен с решениями, Иркутск, Варианты 1-4, декабрь 2013
- ЕГЭ 2014, Математика, Репетиционный экзамен с решениями, Санкт-Петербург, Варианты 1-2, 14.04.2014
- ЕГЭ 2014, Математика, Самара, Пробный экзамен, Варианты 1-4, март 2014
Предыдущие статьи:
- ЕГЭ 2014, Математика, ФЦТ, ФИПИ, Варианты 4-7
- ЕГЭ, Математика, Учебно-практический справочник, Каплун А.И., 2014
- ЕГЭ 2014, Математика, Практикум по выполнению типовых тестовых заданий, Лаппо Л.Д., Попов М.А., 2014
- Подготовка к ЕГЭ по математике, Новая демонстрационная версия, Ященко И.В., Шестаков С.А., Трепалин А.С., 2014




 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 





 спасибо большое, Михаил Николаевич!
спасибо большое, Михаил Николаевич!