Задание 1
Решите уравнение: $$4^x-2^x-2=0$$
Ответ: 1
Скрыть
$$4^x-2^x-2=0$$
$$2^2x-2^x-2=0$$
$$2^x=t, t>0$$
$$t^2-t-2=0$$
$$t=-1$$ и $$t=2$$
$$2^x=-1$$
$$varnothing$$
$$2^x=2$$
$$x=1$$
Задание 2
Лампочки выпускают только два завода. На первом заводе выпускают 20 % таких лампочек, остальные — на втором заводе. Вероятность того, что случайно выбранная лампочка с первого завода окажется бракованной, равна 0,025, а со второго завода — 0,015. Найдите вероятность того, что случайно выбранная такая лампочка бракованная.
Ответ: 0,017
Скрыть
$$P(л.б.)=P(л.б., з.1)+P(л.б., з.2)=0,025cdot0,2+0,015cdot0,8=0,017$$
Задание 3
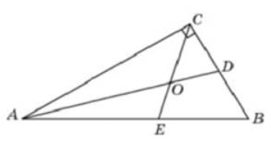
Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Ответ: 61
Скрыть
Острый угол пересечения биссектрис можно найти по формуле:
$$angle AOE=frac{1}{2}(angle A+angle C)=frac{90^{circ}+32^{circ}}{2}=61^{circ}.$$
Задание 4
Найдите $$frac{g(6-x)}{g(6+x)},$$ если $$g(x)=sqrt[11]{x(12-x)},$$ при $$|x|neq6$$
Ответ: 1
Скрыть
$$g(6-x)=sqrt[11]{(6-x)(12-(6-x))}=sqrt[11]{(6-x)(6+x)}$$
$$g(6+x)=sqrt[11]{(6+x)(12-(6+x))}=sqrt[11]{(6+x)(6-x)}$$
$$frac{g(6-x)}{g(6+x)}=frac{sqrt[11]{(6-x)(6+x)}}{sqrt[11]{(6+x)(6-x)}}=1$$
Задание 5
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра призмы равны $$frac{2}{pi}.$$ Найдите объём цилиндра, описанного около этой призмы.
Ответ: 4
Скрыть
$$D=sqrt{a^2+a^2}=sqrt{2a^2}=asqrt{2}=2sqrt{2}$$
$$V=frac{pi D^2}{4}cdot H=frac{picdot4cdot2}{4}cdotfrac{2}{pi}=4$$
Задание 6
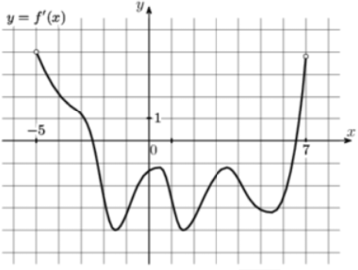
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x)$$ определенной на интервале $$(-5;7).$$ Найдите промежутки убывания функции $$f(x).$$ В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ: 18
Скрыть
Функция убывает там, где $$f'(x)<0,$$ т.е. график производной под $$Ox$$: тогда целые от $$-2$$ до $$6$$ включительно.
$$-2-1+0+1+2+3+4+5+6=18$$
Задание 7
Скорость колеблющегося на пружине груза меняется по закону $$v(t)=5sin(pi t)$$ (см/с), где $$t$$ — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: 0,67
Скрыть
$$5sinpi tgeq2,5$$
$$sinpi tgeq0,5$$
$$frac{pi}{6}+2pi nleqpi tleqfrac{5pi}{6}+2pi n$$
Так как просят в течении первой секунды, то $$n=0$$
$$frac{1}{6}leq tleqfrac{5}{6}$$
$$tau=frac{frac{5}{6}-frac{1}{6}}{1}=frac{2}{3}approx0,67$$
Задание 8
Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
Ответ: 18
Скрыть
Пусть $$a_1=10$$ км прошел турист в первый день;
$$n = 6$$ дней,
$$a_3$$ – в третий день,
$$a_6$$ – в последний ($$n$$-ый) день.
Тогда за 6 дней турист прошел 120 км.
$$S_n=frac{(a_1+a_n)n}{2}$$
$$120=frac{(10+a_6)6}{2}$$
$$frac{120}{3}=10+a_6$$
$$a_n=a_1+(n-1)d$$
$$30=10+(6-1)d$$
$$d=4$$ км — ежедневная прибавка
$$a_3=10+(3-1)4=18$$ км — в третий день
Задание 9
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ: 1,2
Скрыть
Первая прямая проходит через $$(2;-1)$$ и $$(3;1).$$
Тогда: $$left{begin{matrix} -1=2k+b\ 1=3k+b end{matrix}right.Leftrightarrowleft{begin{matrix} -1=4+b\ 2=k end{matrix}right.Leftrightarrowleft{begin{matrix} b=-5\ k=2 end{matrix}right.$$
Получим: $$y=2x-5.$$
Вторая проходит через точки $$(0;1)$$ и $$(1;-2).$$
Тогда: $$left{begin{matrix} 1=0cdot k+b\ -2=1cdot k+b end{matrix}right.Leftrightarrowleft{begin{matrix} b=1\ k=-3 end{matrix}right.$$
Получим: $$y=-3x+1.$$
Тогда: $$2x-5=-3x+1Leftrightarrow 5x=6Leftrightarrow x=1,2$$
Задание 10
Монету подбрасывают до тех пор, пока орёл не выпадет два раза (не обязательно подряд). Найдите математическое ожидание числа бросков.
Ответ: 4
Скрыть
Если сделано 2 броска, то общее количество исходов 4 штуки (ОО; ОР; РО; РР) и только один с двумя орлами, то есть $$frac{1}{4}$$ — вероятность 2 орлов за 2 броска.
Далее за 3 считаем: всего исходов 8, с 2 орлами 3 (ООР; ОРО; РОО), но ООР мы не считаем, так как если бы первыми двумя бросками выпали орлы, то третий не делали бы. Значит $$2Rightarrow P=frac{2}{8}=frac{1}{4}.$$
За 4 броска: всего 16 исходов, 2 орла: ОРРО; РОРО; РРОО (такие как ООРР или РООР исключаем). Итого $$P=frac{3}{8}.$$
И так далее. Получается:
| Кол-во бросков | 1 | 2 | 3 | 4 | 5 | … | n |
| Вероятность | 0 | $$0,5^2$$ | $$2cdot0,5^3$$ | $$3cdot0,5^4$$ | $$4cdot0,5^5$$ | … | $$(n-1)cdot0,5^n$$ |
При этом математическое ожидание есть сумма всех произведений количества бросков на соответствующую вероятность:
$$M(x)=sum^{infty}_{n=2}ncdotfrac{n-1}{2^n}=4$$
Задание 11
Найдите точку максимума функции $$y=(2x-3)cos x-2sin x+5,$$ принадлежащую промежутку $$(0;frac{pi}{2}).$$
Ответ: 1,5
Скрыть
$$y’ = (2x – 3)’·cos x + (2x – 3)·(cos x)’ – (2sin x)´$$
$$y’ = 2cos x – (2x – 3)sin x – 2cos x = – (2x – 3)sin x$$
$$y’ = – (2x – 3)sin x$$
$$y’ = 0$$
$$– (2x – 3)sin x = 0$$
$$(3 – 2x)sin x = 0$$
$$3 – 2x = 0$$ и $$sin x = 0$$
Решим 1 уравнение:
$$3 – 2x = 0$$
$$x = frac{3}{2}$$
$$x = 1,5$$
Решим 2 уравнение:
$$sin x = 0$$
$$x = 0$$ не принадлежит промежутку $$(0;frac{pi}{2})$$
Отметим точку $$x = 1,5$$ на числовой прямой, учитывая промежуток $$(0;frac{pi}{2})$$ и найдем знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
В точке $$x = 1,5$$ производная функции меняет знак с положительного на отрицательный, значит, это искомая точка максимума.
Задание 12
А) Решите уравнение $$frac{2sin^2x-sin x-1}{log_2(cos x)}=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[pi;frac{5pi}{2}]$$
Ответ: А)$$-frac{pi}{6}+2pi n,nin Z$$ Б)$$frac{11pi}{6}$$
Задание 13
В прямоугольном параллелепипеде $$ABCDA_1B_1C_1D_1$$ известны ребра $$ВС=5$$ и $$АВ=АА_1=8,$$ M и N — середины ребер $$CD$$ и $$АА_1$$ соответственно. Плоскость $$alpha$$ проходит через точки $$М$$ и $$В$$ и параллельна прямой $$CD_1.$$
А) Докажите, что прямая $$DN$$ параллельна плоскости $$alpha$$
Б) Найдите расстояние между прямыми $$C_1D$$ и $$BD_1$$
Ответ: $$frac{20sqrt{34}}{51}$$
Задание 14
Решите неравенство: $$2xgeqlog_2(frac{35}{3}cdot6^{x-1}-2cdot9^{x-frac{1}{2}})$$
Ответ: $$(-infty;-1],[2;log_{1,5}frac{35}{12})$$
Задание 15
В июле 2022 года планируется взять кредит в банке на некоторую сумму сроком на 5 лет. Условия возврата таковы:
— в январе долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь необходимо внести единым платежом часть долга;
— в июле 2023, 2024 годов долг должен быть на одну и ту же сумму меньше долга июля предыдущего года;
— в июле 2024 года долг составляет 80% от первоначальной суммы кредита;
— выплаты в 2025 и 2026 годах равны по 202 тыс. рублей;
— долг в июле 2026 года составляет 20% от суммы долга на июль 2024 года;
— в июле 2027 года долг должен быть полностью погашен.
Определите, чему равна общая сумма выплат.
Ответ: 701,15 тыс. руб.
Задание 16
В равнобедренной трапеции ABCD угол BCD — тупой. Через точку В проведена прямая, параллельная прямой CD и пересекающая прямую AD в точке Е. На продолжении ВЕ за точку Е отмечена точка F такая, что DE=DF.
А) Докажите, что точки A, F, C и D лежат на одной окружности.
Б) Найдите расстояние от точки С до прямой AF, если $$BD=10$$ и $$cosangle ADC = 0,6$$
Ответ: 8
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение
$$sqrt{x-2a}+sqrt{x^2+4ax+4a^2}=2$$
имеет хотя бы одно решение
Ответ: $$[-1;frac{1}{2}]$$
Задание 18
Составим две последовательности натуральных чисел $$left{a_nright}$$ и $$left{b_nright}.$$
$$a_1 = 1, a_n =frac{n}{p} (n > 1),$$ где $$p$$ — наименьший простой делитель числа $$n.$$
$$b_1 = 1, b_n (n > 1)$$ — количество таких чисел $$m,$$ для которых $$a_m = n.$$ Оно показывает, сколько раз число $$n$$ встречается в последовательности $$left{a_nright}.$$
А) Найдите $$b_187.$$
Б) Для каких чисел $$n > 1$$ и $$m > 1$$ выполняется равенство $$b_n= b_m?$$
В) Чему равно $$b_m,$$ если $$m = 8n^3+12n^2- 2n-3?$$
(Автор задачи Сергей Андреевич Тюрин)
Ответ: А) 5, Б) числа n и m должны иметь одинаковый наименьший простой делитель, В) 2

Новый тренировочный вариант №388 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 2.04.2022 (2 апреля 2022 года)
скачать вариант 388 Ларина
Вариант Алекса Ларина №388 ЕГЭ 2022 по математике 11 класс:
Тренировочный вариант Ларина ЕГЭ состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 cодержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
Решение варианта №388 и разбор:
2)Лампочки выпускают только два завода. На первом заводе выпускают 20 % таких лампочек, остальные ‐ на втором заводе. Вероятность того, что случайно выбранная лампочка с первого завода окажется бракованной, равна 0,025, а со второго завода ‐ 0,015. Найдите вероятность того, что случайно выбранная такая лампочка бракованная.
Правильный ответ: 0,017
3)Острый угол прямоугольного треугольника. равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Правильный ответ: 61
8)Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
Правильный ответ: 18
10)Монету подбрасывают до тех пор, пока орёл не выпадет два раза (не обязательно подряд). Найдите математическое ожидание числа бросков.
Правильный ответ: 4
15)В июле 2022 года планируется взять кредит в банке на некоторую сумму сроком на 5 лет. Условия возврата таковы: – в январе долг возрастает на 10% по сравнению с концом предыдущего года; – с февраля по июнь необходимо внести единым платежом часть долга; – в июле 2023, 2024 годов долг должен быть на одну и ту же сумму меньше долга июля предыдущего года; – в июле 2024 года долг составляет 80% от первоначальной суммы кредита; – выплаты в 2025 и 2026 годах равны по 202 тыс. рублей; – долг в июле 2026 года составляет 20% от суммы долга на июль 2024 года; – в июле 2027 года долг должен быть полностью погашен. Определите, чему равна общая сумма выплат.
Правильный ответ: 701, 15 тыс.руб
Смотрите также на нашем сайте:
Задание 16 планиметрия ЕГЭ 2022 математика профиль задачи с ответами
Задание 15 ЕГЭ 2022 математика профиль задачи на вклады, кредиты, оптимизацию
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 00:01
Зарегистрирован: 08 мар 2017, 23:11
Сообщений: 545
Откуда: Пущино
Задача 10
Набросок решения


Владимiръ
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 00:03
Зарегистрирован: 08 мар 2017, 23:11
Сообщений: 545
Откуда: Пущино


netka
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 00:48
Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань
Всем здравствуйте! 

Решение задания 12.
Решение задания 14.
Решение задания 17.


netka
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 00:50
Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань
Решение задания 13.
Вложение:
388-13.ggb [12.42 KIB]
Скачиваний: 814
скрин решения


rgg
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 04:23
Зарегистрирован: 29 окт 2014, 22:13
Сообщений: 3763
Выкладываю подробное решение задачи 15.
Поправка: по чистой случайности допущена мной опечатка.
Просьба сумму всех выплат считать равной 701,15 тыс. руб., а ответ к задаче равным 701 150 рублей.
Последний раз редактировалось rgg 08 апр 2022, 00:20, всего редактировалось 3 раз(а).


khazh
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 08:31
|
Зарегистрирован: 23 мар 2012, 10:13
Сообщений: 5392


Raisa
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 10:03
Зарегистрирован: 23 янв 2014, 20:36
Сообщений: 1463
Откуда: г. Дубна МО
Последний раз редактировалось Raisa 07 апр 2022, 22:39, всего редактировалось 1 раз.


Raisa
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 10:04
Зарегистрирован: 23 янв 2014, 20:36
Сообщений: 1463
Откуда: г. Дубна МО
Последний раз редактировалось Raisa 07 апр 2022, 22:35, всего редактировалось 1 раз.


SergeiB
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 07 апр 2022, 14:35
|
Зарегистрирован: 13 янв 2019, 09:04
Сообщений: 512


Владимiръ
Заголовок сообщения: Re: Тренировочный вариант №388
Добавлено: 08 апр 2022, 15:49
Зарегистрирован: 08 мар 2017, 23:11
Сообщений: 545
Откуда: Пущино
SergeiB писал(а):
Сергей, мне понравился ваш подход, и я захотел чуть-чуть подправить решение для лучшей читабельности (на мой взгляд). А получилось вот что…


А. Ларин. Тренировочный вариант № 388.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра BC = 5 и AB = AA1 = 8, M и N — середины ребер CD и АА1 соответственно. Плоскость α проходит через точки M и B и параллельна прямой CD1.
а) Докажите, что прямая DN параллельна плоскости α.
б) Найдите расстояние между прямыми C1D и BD1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В июле 2022 года планируется взять кредит в банке на некоторую сумму сроком на 5 лет. Условия возврата таковы:
— в январе долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь необходимо внести единым платежом часть долга;
— в июле 2023, 2024 годов долг должен быть на одну и ту же сумму меньше долга июля предыдущего года;
— в июле 2024 года долг составляет 80% от первоначальной суммы кредита;
— выплаты в 2025 и 2026 годах равны по 202 тыс. рублей;
— долг в июле 2026 года составляет 20% от суммы долга на июль 2024 года;
— в июле 2027 года долг должен быть полностью погашен.
Определите, чему равна общая сумма выплат.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В равнобедренной трапеции ABCD угол BCD — тупой. Через точку B проведена прямая, параллельная прямой CD и пересекающая прямую AD в точке E. На продолжении BE за точку E отмечена точка F такая, что DE = DF.
а) Докажите, что точки A, F, C и D лежат на одной окружности.
б) Найдите расстояние от точки C до прямой AF, если BD = 10 и
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых уравнение
имеет хотя бы одно решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Составим две последовательности натуральных чисел {an} и {bn}:
a1 = 1, (n > 1), где p — наименьший простой делитель числа n;
b1 = 1, bn (n > 1) — количество таких чисел m, для которых am = n. Оно показывает, сколько раз число n встречается в последовательности {an}.
а) Найдите b187.
б) Для каких чисел n > 1 и m > 1 выполняется равенство bn = bm?
в) Чему равно bm, если ?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |