А. Ларин. Тренировочный вариант № 377.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Основанием прямой треугольной призмы PQRP1Q1R1 является прямоугольный треугольник PQR с прямым углом R. Диагонали боковых граней PP1Q1Q и PP1R1R равны 17 и 15 соответственно, PQ = 10.
а) Докажите, что треугольник P1QR прямоугольный.
б) Найдите объем пирамиды P1QRR1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Производство x тысяч единиц продукции обходится в миллионов рублей в год. При цене p тыс. руб. за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через шесть лет суммарная прибыль может составить не менее 150 млн руб. при некотором значении x?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Дана равнобедренная трапеция ABCD c основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает основание AD в точке L, точка M — середина CD.
а) Докажите, что четырехугольник DLOM — параллелограмм.
б) Найдите AD, если BC = 3.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых три различных корня уравнения
образуют геометрическую прогрессию. Найдите эти корни.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Тридцать пять шариков массой 1 г, 2 г, …, 35 г разложили по двум коробкам, в каждой коробке находится хотя бы один шарик. Масса каждого шарика выражается целым числом граммов. Затем из второй коробки переложили в первую один шарик. После этого средняя масса шариков в первой коробке увеличилась на 4 г.
а) Можно ли такое быть, если первоначально в первой коробке лежали только шарики массой 3 г, 12 г и 27 г?
б) Могла ли средняя масса шариков в первой коробке первоначально равняться 12,6 г?
в) Какое наибольшее число шариков могло быть первоначально в первой коробке?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.

Тренировочный вариант №377 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 15.01.2022 (15 января 2022 года)
-
Скачать вариант Ларина
-
Ответы для варианта
Решать вариант Алекса Ларина №377 ЕГЭ 2022 по математике 11 класс:
2)Найдите вероятность того, что при первых трех подбрасываниях выпадет одна и та же сторона монеты.
Ответ: 0,25
3)В трапеции АВСD известны длины оснований: AD = 36, BC = 12. Диагонали АС и BD пересекаются в точке О. Найдите площадь трапеции АВСD, если площадь треугольника AOD равна 216.
Ответ: 384
5)Высота правильной четырехугольной пирамиды равна 24, а объем пирамиды равен 784. Найдите боковое ребро этой пирамиды.
Ответ: 25
8)Для приготовления молочного коктейля использовали 200 г мороженого жирностью 10% и 300 г молока 6%‐ой жирности. Определите жирность полученного коктейля (в процентах).
Ответ: 7,6
10)Дана симметричная монета – при каждом ее подбрасывании выпадение «орла» или «решки» равновероятно. Эту монету подбросили шесть раз. Известно, что «решка» выпала ровно три раза. Найдите вероятность того, что при первых трех подбрасываниях монеты выпал «орел».
Ответ: 0,05
13)Основанием прямой треугольной призмы PQRP1Q1R1 является прямоугольный треугольник PQR с прямым углом R. Диагонали боковых граней PP1Q1Q и PP1R1R равны 17 и 15 соответственно, PQ = 10. А) Докажите, что треугольник P1QR прямоугольный. Б) Найдите объем пирамиды P1QRR1.
Ответ: б)24 корень из 21
18)Тридцать пять шариков массой 1 г, 2 г, …, 35 г разложили по двум коробкам, в каждой коробке находится хотя бы один шарик. Масса каждого шарика выражается целым числом граммов. Затем из второй коробки переложили в первую один шарик. После этого средняя масса шариков в первой коробке увеличилась на 4 г. А) Можно ли такое быть, если первоначально в первой коробке лежали только шарики массой 3г, 12 г и 27 г? Б) Могла ли средняя масса шариков в первой коробке первоначально равняться 12,6г? В) Какое наибольшее число шариков могло быть первоначально в первой коробке?
Ответ: а-да, б-нет, в-6
Смотрите другие варианты ЕГЭ 2022 по математике 11 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Регистрация Форум Текущее время: 10 мар 2023, 16:19 Сообщения без ответов | Активные темы Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След. Начать новую тему»> Ответить Тренировочный вариант №377
Тренировочный вариант №377
Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След. Текущее время: 10 мар 2023, 16:19 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
Решаем ЕГЭ 264 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №264 (alexlarin.com)
Решаем ЕГЭ 264 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №264 (alexlarin.com)
Задание 1
Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12500 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
Ответ: 10875
Скрыть
После вычета он получит 100-13=87% от своей зарплаты , т.е : 12500*0,87=10875 рублей.
Задание 2
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8‐го класса по математике в 2007 году (по 1000‐бальной шкале). Найдите средний балл участников страны, занимающей третье место в данном списке.
Ответ: 495
Скрыть
Третье место занимает Австралия и ее средний бал 495
Задание 3
Из фанерного листа размером 60 см х 60 см нужно выпилить закрашенный многоугольник. Найдите его массу (в граммах), если известно, что плотность данной фанеры равна 0,5 г/см2.
Ответ: 575
Скрыть
Найдем площадь данной фигуры: $$S=60*60-frac{1}{2} (60*50+60*10+40*10)-frac{40+50}{2}*10=$$$$3600-2000-450=1150$$ см2
Найдем его массу: $$m=1150*0,5=575$$ грамм
Задание 4
На тренировке баскетболист Майкл попадает 3‐очковый бросок с вероятностью 0,9, если бросает мячом фирмы «Nike». Если Майкл выполняет 3‐очковый бросок мячом фирмы «Adidas», то попадает с вероятностью 0,7. В корзине лежат 10 тренировочных мячей: 6 фирмы «Nike» и 4 фирмы «Adidas». Майкл наудачу берет из корзины первый попавшийся мяч и совершает 3‐очковый бросок. Найдите вероятность того, что бросок Майкла будет точен.
Ответ: 0,82
Скрыть
Вероятность выбрать Nike и попасть им: $$P_{1}=frac{6}{6+4}*0,9=0,54$$; выбрать Adidas и попасть им: $$P_{2}=frac{4}{6+4}*0,7=0,28$$. Тогда вероятность вообще попасть: $$P=0,54+0,28=0,82$$
Задание 5
Найдите корень уравнения $$frac{2}{log_{2} (-5x-1)}=-1$$
Ответ: -0,25
Скрыть
$$frac{2}{log_{2}(-5x-1)}=-1Leftrightarrow$$ $$left{begin{matrix}-5x-1>0log_{2}(-5x-1)neq 0-log_{2}(-5x-1)=2(1)end{matrix}right.$$
(1): $$log_{2}(-5x-1)=-2Leftrightarrow$$ $$-5x-1=2^{-2}Leftrightarrow$$ $$-5x=frac{1}{4} +1Leftrightarrow$$ $$-5x=frac{5}{4} Leftrightarrow$$ $$x=-0,25$$.
Задание 6
В треугольнике АВС проведена биссектриса ВК. Определите длину отрезка АК, если известно, что АВ=7,5, ВС=6, СК=4.
Ответ: 5
Скрыть
По свойству биссектрисы: $$frac{BC}{AB}=frac{KC}{AK}Leftrightarrow$$ $$AK=frac{AB*KC}{BC}=frac{7,5*4}{6}=5$$
Задание 7
Движение автомобиля во время торможения описывается формулой $$S(t)=36t-5t^{2}$$ , где S – путь в метрах, t – время в секундах. Сколько секунд автомобиль будет двигаться с момента начала торможения до его полной остановки?
Ответ: 3,6
Скрыть
Производная функции расстояния есть функция скорости, найдем ее и приравняем к 0: $${S}'(t)=v(t)=36-10tRightarrow$$ $$v(t)=0$$ или $$t=3,6$$
Задание 8
В прямоугольном параллелепипеде ABCDA1В1C1D1 , АВ=5, AD=3, AA1=4. Найдите тангенс угла между прямыми BD1 и DC.
Ответ: 1
Скрыть
1) $$ADperp AB$$ ; $$DD_{1}perp (ABC)Rightarrow$$ $$D_{1}Aperp AB$$ по теореме о трех перпендикулярах; $$ABleft | right |DC$$. Тогда $$tg (BD_{1}; DC)=tg(BD_{1}, AB)=frac{AD_{1}}{AB}$$
2) из $$Delta AD_{1}D$$: $$AD_{1}=sqrt{AD^{2}+AD_{1}^{2}}=5$$
3) $$tg (BD_{1}; AB)=frac{5}{5}=1$$
Задание 9
Найдите значение выражения $$log_{2} ^{3} (log_{3} sqrt[4]{3})$$
Ответ: -8
Скрыть
$$log_{2}^{3}(log_{3}sqrt[4]{3})=$$$$log_{2}^{3}log_{3}3^{frac{1}{4}}=$$$$log_{2}^{3}frac{1}{4}=$$$$log_{2}^{3}2^{-2}=(-2)^{3}=-8$$
Задание 10
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m=8 кг и радиуса R=5 см, и двух боковых с массами M=2 кг и с радиусами R+h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг*см2 , задаётся формулой $$I=frac{(m+2M)R^{2}}{2}+M(2Rh+h^{2})$$ . При каком максимальном значении h момент инерции катушки не превышает предельного значения 1900 кг*см2? Ответ выразите в сантиметрах.
Ответ: 25
Скрыть
Подставим имеющееся значение : $$1900=frac{(8+2*2)*5^{2}}{2}+2*(2*5*h+h^{2})Leftrightarrow$$ $$3800=300+40h+4h^{2}Leftrightarrow$$ $$4h^{2}+40h-3500=0Leftrightarrow$$ $$h^{2}+10h-875=0$$
$$D=100+3500=3600Leftrightarrow$$ $$h_{1}=frac{-10+60}{2}=25$$; $$h_{2}=frac{-10-60}{2}=-35$$
Тогда $$h_{max}=25$$, так как не может быть отрицательной
Задание 11
Три числа составляют арифметическую прогрессию. Если первые два оставить, а к третьему прибавить сумму двух первых, то полученные числа составят геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
Ответ: 3
Скрыть
Пусть первое число – x, третье — y, тогда по свойству арифметической прогрессии, второе: $$frac{x+y}{2}$$
Прибавим к третьему сумму первых двух, тогда она составит : $$y+x+frac{x+y}{2}=frac{3(x+y)}{2}$$
Знаменатель геометрической прогрессии- отношение последующего члена к предыдущему (третьего ко второму) : $$q=frac{3(x+y)}{2} frac{x+y}{2}=3$$
Задание 12
Найдите точку минимума функции $$f(x)=2sqrt[3]{x^{2}}-frac{sqrt[3]{x^{4}}}{4}$$
Ответ: 0
Скрыть
Найдем производную для данной функции : $${y}’=(2*sqrt[3]{x^{2}}-frac{sqrt[3]{x^{4}}}{4})=$$$$2{(x^{frac{2}{3}})}’-frac{1}{4}{(x^{frac{4}{3}})}’=$$$$2*frac{2}{3}*x^{-frac{1}{3}}-frac{1}{4}*frac{4}{3}x^{frac{1}{3}}=0Leftrightarrow$$$$frac{4}{3} *frac{1}{sqrt[3]{x}}-frac{1}{3}*sqrt[3]{x}=0Leftrightarrow$$ $$frac{1}{3}(frac{4}{sqrt[3]{x}}-sqrt[3]{x})=0Leftrightarrow$$ $$frac{4-sqrt[3]{x^{2}}}{sqrt[3]{x}}=0Leftrightarrow$$ $$sqrt[3]{x^{2}}=4Leftrightarrow$$ $$x^{2}=64Leftrightarrow$$ $$x=pm 8$$ Тогда $$x=0$$ –точка минимума
Задание 13
а) Решите уравнение $$2|sin x|+log_{tg x} (-frac{|cos x|}{sin x})=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{3pi}{2};0]$$
Ответ: А)$$-frac{5pi }{6} +2 pi n,n in Z$$ Б)$$-frac{5pi}{6}$$
Скрыть
А) $$2 left | sin x right |+log_{tg x}(-frac{left | cos x right |}{sin x})=0$$
ОДЗ: $$left{begin{matrix}frac{-left | cos x right |}{sin x}>0tg x>0tg x neq 1sin xneq 0cos xneq 0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}sin x<0cos x<0 (1)tg xneq 1end{matrix}right.$$
Решение с учетом ОДЗ: $$-2 sin x+log_{tg x}frac{cos x}{sin x}=0Leftrightarrow$$ $$-log_{tg x}frac{sin x}{cos x}=2 sin xLeftrightarrow$$ $$2 sin x=-1Leftrightarrow$$ $$sin x=-frac{1}{2}Leftrightarrow$$$$left[begin{matrix}x=-frac{pi}{6}+2 pi n notin (1)x=-frac{5pi }{6} +2 pi nend{matrix}right.$$$$n in Z$$
Б) На промежутке: $$[-frac{3pi}{2};0]$$ : $$-frac{5pi}{6}$$
Задание 14
В правильной шестиугольной пирамиде SABCDEF сторона основания ABCDEF равна 2, а боковое ребро 3.
а) Докажите, что плоскость AFM , где M ‐ середина ребра SC, делит ребро SB в отношении 2:1, считая от вершины S.
б) Найдите площадь сечения пирамиды SABCDEF плоскостью AFM .
Ответ: А)2:1 Б) $$frac{13sqrt{2}}{3}$$
Скрыть
A) 1) Соединим AM , через M проведем прямую $$aleft | right |AF$$; $$acap SD=NRightarrow$$ $$MNleft | right |AF$$
2) AC-проекция AM ; Пусть SR-высота в $$Delta ASC$$; $$SRcap AM =K Rightarrow$$ через K пойдет прямая , параллельная AF ( по ней пересекаются сечение и (SEB) ); пусть она пересекает SE и SB в H и G соответственно , тогда (AGMNF)-искомое сечение
3) из $$Delta AMC$$ и точки $$S in GM$$ по т. Менелая : $$frac{SK}{KR}=frac{RA}{AC}*frac{CM}{MS}=1$$; $$Delta SAC$$ равнобедренный $$Rightarrow$$ $$AR=RCRightarrow$$ $$frac{SK}{KR}*frac{1}{2}*frac{1}{1}=1Rightarrow$$ $$frac{SC}{KR}=frac{2}{1}(*)$$ ( можно сразу сказать , что K-точка пересечения медиан $$Rightarrow$$ 2: 1)
4) $$Delta SHGsim Delta SEBRightarrow$$ $$Delta SGKsim Delta SBKRightarrow$$ $$frac{SK}{KR}=frac{SC}{SB}=frac{2}{1}$$
Б) 1) Пусть SO-высота пирамиды $$Rightarrow$$ из $$Delta SOB$$: $$SO=sqrt{SB^{2}-OB^{2}}=sqrt{5}Rightarrow$$ $$YO=frac{1}{3} SO=frac{sqrt{5}}{3}$$;
2) из $$Delta FOA$$: $$OZ=OA*sin A=2*frac{sqrt{3}}{2}=sqrt{3}Rightarrow$$ из $$Delta ZOY$$: $$ZY=sqrt{ZO^{2}+OY^{2}}=frac{sqrt{32}}{3}Rightarrow$$ $$cos YZO=frac{ZO}{ZY}=frac{3sqrt{3}}{sqrt{32}}$$
3) Пусть $$AG^{‘}M^{‘}N^{‘}H^{‘}F$$- проекция сечения на (ABC) и $$S _{AC_{1}^{‘}M^{‘}N^{‘}H^{‘}F}=S_{1}$$. Пусть S-площадь сечения $$Rightarrow$$ $$S=frac{S_{1}}{cos YZO}$$
4) $$S_{ZOA}=x=frac{1}{2} *2*2*frac{sqrt{3}}{2}=sqrt{3}$$;
$$S_{AOC_{1}^{‘}}=S_{ZOH^{‘}}=$$$$frac{OC_{1}^{‘}}{OB}*x=$$$$frac{SC_{1}}{SB}*x=frac{2}{3}x=frac{2sqrt{3}}{3}$$
Аналогично: $$S_{G^{‘}OM^{‘}}=S_{H^{‘}ON^{‘}}=$$$$frac{2}{3}*frac{1}{2}x=frac{1}{3}x$$ и $$S_{N^{‘}OM^{‘}}=frac{1}{4}x$$
Тогда $$S_{1}=sqrt{3} (1+2*frac{2}{3}+2*frac{1}{3}+frac{1}{4})=frac{13sqrt{3}}{4}$$
$$S=frac{13sqrt{3}}{4} :frac{3sqrt{3}}{sqrt{32}}=$$$$frac{13sqrt{3}*4sqrt{2}}{4*3sqrt{3}}=$$$$frac{13sqrt{2}}{3}$$
Задание 15
Решите неравенство $$log_{frac{1}{4}} (sqrt{x+3}-x+3) geq -2+log_{frac{1}{4}} frac{3}{8}$$
Ответ: $${-3}cup [-2 ;6)$$
Скрыть
$$log_{frac{1}{4}}(sqrt{x+3}-x+3)geq -2+log_{frac{1}{4}} frac{3}{8}$$
ОДЗ: $$left{begin{matrix}x+3geq 0sqrt{x+3}-x+3>0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}xgeq -3sqrt{x+3}>x-3 (1)end{matrix}right.$$
(1) :решим графически: $$x in [-3 ; 6]$$
Решение: $$log_{frac{1}{4}}(sqrt{x+3}-x+3)geq log_{frac{1}{4}}16+log_{frac{1}{4}}frac{3}{8}Leftrightarrow$$
$$log_{frac{1}{4}}(sqrt{x+3}-x+3)geq log_{frac{1}{4}}16*frac{3}{8}Leftrightarrow$$ $$sqrt{x+3}-x+3leq 6Leftrightarrow sqrt{x+3}leq x+3$$
Пусть $$sqrt{x+3}=ygeq 0Leftrightarrow$$ $$x+3=y^{2}$$:$$left{begin{matrix}yleq y^{2}ygeq 0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}y^{2}-ygeq 0ygeq 0end{matrix}right.Leftrightarrow$$$$left{begin{matrix}(y-1)ygeq 0ygeq 0end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}ygeq 0left{begin{matrix}yleq 0ygeq 0end{matrix}right.end{matrix}right. Leftrightarrow$$ $$left{begin{matrix}y=0ygeq 1end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}sqrt{x+3}=0sqrt{x+3}geq 1end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x=-3xgeq -2end{matrix}right.$$
С учетом ОДЗ : $$x in$$ $${-3}cup [-2 ;6)$$
Задание 16
В треугольнике АВС длина АВ равна 3, $$angle ACB=arcsin frac{3}{5}$$ , хорда KN окружности, описанной около треугольника АВС, пересекает отрезки АС и ВC в точках M и L соответственно. Известно, что $$angle ABC=angle CML$$ , площадь четырехугольника ABLM равна 2, а длина LM равна 1.
А) Найдите высоту треугольника KNC, опущенную из вершины С
Б) Найдите площадь треугольника KNC
Ответ: А)$$frac{1}{2}$$ Б)$$frac{3}{4}$$
Скрыть
A) $$angle C$$ – общий ; $$angle ABC =angle CMLRightarrow$$ $$Delta ABCsim Delta CML$$: $$frac{MC}{BC}=frac{CN}{AC}=frac{MN}{AB}=frac{1}{3}Rightarrow$$ $$S_{MCN}=(frac{1}{3})^{2} S_{ABC}Rightarrow$$ $$S_{AMNB}=frac{8}{9}S_{ABC}Rightarrow$$ $$S_{ABC}=frac{9 S_{AMNB}}{8}=frac{9}{4}$$$$Rightarrow$$ $$S_{MCN}=frac{1}{4}=frac{1}{2} MN*h$$ ,где h-высота из $$CRightarrow h=frac{1}{2}$$
Б) 1) Пусть O — центр описанной около $$Delta ABC$$ окружности , тогда $$OC=OB=OA$$ — радиусы и $$OC=frac{AB}{2 sin ACB}=frac{5}{2}$$
2) Пусть $$angle ABC=alpha Rightarrow$$ $$smile AC=2alpha$$ (вписанный угол) и $$angle LMC=alpha$$ .
3) $$angle LMC$$ — угол между хордами AC и KN $$Rightarrow$$ $$frac{smile AK+smile CN}{2}=alpha Rightarrow$$ $$smile AK+smile CN=2alpha$$. При этом $$smile AC=smile AK+smile KC=2alpha Rightarrow$$ $$smile CN=smile KCRightarrow$$ $$KC=CN$$
4) Пусть $$OCcap KN=DRightarrow$$ $$CD=h=frac{1}{2}$$( расстояние от C до ML ) $$Rightarrow$$ $$OD=OC-DC=frac{5}{2}-frac{1}{2}=2Rightarrow$$ $$KD=sqrt{OK^{2}-OD^{2}}=1,5Rightarrow$$ $$KN=3Rightarrow$$ $$S_{KCN}=frac{1}{2}*CD*KN=frac{3}{4}$$
Задание 17
На счет, который вкладчик имел в начале первого квартала, начисляется в конце этого квартала r1 процентов, а на тот счет, который вкладчик имел в конце второго квартала, начисляется в конце этого квартала r2 процентов, причем r1+r2=150 . Вкладчик положил на счет в начале первого квартала некоторую сумму и снял в конце того же квартала половину этой суммы. При каком значении r1 счет вкладчика в конце второго квартала окажется максимально возможным?
Ответ: 100
Скрыть
Пусть S-первоначальная сумма вклада, тогда после первого начисления на счете $$S(1+frac{r_{1}}{100})$$, а после снятия половины первоначального вклада: $$S(1+frac{r_{1}}{100})-frac{S}{2}$$. Учтем, что $$r_{2}=150-r_{1}$$.
После второго начисления на счету : $$(S(1+frac{r_{1}}{100})-frac{S}{2})(1+frac{150-r_{1}}{100})=S(r_{1})$$
Необходимо найти точку максимума: $$S^{‘}(r_{1})=(S(frac{1}{2}+frac{r_{1}}{100})(frac{250-r_{1}}{100}))^{‘}=$$$$(S(frac{50+r_{1}}{200})(frac{250-r_{1}}{100}))^{‘}$$
При этом максимум $$S(r_{1})$$ совпадает с максимумом $$K(r_{1})=(50+r_{1})(250-r_{1})$$
$$K^{‘}(r_{1})=(250-r_{1})-(50+r_{1})=0Leftrightarrow$$ $$200-2r_{1}=0Leftrightarrow$$ $$r_{1}=100$$
Задание 18
При каких значениях параметра a неравенство $$log_{frac{-2a-13}{5}} (frac{sin x -sqrt{3}cos x -a-4}{5})>0$$ выполняется для любых значений x ?
Ответ: $$(-infty ;-11)cup (-7;-6,5)$$
Скрыть
Пусть $$m(x) =sin x-sqrt{3}cos x$$, тогда $$m^{‘}(x)=cos x+sqrt{3}sin x=0Leftrightarrow$$ $$sqrt{3}tg x=-1Leftrightarrow$$ $$x=-frac{pi}{6}+pi n , n in Z$$
$$m(-frac{pi}{6})=sin -frac{pi}{6}-sqrt{3}cos -frac{pi}{6}=-frac{1}{2}-frac{3}{2}=-2rightarrow m_{min}$$
$$m(frac{5pi}{6})=sin frac{5 pi}{6}-sqrt{3} cos frac{5 pi}{6}=2rightarrow m_{max}$$
Получим систему:
$$left{begin{matrix}(frac{-2a-13}{5}-1)(frac{m-a-4}{5}-1)>0(4)frac{-2a-13}{5}>0(1)frac{m-a-4}{5}>0(3)frac{-2a-13}{5}neq 1(2)end{matrix}right.$$
$$ (1): -2a-13>0Leftrightarrow a<-6,5$$
$$(2): -2a-13neq 5Leftrightarrow aneq -9$$
$$(3) :a<-6,5 , -a-4>2,5 Rightarrow frac{m-a-4}{5}>0$$ при любом m( и ,следовательно, x)
$$(4) :(-2a-18)(m-a-9)>0Leftrightarrow$$ $$left[begin{matrix}left{begin{matrix}-2a-18>0m-a-9>0end{matrix}right. left{begin{matrix}-2a-18<0m-a-9<0end{matrix}right.end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}left{begin{matrix}x<-9m-a-9>0end{matrix}right. (5)left{begin{matrix}x>-9m-a-9<0end{matrix}right.(6)end{matrix}right.$$
$$(5)$$: при $$a<-9$$: $$-a-9>0$$ при любом a , следовательно, чтобы было решение для любого m должно выполняться: $$m_{min}-a-9>0Leftrightarrow$$ $$-2-a-9>0Leftrightarrow$$ $$a<-11$$. Получим $$a in (-infty ;-11)$$
$$(6)$$ : аналогично $$m_{max}-a-9<0Rightarrow$$ $$2-a-9<0Rightarrow a>-7$$. Получим $$a in (-7; +infty )$$
С учетом (1): $$a in (-infty ;-11)cup (-7;-6,5)$$
Задание 19
Задано число от 1 до n. За один ход можно выбрать произвольное подмножество множества чисел от 1 до n и спросить, принадлежит ли ему заданное число. При ответе «да» будет начислено a баллов, при ответе «нет» – b баллов.
а) Можно ли наверняка угадать число, получив не менее 16 и не более 21 баллов, если $$a=3, b=1, n=128$$
б) Может ли n быть равным 144, если известно, что число можно наверняка угадать, получив не менее 11 баллов, и при этом $$a=2, 1leq bleq 4$$ ?
в) Какую наименьшую сумму баллов можно получить, чтобы наверняка угадать число, если $$a=3,b=1, 128leq nleq 170$$ ?
Ответ: а) да; б) нет; в) 8
Решение и ответы заданий № 1–12 варианта №345 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).
Задание 1.
Оплата за использование природного газа составляла 20 рублей на одного человека в месяц. С нового года она повысилась на 20%. Сколько рублей должна заплатить семья из трех человек за использование природного газа за три месяца в новом году?
Задание 2.
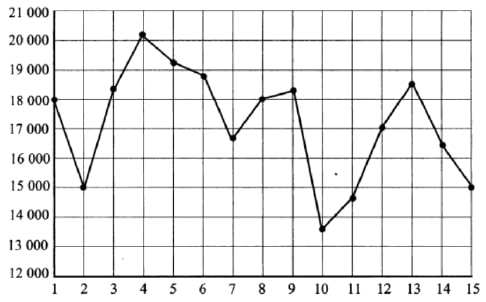
На рисунке жирными точками показана дневная аудитория некоторого сайта во все дни с 1 по 15 апреля 2020 года. По горизонтали указываются числа месяца, по вертикали – количество человек, посетивших сайт хотя бы раз за день. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько суток из данного периода дневная аудитория сайта была между 16000 и 19000 человек.
Задание 3.
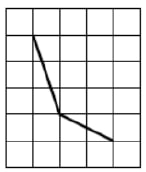
На клетчатой бумаге изображен угол. Найдите его величину. Ответ дайте в градусах.
Задание 4.
Пресс изготавливает стеклянные тарелки. Вероятность того, что готовая тарелка будет с дефектом, равна 0,05. Перед упаковкой каждая тарелка проходит систему контроля. Вероятность того, что система забракует тарелку с дефектом, равна 0,94. Вероятность того, что система по ошибке забракует тарелку без дефектов, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная тарелка будет забраковано системой контроля.
Задание 5.
Решите уравнение Если корней несколько, то в ответе укажите сумму всех корней уравнения.
Задание 6.
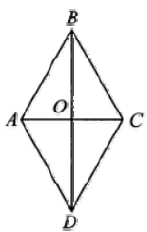
Диагонали ромба относятся как 5:12. Площадь ромба равна 30. Найдите периметр ромба.
Задание 7.
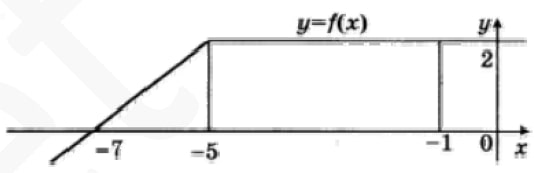
На рисунке изображен график некоторой функции y = f(x). Пользуясь рисунком, найдите интеграл .
Задание 8.
Найдите объём правильной шестиугольной пирамиды, если её боковое ребро равно 6, а радиус окружности, описанной около основания, равен 3.
Задание 9.
Найдите значение выражения
Задание 10.
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле 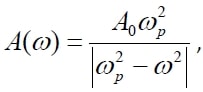
. Ответ выразите в с‐1.
Задание 11.
Петя и Вася живут в деревне в соседних домах и учатся в одной школе. Петя вышел в школу в 7:34, а Вася – в 7:40. Вася догнал Петю в 8:04 и 10 минут шли вместе. Затем Вася зашагал в своем привычном темпе. На сколько минут опоздал Петя, если урок начинается в 8:30, а Вася вошел в класс со звонком?
(Автор задачи Николай Журавлев)
Задание 12.
Найдите наибольшее значение функции y = 3cos x + – 3 на отрезке [
; 0]
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Сайт заблокирован за не оплату услуг хостинга или нарушения правил.
Бесплатный конструктор сайтов
Создайте сайт без технических знаний!
Большой выбор готовых шаблонов для создания сайта
Подробнее
Хостинг сайтов SSD от 55 рублей
У нас можно купить хостинг и получить бесплатно домен и SSL сертификат
Бесплатное тестирование хостинга
Подробнее
Регистрация доменов от 99 рублей
Мы гарантируем самые низкие цены на регистрацию доменов в популярных зонах
Подробнее
SSL сертификаты для сата от 399 рублей
Купите SSL сертификат для сайта и получите месяц хостинга бесплатно
Подробнее
VPS сервера от 209 рублей
Виртуальные серверы VPS с быстрой активацией услуг
Подробнее
Выделенный сервера от 3499 рублей
Огромный выбор выделенных серверов по всему миру
Подробнее
Ссылка на вариант —
https://alexlarin.net/ege/2022/trvar377.html
Друзья, нам очень нужна ваша помощь!
Пожалуйста, помогите развитию канала и пройдите небольшой опрос. Это займет 2-3 минуты. Мы будем вам за это очень признательны и в качестве благодарности отправим вам нашу СУПЕР методичку по параметрам.
Опрос: https://forms.gle/hRHftUiC1Gi65UDw8
Понравилось видео? Подпишись на канал!
Больше полезного контента:
Instagram: https://www.instagram.com/profimatika
VK: https://vk.com/profimatika
ПОДЕЛИТЬСЯ
Тренировочный вариант №377 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 15.01.2022 (15 января 2022 года)
-
Скачать вариант Ларина
-
Ответы для варианта
Решать вариант Алекса Ларина №377 ЕГЭ 2022 по математике 11 класс:
2)Найдите вероятность того, что при первых трех подбрасываниях выпадет одна и та же сторона монеты.
Ответ: 0,25
3)В трапеции АВСD известны длины оснований: AD = 36, BC = 12. Диагонали АС и BD пересекаются в точке О. Найдите площадь трапеции АВСD, если площадь треугольника AOD равна 216.
Ответ: 384
5)Высота правильной четырехугольной пирамиды равна 24, а объем пирамиды равен 784. Найдите боковое ребро этой пирамиды.
Ответ: 25
8)Для приготовления молочного коктейля использовали 200 г мороженого жирностью 10% и 300 г молока 6%‐ой жирности. Определите жирность полученного коктейля (в процентах).
Ответ: 7,6
10)Дана симметричная монета – при каждом ее подбрасывании выпадение «орла» или «решки» равновероятно. Эту монету подбросили шесть раз. Известно, что «решка» выпала ровно три раза. Найдите вероятность того, что при первых трех подбрасываниях монеты выпал «орел».
Ответ: 0,05
13)Основанием прямой треугольной призмы PQRP1Q1R1 является прямоугольный треугольник PQR с прямым углом R. Диагонали боковых граней PP1Q1Q и PP1R1R равны 17 и 15 соответственно, PQ = 10. А) Докажите, что треугольник P1QR прямоугольный. Б) Найдите объем пирамиды P1QRR1.
Ответ: б)24 корень из 21
18)Тридцать пять шариков массой 1 г, 2 г, …, 35 г разложили по двум коробкам, в каждой коробке находится хотя бы один шарик. Масса каждого шарика выражается целым числом граммов. Затем из второй коробки переложили в первую один шарик. После этого средняя масса шариков в первой коробке увеличилась на 4 г. А) Можно ли такое быть, если первоначально в первой коробке лежали только шарики массой 3г, 12 г и 27 г? Б) Могла ли средняя масса шариков в первой коробке первоначально равняться 12,6г? В) Какое наибольшее число шариков могло быть первоначально в первой коробке?
Ответ: а-да, б-нет, в-6
Смотрите другие варианты ЕГЭ 2022 по математике 11 класс
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.
| 3471 | а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. |
а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12 | |
| 3470 | В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней |
В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13 | |
| 3469 | Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x). |
Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14 |
|
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN |
На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ |
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3466 | Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) |
Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6 | |
| 3465 | Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? |
Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9 | |
| 3464 | а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. |
а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12 | |
| 3463 | SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 |
SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13 | |
| 3462 | Решите неравенство 2^(x/(x+1))-2^((5x+3)/(x+1))+8<=2^((2x)/(x+1)) |
Решите неравенство 2 x/x+1 -2 5x+3 / x+1 +8 <= 2 2x/x+1 ! Тренировочный вариант 398 от Ларина Задание 14 |
|

Показана страница 1 из 89




 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема