Задание 1
Решите уравнение $$11^{79}cdot(frac{1}{11})^xcdot(frac{1}{11})^{sqrt{x+11}}=1$$
Ответ: 70
Скрыть
$$79−x−sqrt{x+11}=0$$
$$sqrt{x+11}=79−x$$
ОДЗ: $$x<79$$
Возводим в квадрат
$$x+11=(79−x)^2$$
$$x^2−159x+6230=0$$
$$x=89$$ – не подходит под ОДЗ
$$x=70$$
Задание 2
Найдите вероятность того, что случайно выбранное трехзначное число делится на 34.
Ответ: 0,03
Скрыть
Всего трехзначных чисел $$900$$
Из них на $$34$$ делятся $$102, 136, 170, 204,…,986 (=34cdot3, 34cdot4, 34cdot5,…)$$ – всего их $$27$$ штук $$([900/34]=27)$$
$$P(A)=frac{27}{900}approx0,03$$
Задание 3
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 4 : 7 : 9. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 338.
Ответ: 117
Скрыть
Пусть $$y$$ – неизвестная сторона
Одно из свойств описанного четырехугольника это суммы противоположных сторон равны друг другу
$$4x+9x=7x+y$$
$$6x=y$$
$$x=frac{y}{6}$$
$$P=4x+7x+9x+y=338$$
$$20x+y=338$$
$$20x+6x=338$$
$$x=13$$
Большая сторона $$9x=117$$
Задание 4
Вычислите $$sin555^{circ}cdotsin1185^{circ}cdottg405^{circ}.$$
Ответ: -0,25
Скрыть
$$sin555°=sin(180°cdot3+15°)=−sin15°$$
$$sin1185°=sin(180°cdot6+105°)=sin105°=sin(90°+15°)=cos15°$$
$$tg405°=tg(360°+45°)=tg45°$$
$$−sin15°cdotcos15°cdottg45°=−0,5sin30°cdot1=−0,25$$
Задание 5
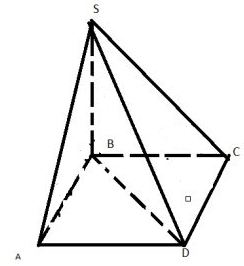
В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы $$30^{circ}$$ и $$45^{circ}$$. Найдите диагональ прямоугольника, если высота пирамиды равна 4.
Ответ: 8
Скрыть
$$SB⟂(ABCD)$$
$$BC$$ – проекция $$SC$$ на $$ABCD$$
$$BC⟂DC$$ (т.к прямоугольник)
Значит по теореме о 3-х перпендикулярах $$SC⟂DC$$, значит $$∠BCS$$ – есть линейный угол двугранного угла $$∠SBCD$$
Аналогично с $$∠ABS$$
Пусть $$∠BCS=45$$ и $$∠ABS=30$$
$$△SBC$$ – прямоугольный и р/б значит $$BC=SB=4$$
$$AB=frac{SB}{tg30}=4sqrt{3}$$
$$BD=sqrt{AB^2+BC^2}=8$$
Задание 6
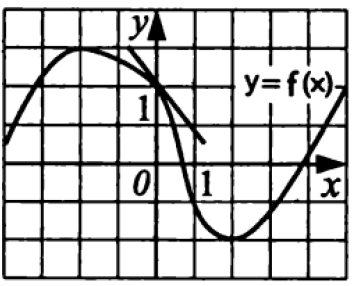
На рисунке изображены участки графика функции $$y=f(x)$$ и касательной к нему в точке с абсциссой $$x=0.$$ Известно, что данная касательная параллельна прямой, проходящей через точки графика с абсциссами $$x=-2$$ и $$x=2$$. Используя это, найдите значение производной $$f'(0)$$.
Ответ: -1,25
Скрыть
Если две прямые параллельные, то их угловые коэффициенты равны.
По геометрическому смыслу производной $$tgα=k$$
$$tgα=tg(180−β)=−tgβ$$
$$tgβ=frac{5}{4}=1,25Rightarrow -1,25$$
Задание 7
Автомобиль, масса которого равна $$m = 1200$$ кг, начинает двигаться с ускорением, которое в течение $$t$$ секунд остается неизменным, и проходит за это время путь $$S = 300$$ метров. Значение силы (в ньютонах), приложенное в это время к автомобилю, можно вычислить по формуле по формуле $$F = frac{2mS}{t^2}$$. Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила $$F$$, приложенная к автомобилю, не меньше 1800 Н. Ответ выразите в секундах.
Ответ: 20
Скрыть
$$frac{2cdot1200cdot300}{t^2}geq1800$$
$$t^2leq400$$
$$−20leq tleq 20$$
Наибольшее время $$t=20$$
Задание 8
Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач. Приобретая опыт, он в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Какое количество задач успеет прорешать школьник за остающиеся до олимпиады 4 недели, если будет увеличивать количество еженедельно решаемых задач прежним образом?
Ответ: 560
Скрыть
Из условия понятно, что задача на арифметическую прогрессию.
$$d=10$$
$$S_{10}=frac{2a_1+10cdot9}{2}cdot10=700$$
$$a_1=25$$
$$S_{14}=frac{2cdot25+10cdot13}{2}cdot14=1260$$
$$S_{14}−S_{10}=560$$
Задание 9
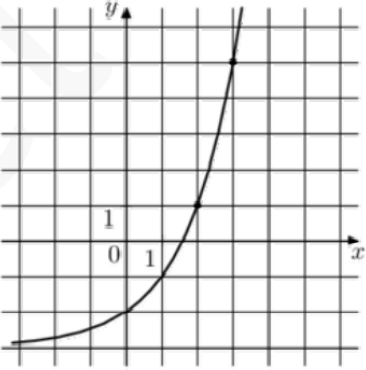
На рисунке изображен график функции $$f(x)=a^{x+b}$$. Найдите $$f(6)$$.
Ответ: 61
Скрыть
Из рисунка видно, какие точки удобнее всего взять
$$1=a^2+b$$
$$5=a^3+b$$
Вычтем одно из другого
$$a^3−a^2=4$$
$$a(a^2−a)=4$$, очевидно, что $$a=2$$
Значит, $$b=3$$
$$f(x)=2^x−3$$
$$f(6)=61$$
Задание 10
Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1, а если гвоздь медный, то он согнется с вероятностью 0,3. На столе вперемешку лежат 6 стальных и 4 медных гвоздя. Вася берет первый попавшийся гвоздь со стола и пытается забить его в доску. Найдите вероятность того, что этот гвоздь не согнется.
Ответ: 0,82
Скрыть
События:
$$A_1$$ — достанет стальной гвоздь и он не согнется
$$A_2$$ - достанет медный гвоздь и он не согнется
Они несовместные, значит
$$P(A)=P(A_1+A_2)=P(A_1)+P(A_2)$$
$$P(A_1)=frac{6}{10}cdot0,9=0,54$$
$$P(A_2)=frac{4}{10}cdot0,7=0,28$$
$$P(A)=0,54+0,28=0,82$$
Задание 11
Найдите наибольшее значение функции $$y=frac{3x-pi}{pi}cdotcos x-frac{3}{pi}cdotsin x+21$$ на отрезке $$[0;2pi]$$
Ответ: 26
Скрыть
Найдём критические точки $$y’=0$$
$$frac{3}{π}cdotcos x−frac{3x−π}{π}cdotsin x−frac{3}{π}cos x=0$$
$$−frac{3x−π}{π}cdotsin x=0$$
$$sin x=0x=πn$$
$$x=frac{π}{3}$$
Так как отрезок $$[0;2pi]$$, то подозрительные точки:
$$x=0,frac{π}{3},π,2π$$
Проверяем все.
$$y(2π)=26$$
Задание 12
А) Решите уравнение $$sqrt{3}sin^2 2x-2sin 4x+sqrt{3}cos^2 2x=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-1; 1]$$
Ответ: А)$$frac{pi}{12}+frac{pi n}{2};frac{pi}{6}+frac{pi n}{2},nin Z$$ Б)$$frac{pi}{12};frac{pi}{6}$$
Задание 13
Дана правильная шестиугольная призма $$ABCDEFA_1В_1С_1D_1E_1F_1$$ со стороной основания $$sqrt{3}$$ и боковым ребром $$1$$.
а) Докажите, что плоскости $$АСА_1$$ и $$В_1СЕ_1$$ перпендикулярны.
б) Найдите угол между плоскостями $$В_1СЕ_1$$ и $$АВС$$.
Ответ: $$arctgfrac{2}{3}$$
Задание 14
Решите неравенство: $$(x-1)(2log_3^2 x-5log_3 x+2)<0$$
Ответ: $$(0;1),(sqrt{3};9)$$
Задание 15
Билл несколько лет назад вложил деньги в акции некоего предприятия. Ежегодно он получал прибыль по акциям сначала $$9frac{1}{11}%$$ в год, потом $$37,5%$$ в год и, наконец, $$6frac{2}{3}%$$ в год и сразу же вкладывал деньги в те же акции. Известно, что одинаковые процентные ставки сохранялись равное число лет, в результате стоимость акций увеличилась на $$156%$$. Определите, сколько лет Билл получал прибыль по акциям.
Ответ: 6
Задание 16
Диагонали АС и BD трапеции ABCD пересекаются в точке О, ВС и AD — основания трапеции.
a) Докажите, что $$frac{S_{Delta ABO}}{S_{Delta AOD}}=frac{BC}{AD}$$.
б) Найдите площадь трапеции, если $$AD=4BC, S_{Delta AOB}=2$$.
Ответ: 12,5
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых уравнение:
$$frac{a}{25^x}-a=2-frac{25^{-2x}}{5}$$
имеет ровно 2 корня, хотя бы один из которых не менее 0,5.
Ответ: $$[-2,49;-2)$$
Задание 18
Натуральные числа от $$1$$ до $$n$$ в порядке возрастания записаны в строчку. Под ними записаны те же числа в другом порядке. Можно ли добиться того, что сумма каждого числа и записанного под ним была бы точным квадратом:
а) при $$n = 7$$;
б) при $$n = 12$$;
в) при $$n = 2015$$?
Ответ: А) нет, Б) да, В) да
| 3019 | Два бегуна одновременно побежали по круговому маршруту из одной и той же точки в противоположных направлениях. Первый бегун пробежал к месту их встречи на 500 м больше, чем второй. Продолжая бежать в том же направлении, первый прибежал к месту старта через 9 минут после встречи со вторым бегуном, а второй – через 16 минут после встречи. Какова длина кругового маршрута в метрах? Скорости обоих бегунов постоянны |
Два бегуна одновременно побежали по круговому маршруту из одной и той же точки в противоположных направлениях ! Тренировочный вариант 363 от Ларина Задание 8 (11) ЕГЭ | |
| 3006 | На рисунке изображен график функции f(x)=a^x+b. Найдите f(6) |
На рисунке изображен график функции f(x)=a^x+b. Найдите f(6) ! Тренировочный вариант 362 от Ларина Задание 9 ЕГЭ | |
| 3005 | В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 300 и 450. Найдите диагональ прямоугольника, если высота пирамиды равна 4 |
Найдите диагональ прямоугольника, если высота пирамиды равна 4 ! Тренировочный вариант 362 от Ларина Задание 5 (8) ЕГЭ | |
| 3004 | Вычислите sin(555^@)*sin(1185^@)*tg 405^@ |
Тренировочный вариант 362 от Ларина Задание 4 (9) | |
| 3003 | Найдите наибольшее значение функции y=(3x-pi)/pi*cos(x)-3/pi*sin(x)+21 на отрезке [0; 2pi]. |
Найдите наибольшее значение функции y= 3x -pi / pi cosx -3 /pi sinx +21 ! Тренировочный вариант 362 от Ларина Задание 11 (12) ЕГЭ | |
| 3002 | Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач. Приобретая опыт, он в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Какое количество задач успеет прорешать школьник за остающиеся до олимпиады 4 недели, если будет увеличивать количество еженедельно решаемых задач прежним образом? |
Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач ! Тренировочный вариант 362 от Ларина Задание 8 (11) ЕГЭ | |
| 2999 | Автомобиль, масса которого равна m = 1200 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S=300 метров. Значение силы (в ньютонах), приложенное в это время к автомобилю, можно вычислить по формуле F=(2mS)/t^2 Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 1800 Н. Ответ выразите в секундах |
Автомобиль, масса которого равна m = 1200 кг, начинает двигаться с ускорением !Тренировочный вариант 362 от Ларина Задание 7 (10) | |
| 2998 | Найдите вероятность того, что случайно выбранное трехзначное число делится на 34 |
Найдите вероятность того, что случайно выбранное трехзначное число делится на 34 !Тренировочный вариант 362 от Ларина Задание 2 (4) | |
| 2997 | Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1, а если гвоздь медный, то он согнется с вероятностью 0,3. На столе вперемешку лежат 6 стальных и 4 медных гвоздя. Вася берет первый попавшийся гвоздь со стола и пытается забить его в доску. Найдите вероятность того, что этот гвоздь не согнется |
Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1 !Тренировочный вариант 362 от Ларина Задание 10 (4) | |
| 2996 | Дана правильная шестиугольная призма АВСDEFА1В1С1D1E1F1 cо стороной основания sqrt3 и боковым ребром 1. а) Докажите, что плоскости АСА1 и В1СЕ1 перпендикулярны. б) Найдите угол между плоскостями В1СЕ1 и АВС |
Дана правильная шестиугольная призма АВСDEFА1В1С1D1E1F1 cо стороной основания корень из 3 и боковым ребром 1 ! Тренировочный вариант 362 от Ларина Задание 13 (14) | |

Показана страница 1 из 2
| Clear |
Тренировочный вариант №362 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 02.10.2021 (2 октября 2021 года)
Задания варианта №362 ЕГЭ 2022: скачать
Ответы для варианта: скачать
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 cодержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
Решать тренировочный вариант Ларина №362 ЕГЭ 2022 по математике:
Ответы для варианта
Сложные задания и ответы с варианта:
2)Найдите вероятность того, что случайно выбранное трехзначное число делится на 34.
Ответ: 0,03
3)Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 4 : 7 : 9. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 338.
Ответ: 117
5)В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 300 и 450. Найдите диагональ прямоугольника, если высота пирамиды равна 4.
Ответ: 8
8)Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач. Приобретая опыт, он в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Какое количество задач успеет прорешать школьник за остающиеся до олимпиады 4 недели, если будет увеличивать количество еженедельно решаемых задач прежним образом?
Ответ: 560
10)Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1, а если гвоздь медный, то он согнется с вероятностью 0,3. На столе вперемешку лежат 6 стальных и 4 медных гвоздя. Вася берет первый попавшийся гвоздь со стола и пытается забить его в доску. Найдите вероятность того, что этот гвоздь не согнется.
Ответ: 0,82
15)Билл несколько лет назад вложил деньги в акции некоего предприятия. Ежегодно он получал прибыль по акциям сначала 1 9 % в год, потом в год и, наконец, 11 37,5% 2 6 % 3 в год и сразу же вкладывал деньги в те же акции. Известно, что одинаковые процентные ставки сохранялись равное число лет, в результате стоимость акций увеличилась на 156% . Определите, сколько лет Билл получал прибыль по акциям.
Ответ: 6
18)Натуральные числа от 1 до в порядке возрастания записаны в строчку. Под ними записаны те же числа в другом порядке. Можно ли добиться того, что сумма каждого числа и записанного под ним была бы точным квадратом: n n Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания. а) при = 7; б) при n = 12; в) при n = 2015?
Ответ: а-нет, б-да, в-да
Видео разбор каждого задания варианта
Смотрите также другие варианты ЕГЭ 2022 Ларина:
-
Тренировочный вариант Ларина №360 ЕГЭ 2022 по математике с ответами
-
Тренировочный вариант Ларина №361 ЕГЭ 2022 по математике с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
А. Ларин. Тренировочный вариант № 362.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1 cо стороной основания и боковым ребром 1.
а) Докажите, что плоскости ACA1 и B1CE1 перпендикулярны.
б) Найдите угол между плоскостями B1CE1 и ABC.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Билл несколько лет назад вложил деньги в акции некоего предприятия. Ежегодно он получал прибыль по акциям сначала % в год, потом 37,5% в год и, наконец,
% в год и сразу же вкладывал деньги в те же акции. Известно, что одинаковые процентные ставки сохранялись равное число лет, в результате стоимость акций увеличилась на 156%. Определите, сколько лет Билл получал прибыль по акциям.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Диагонали AC и BD трапеции ABCD пересекаются в точке O, BC и AD — основания трапеции.
а) Докажите, что
б) Найдите площадь трапеции, если AD = 4BC,
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых уравнение
имеет ровно 2 корня, хотя бы один из которых не менее 0,5.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Натуральные числа от 1 до n в порядке возрастания записаны в строчку. Под ними записаны те же числа в другом порядке. Можно ли добиться того, что сумма каждого числа и записанного под ним была бы точным квадратом:
а) при n = 7;
б) при n = 12;
в) при n = 2015?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Канал видеоролика: Математикс
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #учиться #e_math #егэматематика
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
Разбор Задачи №19 из Варианта Ларина №276
Математикс

Разбор Задачи №13 из Варианта Ларина №277
Математикс

Разбор Задачи №15 из Варианта Ларина №277
Математикс

Разбор Задачи №18 из Варианта Ларина №277
Математикс
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
03.10.2021
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Сайт заблокирован за не оплату услуг хостинга или нарушения правил.
Бесплатный конструктор сайтов
Создайте сайт без технических знаний!
Большой выбор готовых шаблонов для создания сайта
Подробнее
Хостинг сайтов SSD от 55 рублей
У нас можно купить хостинг и получить бесплатно домен и SSL сертификат
Бесплатное тестирование хостинга
Подробнее
Регистрация доменов от 99 рублей
Мы гарантируем самые низкие цены на регистрацию доменов в популярных зонах
Подробнее
SSL сертификаты для сата от 399 рублей
Купите SSL сертификат для сайта и получите месяц хостинга бесплатно
Подробнее
VPS сервера от 209 рублей
Виртуальные серверы VPS с быстрой активацией услуг
Подробнее
Выделенный сервера от 3499 рублей
Огромный выбор выделенных серверов по всему миру
Подробнее
вариант 295 ответы#295
************************
алекс ларин 293 вариант егэ, алекс ларин вариант 293, алекс ларин решение варианта 293, александр ларин вариант 293, вариант ларина 293, ларин 293 вариант, ларин вариант 293 решение, ларин егэ, ларин егэ 293 вариант, математика вариант, решение 293 варианта ларина, решение варианта 293, решение варианта 293 егэ ларин, тренировочный вариант, тренировочный вариант математика
Решаем ЕГЭ 262 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №262 (alexlarin.com)
Решаем ЕГЭ 262 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №262 (alexlarin.com)
Задание 1
В магазине «Сделай сам» мебель продается в разобранном виде. Если покупателю необходимо, он может купить собранную мебель, но в таком случае он должен оплатить сборку, которая составляет 15% от стоимости покупки. Сколько стоит собранный кухонный шкаф, если без сборки он продается за 3200 руб.?
Ответ: 3680
Скрыть
Пусть x руб. – стоимость собранно шкафа, тогда :
x руб.-115%
3200 руб.-100%
$$x=frac{3200*115}{100}=3680$$ рублей.
Задание 2
На диаграмме показана среднемесячная температура воздуха в Санкт‐Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной среднемесячной температурой.
Ответ: 5
Скрыть
Отрицательная была : январь, февраль , март, ноябрь, декабрь — 5 месяцев .
Задание 3
Клетка имеет размер 1 см 1 см. Найдите площадь закрашенной фигуры в квадратных сантиметрах.
Ответ: 11
Скрыть
Разобьем данною фигуру на несколько других:
$$S_{1}=frac{1}{2}*6*1=3$$
$$S_{2}=frac{6+2}{2}*1=4$$
$$S_{3}=2*4-frac{1}{2}*2*1*4=4$$
Тогда площадь данной составляет сумму площадей найденных: $$S=S_{1}+S_{2}+S_{3}=3+4+4=11$$
Задание 4
На чашке с ампицилином в среднем из 100 бактерий 1–го вида выживает 20, а из 100 бактерий 2‐го вида выживает 5. Какова вероятность выживания бактерии в условиях этого эксперимента, если соотношение бактерий 1‐го и 2‐го видов в посеве 1:2?
Ответ: 0,1
Скрыть
Пусть x-кол-во первого вида, тогда 2x-второго вида. Выживут из первого : $$frac{20}{100}x=0,2x$$. Из второго: $$frac{5}{100}*2x=0,1x$$. Всего бактерий: $$2+2x=3x$$. Всего выживут: $$0,2+0,1x=0,3x$$. Вероятность выживания: $$P=frac{0,3x}{3x}=0,1$$
Задание 5
Решите уравнение $$2^{7-x}=100*5^{x-7}$$
Ответ: 5
Скрыть
$$2^{7-x}=100*5^{x-7}Leftrightarrow$$ $$frac{2^{7-x}}{5^{x-7}}=2^{2}*5^{2}Leftrightarrow$$ $$2^{7-x}*5^{7-x}=2^{2}*5^{2}Leftrightarrow$$ $$(2*5)^{7-x}=(2*5)^{2}Leftrightarrow$$ $$7-x=2Leftrightarrow$$ $$x=5$$
Задание 6
В треугольнике ABC, в котором $$angle A=30^{circ}, angle B=105^{circ}$$ проведена медиана CM. Найдите $$angle MCA$$. Ответ дайте в градусах.
Ответ: 15
Скрыть
- $$angle C=180-angle A-angle B=45$$
- Пусть BN – высота $$Rightarrow$$ из $$Delta ABN$$: $$angle ABN=60Rightarrow$$ $$angle NBC=45$$ $$Rightarrow$$ из $$Delta BNC$$: $$angle NCB=45$$ $$Rightarrow$$ $$BN=NC=alpha$$
- из $$Delta ABN$$: $$AB=frac{BN}{sin 30}=frac{x}{frac{1}{2}}=2xRightarrow$$ $$NM=frac{AB}{2}=x$$ (медиана в прямоугольном треугольнике)
- из $$Delta MBN$$: $$angle MNB =60Rightarrow$$ $$angle MNC=60+90=150Rightarrow$$ $$angle MCA=frac{180-150}{2}=15$$
Задание 7
Прямая, параллельная оси абсцисс, касается графика функции $$f(x)=-2x^{2}+6x-7$$ . Найдите ординату точки касания.
Ответ: -2,5
Скрыть
Пусть y=a — прямая, параллельная Ox $$Rightarrow$$ $${y}’=0$$. Раз касается f(x) , то и $${f}'(x)=0$$ ( в точке касания ): $$-4x+6=0 Rightarrow$$ $$x=1,5$$. Найдем ординату точки касания: $$f(1,5)=-2*1,5^{2}+6*1,5-7=-2,5$$
Задание 8
Найдите объём пирамиды, изображённой на рисунке. Её основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых рёбер перпендикулярно плоскости основания и равно 3.
Ответ: 27
Скрыть
Найдем объем пирамиды без учета выреза: $$V_{1}=frac{1}{3}*6*6*3=36$$
Найдем объем вырезанной: $$V_{2}=frac{1}{3}*3*3*3=9$$
Найдем объем оставшейся: $$V=V_{1}-V_{2}=27$$
Задание 9
Найдите значение выражения $$frac{(sqrt[7]{8}*sqrt[3]{81})^{21}}{18^{12}}$$
Ответ: 10,125
Скрыть
$$frac{(sqrt[7]{8}*sqrt[3]{81})^{21}}{18^{12}}=$$$$frac{(8^{frac{1}{7}}*81^{frac{1}{3}})^{21}}{(2*3^{2})^{12}}=$$$$frac{8^{3}*81^{7}}{2^{12}*3^{24}}=$$$$frac{((2^{3})^{3})*(3^{4})^{7}}{2^{12}*3^{24}}=$$$$frac{2^{9}*3^{28}}{2^{12}*3^{24}}=frac{3^{4}}{2^{3}}=10,125$$
Задание 10
В дне цилиндрического бака имеется кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в сантиметрах, меняется по закону $$H(t)=at^{2}+bt+c$$ , где $$a=0,6$$ см/мин2, b (см/мин)– постоянные параметры, t – время в минутах, прошедшее с момента открытия крана. Известно, что через 10 минут после открытия крана вся воды вытечет из бака. Каким будет уровень воды в баке через 6 минут после открытия крана? Ответ выразите в см.
Ответ: 24
Скрыть
Найдем b : $$H(10)=0=0,6*10^{2}+b*10+96Leftrightarrow$$ $$60+10b+96=0Leftrightarrow$$ $$b=15,6$$
Тогда через 6 минут: $$H(6)=0,6*6^{2}-15,6*6+96=117,6-93,6=24$$
Задание 11
Товарный поезд каждую минуту проезжает на 500 метров меньше, чем скорый, и на путь в 120 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Ответ: 30
Скрыть
За минуту на 500м =0,5 км. , следовательно, за час: 0,5*60=30км. Пусть x кмч – скорость товарного, тогда x+30 кмч – скорость скорого. $$frac{120}{x}$$ — время товарного , $$frac{120}{x+30}$$ – время скорого.
$$frac{120}{x}-frac{120}{x+30}=2Leftrightarrow$$ $$frac{60}{x}-frac{60}{x+30}=1Leftrightarrow$$$$60x+1800-60x=x^{2}+30xLeftrightarrow$$ $$x^{2}+30x-1800=0$$
$$left{begin{matrix}x_{1}+x_{2}=-30x_{1}*x_{2}=-1800end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x_{1}=-60x_{2}=30end{matrix}right.$$.
Скорость не может быть отрицательной $$Rightarrow$$ 30 км/ч
Задание 12
Найдите точку максимума функции $$y=x^{2}e^{x}$$
Ответ: -2
Скрыть
$$y=x^{2}*e^{x}Rightarrow$$ $${y}’={(x^{2})}’e^{x}+{e^{x}}’*x^{2}=$$$$2xe^{x}+e^{x}*x^{2}Leftrightarrow$$ $$e^{x}(2x+x^{2})=0$$
Т.к. $$e^{x}>0$$ при любом x $$Rightarrow$$ $$x(2+x)=0Leftrightarrow$$ $$left{begin{matrix}x=0 rightarrow minx=-2rightarrow maxend{matrix}right.$$
Задание 13
а) Решите уравнение $$sqrt{21}cos x*ctg x-sqrt{7}cos x-sqrt{7}ctg x=0$$ б) Укажите корни этого уравнения, принадлежащие отрезку $$[-pi;pi]$$
Ответ: А) $$x=frac{pi}{2} + pi n , n in Z$$; $$frac{pi}{6}+2 pi k , k in Z$$ Б) $$pm frac{pi}{2};frac{pi}{6}$$
Скрыть
А) ОДЗ: $$sin xneq 0 Leftrightarrow$$ $$xneq pi n , n in Z$$
$$sqrt{7} cos x(sqrt{3} ctg x-1-frac{1}{sin x})=0Leftrightarrow$$$$left{begin{matrix}cos x=0(1)sqrt{3} ctg x-1-frac{1}{sin x}=0 (2)end{matrix}right.$$
1) $$cos x=0Leftrightarrow$$ $$x=frac{pi }{2}+pi n , n in Z$$
2) $$frac{sqrt{3}cos x}{sin x}-frac{1}{sin x}-1=0Leftrightarrow$$ $$frac{sqrt{3 } cos x-sin x-1}{sin x}=0Leftrightarrow$$ $$sqrt{3} cos x-sin x=1 Leftrightarrow$$ $$frac{sqrt{3}}{2} cos x-frac{1}{2}sin x=frac{1}{2}Leftrightarrow$$ $$sin frac{pi}{3} cos x-cos frac{pi}{3}sin x=frac{1}{2}Leftrightarrow$$ $$sin x cos frac{pi}{3}-cos x sin frac{pi}{3}=-frac{1}{2}Leftrightarrow$$ $$sin (x-frac{pi}{3})=-frac{1}{2}Leftrightarrow$$ $$left[begin{matrix}x-frac{pi}{3}=-frac{pi}{6}+2 pi k , k in Zx-frac{pi}{3}=-frac{5 pi}{6}+2 pi kend{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x=frac{pi}{6}+2 pi kx=-frac{pi}{2}+2 pi k , k in Zend{matrix}right.$$
Б) На промежутке $$[-pi;pi]$$:
$$frac{pi}{2}+pi n: -frac{pi}{2}; frac{pi}{2}$$
$$frac{pi}{6}+2 pi k: frac{pi}{6}$$
Задание 14
Основанием пирамиды SABC является правильный треугольник, длина стороны которого равна $$sqrt{3}$$. Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника АВС. Расстояние от точки О до стороны АС равно 1. Синус угла ОВА относится к синусу угла ОВС как 2:1. Площадь грани SAB равна $$sqrt{frac{5}{6}}$$.
А) Найдите объем пирамиды
Б) Найдите расстояние от точки А до плоскости SBC
Ответ: $$frac{9}{sqrt{37}}$$
Скрыть
A) 1) Пусть $$OL perp CB$$; $$OMperp AB$$; $$OKperp AC$$ .
Из $$Delta MOB$$: $$sin angle OBA=frac{OM}{OB}$$
Из $$Delta OLB$$: $$sin angle OBL =frac{OL}{OB}$$
По условию $$frac{sin angle OBA}{sin angle OBL}=2Rightarrow$$ $$OM=2OL$$. Пусть $$OM=2xRightarrow$$ $$OL=x$$
2) $$S_{ABC}=S_{AOB}+S_{AOC}+S_{COB}Leftrightarrow$$ $$frac{1}{2} AC^{2} sin 60=frac{1}{2} AB(OM+OL+OK)Leftrightarrow$$ $$sqrt{3} frac{sqrt{3}}{2}=1+x+2xLeftrightarrow$$ $$3x=frac{1}{2}Leftrightarrow$$ $$x=frac{1}{6}Rightarrow$$ $$OM=frac{1}{3}; OL=frac{1}{6}$$
3) $$S_{ABS}=frac{sqrt{5}}{sqrt{6}}=frac{1}{2}AB*SM$$ ($$OMperp AB$$; $$SOperp (ABC)$$$$Rightarrow$$ $$AMperp AB$$), тогда : $$SM=frac{sqrt{5}}{sqrt{6}}*frac{2}{1}*frac{1}{sqrt{3}}=frac{sqrt{10}}{3}$$
4) из $$Delta MOS$$: $$SO=sqrt{SM^{2}-OM^{2}}=1$$
5) $$V_{ABC}=frac{1}{3} S_{ABC}*SO=$$$$frac{1}{3}*frac{3sqrt{3}}{4}*1=frac{sqrt{3}}{4}$$
Б) 1) Аналогично (3): $$SLperp CB$$. Пусть $$ONperp SLRightarrow$$ $$ON$$ – расстояние от O до (SBC). Пусть $$AL_{1}left | right |AL$$ и $$AN_{1}$$ — расстояние от A до (SBC) , тогда $$Delta AL_{1}N_{1}sim Delta OLN$$ и $$frac{AN_{1}}{ON}=frac{AL_{1}}{OL}$$
2) из $$Delta OSL$$: $$SL=sqrt{OS^{2}+OL^{2}}=frac{sqrt{37}}{6}$$; $$ON=frac{OS*OL}{SL}=frac{1}{sqrt{37}}$$
3) из $$Delta ABC$$ : $$AL_{1} =AB sin 60=frac{3}{2}Rightarrow$$ $$AN_{1} :frac{1}{sqrt{37}}=frac{3}{2}:frac{1}{6}Rightarrow$$ $$AN_{1}=frac{9}{sqrt{37}}$$
Задание 15
Решите неравенство $$log_{(x+1)^{2}}8+3log_{4}(x+1)geq frac{37}{4}$$
Ответ: $$(0; sqrt[6]{2}-1]cup [63; +infty )$$
Скрыть
ОДЗ: $$left{begin{matrix}(x+1)^{2}>0(x+1)^{2}neq 1x+1>0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x+1neq 0x+1neq 1xneq 1=-1x>-1end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}xneq -1xneq 0xneq -2x>-1end{matrix}right.Leftrightarrow$$$$x in (-1; 0)cup (0; +infty )$$
Решение: $$log_{(x+1)^{2}}2^{3}+3log_{2^{2}}(x+1)geq frac{37}{4}Leftrightarrow$$$$frac{3}{2}log_{left | x+1 right |}2+frac{3}{2}log_{2}(x+1)geq frac{37}{4}$$
С учетом, что $$x+1>0$$: $$left | x+1 right |=x+1$$: $$frac{1}{log_{2}(x+1)}+log_{2}(x+1)geq frac{37}{6}$$
Пусть $$log_{2}(x+1)=y$$: $$frac{1}{y}+y-frac{37}{6}geq 0Leftrightarrow$$ $$frac{6y^{2}-37y+6}{y}geq 0Leftrightarrow$$ $$frac{6(y-6)(y-frac{1}{6})}{y}geq 0$$
$$left[begin{matrix}left{begin{matrix}y>0xleq frac{1}{6}end{matrix}right.ygeq 6end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}left{begin{matrix}log_{2}(x+1)>0log_{2}(x+1)leq frac{1}{6}end{matrix}right.log_{2}(x+1)geq 6end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}left{begin{matrix}x+1>1x+1leq sqrt[6]{2}end{matrix}right.x+1geq 64end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}left{begin{matrix}x>0xleq sqrt[6]{2}-1end{matrix}right.xgeq 63end{matrix}right.$$
С учетом ОДЗ: $$x in (0; sqrt[6]{2}-1]cup [63; +infty )$$
Задание 16
Окружность, вписанная в равнобедренный треугольник АВС, касается основания АС в точке D и боковой стороны АВ в точке Е. Точка F – середина стороны АВ, а точка G – точка пересечения окружности и отрезка FD, отличная от D. Касательная к окружности, проходящая через точку G, пересекает сторону АВ в точке Н. Известно, что FH:HE=2:3.
А) Докажите, что $$angle HGE=angle EDG$$
Б) Найдите $$angle BCA$$
Ответ: $$arccos frac{3}{4}$$
Скрыть
А) 1) $$angle HGE$$ — угол между хордой EG и касательной HG$$Rightarrow$$ $$angle HGE=frac{smile EG}{2}$$
2) $$angle EDG$$ — вписанный $$Rightarrow$$ $$angle EDG=frac{smile EG}{2}Rightarrow$$ $$angle HGE=angle EDG$$
Б) 1) $$AF=FD$$ (по условию ) $$AD=DCRightarrow$$ FD-средняя линия и $$FD=frac{AB}{2}=frac{BC}{2}$$; $$angle HAD=angle FDA$$
2) Пусть $$H in BE$$; $$angle A=angle C=alpha Rightarrow$$ $$angle FDA=alpha$$; $$FH=2xRightarrow$$ $$HE=3x$$
3) из $$Delta AFD$$: $$angle AFD=180-2angle A=180-2alpha$$; Из AEOD: $$angle O=180-angle A=180-alpha$$; $$angle DGE=frac{smile ED}{2}=frac{angle O}{2}=90-frac{alpha }{2}$$
Из $$Delta EFG$$: $$angle FEG +angle EFG=angle DGERightarrow$$ $$angle FEG=angle DGE-angle EFG=frac{3alpha }{2}-90$$
4) $$Delta EGH$$ – равнобедренный (образован касательными) $$Rightarrow$$ $$angle HGE=HEG=frac{3alpha }{2}-90Rightarrow$$ $$angle GHF=2angle HGE=3alpha -180$$(внешний угол $$Delta EGH$$)
5) $$Delta FGH=180-angle GHF-angle F=180-alpha$$ (из $$Delta EGH$$)
6) из $$Delta FHG$$: по т. Синусов: $$frac{FH}{sin angle FGH}=frac{HG}{sin angle GHF}$$, но $$HG=HERightarrow$$ $$frac{2x}{sin (180-alpha )}=frac{3x}{sin (180-2alpha )}Leftrightarrow$$ $$frac{2}{sin alpha }=frac{3}{sin 2alpha }Leftrightarrow$$ $$2 sin 2alpha -3 sin alpha =0Leftrightarrow$$ $$4 sin alpha cos alpha -3 sin alpha =0 Leftrightarrow$$ $$sin alpha (4 cos alpha -3)=0 Leftrightarrow$$ $$cos alpha =frac{3}{4}Rightarrow$$ $$alpha =arccos frac{3}{4}$$($$sin alpha$$ не может быть 0 )
Задание 17
Два одинаковых поля требуется вспахать тремя тракторами. При работе в одиночку первый трактор вспашет одно поле втрое быстрее, чем второй, а третьему на ту же работу потребуется времени на два часа больше, чем первому. Работая вместе, все три трактора могут вспахать одно поле за семь часов двенадцать минут. Найти наименьшее время, за которое можно вспахать оба поля при условии, что все тракторы начинают работу одновременно, а для переезда с одного поля другое трактору требуется сорок минут.
Ответ: 14,5
Скрыть
Пусть объем всего поля равен 1. x — производительность 1-го трактора (часть объема в час) , y, z — второго и третьего, t — время первого в часах . Раз первый вспахает втрое быстрее , то $$y=frac{x}{3}$$. Получим ( раз втроем вспахивают за 7 ч 12 мин.):
$$frac{1}{x+y+z}=7frac{12}{60}Leftrightarrow$$ $$frac{1}{x+frac{x}{3}+z}=frac{36}{5}Leftrightarrow$$ $$5=frac{4x}{3}*36+36zLeftrightarrow$$ $$z=frac{5-48x}{36}$$
Так как третий на 2 часа больше, то : $$left{begin{matrix}frac{1}{x}=tfrac{1}{z}=t+2end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}frac{1}{x}=tfrac{36}{5-48x}=frac{1}{x}+2end{matrix}right.$$
$$frac{36}{5-48x}=frac{1+2x}{x}Leftrightarrow$$ $$36x=5+10x-48x-96x^{2}Leftrightarrow$$ $$96x^{2}+74x-5=0Leftrightarrow$$ $$left{begin{matrix}x_{1}=frac{1}{16}x_{2}<0end{matrix}right.$$
Пусть три трактора работают x часов на каких-то полях, тогда они выполняют $$frac{5}{36}x$$ объема. Затем один или несколько переезжают (чтобы ускорить другое поле и закончить оба одновременно), тогда производительность оставшихся S и выполнят они $$S*frac{2}{3}$$ объема . Потом все трое дорабатывают вместе y часов: $$frac{5}{36}x+frac{2}{3}S+frac{5}{36}y=2Leftrightarrow$$ $$frac{5}{36}(x+y)=2-frac{2}{3}S$$
Очевидно, что $$x+yrightarrow min$$, при $$Srightarrow max$$: $$S_{max}=frac{1}{16}+frac{1}{18}=frac{17}{144}$$. Тогда : $$x+y=(2-frac{2}{3}*frac{17}{144})*frac{36}{5}=$$$$frac{415}{216}*frac{36}{5}=frac{83}{6}$$
Тогда общее время: $$frac{83}{6}+frac{2}{3}=14,5$$
Задание 18
Найдите все значения параметра a, при которых уравнение $$left | frac{x(3^{x}-1)}{3^{x}+1} -2aright |=a^{2}+1$$ имеет нечетное число решений.
Ответ: $$pm 1$$
Скрыть
Пусть $$(x)=frac{x(3^{x}-1)}{3^{x}+1}$$ и $$g(x)=a^{2}+1$$
1) $$f(x) geq 0$$ при любом x. Найдем промежутки возрастания и убывания: $${f}'(x)=frac{(x{(3^{x}-1)}'(3^{x}+1)-{(3^{x}+1)}'(x(3^{x}-1)))}{(3^{x}+1)^{2}}=0|* (3^{x}+1)^{2}Leftrightarrow$$$$((3^{x}-1)+x*3^{x}ln 3)(3^{x}+1)-3 ^{x}ln 3* x(3^{x}-1)=0Leftrightarrow$$ $$3 ^{2x}-1+3^{2x}*xln 3+x*3^{x}ln 3-x*3^{2x}ln 3 +3 ^{x}*xln 3=0Leftrightarrow$$ $$3 ^{2x}-1+2x*3^{2x}ln 3=0Leftrightarrow$$ $$3^{2x}+2x*3 ^{x}ln 3=1Leftrightarrow$$ $$1-2xln3=3^{x}$$
Пусть $$m(x)=1-2xln 3$$ и $$n(x) =3^{x}$$: m(x) — линейная убывающая и n (x)-степенная возрастающая $$Rightarrow$$ одна точка пересечения x=0
Для f(x): x=0 — точка минимума $$Rightarrow$$ $$(-infty ; 0)$$ – убывает монотонно, $$(0; +infty )$$ — возрастает . При этом
$$left | frac{x(3^{x}-1)}{3^{x}+1}-2a right |=f_{1}(x)$$ — это график f(x), у которого вся часть графика под Ox отражается симметрично относительно Ox. g(x) –прямая, параллельная Ox ($$a^{2}+1>0$$, при любом a ). Тогда возможен только один вариант нечетного числа корней, когда $$left | 2a right |=a^{1}+1Leftrightarrow$$ $$a^{2}-left | 2a right |+1=0Leftrightarrow$$ $$(left | a right |-1)^{2}=0Leftrightarrow$$ $$a=pm 1$$
2) Возможно решение с использованием инвариантности: доказать четность левой функции (f(-x)=f(x)), тогда нечетное количество решений будет лишь в том случае, когда один из корней равен 1. Подставить вместо х в начальное уравнение 1 и получим сразу уравнение отностильно а
Задание 19
В последовательности 19752… каждая цифра, начиная с пятой, равна последней цифре суммы предыдущих четырёх цифр. Встретится ли в этой последовательности:
а) набор цифр 1234; 3269;
б) вторично набор 1975;
в) набор 8197?
Ответ: нет, да, да
Скрыть
А) Рассмотрим последовательность: 19752.. Сначала идет сумма 4 нечетных , что даст четное. Затем получим 19752d , где d –нечетное (т.к. получается из суммы трех нечетных (9,7,5) и четного) Далее , аналогично , из 19752defgh, цифры e,f,g-нечетные и h-четные . Т.е. будет всегда на 4 нечетных и 1 четное , тогда 1234 и 3269 не получается никак.
Б) Докажем, что четверка цифр однозначно и единственно определяет последующее и предыдущее . Пусть дано a b c d. Допустим, что не определяет, тогда есть числа m и n такие, что $$frac{m+a+b+c}{10}$$ и $$frac{n+a+b+c}{10}$$ в остатке даст d. Тогда $$m-n$$ кратно 10 , но m и n цифры от 0 до 9 и не могут в разности быть кратны 10. Значит доказано. Но последовательность вида a b c d не могут быть больше 10^{4} (каждая цифра от 0 до 9 — 10 штук и всего их 4), то есть они могут повториться в силу единственности определения последующего $$Rightarrow$$ 1975 снова появится.
В) Раз 1975 снова появятся , то перед ним однозначно будет 8, т.к. $$frac{8+1+9+7}{10}$$ в остатке дает 5.