Задание 1
Решите уравнение $$2^{x^2-3}cdot5^{x^2-3}=0,01cdot(10^{x-1})^3$$. В ответе запишите сумму всех корней уравнения.
Ответ: 3
Скрыть
$$10^{x^2−3}=10^{−2}cdot10^{3(x−1)}$$
$$x^2−3=3(x−1)−2$$
$$x^2−3x+2=0$$
$$x=1$$
$$x=2$$
Задание 2
Игральный кубик бросают дважды. Найдите вероятность того, что сумма выпавших очков будет меньше, чем 4. Ответ округлите до сотых.
Ответ: 0,08
Скрыть
Всего $$6cdot6=36$$ вариантов
Благоприятные {1,1},{1,2},{2,1} – 3 исхода
$$P(A)=frac{3}{36}approx0,08$$
Задание 3
Радиус окружности, вписанной в прямоугольный треугольник, равен 6. Найдите гипотенузу, если точка касания с вписанной окружностью делит ее на отрезки, длины которых относятся как 5 : 12.
Ответ: 34
Скрыть
Отрезки касательных, проведённые из одной точки, равны.
Значит, по теореме Пифагора:
$$(17x)^2=(5x+6)^2+(12x+6)^2$$, $$(r=6)$$
Решаем квадратное уравнение:
$$left{begin{matrix} x=-frac{3}{10}; -; не; подходит; x>0\ x=2 end{matrix}right.$$
$$AC=17x=17cdot2=34$$
Задание 4
Вычислите $$log_{16}a-log_{16}b$$, если $$a — 4b = 0$$.
Ответ: 0,5
Скрыть
$$frac{a}{b}=4$$
$$log_{16}a−log_{16}b=log_{16}frac{a}{b}=log_{16}4=0,5$$
Задание 5
В правильной треугольной пирамиде боковое ребро равно 15, а тангенс угла между боковой гранью и плоскостью основания равен $$sqrt{23}$$. Найдите сторону основания пирамиды.
Ответ: 10
Скрыть
Пусть сторона основания $$a$$
$$OM=frac{asqrt{3}}{6}$$
$$SO=frac{asqrt{3}cdotsqrt{23}}{6}=frac{asqrt{69}}{36}$$
$$OC=frac{asqrt{3}}{3}$$
$$SO^2+OC^2=225$$
$$frac{69a^2}{36^2}+frac{3a^2}{9}=225$$
$$15=sqrt{frac{69a^2}{36}+frac{3a^2}{9}}$$
$$sqrt{frac{81a^2}{36}}=15$$
$$a=10$$
Задание 6
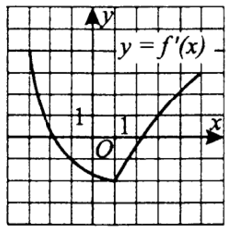
К графику функции $$y=f(x)$$ проведена касательная в точке с абсциссой $$x_0 = 3$$. Определите градусную меру угла наклона касательной, если на рисунке изображен график производной этой функции.
Ответ: 45
Скрыть
$$f'(3)=1$$ и по геометрическому смыслу производной
$$tgalpha=1Rightarrow$$ угол $$45^{circ}$$
Задание 7
Глубоководники проектируют новый батискаф в виде сферы радиуса R. Выталкивающая сила Архимеда, действующая на батискаф, вычисляется по формуле $$F_A = pgV = pgcdotfrac{4}{3}pi R^3$$. Определите максимальный радиус батискафа (в метрах), если сила Архимеда по технологии не должна превосходить 1130400 Н. При расчёте примите следующие значения постоянных: $$p =1000$$ кг/м3, $$g =10$$ Н/кг, $$pi = 3,14$$.
Ответ: 3
Скрыть
$$1000cdot10cdotfrac{4}{3}cdot3,14cdot R^3leq1130400$$
$$Rleq3$$
Задание 8
В бутыли содержится 25 %-ый раствор соли. Из нее вылили некоторую часть раствора и добавили такое же количество воды. В результате получили 12 %-ый раствор соли. Какая часть первоначального раствора была заменена водой?
Ответ: 0,52
Скрыть
Пусть $$A$$ - сколько было в бутыли, $$x$$ — сколько отлили
$$0,25A−0,25x=0,12A$$
отсюда $$frac{x}{A}=0,52$$ – это и есть часть раствора, которая была заменена водой
Задание 9
На рисунке изображен график функции вида $$f(x) = b + log_a x$$. Найдите $$f(32)$$.
Ответ: 2
Скрыть
Составим систему (на рисунке отмечены точки, которые нужно брать)
$$left{begin{matrix} -1=b+log_a4\ -2=b+log_a2 end{matrix}right.$$
Вычтем одно из другого
$$log_a4−log_a2=1$$
$$log_a2=1$$
$$a=2$$
$$b=−2−log_22=−3$$
$$f(x)=−3+log_2x$$
$$f(32)=−3+log_232=−3+5=2$$
Задание 10
В бутике модной обуви в случайный момент каждый продавец занят с покупателем с вероятностью 0,1. Всего продавцов трое. Найдите вероятность того, что в случайно выбранный момент хотя бы один из продавцов свободен.
Ответ: 0,999
Скрыть
Тут легче найти обратное.
$$P(B)=0,1cdot0,1cdot0,1$$ – все продавцы будут заняты делом
$$P_{иск}=1−0,1^3=0,999$$
Задание 11
Найдите наименьшее значение функции $$y=frac{5x^2+2}{3x^2+20}+frac{3x^2+20}{5x^2+2}$$ на отрезке $$[-1;4]$$
Ответ: 2
Скрыть
Пусть $$t=frac{5x^2+2}{3x^2+20}$$
$$f(t)=t+frac{1}{t}$$
$$f'(t)=1−frac{1}{t^2}$$
Найдем критические точки:
$$f'(t)=0$$
$$frac{t^2−1}{t^2}=0$$
$$t=−1$$ – точка максимума
$$t=1$$ – точка минимума
$$t=0$$
$$y(1)=2$$
Задание 12
А) Решите уравнение $$sin3x=4sin xcos2x$$
Б) Найдите все корни уравнения, принадлежащие интервалу $$(0;frac{3pi}{2})$$
Ответ: А)$$pi n;pmfrac{pi}{6}+pi n,nin Z$$ Б)$$frac{pi}{6};pi;frac{5pi}{6};frac{7pi}{6}$$
Задание 13
Две правильные четырехугольные пирамиды EABCD и FABCD имеют общее основание ABCD и расположены по разные стороны от него. Точки M и N — середины ребер ВС и АВ соответственно. Все ребра пирамид равны.
а) Докажите, что угол между прямыми АЕ и BF равен 60o.
б) Найдите угол между прямыми EM и FN.
Ответ: $$arccosfrac{2}{3}$$
Задание 14
Решите неравенство: $$sqrt{x^3-2x^2+4x-2}geq x$$
Ответ: $$[1;+infty)$$
Задание 15
Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму (в тыс. руб.) Владимир ежегодно добавлял к вкладу?
Ответ: 240
Задание 16
Дан прямоугольник ABCD. Окружности, вписанные в треугольники ABD и BDC, касаются диагонали BD в точках M и N соответственно. Окружности, вписанные в треугольники АВС и ADC, касаются диагонали АС в точках K и L соответственно.
а) Докажите, что MNKL — прямоугольник, подобный исходному.
б) Найдите коэффициент подобия, если косинус угла между диагоналями исходного прямоугольника равен $$frac{7}{25}$$.
Ответ: $$frac{1}{5}$$
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых система уравнений имеет хотя бы одно решение:
$$left{begin{matrix}
4x^2-12xy+9y^2+2x-6y=0,\
5x^2-16xy+13y^2-6x+10y+2ax-4ay+a^2-2a-5=0
end{matrix}right.$$
Ответ: $$[frac{5-6sqrt{7}}{6};frac{5+6sqrt{7}}{6}]$$
Задание 18
На доске написано несколько различных натуральных чисел, в записи которых могут быть только цифры 1 и 6.
а) Может ли сумма этих чисел быть равна 173?
б) Может ли сумма этих чисел быть равна 109?
в) Какое наименьшее количество чисел может быть на доске, если их сумма равна 1021?
Ответ: А) да, Б) нет, В) 6
Тренировочный вариант №360 Алекса Ларина по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 18.09.2021 (18 сентября 2021 года)
Тренировочный вариант №360 ЕГЭ 2022: скачать
Ответы для варианта: скачать
Решать тренировочный вариант Ларина №360 ЕГЭ 2022 по математике:
Разбор варианта с ответами:
Сложные задания с варианта:
2)Игральный кубик бросают дважды. Найдите вероятность того, что сумма выпавших очков будет меньше, чем 4. Ответ округлите до сотых.
Ответ: 3
3)Радиус окружности, вписанной в прямоугольный треугольник, равен 6. Найдите гипотенузу, если точка касания с вписанной окружностью делит ее на отрезки, длины которых относятся как 5 : 12.
Ответ: 34
5)В правильной треугольной пирамиде боковое ребро равно 15, а тангенс угла между боковой гранью и плоскостью основания равен корень из 23. Найдите сторону основания пирамиды.
Ответ: 10
8)В бутыли содержится 25 %‐ый раствор соли. Из нее вылили некоторую часть раствора и добавили такое же количество воды. В результате получили 12 %‐ый раствор соли. Какая часть первоначального раствора была заменена водой?
Ответ: 0,52
10)В бутике модной обуви в случайный момент каждый продавец занят с покупателем с вероятностью 0,1. Всего продавцов трое. Найдите вероятность того, что в случайно выбранный момент хотя бы один из продавцов свободен.
Ответ: 0,999
13)Две правильные четырехугольные пирамиды EABCD и FABCD имеют общее основание ABCD и расположены по разные стороны от него. Точки M и N – середины ребер ВС и АВ соответственно. Все ребра пирамид равны. а) Докажите, что угол между прямыми АЕ и BF равен 600. б) Найдите угол между прямыми EM и FN.
15)Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму (в тыс. руб.) Владимир ежегодно добавлял к вкладу?
Ответ: 240
16)Дан прямоугольник ABCD. Окружности, вписанные в треугольники ABD и BDC, касаются диагонали BD в точках M и N соответственно. Окружности, вписанные в треугольники ABС и АDC, касаются диагонали АС в точках K и L соответственно. a) Докажите, что MNKL – прямоугольник, подобный исходному. б) Найдите коэффициент подобия, если косинус угла между диагоналями исходного прямоугольника равен 7/25.
18)На доске написано несколько различных натуральных чисел, в записи которых могут быть только цифры 1 и 6. а) Может ли сумма этих чисел быть равна 173? б) Может ли сумма этих чисел быть равна 109? в) Какое наименьшее количество чисел может быть на доске, если их сумма равна 1021?
Смотрите также другие варианты Ларина:
Тренировочный вариант Ларина №359 ЕГЭ 2022 по математике с ответами
Тренировочный вариант Ларина №358 ЕГЭ 2022 по математике с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
| 2968 | Дан прямоугольник ABCD. Окружности, вписанные в треугольники ABD и BDC, касаются диагонали BD в точках M и N соответственно. Окружности, вписанные в треугольники ABС и АDC, касаются диагонали АС в точках K и L соответственно. a) Докажите, что MNKL – прямоугольник, подобный исходному. б) Найдите коэффициент подобия, если косинус угла между диагоналями исходного прямоугольника равен 7/25 |
Дан прямоугольник ABCD. Окружности, вписанные в треугольники ABD и BDC, касаются диагонали BD в точках M и N соответственно ! Тренировочный вариант 360 от Ларина Задание 16 # Решение — Елены Ильиничны Хажинской | |
| 2967 | Две правильные четырехугольные пирамиды EABCD и FABCD имеют общее основание ABCD и расположены по разные стороны от него. Точки M и N – середины ребер ВС и АВ соответственно. Все ребра пирамид равны. а) Докажите, что угол между прямыми АЕ и BF равен 60 градусов. б) Найдите угол между прямыми EM и FN |
Две правильные четырехугольные пирамиды EABCD и FABCD имеют общее основание ABCD и расположены по разные стороны от него ! Тренировочный вариант 360 от Ларина Задание 13 (14) # Векторный способ | |
| 2966 | Игральный кубик бросают дважды. Найдите вероятность того, что сумма выпавших очков будет меньше, чем 4. Ответ округлите до сотых |
Игральный кубик бросают дважды ! Тренировочный вариант 360 от Ларина Задание 2 (4) | |
| 2965 | Радиус окружности, вписанной в прямоугольный треугольник, равен 6. Найдите гипотенузу, если точка касания с вписанной окружностью делит ее на отрезки, длины которых относятся как 5 : 12 |
Радиус окружности, вписанной в прямоугольный треугольник, равен 6 ! Тренировочный вариант 399 от Ларина Задание 1 # Тренировочный вариант 360 от Ларина Задание 3 (6) | |
| 2964 | В бутике модной обуви в случайный момент каждый продавец занят с покупателем с вероятностью 0,1. Всего продавцов трое. Найдите вероятность того, что в случайно выбранный момент хотя бы один из продавцов свободен |
В бутике модной обуви в случайный момент каждый продавец занят с покупателем с вероятностью 0,1 ! Тренировочный вариант 360 от Ларина Задание 10 (4) | |
| 2963 | В бутыли содержится 25 %‐ый раствор соли. Из нее вылили некоторую часть раствора и добавили такое же количество воды. В результате получили 12 %‐ый раствор соли. Какая часть первоначального раствора была заменена водой? |
В бутыли содержится 25 %‐ый раствор соли ! Тренировочный вариант 360 от Ларина Задание 8 (11) ЕГЭ | |
| 2962 | В правильной треугольной пирамиде боковое ребро равно 15, а тангенс угла между боковой гранью и плоскостью основания равен sqrt23. Найдите сторону основания пирамиды |
В правильной треугольной пирамиде боковое ребро равно 15, а тангенс угла между боковой гранью и плоскостью основания равен ! Тренировочный вариант 360 от Ларина Задание 5 (8) ЕГЭ | |
| 2961 | а) Решите уравнение sin(3x)=4sin(x)cos(2x) б) Найдите все корни уравнения, принадлежащие интервалу (0; (3pi)/2). |
Тренировочный вариант 360 от Ларина Задание 12 (13) ЕГЭ | |
| 2960 | Решите неравенство sqrt(x^3-2x^2+4x-2) >= x |
Тренировочный вариант 360 от Ларина Задание 14 (15) | |
А. Ларин. Тренировочный вариант № 360.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие интервалу
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Две правильные четырехугольные пирамиды EABCD и FABCD имеют общее основание ABCD и расположены по разные стороны от него. Точки M и N — середины рёбер AB и BC соответственно. Все ребра пирамид равны.
а) Докажите, что угол между прямыми AE и BF равен 60°.
б) Найдите угол между прямыми EM и FN.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму (в тысячах рублей) Владимир ежегодно добавлял к вкладу?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Дан прямоугольник ABCD. Окружности, вписанные в треугольники ABD и BDC, касаются диагонали BD в точках M и N соответственно. Окружности, вписанные в треугольники ABC и ADC, касаются диагонали AC в точках K и L соответственно.
а) Докажите, что MNKL — прямоугольник, подобный исходному.
б) Найдите коэффициент подобия, если косинус угла между диагоналями исходного прямоугольника равен
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых система уравнений
имеет хотя бы одно решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
На доске написано несколько различных натуральных чисел, в записи которых могут быть только цифры 1 и 6.
а) Может ли сумма этих чисел быть равна 173?
б) Может ли сумма этих чисел быть равна 109?
в) Какое наименьшее количество чисел может быть на доске, если их сумма равна 1021?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Канал видеоролика: Математикс
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #учиться #e_math #егэматематика
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
Разбор Задачи №19 из Варианта Ларина №276
Математикс

Разбор Задачи №13 из Варианта Ларина №277
Математикс

Разбор Задачи №15 из Варианта Ларина №277
Математикс

Разбор Задачи №18 из Варианта Ларина №277
Математикс
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
19.09.2021
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №360
|
|||||||
|
https://alexlarin.net/ege/2022/trvar360.html |
||||||
  |
|||||||
|
|
|||||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Спасибо за интересный вариант! Подробности: 18 Подробности: |
||||||
  |
|||||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Kirill Kolokolcev писал(а): Спасибо за интересный вариант! Подробности: Так же. |
||||||
  |
|||||||
|
ОГЭ_ЕГЭ |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Доброго времени суток ! 12) а) пn, n — целое; п/6+пk, k — целое; -п/6+пm, m — целое |
||||||
  |
|||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Всем здравствуйте! большое спасибо за интересный вариант! ОГЭ_ЕГЭ писал(а): Доброго времени суток ! 12) а) пn, n — целое; п/6+пk, k — целое; -п/6+пm, m — целое такие же ответы 13 Подробности: |
||||||
  |
|||||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Всем доброй ночи! Подробности:
|
||||||
  |
|||||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Всем доброй ночи! Подробности: Решение 18 Подробности:
|
||||||
  |
|||||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Задача 18 Подробности:
|
||||||
  |
|||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Всем здравствуйте! Решение заданий 12 и 14. Подробности: Решение задания 17. Подробности:
|
||||||
  |
|||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №360
|
||||||
|
Решение задания 13. Вложение:
скрин решения Подробности: |
||||||
  |
|||||||
| Показать сообщения за: Сортировать по: |