Задание 1
Яблоки подешевели на 20%. Сколько килограмм яблок можно теперь купить на те же деньги, на которые раньше покупали 2,8 кг яблок?
Ответ: 3,5
Скрыть
Задание 2
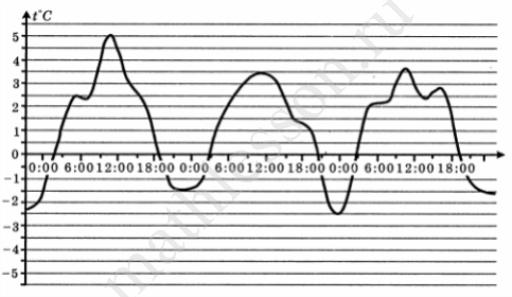
На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов 2 марта. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Найдите по графику наибольшую температуру воздуха 3 марта в градусах Цельсия.
Ответ: 3,5
Задание 3
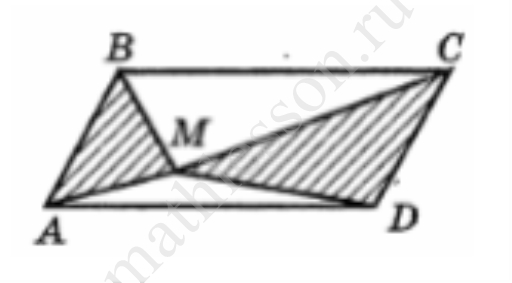
Внутри параллелограмма ABCD, площадь которого равна 10, отмечена точка М. Найдите сумму площадей треугольников AMВ и CMD.
Ответ: 5
Скрыть
Задание 4
Бросаются одновременно две игральные кости. Найдите вероятность того, что сумма выпавших очков будет больше, чем их произведение. Ответ округлите до сотых.
Ответ: 0,31
Скрыть
Задание 5
В равнобедренном треугольнике АВС с основанием АС высоты ВМ и АН пересекаются в точке К, причем АК=5, КН=3. Найдите площадь треугольника АВК.
Ответ: 15
Скрыть
Задание 6
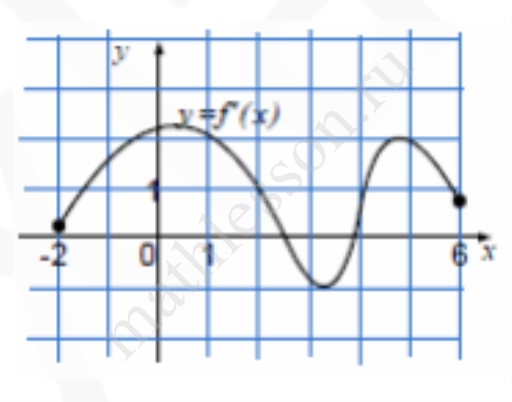
На рисунке изображен график производной функции $$y=f(x)$$, заданной на отрезке [‒ 2; 6]. Найдите число точек на этом отрезке, в которых касательная к графику функции $$f(x)$$ параллельна биссектрисе первой четверти.
Ответ: 4
Скрыть
Задание 7
Боковое ребро правильной треугольной призмы на 20% больше ее стороны основания. Расстояние между серединами двух непараллельных ребер, принадлежащих разным основаниям, равно 13. Найдите площадь боковой поверхности призмы.
Ответ: 360
Скрыть
Задание 8
Найдите значение выражения $$(7,3cdot sqrt[3]{49cdotsqrt{7}}-0,3cdotsqrt{7cdotsqrt[3]{49}})^{frac{6}{11}}$$
Ответ: 7
Скрыть
Задание 9
В ходе распада радиоактивного изотопа его масса уменьшается по закону $$m(t)=m_{0}cdot 2-frac{t}{T}$$, где $$m_{0}$$ ‐ начальная масса изотопа, t (мин) – прошедшее от начального момента время, T ‐ период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени m0=156 мг изотопа, период полураспада которого T=8 мин. В течение скольких минут масса изотопа будет не меньше 39 мг?
Ответ: 16
Скрыть
Задание 10
Двум операторам поручили набрать на компьютере текст книги объемом 315 страниц. Один оператор, отдав второму 144 страницы книги, взял остальные страницы себе. Первый выполнил свою работу за 19 дней, а второй свою – за 12. На сколько процентов нужно было увеличить часть работы второго оператора (уменьшив часть работы первого), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое число дней?
Ответ: 25
Скрыть
Задание 11
Найдите наибольшее значение функции $$y=3x-e^{3x}$$ на отрезке $$[-1;1]$$
Ответ: -1
Скрыть
Задание 12
а) Решите уравнение $$|2cdot tg x-5|-|2cdot tg x-1|=2$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{pi}{2};frac{pi}{2}]$$
Ответ: А)$$frac{pi}{4}+pi n,n in Z$$ Б)$$frac{pi}{4}$$
Скрыть
Задание 13
Основание пирамиды SABCD – квадрат ABCD, боковое ребро SA перпендикулярно плоскости основания. BC=2SA. Точка М – середина ребра АВ.
а) Докажите, что сечение пирамиды плоскостью, проходящей через прямую SM параллельно BD, ‐ равносторонний треугольник
б) Найдите расстояние между прямыми SM и BD, если $$AB=6sqrt{3}$$
Ответ: 3
Задание 14
Решите неравенство: $$log_{x+4}(x^2-8x+12)<frac{1}{2}log_{|x-2|}(2-x)^2$$
Ответ: $$(-4;-3)cup(1;2)cup(6;8)$$
Скрыть
Задание 15
В треугольнике АВС $$angle B=70^{circ}$$, $$angle C=25^{circ}$$, BD — диаметр описанной около треугольника АВС окружности. Продолжение высоты ВН пересекает окружность в точке L.
а) Докажите, что $$angle ACD$$=$$angle CAL$$
б) Найдите длину отрезка DL , если радиус описанной окружности равен $$4sqrt{3}$$
Ответ: 12
Задание 16
Правительство решило закрыть нерентабельные шахты и построить новые фабрики и заводы. В результате закрытия одной шахты увольняется 180 человек, при этом на консервацию шахты и выплату пособий увольняемым тратится 52 млн. рублей. Строительство одного нового завода с персоналом 170 человек стоит 43 млн. рублей, а одной фабрики с персоналом 110 человек – 20 млн. рублей. Чему равно максимально возможное увеличение суммарного числа новых рабочих мест, если известно, что сумма всех затрат правительства составила ровно 714 млн. рублей?
Ответ: 2530
Скрыть
Задание 17
Найдите все значения параметра a , при каждом из которых функция $$f(x)=x(1-a)+3(1-2a)sin frac{x}{3}+frac{3}{2}sin frac{2x}{3}+pi a$$ имеет не более двух экстремумов на промежутке $$(pi;5pi)$$
Ответ: $$(-infty;-1]cup {-frac{1}{2}}cup [frac{1}{2};+infty)$$
Задание 18
За круглым столом сидели 110 человек, а на столе лежали абрикосы. Для каждой пары соседей число съеденных ими абрикосов отличается на 3.
а) Могли ли быть съедены все абрикосы, если изначально их было 1000?
б) Какое наименьшее число абрикосов могло остаться, если изначально их было 1000?
в) Пусть один из присутствующих съел a абрикосов, а другой b. Найдите наибольшее возможное значение a-b при условии, что изначально было 10 000 абрикосов?
Ответ: нет; 1; 165
А. Ларин. Тренировочный вариант № 310. (Часть C)
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Основание пирамиды SABCD — квадрат ABCD боковое ребро SA перпендикулярно плоскости основания. BC = 2SA. Точка M — середина ребра AD.
а) Докажите, что сечение пирамиды плоскостью, проходящей через прямую SM параллельно BD, — равносторонний треугольник.
б) Найдите расстояние между прямыми SM и BD, если
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В треугольнике ABC
BD — диаметр описанной около треугольника ABC окружности. Продолжение высоты BH пересекает окружность в точке L.
а) Докажите, что
б) Найдите длину отрезка DL, если радиус описанной окружности равен
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Правительство решило закрыть нерентабельные шахты и построить новые фабрики и заводы. В результате закрытия одной шахты увольняется 180 человек, при этом на консервацию шахты и выплату пособий увольняемым тратится 52 миллиона рублей. Строительство одного нового завода с персоналом 170 человек стоит 43 млн руб., а одной фабрики с персоналом 110 человек — 20 млн руб. Чему равно максимально возможное увеличение суммарного числа новых рабочих мест, если известно, что сумма всех затрат правительства составила ровно 714 млн руб.?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых функция имеет не более двух экстремумов на промежутке
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
За круглым столом сидели 110 человек, а на столе лежали абрикосы. Для каждой пары соседей число съеденных ими абрикосов отличается на 3.
а) Могли ли быть съедены все абрикосы, если изначально их было 1000?
б) Какое наименьшее число абрикосов могло остаться, если изначально их было 1000?
в) Пусть один из присутствующих съел a абрикосов, а другой b. Найдите наибольшее возможное значение a − b при условии, что изначально было 10 000 абрикосов.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Регистрация Форум Текущее время: 10 мар 2023, 16:20 Сообщения без ответов | Активные темы Страница 4 из 5 [ Сообщений: 43 ] На страницу Пред. 1, 2, 3, 4, 5 След. Начать новую тему»> Ответить Тренировочный вариант №310
Тренировочный вариант №310
Страница 4 из 5 [ Сообщений: 43 ] На страницу Пред. 1, 2, 3, 4, 5 След. Текущее время: 10 мар 2023, 16:20 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
2 новых тренировочных варианта №310 Алекса Ларина пробный ОГЭ 2022 по математике 9 класс с ответами и решением по новой демоверсии ФИПИ ОГЭ 2022 года для подготовки к экзамену, дата выхода варианта на сайте: 26.01.2022 (26 января 2022 года)
Тренировочный вариант №310: скачать
Усложненная версия варианта: скачать
Вариант Алекса Ларина №310 ОГЭ 2022 по математике 9 класс:
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус‐малус (КБМ) зависит от класса водителя.
Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества дорожно‐транспортных происшествий (ДТП) в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя присваивается в зависимости от числа страховых выплат в течение истекшего года, в соответствии с таблицей (см. таблицу выше).
1)Игорь страховал свою гражданскую ответственность три года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Какой класс будет присвоен Игорю на начало четвёртого года страхования?
Ответ: 3
2)Чему равен КБМ на начало четвёртого года страхования?
Ответ: 1
3)Когда Игорь получил водительские права и впервые оформил полис, ему было 22 года. Чему равен КВС на начало 4‐го года страхования?
Ответ: 1,04
4)В начале третьего года страхования Игорь заплатил за полис 18 585 руб. Во сколько рублей обойдётся Игорю полис на четвёртый год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Ответ: 7800
5)Игорь въехал на участок дороги протяжённостью 2,6 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 100 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Игорь въехал на участок в 11:10:33, а покинул его в 11:11:51. Нарушил ли Игорь скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Ответ: 20
10)Игральную кость бросают дважды. Найдите вероятность того, что наименьшее из двух выпавших чисел равно 2.
Ответ: 0,25
14)Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из‐под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.
Ответ: 204,8
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Сумма углов прямоугольного треугольника равна 90 градусам. 3) Каждая из биссектрис равнобедренного треугольника является его медианой.
Ответ: 1
21)Баржа прошла по течению реки 32 км и, повернув обратно, прошла ещё 24 км, затратив на весь путь 4 часа. Найдите собственную скорость (в км/ч) баржи, если скорость течения реки равна 5 км/ч.
Ответ: 15
24)В параллелограмме проведены биссектрисы противоположных углов. Докажите, что отрезки биссектрис, заключенные внутри параллелограмма, равны.
25)Углы при одном из оснований трапеции равны а отрезки, соединяющие середины противоположных сторон трапеции, р Найдите большее основание трапеции.
Ответ: 22
Сложная версия варианта:
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2 (см. рис. выше). И так далее. Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны.
Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта, если изменяется формат листа. В таблице (см. ниже) даны размеры (с точностью до мм) четырёх листов, имеющих форматы А3, А4, А5 и А6.
1)Установите соответствие между форматами и номерами листов. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов и других разделительных символов.
Ответ: 3412
2)Сколько листов бумаги формата А4 получится из одного листа бумаги формата А2?
Ответ: 4
3)Найдите длину (в мм) большей стороны листа бумаги формата А4. Результат округлите до десятков.
Ответ: 300
4)Найдите длины большей стороны листа формата А1 к меньшей. Ответ округлите до десятых.
Ответ: 1,4
5)Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 03528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 27 пунктов на листе формата А5? Результат округлите до целого.
Ответ: 38
10)У Пети всего 28 одноклассников. У каждых двух из 28 различное число друзей в этом классе. Сколько друзей у Пети?
Ответ: 14
14)В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. Если сдвинуть 3 квадратных столика вдоль одной линии, то получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 21 квадратный столик вдоль одной линии?
Ответ: 44
16)В окружности радиуса 5 проведён диаметр и на нём взята точка A на расстоянии 4 от центра. Найдите радиус окружности, которая касается этого диаметра в точке A и изнутри касается данной окружности.
Ответ: 0,9
17)В прямоугольной трапеции меньшее основание равно высоте, а большее основание равно . Найдите боковые стороны трапеции, если известно, что одна из них касается окружности, проходящей через концы меньшего основания и касающейся большего основания. В ответе запишите произведение найденных значений.
Ответ: 180
18)Катеты прямоугольного треугольника равны 7 и 24. Найдите высоту этого треугольника, проведённую к гипотенузе.
Ответ: 6,72
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180 . 2) Диагонали ромба перпендикулярны. 3) Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.
Ответ: 2
21)В группе поровну юношей и девушек. Юноши отправили электронные письма девушкам. Каждый юноша отправил или 4 письма, или 21 письмо, причём и тех, и других юношей было не менее двух. Возможно, что какой‐то юноша отправил какой‐то девушке несколько писем. Пусть все девушки получили различное количество писем (возможно, какая‐то девушка не получила писем вообще). Каково наибольшее возможное количество девушек в группе?
Ответ: 41
24)ABCD – вписанный четырехугольник, диагонали которого перпендикулярны. P – точка пересечения диагоналей. Докажите, что середины сторон четырехугольника ABCD и проекции точки P на стороны лежат на одной окружности.
25)В окружность вписан четырехугольник ABCD ; H и G — ортоцентры треугольников ABD и ABC соответственно. Найдите DH , если известно, что CG 7 .
Ответ: 7
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Главная страница » Работы статград март 2023 год варианты ответы и решения
Автор admin На чтение 2 мин Просмотров 2.7к. Опубликовано 2 марта, 2023
Вам также может понравиться
Почвенное и воздушное питание растений Решение и ответы
01
Рабочая программа по биологии (7 класс) Решение и ответы
01
Рабочая программа по биологии (9 класс) Решение и ответы
03
Рабочая программа по биологии (10 класс) Решение и
01
Рабочая программа по биологии (11 класс) Решение и
01
Рабочая программа по биологии (8 класс) Решение и ответы
01
Влияние фосфатов на скорость роста вегетативных органов
01
Презентация к уроку «Лишайники»
01




 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 



