Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
а) Чтобы делилось на 15, то должно делиться и на 5, и на 3 $$Rightarrow$$ оканчивается на 0 или 5 (на 0 не может $$Rightarrow$$ на 5) и сумма цифр делится на 3.
Например: $$5a5$$ $$Rightarrow$$ $$frac{5+a+5}{3}in N$$
$$Rightarrow$$ $$frac{10+a}{3}in N$$ $$Rightarrow$$ $$a=2$$; $$a=8$$
$$Rightarrow$$ $$525;585$$
б) Пусть $$5aba5$$ — число $$Rightarrow$$
$$frac{5+a+b+a+5}{3}in N,a,bin Nin[0….9]$$
$$frac{10+2a+b}{3}in N$$, при этом $$2a+bin[0…27]$$
$$Rightarrow$$ $$10+2a+bin[10…37]$$.
Выберем все кратные 3 из этого диапазона: $$12;15;18;21;24;27;30;33;36$$
1) $$10+2a+b=12$$
$$2a+b=2$$ $$Rightarrow$$ $$a=1;b=0$$ или $$a=0;b=2$$
$$52025;20205$$
2) $$10+2a+b=15$$
$$2a+b=5$$
$$a=frac{5-b}{2}$$ $$Rightarrow$$ $$a=0;b=5$$ или $$a=2;b=1$$
или $$a=2;b=1$$
$$50505;52125;51315$$
3) $$10+2a+b=18$$
$$2a+b=8$$ $$Rightarrow$$ $$a=4;b=0$$
$$a=3;b=2$$ или $$a=2;b=4$$
$$a=1;b=6$$ или $$a=0;b=0$$
4) $$10+2a+b=21$$
$$2a+b=11$$ $$Rightarrow$$ $$a=5;b=1$$ или $$a=4;b=3$$
$$a=3;b=5$$ или $$a=2;b=7$$
$$a=1;b=9$$
5) $$10+2a+b=24$$
$$2a+b=14$$ $$Rightarrow$$
$$a=7;b=0$$ или $$a=6;b=2$$
$$a=5;b=4$$ или $$a=4;b=6$$
$$a=3;b=8$$
6) $$10+2a+b=27$$
$$2a+b=17$$ $$Rightarrow$$
$$a=8;b=1$$
$$a=7;b=3$$ или $$a=6;b=5$$
$$a=5;b=7$$ или $$a=4;b=9$$
7) $$10+2a+b=30$$
$$2a+b=20$$ $$Rightarrow$$
$$a=9;b=2$$ или $$a=8;b=4$$
$$a=7;b=6$$ или $$a=6;b=8$$

$$2a+b=23$$ $$Rightarrow$$
$$a=9;b=5$$ или $$a=8;b=7$$
$$a=7;b=9$$
9) $$10+2a+b=36$$
$$2a+b=26$$ $$Rightarrow$$
$$a=9;b=8$$
Всего: $$2+3+5+5+5+5+4+3+1=33$$ числа
в) С учетом пункта б) получим: 3хзначных чисел 3 штуки
4х: $$frac{5aa5}{3}=N$$
$$frac{10+2a}{3}=N$$
$$2ain[0…18]$$ $$Rightarrow$$ $$10+2ain[10…18]$$
12: $$2a=2$$ $$Rightarrow$$ $$a=1$$
15: $$2a=5$$ $$Rightarrow$$ $$varnothing$$
18: $$2a=8$$ $$Rightarrow$$ $$a=4$$
21: $$2a=11$$ $$Rightarrow$$ $$varnothing$$
24: $$2a=14$$ $$Rightarrow$$ $$a=7$$
27: $$2a=17$$ $$Rightarrow$$ $$varnothing$$
Всего 3 числа.
То есть 3х и 4х значных в сумме 6 штук.
5ти всего 33 $$Rightarrow$$ вместе 39, нам нужно 37, то есть предпоследнее $$Rightarrow$$ 59295
А. Ларин: Тренировочный вариант № 221.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Основание пирамиды DABC — прямоугольный треугольник ABC с прямым углом C. Высота пирамиды проходит через середину ребра AC, а боковая грань ACD — равносторонний треугольник.
а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и произвольную точку M ребра AD, — прямоугольный треугольник.
б) Найдите расстояние от вершины D до этой плоскости, если M — середина ребра AD, а высота пирамиды равна 6.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Площадь трапеции ABCD равна 30. Точка Р — середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD = 3RD. Прямые AR и PD пересекаются в точке Q, AD = 2BC.
а) Докажите, что точка Q — середина отрезка AR
б) Найдите площадь треугольника APQ.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В двух областях есть по 20 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,2 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко‐часов труда, а для добычи y кг никеля в день требуется y2 человеко‐часов труда. Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
(Человеко‐час — единица учёта рабочего времени, соответствует часу работы одного человека, То есть 40 человеко‐часов формируют: 1 человек, работающий 40 часов; или 2 человека, работающие 20 часов; или 4 человека, работающие 10 часов; и т. д.)
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при которых система
имеет хотя бы одно решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Назовем натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично (совпадает первая и последняя цифры, вторая и предпоследняя, и т. д. Например, числа 121 и 123321 являются палиндромами.
а) Приведите пример числа‐палиндрома, которое делится на 15
б) Сколько существует пятизначных чисел‐палиндромов, делящихся на 15?
в) Найдите 37‐е по величине число‐палиндром, которое делится 15.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Продолжаем решать тренировочный вариант 221 Ларин. Разбираем 2 часть профильного уровня с 9 по 12 задание.
Задания с 1 по 8 тренировочного варианта 221 Алекс Ларин разобраны здесь.
Вариант 221 Ларин решение 9- 12 задания (2 часть профиль)
Задание 9 вариант 221 Ларин
Преобразуем корни в степени и при нахождении значения выражения воспользуемся свойствами степеней, чтобы упростить его.
Ответ: 64.
Задание 10 вариант 221 Ларин
Пусть у = 9 + 1 = 10(м) — высота камня над землей.
Подставим все значения в искомую формулу и найдем x.
1/25x2 + 7/5x — 10 = 0,
Умножим обе части уравнения на 25.
x2 + 35x — 350 = 0,
По теореме, обратной теореме Виета находим два корня уравнения: 25 и 10.
Итак, максимальное расстояние, на которое нужно расположить машину равно 25 м.
Ответ: 25 м.
Задание 11 вариант 221 Ларин
Из городов A и B навстречу друг другу одновременно выехали с постоянными скоростями два автомобиля. Скорость первого автомобиля была в два раза больше скорости второго. Второй автомобиль прибыл в A на 1 час позже, чем первый прибыл в B. На сколько минут раньше произошла бы встреча автомобилей, если бы второй автомобиль ехал с той же скоростью, что и первый?
Обозначим расстояние между городами за 1.
x км/ч — скорость второго автомобиля,
2x км/ч — скорость первого автомобиля.
1/x ч — время второго автомобиля, 1/2x ч — первого.
Второй автомобиль прибыл в пункт В на час позже.
Составим уравнение
1/x — 1/2x = 1,
x = 0,5(км/ч) — скорость второго автомобиля.
2x = 1(км/ч) — скорость первого автомобиля.
Найдем время, через которое произошла бы встреча автомобилей, если бы они ехали с первоначальной скоростью.
t = 1/(x +2x) = 1/1,5 = 2/3.
Найдем время, через которое произошла бы встреча, если бы второй автомобиль ехал с той же скоростью, что и первый.
t = 1/(2x + 2x) = 1/2 .
Найдем на сколько минут раньше произошла бы встреча автомобилей
2/3 — 1/3 = 1/6(ч)
1/6 часа = 10 мин.
Ответ: 10.
Задание 12 вариант 221 Ларин
Область определения функции — все значения x кроме 0.
Выясним как ведет себя функция на отрезке[3,9].
Найдем производную функцию и,преобразовав ее, получим:
y’ =x2 — 36.
Приравняем производную к нулю и найдем критические точки: 6 и -6.
На отрезке от 3 до 6 производная меньше 0, функция убывает.
На отрезке от 6 до 9 производная больше 0, функция возрастает.
Точка 6 — точка минимума функции.
Наименьшее значение на [3,9] достигает функция в точке x = 6 и равно:
y(6) = (36-36+36)/6 = 6.
Ответ: 6.
Задание 13 вариант 221 Алекс Ларин
25
Янв 2018
Категория: Справочные материалы
Елена Репина
2018-01-25
2018-01-25
Автор: egeMax |
Нет комментариев
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Печать страницы
Добавить комментарий
- Материалы для подготовки к ЕГЭ
-
- Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
- II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
- Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
- Свежие записи
- Тест «Гиперболы»
- Тест. Графики функций. Комбинированные задачи
- 10. Графики функций. Комбинированные задачи
- Тест. Тригонометрические функции
- 10. Тригонометрическая функция
- Тест. Кусочно-линейная функция
- 10. Кусочно-линейная функция
- Архивы Архивы
Регистрация Форум Текущее время: 10 мар 2023, 16:20 Сообщения без ответов | Активные темы Страница 1 из 11 [ Сообщений: 106 ] На страницу 1, 2, 3, 4, 5 … 11 След. Начать новую тему»> Ответить Тренировочный вариант №221
Тренировочный вариант №221
Страница 1 из 11 [ Сообщений: 106 ] На страницу 1, 2, 3, 4, 5 … 11 След. Текущее время: 10 мар 2023, 16:20 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|


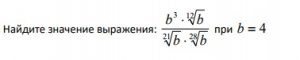






 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 




