Задание 1
Жильцы 9‐этажки ежемесячно платят управляющей компании на капитальный ремонт дома по 250 рублей (с каждой квартиры). В доме 3 подъезда, на каждой площадке по 4 квартиры. Какую сумму выплачивают за год жильцы дома управляющей компании? Ответ дайте в рублях.
Ответ: 324000
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
В каждом подъезде по: 9 * 4 = 36 квартир Всего в доме: 36 * 3 = 108 квартир В месяц с дома в сумме поступает: 108 * 250 = 27000 рублей Значит в год в итоге: 27 000 * 12 = 324 000
Задание 2
В 11А классе 25 учащихся. За контрольную по геометрии 5 человек получили отметку «5», 11 человек – «4», 8 человек – «3», и один ученик получил «2». Определите средний балл учащихся 11А класса за контрольную работу по геометрии.
Ответ: 3.8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Чтобы определить средний был, мы должны сложить все оценки и поделить на количество людей, то есть найти среднее арифметическое: $$frac{5*5+11*4+8*3+1*2}{5+11+8+1}=3.8$$
Задание 3
Площадь маленького круга равна 4. Найдите площадь закрашенной фигуры (рис.).
Ответ: 10.5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь большего круга в 4 раза больше площади маленького (так как радиус в два раза больше) => 4*4 = 16. Отсюда внешнего кольца : 16-4=12 Угол равен сорока пяти градусам, получается, что закрашенная область 315 градусов (360-45). Отсюда ее площадь: 12*315/360= 10.5
Задание 4
Генератор случайных чисел выводит на экран натуральное число, не превосходящее 100. Какова вероятность, что это число окажется простым?
Ответ: 0.25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Всего натуральных чисел, не превосходящих сто, собственно, сто штук. Простых чисел среди них 25. Следовательно, вероятность будет: $$frac{25}{100}*4=0.25$$
Задание 5
Найдите периметр равностороннего треугольника, если радиус вписанной в него окружности равен $$2sqrt{3}$$
Ответ: 36
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Если радиус вписанной в него окружности равен $$2sqrt{3}$$, то вся медиана этого треугольника будет $$2sqrt{3}*3=6sqrt{3}$$ (медиана в равностороннем треугольнике она и высота и биссекриса, следовательно, делится на радиус описанной и писанной окружностей, в отношении два к одному, поэтому радиус вписанной составляет одну треть от медианы) Сторона равностороннего треугольника будет равна : $$6sqrt{3} : sin 60 =6sqrt{3} :frac{sqrt{3}}{2} =12$$ Значит периметр равен 12*3=36
Задание 6
На графике производной функции у = f‘ / (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых угловой коэффициент касательной к графику функции f (x) положительный. В ответе укажите количество этих точек.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Угловой коэффициент касательной к графику это и есть значение производной, следовательно, мы ищем, где производная положительная. Так как дан нам график производной, то мы просто найдем количество точек, которые располагаются над осью ОХ: x1,x3,x4,x6 всего 4
Задание 7
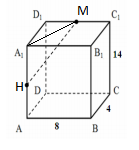
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно ВС=4, АВ=8, СС1=14. Найдите расстояние между серединами ребер АА1 и С1D1.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
|
Для этого рассмотрим треугольник HA1M: HA1=0.5AA1=7 A1M=$$sqrt{A_{1}D_{1}^{2}+D_{1}M^{2}}=sqrt{4^{2}+4^{2}}=sqrt{32}$$ MH=$$sqrt{A_{1}H^{2}+A_{1}M^{2}}=sqrt{7^{2}+32}=sqrt{81}=9$$ |
|
Задание 8
Известно, что $$log_a b *log_b c = -5$$ . Найдите значение выражения $$log_c a$$
Ответ: -0.2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$log_a b *log_b c = frac{1}{log_b a}*log_b c=frac{log_b c}{log_b a}=log_a c=-5$$ $$log_c a=frac{1}{log_a c}=frac{1}{-5}=-0.2$$
Задание 9
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле а=ω2R, где ω – угловая скорость (в с‐1), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с‐1, а центростремительное ускорение равно 650,25 м/с2.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Выразим R: $$R=frac{a}{omega ^{2}}=frac{650.25}{8.5^{2}}=9$$
Задание 10
Свежие плоды содержат 60% воды. При сушке плоды теряют 40% своей влаги. Сколько килограммов свежих плодов потребуется для получения 1520 кг сухих?
Ответ: 2000
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть S — первоначальная масса свежих плодов. Тогда воды в них X
S — 100%
x — 60%
x = 0.6S
При сушке теряется 40% воды, пусть эта масса Y:
0.6S — 100%
y — 40%
y = 0.6S*40/100=0.24S
Значит от первоначальной массы остается : S — 0.24S = 0.76S. Это и есть масса сухих плодов.
Найдем массу свежих: 0.76S=1520 S=1520/0.76=2000
Задание 11
Найдите наименьшее значение функции $$f(x)=(x^{2}-8x+8)*e^{2-x}$$ на отрезке [1; 7].
Ответ: -4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную функции: $$f^{‘}(x)=(2x-8)e^{2-x}+(-1)e^{2-x}(x^{2}-8x+8)=$$
$$=e^{2-x}(2x-8-x^{2}+8x-8)=e^{2-x}(-x^{2}+10x-16)$$
Приравняем производную к нулю:
$$e^{2-x}(-x^{2}+10x-16)=0$$ $$e^{2-x}=0$$
решений не имеет $$(-x^{2}+10x-16)=0$$ x1=2 и x2 =8
Отметим эти точки на координатной прямой и расставим знаки производной:
Точка минимума там, где производная меняет знак с — на +, то есть в точке 2
Подставим данное значение в первоначальную функцию и получим:
$$f(2)=(2^{2}-8*2+8)*e^{2-2}=(4-16+8)*1=-4$$
Задание 12
Дано уравнение $$2^{2+2sin x}-3cdot (sqrt{2})^{1+2sin x}+1=0$$.
a) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку $$[4pi;frac{23pi}{4}]$$.
Ответ: А)$$-frac{pi}{6}+2pi n; -frac{5pi}{6}+2pi m,n,min Z$$ Б)$$frac{31pi}{6}$$
Задание 13
На продолжении высоты $$PO$$ правильной четырехугольной пирамиды $$PABCD$$ отмечена точка $$K$$ так, что $$OP=OK$$.
а) Докажите, что плоскости $$PBC$$ и $$KAD$$ параллельны.
б) Найдите расстояние между плоскостями $$PBC$$ и $$KAD$$ , если $$AB=2, PO=2sqrt{2}$$.
Ответ: $$frac{4sqrt{2}}{3}$$
Задание 14
Решите неравенство
$$log_{2}x+5sqrt{log_{2}x}+15leq frac{92-46sqrt{log_{2}x}}{log_{2}x-5sqrt{log_{2}x}+6}$$
Ответ: $$[1;16);(16;512)$$
Задание 15
Дан квадрат $$ABCD$$. На сторонах $$AB$$ и $$BC$$ отмечены точки $$P$$ и $$K$$ соответственно, причем $$BP:AP=1:3$$, $$BK:CK=3:13$$.
а) Докажите, что углы $$PDK$$ и $$PCK$$ равны.
б) Пусть $$M$$ – точка пересечения $$CP$$ и $$DK$$. Найдите отношение длин отрезков $$CM$$ и $$PM$$.
Ответ: $$frac{52}{25}$$
Задание 16
Али‐Баба пришел в пещеру, где есть золото и алмазы. У Али‐Бабы с собой оказался мешок. Известно, что полный мешок золота весит 200 кг, полный мешок алмазов – 40 кг, а пустой мешок ничего не весит. Килограмм золота стоит 20 динаров, а килограмм алмазов – 60 динаров. Какую наибольшую сумму денег может выручить Али‐Баба за сокровища, если он может унести с собой не более 100 кг?
Ответ: 3000 динаров
Задание 17
Найдите все значения $$a$$, при каждом из которых система $$left{begin{matrix} x^2+y^2-4=2|x-2y|\ x+y=a end{matrix}right.$$ имеет ровно два решения.
Ответ: $$(-3sqrt{2}-1;-3sqrt{2}+1);$$$$(-frac{6sqrt{5}}{5};frac{6sqrt{5}}{5});$$$$(3sqrt{2}-1;3sqrt{2}+1)$$
Задание 18
Дана последовательность $$(a_{n})$$: $$a_{n}=(n-1)cdot ncdot (n+1)+133$$.
а) Найдите два соседних члена этой последовательности, разность которых равна 29700.
б) Найдите сумму всех $$n$$, при каждом из которых $$1033<a_{n}<1000033$$.
в) Найдите все члены этой последовательности, являющиеся точными кубами.
Ответ: А)$$a_{99}=970333, a_{100}=1000033$$ Б)$$4905$$ В)$$a_{6}=7^{3}, a_{133}=133^{3}$$
А. Ларин: Тренировочный вариант № 192.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
На продолжении высоты PО правильной четырехугольной пирамиды РАВСD отмечена точка К так, что ОР = ОК.
а) Докажите, что плоскости РВС и КАD параллельны.
б) Найдите расстояние между плоскостями РВС и КАD, если
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Дан квадрат ABCD. На сторонах АВ и ВС отмечены точки Р и К соответственно, причем ВР : АР = 1 : 3, ВК : СК = 3 : 13.
а) Докажите, что углы РDK и РСК равны.
б) Пусть М — точка пересечения CP и DK. Найдите отношение длин отрезков СM и PM.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Али‐Баба пришел в пещеру, где есть золото и алмазы. У Али‐Бабы с собой оказался мешок. Известно, что полный мешок золота весит 200 кг, полный мешок алмазов — 40 кг, а пустой мешок ничего не весит. Килограмм золота стоит 20 динаров, а килограмм алмазов — 60 динаров. Какую наибольшую сумму денег может выручить Али‐Баба за сокровища, если он может унести с собой не более 100 кг?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых система
имеет ровно два решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Дана последовательность
а) Найдите два соседних члена этой последовательности, разность которых равна 29700.
б) Найдите сумму всех n, при каждом из которых 1033 < an < 1000033.
в) Найдите все члены этой последовательности, являющиеся точными кубами.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Contents
- 1 Задание №1. Решение варианта №192 ОГЭ по математике Ларин
- 1.1 Решение
- 2
- 3 Задание №2
- 3.1 Решение
- 4 Задание №3. Решение варианта №192 ОГЭ по математике Ларин
- 4.1 Решение
- 5 Задание №4
- 5.1 Решение
- 6 Задание №5
- 6.1 Решение
- 7 Задание №6. Решение варианта №192 ОГЭ по математике Ларин
- 7.1 Решение
- 8 Задание №7. Решение варианта №192 ОГЭ по математике Ларин
- 8.1 Решение
- 9 Задание №8. Решение варианта №192 ОГЭ по математике Ларин
- 9.1 Решение
- 10 Задание №9. Решение варианта №192 ОГЭ по математике Ларин
- 10.1 Решение
- 11 Задание №10
- 11.1 Решение
- 12 Задание №11. Решение варианта №192 ОГЭ по математике Ларин
- 12.1 Решение
- 13 Задание №12
- 13.1 Решение
- 14 Задание №13. Решение варианта №192 ОГЭ по математике Ларин
- 14.1 Решение
- 15 Задание №14. Решение варианта №192 ОГЭ по математике Ларин
- 15.1 Решение
- 16 Задание №15
- 16.1 Решение
- 17 Задание №16
- 17.1 Решение
- 18 Задание №17
- 18.1 Решение
- 19 Задание №18
- 19.1 Решение
- 20 Задание №19
- 20.1 Решение
- 21 Задание №20. Решение варианта №192 ОГЭ по математике Ларин
- 21.1 Решение
- 22 Задание №21
- 22.1 Решение
- 23 Задание №22. Решение варианта №192 ОГЭ по математике Ларин
- 23.1 Решение
- 24 Задание №23
- 24.1 Решение
- 25 Задание №24
- 25.1 Решение
- 26 Задание №25
- 26.1 Решение
- 27 Задание №26. Решение варианта №192 ОГЭ по математике Ларин
- 27.1 Решение
- 28 Видео: Разбор Варианта ОГЭ Ларина №192 (№1-20)
- 29 Видео: Разбор Варианта ОГЭ Ларина №192 (№21-26)
Найдите значение выражения:
Решение
Ответ: 3.
Задание №2
В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты:
|
Команда, мин. |
I эстафета |
II эстафета |
III эстафета |
IV эстафета |
|
«Непобедимые» |
3,4 |
5,9 |
2,9 |
5,8 |
|
«Прорыв» |
4,5 |
4,3 |
3,2 |
5,4 |
|
«Чемпионы» |
4,9 |
4,8 |
2,7 |
6,3 |
|
«Тайфун» |
3,7 |
4,5 |
2,4 |
5,1 |
За каждую эстафету команда получает количество баллов, равное занятому в этой эстафете месту, затем баллы по всем эстафетам суммируются. Какое итоговое место заняла команда «Чемпионы», если победителем считается команда, набравшая наименьшее количество очков?
В ответе укажите номер правильного варианта.
- 1.
- 2.
- 3.
- 4.
Решение
Ответ: 4.
Задание №3. Решение варианта №192 ОГЭ по математике Ларин
Между какими числами заключено число 2√5.
Варианты ответа
1) 9 и 11 2) 5 и 6 3) 24 и 26 4) 4 и 5.
Решение
Представим 2√ в виде корня:
⇒ располагается между и или 4 и 5, ⇒ 4 вариант ответа. Ответ: 4.
Задание №4
Решение
Ответ: 3.
Задание №5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наименьшим и наибольшим значениями температуры. Ответ дайте в градусах Цельсия.
Решение
(между 21:00 и 00:00).
(между 12:00 и 15:00).
tmax = 8 — 24 = -16.
Ответ: -16.
Задание №6. Решение варианта №192 ОГЭ по математике Ларин
Решите уравнение:
−2(x+1)−3(2−3x) = 34.
Решение
x = 6.
Ответ: 6.
Задание №7. Решение варианта №192 ОГЭ по математике Ларин
Решение
Пропорция:
40 млн. р. / 100% = х / (100% — 60%)
х = [40*(100-60)]/100=16 млн. р.
Задание №8. Решение варианта №192 ОГЭ по математике Ларин
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей. Какие из следующих утверждений неверны?
- пользователей из России больше, чем пользователей из Украины;
- больше трети пользователей сети — из Украины;
- пользователей из Беларуси больше, чем пользователей из Украины;
- пользователей из России больше 4 миллионов человек.
Решение
Исходя из рисунка:
- да.
- нет (сегмент меньше трети круга).
- нет (сегмент Беларуси меньше).
- да.
Задание №9. Решение варианта №192 ОГЭ по математике Ларин
На одной тарелке 12 пирожков, 4 из которых с капустой, а на другой тарелке 8 пирожков, 6 из которых с капустой. Из каждой тарелки взяли по одному пирожку. Какова вероятность того, что оба пирожка с капустой?
Решение
Вероятность взять с капустой из первой:
Из второй:
Общая вероятность:
Ответ: 0,25.
Задание №10
Установите соответствие между графиками функций и формулами, которые их задают.
Решение
A-парабола
Б-прямая
B-гипербола
Ответ: 214.
Задание №11. Решение варианта №192 ОГЭ по математике Ларин
Укажите номер первого отрицательного члена арифметической прогрессии: 18; 15; …
Решение
Первый член прогрессии:
, ее разность:
ana1 + d(n-1) = 18-3(n-1) = -3n <- 21
Так как
Ответ: 8.
Задание №12
Найдите значение выражения:
Решение
Ответ: 4,5.
Задание №13. Решение варианта №192 ОГЭ по математике Ларин
Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула F=1,8C+32, где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 194 по шкале Фаренгейта? Ответ округлите до десятых.
Решение
1,8C = F-32 C = (
C = (
Ответ: 90.
Задание №14. Решение варианта №192 ОГЭ по математике Ларин
На каком рисунке изображено множество решений неравенства x² — 2x -3 ≤ 0. Укажите неравенство, которое не имеет решений.
Решение
⇒ ответ 1 вариант.
Ответ: 1.
Задание №15
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,6 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 1,5 м. Найдите длину троса. Ответ дайте в метрах.
Решение
Флагшток — первый катет, расстояние от основания флагштока до крепления троса — второй катет)
Первый катет равен 3,6 м, второй — 1,5 м ⇒
3,6² + 1,5² = 12,96+2,25 = 15,21 м².
√15,21 м² = 3,9 м.
Задание №16
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 42° и 78°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Решение
По свойству углов параллелограмма:
Ответ: 60.
Задание №17
Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка.
Каковы длины этих отрезков?
Решение
Из ABH:
Ответ: 13.
Задание №18
Найдите площадь квадрата, если его диагональ равна 8.
Решение
Пусть AB = BC = a.
По т. Пифагора :
Ответ: 32.
Задание №19
Найдите угол ABC. Ответ дайте в градусах.
Решение
Ответ: 45º.
Задание №20. Решение варианта №192 ОГЭ по математике Ларин
Какие из следующих утверждений верны?
- Диагонали ромба равны.
- Площадь ромба равна половине произведения его диагоналей.
- Средняя линия трапеции равна половине основания трапеции.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Решение
- Нет.
- Да.
- Нет.
Ответ: 2.
Задание №21
Решите систему уравнений:
Решение
Ответ: (-3;-4) (4;3).
Задание №22. Решение варианта №192 ОГЭ по математике Ларин
Велосипедист проехал 25 км. При этом один час он ехал по ровной дороге, а один час — в гору. Какова скорость (в км/ч) велосипедиста по ровной дороге, если каждый километр по ровной дороге он проезжал на 2 минуты быстрее, чем в гору?
Решение
По ровной дороге он проехал «х», в гору «у» километров ⇒ х + у = 25.
Пусть по ровной дороге его скорость Vкм/мин ⇒ один км он проезжает за время 1/ V, а «х» км он проедет за х/ V=60 мин.
В гору у*(1/ V + 2) = 60 мин.
60 V + 60/(1/ V + 2) = 25.
V = 1/4*60 = 15 км/мин.
Ответ: 15.
Задание №23
Постройте график функции: y = ∣x2−4x−2∣ и определите, при каких значениях с прямая у=с имеет с графиком три общие точки.
Решение
Парабола: , у которой часть ,которая располагается по Ox отображается симметрично Ox.
Вершина параболы:
— параллельна Ox, тогда при точки при y = 6 , то есть c = 6.
Ответ: 6.
Задание №24
В параллелограмме ABCD биссектриса тупого угла B пересекает сторону АD в точке К. Найти периметр параллелограмма, если АВ = 12 и АК:КD = 4:3
Решение
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ( угол при В делится пополам, а углы ∠AFB=∠CBF — накрест лежащие, поэтому углы при ВF равны и АF=AB).
Примем коэффициент отношения AF:FD равным а.
Тогда AF=4a, FD=3a Из равенства АF=AB находим а=12:4=3. ⇒ FD=3•3=9.⇒ AD=12+9=21.
Противоположные стороны параллелограмма равны. Р(АВСD)=2•(21+12)=66 (ед. длины).
Ответ: 66 или 30.
Задание №25
На основаниях АВ и СD вне трапеции построены квадраты. Докажите, что прямая, соединяющая их центры, проходит через точку пересечения диагоналей трапеции.
Решение
Задание №26. Решение варианта №192 ОГЭ по математике Ларин
В равнобедренной трапеции ABCD длина боковой стороны АВ равна 2 и длина меньшего основания ВС равна 2. Найдите площадь трапеции, если BD ⊥ АВ.
Решение
Обозначим ∠ADB = α. Тогда: ∠CBD = ∠ADB = α.
Треугольник BCD равнобедренный ⇒ ∠CDB = ∠CBD = α.
Поэтому ∠ADC = 2α.
∠BAD = 90o — ∠ADB = 90o — α и ∠BAD = ∠ADC,
то 90o — α = 2α. Отсюда находим, что α = 30o и ∠BAD = 60o.
Пусть BK — высота трапеции ⇒ BK = AB sin 60o = (2√) = √
Т.к. AD = 2AB = 4, то SABCD = ½(AD + BC)BK = ½(4 + 2) *√ = 3√
Ответ: 3√
Разбор Варианта ОГЭ Ларина №192 (№1-20)
Видео: Разбор Варианта ОГЭ Ларина №192 (№21-26)
Разбор Варианта ОГЭ Ларина №192 по математике 2019. Решение варианта Ларина №192. Подробный разбор заданий. Варианты ОГЭ 2019 по математике. mrMathlesson Виктор Осипов
№1-20
№21-26
Смотрите также: