Задание 1
Жильцы 9‐этажки ежемесячно платят управляющей компании на капитальный ремонт дома по 250 рублей (с каждой квартиры). В доме 3 подъезда, на каждой площадке по 4 квартиры. Какую сумму выплачивают за год жильцы дома управляющей компании? Ответ дайте в рублях.
Ответ: 324000
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
В каждом подъезде по: 9 * 4 = 36 квартир Всего в доме: 36 * 3 = 108 квартир В месяц с дома в сумме поступает: 108 * 250 = 27000 рублей Значит в год в итоге: 27 000 * 12 = 324 000
Задание 2
В 11А классе 25 учащихся. За контрольную по геометрии 5 человек получили отметку «5», 11 человек – «4», 8 человек – «3», и один ученик получил «2». Определите средний балл учащихся 11А класса за контрольную работу по геометрии.
Ответ: 3.8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Чтобы определить средний был, мы должны сложить все оценки и поделить на количество людей, то есть найти среднее арифметическое: $$frac{5*5+11*4+8*3+1*2}{5+11+8+1}=3.8$$
Задание 3
Площадь маленького круга равна 4. Найдите площадь закрашенной фигуры (рис.).
Ответ: 10.5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь большего круга в 4 раза больше площади маленького (так как радиус в два раза больше) => 4*4 = 16. Отсюда внешнего кольца : 16-4=12 Угол равен сорока пяти градусам, получается, что закрашенная область 315 градусов (360-45). Отсюда ее площадь: 12*315/360= 10.5
Задание 4
Генератор случайных чисел выводит на экран натуральное число, не превосходящее 100. Какова вероятность, что это число окажется простым?
Ответ: 0.25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Всего натуральных чисел, не превосходящих сто, собственно, сто штук. Простых чисел среди них 25. Следовательно, вероятность будет: $$frac{25}{100}*4=0.25$$
Задание 5
Найдите периметр равностороннего треугольника, если радиус вписанной в него окружности равен $$2sqrt{3}$$
Ответ: 36
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Если радиус вписанной в него окружности равен $$2sqrt{3}$$, то вся медиана этого треугольника будет $$2sqrt{3}*3=6sqrt{3}$$ (медиана в равностороннем треугольнике она и высота и биссекриса, следовательно, делится на радиус описанной и писанной окружностей, в отношении два к одному, поэтому радиус вписанной составляет одну треть от медианы) Сторона равностороннего треугольника будет равна : $$6sqrt{3} : sin 60 =6sqrt{3} :frac{sqrt{3}}{2} =12$$ Значит периметр равен 12*3=36
Задание 6
На графике производной функции у = f‘ / (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых угловой коэффициент касательной к графику функции f (x) положительный. В ответе укажите количество этих точек.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Угловой коэффициент касательной к графику это и есть значение производной, следовательно, мы ищем, где производная положительная. Так как дан нам график производной, то мы просто найдем количество точек, которые располагаются над осью ОХ: x1,x3,x4,x6 всего 4
Задание 7
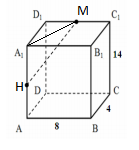
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно ВС=4, АВ=8, СС1=14. Найдите расстояние между серединами ребер АА1 и С1D1.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
|
Для этого рассмотрим треугольник HA1M: HA1=0.5AA1=7 A1M=$$sqrt{A_{1}D_{1}^{2}+D_{1}M^{2}}=sqrt{4^{2}+4^{2}}=sqrt{32}$$ MH=$$sqrt{A_{1}H^{2}+A_{1}M^{2}}=sqrt{7^{2}+32}=sqrt{81}=9$$ |
|
Задание 8
Известно, что $$log_a b *log_b c = -5$$ . Найдите значение выражения $$log_c a$$
Ответ: -0.2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$log_a b *log_b c = frac{1}{log_b a}*log_b c=frac{log_b c}{log_b a}=log_a c=-5$$ $$log_c a=frac{1}{log_a c}=frac{1}{-5}=-0.2$$
Задание 9
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле а=ω2R, где ω – угловая скорость (в с‐1), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с‐1, а центростремительное ускорение равно 650,25 м/с2.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Выразим R: $$R=frac{a}{omega ^{2}}=frac{650.25}{8.5^{2}}=9$$
Задание 10
Свежие плоды содержат 60% воды. При сушке плоды теряют 40% своей влаги. Сколько килограммов свежих плодов потребуется для получения 1520 кг сухих?
Ответ: 2000
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть S — первоначальная масса свежих плодов. Тогда воды в них X
S — 100%
x — 60%
x = 0.6S
При сушке теряется 40% воды, пусть эта масса Y:
0.6S — 100%
y — 40%
y = 0.6S*40/100=0.24S
Значит от первоначальной массы остается : S — 0.24S = 0.76S. Это и есть масса сухих плодов.
Найдем массу свежих: 0.76S=1520 S=1520/0.76=2000
Задание 11
Найдите наименьшее значение функции $$f(x)=(x^{2}-8x+8)*e^{2-x}$$ на отрезке [1; 7].
Ответ: -4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную функции: $$f^{‘}(x)=(2x-8)e^{2-x}+(-1)e^{2-x}(x^{2}-8x+8)=$$
$$=e^{2-x}(2x-8-x^{2}+8x-8)=e^{2-x}(-x^{2}+10x-16)$$
Приравняем производную к нулю:
$$e^{2-x}(-x^{2}+10x-16)=0$$ $$e^{2-x}=0$$
решений не имеет $$(-x^{2}+10x-16)=0$$ x1=2 и x2 =8
Отметим эти точки на координатной прямой и расставим знаки производной:
Точка минимума там, где производная меняет знак с — на +, то есть в точке 2
Подставим данное значение в первоначальную функцию и получим:
$$f(2)=(2^{2}-8*2+8)*e^{2-2}=(4-16+8)*1=-4$$
Задание 12
Дано уравнение $$2^{2+2sin x}-3cdot (sqrt{2})^{1+2sin x}+1=0$$.
a) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку $$[4pi;frac{23pi}{4}]$$.
Ответ: А)$$-frac{pi}{6}+2pi n; -frac{5pi}{6}+2pi m,n,min Z$$ Б)$$frac{31pi}{6}$$
Задание 13
На продолжении высоты $$PO$$ правильной четырехугольной пирамиды $$PABCD$$ отмечена точка $$K$$ так, что $$OP=OK$$.
а) Докажите, что плоскости $$PBC$$ и $$KAD$$ параллельны.
б) Найдите расстояние между плоскостями $$PBC$$ и $$KAD$$ , если $$AB=2, PO=2sqrt{2}$$.
Ответ: $$frac{4sqrt{2}}{3}$$
Задание 14
Решите неравенство
$$log_{2}x+5sqrt{log_{2}x}+15leq frac{92-46sqrt{log_{2}x}}{log_{2}x-5sqrt{log_{2}x}+6}$$
Ответ: $$[1;16);(16;512)$$
Задание 15
Дан квадрат $$ABCD$$. На сторонах $$AB$$ и $$BC$$ отмечены точки $$P$$ и $$K$$ соответственно, причем $$BP:AP=1:3$$, $$BK:CK=3:13$$.
а) Докажите, что углы $$PDK$$ и $$PCK$$ равны.
б) Пусть $$M$$ – точка пересечения $$CP$$ и $$DK$$. Найдите отношение длин отрезков $$CM$$ и $$PM$$.
Ответ: $$frac{52}{25}$$
Задание 16
Али‐Баба пришел в пещеру, где есть золото и алмазы. У Али‐Бабы с собой оказался мешок. Известно, что полный мешок золота весит 200 кг, полный мешок алмазов – 40 кг, а пустой мешок ничего не весит. Килограмм золота стоит 20 динаров, а килограмм алмазов – 60 динаров. Какую наибольшую сумму денег может выручить Али‐Баба за сокровища, если он может унести с собой не более 100 кг?
Ответ: 3000 динаров
Задание 17
Найдите все значения $$a$$, при каждом из которых система $$left{begin{matrix} x^2+y^2-4=2|x-2y|\ x+y=a end{matrix}right.$$ имеет ровно два решения.
Ответ: $$(-3sqrt{2}-1;-3sqrt{2}+1);$$$$(-frac{6sqrt{5}}{5};frac{6sqrt{5}}{5});$$$$(3sqrt{2}-1;3sqrt{2}+1)$$
Задание 18
Дана последовательность $$(a_{n})$$: $$a_{n}=(n-1)cdot ncdot (n+1)+133$$.
а) Найдите два соседних члена этой последовательности, разность которых равна 29700.
б) Найдите сумму всех $$n$$, при каждом из которых $$1033<a_{n}<1000033$$.
в) Найдите все члены этой последовательности, являющиеся точными кубами.
Ответ: А)$$a_{99}=970333, a_{100}=1000033$$ Б)$$4905$$ В)$$a_{6}=7^{3}, a_{133}=133^{3}$$
А. Ларин: Тренировочный вариант № 192.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
На продолжении высоты PО правильной четырехугольной пирамиды РАВСD отмечена точка К так, что ОР = ОК.
а) Докажите, что плоскости РВС и КАD параллельны.
б) Найдите расстояние между плоскостями РВС и КАD, если
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Дан квадрат ABCD. На сторонах АВ и ВС отмечены точки Р и К соответственно, причем ВР : АР = 1 : 3, ВК : СК = 3 : 13.
а) Докажите, что углы РDK и РСК равны.
б) Пусть М — точка пересечения CP и DK. Найдите отношение длин отрезков СM и PM.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Али‐Баба пришел в пещеру, где есть золото и алмазы. У Али‐Бабы с собой оказался мешок. Известно, что полный мешок золота весит 200 кг, полный мешок алмазов — 40 кг, а пустой мешок ничего не весит. Килограмм золота стоит 20 динаров, а килограмм алмазов — 60 динаров. Какую наибольшую сумму денег может выручить Али‐Баба за сокровища, если он может унести с собой не более 100 кг?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых система
имеет ровно два решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Дана последовательность
а) Найдите два соседних члена этой последовательности, разность которых равна 29700.
б) Найдите сумму всех n, при каждом из которых 1033 < an < 1000033.
в) Найдите все члены этой последовательности, являющиеся точными кубами.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Структура профильного уровня ЕГЭ по математике
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий:
- 8 заданий первой части (задания 1–8) с кратким ответом в виде целого числа или конечной десятичной дроби
- 4 задания второй части (задания 9–12) с кратким ответом в виде целого числа или конечной десятичной дроби
- 7 заданий второй части (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий)
Задания первой части направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий второй части осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
По уровню сложности задания распределяются следующим образом:
- задания 1–8 имеют базовый уровень
- задания 9–17 – повышенный уровень
- задания 18 и 19 относятся к высокому уровню сложности
При выполнении заданий с развернутым ответом части 2 экзаменационной работы в бланке ответов № 2 должны быть записаны полное обоснованное решение и ответ для каждой задачи.
Распределение заданий по частям экзаменационной работы
| Части работы | Количество заданий | Максимальный первичный бал | Тип заданий |
| 1 часть | 8 | 8 | Краткий ответ |
| 2 часть | 11 | 24 | Развернутый ответ |
| Итого | 19 | 32 |
Разбор заданий ЕГЭ по математике (профиль)
Напиши мне, решений каких вариантов не хватает на сайте?
Например: «Сборник Лысенко ЕГЭ 2023 профиль 40 вариантов», «Варианты Ларина ЕГЭ 2023 профиль», «Варианты СтатГрад ЕГЭ 2023 профиль» и т.п.
Варианты СтатГрад ЕГЭ 2023 (профильный уровень)
Варианты сборника И.В. Ященко ЕГЭ 2023 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2022 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2021 (профильный уровень), 36 вариантов.
Варианты сборника Ф.Ф. Лысенко ЕГЭ 2021 (профильный уровень), 40 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2020 (профильный уровень), 36 вариантов.
Сборники тренировочных тестов по математике профильного уровня для ЕГЭ в 2023 году и для ЕГЭ прошлых лет. Все тренировочные варианты/пробники содержат ответы и решения ко 2-й части кима. Обсудить решение и задания каждого варианта вы можете в комментариях под ними. РЕШАТЬ ТЕСТЫ
Обращайте внимание на уровень пробника — здесь только профильный! Базовый уровень смотрите здесь.
- Всё про ЕГЭ 2023
- Демоверсия 2023 + изменения 2023
Что почитать?
- Из актуального: рекомендации от ФИПИ по профильной математике
Что изменилось в ЕГЭ 2023 по математике
Представляете — ничего 
Теория для подготовки к ЕГЭ 2023 по математике
Для теории у нас создан особый раздел «Теория для ЕГЭ по математике». Отдельно может порекомендовать посмотреть сборник шпаргалок для ЕГЭ по математике и на проекте ЕГЭ100Баллов целая ветка, посвященная шпаргалкам.
Что можно брать с собой на ЕГЭ по профильной математике?
На ЕГЭ по математике как всегда с собой можно взять только линейку. Никаких калькуляторов и мобильных телефонов, конечно же. Вода и шоколадка разрешаются 
Выбирайте вариант, сверяйте с ответами, оставляйте комментарии НИЖЕ
Реальные варианты ЕГЭ по математике
Дорогие друзья! На этой странице вы можете найти варианты реальных КИМ ЕГЭ по математике (база и профиль). На сайте размещены только ссылки на варианты КИМ ЕГЭ и их решения. Здесь вы можете сказать тренировочный и реальный вариант ЕГЭ по математике (профиль и база) 2022 и 2023 гг с ответами и решениями. Если материалы вам пригодились, можете финансово поддержать работу сайта через форму ниже:
2022-2023 учебный год
| Реальный вариант ЕГЭ по математике-2023 | ||
| Скачать вариант (профиль) | Решение и ответы | 02.06.2023 |
| Досрочные варианты ЕГЭ по математике-2023 | ||
| Скачать вариант 1 (профиль) | Решение и ответы | 28.03.2023 |
| Открытый вариант досрочного ЕГЭ по математике-2023 | ||
| Скачать вариант (профиль) |
Решение и ответы | 28.03.2023 |
| Скачать вариант (база) | Решение и ответы | 28.03.2023 |
| Демонстрационный вариант ЕГЭ по математике-2023 | ||
| Вариант (профиль) | Спецификация | Кодификатор |
| Вариант (база) | Спецификация | |
| Тренировочные работы Статград в формате ЕГЭ по математике-2023 | ||
| Тренировочная работа №1
Профиль База |
Ответы и решения | 28 сентября 2021 г. |
| Тренировочная работа №2
Профиль База |
Ответы и решения | 15 декабря 2021 г. |
| Тренировочная работа №3
Профиль База |
Ответы и решения (профиль) | 27 января 2022 г. |
| Тренировочная работа №4
Профиль База |
||
| Тренировочная работа №5
Профиль База |
Ответы и решения | 28 апреля 2022 г. |
2021-2022 учебный год
| Реальный вариант ЕГЭ по математике-2022 | ||
| Скачать вариант (профиль) Дальний Восток | Решение и ответы | 02.06.2022 |
| Досрочные варианты ЕГЭ по математике-2022 | ||
| Скачать вариант 1 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 2 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 3 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 4 (профиль) | Решение и ответы | 28.03.2022 |
| Открытый вариант досрочного ЕГЭ по математике-2022 | ||
| Скачать вариант (профиль) |
Решение и ответы | 28.03.2022 |
| Скачать вариант (база) | Решение и ответы | 28.03.2022 |
| Демонстрационный вариант ЕГЭ по математике-2022 | ||
| Вариант (профиль) | Спецификация | Кодификатор |
| Вариант (база) | Спецификация | |
| Перспективный вариант демо-версии КИМ ЕГЭ по математике-2022 |
||
| Вариант | Спецификация | |
| Тренировочные работы Статград в формате ЕГЭ по математике-2022 | ||
| Тренировочная работа №1 (профиль)
Тренировочная работа №1 (база) |
Ответы и решения | 28 сентября 2021 г. |
| Тренировочная работа №2 (профиль) Варианты 1 и 2Варианты 3 и 4 |
Ответы и решения | 15 декабря 2021 г. |
| Тренировочная работа №3 (профиль)
Тренировочная работа №3 (база) |
Ответы и решения (профиль) | 27 января 2022 г. |
| Тренировочная работа №4 | ||
| Тренировочная работа №5 (база)
Тренировочная работа №5, варианты 1 и 2 (профиль) Тренировочная работа №5, варианты 3 и 4 (профиль) |
Ответы и решения | 28 апреля 2022 г. |
2020-2021 учебный год
| Реальные варианты КИМ ЕГЭ по математике | ||
| Основная волна ЕГЭ по математике-2021 | ||
| Вариант 1 | Ответы и решения | |
| Открытый вариант ЕГЭ по математике-2021 от ФИПИ | ||
| Вариант (профиль) | Ответы и решения | |
| Демонстрационный вариант ЕГЭ по математике-2021 (проект) | ||
| Вариант Ответы | Кодификатор | Спецификация |
|
Тренировочные варианты ЕГЭ по математике-2021 |
||
| Вариант 1
Вариант 2 |
Вариант 1 — ответы и решения
Вариант 2 — ответы, критерии |
Admin
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.