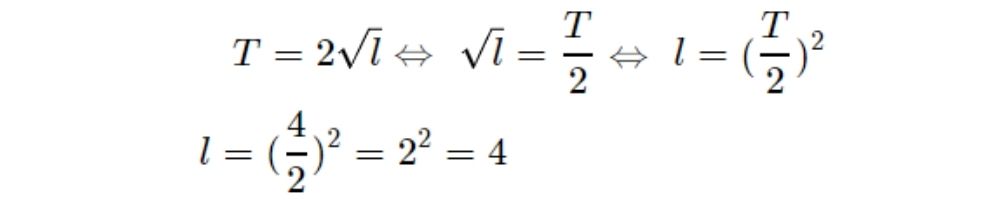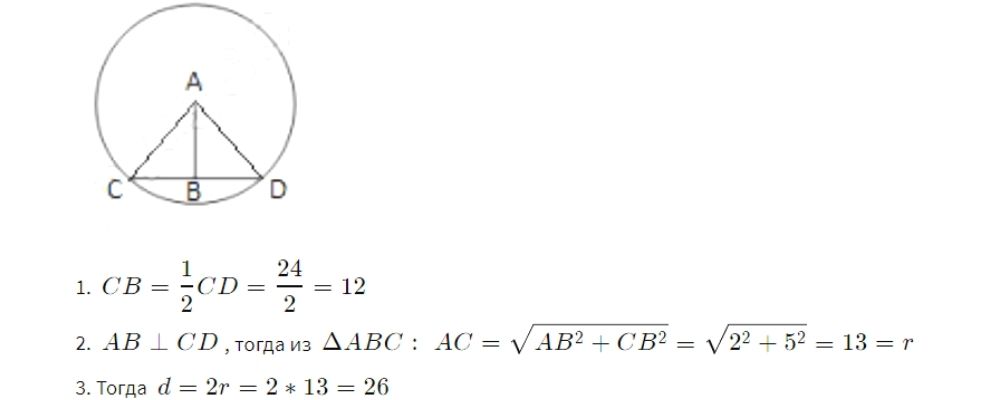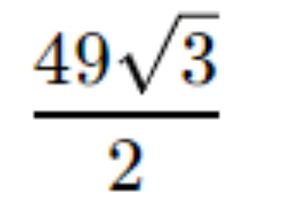А. Ларин: Тренировочный вариант № 190.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение:
б) Найдите все решения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В правильной треугольной пирамиде SABC точки M, N и K — середины ребер основания, а P, Q и R делят боковые ребра SA, SB и SC в отношении 1 : 2, считая от вершины.
а) Доказать, что точки M, N, K, P, Q, R — лежат на одной сфере.
б) При каких углах наклона бокового ребра к основанию центр сферы лежит вне пирамиды SABC.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Первая окружность вписана в треугольник АВС и касается ВС в точке М. Вторая окружность касается ВС в точке N и продолжений сторон АС и АВ.
а) Докажите, что длина МN равна модулю разности длин АВ и АС.
б) Найдите площадь треугольника АВС, если известно, что радиусы окружностей относятся как 1 : 3, ВС = 12, MN = 4.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Гражданин положил в каждый из двух банков по 5 млн руб. В первом банке в конце года начисляется одно и то же количество процентов на сумму, лежащую в банке в начале года. Во втором банке принцип начисления процентов следующий: в первый год процентная ставка на 3 меньше, чем в первом банке, а затем она каждый год увеличивается на 2%. В итоге, к концу четвертого года на счету у гражданина в первом банке было на 5617 руб. 55 коп. больше, чем во втором. Найти процентную ставку в первом банке.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
При каких значениях параметра a область значений функции
содержит отрезок [1; 4]?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Назовем квадратное уравнение с натуральными коэффициентами a ,b и c «простым», если a ,b и c не имеют кроме 1, других общих делителей.
а) Найти все значения b , для которых «простое» уравнение имеет хотя бы одно целое решение,
б) Докажите, что «простое» уравнение не имеет целых решений, если b кратно 3,
в) Докажите, что если и не кратно 3, найдется такое «с», что простое уравнение
имеет целое решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
ЕГЭ по математике, Вариант № 190, 11 класс, 2010.
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 18 заданий. Часть 1 содержит 12 заданий с кратким ответом (В1–В12) базового уровня по материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1–С6) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Примеры.
1. На рисунке жирными точками показана цена олова на момент закрытия биржевых торгов во все рабочие дни с 7 по 20 сентября 2007 года. По горизонтали указываются числа месяца, по вертикали – цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена олова на момент закрытия торгов была наибольшей.
2. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 450 рублей после понижения цены на 10%?
3. В треугольнике ABC угол C равен 90° , AB = 30, AC = 24. Найдите sin A.
4. Строительной фирме нужно приобрести 50 кубометров строительного бруса у одного из трех поставщиков. Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и условия доставки приведены в таблице.
5. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.
6. Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: q =160 −10 p . Определите максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприятия за месяц r = q ⋅ p составит не менее 550 тыс. руб.
7. Перед каждым из чисел 11, 12, …, 19 и 6, 7, …, 10 произвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 45 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
8. Моторная лодка в 11:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 15 минут, лодка отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки равна 3 км/ч.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ по математике, Вариант № 190, 11 класс, 2010 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ по математике, Вариант № 190, 11 класс, 2010 — pdf — depositfiles.
Скачать книгу ЕГЭ по математике, Вариант № 190, 11 класс, 2010
— pdf — Яндекс.Диск.
Дата публикации: 31.05.2013 17:52 UTC
Теги:
математика :: ЕГЭ по математике :: 11 класс
Следующие учебники и книги:
- ЕГЭ 2010, Математика, Экспресс-консультация, Жафяров А.Ж.
- ЕГЭ 2010, Математика, Задача B4, Рабочая тетрадь, Смирнов В.А., Семенов А.Л., Ященко И.В.
- ЕГЭ 2013, Математика, 30 типовых вариантов заданий, Семенов А.Л., Ященко И.В.
- Геометрия, Все типы заданий ГИА и ЕГЭ, Решаем задачи повторяем теорию, Вольфсон Б.И., 2013
Предыдущие статьи:
- ЕГЭ по математике, Вариант № 189, 11 класс, 2010
- ЕГЭ по математике, Вариант № 188, 11 класс, 2010
- ЕГЭ по математике, Вариант № 187, 11 класс, 2010
- ЕГЭ по математике, Вариант № 186, 11 класс, 2010
Регистрация Форум Текущее время: 10 мар 2023, 16:20 Сообщения без ответов | Активные темы Страница 1 из 17 [ Сообщений: 162 ] На страницу 1, 2, 3, 4, 5 … 17 След. Начать новую тему»> Ответить Тренировочный вариант №190
Тренировочный вариант №190
Страница 1 из 17 [ Сообщений: 162 ] На страницу 1, 2, 3, 4, 5 … 17 След. Текущее время: 10 мар 2023, 16:20 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
Задание 1
Найдите значение выражения: $$frac{6,9}{3,9-6,2}$$
Ответ: -3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{6,9}{3,9*6,2}=-frac{6,9}{2,3}=-frac{69}{23}=-3$$
Задание 2
Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 63,5 г.
| Категория | Масса одного яйца, не менее, г |
| Высшая | 75,0 |
| Отборная | 65,0 |
| Первая | 55,0 |
| Вторая | 45,0 |
| Третья | 35,0 |
Варианты ответа
- Высшая
- Отборная
- Первая
- Вторая
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$63,5 in (55; 65)$$ следовательно, попадает в первую категорию.
Задание 3
Одно из чисел $$sqrt{5}, sqrt{7}, sqrt{11}, sqrt{14}$$ отмечено на прямой точкой A. Какое это число?
Варианты ответа
- $$sqrt{5}$$
- $$sqrt{7}$$
- $$sqrt{11}$$
- $$sqrt{14}$$
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$2=sqrt{4}; 3=sqrt{9}$$ . Тогда $$A=sqrt{5}$$ или $$A=sqrt{7}$$. Так как число А ближе к 2, то оно равно $$sqrt{5}$$, что соответствует 1 варианту ответа
Задание 4
Представьте выражение $$(m^{-3})^{-5}:m^{-3}$$ в виде степени с основанием m
Варианты ответа
- $$m^{12}$$
- $$m^{-12}$$
- $$m^{18}$$
- $$m^{-4}$$
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(m^{-3})^{-5}:m^{-3}=m^{(-3)(-5)-(-3)}=m^{15+3}=m^{18}$$, что соответствует 3 варианту ответа
Задание 5
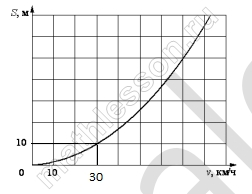
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 30 км/ч. Ответ дайте в метрах.
Ответ: 10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Координате v=30 соответствует S=10 (смотреть рисунок)
Задание 6
Решите уравнение $$frac{x}{5}+frac{x}{15}+x=-3frac{4}{5}$$
Ответ: -3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{x}{5}+frac{x}{15}+x=-3frac{4}{5}$$ $$frac{3x+x+15x}{15}=frac{-19}{5}$$ $$frac{19x}{15}=frac{-19*3}{15}$$ $$x=-3$$
Задание 7
В поселке в настоящее время 40824 жителя. Известно, что население этого поселка увеличивалось ежегодно на 8%. Сколько жителей было в поселке два года назад?
Ответ: 35000
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x –два года назад, тогда x*1,08 –год назад и (x*1,08)*1,08 –в этом году $$x*1,08^{2}=40824$$ $$x=frac{40824}{1,08}=3500$$
Задание 8
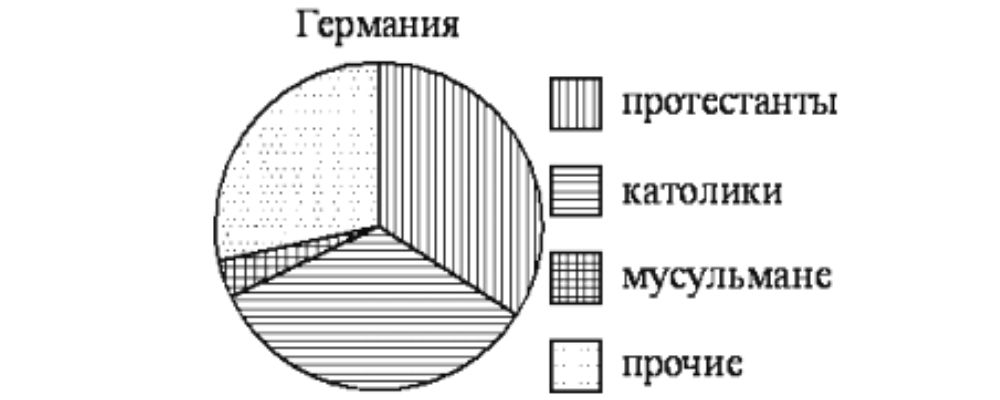
На диаграмме показан религиозный состав населения Германии. Определите по диаграмме, в каких пределах находится доля католиков.
Варианты ответа:
- 0-10%
- 10-15%
- 15-25%
- 25-45%
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Сегмент католиков составляет третью часть круга, то есть около 33%, что попадает в четвертый вариант ответа
Задание 9
На олимпиаде по математике 250 участников разместили в трёх аудиториях. В первых двух удалось разместить по 95 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Ответ: 0,24
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
В запасной аудитории 250-2*95=60 человек. Тогда вероятность туда попасть: $$P=frac{60}{250}=0,24.$$
Задание 10
График какой из приведенных ниже функций изображён на рисунке?
- $$y=x^{2}+2$$
- $$y=-x^{2}+2$$
- $$y=x^{2}+4$$
- $$y=-x^{2}+4$$
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Ветви вниз, значит a<0. Вершина смещена на 4 вверх, значит b=4(рассматриваем квадратичную функцию $$y=ax^2+b$$), следовательно, ответ 4.
Задание 11
Арифметическая прогрессия задана условием $$a_{n}=-29+5,8*n$$ . Найдите $$a_{10}$$
Ответ: 29
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$a_{10}=-29+5,8*10=-29+58=29$$
Задание 12
Найдите значение выражения $$frac{35}{7a-a^{2}}-frac{5}{a}$$, при $$a=-18$$
Ответ: 0,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{35}{7a-a^{2}}-frac{5}{a}=frac{35-5(7-a)}{a(7-a)}=$$$$frac{35-35+5a}{a(7-a)}=frac{5}{7-a}=$$$$frac{5}{7-(-8)}=frac{5}{25}=0,2$$
Задание 13
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле $$T=2sqrt{l}$$ , где l — длина нити в метрах. Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 4 секунды.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$T=2sqrt{l}Leftrightarrow$$ $$sqrt{l}=frac{T}{2}Leftrightarrow$$ $$l=(frac{T}{2})^{2}$$ $$l=(frac{4}{2})^{2}=2^{2}=4$$
Задание 14
Решите неравенство $$3x-59(x+2)>-2$$
Варианты ответа:
- $$(-4;+infty )$$
- $$(-12;+infty)$$
- $$(-infty;-4)$$
- $$(infty;-12)$$
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$3x-5(x+2)>-2$$
$$3x-5x-10+2>0$$
$$-2x-8>0$$
$$-2x>8$$
$$x<4$$, что соответствует 3 варианту ответа
Задание 15
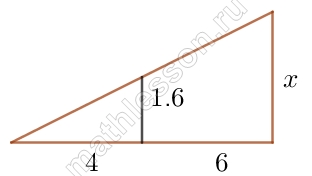
Человек ростом 1,6 м стоит на расстоянии 6 шагов от столба, на котором висит фонарь. Тень человека равна четырём шагам. На какой высоте (в метрах) расположен фонарь?
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x –высота фонаря, тогда $$frac{1,6}{x}=frac{4}{10}Leftrightarrow$$ $$x=frac{1,6*10}{4}=frac{16}{4}=4$$
Задание 16
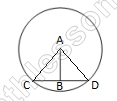
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=44°. Найдите угол NMB. Ответ дайте в градусах.
Ответ: 46
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- $$angle NBA=frac{1}{2}cup ANRightarrow cup AN=44*2=88$$
- $$cup NB=180-cup NA=180-88=92$$
- $$angle NMB=frac{1}{2}cup NB=frac{92}{2}=46$$
Задание 17
Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 5. Найдите диаметр окружности.
Ответ: 26
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- $$CB=frac{1}{2}CD=frac{24}{2}=12$$
- $$ABperp CD$$, тогда из $$Delta ABC:$$ $$AC=sqrt{AB^{2}+CB^{2}}=sqrt{2^{2}+5^{2}}=13=r$$
- Тогда $$d=2r=2*13=26$$
Задание 18
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь
Ответ: 10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь одного квадрата составляет 1*1=1, тогда площадь фигуры равна 1*10=10
Задание 19
В треугольнике ABC угол C равен 90°, BC=9, sin A=0,6. Найдите AB
Ответ: 15
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$sin A=frac{CB}{AB}$$, тогда $$AB=frac{CB}{sin A}=frac{9}{0,6}=15$$
Задание 20
Какие из следующих утверждений верны?
1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
2. Диагонали параллелограмма равны.
3. Радиус окружности равен половине диаметра этой окружности.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- нет — так как половине гипотенузы равна медиана, к ней проведенная
- нет — только в прямоугольнике и квадрате
- верно
Задание 21
Решите уравнение: $$x^{2}(x-2)^{3}=x^{4}(x-2)$$
Ответ: 0;1;2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$x^{2}(x-2)^{3}=x^{4}(x-2)$$ $$x^{4}(x-2)-x^{2}(x-2)^{3}=0$$ $$x^{2}(x-2)((x-2)^{2}-x^{2})=0$$ $$x^{2}(x-2)(x-2-x)(x-2+x)=0$$ $$left{begin{matrix}x=0 \x-2=0 \2x-2=0end{matrix}right.Leftrightarrow$$$$left{begin{matrix}x=0 \x=2 \x=1end{matrix}right.$$
Задание 22
В первую поездку автомобиль израсходовал 10% бензина, имеющегося в баке, затем во вторую поездку – 25% остатка. После этого в баке осталось на 13 л меньше, чем было первоначально. Сколько литров бензина находилось в баке первоначально?
Ответ: 40
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть изначально было литров. Израсходовал 0,1x , осталось 0,9x . Затем израсходовал 25% от $$0,9x=0,25*0,9x=0,225x$$. Тогда всего израсходовали: $$0,1x+0,25x=13$$ $$0,325x=13Leftrightarrow x=40$$ (литров) было в баке.
Задание 23
Постройте график функции $$y=left{begin{matrix}-x^{2},|x|leq 2\ frac{8}{x},|x|>2end{matrix}right.$$
и определите, при каких значениях а прямая y=аx будет иметь с графиком единственную общую точку
Ответ: $$[0;4)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Начертим график данной функции $$y=left{begin{matrix} -x^{2}, left | x right |leq 2\ frac{8}{x}, left | x right |>0end{matrix}right.$$
Учтем, что график $$y=-x^{2}$$ при $$xin [-2;2]$$ (на концах закрашенные точки, так как неравенство нестрогое), на остальной части область определения $$y=frac{8}{x}$$.
$$y=a$$ — прямая, параллельная оси Ox, тогда одну точку будет иметь при $$ain [0;4)$$
Задание 24
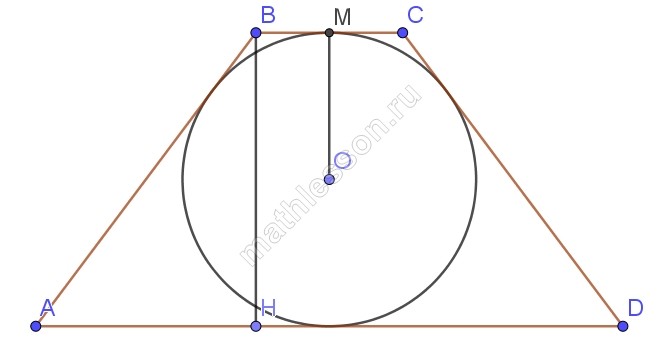
Около круга радиуса 2 см описана равнобедренная трапеция с острым углом 30. Найдите длину средней линии трапеции.
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- Пусть BH-высота, тогда BH=2ч=4
- из $$Delta ABH$$: $$AB=BH sin A=frac{4}{frac{1}{2}}=8=CD$$
- т.к. $$AB+CD=BC+AD$$(свойство описанного выпуклого четырехугольника) , то $$BC+AD=16$$, тогда средняя линия $$frac{16}{2}=8$$
Задание 25
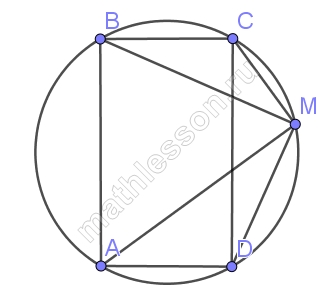
Точка М лежит на окружности радиуса R, описанной около прямоугольника ABCD. Докажите, что МА2 + МВ2 + МС2 + МD2 = 8R2
Ответ:
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- $$angle CMA=90$$, AC-диаметр окружности . Тогда из $$Delta ACM$$
- $$AC^{2}=MC^{2}+MA^{2}Leftrightarrow (2R)^{2}=MC^{2}+MA^{2}(1)$$
- Аналогично , из $$Delta BMD: (2R)^{2}=MB^{2}+MD^{2}(2)$$
- Сложим (1)и(2): $$MA^{2}+MB^{2}+MC^{2}+MD^{2}=8R^{2}$$
Задание 26
Внутри параллелограмма ABCD взята точка K так, что треугольник CKD равносторонний. Известно, что расстояния от точки K до прямых AD, AB и BC равны соответственно 3, 6 и 5. Найдите периметр параллелограмма.
Ответ: $$frac{49sqrt{3}}{2}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) Пусть KN=3, KP=5, KM=6,$$KQperp DC$$
KD=KC=DC=Q, тогда:
$$Delta KDC ND=sqrt{a^{2}-3^{2}}$$
$$Delta KPC PC=sqrt{a^{2}-5^{2}}$$
2) Опустим $$DHperp BC$$, тогда DH=NP=8,
$$CH=ND-PC=sqrt{a^{2}-3^{2}}-sqrt{a^{2}-5^{2}}$$
Тогда из $$Delta DHC:$$
$$a^{2}=8^{2}+(sqrt{a^{2}-3^{2}}-sqrt{a^{2}-5^{2}})^{2}$$
$$a^{2}-8^{2}=a^{2}-9+a^{2}-25-2sqrt{a^{4}-34a^{2}+225}$$
$$2sqrt{a^{4}-34a^{2}+225}=a^{2}+30$$
$$4a^{4}-136a^{2}+900=a^{4}+60a^{2}+900$$
$$3a^{4}-196a^{2}=0$$
$$3a^{2}(a^{2}-frac{96}{3})=0$$
a=0-не может быть
$$a=pm sqrt{frac{196}{3}}=pm frac{14}{sqrt{3}}$$ отрицательным не может быть
3) Из $$Delta KDC KQ=KC*sin C=frac{14}{sqrt{3}}*frac{sqrt{3}}{2}=7Rightarrow MQ=13$$
4) $$S_{ABCD}=MP*BC=MQ*DC$$
$$BC=frac{MQ*DC}{NP}=frac{13*14}{sqrt{3}}{8}=frac{91}{4sqrt{3}}$$
5) $$P_{ABCD}=2(frac{14}{sqrt{3}}+frac{91}{4sqrt{3}})=frac{147}{2sqrt{3}}=frac{49sqrt{3}}{2}$$
Contents
- 1 Задание №1
- 1.1 Решение
- 2 Задание №2. Решение варианта №190 ОГЭ по математике. Ларин
- 2.1 Решение
- 3 Задание №3. Решение варианта №190 ОГЭ по математике. Ларин
- 3.1 Решение
- 4 Задание №4
- 4.1 Решение
- 5 Задание №5. Решение варианта №190 ОГЭ по математике. Ларин
- 5.1 Решение
- 6 Задание №6
- 6.1 Решение
- 7 Задание №7. Решение варианта №190 ОГЭ по математике. Ларин
- 7.1 Решение
- 8 Задание №8. Решение варианта №190 ОГЭ по математике. Ларин
- 8.1 Решение
- 9 Задание №9. Решение варианта №190 ОГЭ по математике. Ларин
- 9.1 Решение
- 10 Задание №10. Решение варианта №190 ОГЭ по математике. Ларин
- 10.1 Решение
- 11 Задание №11. Решение варианта №190 ОГЭ по математике. Ларин
- 11.1 Решение
- 12 Задание №12
- 12.1 Решение
- 13 Задание №13
- 13.1 Решение
- 14 Задание №14. Решение варианта №190 ОГЭ по математике. Ларин
- 14.1 Решение
- 15 Задание №15. Решение варианта №190 ОГЭ по математике. Ларин
- 15.1 Решение
- 16 Задание №16. Решение варианта №190 ОГЭ по математике. Ларин
- 16.1 Решение
- 17 Задание №17
- 17.1 Решение
- 18 Задание №18
- 18.1 Решение
- 19 Задание №19. Решение варианта №190 ОГЭ по математике. Ларин
- 19.1 Решение
- 20 Задание №20. Решение варианта №190 ОГЭ по математике. Ларин
- 20.1 Решение
- 21 Задание №21
- 21.1 Решение
- 22 Задание №22. Решение варианта №190 ОГЭ по математике. Ларин
- 22.1 Решение
- 23 Задание №23. Решение варианта №190 ОГЭ по математике. Ларин
- 23.1 Решение
- 24 Задание №24. Решение варианта №190 ОГЭ по математике. Ларин
- 24.1 Решение
- 25 Задание №25
- 25.1 Решение
- 26 Задание №26. Решение варианта №190 ОГЭ по математике. Ларин
- 26.1 Решение
- 27 Видео: Разбор Варианта ОГЭ Ларина №190 (№1-20)
- 28 Видео: Разбор Варианта ОГЭ Ларина №190 (№21-26)
Задание №1
Найдите значение выражения:
Решение
Ответ: -3.
Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья.
| Категория | Масса одного яйца, не менее, г |
| Высшая | 75,0 |
| Отборная | 65,0 |
| Первая | 55,0 |
| Вторая | 45,0 |
| Третья | 35,0 |
Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 63,5 г.
Варианты ответа: 1. высшая 2. отборная 3. первая 4. вторая.
Решение
следовательно, первая категория.
Ответ: 3.
Задание №3. Решение варианта №190 ОГЭ по математике. Ларин
Одно из чисел √5, √7, √11, √14 отмечено на прямой точкой A.
Какое это число? 1.√5 2.√7 3.√11 4.√14
Решение
.
ТогдаA = илиA = .
Так как число А ближе к 2, то оно равно , что соответствует 1 варианту.
Ответ: 1.
Задание №4
Представьте выражение:
в виде степени с основанием m.
Варианты ответа
- 1. m12 .
- 2.m-12 .
- 3.18 .
- 4.-4.
Решение
соответствует 3 варианту ответа.
Ответ: 3.
Задание №5. Решение варианта №190 ОГЭ по математике. Ларин
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости.
По горизонтальной оси откладывается скорость (в км/ч), по вертикальной — тормозной путь (в метрах).
Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 30 км/ч. Ответ дайте в метрах.
Решение
Координате v=30 соответствует S=10.
Ответ: 10.
Задание №6
Решите уравнение:
Решение
Ответ: -3.
Задание №7. Решение варианта №190 ОГЭ по математике. Ларин
В поселке в настоящее время 40824 жителя. Известно, что население этого поселка увеличивалось ежегодно на 8%.
Сколько жителей было в поселке два года назад?
Решение
Пусть x –два года назад, тогда x*1,08 –год назад и (x*1,08)*1,08 в этом году.
Ответ: 35000.
Задание №8. Решение варианта №190 ОГЭ по математике. Ларин
На диаграмме показан религиозный состав населения Германии.
Определите по диаграмме, в каких пределах находится доля католиков.
- 1. 0-10%
- 2. 10-15%
- 3. 15-25%
- 4. 25-45%
Решение
Сегмент католиков составляет третью часть круга, то есть около 33%, что попадает в 4 вариант ответа.
Ответ: 4.
Задание №9. Решение варианта №190 ОГЭ по математике. Ларин
На олимпиаде по математике 250 участников разместили в трёх аудиториях. В первых двух удалось разместить по 95 человек, оставшихся перевели в запасную аудиторию в другом корпусе.
Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Решение
В запасной аудитории 250-2*95=60 человек.
Следовательно вероятность попасть:
Ответ: 0,24.
Задание №10. Решение варианта №190 ОГЭ по математике. Ларин
График какой из приведенных ниже функций изображён на рисунке?
Решение
Ветви вниз, значит a<0. Вершина смещена на 4 вверх, значит b=4 (рассматриваем квадратичную функцию ), следовательно, ответ 4.
Ответ: 4.
Задание №11. Решение варианта №190 ОГЭ по математике. Ларин
Арифметическая прогрессия задана условием:
an = -29 + 5.8n.
Найдите a10.
Решение
Ответ: 29.
Задание №12
Найдите значение выражения:
при а = — 18.
Решение
Ответ: 0,2.
Задание №13
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле T=2√l , где l — длина нити в метрах. Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 4 секунды.
Решение
Ответ: 4.
Задание №14. Решение варианта №190 ОГЭ по математике. Ларин
Решите неравенство 3x — 5(x+2) > -2.
Варианты ответа:
Решение
x < 4, что соответствует ответу 3.
Ответ: 3.
Задание №15. Решение варианта №190 ОГЭ по математике. Ларин
Человек ростом 1,6 м стоит на расстоянии 6 шагов от столба, на котором висит фонарь. Тень человека равна четырём шагам.
На какой высоте (в метрах) расположен фонарь?
Решение
Ответ: 4.
Задание №16. Решение варианта №190 ОГЭ по математике. Ларин
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что угол NBA=44°.
Найдите угол NMB. Ответ дайте в градусах.
Решение
Ответ: 46.
Задание №17
Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 5.
Найдите диаметр окружности.
Решение
Ответ: 26.
Задание №18
На клетчатой бумаге с размером клетки 1*1 изображена фигура.
Найдите её площадь.
Решение
Площадь одного квадрата составляет 1*1=1, тогда площадь фигуры равна 1*10=10.
Задание №19. Решение варианта №190 ОГЭ по математике. Ларин
В треугольнике ABC угол C равен 90°, BC=9, sinA=0,6.
Найдите AB.
Решение
Ответ: 15.
Задание №20. Решение варианта №190 ОГЭ по математике. Ларин
Какие из следующих утверждений верны?
- 1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
- 2. Диагонали параллелограмма равны.
- 3. Радиус окружности равен половине диаметра этой окружности.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение
- нет — так как половине гипотенузы равна медиана, к ней проведенная.
- нет — только в прямоугольнике и квадрате.
- верно.
Ответ: 3.
Задание №21
Решите уравнение:
Решение
Ответ: 0; 1; 2.
Задание №22. Решение варианта №190 ОГЭ по математике. Ларин
В первую поездку автомобиль израсходовал 10% бензина, имеющегося в баке, затем во вторую поездку — 25% остатка. После этого в баке осталось на 13 л меньше, чем было первоначально. Сколько литров бензина находилось в баке первоначально?
Решение
Пусть изначально было литров.
Израсходовал 0,1x , осталось 0,9x.
Затем израсходовал:
25% от 0,9x = 0,25*0,9x = .
Тогда всего израсходовали:
0,1x + 0,25x = 13.
0,325x = (литров) было в баке.
Ответ: 40.
Задание №23. Решение варианта №190 ОГЭ по математике. Ларин
Постройте график функции:
и определите, при каких значениях а прямая y=а будет иметь с графиком единственную общую точку.
Решение
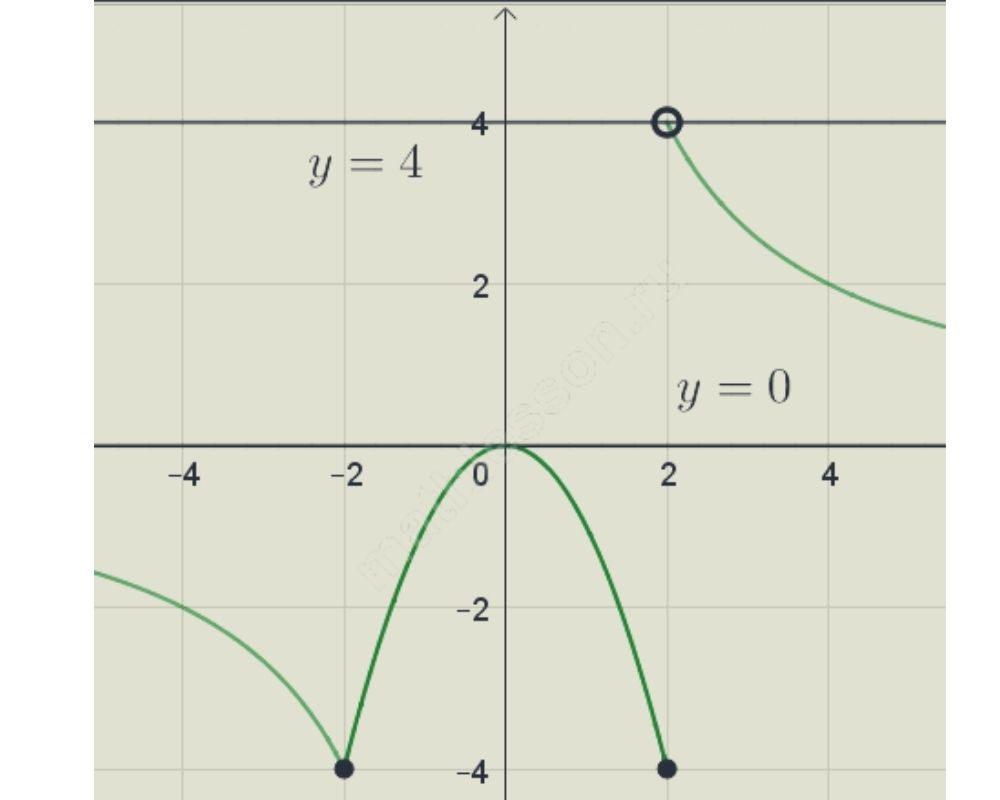
Ответ: [0;4).
Задание №24. Решение варианта №190 ОГЭ по математике. Ларин
Около круга радиуса 2 см описана равнобедренная трапеция с острым углом 30°.
Найдите длину средней линии трапеции.
Решение
Ответ: 8.
Задание №25
Точка М лежит на окружности радиуса R, описанной около прямоугольника ABCD.
Докажите, что МА2 + МВ2 + МС2 + МD2 = 8R2
Решение
Решение
Ответ:





 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема