А. Ларин: Тренировочный вариант № 186.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) При каких значениях x числа взятые в указанном порядке, являются последовательными членами арифметической прогрессии?
б) При каких значениях x прогрессия является возрастающей? Найти сумму первых 70 членов прогрессии.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В конус вписан цилиндр так, что нижнее основание цилиндра лежит на основании конуса, а окружность верхнего основания принадлежит боковой поверхности конуса. Объем конуса равен 72.
а) Найти объем цилиндра, верхнее основание которого делит высоту конуса пополам.
б) Найти наибольший объем вписанного цилиндра.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Равнобедренные треугольники АВС (АВ = ВС) и KLM (KM = LM) расположены так, что М — середина АС, В — середина KL, прямая KL параллельна прямой AC. Точки R — точка пересечения KM и АВ, Т — ВС и МL.
а) Доказать, что прямая RT параллельна прямой АС.
б) Найти площадь треугольника АВС, если и площадь четырехугольника BTMR равна 24.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
На следующей странице вам будет предложено проверить их самостоятельно.
6
При каких значениях параметра a, уравнение
имеет хотя бы одно решение на отрезке
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Натуральное число х имеет остаток 5 при делении на 8 и остаток 41 при делении на 64.
а) Найти остаток при делении числа х на 32;
б) Найти сумму таких чисел х, которые принадлежат отрезку [2000, 3000].
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Задание 1
Найдите значение выражения: $$(frac{4}{15}+2frac{2}{9}):frac{4}{27}$$
Ответ: 16,8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$left ( frac{4}{15}+2frac{2}{9} right ):frac{4}{27}= $$$$left ( frac{4}{15}+frac{20}{9} right )*frac{27}{4}=$$$$frac{12+100}{5}*frac{3}{4}=frac{56*3}{5*2}=frac{168}{10}=16,8$$
Задание 2
В таблице представлены налоговые ставки на автомобили в Москве с 1.01. 2014 г.
| Мощность автомобиля (в л.с.) | Налоговая ставка (в руб. за л. с. в год) |
| не более 7 | 0 |
| 71-100 | 12 |
| 101-125 | 25 |
| 126-150 | 35 |
| 151-175 | 45 |
| 176-200 | 50 |
| 201-225 | 65 |
| 226-250 | 75 |
| свыше 250 | 150 |
Сколько рублей должен заплатить владелец автомобиля мощностью 286 л.с. в качестве налога за один год?
Варианты ответа
1. 21450
2. 42900
3. 75
4. 150
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
286 л.с. попадает под категорию «свыше 250», следовательно, ставка за 1 л.с. составит 150 рублей. Найдем величину налога: $$286*150=42900$$ рублей. Что соответствует 2 варианту ответа
Задание 3
Между какими числами заключено число $$7sqrt{2}$$ Варианты ответа: 1)10 и 11 2)7 и 9 3)9 и 10 4)11 и 12
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Занесем число 7 под квадратный корень: $$7sqrt{2}=sqrt{7^{2}*2}=$$$$sqrt{49*2}=sqrt{98}$$. Данное число расположено между $$sqrt{81}=9$$ и $$sqrt{100}=10$$, то есть между 9 и 10, что соответствует 3 варианту ответа.
Задание 4
Найдите значение выражения $$sqrt{3^{4}cdot 7^{2} cdot 11^{2}}$$
Ответ: 693
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$sqrt{4^{3}*2^{7}*2^{11}}=2^{3}*7*11=9*77=693.$$
Задание 5
На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Какое место занимала Польша?
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Польша выплавляет больше Казахстана и Замбии. Так как Казахстан занимает 10 место, то Польша будет занимать 8 место
Задание 6
Решите уравнение $$(2x+9)^{2}=(x-12)^{2}$$ . Если уравнение имеет более одного корня, укажите больший из них.
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$left ( 2x +9 right )^{2}=left ( x -12 right )^{2}$$
$$left ( 2x +9 right )^{2}-left ( x -12 right )^{2}=0$$
$$left ( 2x +9-left ( x -12 right ) right )*(2x +9+left ( x -12 right ))=0$$
$$left ( x +21 right )*left ( 3x -3 right )=0$$
$$x_{1} =-21$$
$$x_{2} =1.$$
В ответе необходимо указать больший корень, следовательно, напишем 1
Задание 7
Электрический чайник, который стоил 3500 рублей, продаётся с 15-процентной скидкой. При покупке этого чайника покупатель отдал кассиру 5000 рублей. Сколько рублей сдачи он должен получить?
Ответ: 2025
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем стоимость чайника с учетом 15-процентной скидки: $$3500*0,85=2975$$ рублей Найдем сдачу с 5000: $$5000-2975=2025$$ рублей
Задание 8
На диаграмме показаны религиозные составы населения Германии, США, Австрии и Великобритании. Определите по диаграмме, в каких странах суммарная доля протестантов и католиков превышает 75%.
Варианты ответа:
1. Германия
2. США
3. Австрия
4. Великобритания
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Из всех представленных вариантов количество католиков и протестантов превышает 75% (3/4 круга) только в Австрии, следовательно, в ответе укажем 3 вариант ответа.
Задание 9
На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,35. Вероятность того, что это окажется задача по теме «Треугольник», равна 0,3. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
Ответ: 0,65
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Для того, чтобы найти вероятность того, что достанется задача по одной из двух тем, необходимо сложить вероятности получения каждой темы по отдельности: $$0.3+0.35=0.65$$
Задание 10
На рисунке изображены графики функций вида $$y=ax^{2}+bx+c$$ . Установите соответствие между знаками коэффициентов a и c и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, c<0
Б) a<0, c>0
В) a>0, c>0
Ответ: 132
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) a>0, c<0 — в данном случае ветви параболы направлены вверх, ордината (координата у) точки пересечения параболой оси Оу находится под осью Ох. Соответствует 1 варианту ответа
Б) a<0, c>0 — в данном случае ветви параболы направлены вниз, ордината (координата у) точки пересечения параболой оси Оу находится над осью Ох. Соответствует 3 варианту ответа
В) a>0, c>0 — в данном случае ветви параболы направлены вверх, ордината (координата у) точки пересечения параболой оси Оу находится над осью Ох. Соответствует 2 варианту ответа
Задание 11
Дана арифметическая прогрессия (an), для которой a4 = — 121, a9 = — 256. Найдите разность прогрессии.
Ответ: -27
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Воспользуемся формулой для нахождения разности арифметической прогрессии: $$d=frac{ a _{9 }-a _{4 }}{9-4}=$$$$frac{-256-(-121)}{5}=$$$$frac{-135}{5}=-27;$$
Задание 12
Найдите значение выражения $$frac{3ac^{2}}{a^{2}-16c^{2}}frac{a-4c}{ac}$$
Ответ: -3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{3*alpha*c^{2} }{alpha ^{2}-16*c^{2}}*frac{alpha -4*c}{alpha *c}=$$$$frac{3*c}{alpha +4*c}=frac{3(-0,2)}{1+4*(-0,2)}=frac{-0,6}{0,2}=-3;$$
Задание 13
Закон Джоуля–Ленца можно записать в виде $$Q=I^{2}Rt$$, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q=40,5Дж, I=1,5A, R=9 Ом.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Выразим t из формулы: $$t=frac{Q }{I^{2}*R}$$ Подставим данные по условию значения: $$t=frac{40,5}{1,5^{2}*9}=frac{27}{1,5*9}=2$$
Задание 14
На каком рисунке изображено множество решений неравенства $$x^{2}-7x+12<0$$?
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Рассмотрим выражение $$x ^{2}-7x +12$$. Приравняем его к 0 и найдем корни:
$$x ^{2}-7x +12= 0;left{begin{matrix}x _{1}+x _{2} =7 \x _{1}*x _{2}=12 end{matrix}right.Leftrightarrow x _{1}=3; x _{2}=4;$$
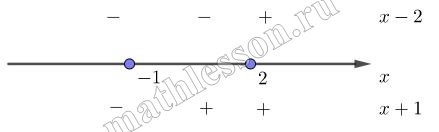
Начертим координатную прямую, отметим на ней корни (точки пустые, так как неравенство строгое) и расставим знаки, которое принимает данное выражение на полученных промежутках:
Выберем тот, на котором принимает отрицательные значения. В итоге получаем 1 вариант ответа
Задание 15
Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,8 м?
Ответ: 408
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем площадь стены: $$S=3,4*4,8$$ м2
Найдем площадь одной плитки $$S_{1}=0,2*0,2=0,04$$ м2
Найдем количество плиток: $$n=frac{S}{S_{1}}=frac{3,4*4,8}{0,2*0,2}=$$$$17*24=408$$
Задание 16
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 34°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Ответ: 73
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Так как О — цент окружности, то $$angle BOC=angle AOD$$ (вертикальные) и BO и OC — радиусы. Тогда: $$angle ACB=frac{180-angle AOD}{2}=frac{180-34}{2}=73$$
Задание 17
Основания трапеции равны 10 и 18. Найдите длину отрезка, соединяющего середины диагоналей трапеции
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Построим среднюю линию и диагонали как показано на рисунке. MK — средняя линия в треугольнике ABD, следовательно, $$MK=frac{1}{2}AD=9$$. Аналогично, MN — средняя линия в треугольнике ABC, следовательно, $$MN=frac{1}{2}BC=5$$. Тогда $$NK=9-5=4$$
Задание 18
Найдите длину средней линии трапеции, изображённой на рисунке.
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Средняя линия вычисляется как полусумма оснований на высоту: $$frac{5+9}{2}=7$$
Задание 19
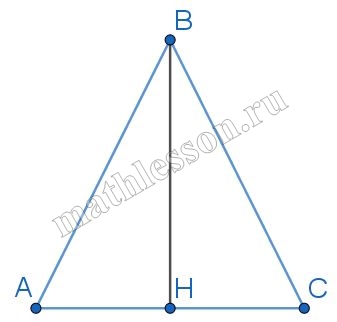
В треугольнике ABC АВ = ВС = 13, AС = 10. Найдите tg A.
Ответ: 2,4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Проведем высоту BH. Так как треугольник равнобедренный, то BH — медиана, тогда: $$AH=5$$
По теореме Пифагора из треугольника ABH: $$BH=sqrt{13^{2}-5^{2}}=12$$.
Следовательно, $$tg A=frac{BH}{AH}=frac{12}{5}=2,4$$
Задание 20
Какие из следующих утверждений верны?
1. Площадь квадрата равна произведению его диагоналей.
2. Площадь параллелограмма равна произведению его соседних сторон
3. Площадь трапеции равна произведению средней линии и высоты этой трапеции.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1. Площадь квадрата равна произведению его диагоналей. — неверно, равна половине произведения диагоналей 2. Площадь параллелограмма равна произведению его соседних сторон — неверно, равна произведению сторон на синус угла между ними 3. Площадь трапеции равна произведению средней линии и высоты этой трапеции. — верно
Задание 21
Сократите дробь $$frac{900^{n}}{5^{2n+3}*6^{2n-3}}$$
Ответ: 1,728
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{900^{n}}{5^{2n+3}*6^{2n-3}}=$$$$frac{(30^{2})^{n}}{5^{2n+3}*6^{2n-3}}=$$$$frac{(5*6)^{2n}}{5^{2n+3}*6^{2n-3}}=$$$$frac{5^{2n}*6^{2n}}{5^{2n+3}*6^{2n-3}}=$$$$6^{2n-2n+3}*5^{2n-2-3}=frac{6^{3}}{5^{3}}=1,728;$$
Задание 22
Из пункта А в пункт В с определённой скоростью выехал автомобилист. Если бы он ехал со скоростью на 12 км/ч меньше, то затратил бы на весь путь на один час больше, а если бы ехал со скоростью на 20 км/ч больше, то затратил бы на весь путь на один час меньше. С какой скоростью планировал проехать весь путь автомобилист?
Ответ: 60
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть х кмч –скорость; у-расстояние, тогда время первого: $$frac{y}{x }=t_{1}$$, время второго:$$frac{y}{x -12}=t_{2}$$, время третьего: $$frac{y}{x +70}=t_{3}$$. Составим систему уравнений в соответствии с условием задания: $$left{begin{matrix}t_{2}-t_{1}=1 & & \t_{1}-t_{3}=1 & &end{matrix}right. Leftrightarrow $$$$left{begin{matrix}frac{4}{x -12}-frac{y}{x }=1 & & \frac{y}{x }-frac{y}{x +20}=1 & &end{matrix}right.Leftrightarrow$$$$ left{begin{matrix}yleft ( frac{x -left ( x -12 right )}{left ( x -12 right )*x } right )=1 & & \yleft ( frac{x +20-x }{x *left ( x +20 right )} right )=1 & &end{matrix}right.;$$ Поделим первое уравнение на второе: $$frac{12}{-x left ( x -12 right )}:frac{20}{-x *left ( x +20 right )}=1;$$ $$frac{3*left ( x +20 right )}{5*left ( x -12 right )}=1;$$ $$5x -60=3x +60;$$ $$2x =120Rightarrow x =60;$$ км/ч скорость автобуса.
Задание 23
Постройте график функции $$y=|x-2|-|x+1|$$ и определите, при каких значениях k прямая y=kx имеет с графиком ровно три общие точки.
Ответ: $$(-1,5;0)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$y=left | x -2 right |-left | x +1 right |$$. Уберем модули. $$x -2=0$$ при $$x=2$$, а $$x+1=0$$, при х=-1$$. Отметим полученные точки на координатной прямой и посмотрим, какие значения принимают подмодульные выражения на различных промежутках:
Получили три интервала:
1)$$left{begin{matrix}x leq -1\y=-x +2+x +1=3 end{matrix}right.$$
2)$$left{begin{matrix} -1<x<2\y=-x +2-x -1=-2*x +1end{matrix}right.$$
3)$$left{begin{matrix}x geq 2 \y=x -2-x -1=-3 end{matrix}right.$$
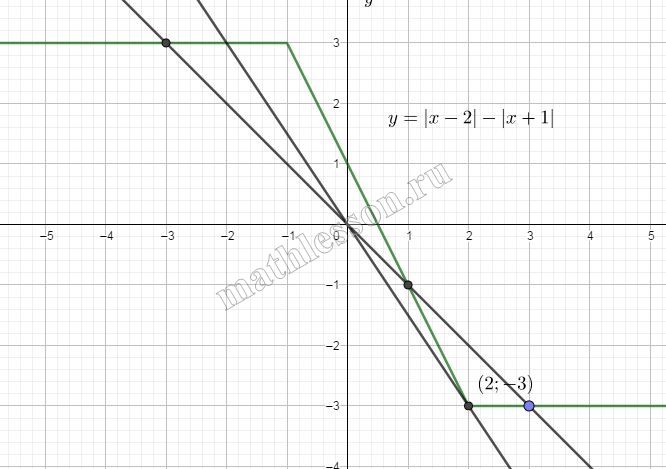
Построим график с учетом полученных интервалов и их кусочных функций:
Графиком функции $$y=kx$$ является прямая, проходящая через начало координат. Очевидно, что для 2х пересечений прямая должна пройти через координату (2;-3).
Найдем коэффициент k:
$$-3=k*2Leftrightarrow$$$$k=-1,5$$
Тогда, для 3х пересечений, коэффициент должен быть больше, чем -1,5, но меньше 0, то есть $$k in(-1,5;0)$$
Задание 24
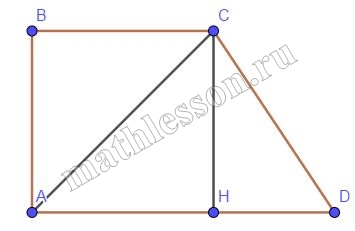
Высота прямоугольной трапеции в три раза больше меньшего основания, а большее основание равно 5. Найдите площадь трапеции, если её диагональ является биссектрисой угла при меньшем основании.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1)AC-биссектриса $$Rightarrow angle BCA=angle DCA;$$
$$angle DAC=angle BCA$$(накрест)$$Rightarrow angle DCA=angle DACRightarrow AD=CD=5;$$
2)$$CH||ABRightarrow AH=BC=xRightarrow HD=5-x$$ $$CH=3*x Rightarrow Delta CHD:5^{2}=left ( 5-x right )^{2}+3*x ^{2};$$
$$25=25-10x +x ^{2}+9x ^{2}Rightarrow$$ $$10x ^{2}-10x =0Rightarrow$$ $$10x left ( x -1 right )=0Rightarrow$$$$x =0; x =1;$$
3)$$S=frac{5+1}{2}*3=9;$$
Задание 25
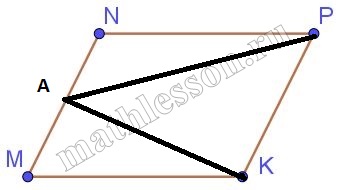
В параллелограмме MNPK точка A — середина стороны MN. Известно, что AP=AK. Докажите, что данный параллелограмм — прямоугольник.
Ответ:
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) По свойству параллелограмма: MN=NP. По условию AN=AM и AP=AK. Тогда треугольники ANP и AMK равны по трем сторонам, следовательно $$angle ANP=angle AMK=x$$
2) По свойству параллелограмма: $$angle ANP+angle AMK=180$$, следовательно $$angle ANP=angle AMK=90$$, тогда MNPK — прямоугольник
Задание 26
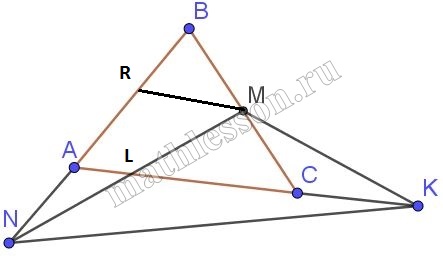
В треугольнике АВС, площадь которого равна S, точка М середина стороны ВС, точка N на продолжении стороны АВ и точка К на продолжении стороны АС выбраны так, что AN = ½ AB, CK = ½ AC. Найти площадь треугольника MNK.
Ответ: $$frac{5S}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1)$$S_{MCR}=frac{1}{4}*S$$
2)Пусть $$MRleft | right |ACRightarrow AR=RB$$(RM-средняя линия)$$Rightarrow AR=0,5*y=NARightarrow AL$$-средняя линия $$Rightarrow NL=LMRightarrow AL=frac{1}{2}*RM=frac{1}{4}*AC=frac{1}{4}x ; LC=frac{3}{4}x ;$$
3)$$S_{NMK}=S_{MCK}+S_{MCL}+S_{NLK}$$ $$S_{MCL}=frac{1}{2}*frac{3}{4}*S=frac{3}{8}*SRightarrow S_{LMK}=frac{3}{8}*S=frac{5*S}{8};$$
4)KL-медиана$$Rightarrow S_{MLK}=S_{KLN}=frac{5*S}{8};$$
5) $$S_{MNK}=2*frac{5*S}{8}=frac{109}{8}=frac{5S}{4};$$
Регистрация Форум Текущее время: 10 мар 2023, 16:20 Сообщения без ответов | Активные темы Страница 15 из 17 [ Сообщений: 167 ] На страницу Пред. 1 … 12, 13, 14, 15, 16, 17 След. Начать новую тему»> Ответить Тренировочный вариант №186
Тренировочный вариант №186
Страница 15 из 17 [ Сообщений: 167 ] На страницу Пред. 1 … 12, 13, 14, 15, 16, 17 След. Текущее время: 10 мар 2023, 16:20 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
ОГЭ по математике 2018 Решение варианта Александр Ларина №186 Разбор Варианта ОГЭ Ларина ОГЭ математика, Подробный разбор заданий
скачать
Решение
1.
2.
286>250 ⇒ 150 руб. за л.с. в год
286 · 150 = 42900 руб.
3.
3) 9 и 10
4.
5. 7
6.
7.
3500 · 0,85 = 2975
5000 — 2975 = 2025
8. 3
9.
0,35 + 0,3 = 0,65
10.
А=1; Б=3; В=2
11.
12.
13.
14.
x2-7x+12=0
x=3, x=4
15.
16.
AD=34
AB=180-34=146
∠ACB=146/2 = 73
17.
9-5 =4
18.
19.
h2=132-52
h2=144
h=12
20.
3. Площадь трапеции равна произведению средней линии и высоты этой трапеции.
1-20 задания
21-26 задания








 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 



