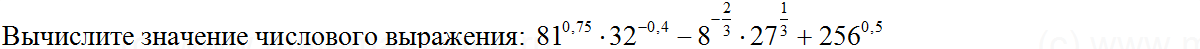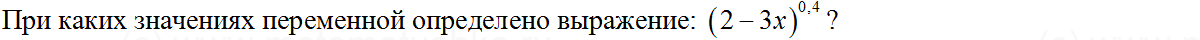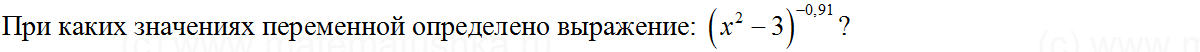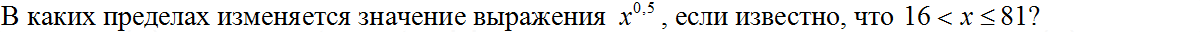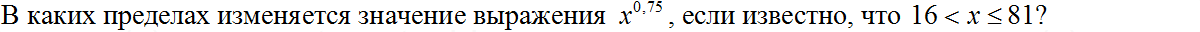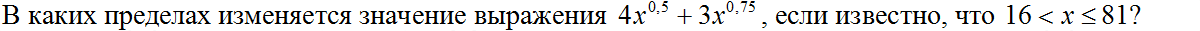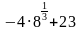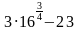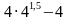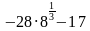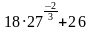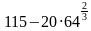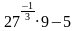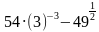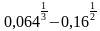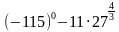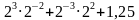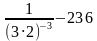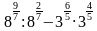Степень с рациональным показателем задания егэ

Всего: 102    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Всего: 102    1–20 | 21–40 | 41–60 | 61–80 …

Задачи ЕГЭ по математике

Инфоурок

›

Алгебра

›Другие методич. материалы›Карточки-тренажеры по теме «Степени» (подготовка к ЕГЭ)

Карточки-тренажеры по теме «Степени» (подготовка к ЕГЭ)

  Муниципальное казенное общеобразовательное учреждение

средняя общеобразовательная школа № 2

Открытый урок

по алгебре и началам анализа

«  Степень с рациональным показателем. Подготовка к ЕГЭ»

для учащихся  11 класса

подготовила учитель математики

Данилова Оксана  Михайловна.

с. Труновское

2016

  Степень с рациональным показателем. Подготовка к ЕГЭ.

Тип урока: урок формирования первоначальных предметных навыков, овладения предметными умениями.

Цель: 
Успешная сдача итоговой аттестации в форме ЕГЭ и последующий выбор дисциплины как специального предмета в будущей профессиональной деятельности. Задачи: 
Образовательные: 
Организовать деятельность учащихся по изучению и осмыслению понятия степени с рациональным показателем ,при котором сохраняются основные свойства  степеней.
Способствовать формированию у учащихся новых способов деятельности по одновременному применению свойств корня и степени в преобразованиях и вычислениях выражений.
Организовать работу учащихся с материалами ЕГЭ. 
Воспитательные:
Способствовать привитию у учащихся организованности, внимательности, настойчивости. 
Развивающие: 
Создать условия для развития у учащихся умений формулировать проблемы, сравнивать познавательные объекты и выделять основную мысль. 
Приучать учащихся контролировать свою деятельность с целью оправданного использования рабочего времени при сдаче ЕГЭ. 

                                                    План урока.

1  Организационный этап.

Добрый день, дорогие друзья! Сегодня у нас необычный урок. К нам приехали в гости, уважаемые учителя математики. Но всё же я попрошу вас  принять царственную осанку — спина прямая, мышцы головы без напряжения, выражение лица значительное, ведь вы сейчас знаете такое количество формул, которое не под силу даже царственным особам. 

А пока вы входите в образ, послушайте притчу.

Притча:

«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному замку. «Кто первым откроет, тот и будет первым помощником». Никто даже не притронулся к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, а надеешься на собственные силы и не боишься сделать попытку».
И мы сегодня будем пытаться, пробовать, чтобы прийти к правильному решению.

Итак, вы успокоились. сосредоточились? Готовы работать?

Сегодня вы будете проводить исследования, направленные на укрепление не только знаний по алгебре, но и здоровья.
Для этого ответьте на вопрос: Как при таком объёме информации сохранить здоровье во время урока, накануне и во время экзамена? 
Правильная осанка, хорошее освещение, сбалансированное питание с витаминами и минералами, не волноваться, избегать стрессов. 
А чтобы на экзаменах у вас не было стресса, вы должны уже сейчас свободно выполнять задания из материалов ЕГЭ, уметь жёстко работать по времени, контролировать свою деятельность, уметь методом прикидки и минимальной подстановки выполнять проверку и тогда вы будете уверенными в себе. 

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Итак! Посмотрите внимательно несколько секунд на рисунок, запомните. 

Ответьте на мои вопросы:

• Перечислите все корни, которые вы видели
• В какой геометрической фигуре расположен ? (в окружности)
• Какого цвета эта окружность? (синяя)
• Квадратный корень из какого числа находится в квадрате? (из 5)
• Какого цвета этот квадрат? (зелёного)
• В какой геометрической фигуре  расположен корень кубический? (в треугольнике)
• Какого цвета этот треугольник? (красного)

Молодцы! Вы хорошо справились с первым испытанием!  Внимательность очень нужна на экзаменах.

1. С каким математическим понятием связаны слова:

Основание
Показатель (Степень)
Какими словами можно объединить слова:
Целое число
Натуральное число
(Рациональное число)
Сформулируйте тему урока. (Степень с рациональным показателем)

2.  Какая наша стратегическая цель? (ЕГЭ)
Какова цель нашего урока?
– Продолжить работу над степенями с рациональным показателем.

Задачи:

– повторить свойства степеней и корней
– рассмотреть применение свойств степени при вычислениях и упрощениях выражений
– отработка вычислительных навыков.

3. Воспроизведение и коррекция опорных знаний учащихся. Актуализация знаний.

1. Какие действия (математические операции) можно выполнять со степенями?

Установите соответствие:

ОТВЕТ        3 5 1 6 4 2                        

Поменяться тетрадями и оценить работу соседа.(взаимопроверка)

Пока все выполняют задание на соответсвие, двое учащихся у доски: пишут свойства степеней с рациональным показателем свойства корней с натуральным показателем.

Знание теории и формул не достаточно для успешной сдачи ЕГЭ. Но вы справились и со вторым испытанием: знание необходимого материала на ЕГЭ по теме.

Аристотель  сказал:  «Ум заключается не только в знании, но и в умении прилагать знание на деле.» Так вот и мы с вами перейдём от слов к делу.

4 Отработка знаний умений и навыков.

Сейчас, мы проведём эксперимент — сколько баллов можно набрать за 5 минут. 

Самопроверка.
А теперь проверим и проанализируем с чем вы справились, а над чем надо поработать?

Вот вы справились и с третьим испытанием-  работа по времени и контроль своей деятельности.

Динамическая пауза

1. Упражнение на релаксацию

Принять удобное положение. Расслабиться. Закрыть глаза и представить большой белый экран. Мысленно раскрасить этот экран любимым цветом. Получается ровно, красиво, радует глаз, залюбуешься.

Раз, два, три – открыли глаза. Каким цветом был ваш экран?

1. Упражнение на сосредоточение внимания – «пальчики»

Одновременно под счёт пальчиками левой и правой руки касаться большого пальца.

.

Работа в парах.

Заполните пропуски. Знание формул сокращённого умножения.

а) х – 2х

= … * (х – …)

б) 6

 – 2… = 2* (… –2 )

в) а – b = (а 

+ b) * (… – …)

г) а + b = (… + …) *(а

— а b + b)

Ответы

а) х – 2х= х * (х – 2)

б) 6

 – 2… = 2* (3 –2 )

в) а – b = (а 

+ b) * (а  – b )

г) а + b = (а

+ b) *(а— а b + b)

2 задания- «3»

3задания- «4»

4задания- «5»

Взаимопроверка.

Какие витамины и минералы необходимы человеку, чтобы быть здоровым? 

Давайте вычислим суточную потребность организма в витаминах В1, В2 , Fe, в миллиграммах.

Выполнение заданий по рядам.

ОТВЕТЫ на слайде, самопроверка

Дефицит витамина В1 может привести к нарушению обмена углеводов. Витамин В2 отвечает за состояние зрения, он необходим для построения защитного слоя сетчатки. 
Дефицит железа сказывается на росте и устойчивости к инфекциям. От железа зависит построение гемоглобина – переносчика кислорода ко всем органам. 

5. Этап закрепления и осмысления изученного материала. Дифференцированная работа с модульными карточками 5 мин

Данная тема также используется на ЕГЭ, я подобрала вам задания из 
материалов ЕГЭ.
Каждый учащийся работают самостоятельно с модульной карточкой 1,2,3 уровня,  выбрав по силам задания. Выполненные задания проверяет и оценивает учитель.

Резерв: 6.Этап информирования и инструктажа домашнего задания 

1.В учебнике на стр.219 повторить свойства степеней с рациональным показателем и на стр. 220 самостоятельно разобрать свойства 6,7.

2. Работать по карточкам (внимательно читать рекомендации).

Карточка № 1

Цель: закрепить навык преобразования выражений, содержащих рациональные степени, пользуясь формулами сокращенного умножения.

Вспомните определение степени с рациональным показателем и формулы сокращенного умножения. Рассмотрите пример 4 на стр.220 учебника под ред. А.Н.Колмогорова.

Выполните письменную работу.

Упростить выражение:

Корректирующий вариант

а)                                                                              

б)                                                                     

в) + (1+х) (1 — х +х )                                     + (1-х) (1+х +х )  

Желаю успеха!

——————————————————————————————————

Карточка № 2

Цель: закрепить навык сравнения чисел, представленных в виде степени с рациональным показателем.

Вспомните свойства степени с рациональным показателем.

Рассмотрите примеры 5, 6 на стр. 221 учебника под ред. А.Н. Колмогорова.

Выполните письменную работу.

Сравните числа:

Корректирующий вариант

а)  и  2                                                                              и  5

б) ()   и                                                              ()       и    ×  2

в) 3  и   5                                                                          7      и       4

Желаю успеха!
7. Этап подведение итогов занятия

Вернемся к целям урока, которые себе поставили. Давайте отметим то, что у нас получилось из намеченного. Что нового сегодня вы узнали?

Молодцы, вы активно работали на разных этапах занятия.

Ответы достаточно аргументированы, оперировали понятиями, сочетая теоретические знания с практическими, активно вносили поправки.

_____________работали особенно старательно.

 8 Этап рефлексии:

Что я  усвоил для себя:

Зелёный цвет- всё получилось, я спокоен за себя при сдаче ЕГЭ;

Жёлтый цвет- есть небольшие пробелы, но я с ними справлюсь;

Красный цвет- я ничего не понимаю и очень боюсь сдавать ЕГЭ.

Из ТРЁХ ЦВЕТОВ БУМАГИ выберите, пожалуйста, тот, который лучше всего отражает ваше внутреннее состояние и с помощью которой вы могли бы рассказать нам о своем настроении, о своем самочувствии и о степени своей удовлетворенности, готовности по данной теме к ЕГЭ. Наклейте, пожалуйста, выбранные вами листочки с соответствующим цветом на куб. Итак, что у нас с вами получилось? Куб должен быть одного цвета в том случае. если всё у вас уже получается, но он разных цветов —  есть ещё над чем работать.

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их
(Д. Пойа)

Урок закончен. Спасибо за урок!

Оценочный лист                                                                                           (Ф.И.)

Мы уже знакомы с понятием степени с ЦЕЛЫМ показателем, когда в степени стоит целое число (n). Давайте разберемся, что такое степень с РАЦИОНАЛЬНЫМ показателем, когда в степени обыкновенная дробь — (a^{frac{p}{q}}).

Рациональный показатель – это выражение вида (frac{p}{q}), где (p)-некоторое целое число, а (q) – натуральное число, причем (qge2). Это строгое определение рационального показателя, но простыми словами мы будем изучать дробные степени, когда у вас в показателе стоит обыкновенная дробь.

Определение

Положительное число (a) в степени (frac{p}{q}) является арифметическим корнем степени (q) из числа (a) в степени (p):

$$ a^{frac{p}{q}}=sqrt[q]{a^p}. $$

Для того, чтобы научиться считать дробные степени, достаточно запомнить формулу из определения. Разберемся на примерах, как это работает, но нам понадобится хорошее знание арифметического корня n-й степени.

И обращаем ваше внимание, что

$$ sqrt[q]{a^p}=(sqrt[q]{a})^p,$$

Неважно в каком порядке – сначала извлечь корень и потом возвести в степень, или возвести в степень, а потом уже извлечь корень, от этого смысл выражения не теряется. Как удобнее, так и считайте. Рассмотрим несколько примеров:

Пример 1
$$ 8^{frac{2}{3}}=sqrt[3]{8^2}=(sqrt[3]{8})^2=2^2=4; $$
$$ 27^{frac{1}{3}}=sqrt[3]{27^1}=sqrt[3]{27}=3;$$
$$ 3^{frac{1}{5}}=sqrt[5]{3}; $$
$$ 7^{-frac{5}{6}}=sqrt[6]{7^{-5}}=sqrt[6]{frac{1}{7^5}}=frac{1}{sqrt[6]{7^{5}}};$$

Обратите внимание, что у обыкновенного квадратного корня двойка в показателе не пишется: пишем так (sqrt{a}), а имеем в виду (sqrt[2]{a}.)
$$ 7^{frac{1}{2}}=sqrt{7};$$
$$ 5^{frac{3}{2}}=sqrt{5^3}.$$

Пусть есть некоторое положительное число (a), целое число (p) и натуральное число (q), тогда справедливы следующие соотношения:

$$1.; a^{frac{p}{q}}=(a^{frac{1}{q}})^p,$$
$$2.; a^{frac{p}{q}}=a^{frac{p*k}{q*k}},$$
$$ 3.;a^p= a^{frac{pq}{q}}, $$

где (k) и (q) – натуральные числа большие 1.

Давайте попробуем их доказать:

Из определения степени с рациональным показателем следует, что:

$$ a^{frac{p}{q}}=sqrt[q]{a^p}=(sqrt[p]{a})^p=(a^{frac{1}{q}})^p,$$

Опять из определения и свойства корня n-й степени следует:

$$ a^{frac{p}{q}}=sqrt[q]{a^p}=sqrt[q*k]{a^{p*k}}= a^{frac{p*l}{q*k}}, $$

Третья формула на наш взгляд очевидна, просто сократить степень справа и получите исходное выражение.

Пример 2
$$8^{frac{4}{3}}=(8^{frac{1}{3}})^4=2^4=16;$$
$$4^{frac{15}{5}}=4^{frac{3}{1}}=4^3=64;$$
$$3^{-frac{6}{2}}=3^{-3}=frac{1}{3^3}=frac{1}{27}.$$

Свойства степени с рациональным показателем

Пусть (a) и (b) – некоторые положительные числа, а числа (frac{m}{n}) и (frac{c}{d}) – рациональные числа. Тогда выполняются соотношения:

$$ mathbf {1. ;a^{frac{m}{n}}*a^{frac{c}{d}}=a^{frac{m}{n}+frac{c}{d}}} $$
$$ 3^{frac{2}{5}}*3^{frac{8}{5}}=3^{frac{2}{5}+frac{8}{5}}=3^{frac{10}{5}}=3^2=9; $$
$$ 2^{frac{1}{3}}*4^{frac{4}{3}}=2^{frac{1}{3}}*(2^2)^{frac{4}{3}}=2^{frac{1}{3}}*2^{frac{8}{3}}=2^{frac{1}{3}+frac{8}{3}}=2^{frac{9}{3}}=2^3=8;$$

При умножении степеней с рациональным показателем и одинаковым основанием их показатели складываются.

$$mathbf {2. ; a^{frac{m}{n}}:a^{frac{c}{d}}=a^{frac{m}{n}-frac{c}{d}}}$$
$$ 5^{frac{8}{3}}:5^{frac{2}{3}}=5^{frac{8}{3}-frac{2}{3}}=5^{frac{6}{3}}=5^2=25;$$

При делении степеней с рациональным показателем и одинаковым основанием их показатели вычитаются.

$$mathbf {3. ; (a^{frac{m}{n}})^{frac{c}{d}}=a^{frac{m}{n}*frac{c}{d}}}$$
$$ (9^{frac{1}{3}})^{frac{3}{2}}=9^{frac{1}{3}*frac{3}{2}}=9^{frac{1}{2}}=sqrt[2]{9^1}=sqrt{9}=3;$$

При возведении степени с рациональным показателем в степень с рациональным показателем их показатели перемножаются.

$$mathbf {4. ; (a*b)^{frac{m}{n}}=a^{frac{m}{n}}*b^{frac{m}{n}}}$$
$$ (27*8)^{frac{2}{3}}=27^{frac{2}{3}}*8^{frac{2}{3}}=sqrt[3]{27^2}*sqrt[3]{8^2}=(sqrt[3]{27})^2*(sqrt[3]{8})^2=3^2*2^2=9*4=36;$$

Степень с рациональным показателем от произведения двух положительных чисел равна произведению степеней этих множителей.

$$ mathbf {5.; left(frac{a}{b}right)^{frac{m}{n}}=frac{a^{frac{m}{n}}}{b^{frac{m}{n}}}}$$

Степень с рациональным показателем от частного двух положительных чисел равна частному степеней этих чисел.

И еще два очень важных свойства степеней. Они вам понадобятся при решении показательных уравнений и неравенств.

Пусть опять есть некоторое положительное число (a>1) и дроби (frac{m}{n}) и (frac{c}{d}).

$$mathbf {6. ; При ; n gt 0 qquad a^n gt 1},$$
$$mathbf {При ; n lt 0 qquad 0 lt a^n lt 1}.$$

7. Если же (a gt 1) и (n gt m), то

$$ a^n>a^m.$$

Если ( 0 lt a lt 1 ) и (n gt m), то

$$ a^n lt a^m.$$

Разберем несколько примеров:

Пример 3
$$ 3^{-frac{3}{4}}*3^{-frac{1}{4}}=3^{-frac{3}{4}-frac{1}{4}}=3^{-1}=frac{1}{3};$$
$$ 2^{frac{1}{2}}:2^{frac{1}{4}}=2^{frac{1}{2}-frac{1}{4}}=2^{frac{1}{4}}=sqrt[4]{3};$$
$$ (5^{-frac{1}{2}})^{-4}=5^{(-frac{1}{2})*(-4)}=5^2=25; $$
$$ (0,125)^{-frac{2}{3}}*8^{-frac{2}{3}}=(0,125*8)^{-frac{2}{3}}=1^{-frac{2}{3}}=1; $$
$$ (4,4)^{frac{1}{3}}:(0,55)^{frac{1}{3}}=(frac{4,4}{0,55})^{frac{1}{3}}=8^{frac{1}{3}}=sqrt[3]{8}=2;$$

$$ 3^{frac{1}{3}} lt 3^{frac{1}{2}},$$

Так как основание степени больше единицы (3 gt 1) и (frac{1}{3} lt frac{1}{2}).

$$ (frac{1}{5})^{frac{1}{3}} gt (frac{1}{5})^{frac{1}{2}}, $$

Так как (0 lt frac{1}{5} lt 1) и (frac{1}{3} lt frac{1}{2}).

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Все материалы доступны по лицензии Creative Commons — «Attribution-NonCommercial»

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2023 Все права на дизайн сайта принадлежат С.Є.А.