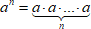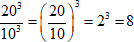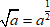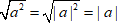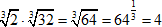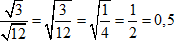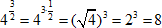Поиск
Всего: 105 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите значение выражения
Источник: ЕГЭ по математике 28.03.2022. Досрочная волна. ФИПИ. Вариант 4
Найдите значение выражения при
Найдите значение выражения:
Найдите значение выражения: при
Найдите значение выражения
Найдите значение выражения
Найдите значение выражения при
Найдите значение выражения при
Найдите значение выражения если
Найдите значение выражения если
Найдите значение выражения при
Найдите значение выражения при
Найдите значение выражения
Источник: ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 101
Найдите значение выражения при a = −1,9 и b = 4,8.
Найдите значение выражения
Найдите значение выражения
Найдите значение выражения при
Найдите значение выражения при
Найдите значение выражения при
Найдите значение выражения при
Всего: 105 1–20 | 21–40 | 41–60 | 61–80 …
Видеоурок 1: Свойства степени с натуральным показателем
Видеоурок 2: Степень с натуральным показателем и ее свойства
Лекция: Степень с натуральным показателем

Под степенью некоторого числа «а» с некоторым показателем «n» понимают произведение числа «а» само на себя «n» раз.
Когда говорят о степени с натуральным показателем, это означает, что число «n» должно быть целым и не отрицательным.
а — основание степени, которое показывает, какое число следует умножать само на себя,
n — показатель степени — он говорит, сколько раз основание нужно умножить само на себя.
Например:
84 = 8 * 8 * 8 * 8 = 4096.
В данном случае под основанием степени понимают число «8», показателем степени считается число «4», под значением степени понимается число «4096».
Самой большой и распространенной ошибкой при подсчете степени является умножение показателя на основание — ЭТО НЕ ВЕРНО!
Когда речь идет о степени с натуральным показателем, имеется в виду, что только показатель степени (n) должен быть натуральным числом.
В качестве основания можно брать любые числа с числовой прямой.
Например,
(-0,1)3 = (-0,1) * (-0,1) * (-0,1) = (-0,001).
Математическое действие, которое совершается над основанием и показателем степени, называется возведение в степень.
Сложение вычитание — математические действия первой ступени, умножение деление — действие второй ступени, возведение степени — это математическое действие третьей ступени, то есть одной из высших.
Данная иерархия математических действий определяет порядок при расчете. Если данное действие встречается в задачах среди двух предыдущих, то оно делается в первую очередь.
Например:
15 + 6 *22 = 39
В данном примере необходимо сначала возвести 2 в степень, то есть
22 = 4,
затем полученный результат умножить на 6, то есть
4 * 6 = 24,
затем
24 + 15 = 39.
Степень с натуральным показателем используется не только для конкретных вычислений, но и для удобства записи больших чисел. В данном случае еще используется понятие «стандартный вид числа». Данная запись подразумевает умножение некоторого числа от 1 до 9 на основание степени равное 10 с некоторым показателем степени.
Например, для записи радиуса Земли в стандартном виде используют следующую запись:
6400000 м = 6,4 * 106 м,
а масса Земли, например, записывается следующим образом:
6 * 1024 кг.

Для удобства решений примеров со степенями необходимо знать основные их свойства:
1. Если Вам необходимо умножить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.
an * am = an+m
Например:
52 * 54 = 56.
2. Если необходимо разделить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть. Обратите внимани, для действий со степенями с натуральным показателем показатель степени делимого должен быть больше показателя степени делителя. В противном случае, частным данного действия будет число с отрицательным показателем степени.
an / am = an-m
Например,
54 * 52 = 52.
3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.
(an )m = an*m
Например,
(54 )2 = 58.
4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.
(a * b)m = am * bm
Например,
(5 * 8 )2 = 52 * 82.
5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.
(a / b)m = am / bm
6. Любое число, которое возводится в показатель степени, равный единице, равно первоначальному числу.
а1 = а
Например,
51 = 5.
7. При возведении любого числа в степень с показателем ноль, результатом данного вычисления всегда будет единица.
а0 = 1
Например,
70 = 1.
Для того, чтобы возвести число в степень с натуральным показателем 

В этой записи 

Для проведения вычислений удобно использовать формулы преобразования выражений со степенями. Они универсальны и работают для любых показателей (целых, рациональных или иррациональных).
Применим эти правила для решения следующих задач.
Пример 1
Воспользуемся формулой для частного степеней с одинаковыми основаниями.
Пример 2
Так как степень частного равна частному степеней, занесем всю дробь под одну степень.
Пример 3
Для удобства представим 
Иногда для записи дробных степеней используют специальный знак – корень. На самом деле корень — всего лишь дробная степень:
Чаще всего встречается квадратный корень из числа:
Выражения с корнями преобразуется по тем же правилам, что и все остальные степени.
Следует различать корни нечетной степени 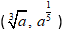

Корень нечетной степени из отрицательного числа – отрицательное число; из положительного – положительное.
Корень четной степени берется только из неотрицательного числа. Само значение корня четной степени может быть только неотрицательным.

Пример 4
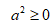

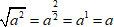
В случае отрицательного 
Пример 5
Так как корень – это степень, то можем воспользоваться правилом «степень произведения равна произведению степеней».
Пример 6
Частное степеней равно степени частного, поэтому занесем всю дробь под общий корень.
Пример 7
Представим число 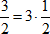
Помимо выражений с числами, в заданиях часто встречаются выражения с символьными переменными. К счастью, выписанные нами формулы, продолжают работать и в этом случае.
Пример 8
Возведем степень в степень, перемножая показатели. Так как все основания одинаковые, то заменим произведение степеней на сумму показателей, а частное – на разность. Основание при этом не меняем.
Пример 9
Перепишем корень как дробный показатель. Заменим возведение степени в степень на произведение показателей. Затем преобразуем произведение степеней, сложив их показатели.
Для того, чтобы возвести число в степень с натуральным показателем $ n $ , нужно умножить число само на себя $ n $ раз:
$ a^{n}underbrace{acdot a cdot…cdot a}_n $
В этой записи $ a $ – основание, $ n $ – показатель степень.
Для проведения вычислений удобно использовать формулы преобразования выражений со степенями. Они универсальны и работают для любых показателей (целых, рациональных или иррациональных).
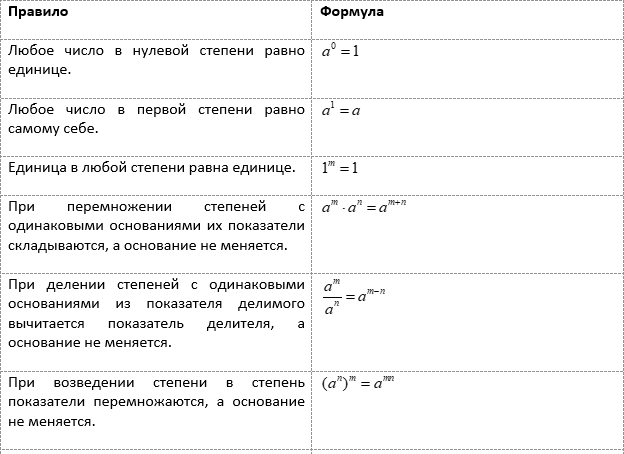
| Правило | Формула |
|---|---|
| Любое число в нулевой степени равно единице | $ a^{0}=1 $ |
| Любое число в первой степени равно самом себе | $ a^{1}=a $ |
| Единица в любой степени равна единице | $ 1^{m}=1 $ |
| При перемножении степеней одинаковыми основаниями их показатели складываются, а основание не меняется | $ a^{m} cdot a^{n}=a^{m+n} $ |
| При делении степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя, а основание не меняется | $ frac {a^{m}}{a^{n}}=a^{m-n} $ |
| При возведение степени в степень показатели перемножаются, а основание не меняется | $ (a^{n})^{m}=a^{mn} $ |
| Степень произведения равна произведению степеней | $ (ab)^{n}=a^{n} cdot b^{n} $ |
| Степень частного равна частному степеней | $ big( frac{a}{b} big)^{m}=frac{a^{m}}{b^{m}}$ |
| При возведении в отрицательную степень, основание степени «переворачивается», и знак показателя степени меняется на противоположный | $ a^{-n}= frac {1}{a^{n}}= big( frac {1}{a} big)^{n} $ |
Применим эти правила для решения следующих задач.
Пример 1
$ frac{3^{5}}{3^{3}}=3^{5-3}=3^{2}=9 $
Воспользуемся формулой для частного степеней с одинаковыми основаниями.
Пример 2
$ frac {20^{3}}{10^{3}} = big( frac {20}{10} big)^{3}=2^{3}=8 $
Так как степень частного равна частному степеней, занесем всю дробь под одну степень.
Пример 3
$ frac {1}{2^{-2}} = frac {1^{-2}}{2^{-2}} = big( frac {1}{2} big)^{-2}=2^{2}=4 $
Для удобства представим $ 1=1^{-2} $ и занесем всю дробь под одну степень.
Иногда для записи дробных степеней используют специальный знак – корень. На самом деле корень — всего лишь дробная степень:
$ sqrt[n]{a}=a^{ frac {1}{n}} $
Чаще всего встречается квадратный корень из числа:
$ sqrt{a}=a^{ frac {1}{2}} $
Выражения с корнями преобразуется по тем же правилам, что и все остальные степени.
Следует различать корни нечетной степени $ sqrt[3]{a}, ; a^{ frac {1}{5}} $ и корни четной степени $ sqrt{a},; a^{ frac {3}{8}} $ .
Корень нечетной степени из отрицательного числа – отрицательное число; из положительного – положительное.
$ sqrt[3]{-27}=-3 $
Корень четной степени берется только из неотрицательного числа. Само значение корня четной степени может быть только неотрицательным.
$ sqrt{4}=2 $,
$ sqrt{-4} $ — не существует.
Пример 4
$ sqrt{a^{2}} = sqrt {|a|^{2}} = |a| $
$ a^{2} geq 0 $, следовательно, корень из этого выражения существует. При этом значение $ a $ может быть любым. Если действовать по правилам степеней без модуля, имеем:
$ sqrt{a^{2}} = a^{ frac {2}{2}}=a^{1}=a $.
В случае отрицательного $ a $ получаем, что корень четной степени равен отрицательному числу, что невозможно.
Пример 5
$ sqrt[3]{2} cdot sqrt[3]{32}=sqrt[3]{64}=64^{frac {1}{3}}=4 $
Так как корень – это степень, то можем воспользоваться правилом «степень произведения равна произведению степеней».
Пример 6
$ frac {sqrt{3}}{sqrt{12}}=sqrt {frac {3}{12}}=sqrt {frac {1}{4}}=frac {1}{2}=0,5 $
Частное степеней равно степени частного, поэтому занесем всю дробь под общий корень.
Пример 7
$ 4^{frac {3}{2}}=4^{3 cdot frac {1}{2}}=(sqrt {4})^{3}=2^{3}=8 $
Представим число $ frac {3}{2}=3 cdot frac {1}{2} $ в виде произведения, чтобы можно было воспользоваться правилом «При возведении степени в степень показатели перемножаются, а основание не меняется» в обратную сторону.
Помимо выражений с числами, в заданиях часто встречаются выражения с символьными переменными. К счастью, выписанные нами формулы, продолжают работать и в этом случае.
Пример 8
$ frac {a^{2} cdot (a^{frac {5}{2}})^{2}}{a^{7}}=frac {a^{2} cdot a^{frac {5}{2} cdot 2}}{a^{7}}=a^{2+5-7}=a^{0}=1 $
Возведем степень в степень, перемножая показатели. Так как все основания одинаковые, то заменим произведение степеней на сумму показателей, а частное – на разность. Основание при этом не меняем.
Пример 9
$ sqrt [7]{b^{10}} cdot big( sqrt[7]{b} big)^{-3}=b^{frac {10}{7}} cdot big( b^{frac {1}{7}} big)^{-3}=b^{frac {10}{7}} cdot b^{frac {-3}{7}}=b^{frac {10}{7} — frac {3}{7}}=b^{1}=b $
Перепишем корень как дробный показатель. Заменим возведение степени в степень на произведение показателей. Затем преобразуем произведение степеней, сложив их показатели.
Правило чтения и записи степеней с натуральным показателем
Краткую запись произведения одинаковых сомножителей очень удобно использовать, — длинная строка описания математических действий сокращается до записи нескольких шагов:
17^5=17 cdot 17 cdot 17 cdot 17 cdot 17=1,419,857
17 — основание степени,
5 — показатель степени,
1419857 — значение степени.
Степень с нулевым показателем равна 1, при условии, что a neq 0:
a^0=1.
Например: 2^0=1
Когда нужно записать большое число обычно используют степень числа 10.
Например, один из самых древних динозавров на Земле жил около 280 млн. лет назад. Его возраст записывается следующим образом: 2,8 cdot 10^8.
Каждое число большее 10 можно записать в виде a cdot 10^n, при условии, что 1 < a < 10 и n является положительным целым числом. Такую запись называют стандартным видом числа.
Примеры таких чисел: 6978=6,978 cdot 10^3, 569000=5,69 cdot 10^5.
Можно говорить как и «a в n-ой степени», так и «n-ая степень числа a» и «a в степени n».
4^5 — «четыре в степени 5 » или «4 в пятой степени» или также можно сказать «пятая степень числа 4»
В данном примере 4 — основание степени, 5 — показатель степени.
Приведем теперь пример с дробями и отрицательными числами. Для избежания путаницы принято записывать основания, отличные от натуральных чисел, в скобках:
(7,38)^2, left(frac 12 right)^7, (-1)^4 и др.
Заметьте также разницу:
(-5)^6 — означает степень отрицательного числа −5 с натуральным показателем 6.
-5^6 — соответствует числу противоположному 5^6.
Свойства степеней с натуральным показателем
Основное свойство степени
a^n cdot a^k = a^{n+k}
Основание остается прежним, а складываются показатели степеней.
Например: 2^3 cdot 2^2 = 2^{3+2}=2^5
Свойство частного степеней с одинаковыми основаниями
a^n : a^k=a^{n-k}, если n > k.
Показатели степени вычитаются, а основание остается прежним.
Данное ограничение n > k вводится для того, чтобы не выходить за рамки натуральных показателей степени. Действительно, при n > k показатель степени a^{n-k} будет являться натуральным числом, иначе он будет либо отрицательным числом (k < n), либо нулем (k-n).
Например: 2^3 : 2^2 = 2^{3-2}=2^1
Свойство возведения степени в степень
(a^n)^k=a^{nk}
Основание остается прежним, перемножаются лишь показатели степеней.
Например: (2^3)^6 = 2^{3 cdot 6}=2^{18}
Свойство возведения в степень произведения
В степень n возводится каждый множитель.
a^n cdot b^n = (ab)^n
Например: 2^3 cdot 3^3 = (2 cdot 3)^3=6^3
Свойство возведения в степень дроби
frac{a^n}{b^n}=left(frac{a}{b} right) ^n, b neq 0
В степень возводится и числитель и знаменатель дроби. left(frac{2}{5} right)^3=frac{2^3}{5^3}=frac{8}{125}