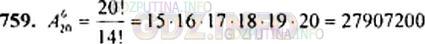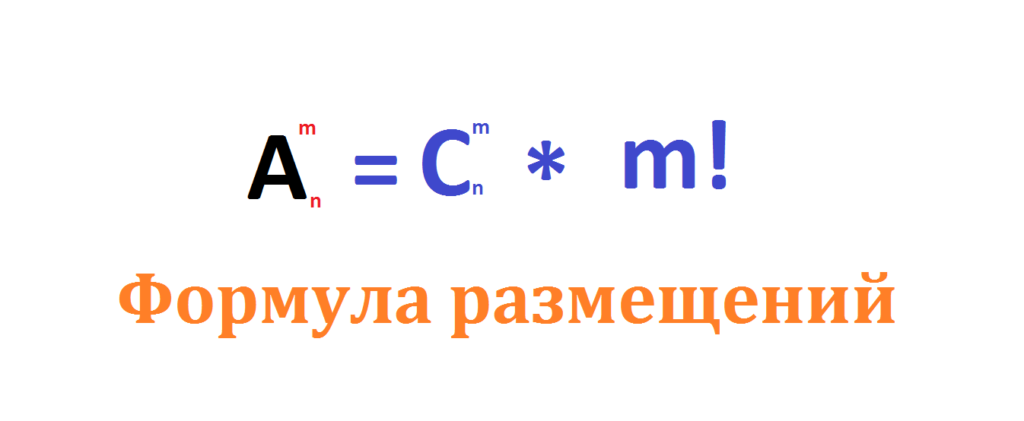ГДЗ (готовое домашние задание из решебника) на Номер задания №759 по учебнику Алгебра. 9 класс : учебник для общеобразовательных организаций: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова — 21-е издание — Просвещение, 2014-2022г.
Условие
Сколькими способами 6 студентов, сдающих экзамен, могут занять места в аудитории, в которой стоит 20 одноместных столов?
Решение 1
Подробное решение

Белый фонпереписывать в тетрадь
Цветной фонтеория и пояснения
Решение 2
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Комбинаторика
В науке и практике
часто встречаются задачи, решая которые, приходится составлять различные
комбинации из конечного числа элементов и подсчитывать число комбинаций. Решать
такие задачи помогает комбинаторика – раздел математики, в котором исследуются
и решаются задачи выбора элементов из исходного множества и расположения их в
некоторой комбинации, составленной по заданным правилам.
Простейшими комбинациями,
которые можно составить из элементов конечного множества, являются
перестановки.
Определение. Перестановкой из элементов называется каждое расположение этих элементов в определенном порядке.
Обозначается .
где называется факториалом
числа . Это произведение
натуральных чисел от 1 до , т.е.
Пример 1. Сколькими
способами можно расставить на игровой площадке 6 волейболистов?
Решение.
Ответ. Волейболистов можно
расставить на площадке 720 способами.
Пример 2. Сколько
различных последовательностей можно составить из букв слова (необязательно
осмысленных)?
а) привет; б) задача.
Решение. а) В слове «привет»
6 букв, следовательно, чтобы найти, сколько последовательностей можно составить
из букв этого слова, надо найти число перестановок из 6 элементов, т.е.
б) Если бы в слове
«задача» все буквы были бы разными, то перестановок было бы 6! Но три
одинаковых буквы «а» не дадут новых 3! перестановок, т.е. их будет в 3! раз
меньше. Значит, ответ: .
Ответ: а) 720; б) 120 последовательностей.
Определение. Размещением из элементов по
называется любое множество,
состоящее из любых элементов, взятых в
определенном порядке из данных элементов. Обозначается
.
Пример 3. Сколькими
способами 6 студентов, сдающих экзамен, могут занять место в аудитории, в
которой стоит 10 одноместных столов?
Решение. Для того чтобы
посчитать количество способов воспользуемся формулой размещения из 10 элементов
по 6:
Ответ: 151200 способов.
Замечание. Если , то
. Т.е., перестановка –
частный случай размещения.
Определение. Сочетанием из элементов по
называется любое множество,
составленное из элементов, выбранных из
данных элементов. Обозначается
.
Договорились считать:
Пример 4. В группе 25
студентов. Сколькими способами из 25 студентов выбрать 3 дежурных.
Решение. Выбор 3 дежурных
из 25 студентов – это комбинация из 25 по 3. Т.е.,
Ответ: 2300 способами.
Комбинации, размещения и
перестановки вместе называются сочетаниями. При решении простых комбинаторных
задач сначала следует определить вид сочетания, учитывая, что:
¾
Перестановки отличаются друг от друга порядком
размещения элементов;
¾
Размещения отличаются или выбором элементов, или
порядком их размещения;
¾
Комбинации отличаются только выбором элементов
(порядок размещения элементов не учитывается).
Как выбрать формулу
 |
Комбинаторные
задачи бывают разных видов, но большинство из них решают с помощью основных
правил: правила суммы и правила произведения.
Пример
5. Сборы из 30 человек выбирают председателя, секретаря и трех членов
редакционной комиссии. Сколькими способами это можно сделать?
Решение.
В выборе председателя и секретаря порядок размещения элементов учитывается и не
все элементы входят в соединение, следовательно, используем формулу размещение
из 30 по 2; таким образом, в дальнейших выборах будут участвовать 30-2=28
человек. При выборе членов комиссии порядок размещения элементов не
учитывается, следовательно используем формулу сочетаний из 28 по 3. Т.к. нам
необходимо выбрать и председателя с секретарем и членов комиссии,
следовательно, используем правило произведения:
Ответ: 2850120
способами.
Пример 6. Из 7 бегунов
и 3 прыгунов надо собрать команду из 5 человек, в которую войдет хотя бы один
прыгун. Сколькими способами это можно сделать?
Решение. Рассмотрим
все варианты:
¾
в команде один прыгун и, соответственно, 4
бегуна ;
¾
2 прыгуна и 3 бегуна ;
¾
3 прыгуна и 2 бегуна .
Т.к.
собрать команду можно или первым или вторым или третьим
способом, то используем правило суммы:
Ответ:
231 способом.
Содержание
- Комбинаторика. Перестановки. Размещения. Сочетания
- Буклет «Повторим комбинаторику» 9 класс
- 06. Размещения
Комбинаторика. Перестановки. Размещения. Сочетания
Комбинаторика. Перестановки. Размещения. Сочетания.
В науке и практике часто встречаются задачи, решая которые, приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Решать такие задачи помогает комбинаторика — раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составленной по заданным правилам.
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Задача 1. Сколькими способами можно построить 3 человек в шеренгу?
Решение: а в с, а с в
Рп — число перестановок. Р3 = 3 *2 *1= 6.
Перестановкой из п элементов называется каждое расположение этих элементов в определенном порядке.
где п! называется факториалом числа п. Это произведение первых натуральных n чисел от 1 до n.
Задача 2. В автосервис приехали 5 машин для ремонта. Сколько существует способов выстроить их в очередь на обслуживание?
Решение: Р5 = 5!= 5*4 *3 *2 *1 =120.
Задача 3. Сколько различных последовательностей можно составить из букв слова (необязательно осмысленных)?
Решение: Р7 = 7*6*5*4*3*2* 1 = 5040.
Р5 = 5 * 4 * 3 * 2 * 1 = 120.
Р6 = 6 * 5 * 4 * 3 * 2 * 1 = 720.
Задача 4. На дверях четырех одинаковых кабинетов надо повесить таблички с фамилиями четырех заместителей директора. Сколькими способами это можно сделать?
Решение: Р4 = 4! = 4 • 3 • 2 • 1 = 24.
Размещением из п элементов по к (к
Источник
Буклет «Повторим комбинаторику» 9 класс
В науке и практике часто встречаются задачи, решая которые, приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Решать такие задачи помогает комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составленной по заданным правилам.
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Определение. Перестановкой из 

где 


Пример 1. Сколькими способами можно расставить на игровой площадке 6 волейболистов?
Решение.
Ответ. Волейболистов можно расставить на площадке 720 способами.
Пример 2. Сколько различных последовательностей можно составить из букв слова (необязательно осмысленных)?
а) привет; б) задача.
Решение. а) В слове «привет» 6 букв, следовательно, чтобы найти, сколько последовательностей можно составить из букв этого слова, надо найти число перестановок из 6 элементов, т.е.
б) Если бы в слове «задача» все буквы были бы разными, то перестановок было бы 6! Но три одинаковых буквы «а» не дадут новых 3! перестановок, т.е. их будет в 3! раз меньше. Значит, ответ: 
Ответ: а) 720; б) 120 последовательностей.
Определение. Размещением из 




Пример 3. Сколькими способами 6 студентов, сдающих экзамен, могут занять место в аудитории, в которой стоит 10 одноместных столов?
Решение. Для того чтобы посчитать количество способов воспользуемся формулой размещения из 10 элементов по 6:
Ответ: 151200 способов.
Замечание. Если 

Определение. Сочетанием из 




Договорились считать:
Пример 4. В группе 25 студентов. Сколькими способами из 25 студентов выбрать 3 дежурных.
Решение. Выбор 3 дежурных из 25 студентов – это комбинация из 25 по 3. Т.е.,
Ответ: 2300 способами.
Комбинации, размещения и перестановки вместе называются сочетаниями. При решении простых комбинаторных задач сначала следует определить вид сочетания, учитывая, что:
Перестановки отличаются друг от друга порядком размещения элементов;
Размещения отличаются или выбором элементов, или порядком их размещения;
Комбинации отличаются только выбором элементов (порядок размещения элементов не учитывается).
Источник
06. Размещения
Пусть имеется некоторое множество, содержащее n элементов. Выберем из этого множества k элементов без возвращения, но упорядочивая их по мере их выбора в последовательную цепочку. Такие цепочки называются размещениями.
Размещениями из n элементов по k элементов называются такие комбинации, из которых каждое содержит k элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одного), либо порядком их расположения.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить шесть размещений по два элемента: ab, ac, ba, bc, ca, cb. Все приведённые размещения отличаются друг от друга хотя бы одним элементом или порядком их расположения.
Число размещений 

Легко понять, что 
Пример 4.1. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить 4 различных фотографии. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение. Для размещения фотографий следует отобрать 4 различных страницы из 12 имеющихся. Затем нужно отобранные страницы упорядочить, т. е. определить, на какую страницу поместить первую фотографию, на какую – вторую и т. д. Полученная упорядоченная совокупность страниц является, согласно определению, размещением из 12 элементов по 4, а число таких размещений является искомым результатом:

Пример 4.2. Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани пяти различных цветов? Решите эту же задачу при условии, что одна полоса должна быть красной.
Решение. Поскольку в данной задаче важен порядок следования полос и все цвета во флаге должны быть разными, то исходная задача сводится к подсчету числа размещений из 5 по 3:

При условии, что одна полоса должна быть красной, получаем, что для выбора места для красной полосы существует 3 способа, а для оставшихся двух полос останется 

Пример 4.3. Сколькими способами 10 человек можно поставить парами в ряд?
Решение. Первую пару можно выбрать 


4.1. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?
Ответ: В этом случае надо число размещений из 25 элементов по 4. Здесь играет роль и то, кто будет выбран в руководство общества, и то, какие посты займут выбранные. Поэтому ответ дается формулой 
4.2. В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление различных видов деталей (по одному виду на каждого).
Ответ: 
4.3. Из 10 книг выбирают 4 для рассылки по разным адресам. Сколькими способами это можно сделать?
Ответ: 
4.4. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?
Ответ: 
4.5. Студенту необходимо сдать 5 экзаменов в течение 12 дней. Сколькими способами можно составить расписание экзаменов, если в течение дня он может сдать не более одного экзамена?
Ответ: 
4.6. Сколькими способами можно преподнести 4 различных подарка 6 ученикам таким образом, чтобы каждый ученик получил не более одного подарка?
Ответ: 
4.7. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, …, 9, если каждая цифра в обозначении числа встречается не более одного раза? (Учесть, что число не может начинаться с нуля.)
Ответ: 
Источник
Задачи на размещение для 5-6 классов на этой странице! Научим решать и покажем формулу. 10 задач на размещение в интересном формате. Решайте!
- Сколькими способами семья из трёх человек может разместиться в 4-местном купе (других пассажиров нет)?
Значит, надо искать кол-во размещений:
И получим: 24 способа.
3. На станции 7 запасных путей. Сколькими способами на них можно расставить 5 поездов? (по 1 на путь)
4. Сколькими способами могут быть распределены первая, вторая и третья премия между 15 участниками конкурса?
5. На странице альбома 6 свободных мест. Сколькими способами можно вложить в свободные места 4 фотографии?
7. Из 20 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?
8. Сколькими способами могут занять 1-ое, 2-ое, 3-ое, 4-ое и 5-ое место 8 участниц финального забега?
Задачи на размещение и олимпиадные задачи по математике 4 класс — https://matematika-online.ru/2019/11/23/olimpiadnye-zadachi-4-klass/
9. Сколькими способами 6 студентов, сдающих экзамен, могут занять места в аудитории, где стоит 20 одноместных столов?