в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 93 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
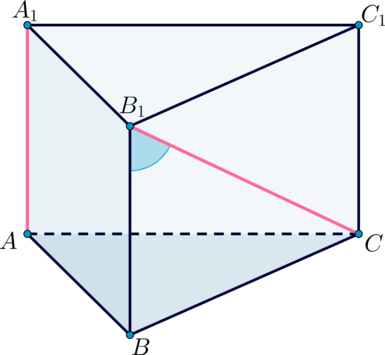
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 5, а боковые рёбра равны 11.
а) Докажите, что прямые CA1 и C1D1 перпендикулярны.
б) Найдите площадь сечения призмы плоскостью, проходящей через вершины C, A1 и F1.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 2. (Часть C)., Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С2, C4.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. Через точки B, D1, F1 проведена плоскость β.
а) Докажите, что плоскость β пересекает ребро AA1 в такой точке M, что AM : A1M = 1 : 2.
б) Найдите угол, который образует плоскость β с плоскостью основания призмы, если известно, что AB = 1, AA1 = 3.
Источник: А. Ларин: Тренировочный вариант № 122.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. Через точки B, D1, F1 проведена плоскость
а) Докажите, что плоскость α перпендикулярна плоскости DCC1.
б) Найдите площадь сечения призмы плоскостью α, если известно, что AB = 1, AA1 = 3.
Источник: А. Ларин: Тренировочный вариант № 123.
Все ребра правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 равны
а) Построить сечение призмы плоскостью AFC1.
б) Найдите площадь этого сечения.
Источник: А. Ларин: Тренировочный вариант № 133.
Источник: А. Ларин: Тренировочный вариант № 9.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 AB = 2, AA1 = 3.
а) Докажите, что прямые AC1 и BE перпендикулярны.
б) Найдите расстояние между прямыми AC1 и BE.
Источник: А. Ларин: Тренировочный вариант № 118.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. Через точки B, D1, F1 проведена плоскость α.
а) Докажите, что плоскость α пересекает ребро CC1 в такой точке М, что MC : MC1 = 1 : 2.
б) Найдите отношение объемов многогранников, на которые данную призму делит плоскость α.
Источник: А. Ларин: Тренировочный вариант № 163.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 на ребре CC1 отмечена точка М так, что СМ : С1М = 1 : 3. Плоскость АЕМ пересекает ребро ВВ1 в точке К.
А) Докажите, что ВК : В1К = 1 : 5.
Б) Найдите площадь сечения призмы плоскостью АЕМ, если АВ = 3, СС1 = 8.
Источник: А. Ларин: Тренировочный вариант № 171.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1.
а) Докажите, что плоскости AA1D1 и DB1F1 перпендикулярны.
б) Найдите тангенс угла между плоскостями ABC и DB1F1.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. O — точка пересечения А1D и AD1.
а) Докажите, что плоскости OB1C1 и СЕЕ1 перпендикулярны.
б) Найдите расстояние между прямыми B1C1 и СЕ1, если известно, что АВ = 1, АА1 = 3.
Источник: А. Ларин: Тренировочный вариант № 167.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ребро основания AB = 2, высота AA1 = 6, точка M — середина F1E1, проведено сечение через точки A, C и M.
а) Докажите, что сечение проходит через середину ребра D1E1.
б) Найдите площадь этого сечения.
Источник: А. Ларин. Тренировочный вариант № 281.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 3, а боковые ребра равны 4.
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите расстояние от точки С до прямой D1E1.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1.
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите расстояние от точки B до плоскости DEA1.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1 все рёбра которой равны 1.
а) Докажите, что
б) Найдите косинус угла между прямыми AB1 и BC1.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 на ребре DD1 отмечена точка O так, что
а) Докажите, что объём данной призмы в 4,5 раза больше, чем объём пирамиды OABB1A1.
б) Найдите площадь боковой поверхности пирамиды OABB1A1, если известно, что AB = 1, DD1=3.
Источник: А. Ларин: Тренировочный вариант № 158.
В правильной шестиугольной призме ABCDEFA’B’C’D’E’F’ все ребра равны 1.
а) Докажите, что AC’ перпендикулярна прямой BE.
б) Найдите угол между прямой AC’ и плоскостью ACD’.
Источник: А. Ларин: Тренировочный вариант № 13.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. На ребре AA1 отмечена точка M так, что А1М : АМ = 1 : 3. Через точки М и В1 параллельно АD1 проведена плоскость Ω.
а) Докажите, что плоскость Ω проходит через вершину F1.
б) Найдите расстояние от точки А до плоскости Ω, если АВ = 2, АА1 = 4.
Источник: А. Ларин: Тренировочный вариант № 168.
Дана правильная шестиугольная призма
а) Докажите, что прямые СF и перпендикулярны.
б) Найдите расстояние между прямыми СF и если
.
Источник: А. Ларин: Тренировочный вариант № 191.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 4, а боковые ребра 5.
а) Докажите, что плоскость A1C1E1 перпендикулярна плоскости BB1E1.
б) Найдите угол между плоскостями A1C1E1 и ABC.
Источник: А. Ларин: Тренировочный вариант № 235.
Всего: 93 1–20 | 21–40 | 41–60 | 61–80 …
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 93 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 5, а боковые рёбра равны 11.
а) Докажите, что прямые CA1 и C1D1 перпендикулярны.
б) Найдите площадь сечения призмы плоскостью, проходящей через вершины C, A1 и F1.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 2. (Часть C)., Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С2, C4.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. Через точки B, D1, F1 проведена плоскость β.
а) Докажите, что плоскость β пересекает ребро AA1 в такой точке M, что AM : A1M = 1 : 2.
б) Найдите угол, который образует плоскость β с плоскостью основания призмы, если известно, что AB = 1, AA1 = 3.
Источник: А. Ларин: Тренировочный вариант № 122.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. Через точки B, D1, F1 проведена плоскость
а) Докажите, что плоскость α перпендикулярна плоскости DCC1.
б) Найдите площадь сечения призмы плоскостью α, если известно, что AB = 1, AA1 = 3.
Источник: А. Ларин: Тренировочный вариант № 123.
Все ребра правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 равны
а) Построить сечение призмы плоскостью AFC1.
б) Найдите площадь этого сечения.
Источник: А. Ларин: Тренировочный вариант № 133.
Источник: А. Ларин: Тренировочный вариант № 9.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 AB = 2, AA1 = 3.
а) Докажите, что прямые AC1 и BE перпендикулярны.
б) Найдите расстояние между прямыми AC1 и BE.
Источник: А. Ларин: Тренировочный вариант № 118.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. Через точки B, D1, F1 проведена плоскость α.
а) Докажите, что плоскость α пересекает ребро CC1 в такой точке М, что MC : MC1 = 1 : 2.
б) Найдите отношение объемов многогранников, на которые данную призму делит плоскость α.
Источник: А. Ларин: Тренировочный вариант № 163.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 на ребре CC1 отмечена точка М так, что СМ : С1М = 1 : 3. Плоскость АЕМ пересекает ребро ВВ1 в точке К.
А) Докажите, что ВК : В1К = 1 : 5.
Б) Найдите площадь сечения призмы плоскостью АЕМ, если АВ = 3, СС1 = 8.
Источник: А. Ларин: Тренировочный вариант № 171.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1.
а) Докажите, что плоскости AA1D1 и DB1F1 перпендикулярны.
б) Найдите тангенс угла между плоскостями ABC и DB1F1.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. O — точка пересечения А1D и AD1.
а) Докажите, что плоскости OB1C1 и СЕЕ1 перпендикулярны.
б) Найдите расстояние между прямыми B1C1 и СЕ1, если известно, что АВ = 1, АА1 = 3.
Источник: А. Ларин: Тренировочный вариант № 167.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ребро основания AB = 2, высота AA1 = 6, точка M — середина F1E1, проведено сечение через точки A, C и M.
а) Докажите, что сечение проходит через середину ребра D1E1.
б) Найдите площадь этого сечения.
Источник: А. Ларин. Тренировочный вариант № 281.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 3, а боковые ребра равны 4.
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите расстояние от точки С до прямой D1E1.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1.
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите расстояние от точки B до плоскости DEA1.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1 все рёбра которой равны 1.
а) Докажите, что
б) Найдите косинус угла между прямыми AB1 и BC1.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 на ребре DD1 отмечена точка O так, что
а) Докажите, что объём данной призмы в 4,5 раза больше, чем объём пирамиды OABB1A1.
б) Найдите площадь боковой поверхности пирамиды OABB1A1, если известно, что AB = 1, DD1=3.
Источник: А. Ларин: Тренировочный вариант № 158.
В правильной шестиугольной призме ABCDEFA’B’C’D’E’F’ все ребра равны 1.
а) Докажите, что AC’ перпендикулярна прямой BE.
б) Найдите угол между прямой AC’ и плоскостью ACD’.
Источник: А. Ларин: Тренировочный вариант № 13.
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. На ребре AA1 отмечена точка M так, что А1М : АМ = 1 : 3. Через точки М и В1 параллельно АD1 проведена плоскость Ω.
а) Докажите, что плоскость Ω проходит через вершину F1.
б) Найдите расстояние от точки А до плоскости Ω, если АВ = 2, АА1 = 4.
Источник: А. Ларин: Тренировочный вариант № 168.
Дана правильная шестиугольная призма
а) Докажите, что прямые СF и перпендикулярны.
б) Найдите расстояние между прямыми СF и если
.
Источник: А. Ларин: Тренировочный вариант № 191.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 4, а боковые ребра 5.
а) Докажите, что плоскость A1C1E1 перпендикулярна плоскости BB1E1.
б) Найдите угол между плоскостями A1C1E1 и ABC.
Источник: А. Ларин: Тренировочный вариант № 235.
Всего: 93 1–20 | 21–40 | 41–60 | 61–80 …
Задача 1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна а площадь поверхности равна
Решение: + показать
Задача 2. В правильной четырёхугольной призме известно, что
Найдите угол между диагоналями
и
Ответ дайте в градусах.
Решение: + показать
Задача 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и
боковое ребро равно
Найдите объем призмы.
Решение: + показать
Задача 4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и
высота призмы равна
Найдите площадь ее поверхности.
Решение: + показать
Задача 5. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и
Площадь ее поверхности равна
. Найдите высоту призмы.
Решение: + показать
Задача 6. Площадь поверхности правильной треугольной призмы равна Какой будет площадь поверхности призмы, если все ее ребра увеличить в два раза?
Решение: + показать
Задача 7. В правильной треугольной призме , все ребра которой равны
найдите угол между прямыми
и
. Ответ дайте в градусах.
Решение: + показать
Задача 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными и
и боковым ребром, равным
Решение: + показать
Задача 9. Гранью параллелепипеда является ромб со стороной и острым углом
Одно из ребер параллелепипеда составляет с этой гранью угол в
и равно
Найдите объем параллелепипеда.
Решение: + показать
Задача 10. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна а высота —
Решение: + показать
Задача 11. Найдите объем правильной шестиугольной призмы, стороны основания которой равны а боковые ребра равны
Решение: + показать
Задача 12. В правильной шестиугольной призме все ребра равны
. Найдите расстояние между точками
и
.
Решение: + показать
Задача 13. В правильной шестиугольной призме все ребра равны
Найдите угол
. Ответ дайте в градусах.
Решение: + показать
Задача 14. В правильной шестиугольной призме , все ребра которой равны
найдите угол между прямыми
и
. Ответ дайте в градусах.
Решение: + показать
Задача 15. В правильной шестиугольной призме все ребра равны
Найдите тангенс угла
Решение: + показать
Задача 16. В сосуд, имеющий форму правильной треугольной призмы, налили см
воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки
см до отметки
см. Найдите объем детали. Ответ выразите в см
Решение: + показать
Задача 17. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в
раза больше, чем у первого? Ответ выразите в сантиметрах.
Решение: + показать
Задача 18. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение: + показать
Задача 19. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен Найдите объем исходной призмы.
Решение: + показать
Задача 20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.
Задача 21. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами а боковые ребра равны
и наклонены к плоскости основания под углом
Решение: + показать
Задача 22. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно и отстоит от других боковых ребер на
и
Найдите площадь боковой поверхности этой призмы.
Решение: + показать
Задача 23. В правильной треугольной призме стороны оснований равны
боковые рёбра равны
Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер
, и
и точку
Решение: + показать
Задача 24. В правильной треугольной призме стороны оснований равны
боковые рёбра равны
Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер
и
Решение: + показать
Задача 25. Объём куба равен
Построено сечение
проходящее через середины рёбер
и
и параллельное ребру
Найдите объём треугольной призмы
Решение: + показать
Задача 26. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы
площадь основания которой равна
а боковое ребро равно
Решение: + показать
Задача 27. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы
площадь основания которой равна
а боковое ребро равно

Задача 28. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы
площадь основания которой равна
а боковое ребро равно
Решение: + показать
Задача 29. Найдите объём многогранника, вершинами которого являются точки правильной шестиугольной призмы
площадь основания которой равна
а боковое ребро равно
Решение: + показать

ЕГЭ Профиль №2. Призма
Скачать файл в формате pdf.
ЕГЭ Профиль №2. Призма
| Задача 1. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в cм3.
Ответ
ОТВЕТ: 184. |
 |
| Задача 2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
Ответ
ОТВЕТ: 5. |
 |
| Задача 3. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Ответ
ОТВЕТ: 300. |
|
| Задача 4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Ответ
ОТВЕТ: 248. |
|
| Задача 5. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 5, а площадь поверхности равна 190.
Ответ
ОТВЕТ: 7. |
|
| Задача 6. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Ответ
ОТВЕТ: 12. |
|
| Задача 7. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Ответ
ОТВЕТ: 4. |
 |
| Задача 8. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны (sqrt 3 ).
Ответ
ОТВЕТ: 4,5. |
|
| Задача 9. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Ответ
ОТВЕТ: 8. |
|
| Задача 10. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Ответ
ОТВЕТ: 20. |
|
| Задача 11. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны (2sqrt 3 ) и наклонены к плоскости основания под углом 30o.
Ответ
ОТВЕТ: 18. |
|
| Задача 12. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Ответ
ОТВЕТ: 4. |
|
| Задача 13. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Ответ
ОТВЕТ: 288. |
|
| Задача 14. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Ответ
ОТВЕТ: 10. |
|
| Задача 15. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Ответ
ОТВЕТ: 240. |
|
| Задача 16. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Ответ
ОТВЕТ: 10. |
|
| Задача 17. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Ответ
ОТВЕТ: 16. |
|
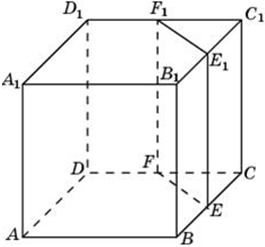
| Задача 18. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
Ответ
ОТВЕТ: 1,5. |
 |
| Задача 19. Найдите объем многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 2, а боковое ребро равно 3.
Ответ
ОТВЕТ: 2. |
| Задача 20. Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 2.
Ответ
ОТВЕТ: 4. |
| Задача 21. Найдите объем многогранника, вершинами которого являются точки A1, B1, B, C правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 3.
Ответ
ОТВЕТ: 4. |
| Задача 22. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, E, F, A1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 4, а боковое ребро равно 3.
Ответ
ОТВЕТ: 4. |
| Задача 23. Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3.
Ответ
ОТВЕТ: 3. |
| Задача 24. Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Ответ
ОТВЕТ: 8. |
| Задача 25. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Ответ
ОТВЕТ: 6. |
| Задача 26. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?
Ответ
ОТВЕТ: 54. |
| Задача 27. Найдите объем правильной шестиугольной призмы, все ребра которой равны (sqrt 3 ).
Ответ
ОТВЕТ: 13,5. |
| Задача 28. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1.
Ответ
ОТВЕТ: 2. |
| Задача 29. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.
Ответ
ОТВЕТ: 2. |
| Задача 30. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны (sqrt 5 ). Найдите расстояние между точками B и E1.
Ответ
ОТВЕТ: 5. |
| Задача 31. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
Ответ
ОТВЕТ: 2. |
| Задача 32. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
| Задача 33. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
| Задача 34. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 3, найдите угол между прямыми AA1 и BC1. Ответ дайте в градусах.
Ответ
ОТВЕТ: 45. |
| Задача 35. В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что (A{C_1} = 2BC). Найдите угол между диагоналями BD1 и CA1. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
| Задача 36. В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые ребра равны 5.Найдите площадь сечения призмы плоскостью, проходящей через середины ребер AB, AC, A1B1 и A1C1.
Ответ
ОТВЕТ: 5. |
| Задача 37. В правильной четырехугольной призме ABCDA1B1C1D1 ребро AA1 равно 15, а диагональ BD1 равна 17. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C.
Ответ
ОТВЕТ: 120. |
| Задача 38. В правильной треугольной призме ABCA1B1C1 известно, что (AB = sqrt 3 A{A_1}.) Найдите угол между прямыми AB1 и CC1. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Призма»
Открытый банк заданий по теме призма. Задания B8 из ЕГЭ по математике (профильный уровень)
Производная и первообразная функции
Задание №1084
Тип задания: 8
Тема:
Призма
Условие
В правильной треугольной призме ABCA_1B_1C_1 стороны основания равны 4, а боковые рёбра равны 10. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A_1B_1 и A_1C_1.
Показать решение
Решение
Рассмотрим следующий рисунок.
Отрезок MN является средней линией треугольника A_1B_1C_1, поэтому MN = frac12 B_1C_1=2. Аналогично, KL=frac12BC=2. Кроме того, MK = NL = 10. Отсюда следует, что четырёхугольник MNLK является параллелограммом. Так как MKparallel AA_1, то MKperp ABC и MKperp KL. Следовательно, четырёхугольник MNLK является прямоугольником. S_{MNLK} = MKcdot KL = 10cdot 2 = 20.
Ответ
20
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1082
Тип задания: 8
Тема:
Призма
Условие
Объём правильной четырёхугольной призмы ABCDA_1B_1C_1D_1 равен 24. Точка K — середина ребра CC_1. Найдите объём пирамиды KBCD.
Показать решение
Решение
Согласно условию, KC является высотой пирамиды KBCD. CC_1 является высотой призмы ABCDA_1B_1C_1D_1.
Так как K является серединой CC_1, то KC=frac12CC_1. Пусть CC_1=H, тогдаKC=frac12H. Заметим также, что S_{BCD}=frac12S_{ABCD}. Тогда, V_{KBCD}= frac13S_{BCD}cdotfrac{H}{2}= frac13cdotfrac12S_{ABCD}cdotfrac{H}{2}= frac{1}{12}cdot S_{ABCD}cdot H= frac{1}{12}V_{ABCDA_1B_1C_1D_1}. Следовательно, V_{KBCD}=frac{1}{12}cdot24=2.
Ответ
2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1077
Тип задания: 8
Тема:
Призма
Условие
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота — 8.
Показать решение
Решение
Площадь боковой поверхности призмы находим по формуле Sбок. = Pосн. · h = 6acdot h, где Pосн. и h — соответственно периметр основания и высота призмы, равная 8, и a — сторона правильного шестиугольника, равная 6. Следовательно, Sбок. = 6cdot 6cdot 8 = 288.
Ответ
288
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1076
Тип задания: 8
Тема:
Призма
Условие
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 40 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в два раза больше, чем у первого? Ответ выразите в сантиметрах.
Показать решение
Решение
Пусть a — сторона основания первого сосуда, тогда 2a — сторона основания второго сосуда. По условию объём жидкости V в первом и втором сосуде один и тот же. Обозначим через H уровень, на который поднялась жидкость во втором сосуде. Тогда V= frac12cdot a^2cdotsin60^{circ}cdot40= frac{a^2sqrt3}{4}cdot40, и, V=frac{(2a)^2sqrt3}{4}cdot H. Отсюда frac{a^2sqrt3}{4}cdot40=frac{(2a)^2sqrt3}{4}cdot H, 40=4H, H=10.
Ответ
10
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №916
Тип задания: 8
Тема:
Призма
Условие
В правильной шестиугольной призме ABCDEFA_1B_1C_1D_1E_1F_1 все рёбра равны 2. Найдите расстояние между точками A и E_1.
Показать решение
Решение
Треугольник AEE_1 — прямоугольный, так как ребро EE_1 перпендикулярно плоскости основания призмы, прямым углом будет угол AEE_1.
Тогда по теореме Пифагора AE_1^2 = AE^2 + EE_1^2. Найдём AE из треугольника AFE по теореме косинусов. Каждый внутренний угол правильного шестиугольника равен 120^{circ}. Тогда AE^2= AF^2+FE^2-2cdot AFcdot FEcdotcos120^{circ}= 2^2+2^2-2cdot2cdot2cdotleft ( -frac12 right ).
Отсюда, AE^2=4+4+4=12,
AE_1^2=12+4=16,
AE_1=4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №912
Тип задания: 8
Тема:
Призма
Условие
Найдите площадь боковой поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 4sqrt5 и 8, и боковым ребром, равным 5.
Показать решение
Решение
Площадь боковой поверхности прямой призмы находим по формуле Sбок. = Pосн. · h = 4acdot h, где Pосн. и h соответственно периметр основания и высота призмы, равная 5, и a — сторона ромба. Найдём сторону ромба, пользуясь тем, что диагонали ромба ABCD взаимно перпендикулярны и точкой пересечения делятся пополам.
Из треугольника BOC по теореме Пифагора находим BC^2=BO^2+OC^2= left ( frac82 right )^2+left ( frac{4sqrt5}{2} right)^2= 16+20=36, BC=6.
Следовательно, Sбок. = 4cdot6cdot5=120.
Ответ
120
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №313
Тип задания: 8
Тема:
Призма
Условие
В сосуде, имеющем форму правильной треугольной призмы содержится 357 см3 воды. При полном погружении детали в воду, уровень жидкости поднялся с отметки 14 см до отметки 18 см. Найдите объем детали. Ответ выразите в кубических сантиметрах.
Показать решение
Решение
Пусть V_B — объем воды в призме, V_D — искомый объем детали.
По условию V_B=14S, V_B+V_D=18S, где S — площадь основания призмы.
Так как V_B=14S=357, то S=frac{357}{14}=frac{51}{2} (см3).
Тогда V_D= (V_B+V_D)-V_B= 18S-14S= 4S= 4cdotfrac{51}{2}= 2cdot51= 102 (см3).
Ответ
102
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №310
Тип задания: 8
Тема:
Призма
Условие
Треугольная призма содержит плоскость, проведенную параллельно ее боковому ребру через среднюю линию основания. Найдите объем отсеченной плоскостью призмы, если объем исходной призмы равен 36.
Показать решение
Решение
Плоскость, параллельная боковому ребру, проходит через среднюю линию основания, значит, площадь основания отвеченной призмы уменьшилась в 2^2 раза по сравнению с площадью основания заданной призмы (средняя линия в 2 раза меньше стороны, которой она параллельна). Высота отсеченной призмы равна высоте заданной призмы.
Следовательно, объем отсеченной призмы уменьшился в 4 раза и стал равным 36:4=9.
Ответ
9
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №109
Тип задания: 8
Тема:
Призма
Условие
В правильной треугольной призме ABCA_1B_1C_1 площадь основания равна 9, а боковое ребро равно 7. Найдите объем многогранника ABCB_1C_1.
Показать решение
Решение
Объем многогранника ABCB_1C_1 мы можем найти из разности объема пирамиды AA_1B_1C_1 от общего объема призмы.
Формула объема пирамиды имеет вид: V=frac13Sh
Формула объема призмы имеет вид: V=Sh
где S – площадь основания, а h – высота пирамиды
Площадь основания нам известна, поэтому объем пирамиды AA_1B_1C_1 равен frac13cdot 9cdot 7 = 21
Объем призмы равен: 9·7 = 63
Значит объем многогранника ABCB_1C_1 равен 63 − 21 = 42
Ответ
42
Задание №84
Тип задания: 8
Тема:
Призма
Условие
В основании треугольной призмы ABCA_1B_1C_1 провели среднюю линию MN, из которой, параллельно боковому ребру, подняли плоскость MNM_1N_1. Определите площадь боковой поверхности исходной призмы BCB_1C_1, если площадь боковой поверхности отсеченной треугольной призмы BNN_1B_1 составляет 79 см2. Ответ выразите в квадратных сантиметрах.
Показать решение
Решение
Боковыми поверхностями и сечением треугольной призмы являются прямоугольники. Искомая площадь боковой поверхности равна произведению длины основания на высоту:
S_{BCB_1C_1} = BC cdot BB_1
Площадь боковой поверхности отсеченной призмы BNB_1N_1 вычисляется как произведение высоты призмы BB_1 и длины ребра BN.
S_{BNB_1N_1} = BN cdot BB_1
Т.к. MN – средняя линия треугольника ABC, точка N делит прямую BC пополам (BN = NC), и, следовательно, BC = 2 · BN. Получаем:
S_{BCB_1C_1} = BC cdot BB_1 = 2 cdot BN cdot BB_1 = 2 cdot S_{BNB_1N_1} = 2 cdot 79 = 158 см2
Ответ
158
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Прямая и правильная призмы»
(blacktriangleright) Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
Тогда:
1) боковые грани представляют собой прямоугольники;
2) боковое ребро является высотой призмы.
(blacktriangleright) Призма называется правильной, если она прямая и ее основания – правильные многоугольники.
Тогда:
боковые грани представляют собой равные прямоугольники.
Задание
1
#2859
Уровень задания: Легче ЕГЭ
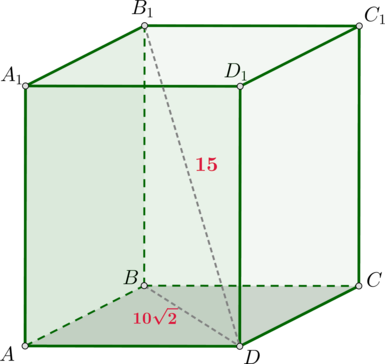
Дана правильная четырехугольная призма, диагональ которой равна (15), а диагональ основания равна (10sqrt2). Найдите площадь полной поверхности призмы.
Пусть (ABCDA_1B_1C_1D_1) – данная призма. Так как она правильная, то в основании лежит квадрат и она является прямой. Тогда (triangle
BB_1D) прямоугольный, следовательно, по теореме Пифагора [BB_1=sqrt{15^2-(10sqrt2)^2}=5.] Так как диагональ квадрата в (sqrt2) раз больше его стороны, то [AB=dfrac{BD}{sqrt2}=10.] Следовательно, [S_{text{пов-ти}}=2S_{ABCD}+4S_{AA_1D_1D}=2cdot 10^2+4cdot 10cdot 5=400.]
Ответ: 400
Задание
2
#2860
Уровень задания: Равен ЕГЭ
Дана прямая призма, в основании которой лежит равнобедренная описанная около окружности трапеция (ABCD) с боковой стороной, равной (5), и высотой, равной (3). Боковое ребро призмы равно (2). Найдите площадь полной поверхности призмы.
Пусть (AB=CD=5). Так как трапеция описанная, то суммы противоположных сторон равны, следовательно, (AD+BC=AB+CD=10). Следовательно, ее площадь равна [S_{ABCD}=dfrac{AD+BC}2cdot h=dfrac{10}2cdot 3=15.] Площадь боковой поверхности призмы равна [S’=(AB+BC+CD+AD)cdot AA_1=(10+10)cdot 2=40.] Следовательно, площадь полной поверхности равна [S_{text{пов-ти}}=40+15+15=70.]
Ответ: 70
Задание
3
#954
Уровень задания: Равен ЕГЭ
(ABCA_1B_1C_1) – правильная треугольная призма, (AB = sqrt[4]{3}), (AA_1 = sqrt[4]{27}). Найдите площадь полной поверхности призмы.
Площадь равностороннего треугольника со стороной (a) равна (dfrac{a^2sqrt{3}}{4}), тогда
[begin{aligned}
&S_{ABC} = S_{A_1B_1C_1} = dfrac{(sqrt[4]{3})^2sqrt{3}}{4} = dfrac{sqrt{3}cdotsqrt{3}}{4} = dfrac{3}{4},\
&S_{AA_1C_1C} = S_{CC_1B_1B} = S_{AA_1B_1B} = AA_1cdot AB = sqrt[4]{27}cdotsqrt[4]{3} = sqrt[4]{81} = 3.
end{aligned}]
Таким образом, площадь полной поверхности (ABCA_1B_1C_1) равна [2cdotdfrac{3}{4} + 3cdot 3 = 10,5.]
Ответ: 10,5
Задание
4
#1868
Уровень задания: Равен ЕГЭ
В прямоугольной треугольной призме все боковые грани являются квадратами со стороной (10sqrt3). Найдите объем призмы.
У квадрата все стороны равны (Rightarrow) в основаниях призмы лежат равносторонние треугольники со сторонами, равными (10sqrt3).
Тогда площадь основания:
(displaystyle S_{text{осн.}} = frac{1}{2}cdot10sqrt3cdot10sqrt3cdotsin 60^circ = frac{1}{2}cdot10sqrt3cdot10sqrt3cdotfrac{sqrt3}{2} = 75sqrt3). Высота призмы равна стороне квадрата, тогда объем призмы: [10sqrt3cdot75sqrt3 = 2250.]
Ответ: 2250
Задание
5
#1869
Уровень задания: Равен ЕГЭ
Дана правильная треугольная призма. Площадь основания равна площади одной из боковых граней и равна (4sqrt3). Найдите объем призмы.
Так как призма является правильной, то в основаниях призмы лежат равносторонние треугольники, поэтому все боковые грани равны друг другу и являются прямоугольниками. Обозначим высоту призмы за (h), а сторону правильного треугольника за (x). Тогда найдем площадь основания:
(displaystyle S_{text{осн.}} = frac{1}{2}cdot x^2cdotsin 60^circ = frac{1}{2}cdot x^2cdotfrac{sqrt3}{2} = frac{sqrt3}{4}cdot x^2 = 4sqrt3) (Rightarrow) (x^2 = 16) (Rightarrow) (x = 4). Высоту выразим из формулы для площади боковой грани: (S = 4sqrt3 = xcdot h = 4cdot h) (Rightarrow) (h = sqrt3). Наконец, найдем объем призмы: [V = hcdot S_{text{осн.}} = sqrt3cdot4sqrt3 = 12.]
Ответ: 12
Задание
6
#3116
Уровень задания: Равен ЕГЭ
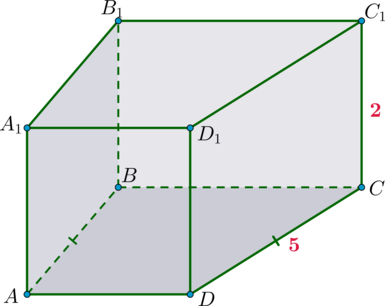
В правильной четырехугольной призме (ABCDA_1B_1C_1D_1) известно, что (DB_1=2CD). Найдите угол между диагоналями (AC_1) и (B_1D). Ответ дайте в градусах.
Так как призма четырехугольная и правильная, то в основании лежит квадрат и она прямая. Следовательно, (AD=CD) и (DB_1=2AD).
Диагонали призмы пересекаются и точкой пересечения (O) делятся пополам, следовательно, (OD=frac12DB_1=AD). Так как призма правильная, то диагонали равны, значит, (AO=OD=AD). Следовательно, (triangle AOD) правильный и (angle AOD=60^circ). Это и есть угол между (DB_1) и (AC_1).
Ответ: 60
Задание
7
#3115
Уровень задания: Равен ЕГЭ
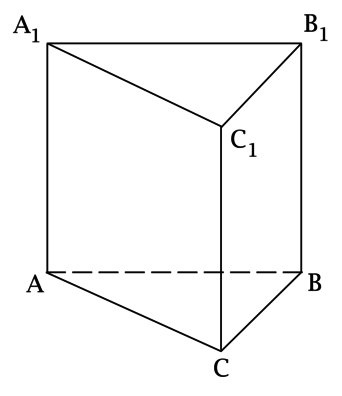
В правильной треугольной призме (ABCA_1B_1C_1), все ребра которой равны (1), найдите угол между прямыми (AA_1) и (CB_1). Ответ дайте в градусах.
Для того, чтобы найти угол между прямыми, не лежащими в одной плоскости, нужно одну из прямых параллельно перенести в плоскость, в которой лежит вторая прямая. Заметим, что (BB_1parallel AA_1). Следовательно, угол между (AA_1) и (CB_1) равен углу между прямыми (BB_1) и (CB_1).
Так как все ребра призмы равны, то грань (BCC_1B_1) представляет собой квадрат, где (CB_1) – диагональ. Следовательно, (angle
BB_1C=45^circ).
Ответ: 45
Школьникам, которые готовятся к сдаче ЕГЭ по математике, обязательно стоит научиться решать задачи на нахождение площади прямой и правильной призмы. Многолетняя практика подтверждает тот факт, что подобные задания по геометрии многие учащиеся считают достаточно сложными.
При этом уметь находить площадь и объем правильной и прямой призмы должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи ЕГЭ.
Основные моменты, которые стоит запомнить
- Если боковые ребра призмы перпендикулярны основанию, она называется прямой. Все боковые грани этой фигуры являются прямоугольниками. Высота прямой призмы совпадает с ее ребром.
- Правильной является призма, боковые ребра которой перпендикулярны основанию, в котором находится правильный многоугольник. Боковые грани этой фигуры — равные прямоугольники. Правильная призма всегда является прямой.
Подготовка к единому госэкзамену вместе со «Школково» — залог вашего успеха!
Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь представлен весь необходимый материал, который поможет подготовиться к прохождению аттестационного испытания.
Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы, теоремы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня.
Базовая информация систематизирована и понятно изложена в разделе «Теоретическая справка». Если вы уже успели повторить необходимый материал, рекомендуем вам попрактиковаться в решении задач на нахождение площади и объема прямой призмы. В разделе «Каталог» представлена большая подборка упражнений различной степени сложности.
Попробуйте рассчитать площадь прямой и правильной призмы или площадь боковой поверхности призмы прямо сейчас. Разберите любое задание. Если оно не вызвало сложностей, можете смело переходить к упражнениям экспертного уровня. А если определенные трудности все же возникли, рекомендуем вам регулярно готовиться к ЕГЭ в онлайн-режиме вместе с математическим порталом «Школково», и задачи по теме «Прямая и правильная призма» будут даваться вам легко.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Всего: 19 1–19
Добавить в вариант
Около цилиндра, осевое сечение которого — квадрат, описана треугольная призма, объем которой равен 672 см3, а площадь полной поверхности — 504 см2. Вычислите площадь полной поверхности цилиндра.
Основанием конуса служит круг, описанный около основания правильной треугольной призмы. Вершина конуса лежит на другом основании призмы. Найдите объем призмы, если объем конуса равен см2.
Сфера радиусом вписана в правильную треугольную призму. Найдите площадь полной поверхности призмы.
Основанием конуса служит круг, вписанный в основание правильной треугольной призмы. Вершина конуса лежит на другом основании призмы. Найдите объем призмы, если объем конуса равен см2.
В конус вписана прямая шестиугольная призма так, что нижнее ее основание лежит на основании конуса, а вершины верхнего основания лежат на боковой поверхности конуса. Все ребра призмы равны. Найдите отношение полных поверхностей конуса и призмы, если осевое сечение конуса является правильным треугольником.
Основание прямой призмы — равнобедренная трапеция с основаниями 9 и 3 см. Найдите площадь боковой поверхности призмы, если диагональ большей боковой грани составляет с боковым ребром призмы угол 45° и известно, что в основание призмы можно вписать окружность.
Основанием прямой призмы является равнобедренная трапеция с основаниями 4 и 8 см. Найдите площадь боковой поверхности призмы, если диагональ меньшей боковой грани составляет с боковым ребром призмы угол 45° и известно, что в основание призмы можно вписать окружность.
Сфера радиусом описана вокруг правильной треугольной призмы. Ребро основания призмы равно
Найдите высоту призмы.
Около цилиндра, осевое сечение которого — квадрат, описана треугольная призма, периметр основания которой равен 14 см, а площадь полной поверхности — 56 см2. Вычислите площадь боковой поверхности цилиндра.
Тип 2 № 52
Стороны основания прямой четырехугольной призмы равны 3, 6, 5,и 7, а боковое ребро призмы равно 8. Тогда площадь боковой поверхности призмы равна:
а)
б)
в)
г)
Тип 2 № 42
Стороны основания прямой треугольной призмы равны 7, 5 и 8, а боковое ребро — 6. Тогда площадь боковой поверхности призмы равна:
а)
б)
в)
г)
В основании прямой призмы лежит равнобедренный треугольник со сторонами 10, 10 и 12 см. Сечение, проходящее через его основание и среднюю линию другого основания, наклонено к основанию призмы под углом 45°. Найдите площадь сечения.
Все боковые грани треугольной призмы ABCA1B1C1 — квадраты. Расстояние от середины ребра AB до вершины C равно 3. Найдите расстояние от середины ребра BC до вершины A1.
Все боковые грани треугольной призмы ABCA1B1C1 — квадраты. Расстояние от середины ребра BC до вершины A1 равно 7. Найдите сторону основания призмы.
ABCDA1B1C1D1 — правильная четырехугольная призма, основанием которой является ромб ABCD. Известно, что SC1OC= 5 см2.Найдите площадь боковой поверхности призмы>:
а) 160 см2
б) 80 см2
в) 40 см2
г) 20 см2
В основании прямой призмы лежит прямоугольный треугольник с катетами AC=6 см и CB=10 см. Сечение, проходящее через катет AC и среднюю линию другого основания, наклонено к основанию призмы под углом 60°. Найдите площадь сечения.
Основание прямой призмы — равнобедренный треугольник с основанием a и углом при основании Диагональ боковой грани, содержащей боковую сторону треугольника, наклонена к плоскости основания под углом
Найдите площадь боковой поверхности цилиндра, вписанного в призму.
Основание прямой призмы — равнобедренный треугольник с боковой стороной b и углом при основании Диагональ боковой грани, содержащей основание треугольника, образует с боковым ребром угол
Найдите площадь боковой поверхности цилиндра, вписанного в призму.
ABCDEFA1B1C1D1E1F1 — правильная шестиугольная призма. Известно, что SEBCD = 18 см2. Найдите площадь четырехугольника A1B1OF1:
а) 18 см2
б) 12 см2
в) 36 см2
г) 6 см2
Всего: 19 1–19



















.png)

.png)