Задания
Версия для печати и копирования в MS Word
Тип 10 № 509109 
На рисунке изображён график функции linebreak$fleft(xright)=a^{x,+,b} $. Найдите значение $x$, при котором $fleft(xright)=64$.
Аналоги к заданию № 509107: 509108 509109 509110 509111 509112 Все
Прототип задания
·
·
Курс Д. Д. Гущина
Задания
Версия для печати и копирования в MS Word
Тип 10 № 509109 
На рисунке изображён график функции linebreak$fleft(xright)=a^{x,+,b} $. Найдите значение $x$, при котором $fleft(xright)=64$.
Аналоги к заданию № 509107: 509108 509109 509110 509111 509112 Все
Прототип задания
·
·
Курс Д. Д. Гущина
Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Тип 10 № 509109
На рисунке изображён график функции linebreak$fleft(xright)=a^{x,+,b} $. Найдите значение $x$, при котором $fleft(xright)=64$.
Аналоги к заданию № 509107: 509108 509109 509110 509111 509112 Все
Прототип задания
·
·
Курс Д. Д. Гущина
Решение 18 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
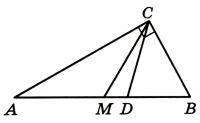
Угол между биссектрисой CD и медианой CM проведёнными из вершины прямого угла C треугольника ABC, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
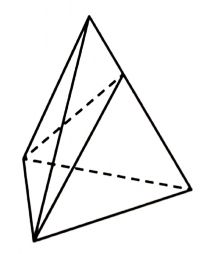
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шашистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шашистом из России.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Найдите корень уравнения (log_4{2^{5x+7}}=3).
Найдите значение выражения (dfrac{a^{3{,}33}}{a^{2{,}11}cdot a^{2{,}22}}) при (a=dfrac{2}{7}).
Прямая (y=9x+6) является касательной к графику (y=ax^2-19x+13). Найдите (a).
Расстояние от наблюдателя, находящегося на высоте (h) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле (l=sqrt{dfrac{Rh}{500}}), где (R = 6400) км − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Первый садовый насос перекачивает 10 литров воды за 5 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литров воды?
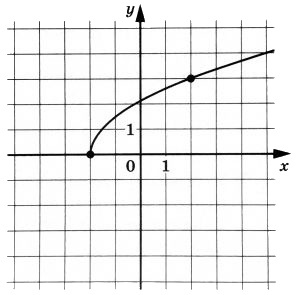
На рисунке изображен график функции (f(x)=ksqrt{x+p}). Найдите (f(0{,}25)).
Найдите наибольшее значение функции (y=2x^2-12x+8ln{x}-5) на отрезке (left[dfrac{12}{13};dfrac{14}{13}right]).
а) Решите уравнение (7cos{x}-4cos^3{x}=2sqrt{3}sin{2x}).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-4pi;-3piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -4π | 18. -23π/6 | 19. -15π/4 | 20. -11π/3 |
| 21. -7π/2 | 22. -10π/3 | 23. -13π/4 | 24. -19π/6 |
| 25. -3π |
Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=2AC.
Решите неравенство (log^2_{5}{left(x^4right)}-28log_{0{,}04}{left(x^2right)}leqslant 8).
Производство (x) тыс. единиц продуктции обходится в (q=3x^2+6x+13) млн рублей в год. При цене (p) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px-q). При каком наименьшем значении (p) через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении (x)?
Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A1CB1, A1BC1 и B1AC1 пересекаются в одной точке.
б) Известно, что AB=AC=17 и BC=16. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} left(x-a+3right)^2+left(y+a-2right)^2=a+dfrac{7}{2}, x-y=a-1 end{cases})имеет единственное решение.
Для действительного числа (x) обозначим через (left[xright]) наибольшее целое число, не превосходящее (x). Например, (left[dfrac{11}{4}right]=2), так как (2leqslantdfrac{11}{4}<3).
а) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{9}right]=n)?
б) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{5}right]=n+2)?
в) Сколько существует различных натуральных (n), для которых (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{8}right]+left[dfrac{n}{23}right]=n+2021)?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
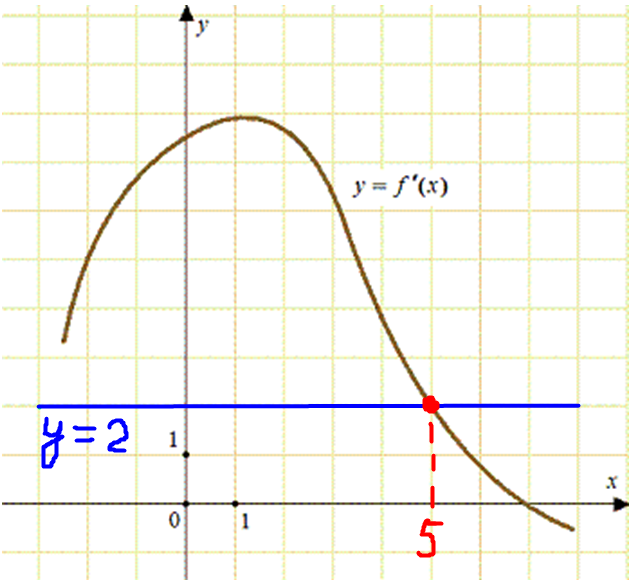
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 10
Задача 10. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)). Найдите абсциссу точки, в которой касательная к графику (y = fleft( x right)) параллельна прямой (y = 2x — 2) или совпадает с ней.
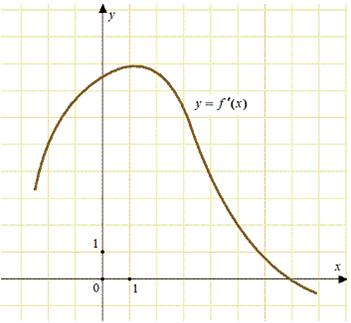
ОТВЕТ: 5.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой (y = 2x — 2) или совпадает с ней, то их угловые коэффициенты равны 2 (коэффициент перед x). Следовательно, необходимо найти точку, в которой (f’left( {{x_0}} right) = 2). Этому соответствует точка пересечения графика производной с прямой (y = 2). Это точка 5 (выделена красным цветом см. рисунок).
Ответ: 5.
Комментарии для сайта Cackle
Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы
Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности
Стереометрия на ЕГЭ по математике присутствует и в 1 части, и во второй. Чтобы решать задачи, для начала надо выучить формулы. Все они есть в наших таблицах:
- Куб, параллелепипед, призма, пирамида. Объем и площадь поверхности
- Цилиндр, конус, шар. Объем и площадь поверхности
Часто в задачах ЕГЭ, посвященных стереометрии, требуется посчитать объем тела или площадь его поверхности. Или как-то использовать эти данные. Поэтому заглянем в толковый словарь русского языка и уточним понятия.
Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар).
Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины», «грани» и «ребра». Вот они, на картинке.
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма», правильная призма», «правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Перейдем к практике.
1. Одна из распространенных задач в части 1 — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького. Получаем: 
А как быть с площадью поверхности? Почему-то многие школьники пытаются посчитать ее по аналогии с объемом, как разность площадей большого и малого «кирпичей». В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется? 
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна 
. А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна 
.
А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна 
! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна . Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.
Ответ: .
2. Следующую задачу, попроще, вы теперь решите без труда. Здесь тоже надо найти площадь поверхности многогранника:
. Из площади поверхности «целого кирпича» вычитаем площади двух квадратиков со стороной 
— на верхней и нижней гранях.
Ответ: 92.
3. А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму».
Ответ: 
.
Следующий тип задач — когда одно объемное тело вписано в другое.
4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна 
, высота равна , объем равен .
Ответ: 4.
5. В основании прямой призмы лежит прямоугольный треугольник с катетами 
и 
. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. В ответ запишите 
.
Очевидно, высота цилиндра равна боковому ребру призмы, то есть . Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна 
. Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ: 
.
Ответ: 100.
6. В прямоугольный параллелепипед вписан шар радиуса . Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: .
Следующий тип задач — такие, в которых увеличили или уменьшили какой-либо линейный размер (или размеры) объемного тела. А узнать нужно, как изменится объем или площадь поверхности.
7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 
см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 
раза больше, чем у первого? Ответ выразите в сантиметрах.
Слова «другой такой же сосуд» означают, что другой сосуд тоже имеет форму правильной треугольной призмы. То есть в его основании — правильный треугольник, у которого все стороны в два раза больше, чем у первого. Мы уже говорили о том, что площадь этого треугольника будет больше в раза. Объем воды остался неизменным. Следовательно, в раза уменьшится высота.
Ответ: 
.
8. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.
Давайте вспомним, как мы решали стандартные задачи, на движение и работу. Мы рисовали таблицу, верно? И здесь тоже нарисуем таблицу. Мы помним, что объем цилиндра равен 
.
| Высота | Радиус | Объем | |
| Первая кружка |  |
 |
|
| Вторая кружка |  |
 |
 |
Считаем объем второй кружки. Он равен 
. Получается, что он в два раза больше, чем объем первой.
Следующая задача тоже решается сразу и без формул.
9. Через среднюю линию основания треугольной призмы, объем которой равен 
, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Высота меньшей призмы такая же, как и у большой. А какой же будет ее площадь основания? Очевидно, в раза меньше. Вспомните свойство средней линии треугольника — она равна половине основания. Значит, объем отсеченной призмы равен .
И еще одна классическая задача. Никаких формул!
10. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раза?
Только не надо обмирать от ужаса при слове «октаэдр». Тем более — он здесь нарисован и представляет собой две сложенные вместе четырехугольные пирамиды. А мы уже говорили — если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в 
раз, поскольку 
.
Ответ: .
Следующий тип задач — такие, в которых надо найти объем части конуса, или части пирамиды. Они тоже решаются элементарно.
11. Найдите объем части цилиндра, изображенной на рисунке. Радиус цилиндра равен 15, высота равна 5. В ответе укажите .
Изображен не целый цилиндр, а его часть. Из него, как из круглого сыра, вырезали кусок. Надо найти объем оставшегося «сыра».
Какая же часть цилиндра изображена? Вырезан кусок с углом 
градусов, а 
— это одна шестая часть полного круга. Значит, от всего объема цилиндра осталось пять шестых. Находим объем всего цилиндра, умножаем на пять шестых, делим на 
, записываем ответ: 
.
Продолжение: другие типы задач по стереометрии. Удачи вам в подготовке к ЕГЭ!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023