Решу егэ математика 508983

Задания

Версия для печати и копирования в MS Word

Тип 10 № 508983

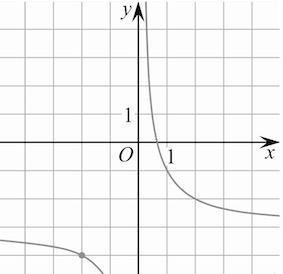
На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка =dfrackx плюс a . Найдите значение x, при котором f левая круглая скобка x правая круглая скобка =0,2.

Спрятать решение

Решение.

График функции имеет вертикальную асимптоту x  =  −1, значит, a  =  1. По графику f(2)  =  1, тогда дробь: числитель: k, знаменатель: 2 плюс 1 конец дроби =1 равносильно k=3. Таким образом,

дробь: числитель: 3, знаменатель: x плюс 1 конец дроби =0,2 равносильно 0,2x=2,8 равносильно x=14.

Ответ: 14.

Аналоги к заданию № 508961: 508983 508962 508963 508964 508965 508966 508967 508968 508969 508970 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Спрятать решение

·

Прототип задания

·

·

Сообщить об ошибке · Помощь

Источник

Каталог заданий.
Гиперболы


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 10 № 508951

На рисунке изображён график функции f левая круглая скобка x правая круглая скобка =dfrackx плюс a. Найдите f левая круглая скобка минус 12 правая круглая скобка .

Аналоги к заданию № 508951: 508971 508952 508953 508954 508955 508956 508957 508958 508959 508960 … Все

Источник: А. Ларин: Тренировочный вариант № 110.

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

2

Тип 10 № 508961

На рисунке изображён график функции f левая круглая скобка x правая круглая скобка =dfrackx плюс a. Найдите, при каком значении x значение функции равно 0,8.

Аналоги к заданию № 508961: 508983 508962 508963 508964 508965 508966 508967 508968 508969 508970 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

3

Тип 10 № 564197

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: a, знаменатель: x плюс b конец дроби плюс c, где числа a, b и c  — целые. Найдите f левая круглая скобка 13 правая круглая скобка .

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

4

Тип 10 № 564198

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: a, знаменатель: x плюс b конец дроби плюс c, где числа a, b и c  — целые. Найдите f левая круглая скобка 9 правая круглая скобка .

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

5

Тип 10 № 564199

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: a, знаменатель: x плюс b конец дроби плюс c, где числа a, b и c  — целые. Найдите f левая круглая скобка минус 13 правая круглая скобка .

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

·

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Skip to content

ЕГЭ Профиль №9. Гиперболаadmin2022-08-17T23:36:10+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Гипербола

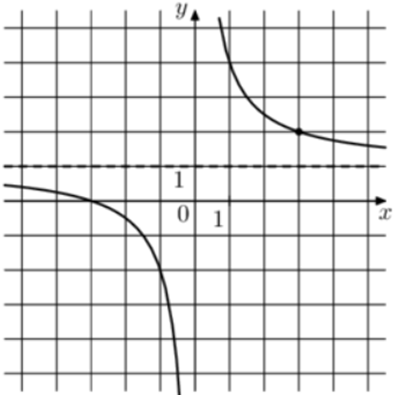
Задача 1. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)   Найдите  (fleft( { — 12} right).)

Ответ

ОТВЕТ: 0,75.
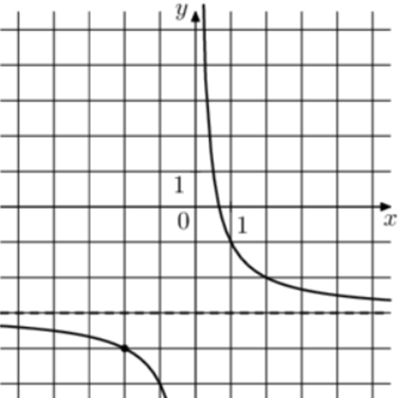
Задача 2. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {50} right).)

Ответ

ОТВЕТ: — 2,96.
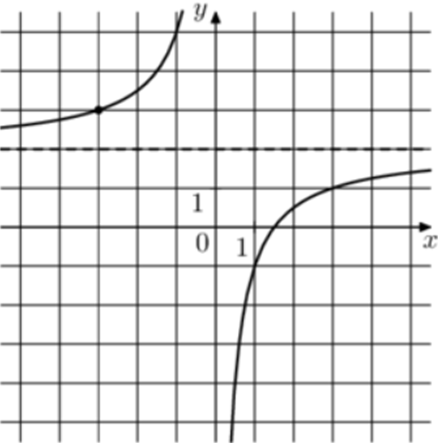
Задача 3. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {7,5} right).)

Ответ

ОТВЕТ: 1,6.
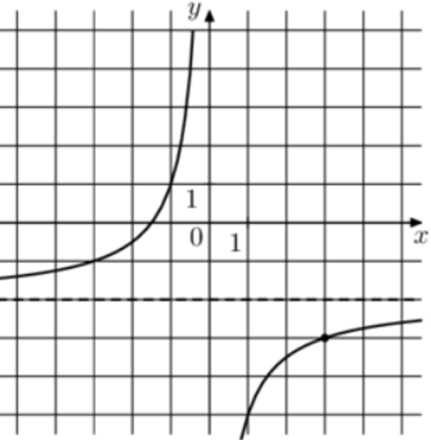
Задача 4. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {0,25} right).)

Ответ

ОТВЕТ: — 14.
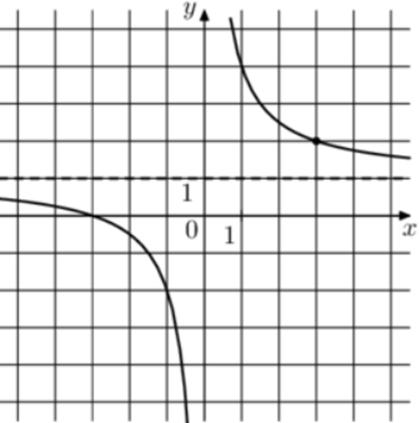
Задача 5. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 0,8.

Ответ

ОТВЕТ: — 15.
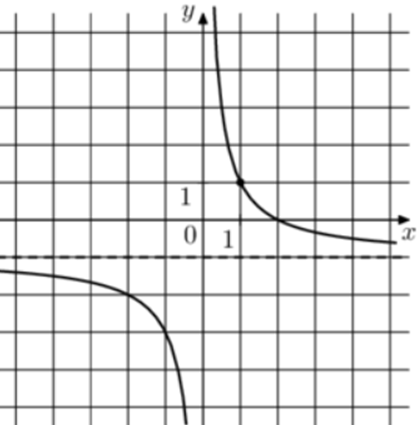
Задача 6. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 19.

Ответ

ОТВЕТ: 0,1.
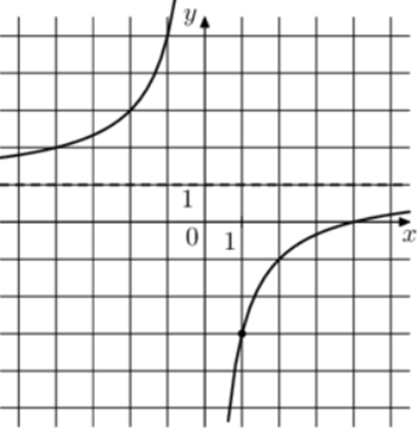
Задача 7. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 0,75.

Ответ

ОТВЕТ: 16.
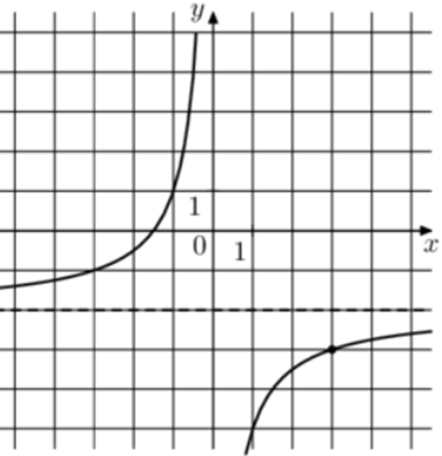
Задача 8. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно ( — 9,5.)

Ответ

ОТВЕТ: 0,4.
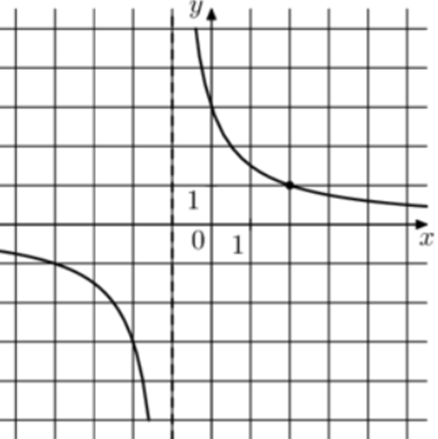
Задача 9. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {19} right).)

Ответ

ОТВЕТ: 0,15.
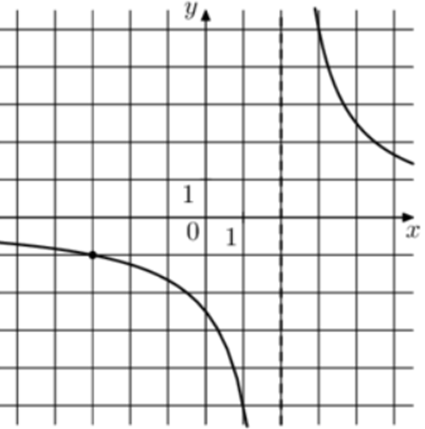
Задача 10. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( { — 4frac{2}{3}} right).)

Ответ

ОТВЕТ: — 0,75.
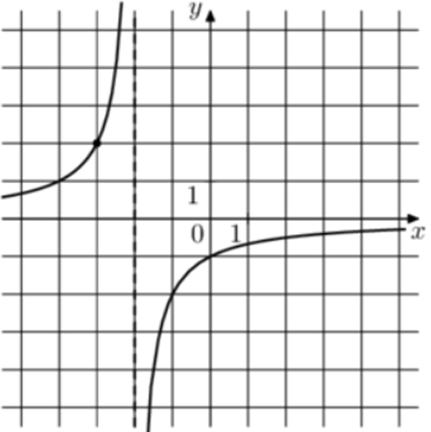
Задача 11. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {18} right).)

Ответ

ОТВЕТ: — 0,1.
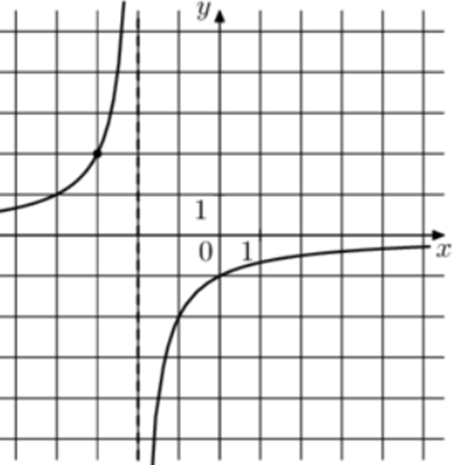
Задача 12. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {6frac{1}{3}} right).)

Ответ

ОТВЕТ: — 0,24.
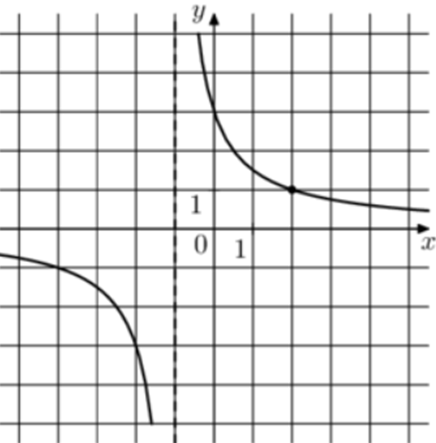
Задача 13. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) = 0,2.)

Ответ

ОТВЕТ: 14.
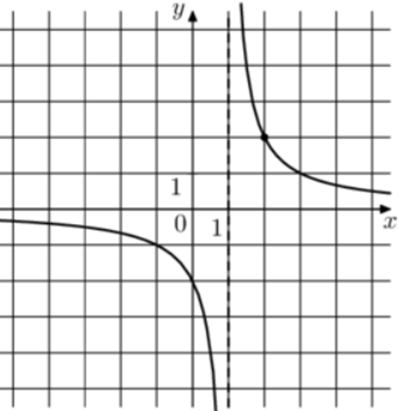
Задача 14. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) =  — 0,08.)

Ответ

ОТВЕТ: — 24.
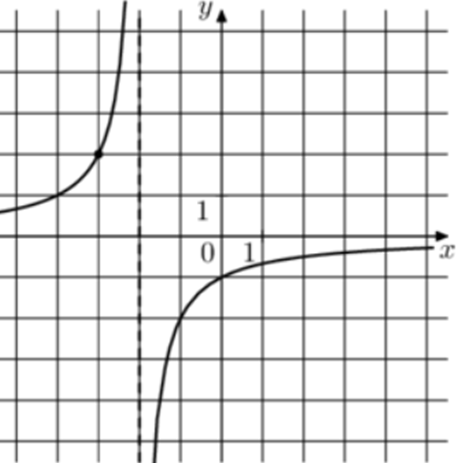
Задача 15. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) =  — 0,04.)

Ответ

ОТВЕТ: 48.
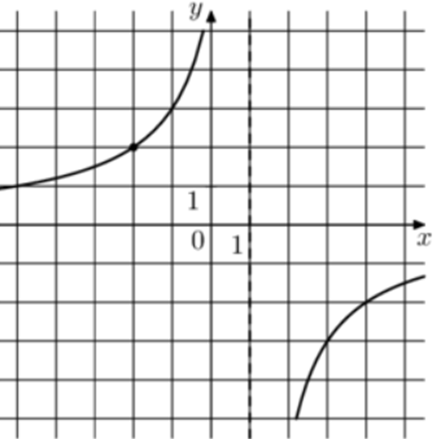
Задача 16. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) = 0,2.)

Ответ

ОТВЕТ: — 29.
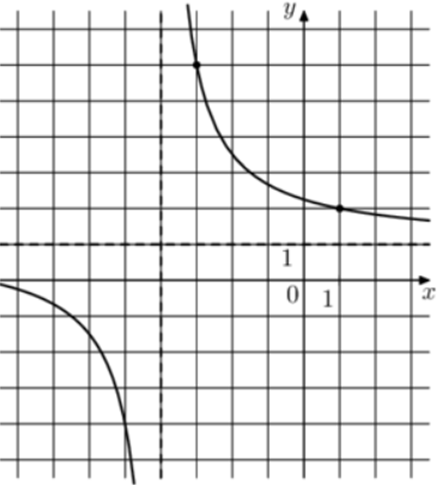
Задача 17. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: 1.
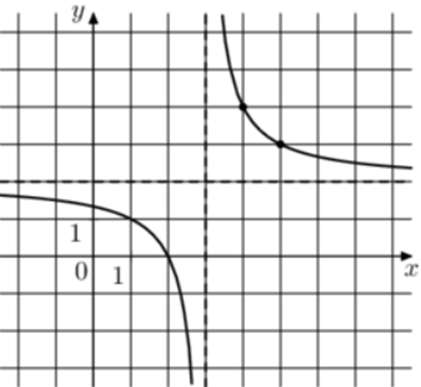
Задача 18. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: 2.
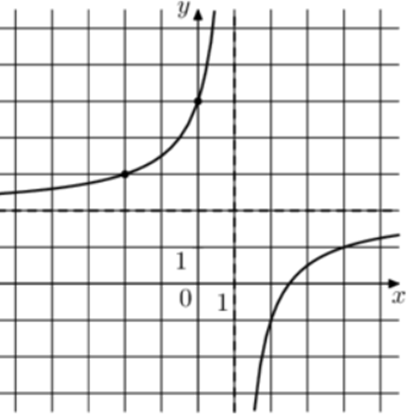
Задача 19. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: 2.
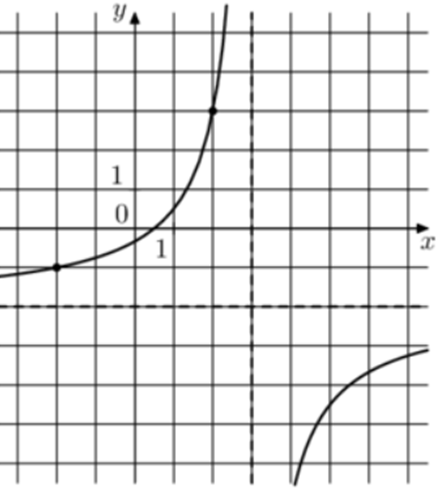
Задача 20. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k.

Ответ

ОТВЕТ: — 2.
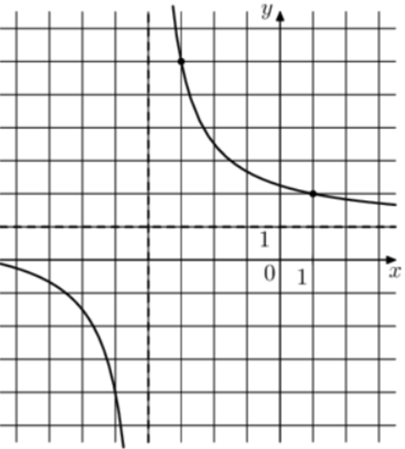
Задача 21. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: 9.
Задача 22. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: — 4.
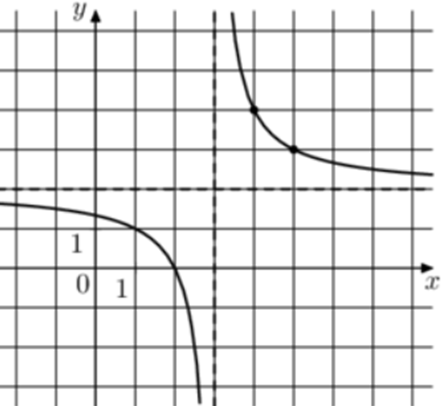Задача 23. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: 1.
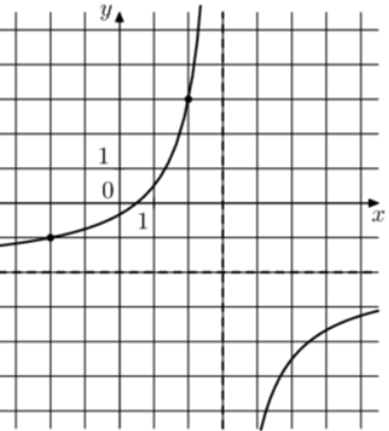Задача 24. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a.

Ответ

ОТВЕТ: — 5.
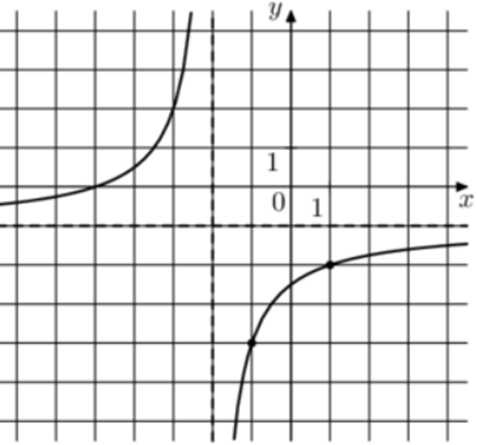Задача 25. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 0,2.
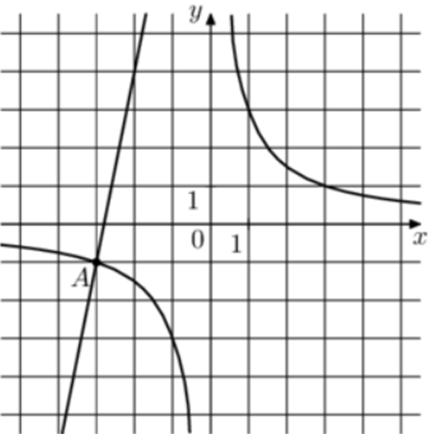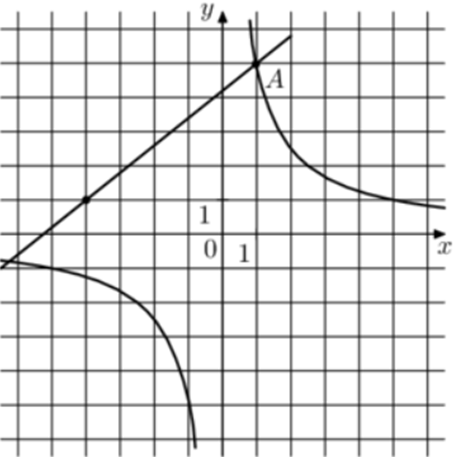
Задача 26. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 6,25.
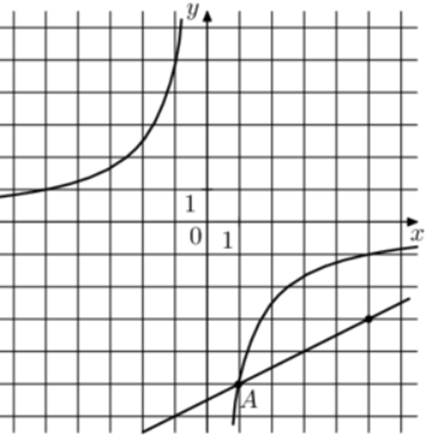
Задача 27. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 10.
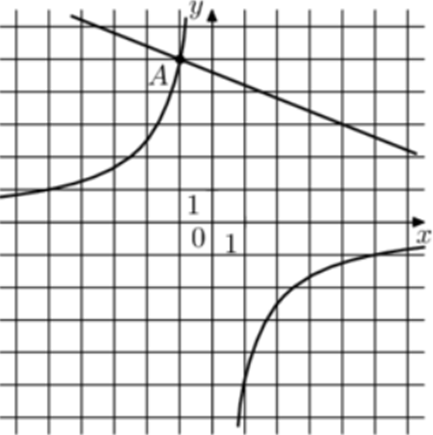
Задача 28. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 12,5.
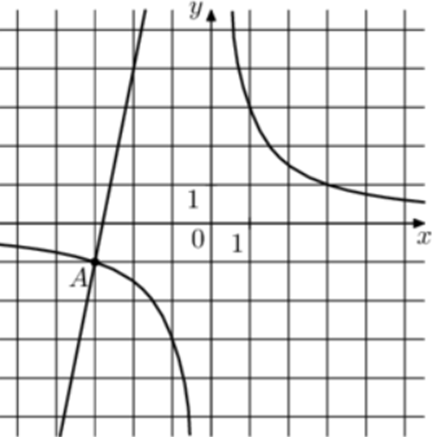
Задача 29. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 15.
Задача 30. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 16.
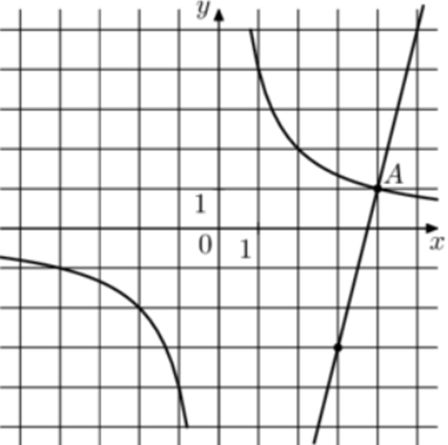Задача 31. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 0,4.
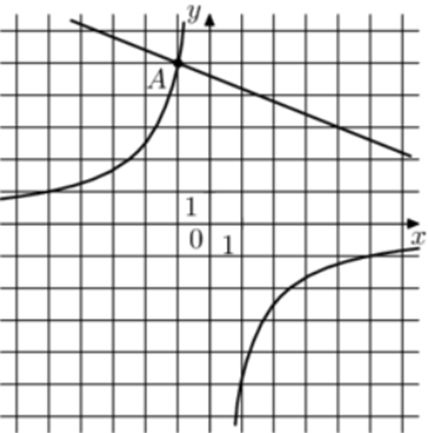Задача 32. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 0,5.

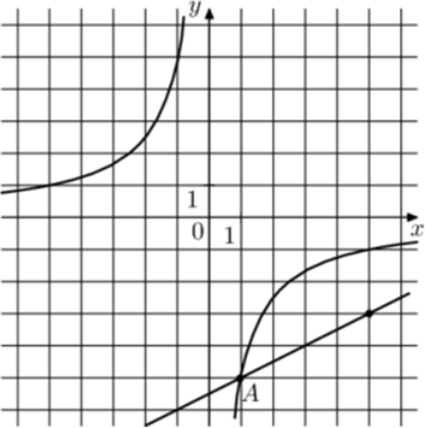09
Янв 2022

Категория: 10 Графики функций

2022-01-09
2022-09-11

Задача 1. На рисунке изображён график функции f(x)=frac{k}{x}+a.  Найдите f(50). 

Решение: + показать

Задача 2. На рисунке изображён график функции вида f(x)=frac{a}{x+b}+c,  где числа a,b и c — целые. Найдите значение x, при котором f(x)=2,5.

Решение: + показать

Задача 3. На рисунке изображён график функции  вида f(x)=frac{a}{x+b}+c, где a,b,c – целые числа.  Найдите f(frac{8}{3}).

Решение: + показать

Задача 4. На рисунке изображён график функции f(x)=frac{kx+a}{x+b}.  Найдите a.

Решение: + показать

Задача 5. На рисунке изображены графики функций f(x)=frac{k}{x}  и g(x)=ax+b и  которые пересекаются в точках A и B. Найдите ординату точки B.

Решение: + показать

Вы можете пройти тест “Гиперболы”

Автор: egeMax |

Нет комментариев

ЕГЭ 2022 ПРОФИЛЬНАЯ МАТЕМАТИКА РАЗБОР ЗАДАНИЯ №9
В этом уроке мы обсудим, как решать задание №9 на гиперболы.

Основные ссылки:
Группа Вконтакте: https://vk.com/path_in_math
Получать уведомления о вебинарах(рассылка Вконтакте): https://vk.com/app5898182_-199426423#…
Есть идеи или предложения? Связаться со мной можно по почте: pathmath2022@gmail.com
Или написать в сообщения группы Вконтакте: https://vk.com/path_in_math

Таймкоды:
00:00 кто убил path in math
01:15 стандартная гипербола
03:18 смещения гиперболы
08:16 практика по смещениям, строим гиперболу
13:44 решаем задание №9
18:28 как поддержать выход видеороликов
18:43 вопрос тысячелетия

Видео Задание №9 на ГИПЕРБОЛЫ. Подробный разбор. Профильная математика ЕГЭ 2022. канала PATH IN MATH: Математика — ЕГЭ, ОГЭ, ОЛИМПИАДЫ

Показать

ЕГЭ по математике профиль

Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.

Для успешного результата необходимо уметь выполнять действия с функциями.

Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы

Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:

3.3.1 Линейная функция, её график

3.3.2  Функция, описывающая обратную пропорциональную зависимость, её график

3.3.3 Квадратичная функция, её график

3.3.4 Степенная функция с натуральным показателем, её график

3.3.5 Тригонометрические функции, их графики

3.3.6 Показательная функция, её график

3.3.7 Логарифмическая функция, её график

Уметь выполнять действия с функциями:  определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:

При отработке данного задания будут полезны книги:

Графики функций ЕГЭ математика профиль

Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля

Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств

Связанные страницы:

верхняя шапка

картинка

MATHM
>>
ЕГЭ
>>
ЕГЭ профиль

>>

Задача 9

картинка

ЗАДАЧА 9
сортировка
по темам

СПИСОК ТЕМ

Тема 1: График параболы
Тема 2: График гиперболы и корня
Тема 3: График модуля
Тема 4: Графики тригонометрических функций
Тема 5: График показательной функции и логарифма
Тема 6: Пересечение графиков

Задачи разделены на темы. Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.

Тема 1: График параболы.

  1. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-12).

    2. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  2. На рисунке изображен график функции вида 𝑓𝑥=𝑎𝑥2+𝑏𝑥−𝑐, где числа 𝑎,𝑏 и 𝑐 – целые. Найдите 𝑓(6).

    3. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  3. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-8).

    4. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  4. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(18).

    5. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  5. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-16).

    6. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  6. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(8).

    7. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  7. На рисунке изображен график функции вида f(x)=〖a(x+1)〗^2+bx+c, где числа a,b и c – целые. Найдите f(-12).

    8. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  8. На рисунке изображен график функции вида f(x)=〖a(x-2)〗^2+b(x+1)+c, где числа a,b и c – целые. Найдите f(-15).

    9. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  9. На рисунке изображен график функции вида f(x)=〖a(x-4)〗^2+b(x+3)+c, где числа a,b и c – целые. Найдите f(-12).

    10. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  10. На рисунке изображен график функции вида f(x)=〖ax〗^2+bx+c, где числа a,b и c – целые. Найдите f(-18).

    11. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  11. На рисунке изображен график функции вида f(x)=x^2/a+bx+c, где числа a,b и c – целые. Найдите f(-12).

    12. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

  12. На рисунке изображен график функции вида 𝑓𝑥=𝑥2𝑎+𝑏𝑥+𝑐, где числа 𝑎,𝑏 и 𝑐 – целые. Найдите 𝑓(20).

    13. посмотреть ответ

    посмотреть решение 1

    посмотреть решение 2

    видеоурок 1 по графику параболы

    yotube

    видеоурок 2 по графику параболы

    yotube

Тема 2: График гиперболы и корня.

  1. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(-14).

    2. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  2. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(12).

    3. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  3. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(15).

    4. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  4. На рисунке изображен график функции вида f(x)=a/(x+b)+c, где числа a,b и c – целые. Найдите f(20).

    5. посмотреть ответ

    посмотреть решение

    видеоурок по графику гиперболы

    yotube

  5. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(160).

    6. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  6. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(399).

    7. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  7. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(-1056).

    8. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  8. На рисунке изображен график функции вида f(x)=√(ax+b)+c, где числа a,b и c – целые. Найдите f(-895).

    9. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  9. На рисунке изображен график функции вида f(x)=-√(ax+b)+c, где числа a,b и c – целые. Найдите f(-1056).

    10. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

  10. На рисунке изображен график функции вида f(x)=-√(ax+b)+c, где числа a,b и c – целые. Найдите f(720).

    11. посмотреть ответ

    посмотреть решение

    видеоурок по графику корня

    yotube

Тема 3: График модуля.

  1. На рисунке изображен график функции вида f(x)=|ax+b|+c, где числа a,b и c – целые. Найдите f(88).

    2. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

  2. На рисунке изображен график функции вида f(x)=|ax+b|+c, где числа a,b и c – целые. Найдите f(-56).

    3. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

  3. На рисунке изображен график функции вида f(x)=-|ax+b|+c, где числа a,b и c – целые. Найдите f(81).

    4. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

  4. На рисунке изображен график функции вида f(x)=-|ax+b|+c, где числа a,b и c – целые. Найдите f(-23).

    5. посмотреть ответ

    посмотреть решение

    видеоурок по графику модуля

    yotube

Тема 4: Графики тригонометрических функций.

  1. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(10/3).

    2. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  2. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(-11/3).

    3. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  3. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(19/3).

    4. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  4. На рисунке изображен график функции вида f(x)=〖a∙cos〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(-22/3).

    5. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  5. На рисунке изображен график функции вида f(x)=〖a∙sin〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(23/6).

    6. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

  6. На рисунке изображен график функции вида f(x)=〖a∙sin〗⁡(bπx)+c, где числа a,b и c – целые. Найдите f(23/6).

    7. посмотреть ответ

    посмотреть решение

    видеоурок 1 по графикам тригонометрических функций

    yotube

    видеоурок 2 по графикам тригонометрических функций

    yotube

Тема 5: График показательной функции и логарифма.

  1. На рисунке изображен график функции вида f(x)=2^(ax+b)+c, где числа a,b и c – целые. Найдите f(4).

    2. посмотреть ответ

    посмотреть решение

  2. На рисунке изображен график функции вида f(x)=3^(ax+b)+c, где числа a,b и c – целые. Найдите f(3).

    3. посмотреть ответ

    посмотреть решение

  3. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(510).

    4. посмотреть ответ

    посмотреть решение

  4. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(257).

    5. посмотреть ответ

    посмотреть решение

  5. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(244).

    6. посмотреть ответ

    посмотреть решение

  6. На рисунке изображен график функции вида f(x)=log_4⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(65).

    7. посмотреть ответ

    посмотреть решение

  7. На рисунке изображен график функции вида f(x)=log_2⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-130).

    8. посмотреть ответ

    посмотреть решение

  8. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-84).

    9. посмотреть ответ

    посмотреть решение

Тема 6: Пересечение графиков.

  1. На рисунке изображен график функции вида f(x)=2^(ax+b)+c, где числа a,b и c – целые. Найдите f(4).

    2. посмотреть ответ

    посмотреть решение

  2. На рисунке изображен график функции вида f(x)=3^(ax+b)+c, где числа a,b и c – целые. Найдите f(3).

    3. посмотреть ответ

    посмотреть решение

  3. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(510).

    4. посмотреть ответ

    посмотреть решение

  4. На рисунке изображен график функции вида f(x)=log_2⁡(x+b)+c, где числа b и c – целые. Найдите f(257).

    5. посмотреть ответ

    посмотреть решение

  5. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(244).

    6. посмотреть ответ

    посмотреть решение

  6. На рисунке изображен график функции вида f(x)=log_4⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(65).

    7. посмотреть ответ

    посмотреть решение

  7. На рисунке изображен график функции вида f(x)=log_2⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-130).

    8. посмотреть ответ

    посмотреть решение

  8. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-84).

    9. посмотреть ответ

    посмотреть решение

  9. На рисунке изображен график функции вида f(x)=log_3⁡(ax+b)+c, где числа a,b и c – целые. Найдите f(-84).

    10. посмотреть ответ

    посмотреть решение

нижняя шапка

29 декабря 2021

В закладки

Обсудить

Жалоба

В версии ЕГЭ-2022 по математике появилось новое 9 задание, в котором требуется работа с функциями.

Эта тема пока вызывает затруднения у учащихся в связи со своей новизной. В презентации представлены решения задач с использованием линейной и квадратичной функций. Некоторые задачи решены 3 способами, чтобы учащиеся смогли выбрать наиболее понятный для себя.

ege9new.pptx
ege9new.pdf

Автор: Лесных Марина Владимировна.

Тест «Витамины»

Проверочная работа по биологии в 8 классе.

Консультация по физике

Онлайн-трансляция по вопросам подготовки к ЕГЭ по физике.

Sorry, your request has been denied.

Решу ЕГЭ 2022 задание №9 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки к экзамену.

  • скачать задания прямая с ответами
  • скачать задания парабола с ответами
  • скачать задания гипербола с ответами
  • скачать задания логарифмические функции с ответами
  • скачать задания иррациональные функции с ответами
  • скачать задания тригонометрические функции с ответами

Решу ЕГЭ 2022 линейные функции 9 задание математика с ответами:

Решу ЕГЭ 2022 парабола 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 гипербола 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 логарифмические функции 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 иррациональные функции 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 тригонометрические функции 9 задание профиль математика с ответами:

Как формулируется новое задание 9 ЕГЭ 2022 по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Как решать 9 задание ЕГЭ 2022 математика профиль видео теория:

1)На рисунке изображён график функции вида f(x)= a3x+b x+c , где числа a, b и c — целые. Найдите a.

2)На рисунке изображён график функции вида f(x)= 2ax+b x+c , где числа a, b и c — целые. Найдите a.

3)На рисунке изображён график функции вида f(x)= ax+b x+c , где числа a, b и c — целые. Найдите a.

4)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(−22).

5)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите решение уравнения f(x)=18.

6)На рисунке изображён график функции вида f(x)= 2ax+b x+c , где числа a, b и c — целые. Найдите a.

7)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(15).

8)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите x, при котором f(x)=21.

9)На рисунке изображён график функции вида f(x)=log5(ax+b)+c, где числа a, b, c  — целые. Найдите наибольшее значение функции g(x)=−x2+ax+b.

10)На рисунке изображён график функции вида f(x)=log1.4(x−a)+b, где числа a, b  — целые. Найдите ab.

11)На рисунке изображён график функции вида f(x)=2ax+b, где числа a, b  — целые. Найдите сумму коэффициентов a+b, если f(1)=10.

12)На рисунке изображён график функции вида f(x)=log2(ax+b)+2, где числа a, b  — целые. Найдите сумму коэффициентов a+b.

13)На рисунке изображён график функции вида f(x)=ln(a+x)+b, где числа a, b  — целые. Найдите сумму коэффициентов a+b, если A(0;ln2e).

Задание №3 ЕГЭ 2022 по математике профиль прототипы с ответами

Задание №4 ЕГЭ 2022 по математике профиль прототипы с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

  • Cайты учителей
  • Все блоги
  • Все файлы
  • Все тесты
  • Мои уведомления
    1
  • Войти
  • Зарегистрироваться / Создать сайт

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 31.01.2022 15:49

Бабошкина Любовь Юрьевна

Учитель математики

66 лет

рейтинг1 728
место23 187

09.11.2021 20:48

Нажмите, чтобы узнать подробности

В презентации разбирается один из способов решения задания №9 ЕГЭ (гиперболы)

Просмотр содержимого документа

«Графики функции. Задание №9 ЕГЭ-2022»

Графики функций Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама

Графики функций

Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама

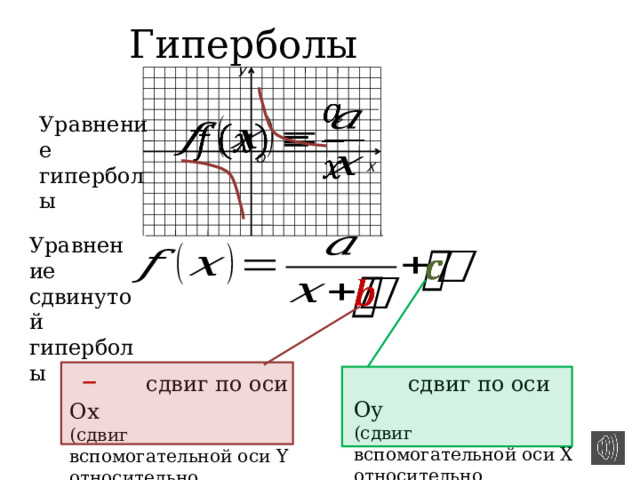
Гиперболы У   Уравнение гиперболы О Х   Уравнение сдвинутой гиперболы     – сдвиг по оси Ох (сдвиг вспомогательной оси Y относительно основной) сдвиг по оси Оу (сдвиг вспомогательной оси Х относительно основной)

Гиперболы

У

Уравнение гиперболы

О

Х

Уравнение

сдвинутой

гиперболы

– сдвиг по оси Ох

(сдвиг вспомогательной оси Y относительно основной)

сдвиг по оси Оу

(сдвиг вспомогательной оси Х относительно основной)

y 1 Пример   f(13). Решение c x 1 (2;1) – b 1) - b = 3, b = - 3 2) c = 2   3)     - уравнение заданной гиперболы   Ответ: 2,1

y 1

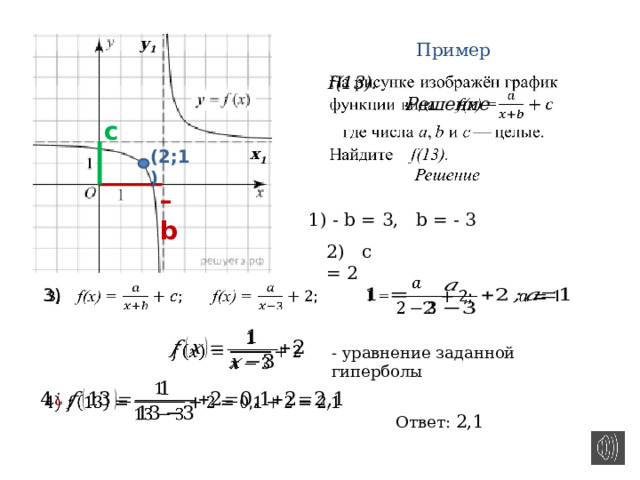
Пример

f(13).

Решение

c

x 1

(2;1)

– b

1) — b = 3, b = — 3

2) c = 2

3)

— уравнение заданной гиперболы

Ответ: 2,1

Рекомендуем курсы ПК и ППК для учителей

Похожие файлы

Источник

Решу егэ профиль математика 517739

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Задание 12 № 517747

Ответ а 3 и 27; б 3.

Ege. sdamgia. ru

12.01.2020 13:48:01

2020-01-12 13:48:01

Источники:

Https://ege. sdamgia. ru/test? likes=517739

Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Б Заметим, что Значит, указанному отрезку принадлежит корень 3.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Dankonoy. com

16.06.2020 6:45:22

2020-06-16 06:45:22

Источники:

Https://dankonoy. com/ege/ege11/archives/10087

Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Материал для подготовки к экзамену по математике 1 курс

Материал для подготовки к экзамену по математике 1 курс.

нажмите, чтобы узнать подробности

Материал для подготовки к экзамену по математике для 1 курса СПО.

Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»

Логарифмические уравнения

1. Задание 5 № 26646

Найдите корень уравнения

2. Задание 5 № 26647

Найдите корень уравнения

3. Задание 5 № 26648

Найдите корень уравнения

4. Задание 5 № 26649

Найдите корень уравнения

5. Задание 5 № 26657

Найдите корень уравнения

6. Задание 5 № 26658

Найдите корень уравнения

7. Задание 5 № 26659

Найдите корень уравнения

8. Задание 5 № 77380

Решите уравнение

9. Задание 5 № 77381

Решите уравнение

10. Задание 5 № 77382

Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

11. Задание 5 № 315120

Найдите корень уравнения

12. Задание 5 № 315535

Найдите корень уравнения

13. Задание 5 № 525399

Решите уравнение

Тригонометрические уравнения

1. Задание 5 № 26669

Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.


Значениям соответствуют положительные корни.

Если, то и

Если, то и

Значениям соответствуют меньшие значения корней.

Следовательно, наибольшим отрицательным корнем является число

2. Задание 5 № 77376

Решите уравнение В ответе напишите наибольший отрицательный корень.

Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.

3. Задание 5 № 77377

Решите уравнение В ответе напишите наименьший положительный корень.

Значениям соответствуют отрицательные корни.

Если, то и

Если, то и

Значениям соответствуют большие положительные корни.

Наименьшим положительным решением является 0,5.

Преобразования числовых логарифмических выражений

1. Задание 9 № 26843

Найдите значение выражения

2. Задание 9 № 26844

Найдите значение выражения

3. Задание 9 № 26845

Найдите значение выражения

4. Задание 9 № 26846

Найдите значение выражения

5. Задание 9 № 26847

Найдите значение выражения

6. Задание 9 № 26848

Найдите значение выражения

7. Задание 9 № 26849

Найдите значение выражения

8. Задание 9 № 26850

Найдите значение выражения

9. Задание 9 № 26851

Найдите значение выражения

10. Задание 9 № 26852

Найдите значение выражения

11. Задание 9 № 26853

Найдите значение выражения

12. Задание 9 № 26854

Найдите значение выражения

13. Задание 9 № 26855

Найдите значение выражения

14. Задание 9 № 26856

Найдите значение выражения

15. Задание 9 № 26857

Найдите значение выражения

16. Задание 9 № 26858

Найдите значение выражения

17. Задание 9 № 26859

Найдите значение выражения

18. Задание 9 № 26860

Найдите значение выражения

19. Задание 9 № 26861

Найдите значение выражения

20. Задание 9 № 26862

Найдите значение выражения

21. Задание 9 № 26882

Найдите значение выражения

22. Задание 9 № 26883

Найдите значение выражения

23. Задание 9 № 26885

Найдите значение выражения

24. Задание 9 № 26889

Найдите значение выражения

25. Задание 9 № 26892

Найдите значение выражения

26. Задание 9 № 26893

Найдите значение выражения

27. Задание 9 № 26894

Найдите значение выражения

28. Задание 9 № 26896

Найдите значение выражения

29. Задание 9 № 77418

Вычислите значение выражения:

30. Задание 9 № 505097

Найдите значение выражения

31. Задание 9 № 509086

Найдите значение выражения

32. Задание 9 № 510939

Найдите значение выражения

33. Задание 9 № 525403

Найдите значение выражения

Вычисление значений тригонометрических выражений

1. Задание 9 № 26775

Найдите, если и

2. Задание 9 № 26776

Найдите, если и

3. Задание 9 № 26777

Найдите, если и

4. Задание 9 № 26778

Найдите, если и

5. Задание 9 № 26779

Найдите, если

6. Задание 9 № 26780

Найдите, если

7. Задание 9 № 26783

Найдите значение выражения, если

8. Задание 9 № 26784

Найдите, если и

9. Задание 9 № 26785

Найдите, если и

10. Задание 9 № 26786

Найдите, если

11. Задание 9 № 26787

Найдите, если

12. Задание 9 № 26788

Найдите, если

13. Задание 9 № 26789

Найдите, если

14. Задание 9 № 26790

Найдите, если

15. Задание 9 № 26791

Найдите, если

16. Задание 9 № 26792

Найдите значение выражения, если

17. Задание 9 № 26793

Найдите значение выражения, если

18. Задание 9 № 26794

Найдите, если

19. Задание 9 № 316350

Найдите, если

20. Задание 9 № 501598

Найдите значение выражения

21. Задание 9 № 502014

Найдите значение выражения

22. Задание 9 № 502045

Найдите значение выражения

23. Задание 9 № 502106

Найдите значение выражения

24. Задание 9 № 502285

Найдите значение выражения

25. Задание 9 № 502305

Найдите значение выражения если и

26. Задание 9 № 504410

Найдите значение выражения:

27. Задание 9 № 504824

Найдите значение выражения

28. Задание 9 № 508966

Найдите если

29. Задание 9 № 510424

Найдите если и

30. Задание 9 № 549336

Найдите если и

Преобразования числовых тригонометрических выражений

1. Задание 9 № 26755

Найдите значение выражения

2. Задание 9 № 26756

Найдите значение выражения

3. Задание 9 № 26757

Найдите значение выражения

4. Задание 9 № 26758

Найдите значение выражения

5. Задание 9 № 26759

Найдите значение выражения

6. Задание 9 № 26760

Найдите значение выражения

7. Задание 9 № 26761

Найдите значение выражения

8. Задание 9 № 26762

Найдите значение выражения

9. Задание 9 № 26763

Найдите значение выражения

10. Задание 9 № 26764

Найдите значение выражения

11. Задание 9 № 26765

Найдите значение выражения

12. Задание 9 № 26766

Найдите значение выражения

13. Задание 9 № 26767

Найдите значение выражения

14. Задание 9 № 26769

Найдите значение выражения

15. Задание 9 № 26770

Найдите значение выражения

16. Задание 9 № 26771

Найдите значение выражения

17. Задание 9 № 26772

Найдите значение выражения

18. Задание 9 № 26773

Найдите значение выражения

19. Задание 9 № 26774

Найдите значение выражения

20. Задание 9 № 77412

Найдите значение выражения

21. Задание 9 № 77413

Найдите значение выражения

22. Задание 9 № 77414

Найдите значение выражения:

23. Задание 9 № 245169

Найдите значение выражения

24. Задание 9 № 245170

Найдите значение выражения

25. Задание 9 № 245171

Найдите значение выражения

26. Задание 9 № 245172

Найдите значение выражения

27. Задание 9 № 501701

Найдите значение выражения

28. Задание 9 № 502994

Найдите значение выражения

29. Задание 9 № 503310

Найдите значения выражения

30. Задание 9 № 510013

Найдите если и

31. Задание 9 № 510312

Найдите значение выражения

32. Задание 9 № 510386

Найдите значение выражения

33. Задание 9 № 510405

Найдите значение выражения

34. Задание 9 № 510824

Найдите значение выражения

35. Задание 9 № 510843

Найдите значение выражения

36. Задание 9 № 525113

Найдите значение выражения

37. Задание 9 № 526009

Найдите значение выражения

Ло­га­риф­ми­че­ские и по­ка­за­тель­ные уравнения

1. Задание 13 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

2. Задание 13 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

3. Задание 13 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

4. Задание 13 № 516760

А) Решите уравнение:

Б) Определите, какие из его корней принадлежат отрезку

5. Задание 13 № 514623

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

6. Задание 13 № 502053

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

7. Задание 13 № 525377

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

8. Задание 13 № 513605

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

9. Задание 13 № 503127

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

10. Задание 13 № 514081

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащего отрезку

11. Задание 13 № 502999

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].

12. Задание 13 № 528517

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

13. Задание 13 № 550261

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие промежутку

14. Задание 13 № 555265

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

15. Задание 13 № 555583

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

16. Задание 13 № 561853

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].

17. Задание 13 № 562032

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

18. Задание 13 № 562757

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение В ответе напишите наименьший положительный корень.

Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»

Б Укажите корни этого уравнения, принадлежащие отрезку.

Multiurok. ru

06.02.2020 18:29:01

2020-02-06 18:29:01

Источники:

Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html

Источник

  • ЗАДАЧИ ЕГЭ С ОТВЕТАМИ

  • АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

  • РубрикиРубрики
  • Задачи по номерам!

    №1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16

  • МЕТКИ

    БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие

  • ОСТЕОХОНДРОЗУ-НЕТ!

Источник

Положительное вещественное
шестизначное

число 508983
является составным числом.
Является полупростым число.
33 — сумма всех цифр данного числа.
4 — количество делителей у числа.
Сумма делителей: 678648.
Обратное число к 508983 – это 0.0000019647021609759067.

Перевод числа в другие системы счисления:
двоичная система счисления: 1111100010000110111, троичная система счисления: 221212012020, восьмеричная система счисления: 1742067, шестнадцатеричная система счисления: 7C437.
В числе байт 508983 содержится 497 килобайтов 55 байтов информации.

Азбука Морзе для числа: ….. —— —.. —-. —.. …—

Косинус 508983: 0.5337, тангенс 508983: 1.5845, синус 508983: 0.8457.
Натуральный логарифм числа: 13.1402.
Логарифм десятичный числа: 5.7067.
713.4304 — корень квадратный из числа 508983, 79.8426 — корень кубический.
Число в квадрате это 2.5906e+11.

Число секунд 508983 можно представить как 5 дней 21 час 23 минуты 3 секунды .
Нумерологическое цифра числа 508983 — 6.

Источник

Ранее, счета за холодную воду приходили отдельно от других коммунальных услуг.

В Санкт-Петербурге было внесено изменение в систему оплаты коммунальных услуг, и теперь жители могут оплачивать свои счета за холодную воду в рамках единой квитанции за ЖКУ. Ранее, счета за холодную воду приходили отдельно от других коммунальных услуг, что иногда приводило к затруднениям и путанице у жителей города.

Это изменение внесено с целью упростить процесс оплаты коммунальных услуг и уменьшить количество счетов, которые должны получать жители. В настоящее время, жители Санкт-Петербурга могут оплачивать все свои коммунальные счета в одной единой квитанции, что существенно облегчает процесс оплаты и снижает вероятность ошибок.

Также, это изменение поможет уменьшить количество неплатежей за коммунальные услуги, так как жители смогут лучше контролировать свои расходы на ЖКУ и, возможно, смогут легче оплачивать свои счета вовремя. В целом, внедрение единой квитанции за ЖКУ в Санкт-Петербурге является положительным шагом в упрощении и улучшении процесса оплаты коммунальных услуг для жителей города.

#Марина Цурикова#2#Общество#Город и горожане

Источник

Новые тренировочные варианты в формате решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ЕГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.

  • Тренировочный вариант №41054170 с ответами

  • Тренировочный вариант №41054171 с ответами

  • Тренировочный вариант №41054172 с ответами

  • Тренировочный вариант №41054173 с ответами

  • Тренировочный вариант №41054174 с ответами

  • Тренировочный вариант №41054175 с ответами

  • Тренировочный вариант №41054176 с ответами

  • Тренировочный вариант №41054177 с ответами

  • Тренировочный вариант №41054178 с ответами

  • Тренировочный вариант №41054179 с ответами

  • Тренировочный вариант №41054180 с ответами

  • Тренировочный вариант №41054181 с ответами

  • Тренировочный вариант №41054182 с ответами

  • Тренировочный вариант №41054183 с ответами

  • Тренировочный вариант №41054184 с ответами

Другие тренировочные варианты ЕГЭ 2022 по математике:

Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами

Пробный вариант ЕГЭ 2022 №211004 по математике 11 класс с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Решу егэ математика 508911
  • Решу егэ математика 508895
  • Решу егэ математика 508795
  • Решу егэ математика 508791
  • Решу егэ математика 508770

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии