Решите неравенство:
Спрятать решение
Решение.
Преобразуем неравенство:
Пусть тогда неравенство примет вид:
Рассмотрим два случая. Первый случай:
Второй случай:
Решение неравенства:
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-14

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
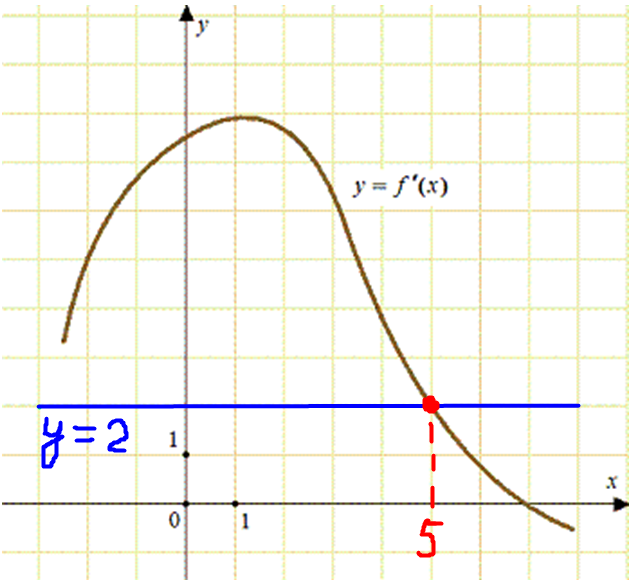
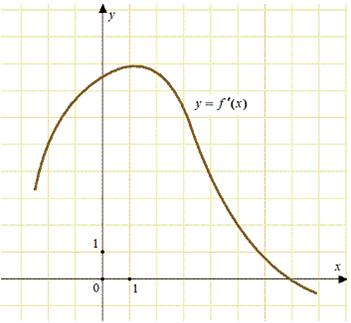
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 10
ОТВЕТ: 5.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой (y = 2x — 2) или совпадает с ней, то их угловые коэффициенты равны 2 (коэффициент перед x). Следовательно, необходимо найти точку, в которой (f’left( {{x_0}} right) = 2). Этому соответствует точка пересечения графика производной с прямой (y = 2). Это точка 5 (выделена красным цветом см. рисунок).
Ответ: 5.
Комментарии для сайта Cackle
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 14 № 508380
Воспользуемся тем, что для суммы возможны четыре случая раскрытия модулей, откуда заключаем:
Приведем другое решение:
Как и в первом решении запишем неравенство в виде:
Заметим, что левая часть представляет из себя кусочно-линейную функцию, которая возрастает при и убывает при Это означает, что в точке –3 она достигает минимума равного 5. Таким образом, правая часть Тогда неравенство принимает вид:
Задание 14 № 508380
—>
508780 решу егэ математика.
Ege. sdamgia. ru
07.03.2017 0:00:13
2017-03-07 00:00:13
Источники:
Https://ege. sdamgia. ru/problem? id=508380
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508781
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?
Задание 10 № 508782
Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?
Задание 10 № 508783
Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508784
Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508785
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508786
Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508787
Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508788
Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508789
Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508790
Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508786
Задание 10 № 508781
Задание 10 508786.
Ege. sdamgia. ru
14.05.2019 20:28:53
2019-05-14 20:28:53
Источники:
Https://ege. sdamgia. ru/test? likes=508780
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508780
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:
Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:
Приведем решение Ирины Шраго.
Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей
—>
Задание 10 № 508780
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege. sdamgia. ru
09.08.2017 16:57:34
2017-08-09 16:57:34
Источники:
Https://ege. sdamgia. ru/problem? id=508780
В подборке вам будут доступно 12 веб-сайтов и видеолекций, которые помогут подготовится к ЕГЭ по математике. Статья актуальна для тех кто выбрал базовый и профильный уровень.
Привет! На связи «Сотка»
Онлайн-школа подготовки к ЕГЭ по математике👇
Ниже вы увидите список из 14 ссылок.
Нажмите на ссылку, чтобы узнать подробнее.
Нажмите кнопку «назад» в браузере, чтобы вернутся к списку.
- Введение
Сайты:
- Sdamgia
- Yandex
- Alexlarin
- Egemaximum
- Uchportal
- Math-prosto
- Aplusclick
- Bymath
- Problems
Видео:
- @Getaclassmath
- @User-rb8ux1no6j
- @ValeryVolkov
Бонус:
- Веб-ресурсы по другим предметам
ЕГЭ математика: введение
ЕГЭ по математике – это стандартное тестирование, который проводится Рособрнадзором — государственным учреждением, отвечающим за надзор в области образования и науки в России. ЕГЭ предназначен для школьников, которые собираются поступать в вузы.
На ЕГЭ по математике есть множество сложных заданий, связанных с алгеброй и геометрией. Результаты экзамена ЕГЭ по математике оценивают уровень знаний и навыков учеников, а также их способность применять математический опыт и решать практические задачи.
ЕГЭ математика: сайты
- Sdamgia.ru – веб-сайт для подготовки к ЕГЭ по математике. Он содержит более 10 000 видеолекций по математике, а также различные инструменты для упражнений и тестирования.
Самым полезным инструментом на площадке является онлайн-тестирование, которое помогает ученикам проверить свои знания и умения, а также привыкнуть к формату ЕГЭ по математике. Пользователи могут выбрать тип теста (стандартный тест, тест по годам, симуляция ЕГЭ) и режим (без ограничений по времени, с ограничением по времени и другие) . Результаты тестирования показываются сразу же после его окончания, что позволяет оценить свой уровень подготовки и выявить слабые места.
На площадке также есть раздел с видеоуроками по теме «ЕГЭ математика», которые помогут ученикам лучше понимать теорию.
ЕГЭ математика | Sdamgia.ru
- Yandex.ru/tutor – платформа предназначена для подготовки к ЕГЭ по математике. На этом веб-ресурсе доступны разнообразные материалы, включая видеоуроки, тесты и другие обучающие материалы, помогающие в изучении математики.
На платформе имеется раздел, посвященный ЕГЭ по математике. Там можно найти уроки для ЕГЭ по математике. Каждый урок сопровождается подробным решением, что позволяет ученикам лучше понимать, как решать задачи и готовиться к ЕГЭ по математике.
На платформе также есть раздел «Тренировки», где ученики могут выбрать уровень сложности. После тестирования результаты будут анализироваться, и ученикам будут предложены рекомендации для дальнейшей подготовки.
Портал также содержит материалы по теории математики, которые помогут ученикам понимать основные концепции и принципы. Эти материалы включают видеоуроки, теоретические статьи и другие образовательные материалы.
ЕГЭ математика | Yandex.ru/tutor
- Alexlarin.net – платформа, представленная на данном сайте, создана для того, чтобы помочь в подготовке к ЕГЭ по математике.
Здесь вы найдете разнообразные обучающие материалы, такие как видеоуроки, тесты, уроки и консультации с опытными преподавателями. Все материалы разбиты на темы.
ЕГЭ математика | Alexlarin.net
- Egemaximum.ru – это отличный портал для всех, кто интересуется темой «ЕГЭ математика». Он занимает четвертое место в списке 12 сайтов, которые мы рекомендуем.
Веб-ресурс удобно организован и легок в использовании. Материалы разбиты на темы и категории, что позволяет быстро находить нужный материал и начинать работу с ним.
Одно из основных преимуществ Egemaximum — это наличие большого количества практических задач. Это позволяет ученикам не только узнать теорию, но и закрепить полученные знания на практике. Кроме того, на площадке вы найдете онлайн-тесты и возможность проверить свои знания в режиме реального времени.
ЕГЭ математика | Egemaximum.ru
- Uchportal.ru – это полезная площадка для тех, кто готовится к ЕГЭ по математике. Здесь вы найдете теоретические материалы, тесты и примеры решения задач.
На веб-ресурсе есть возможность проходить онлайн-тесты, которые позволяют оценить свои знания по каждой теме и подготовиться к ЕГЭ по математике. Также на площадке вы можете найти полезные ссылки на другие ресурсы, которые помогут вам лучше подготовиться к экзамену ЕГЭ по математике.
ЕГЭ математика | Uchportal.ru
- Math-prosto.ru – это веб-портал для тех, кто готовится к ЕГЭ по математике. Одним из главных преимуществ ресурса является то, что на нем представлена большая база задач с подробными решениями. Здесь вы найдете разнообразные задачи, которые позволяют ознакомиться с различными видами задач, которые могут встретиться на экзамене. Также на сайте представлены материалы по всем темам, которые содержат необходимые теоретические сведения и примеры решения задач.
Еще одно преимущество Math-prosto — это удобная система тестирования. Здесь вы можете проходить тесты по разным темам математики и оценивать свой уровень знаний, а также выявлять слабые места, на которые нужно обратить особое внимание.
ЕГЭ математика | Math-prosto.ru
- Aplusclick.org – это интерактивный веб-ресурс с математическими головоломками и задачами для учеников всех возрастов. Он может быть полезен для тех, кто готовится к ЕГЭ по математике.
Площадка содержит более 2000 интерактивных задач и головоломок по математике, которые разделены по уровню сложности и темам.
Одним из главных преимуществ Aplusclick является его интерактивный формат. Задачи часто содержат интерактивные элементы, которые позволяют ученикам более глубоко погрузиться в материал и лучше понимать его. Также интерактивные курсы могут быть более интересными и увлекательными для учеников, что может помочь им улучшить мотивацию к изучению математики.
ЕГЭ математика | Aplusclick.org
- Bymath.net – это онлайн-ресурс, который предлагает материалы и упражнения для учеников и студентов по математике. Он может быть полезен для тех, кто готовится к ЕГЭ по математике, так как здесь представлены различные тесты.
На онлайн-ресурсе представлены материалы по различным темам математики. Вы найдете здесь теорию, примеры и упражнения, которые помогут лучше понять материал. Кроме того, сайт предлагает тесты, которые помогут проверить ваши знания.
Один из главных плюсов Bymath – это его простой и удобный интерфейс.
ЕГЭ математика | Bymath.net
- Problems.ru – интерактивный портал для решения математических задач. На ресурсе можно найти широкий спектр математических задач, в том числе по теме «ЕГЭ математика».
Данный ресурс является бесплатным и не требует регистрации. Пользователи могут выбирать задания в зависимости от уровня сложности, темы и типа задачи. Кроме того, на площадке представлены тесты для проверки уровня знаний.
ЕГЭ математика | Problems.ru
ЕГЭ математика: лекции на Youtube
- @getaclassmath – это канал на YouTube, предоставляющий обучающие математические видеоуроки для школьников. На канале вы найдете различные видеоуроки по математике, в том числе для подготовки к Единому государственному экзамену (ЕГЭ) по математике.
Плейлист «Математика для ЕГЭ» на канале «Get a Class Math» содержит 58 видеоуроков, которые охватывают всю математику, необходимую для сдачи экзамена.
ЕГЭ математика | GetAClass
- @user-rb8ux1no6j – это канал на Ютубе, который ориентирован на тему «ЕГЭ математика». Ресурс создан командой преподавателей математики и разработчиков, которые стараются сделать обучение математике интересным и доступным.
На канале можно найти много видеолекций по темам, которые часто встречаются на ЕГЭ по математике. Видео покрывают все разделы математики, начиная от алгебры и геометрии и заканчивая математической статистикой.
Особенностью канала является то, что в каждом видеоуроке авторы стараются объяснить тему максимально доступно и просто, используя примеры из реальной жизни и задачи, которые могут встретиться на ЕГЭ.
ЕГЭ математика | Маткульт-привет!
- @ValeryVolkov – образовательный канал на Ютуб, посвящен в основном подготовке к ЕГЭ по математике. Он содержит множество видеоуроков, которые помогают ученикам изучать математику и успешно сдавать экзамен.
На канале вы найдете множество различных видеоуроков по темам, которые входят в программу ЕГЭ по математике. Эти видеоуроки разработаны квалифицированными преподавателями математики и являются интерактивными и наглядными.
Кроме того, на канале вы найдете множество практических лекций, которые помогут вам закрепить полученные знания и подготовиться к ЕГЭ по математике.
ЕГЭ математика | Канал Валерия Волкова
Веб-ресурсы по другим предметам
Подготовка к ЕГЭ: 139 бесплатных сайтов
В статье вы найдете 139 бесплатных ресурсов для подготовки к ЕГЭ по следующим предметам: математика, русский язык, обществознание, информатика, физика, английский язык, литература, химия, биология. Статья регулярно обновляется — добавляйте в закладки.
Курсы ЕГЭ: 33 бесплатных сайта
Статья содержит информацию о курсах ЕГЭ по различным предметам, включая: литературу, математику, химию, русский язык, обществознание, информатику, физику, английский язык и биологию. Все курсы ЕГЭ являются бесплатными. Материал регулярно обновляется — сохраняйте в закладки.
Курсы ЕГЭ | youtube.com/c/devinf74
ЕГЭ 2023: расписание, изменения, бесплатные лекции
В статье вы найдете всю необходимую информацию по теме ЕГЭ 2023: расписание, баллы, изменения, а также бесплатные ресурсы для подготовки по любому предмету. Статья регулярно обновляется, поэтому смело добавляйте ее в Закладки.
🗣Понимаем, что это не полный список полезных веб-ресурсов для ЕГЭ по математике, поэтому будет рады, если вы напишите свои рекомендации в комментариях👇
Вариант МА2210301 и ответы
Скачать ответы и
решения для вариантов
1.
Каждый день во время конференции расходуется 60 пакетиковчая.
Конференция длится 9 дней. В пачке чая 50 пакетиков. Какого наименьшего
количества пачек чая хватит на все дни конференции?
2.
Установите соответствие между величинами и их
возможнымизначениями: к каждому элементу первого столбца подберите
соответствующий элемент из второго столбца.
3.
В таблице показано расписание пригородных электропоездовпо
направлению Москва Курская – Крутое – Петушки. Владислав пришёл на станцию
Москва Курская в 18:20 и хочет уехать в Петушки на электропоезде без пересадок.
Найдите номер ближайшего электропоезда, который ему подходит.
5. В коробке вперемешку лежат чайные пакетики с
чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в 4
раза больше, чем пакетиков с зелёным. Найдите вероятность того, что случайно
выбранный из этой коробки пакетик окажется пакетиком с чёрным чаем.
8.
Некоторые учащиеся 10-х классов школы ходили в апреле наспектакль
«Гроза». В мае некоторые десятиклассники пойдут на постановку по пьесе
«Бесприданница», причём среди них не будет тех, кто ходил в апреле на спектакль
«Гроза». Выберите утверждения, которые будут верны при указанных условиях
независимо от того, кто из десятиклассников пойдёт на постановку по пьесе
«Бесприданница».
●
1) Каждый учащийся 10-х классов, который не ходил на спектакль
«Гроза», пойдёт на постановку по пьесе «Бесприданница».
●
2) Нет ни одного десятиклассника, который ходил на спектакль
«Гроза» и пойдёт на постановку по пьесе «Бесприданница».
●
3) Среди учащихся 10-х классов этой школы, которые не пойдут на
постановку по пьесе «Бесприданница», есть хотя бы один, который ходил на
спектакль «Гроза».
●
4) Найдётся десятиклассник, который не ходил на спектакль «Гроза»
и не пойдёт на постановку по пьесе «Бесприданница».
9.
На фрагменте географической карты схематично изображеныграницы
деревни Покровское и очертания озёр (площадь одной клетки равна одному
гектару). Оцените приближённо площадь озера Малого. Ответ дайте в гектарах с
округлением до целого значения.
10.
Диагональ прямоугольного экрана ноутбука равна 40 см, аширина
экрана ― 32 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
11.
Пирамида Снофру имеет форму правильной четырёхугольнойпирамиды,
сторона основания которой равна 220 м, а высота — 104 м. Сторона основания
точной музейной копии этой пирамиды равна 55 см. Найдите высоту музейной копии.
Ответ дайте в сантиметрах.
12.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°
, угол ABC равен 106° . Найдите угол ACB . Ответ дайте в градусах.
13.
Даны два цилиндра. Радиус основания и высота первогоцилиндра
равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго
цилиндра больше объёма первого?
15. В школе мальчики составляют 55 % от числа всех
учащихся. Сколько в этой школе мальчиков, если их на 50 человек больше, чем
девочек?
19.
Цифры четырёхзначного числа, кратного 5, записали вобратном
порядке и получили второе четырёхзначное число. Затем из исходного числа вычли
второе и получили 3366. В ответе укажите какое-нибудь одно такое исходное
число.
20.
Имеется два сплава. Первый содержит 45 % никеля, второй —5 %
никеля. Из этих двух сплавов получили третий сплав, содержащий 15 % никеля.
Масса первого сплава равна 40 кг. На сколько килограммов масса первого сплава
была меньше массы второго?
21.
Прямоугольник разбит на четыре меньших прямоугольникадвумя
прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и
далее по часовой стрелке, равны 2, 3 и 18. Найдите периметр четвёртого
прямоугольника.
Вариант МА2210305 и ответы
Скачать ответы и
решения для вариантов
1. Для покраски 1 кв. м потолка требуется 230 г
краски. Краска продаётся в банках по 2 кг. Какое наименьшее количество банок
краски нужно для покраски потолка площадью 44 кв. м?
3. В таблице представлены налоговые ставки на
автомобили в Москве с 1 января 2013 года. Какова налоговая ставка (в рублях за
1 л. с. в год) на автомобиль мощностью 115 л. с.?
5.
Помещение освещается двумя лампами. Вероятностьперегорания одной
лампы в течение года равна 0,3. Найдите вероятность того, что в течение года
обе лампы перегорят.
6.
В таблице даны результаты олимпиад по русскому языку ибиологии в
9 «А» классе. Похвальные грамоты дают тем школьникам, у кого суммарный балл по
двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60
баллов. Укажите номера учащихся 9 «А» класса, набравших меньше 60 баллов по
русскому языку и получивших похвальные грамоты, без пробелов, запятых и других
дополнительных символов.
7.
На рисунке изображены график функции и касательные,проведённые к
нему в точках с абсциссами A, B, C и D. В правом столбце указаны значения
производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в
соответствие каждой точке значение производной функции в ней.
8.
Некоторые учащиеся 10-х классов школы ходили в ноябре наоперу
«Евгений Онегин». В марте некоторые десятиклассники пойдут на оперу «Руслан и
Людмила», причём среди них не будет тех, кто ходил в ноябре на оперу «Евгений
Онегин». Выберите утверждения, которые будут верны при указанных условиях независимо
от того, кто из десятиклассников пойдёт на оперу «Руслан и Людмила».
●
1) Каждый учащийся 10-х классов, который не ходил на оперу
«Евгений Онегин», пойдёт на оперу «Руслан и Людмила».
●
2) Нет ни одного десятиклассника, который ходил на оперу «Евгений
Онегин» и пойдёт на оперу «Руслан и Людмила».
●
3) Найдётся десятиклассник, который не ходил на оперу
«Евгений Онегин» и не пойдёт на оперу «Руслан и
Людмила».
●
4) Среди учащихся 10-х классов этой школы, которые не пойдут на
оперу «Руслан и Людмила», есть хотя бы один, который ходил на оперу «Евгений
Онегин».
9.
План местности разбит на клетки. Каждая клетка обозначаетквадрат
1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных
метрах.
10.
Пожарную лестницу длиной 10 м приставили к окну дома.Нижний конец
лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец
лестницы? Ответ дайте в метрах.
11.
Прямолинейный участок трубы длиной 4 м, имеющей всечении
окружность, необходимо покрасить снаружи (торцы трубы открыты, их красить не
нужно). Найдите площадь поверхности, которую необходимо покрасить, если внешний
обхват трубы равен 19 см. Ответ дайте в квадратных сантиметрах.
12.
В треугольнике ABC стороны AC и BC равны. Внешний угол при
вершине B равен 146° . Найдите угол C. Ответ дайте в градусах.
13.
Даны два шара радиусами 4 и 2. Во сколько раз объёмбольшего шара
больше объёма меньшего?
15. Число больных гриппом в школе уменьшилось за
месяц в пять раз. На сколько процентов уменьшилось число больных гриппом?
19.
Найдите пятизначное число, кратное 15, любые две соседниецифры
которого отличаются на 3. В ответе укажите какое-нибудь одно такое число.
20.
Теплоход, скорость которого в неподвижной воде равна 19 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт
теплоход возвращается через 43 часа после отправления из него. Сколько
километров проходит теплоход за весь рейс?
21.
На кольцевой дороге расположены четыре бензоколонки: А, Б,В и Г.
Расстояние между А и Б — 55 км, между А и В — 40 км, между В и Г — 40 км, между
Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей
дуге). Найдите расстояние (в километрах) между Б и В.
Вариант МА2210309 и ответы
Скачать ответы и
решения для вариантов
2.
Прямоугольный параллелепипед описан около цилиндра,радиус
основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту
цилиндра.
3.
В группе 16 человек, среди них — Анна и Татьяна. Группуслучайным
образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность
того, что Анна и Татьяна окажутся в одной подгруппе.
4.
Агрофирма закупает куриные яйца только в двух домашниххозяйствах.
Известно, что 40 % яиц из первого хозяйства — яйца высшей категории, а из
второго хозяйства — 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей
категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы,
окажется из первого хозяйства.
9. Пристани A и B расположены на озере, расстояние
между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На
следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч
больше прежней, сделав по пути остановку на 8 часов. В результате она затратила
на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость
баржи на пути из A в B. Ответ дайте в км/ч.
13. Основанием правильной пирамиды PABCD является
квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD
перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра
пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если AB
= 30.
15.
По вкладу «А» банк в конце каждого года планируетувеличивать на
13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать
эту сумму на 7 % в первый год и на целое число n процентов за второй год.
Найдите наименьшее значение n , при котором за два года хранения вклад «Б»
окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16.
В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M
. Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б)
Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22 .
18. У Ани есть 800 рублей. Ей нужно купить конверты
(большие и маленькие). Большой конверт стоит 32 рубля, а маленький — 25 рублей.
При этом число маленьких конвертов не должно отличаться от числа больших
конвертов больше чем на пять. а) Может ли Аня купить 24 конверта? б) Может ли
Аня купить 29 конвертов? в) Какое наибольшее число конвертов может купить Аня?
Вариант МА2210311 и ответы
Скачать ответы и
решения для вариантов
1.
Найдите периметр прямоугольника, если его площадь равна 12,а
отношение соседних сторон равно 1:3.
2.
Шар вписан в цилиндр. Площадь полной поверхностицилиндра равна
78. Найдите площадь поверхности шара.
3.
В магазине в среднем из 120 сумок 15 имеют скрытые
дефекты.Найдите вероятность того, что выбранная в магазине сумка окажется со
скрытыми дефектами.
4.
Игральный кубик бросают дважды. Известно, что в суммевыпало 11
очков. Найдите вероятность того, что во второй раз выпало 5 очков.
9. Игорь и Паша, работая вместе, могут покрасить
забор за 40 часов. Паша и Володя, работая вместе, могут покрасить этот же забор
за 48 часов, а Володя и Игорь, работая вместе, — за 60 часов. За сколько часов
мальчики покрасят забор, работая втроём?
13. Основанием правильной пирамиды PABCD является
квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD
перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра
пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если
AB = 24 .
15.
По вкладу «А» банк в конце каждого года планируетувеличивать на
11 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать
эту сумму на 7 % в первый год и на целое число n процентов за второй год.
Найдите наименьшее значение n , при котором за два года хранения вклад «Б»
окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16.
В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M
. Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б)
Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 18.
18. У Ани есть 400 рублей. Ей нужно купить конверты
(большие и маленькие). Большой конверт стоит 22 рубля, а маленький — 17 рублей.
При этом число маленьких конвертов не должно отличаться от числа больших
конвертов больше чем на пять. а) Может ли Аня купить 19 конвертов? б) Может ли
Аня купить 23 конверта? в) Какое наибольшее число конвертов может купить Аня?
Скачать ответы и
решения для вариантов
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
Раскроем скобки.
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$
$х=-{17}/{5}$
$х = — 3,4$
Ответ: $- 3,4$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
$x = 0; ax + b = 0$
2. Решаем получившиеся уравнения каждое отдельно.
Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$
$4х^2 — 5х = 0$
Вынесем х как общий множитель за скобки:
$х (4х — 5) = 0$
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
$ax^2 + c = 0$
$ax^2 = — c$
$x_2 = {-c}/{a}$
При решении последнего уравнения возможны два случая:
если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$
если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.
$x^2 — 16 = 0$
$x^2 = 16$
$x = ±4$
Ответ: $х_1 = 4, х_2 = — 4$
Решение полного квадратного уравнения
Решение с помощью дискриминанта
Дискриминантом квадратного уравнения D называется выражение
$b^2 — 4ac$.
При решении уравнения с помощью дискриминанта возможны три случая:
1. $D > 0$. Тогда корни уравнения равны:
$x_{1,2}={-b±√D}/{2a}$
2. $D = 0$. В данном случае решение даёт два двукратных корня:
$x_{1}=x_{2}={-b}/{2a}$
3. $D < 0$. В этом случае уравнение не имеет корней.
$3х^2 — 11 = -8х$
Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней
$3х^2 + 8х — 11 = 0$
$a = 3 ,b = 8, c = — 11$
$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$
$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$
$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$
Ответ: $x_1=1, x_2=-3{2}/{3}$
Устные способы
Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$
$4х^2+ 3х — 7 = 0$
$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$
Ответ: $х_1= 1, х_2 = -{7}/{4}$
Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$
$5х^2+ 7х + 2 = 0$
$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$
Ответ: $х_1= -1, х_2 = -{2}/{5}$
Кубические уравнения
Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.
$(x — 3)^3 = 27$
Представим обе части как основания в третьей степени
$(x — 3)^3 = $33
Извлечем кубический корень из обеих частей
$х — 3 = 3$
Соберем известные слагаемые в правой части
$x = 6$
Ответ: $х = 6$
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
$4x + 1 — {3}/{x} = 0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x + 1 — {3}/{x}= 0¦· x$
$4x · x + 1 · x — {3·x}/{x} = 0$
3. решаем полученное уравнение
$4x^2 + x — 3 = 0$
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = {3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = {3}/{4}$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$
${3х-5}/{-2}={1}/{х}$
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х (3х — 5) = -2$
Раскроем скобки и соберем все слагаемые в левой части уравнения
$3х^2- 5х + 2 = 0$
Решим данное квадратное уравнение первым устным способом, т.к.
$a + b + c = 0$
$x_1 = 1, x_2 = {2}/{3}$
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1 = 1, x_2 = {2}/{3}$
Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.
Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.
Например,
${2}/{x}+5x=7$ – рациональное уравнение
$3x+√x=7$ — иррациональное уравнение (содержит корень)
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль общий знаменатель.
Решить уравнение: $4x+1-{3}/{x}=0$
Решение:
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x ≠ 0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x+1-{3}/{x}=0|·x$
$4x·x+1·x-{3·x}/{x}=0$
3. решаем полученное уравнение
$4x^2+x-3=0$
Решим вторым устным способом, т.к. $а+с=b$
Тогда, $x_1=-1, x_2=-{3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=-1, x_2=-{3}/{4}$
При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$
Решить уравнение ${3x-5}/{-2}={1}/{x}$
Решение:
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х(3х-5)=-2$
Раскроем скобки и соберем все слагаемые в левой стороне
$3х^2-5х+2=0$
Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$
$x_1=1, x_2={2}/{3}$
В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=1, x_2={2}/{3}$
Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.
Чтобы решить иррациональное уравнение, необходимо:
- Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
- Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
- Решить полученное рациональное уравнение.
- Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.
Решение:
Обе части уравнение возведем в квадрат:
$√{4х-3}^2=х^2$
Получаем квадратное уравнение:
$4х-3=х^2$
Перенесем все слагаемые в левую часть уравнения:
${-х}^2+4х-3=0$
Решим данное квадратное уравнение устным способом, так как
$a+b+c=0$
$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$√{4·1-3}=1$
$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.
$√{4·(3)-3}=3$
$√9=3$
$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит
$х_1=1$ наименьший корень.
Ответ: $1$
Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
- Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$
Решить уравнение: $х-6=√{8-х}$
Возведем обе части уравнения в квадрат
$(х-6)^2=8-х$
В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение
$х^2-2·6·х+6^2=8-х$
$х^2-12х+36=8-х$
Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.
$х^2-12х+36-8+х=0$
Приводим подобные слагаемые:
$х^2-11х+28=0$
Найдем корни уравнения через дискриминант:
$D=b^2-4ac=121-4·28=121-112=9=3^2$
$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$
$x_1=7; x_2=4$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$x_1=7$
$7-6=√{8-7}$
$1=1$, получили верное равенство, следовательно, корень нам подходит.
$x_2=4$
$4-6=√{8-4}$
$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.
Ответ: $7$
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n⋅a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.
Решить уравнение $25·5^х=1$
Решение:
В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$
$5^2·5^х=5^0$
При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются
$5^{2+х}=5^0$
Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели
$2+х=0$
$х=-2$
Ответ: $-2$
Решить уравнение $2^{3х+2}-2^{3х-2}=30$
Решение:
Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель
$2^{3x+2}-2^{3x-2}=30$
$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$
$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$
$2^{3x-2}(2^4-1)=30$
$2^{3x-2}·15=30$
Разделим обе части уравнения на $15$
$2^{3х-2}=2$
$2^{3х-2}=2^1$
$3х-2=1$
$3х=3$
$х=1$
Ответ: $1$