Решите неравенство:
Спрятать решение
Решение.
Заметим, что решим неравенство, сводящееся к логарифмическому:
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Решите неравенство:
Спрятать решение
Решение.
Заметим, что решим неравенство, сводящееся к логарифмическому:
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
509583 решу егэ математика
Задание 15 № 509930
Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
Пусть Bi — размер долга Жанны на конец месяца I, Xi — платеж Жанны в конце месяца I. Мы знаем, что имеет место соотношение Bi = 1,01BI − 1 − Xi. Кроме того, мы знаем, что последовательность (Bi) является арифметической прогрессией. При этом B0 = 1800 тыс. руб., а B24 = 0, так как в конце срока кредитования долг Жанны должен быть равен нулю. Этих двух точек достаточно, чтобы узнать всю последовательность Bi: Значит,
Поскольку Xi линейно зависит от I, последовательность Xi также является арифметической прогрессией. Значит,
Задание 15 № 509930
Задание 15 509930.
Ege. sdamgia. ru
10.03.2018 14:11:56
2018-03-10 14:11:56
Источники:
Https://ege. sdamgia. ru/test? likes=509583
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 509583 решу егэ математика
509583 решу егэ математика
509583 решу егэ математика
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69 690 821 рубль.
Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Какую сумму Жанна выплатит банку в течение первого года кредитования.
Ege. sdamgia. ru
17.12.2018 1:09:09
2018-12-17 01:09:09
Источники:
Https://ege. sdamgia. ru/test? id=46311834
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 509583 решу егэ математика
509583 решу егэ математика
509583 решу егэ математика
Задание 15 № 506958
Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Пусть сумма кредита S у. е., процентная ставка банка X %.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет:
Общая сумма, выплаченная Антоном за 6 месяцев: (у. е.). А эта сумма по условию задачи равна у. е. Решим уравнение:
«Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину»
«Антон взятую сумму возвращал в банк равными долями.»
При этом решение верное, т. к. для составления формулы использована первая фраза.
S=90тр срок выплаты 3 месяца, ставка 10%
Размер кредита после 1 месяца 99. Что бы сумма долга уменьшалась равномерно (равными долями по 30), первая выплата должна составлять 39
Сумма долга уменьшается равномерно(равными долями по 30тр). Выплаты не равномерны.
Антон, спорить с Антоном по поводу задачи про Антона дело неблагодарное. и всё же
В решении нигде не говорится о том, что выплаты были одинаковыми.
Сказано, что «Антон ВЗЯТУЮ сумму возвращал в банк равными долями.»
В Вашем примере сумму взятую у банка в размере 90тр Антон возвращал равными долями (по 30тр)
Здравствуйте! Необходимо всё это описывать, если пользоваться формулой Дмитрия Гущина?
Если пользоваться формулой Дмитрия Гущина, могут поставить два балла из трех за недостаточное обоснование.
Задание 15 № 509583
Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?
Пусть Bi — размер долга Жанны на конец месяца I, Xi — платеж Жанны в конце месяца I. Мы знаем, что имеет место соотношение Bi = 1,02BI − 1 − Xi. Кроме того, мы знаем, что последовательность (Bi) является арифметической прогрессией. При этом B0 = 1200 тыс. руб., а B24 = 0, так как в конце срока кредитования долг Жанны должен быть равен нулю. Этих двух точек достаточно, чтобы узнать всю последовательность Bi: Значит,
Поскольку Xi линейно зависит от I, последовательность Xi также является арифметической прогрессией. Значит,
Ответ: 822 тыс. рублей.
Приведём другое решение.
Ежемесячно Жанна возвращает банку по 1,2 млн : 24 = 50 тыс. руб. тела долга и выплачивает равномерно уменьшающуюся от максимального значения до нуля сумму процентов за пользование кредитом. За первый месяц это 0,02 · 1,2 млн = 24 тыс. руб. За второй месяц на 1/24 меньше то есть 23 тыс. руб., затем 22 тыс. руб. и так далее. Поэтому выплаты за 12 первых месяцев составят арифметическую прогрессию с первым членом 74, последним — 63 тыс. руб. Ее сумма равна 12(74 + 63)/2 = 822 тыс. руб.
Задание 15 № 511220
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
Если первый платеж банку Аркадия составил X рублей, то второй составит 2X рублей, а третий — 3X рублей, всего 6X рублей, что равно 2 395 800, то есть X = 2 395 800 : 6 = 399 300. Отсюда: 2X = 798 600, 3X = 1 197 900.
Пусть в банке Аркадий взял в кредит S рублей.
Тогда его долг 01.03.2011 составил 1,1S рублей. После первого перечисления Аркадия долг снизился до (1,1S − 399 300) руб.
01.03.2012 банк начислил проценты на долг Аркадия. Долг Аркадия стал (1,1S − 399 300) · 1,1 = 1,21S − 439 230 (руб.)
Аркадий перевел в банк 798 600 руб. Долг снизился до 1,21S − 439230 − 798600 = 1,21S − 1237830 (руб.)
01.03.2013 банк начислил проценты на оставшийся долг Аркадия. Долг Аркадия стал (1,21S − 1237830) · 1,1 = 1,331S − 1 361 613 (руб.)
Аркадий перевел в банк 1 197 900 руб. Кредит погашен полностью, долга у Аркадия нет.
Значит, 1,331S − 1 361 613 − 1 197 900 = 0 ⇔ 1,331S = 2 559 513 ⇔ S = 1 923 000.
Задание 15 № 506958
Задание 15 № 511220
Поскольку X i линейно зависит от i, последовательность X i также является арифметической прогрессией.
Ege. sdamgia. ru
21.05.2019 18:06:29
2019-05-21 18:06:29
Источники:
Https://ege. sdamgia. ru/test? filter=all&category_id=292
Как я в школе относился к математике:)
Автор: Лёва Матрос
(И именно поэтому у меня в аттестате единственные тройки среди хороших оценок — это по алгебре и геометрии…)
Только зарегистрированные пользователи могут оставлять комментарии.
Войдите, пожалуйста.
Написать комментарий

2 913
4
75
Мероприятия
Список действующих конкурсов, марафонов и игр, организованных пользователями Author.Today.
Хотите добавить сюда ещё одну ссылку? Напишите об этом администрации.
Полезное
Подборка полезных статей и записей в блогах.
Хотите добавить сюда ещё одну ссылку? Напишите об этом администрации.
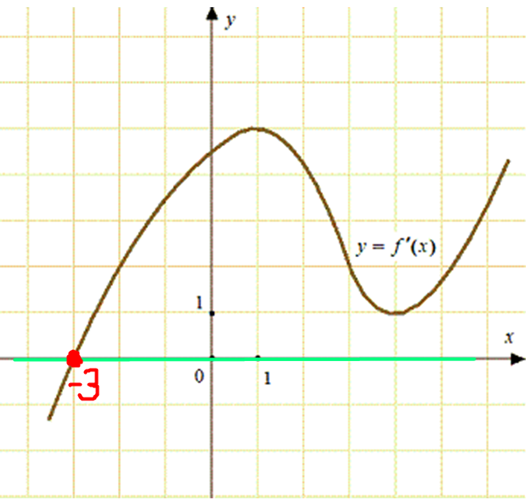
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 11
ОТВЕТ: — 3.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, то её угловой коэффициент равен 0 (коэффициент перед x). Следовательно, необходимо найти точку, в которых (f’left( {{x_0}} right) = 0). Этому соответствует точка пересечения графика производной с прямой (y = 0) (ось Ox). Это точка –3 (выделена красным цветом см. рисунок).
Ответ: –3.
Комментарии для сайта Cackle
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
Раскроем скобки.
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$
$х=-{17}/{5}$
$х = — 3,4$
Ответ: $- 3,4$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
$x = 0; ax + b = 0$
2. Решаем получившиеся уравнения каждое отдельно.
Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$
$4х^2 — 5х = 0$
Вынесем х как общий множитель за скобки:
$х (4х — 5) = 0$
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
$ax^2 + c = 0$
$ax^2 = — c$
$x_2 = {-c}/{a}$
При решении последнего уравнения возможны два случая:
если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$
если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.
$x^2 — 16 = 0$
$x^2 = 16$
$x = ±4$
Ответ: $х_1 = 4, х_2 = — 4$
Решение полного квадратного уравнения
Решение с помощью дискриминанта
Дискриминантом квадратного уравнения D называется выражение
$b^2 — 4ac$.
При решении уравнения с помощью дискриминанта возможны три случая:
1. $D > 0$. Тогда корни уравнения равны:
$x_{1,2}={-b±√D}/{2a}$
2. $D = 0$. В данном случае решение даёт два двукратных корня:
$x_{1}=x_{2}={-b}/{2a}$
3. $D < 0$. В этом случае уравнение не имеет корней.
$3х^2 — 11 = -8х$
Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней
$3х^2 + 8х — 11 = 0$
$a = 3 ,b = 8, c = — 11$
$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$
$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$
$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$
Ответ: $x_1=1, x_2=-3{2}/{3}$
Устные способы
Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$
$4х^2+ 3х — 7 = 0$
$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$
Ответ: $х_1= 1, х_2 = -{7}/{4}$
Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$
$5х^2+ 7х + 2 = 0$
$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$
Ответ: $х_1= -1, х_2 = -{2}/{5}$
Кубические уравнения
Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.
$(x — 3)^3 = 27$
Представим обе части как основания в третьей степени
$(x — 3)^3 = $33
Извлечем кубический корень из обеих частей
$х — 3 = 3$
Соберем известные слагаемые в правой части
$x = 6$
Ответ: $х = 6$
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
$4x + 1 — {3}/{x} = 0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x + 1 — {3}/{x}= 0¦· x$
$4x · x + 1 · x — {3·x}/{x} = 0$
3. решаем полученное уравнение
$4x^2 + x — 3 = 0$
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = {3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = {3}/{4}$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$
${3х-5}/{-2}={1}/{х}$
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х (3х — 5) = -2$
Раскроем скобки и соберем все слагаемые в левой части уравнения
$3х^2- 5х + 2 = 0$
Решим данное квадратное уравнение первым устным способом, т.к.
$a + b + c = 0$
$x_1 = 1, x_2 = {2}/{3}$
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1 = 1, x_2 = {2}/{3}$
Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.
Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.
Например,
${2}/{x}+5x=7$ – рациональное уравнение
$3x+√x=7$ — иррациональное уравнение (содержит корень)
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль общий знаменатель.
Решить уравнение: $4x+1-{3}/{x}=0$
Решение:
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x ≠ 0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x+1-{3}/{x}=0|·x$
$4x·x+1·x-{3·x}/{x}=0$
3. решаем полученное уравнение
$4x^2+x-3=0$
Решим вторым устным способом, т.к. $а+с=b$
Тогда, $x_1=-1, x_2=-{3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=-1, x_2=-{3}/{4}$
При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$
Решить уравнение ${3x-5}/{-2}={1}/{x}$
Решение:
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х(3х-5)=-2$
Раскроем скобки и соберем все слагаемые в левой стороне
$3х^2-5х+2=0$
Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$
$x_1=1, x_2={2}/{3}$
В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=1, x_2={2}/{3}$
Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.
Чтобы решить иррациональное уравнение, необходимо:
- Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
- Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
- Решить полученное рациональное уравнение.
- Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.
Решение:
Обе части уравнение возведем в квадрат:
$√{4х-3}^2=х^2$
Получаем квадратное уравнение:
$4х-3=х^2$
Перенесем все слагаемые в левую часть уравнения:
${-х}^2+4х-3=0$
Решим данное квадратное уравнение устным способом, так как
$a+b+c=0$
$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$√{4·1-3}=1$
$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.
$√{4·(3)-3}=3$
$√9=3$
$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит
$х_1=1$ наименьший корень.
Ответ: $1$
Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
- Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$
Решить уравнение: $х-6=√{8-х}$
Возведем обе части уравнения в квадрат
$(х-6)^2=8-х$
В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение
$х^2-2·6·х+6^2=8-х$
$х^2-12х+36=8-х$
Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.
$х^2-12х+36-8+х=0$
Приводим подобные слагаемые:
$х^2-11х+28=0$
Найдем корни уравнения через дискриминант:
$D=b^2-4ac=121-4·28=121-112=9=3^2$
$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$
$x_1=7; x_2=4$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$x_1=7$
$7-6=√{8-7}$
$1=1$, получили верное равенство, следовательно, корень нам подходит.
$x_2=4$
$4-6=√{8-4}$
$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.
Ответ: $7$
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n⋅a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.
Решить уравнение $25·5^х=1$
Решение:
В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$
$5^2·5^х=5^0$
При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются
$5^{2+х}=5^0$
Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели
$2+х=0$
$х=-2$
Ответ: $-2$
Решить уравнение $2^{3х+2}-2^{3х-2}=30$
Решение:
Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель
$2^{3x+2}-2^{3x-2}=30$
$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$
$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$
$2^{3x-2}(2^4-1)=30$
$2^{3x-2}·15=30$
Разделим обе части уравнения на $15$
$2^{3х-2}=2$
$2^{3х-2}=2^1$
$3х-2=1$
$3х=3$
$х=1$
Ответ: $1$
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
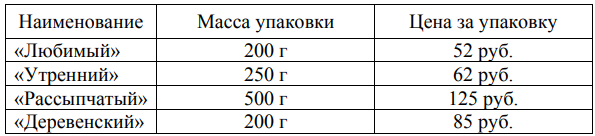
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
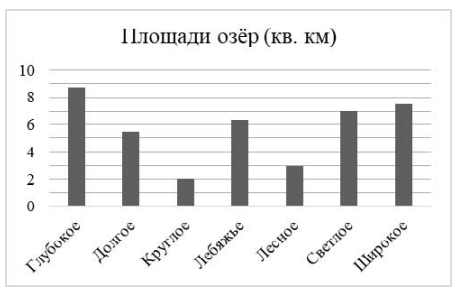
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
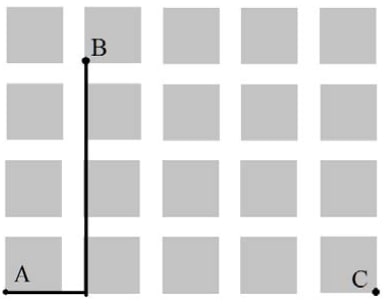
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.