Задания
Версия для печати и копирования в MS Word
Тип 10 № 509966
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Спрятать решение
Решение.
Участок, изображенный на плане, представляет собой прямоугольник, площадь которого равна произведению длин его сторон. Таким образом, площадь участка: 3 · 3 − 1= 8.
Ответ: 8.
Аналоги к заданию № 509793: 509966 Все
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Тип 10 № 509966
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Аналоги к заданию № 509793: 509966 Все
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 14 № 508380
Воспользуемся тем, что для суммы возможны четыре случая раскрытия модулей, откуда заключаем:
Приведем другое решение:
Как и в первом решении запишем неравенство в виде:
Заметим, что левая часть представляет из себя кусочно-линейную функцию, которая возрастает при и убывает при Это означает, что в точке –3 она достигает минимума равного 5. Таким образом, правая часть Тогда неравенство принимает вид:
Задание 14 № 508380
—>
508780 решу егэ математика.
Ege. sdamgia. ru
07.03.2017 0:00:13
2017-03-07 00:00:13
Источники:
Https://ege. sdamgia. ru/problem? id=508380
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508781
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?
Задание 10 № 508782
Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?
Задание 10 № 508783
Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508784
Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508785
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508786
Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508787
Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508788
Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508789
Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508790
Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508786
Задание 10 № 508781
Задание 10 508786.
Ege. sdamgia. ru
14.05.2019 20:28:53
2019-05-14 20:28:53
Источники:
Https://ege. sdamgia. ru/test? likes=508780
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508780
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:
Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:
Приведем решение Ирины Шраго.
Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей
—>
Задание 10 № 508780
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege. sdamgia. ru
09.08.2017 16:57:34
2017-08-09 16:57:34
Источники:
Https://ege. sdamgia. ru/problem? id=508780
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 1 мин. 16 сек.
ЕГЭ по математике (база) 2023 задание 16: номер 441 | gzvne | Механические часы с двенадцат…
35
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки $11$, но не дойдя до отметки $2$ часа.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Найдите значение выражения ${(4^{-6})^2}/{4^{-14}}$.
Найдите $sin x$, если известно, что $cos x = {√7}/{4}$ и $270° < x < 360°$.
Найдите значение выражения ${6√{180}}/{√5}$.
Найдите значение выражения $67·10-4.5·10^2$.
На экранах долгожданный шестой сезон одного из самых популярных и востребованных сериалов на зарубежном телевидении. Проект «Викинги» повествует о выдающемся воинственном народе, который проживает в Скандинавии и управляется безумным, яростным, но при этом очень мудрым правителем Рагнаром Лодброком. Этот человек смог собрать вокруг себя верных людей, смог установить свои правила на родных территориях, а вскоре отправился на покорение европейских земель. Главный герой повёл за собой свою армию, которая дошла с ним до территории Франции, осадив Париж и забрав сокровища одной из самых могущественных стран центральной Европы! Викингам по силам оказалось разбить армии англичан, которых не спасло даже нахождение на море. Ко всему прочему, главные персонажи сумели пробиться вглубь континента, наворотив дел и в других частях Европы.Продолжение истории обещает зрителям ещё более интересные походы. В этот раз главный герой вместе с верными товарищами отправится на восточные земли. Его встреча с Вещим Олегом, роль которого исполнит великолепный российский актёр Данила Козловский будет судьбоносной. Но чем же обернётся новый сезон знаменитого сериала?
- Название: Vikings
- Год выхода: 2013-03-03
- Страна: Канада, Ирландия
- Режиссер: Киаран Доннелли, Кен Джиротти, Стивен Ст.
- Статус сериала: Завершен
- Перевод: LostFilm
- Качество: FHD (1080p) (45 мин)
- Возраст: Сериал для зрителей старше 18+ лет
-
8.2
8.5
- В главных ролях: Кэтрин Уинник, Густаф Скарсгард, Александр Людвиг, Джорджия Хёрст, Алекс Хег Андерсен, Джордан Патрик Смит, Марко Ильсё, Петер Францен, Трэвис Фиммел, Клайв Стэнден
- Жанры: Приключения, Военный, Исторический, Боевик, Мелодрама, Драма
6 сезон 21 серия
Викинги смотреть онлайн в хорошем качестве бесплатно
Смотреть онлайн
Плеер 2
Плеер 3
Свет
К сожалению некоторые диалоги в сериале не переведены, рекомендуем в настройках включить субтитры, чтобы понимать диалоги. Приятного просмотра!
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.
Ответ: 0,4
Задание 2
Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.
Ответ: 5
Задание 3
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.
Ответ: 0,125
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Задание 5
Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$
Ответ: -7
Задание 6
Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$
Ответ: -1
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.
Ответ: 7
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Ответ: 1,8
Задание 9
Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 11
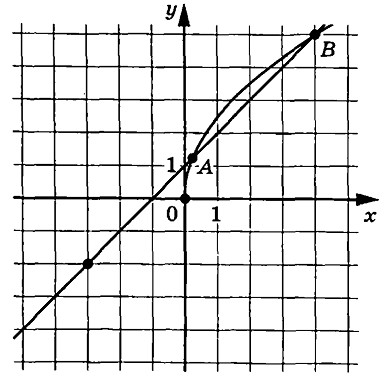
Задание 10
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.
Ответ: 0,25
Задание 11
Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: 17
Задание 12
а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].
Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Ответ: $$6sqrt{3}$$
Задание 14
Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$
Ответ: $$2;[log_{3}12;+infty)$$
Задание 15
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.
Ответ: 13 млн. руб.
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.
Ответ: $$frac{sqrt{6}}{2}$$
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$
Задание 18
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 64?
б) Может ли $$n$$ равняться 78?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)73
Егэ математика задание 18 номер 508050
В городе Z в 2013 году мальчиков родилось больше, чем девочек. Мальчиков чаще всего называли Андрей, а девочек — Мария. Выберите утверждения, которые следуют из приведённых данных.
Среди рождённых в 2013 году в городе Z:
1) девочек с именем Мария больше, чем с именем Светлана.
2) мальчиков с именем Николай больше, чем с именем Аристарх.
3) хотя бы одного из родившихся мальчиков назвали Андреем.
4) мальчиков с именем Андрей больше, чем девочек с именем Мария.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Школа приобрела стол, доску, магнитофон и принтер. Известно, что принтер дороже магнитофона, а доска дешевле магнитофона и дешевле стола. Выберите утверждения, которые верны при указанных условиях.
1) Магнитофон дешевле доски.
2) Принтер дороже доски.
3) Доска — самая дешёвая из покупок.
4) Принтер и доска стоят одинаково.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Перед баскетбольным турниром измерили рост игроков баскетбольной команды города N. Оказалось, что рост каждого из баскетболистов этой команды больше 180 см и меньше 195 см. Выберите утверждения, которые верны при указанных условиях.
1) В баскетбольной команде города N обязательно есть игрок, рост которого равен 200 см.
2) В баскетбольной команде города N нет игроков с ростом 179 см.
3) Рост любого баскетболиста этой команды меньше 195 см.
4) Разница в росте любых двух игроков баскетбольной команды города N составляет более 15 см.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Некоторые сотрудники фирмы летом 2014 года отдыхали на даче, а некоторые — на море. Все сотрудники, которые не отдыхали на море, отдыхали на даче. Выберите утверждения, которые верны при указанных условиях.
1) Каждый сотрудник этой фирмы отдыхал летом 2014 года или на даче, или на море, или и там, и там.
2) Сотрудник этой фирмы, который летом 2014 года не отдыхал на море, не отдыхал и на даче.
3) Если Фаина не отдыхала летом 2014 года ни на даче, ни на море, то она является сотрудником этой фирмы.
4) Если сотрудник этой фирмы не отдыхал на море летом 2014 года, то он отдыхал на даче.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
В классе учатся 20 человек, из них 13 человек посещают кружок по истории, а 10 человек — кружок по математике. Выберите утверждения, которые следуют из приведённых данных. В этом классе
1) нет ученика, который не посещает ни кружок по истории, ни кружок по математике
2) найдутся хотя бы два человека, которые посещают оба кружка
3) если ученик не ходит на кружок по истории, то он обязательно ходит на кружок по математике
4) не найдётся 11 человек, которые посещают оба кружка
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Известно, что Витя выше Коли, Маша выше Ани, а Саша ниже и Коли, и Маши. Выберите утверждения, которые следуют из приведённых данных.
1) Витя выше Саши.
2) Саша ниже Ани.
3) Коля и Маша одного роста.
4) Витя самый высокий из всех.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Пять жильцов многоквартирного дома — Андрей, Борис, Виктор, Денис и Егор — имеют различный возраст. При этом известно, что возраст Андрея больше, чем сумма возрастов Бориса и Виктора, Виктор старше Дениса, но младше Егора. Выберите утверждения, которые следуют из приведённых данных.
1) Андрей самый старший из жильцов
2) Егор старше Бориса
3) Андрей старше Дениса
4) Борис старше Егора
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Какие из приведённых ниже утверждений равносильны утверждению «Если Вы ― слон, значит, Вы ничего не забываете»?
(1) Если Вы ничего не забываете, значит, Вы ― слон.
(2) Если Вы ― не слон, значит, Вы все забываете.
(3) Если Вы ― не слон, значит, Вы что-то забываете.
(4) Если Вы что-то забываете, значит, Вы ― не слон.
В ответе укажите номера выбранных Вами утверждений без пробелов, запятых и других дополнительных символов.
В 2013 году в городе N цена на молоко повысилась на 5% по сравнению с 2012 годом, а в 2014 году — повысились на 7% по сравнению с 2013 годом. Какие из приведённых ниже утверждений следуют из этих данных?
(1) В 2015 году цена на молоко повысится примерно на 9% по сравнению с 2014 годом.
(2) В 2015 году рост цены должен прекратиться.
(3) За два года цена выросла на 13% по сравнению с 2012 годом.
(4) Ни одно из предложенных.
В ответе укажите номера выбранных Вами утверждений без пробелов, запятых и других дополнительных символов.
Известно, что спектр ртутной лампы — линейчатый. Выберите утверждения, которые следуют из этого факта.
1) У любой ртутной лампы линейчатый спектр.
2) Любая лампа с линейчатым спектром — ртутная.
3) У любой нертутной лампы спектр не является линейчатым.
4) Если спектр лампы линейчатый то она может быть ртутной.
В визовом центре работает 35 переводчиков, из них 25 человек знают немецкий язык, а 14 человек — испанский. Выберите утверждение, которое следует из приведённых данных. В визовом центре
1) нет переводчика, который не знал бы ни немецкого, ни испанского языка
2) найдутся хотя бы два человека, которые знают одновременно немецкий и испанский языки
3) найдётся переводчик, который не знает ни немецкого, ни испанского языка
4) не найдётся 12 человек, которые знают оба языка.
В ответе запишите номер выбранного утверждения.
На химическом заводе всего 15 промышленных ёмкостей для реакций. Объём каждой ёмкости меньше 100 литров, но не меньше 50 литров. Выберите утверждения, которые следуют из данной информации.
1) На химическом заводе есть ёмкость объёмом 60 литров.
2) Разница в объёме двух ёмкостей более 15 литров.
3) На заводе нет ёмкости объёмом 40 литров.
4) Объём любой ёмкости на заводе более 30 литров.
Средний балл выпускника школы, сдавшего ЕГЭ по четырём предметам, составляет 75. Самый низкий результат он показал по математике — 66 баллов (по остальным экзаменам баллы выше). Выберите утверждения, которые следуют из приведённых данных.
1) Средний балл по трём экзаменам, кроме математики, равен 78
2) Минимальный балл по любому из трёх предметов, не считая математики, больше 75
3) Ни по одному предмету выпускник не получил 100 баллов
4) По какому-то предмету выпускник получил больше 76 баллов
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
В офисе фирмы компьютеры работают только от сетевого электропитания. Если компьютеры работают, то электричество в офисе есть. Выберите утверждения, которые непосредственно следуют из этих данных.
1) Если в офисе нет электричества, то компьютеры не работают.
2) Если в офисе есть электричество, то компьютеры работают.
3) Если компьютеры не работают, значит, в офисе нет электричества.
4) Если в офисе нет электричества, то не работает компьютер директора.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Пять наиболее длинных рек России (учитывается наибольшая длина с притоками) — это Амур, Енисей, Иртыш, Лена и Обь. При этом Лена длиннее Енисея, но короче Оби, Амур длиннее и Лены и Иртыша. Выберите утверждения, которые следуют из приведённых данных.
1) Амур — первая или вторая по длине река
2) Енисей — вторая или третья река по длине
3) Лена длиннее Иртыша
4) Амур длиннее Оби
В ответе укажите номер выбранного утверждения.
Автолюбителям известно, что если в присутствии инспектора ГИБДД проехать на красный свет, то штраф неминуем. Выберите утверждения, которые непосредственно следуют из этого знания.
1) Если вас оштрафовал инспектор, то вы проехали на красный свет.
2) Если вас не оштрафовали, вы не проезжали на красный свет
3) Если вы не проезжали на красный свет, то вы не будете оштрафованы
4) Если вы проехали на красный свет с непристёгнутым ремнём, то заметивший это инспектор ГИБДД вас оштрафует.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Известно, что все щуки — рыбы, также известно, что все рыбы плавают в воде. Тюлень тоже плавает в воде. Выберите утверждения, которые следуют из приведённых данных.
1) Все тюлени — рыбы
2) Если животное не плавает, то это не тюлень
3) Все щуки плавают в воде
4) Если животное плавает в воде, то оно либо рыба, либо тюлень
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Согласно русской поговорке «Пока гром не грянет, мужик не перекрестится». Выберите утверждения, которые следуют из этой поговорки. Указание: понимайте эту поговорку как условие «Без грома мужик не будет креститься».
1) Если грянул гром, мужик перекрестится
2) Если мужик не крестился, то грома не было
3) Если не было грома, то мужик не крестился
4) Если мужик перекрестился, то был гром
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Отец обещал сыну-студенту подарить ноутбук, если он сдаст сессию без троек. Отец всегда выполняет свои обещания. Выберите утверждения, которые следуют из приведённых фактов.
1) Если сессия сдана на отлично, то ноутбук будет подарен
2) Если сын получит тройку, то отец не подарит ему ноутбук
3) Если ноутбук не был подарен, то сессия не сдана успешно (без троек)
4) Если ноутбук был подарен, то сессия сдана без троек
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Если в маршрутном такси заняты все места, то оно трогается от остановки. Выберите утверждения, которые следуют из приведённых данных.
1) Если в маршрутке есть свободные места, то она не трогается
2) Если маршрутка продолжает стоять, то в ней остались свободные места
3) Если на каждом месте маршрутки сидит пенсионер, то она трогается от остановки
4) Если маршрутка отъехала от остановки, то в ней заняты все места
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Известно, что берёзы — деревья, также известно, что все деревья выделяют кислород. Подсолнухи тоже выделяют кислород. Выберите утверждения, которые следуют из приведённых данных.
1) Все берёзы выделяют кислород
2) Все подсолнухи являются берёзами
3) Некоторые растения, выделяющие кислород, являются берёзами
4) Если растение не выделяет кислород, то оно — не подсолнух
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Игорь Витальевич часто ездит на работу на велосипеде. Он не ездит на велосипеде в те дни, когда идёт дождь или снег, а также по четвергам, когда Игорь Витальевич надевает парадный костюм. Выберите утверждения, которые верны при приведённых условиях.
1) Сегодня Игорь Витальевич приехал на работу на велосипеде, значит, сегодня нет дождя.
2) Каждый раз, когда в течение дня будет ясно, Игорь Витальевич будет добираться на работу на велосипеде.
3) Каждый раз, когда Игорь Витальевич добирается до работы без велосипеда, он одет в парадный костюм.
4) Каждый раз, когда на улице идёт снег, Игорь Витальевич добирается до работы без велосипеда.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
В фирме работает 60 сотрудников, из них 50 человек знают английский язык, а 15 — французский. Выберите утверждения, которые верны при указанных условиях.
1) Если сотрудник этой фирмы знает английский язык, то он знает и французский.
2) Хотя бы три сотрудника этой фирмы знают и английский, и французский языки.
3) Не более 15 сотрудников этой фирмы знают и английский, и французский языки.
4) В этой фирме нет ни одного человека, знающего и английский, и французский языки.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
В фирме работает 50 сотрудников, из них 40 человек знают английский язык, а 20 — немецкий. Выберите утверждения, которые верны при указанных условиях.
1) В этой фирме хотя бы три сотрудника знают и английский, и немецкий языки.
2) В этой фирме нет ни одного сотрудника, знающего и английский, и немецкий языки.
3) Если сотрудник этой фирмы знает английский язык, то он знает и немецкий.
4) Не более 20 сотрудников этой фирмы знают и английский, и немецкий языки.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Маша младше Алисы на год, но старше Кати на два года. Выберите утверждения, которые верны при указанных условиях.
1. Любая девочка, помимо указанных, которая старше Кати, также старше Маши.
2. Среди указанных девочек нет никого младше Кати.
3. Любая девочка, помимо указанных, которая старше Маши, также старше Кати.
4. Алиса и Катя одного возраста.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
В жилых домах, в которых больше 5 этажей, установлен лифт. Выберите утверждения, которые верны при приведённом условии.
1) Если в доме нет лифта, то в этом доме больше 6 этажей
2) Если в доме лифта нет, то в этом доме меньше 6 этажей
3) Если в доме больше 8 этажей, то в нём нет лифта
4) Если в доме больше 7 этажей, то в нём есть лифт
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Во дворе школы растут всего три дерева: ясень, рябина и осина. Ясень выше рябины на 1 метр, но ниже осины на 2 метра. Выберите все утверждения, которые верны при указанных условиях.
1) Среди указанных деревьев не найдётся двух одной высоты.
2) Ясень, растущий во дворе школы, выше осины, растущей там же.
3) Любое дерево, помимо указанных, которое ниже ясеня, растущего во дворе школы, также ниже рябины, растущей там же.
4) Любое дерево, помимо указанных, которое ниже рябины, растущей во дворе школы, также ниже ясеня, растущего там же.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Андрей Сергеевич был в отпуске 9 дней и каждый день ходил куда-нибудь гулять. Два раза он ходил на смотровую площадку и 3 раза ходил на пляж (за день Андрей Сергеевич мог сходить и на смотровую площадку, и на пляж, а мог никуда не ходить, но дважды в день в одно и то же место не ходил). Выберите утверждения, которые верны при указанных условиях вне зависимости от того, в какие дни Андрей Сергеевич ходил на пляж.
1) Не может оказаться, что Андрей Сергеевич 4 дня ходил и на смотровую площадку, и на пляж.
2) Было 2 дня, когда Андрей Сергеевич ходил и на смотровую площадку, и на пляж.
3) Было 3 дня, когда Андрей Сергеевич никуда не ходил.
4) Если Андрей Сергеевич сходил на смотровую площадку, то в этот же день он ходил и на пляж.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Диагностика 30 машин в автосервисе показала, что у 5 машин нужно заменить тормозные колодки, а у 10 машин — заменить воздушный фильтр (колодки и фильтр требуют замены независимо друг от друга). Выберите утверждения, которые верны при указанных условиях вне зависимости от того, какие машины нуждаются в замене фильтра, а какие — в замене колодок.
1) Найдётся 6 машин, в которых нужно поменять и колодки, и фильтр.
2) Найдётся 9 машин, в которых не нужно менять ни колодки, ни фильтр.
3) Не найдётся 7 машин, в которых нужно менять и колодки, и фильтр.
4) Если в машине нужно менять колодки, то фильтр тоже нужно менять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
На столе стоят 20 кружек с чаем. В шести из них чай с сахаром, а в остальных — без сахара. В четыре из этих 20 кружек официант собирается положить по дольке лимона. Выберите утверждения, которые будут верны при указанных условиях независимо от того, в какие кружки официант положит дольки лимона.
1) Найдётся 9 кружек с чаем без сахара и лимона.
2) Найдётся 3 кружки с чаем с лимоном, но без сахара.
3) Если в кружке чай без сахара, то он с лимоном.
4) Не найдётся 8 кружек с чаем без сахара, но с лимоном.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
2 Если Вы не слон, значит, Вы все забываете.
Mathb-ege. sdamgia. ru
20.10.2018 0:10:27
2018-02-26 01:36:12
Источники:
Https://mathb-ege. sdamgia. ru/test? filter=all&category_id=222&ttest=true
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ математика задание 18 номер 508050
Егэ математика задание 18 номер 508050
Егэ математика задание 18 номер 508050
Задание 18 № 514068
В фирме работает 60 сотрудников, из них 50 человек знают английский язык, а 15 — французский. Выберите утверждения, которые верны при указанных условиях.
1) Если сотрудник этой фирмы знает английский язык, то он знает и французский.
2) Хотя бы три сотрудника этой фирмы знают и английский, и французский языки.
3) Не более 15 сотрудников этой фирмы знают и английский, и французский языки.
4) В этой фирме нет ни одного человека, знающего и английский, и французский языки.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение не следует из данного условия.
2) Утверждение следует из данного условия, так как 5 человек, точно, знают и английский, и французский язык.
3) Утверждение следует из данного условия, так как в сумме 65 человек, которые знают либо английский, либо французский, следовательно, 5 человек точно знают оба языка, что не противоречит утверждению.
4) Утверждение не следует из данного условия.
Ответ: 23 или 32.
Задание 18 № 514130
В фирме работает 50 сотрудников, из них 40 человек знают английский язык, а 20 — немецкий. Выберите утверждения, которые верны при указанных условиях.
1) В этой фирме хотя бы три сотрудника знают и английский, и немецкий языки.
2) В этой фирме нет ни одного сотрудника, знающего и английский, и немецкий языки.
3) Если сотрудник этой фирмы знает английский язык, то он знает и немецкий.
4) Не более 20 сотрудников этой фирмы знают и английский, и немецкий языки.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим каждое утверждение
1) Утверждение верно, поскольку в фирме всего 50 человек и из них 40 человек знают английский язык, а 20 человек — немецкий.
2) Второе утверждение противоречит приведённым данным.
3) Утверждение не следует из приведённых данных.
4) Поскольку немецкий знают 20 человек, следовательно, не больше 20 человек знают два иностранных языка. Утверждение верно.
Задание 18 № 514625
В жилых домах, в которых больше 5 этажей, установлен лифт. Выберите утверждения, которые верны при приведённом условии.
1) Если в доме нет лифта, то в этом доме больше 6 этажей
2) Если в доме лифта нет, то в этом доме меньше 6 этажей
3) Если в доме больше 8 этажей, то в нём нет лифта
4) Если в доме больше 7 этажей, то в нём есть лифт
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение не следует из данного условия.
2) Утверждение следует из данного условия, так как лифт устанавливается в те дома, в которых строго больше 5 этажей.
3) Утверждение не следует из данного условия.
4) Утверждение следует из данного условия, так как по условию на сказано, что в домах, в которых больше 5 этажей установлен лифт.
Ответ: 24 или 42.
Задание 18 № 509225
В классе учится 20 человек, из них 13 человек посещают кружок по истории, а 10 — кружок по математике. Выберите утверждения, которые верны при указанных условиях.
1) Каждый ученик этого класса посещает оба кружка.
2) Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике.
3) Найдутся хотя бы двое из этого класса, кто посещает оба кружка.
4) Не найдётся 11 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение не следует из приведённых данных, поскольку возможна ситуация, когда 13 человек посещают кружок по истории, причём трое из них посещают ещё и кружок по математике, а оставшиеся семь человек ходят только в кружок по математике.
2) Утверждение не следует из приведённых данных, поскольку возможна ситуация, когда 10 человек из тринадцати, посещающих кружок по истории, ходят и на кружок по математике. При этом окажется, что семь человек не посещают ни одного кружка.
3) Утверждение следует из приведённых данных. Более того, можно утверждать, что минимум три человека посещают сразу оба кружка. Такая ситуация описана в пункте 1).
4) Кружок по математике посещают 10 человек, поэтому более 10 человек посещать оба кружка не может. Утверждение верно.
Задание 18 № 510283
Повар испёк для вечеринки 45 кексов, из них 15 штук он посыпал марципаном, а 20 кексов посыпал сахарной пудрой. Выберите утверждения, которые верны при указанных условиях.
1) Хотя бы 16 кексов посыпаны и сахарной пудрой, и марципаном.
2) Найдётся 10 кексов, которые ничем не посыпаны.
3) Не может оказаться больше 15 кексов, посыпанных и сахарной пудрой, и марципаном.
4) Если кекс посыпан сахарной пудрой, то он посыпан марципаном.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Проанализируем каждое из утверждений:
1) Неверное утверждение, поскольку кексов, которые посыпаны марципаном, только 15.
2) Верное утверждение, поскольку только про 35 кексов мы знаем, что они чем-то посыпаны.
3) Верное утверждение, так как мы знаем, что только 15 кексов посыпаны марципаном.
4) Неверное утверждение, поскольку могут оказаться кексы, посыпанные сахарной пудрой, но не посыпанные марципаном.
Задание 18 № 508009
В фирме N работают 60 человек, из них 50 человек знают английский язык, а 15 человек — французский. Выберите утверждения, которые следуют из приведённых данных. В фирме N
1) если человек знает французский язык, то он знает и английский
2) хотя бы три человека знают оба языка
3) не больше 15 человек знают два иностранных языка
4) нет ни одного человека, знающего и английский, и французский языки
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение не следует из приведённых данных.
2) Утверждение следует из приведённых данных. Оба языка знают минимум 5 человек.
3) Поскольку французский язык знают 15 человек, следовательно, не больше 15 человек знают два иностранных языка. Утверждение верно.
4) Утверждение не следует из приведённых данных.
Примечание. Сотрудники фирмы могут знать и другие иностранные языки, но в условии об этом ничего не сказано.
Задание 18 № 509683
В фирме N работает 60 сотрудников, из них 50 человек знают английский язык, а 15 — французский. Выберите утверждения, которые верны при указанных условиях.
1) Не более 15 сотрудников этой фирмы знают и английский, и французский языки.
2) Если сотрудник этой фирмы знает английский язык, то он знает и французский.
3) Хотя бы три сотрудника этой фирмы знают и английский, и французский языки.
4) В этой фирме нет ни одного человека, знающего и английский, и французский языки.
1) Утверждение следует из данного условия, так как в сумме 65 человек, которые знают либо английский, либо французский, следовательно, 5 человек точно знают оба языка, что не противоречит утверждению.
2) Утверждение не следует из данного условия.
3) Утверждение следует из данного условия, так как 5 человек, точно, знают и английский, и французский язык.
4) Утверждение не следует из данного условия.
Ответ: 13 или 31.
Задание 18 № 507966
В группе учатся 30 студентов, из них 20 студентов получили зачёт по экономике и 20 студентов получили зачёт по английскому языку. Выберите утверждения, которые следуют из приведённых данных. В этой группе
1) найдутся 11 студентов, не получивших ни одного зачёта
2) хотя бы 10 студентов получили зачёты и по экономике, и по английскому языку
3) не больше 20 студентов получили зачёты и по экономике, и по английскому языку
4) найдётся студент, который не получил зачёта по английскому языку, но получил зачёт по экономике
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение противоречит приведённым данным, поскольку даже если 20 человек получили зачёт по одному предмету, и те же 20 человек по второму, не получивших зачёт будет всего 10.
2) Попытаемся найти минимальное число студентов, получивших оба зачёта при данном условии. Пусть, например, 20 студентов из 30 получили зачёт по экономике, а оставшиеся 10 студентов получили зачёт по английскому языку. Значит, есть ещё 10 студентов, которые получили зачёт по английскому языку и это студенты с необходимостью входят в число тех, кто получил зачёт по экономике. Таким образом, как минимум 10 студентов получат оба зачёта. Утверждение следует из приведённых данных.
3) Утверждение следует из приведённых данных. Максимально число студентов, сдавших хотя бы один зачёт — 20, поэтому и максимальное число тех, кто получил оба зачёта не больше двадцати.
4) Возможно из всей группы одни и те же 20 человек получили зачёт по обоим предметам. Утверждение не следует из приведённых данных.
Задание 18 № 506751
В группе учится 30 студентов, из них 20 студентов получили зачёт по экономике и 20 студентов получили зачёт по английскому языку. Выберите утверждения, которые следуют из приведённых данных.
1) не менее 10 студентов не получили зачёта ни по экономике, ни по английскому языку
2) хотя бы 10 студентов получили зачёты и по экономике, и по английскому языку
3) не больше 20 студентов получили зачёты и по экономике, и по английскому языку
4) найдётся студент, который не получил зачёта по английскому языку, но получил зачёт по экономике.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Студентов, которые не получили ни одного зачёта, от 0 до 10. Но не «не менее 10».
3) Да, так как всего по экономике получили зачёты 20 студентов. То есть больше студентов с зачётом по экономике быть не может.
4) Не факт. Может быть такое, что каждый студент, который получил зачёт по экономике, также получил зачёт и по английскому языку.
Задание 18 № 509643
В классе учится 25 человек, из них 16 человек посещают кружок по английскому языку, а 13 — кружок по немецкому языку. Выберите утверждения, которые верны при указанных условиях.
1) Найдётся 4 человека из этого класса, которые посещают оба кружка.
2) Если ученик из этого класса ходит на кружок по английскому языку, то он обязательно ходит на кружок по немецкому языку.
3) Найдётся хотя бы три человека из этого класса, которые посещают оба кружка.
4) Каждый ученик из этого класса посещает и кружок по английскому языку, и кружок по немецкому языку.
1) Утверждение следует из приведённых данных, так как в сумме 29 человек посещающих кружок по английскому или по немецкому языку, следовательно, 29 − 25 = 4, это и есть те 4 человека, которые посещают оба кружка.
2) Утверждение не следует из приведённых данных.
3) Утверждение следует из приведённых данных, так как есть 4 человека, которые посещают оба кружка.
4) Утверждение не следует из приведённых данных.
Ответ: 13 или 31.
Задание 18 № 509623
В компании из 30 человек 25 пользуются социальной сетью «Одноклассники», а 10 — социальной сетью «ВКонтакте». Выберите утверждения, которые верны при указанных условиях.
1) В этой компании найдётся 10 человек, которые не пользуются ни сетью «Одноклассники», ни сетью «ВКонтакте».
2) В этой компании найдётся хотя бы 5 человек, пользующихся обеими сетями.
3) Не найдётся ни одного человека из этой компании, пользующегося только сетью «Одноклассники».
4) Не более 10 человек из этой компании пользуются обеими сетями.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение не следует из приведённых данных.
2) Утверждение следует из приведённых данных, так как 30 − 25 + 10 = −5, следовательно, 5 человек пользуются двумя социальными сетями.
3) Утверждение не следует из приведённых данных.
4) Утверждение следует из приведённых данных, так как двумя социальными сетями пользуется 5 человек.
Ответ: 24 или 42.
Задание 18 № 506461
В компании из 20 человек 15 человек пользуется социальной сетью «Facebook», а 10 человек — социальной сетью «ВКонтакте». Выберите утверждения, которые следуют из приведённых данных. В этой компании
1) найдётся хотя бы 5 человек, пользующихся обеими сетями
2) найдётся человек, который не пользуется ни сетью «Facebook», ни сетью «ВКонтакте»
3) не больше 10 человек пользуются обеими сетями
4) не найдётся ни одного человека, пользующегося только сетью «Facebook»
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Это так. Пять достигается в случае, когда все пять человек, которые не пользуются «Facebook», пользуются «ВКонтакте». В остальных случаях таких людей ещё больше.
2) В примере из первого пункта все люди пользуются хотя бы одной социальной сетью.
3) Это верно, так как всего 10 человек пользуются «ВКонтакте».
4) Всегда найдётся такой человек, так как пользующихся «Facebook» больше, чем тех, кто пользуется «ВКонтакте».
Задание 18 № 506686
Повар испёк для вечеринки 40 печений, из них 10 штук он посыпал корицей, а 20 печений посыпал сахаром. Выберите утверждения, которые следуют из приведённых данных. Среди испечённых поваром печений
1) хотя бы одно печенье посыпано и сахаром, и корицей
2) не меньше 10 печений ничем не посыпано: ни сахаром, ни корицей
3) не может оказаться больше 10 печений, посыпанных и сахаром, и корицей
4) если печенье посыпано сахаром, то оно не посыпано корицей
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Совсем необязательно.
2) Если нет ни одного печенья, посыпанного и сахаром, и корицей, то тогда есть 10 печений, ничем не посыпанных. Во всех других случаях непосыпанных печений будет ещё больше.
3) Да, не может, так как всего 10 печений посыпано корицей.
Задание 18 № 510754
В классе учится 30 человек, из них 20 человек посещают кружок по биологии, а 16 — кружок по географии. Выберите утверждения, которые верны при указанных условиях.
1) Найдутся хотя бы двое из этого класса, кто посещает оба кружка.
2) Если ученик из этого класса ходит на кружок по биологии, то он обязательно ходит на кружок по географии.
3) Каждый ученик из этого класса посещает оба кружка.
4) Не найдётся 17 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Проанализируем каждое из утверждений:
1) Найдутся хотя бы двое из этого класса, кто посещает оба кружка — поскольку в классе всего 30 человек, 20 посещают кружок по биологии, а 16 — кружок по биологии, то это значит, хотя бы двое посещают два кружка одновременно. Утверждение Верно
2) Если ученик из этого класса ходит на кружок по биологии, то он обязательно ходит на кружок по географии — не все ученики ходят на кружок по географии. Утверждение Неверно
3) Каждый ученик из этого класса посещает оба кружка — не все ученики ходят на оба кружка. Утверждение Неверно
4) Не найдётся 17 человек из этого класса, которые посещают оба кружка — поскольку в классе всего 30 человек, 20 посещают кружок по биологии, а 16 — кружок по биологии, то это значит, только 16 человек найдется, которые могли бы посещать оба кружка. Утверждение Верно
Задание 18 № 511468
В фирме N работают 60 человек, из них 50 человек знают английский язык, а 15 человек — французский. Выберите утверждения, которые следуют из приведённых данных.
1) если человек знает французский язык, то он знает и английский
2) хотя бы три человека знают оба языка
3) не больше 15 человек знают два иностранных языка
4) нет ни одного человека, знающего и английский, и французский языки.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Поскольку в фирме 15 человек знают французский язык, английский язык знают 50 человек, вовсе необязательно, что если человек знает французский язык, то он знает и английский. Утверждение неверно.
2) Поскольку всего в фирме 60 человек, а знающих английский — 50, французский — 15, то 65 − 60 = 5, поэтому минимум 5 человек знают и французский, и английский, следовательно, утверждение верно.
3) Утверждение верно, поскольку 15 человек знают французский.
4) Поскольку всего в фирме 60 человек, а знающих английский — 50, французский — 15, то 65 − 60 = 5, поэтому минимум 5 человек знают и французский, и английский, следовательно, утверждение неверно.
Примечание. Сотрудники фирмы могут знать и другие иностранные языки, но в условии об этом ничего не сказано.
Задание 18 № 512370
В классе учится 25 человек, из них 16 человек посещают кружок по английскому языку, а 13 — кружок по немецкому языку. Выберите утверждения, которые верны при указанных условиях.
1) Каждый ученик из этого класса посещает и кружок по английскому языку, и кружок по немецкому языку.
2) Найдётся хотя бы три человека из этого класса, которые посещают оба кружка.
3) Если ученик из этого класса ходит на кружок по английскому языку, то он обязательно ходит на кружок по немецкому языку.
4) Не более 13 человек из этого класса посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение не следует из приведённых данных.
2) Утверждение следует из приведённых данных, так как 3 человек могут посещают оба кружка.
3) Утверждение не следует из приведённых данных.
4) Утверждение следует из приведённых данных, так как 13 человек могут посещают оба кружка.
Задание 18 № 512506
В группе учится 30 студентов, из них 20 человек сдали зачёт по экономике и 20 сдали зачёт по английскому языку. Выберите утверждения, которые верны при указанных условиях.
1) В этой группе найдётся 11 студентов, не сдавших ни одного из этих двух зачётов.
2) Хотя бы 10 студентов из этой группы сдали зачёты и по экономике, и по английскому языку.
3) Не более 20 студентов из этой группы сдали зачёты и по экономике, и по английскому языку.
4) В этой группе найдётся 20 студентов, которые не сдали зачёта по английскому языку, но сдали зачёт по экономике.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим представленные утверждения:
1) В этой группе может найтись только 10 студентов, не сдавших ни одного из двух зачетов. Утверждение неверно.
2) Минимум 10 человек из группы сдали оба зачета. Утверждение верно.
3) Максимальное количество человек, которые могли сдать оба зачета — 20 человек. Утверждение верно.
4) В этой группе может найтись лишь 10 человек, которые не сдали зачет по экономике, но сдали зачет по английскому языку. Утверждение неверно.
Задание 18 № 512526
Повар испёк 40 печений, из них 10 печений он посыпал корицей, а 20 печений посыпал сахаром. Выберите утверждения, которые верны при указанных условиях.
1) Найдётся 20 печений, посыпанных и сахаром, и корицей.
2) Найдётся 10 печений, которые ничем не посыпаны.
3) Не может оказаться больше 10 печений, посыпанных и сахаром, и корицей.
4) Если печенье посыпано сахаром, то оно посыпано и корицей.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим представленные утверждения:
1) Только 10 печений посыпано корицей. Утверждение неверно.
2) Минимум 10 печений ничем не посыпаны. Утверждение верно.
3) Только 10 печений посыпано корицей. Утверждение верно.
4) Только 10 печений посыпано сахаром, корицей — 20. Утверждение неверно.
Задание 18 № 512566
В классе учится 30 человек, из них 20 человек посещают кружок по биологии, а 16 — кружок по географии. Выберите утверждения, которые верны при указанных условиях.
1) Найдутся хотя бы двое из этого класса, кто посещает оба кружка.
2) Если ученик из этого класса посещает кружок по биологии, то он обязательно посещает кружок по географии.
3) Каждый ученик из этого класса посещает оба кружка.
4) Не найдётся 17 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим представленные утверждения:
1) Минимум 6 человек посещает оба кружка. Утверждение верно.
2) Ученик может посещать исключительно занятия по биологии. Утверждение неверно.
3) Максимум 16 человек посещают оба кружка. Утверждение неверно.
4) Максимум 16 человек посещают оба кружка. Утверждение верно.
Задание 18 № 514041
Повар испёк 50 рогаликов, из них 15 рогаликов он посыпал корицей, а 20 рогаликов посыпал сахаром. Выберите утверждения, которые верны при указанных условиях.
1. Найдётся 10 рогаликов, которые ничем не посыпаны.
2. Если рогалик посыпан сахаром, то он посыпан и корицей.
3. Не может оказаться больше 20 рогаликов, посыпанных и сахаром, и корицей.
4. Найдётся 20 рогаликов, посыпанных и сахаром, и корицей.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Верное утверждение, поскольку только про 35 рогаликов мы знаем, что они чем-то посыпаны.
2) Неверное утверждение, поскольку могут оказаться рогалики, посыпанные сахаром, но не посыпанные корицей.
3) Верное утверждение, так как мы знаем, что только 15 рогаликов посыпаны корицей.
4) Только 15 рогаликов посыпаны корицей
Ответ: 13 или 31.
Задание 18 № 514088
В фирме работает 100 человек, из них 70 человек знают португальский язык, а 50 — французский. Выберите утверждения, которые верны при указанных условиях.
1) В этой фирме хотя бы пять человек знают и португальский, и французский языки.
2) Нет ни одного человека в этой фирме, знающего и португальский, и французский языки.
3) Если человек из этой фирмы знает португальский язык, то он знает и французский.
4) Не более 50 человек из этой фирмы знают и португальский, и французский языки.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение следует из данного условия, так как 20 человек, точно, знают и португальский, и французский языки.
2) Утверждение не следует из данного условия.
3) Утверждение не следует из данного условия.
4) Утверждение следует из данного условия, так как в сумме 120 человек, которые знают либо английский, либо французский, следовательно, 20 человек точно знают оба языка, что не противоречит утверждению.
Ответ: 14 или 41.
Задание 18 № 514204
Повар испёк для вечеринки 45 кексов, из них 15 кексов он посыпал кокосовой стружкой, а 20 кексов посыпал сахарной пудрой. Выберите утверждения, которые верны при указанных условиях.
1) Хотя бы 16 кексов посыпаны и сахарной пудрой, и кокосовой стружкой.
2) Найдётся 10 кексов, которые ничем не посыпаны.
3) Не может оказаться больше 15 кексов, посыпанных и сахарной пудрой, и кокосовой стружкой.
4) Если кекс посыпан сахарной пудрой, то он посыпан кокосовой стружкой.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Проанализируем каждое из утверждений:
1) Неверное утверждение, поскольку кексов, которые посыпаны кокосовой стружкой, только 15.
2) Верное утверждение, поскольку только про 35 кексов мы знаем, что они чем-то посыпаны.
3) Верное утверждение, так как мы знаем, что только 15 кексов посыпаны кокосовой стружкой.
4) Неверное утверждение, поскольку могут оказаться кексы, посыпанные сахарной пудрой, но не посыпанные кокосовой стружкой.
Задание 18 № 514227
В компании из 20 человек 15 пользуются социальной сетью «Одноклассники», а 10 — социальной сетью «ВКонтакте». Выберите утверждения, которые верны при указанных условиях.
1) В этой компании найдётся хотя бы 5 человек, пользующихся обеими сетями.
2) Найдётся 10 человек из этой компании, которые не пользуются ни сетью «Одноклассники», ни сетью «ВКонтакте».
3) Не более 10 человек из этой компании пользуются обеими сетями.
4) В этой компании не найдётся ни одного человека, пользующегося только сетью «Одноклассники».
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение следует из приведённых данных, так как 20 − 15 − 10 = −5, следовательно, 5 человек пользуются двумя социальными сетями.
2) Утверждение не следует из приведённых данных.
3) Утверждение следует из приведённых данных, так как двумя социальными сетями пользуется 5 человек.
4) Утверждение не следует из приведённых данных.
Задание 18 № 518613
Марусе на день рождения подарили 20 шариков, из которых 13 красные, а остальные синие. Маруся на четырёх случайных шариках нарисовала рисунки маркером, чтобы подарить маме, папе, брату и сестре. Выберите все
Утверждения, которые будут верны при указанных условиях независимо от того, на каких шариках Маруся нарисовала рисунки
1) Найдётся 2 синих шарика без рисунков.
2) Если шарик красный, то на нём есть рисунок.
3) Найдётся 4 красных шарика с рисунками.
4) Не найдётся 5 синих шариков с рисунками.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Найдётся 2 синих шарика без рисунков — верно.
2) Если шарик красный, то на нём есть рисунок — неверно.
3) Найдётся 4 красных шарика с рисунками — неверно.
4) Не найдётся 5 синих шариков с рисунками — верно.
Задание 18 № 518669
Тане на день рождения подарили 15 шариков, 8 из которых жёлтые, а остальные зелёные. Таня на трёх шариках нарисовала рисунки маркером, чтобы подарить маме, папе и брату. Выберите все утверждения, которые будут верны при указанных условиях независимо от того, на каких шариках Таня нарисовала рисунки
1) Найдётся 2 зелёных шарика без рисунков.
2) Не найдётся 5 жёлтых шариков с рисунками.
3) Если шарик жёлтый, то на нём Таня нарисует рисунок.
4) Найдётся 3 жёлтых шарика с рисунками.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1) Найдётся 2 зелёных шарика без рисунков — верно.
2) Не найдётся 5 жёлтых шариков с рисунками — верно.
3) Если шарик жёлтый, то на нём Таня нарисует рисунок — неверно.
4) Найдётся 3 жёлтых шарика с рисунками — неверно.
Задание 18 № 522346
Кондитер испёк 40 печений, из них 10 штук он посыпал корицей, а 20 штук собирается посыпать сахаром (кондитер может посыпать одно печенье и корицей, и сахаром, а может вообще ничем не посыпать). Выберите утверждения, которые будут верны при указанных условиях независимо от того, какие печенья кондитер посыплет сахаром.
1) Найдётся 7 печений, которые ничем не посыпаны.
2) Найдётся 8 печений, посыпанных и сахаром, и корицей.
3) Если печенье посыпано корицей, то оно посыпано и сахаром.
4) Не может оказаться 12 печений, посыпанных и сахаром, и корицей.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Найдётся 7 печений, которые ничем не посыпаны. — верно, поскольку он может посыпать 10 печений корицей, 20 печений сахаром, а остальные 10 ничем не посыпать.
2) Найдётся 8 печений, посыпанных и сахаром, и корицей. — неверно, поскольку он может посыпать 10 печений корицей, 20 печений сахаром, а остальные 10 ничем не посыпать.
3) Если печенье посыпано корицей, то оно посыпано и сахаром. — неверно, поскольку он собирается посыпать 20 печений сахаром, а корицей он посыпал только 10 печений.
4) Не может оказаться 12 печений, посыпанных и сахаром, и корицей. — верно, поскольку он собирается посыпать 20 печений сахаром, а корицей он посыпал только 10 печений.
Задание 18 № 522683
На соревнованиях сборная России завоевала медалей больше, чем сборная Канады, сборная Канады — больше, чем сборная Германии, а сборная Норвегии — меньше, чем сборная Канады. Выберите утверждения, которые верны при указанных условиях.
1) Из названных сборных команда Канады заняла второе место по числу медалей.
2) Среди названных сборных есть три, завоевавшие равное количество медалей.
3) Сборная Германии завоевала больше медалей, чем сборная России.
4) Сборная России завоевала больше медалей, чем каждая из остальных трёх сборных.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение соответствует условию, поскольку сборная Канады завоевала медалей меньше, чем Россия, но больше, чем остальные сборные.
2) Утверждение не соответствует условию.
3) Утверждение не соответствует условию.
4) Утверждение соответствует условию, поскольку сборная России завоевала медалей больше, чем остальные сборные.
Ответ: 14 или 41.
Задание 18 № 522725
В доме Маши меньше этажей, чем в доме Стаса, в доме Ксюши больше этажей, чем в доме Стаса, а в доме Нади больше этажей, чем в Машином доме, но меньше, чем в Ксюшином доме. Выберите утверждения, которые верны при указанных условиях.
1) В доме Маши меньше этажей, чем в доме Нади.
2) Дом Ксюши самый многоэтажный среди перечисленных четырёх.
3) Среди этих четырёх домов есть три дома с одинаковым количеством этажей.
4) В Надином доме один этаж.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение соответствует условию, так как в доме Нади больше этажей, чем у Маши.
2) Утверждение соответствует условию, так как в доме Ксюши больше этажей, чем у Стаса, Маши и Нади.
3) Утверждение не соответствует условию.
4) Утверждение не соответствует условию.
Ответ: 12 или 21.
Задание 18 № 525546
В фирме работает 50 сотрудников, из них 40 человек знают английский язык, а 20 — немецкий. Выберите все утверждения, которые верны при указанных условиях.
1) В этой фирме нет ни одного сотрудника, знающего и английский, и немецкий языки.
2) Не больше 20 сотрудников этой фирмы знают и английский, и немецкий языки.
3) В этой фирме хотя бы три сотрудника знают и английский, и немецкий языки.
4) Если сотрудник этой фирмы знает английский язык, то он знает и немецкий.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Неверно. Утверждение противоречит указанным данным.
2) Поскольку немецкий знают 20 человек, следовательно, не больше 20 человек знают два иностранных языка. Утверждение верно.
3) Утверждение верно, поскольку в фирме всего 50 человек и из них 40 человек знают английский язык, немецкий.
4) Утверждение не следует из приведённых данных.
Задание 18 № 510297
Повар испёк 50 рогаликов, из них 15 штук он посыпал корицей, а 20 рогаликов посыпал сахаром. Выберите утверждения, которые верны при указанных условиях.
1) Найдётся 10 рогаликов, которые ничем не посыпаны.
2) Если рогалик посыпан сахаром, то он посыпан и корицей.
3) Не может оказаться больше 20 рогаликов, посыпанных и сахаром, и корицей.
4) Найдётся 20 рогаликов, посыпанных и сахаром, и корицей.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 18 № 510299
Повар испёк 40 печений, из них 10 штук он посыпал корицей, а 20 печений посыпал сахаром. Выберите утверждения, которые верны при указанных условиях.
1) Найдётся 20 печений, посыпанных и сахаром, и корицей.
2) Найдётся 10 печений, которые ничем не посыпаны.
3) Не может оказаться больше 10 печений, посыпанных и сахаром, и корицей.
4) Если печенье посыпано сахаром, то оно посыпано и корицей.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 18 № 512546
В фирме N работает 100 человек, из них 70 человек знают португальский язык, а 50 — французский. Выберите утверждения, которые верны при указанных условиях.
1) В фирме N хотя бы пять человек знают и португальский, и французский языки.
2) Нет ни одного человека в этой фирме, знающего и португальский, и французский языки.
3) Если человек из этой фирмы знает португальский язык, то он знает и французский.
4) Не более 50 человек из этой фирмы знают и португальский, и французский языки.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Это задание ещё не решено, приводим решение прототипа.
В классе учатся 20 человек, из них 13 человек посещают кружок по истории, а 10 человек — кружок по математике. Выберите утверждения, которые следуют из приведённых данных. В этом классе
1) нет ученика, который не посещает ни кружок по истории, ни кружок по математике
2) найдутся хотя бы два человека, которые посещают оба кружка
3) если ученик не ходит на кружок по истории, то он обязательно ходит на кружок по математике
4) не найдётся 11 человек, которые посещают оба кружка
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Утверждение не следует из приведённых данных, поскольку возможна ситуация, когда из 13 человек, посещающих кружок по истории, десять человек посещают ещё и кружок по математике, а оставшиеся семь учеников класса не посещают ни один кружок.
2) Утверждение следует из приведённых данных. Более того, можно утверждать, что минимум три человека посещают сразу оба кружка, поскольку суммарное количество учеников, посещающих кружки, на 3 больше количества учеников в классе.
3) Утверждение не следует из приведённых данных, поскольку возможна ситуация, когда 10 человек из тринадцати, посещающих кружок по истории ходят и на кружок по математике. При этом окажется, что семь человек не посещают ни одного кружка.
4) Кружок по математике посещают 10 человек, поэтому более 10 человек посещать оба кружка не может. Утверждение верно.
Задание 18 № 507966
Задание 18 № 522346
4 Не найдётся 11 человек из этого класса, которые посещают оба кружка.
Mathb-ege. sdamgia. ru
18.08.2020 8:22:47
2019-12-26 09:48:31
Источники:
Https://mathb-ege. sdamgia. ru/test? likes=508050
Задание 18. Числа и их свойства, Профильный ЕГЭ, Математика » /> » /> .keyword { color: red; } Егэ математика задание 18 номер 508050
Задание 18. Числа и их свойства — профильный ЕГЭ по Математике
Задание 18. Числа и их свойства — профильный ЕГЭ по Математике
Вот она! Загадочная. Нестандартная. Задача 18 Профильного ЕГЭ по математике.
Эта задача оценивается в целых 4 первичных балла, и они пересчитываются в 9-10 тестовых.
Можно ничего не знать. И удачно подобрать пример. И получить 1 балл за пункт (а). Во всяком случае, попробовать это сделать.
А можно потратить 2 часа на перебор вариантов… и так ничего и не найти. Если не знаешь секретов решения этой задачи. ОК, некоторые из секретов мы расскажем.
Действительно, пункт (а) в задаче 18 почти всегда решается сразу. Пункт (б) тоже решается быстро, но только если повезет. Пункт (в) без специальной подготовки решить невозможно.
Необходимая теория для решения задач на числа и их свойства — это всего две страницы. Делимость чисел, наибольший общий делитель и наименьшее общее кратное, основная теорема арифметики, признаки делимости на 3, на 4, на 5, на 8, 9, 10 и 11. Ничего сложного.
Затем стоит освоить метод «Оценка плюс пример». Для того чтобы применить этот метод, от строгих оценок, которые даны в условии (со знаками > или < ), переходим к нестрогим (со знаками ≥ или ≤ ).
Узнать больше о решении уравнений в целых числах. В школьных учебниках этого нет.
Один из необходимых навыков для решения пункта (в) – работа с неравенствами. В школьных учебниках этого тоже нет.
Многие считают, что если в этой задаче в пункте (а) ответ «да», то во втором обязательно должно быть «нет». Авторитетно заявляем: нет, необязательно! Может быть любое сочетание из «да» и «нет». И может быть «да» в обоих пунктах, и «нет» в обоих.
Если вопрос в этой задаче (неважно, в каком пункте) формулируется как «Может ли быть…» — и дальше некоторое утверждение, и ваш ответ: «Да», — то одного вашего «Да» недостаточно. Нужен пример. И если вы его подберете, вы не обязаны объяснять, как нашли его.
Если ответ на этот вопрос: «Нет», то вам нужно это доказать. «Нет, потому что…» — и приводите свое доказательство.
В общем, проще показать это на примерах:
1. За прохождение каждого уровня игры на планшете можно получить от одной до трёх звёзд. При этом заряд аккумулятора планшета уменьшается на 3 пункта при получении трёх звёзд, на 6 пунктов при получении двух звёзд и на 9 пунктов при получении одной звезды. Витя прошёл несколько уровней игры подряд.
А) Мог ли заряд аккумулятора уменьшиться ровно на 32 пункта?
Б) Сколько уровней игры было пройдено, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?
В) За пройденный уровень начисляется 9000 очков при получении трёх звёзд, 5000 — при получении двух звёзд и 2000 — при получении одной звезды. Какое наибольшее количество очков мог получить Витя, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?
А) Заметим, что заряд аккумулятора при прохождении уровня уменьшается на 3, 6 или 9 пунктов, и все эти числа делится на 3. Поскольку 32 не делится на 3, заряд не мог уменьшиться на 32 пункта.
Б) Да, на 33 пункта заряд мог уменьшиться.
Пусть на х уровнях получено по 3 звезды, на у уровнях по 2 звезды и на z уровнях по 1 звезде.
Сложив уравнения и, получим, что (пройдено 7 уровней).
Системе удовлетворяют При этом заряд аккумулятора уменьшился на 33 пункта.
В) Поскольку и, получаем, что. Возможны варианты:
, тогда, получено 47 тысяч очков.
, тогда, получено 48 тысяч очков.
, тогда, получено 49 тысяч очков – это максимально возможное количество.
Это была простая задача №18. А вот сложная.
2. В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
А) Мог ли средний балл в школе № 1 вырасти в два раза?
Б) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Мог ли первоначальный балл в школе № 2 равняться 1?
В) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Пусть в первой школе писали тест учеников, а во второй учеников, причем
, .
Пусть учащиеся первой школы набрали в сумме балл, а учащиеся второй баллов.
Тогда средние баллы равны и.
Пусть из первой школы во вторую перешел ученик, набравший за тест баллов.
А) Предположим, что средний балл в школе № 1 вырос в два раза. Тогда.
Поскольку положительно, получаем, что – противоречие с условием.
Ответ в пункте (а): нет.
Б) Во втором пункте ответ тоже «нет». Предположим, что. Получим:
Что будет, если? Тогда.
Подставив эти и в уравнение
, получим: , , противоречие с условием, поскольку – целое. Значит,
С другой стороны, из условия получаем, что
, значит, .
Но если, то и – получили противоречие.
В) По условию, и в первой, и во второй школах первоначально средний балл был целым числом. Он не может быть равен единице (из пункта (б)). Проверим, может ли он быть равен 2, 3, 4…
Пусть первоначально средний балл равен 2. Тогда
. Условие по-прежнему должно выполняться.
Преобразуя эти уравнения, получим:
Значит, и. Подходит и.
При таких значениях уравнение имеет решения или.
Подставим поочередно пары и в уравнение
, получим, что целых решений это уравнение не имеет.
Пусть первоначально средний балл равен 3. Тогда
Например, в первой школе тест писали 2 учащихся и набрали 22 и 18 баллов. В школе № 2 писали тест 49 учащихся и каждый набрал по три балла, а у перешедшего из одной школы в другую учащегося 18 баллов.
Да, непростая это задача, девятнадцатая из варианта ЕГЭ. Но если к ней привыкнуть, потренироваться, — то вполне можно решить и заработать необходимые на ЕГЭ баллы. Мы учим решать эту задачу на наших интенсивах в ЕГЭ-Студии, а также на Онлайн-курсе. Многим нашим выпускникам она обеспечила поступление на бюджетные отделения ведущих вузов.
, тогда, получено 47 тысяч очков.
Ege-study. ru
28.01.2019 16:11:53
2019-01-28 16:11:53
Источники:
Https://ege-study. ru/ru/ege/materialy/matematika/zadanie-19-profilnogo-ege-po-matematike-chisla-i-ix-svojstva/
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
Раскроем скобки.
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$
$х=-{17}/{5}$
$х = — 3,4$
Ответ: $- 3,4$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
$x = 0; ax + b = 0$
2. Решаем получившиеся уравнения каждое отдельно.
Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$
$4х^2 — 5х = 0$
Вынесем х как общий множитель за скобки:
$х (4х — 5) = 0$
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
$ax^2 + c = 0$
$ax^2 = — c$
$x_2 = {-c}/{a}$
При решении последнего уравнения возможны два случая:
если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$
если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.
$x^2 — 16 = 0$
$x^2 = 16$
$x = ±4$
Ответ: $х_1 = 4, х_2 = — 4$
Решение полного квадратного уравнения
Решение с помощью дискриминанта
Дискриминантом квадратного уравнения D называется выражение
$b^2 — 4ac$.
При решении уравнения с помощью дискриминанта возможны три случая:
1. $D > 0$. Тогда корни уравнения равны:
$x_{1,2}={-b±√D}/{2a}$
2. $D = 0$. В данном случае решение даёт два двукратных корня:
$x_{1}=x_{2}={-b}/{2a}$
3. $D < 0$. В этом случае уравнение не имеет корней.
$3х^2 — 11 = -8х$
Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней
$3х^2 + 8х — 11 = 0$
$a = 3 ,b = 8, c = — 11$
$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$
$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$
$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$
Ответ: $x_1=1, x_2=-3{2}/{3}$
Устные способы
Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$
$4х^2+ 3х — 7 = 0$
$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$
Ответ: $х_1= 1, х_2 = -{7}/{4}$
Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$
$5х^2+ 7х + 2 = 0$
$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$
Ответ: $х_1= -1, х_2 = -{2}/{5}$
Кубические уравнения
Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.
$(x — 3)^3 = 27$
Представим обе части как основания в третьей степени
$(x — 3)^3 = $33
Извлечем кубический корень из обеих частей
$х — 3 = 3$
Соберем известные слагаемые в правой части
$x = 6$
Ответ: $х = 6$
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
$4x + 1 — {3}/{x} = 0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x + 1 — {3}/{x}= 0¦· x$
$4x · x + 1 · x — {3·x}/{x} = 0$
3. решаем полученное уравнение
$4x^2 + x — 3 = 0$
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = {3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = {3}/{4}$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$
${3х-5}/{-2}={1}/{х}$
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х (3х — 5) = -2$
Раскроем скобки и соберем все слагаемые в левой части уравнения
$3х^2- 5х + 2 = 0$
Решим данное квадратное уравнение первым устным способом, т.к.
$a + b + c = 0$
$x_1 = 1, x_2 = {2}/{3}$
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1 = 1, x_2 = {2}/{3}$
Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.
Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.
Например,
${2}/{x}+5x=7$ – рациональное уравнение
$3x+√x=7$ — иррациональное уравнение (содержит корень)
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль общий знаменатель.
Решить уравнение: $4x+1-{3}/{x}=0$
Решение:
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x ≠ 0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x+1-{3}/{x}=0|·x$
$4x·x+1·x-{3·x}/{x}=0$
3. решаем полученное уравнение
$4x^2+x-3=0$
Решим вторым устным способом, т.к. $а+с=b$
Тогда, $x_1=-1, x_2=-{3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=-1, x_2=-{3}/{4}$
При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$
Решить уравнение ${3x-5}/{-2}={1}/{x}$
Решение:
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х(3х-5)=-2$
Раскроем скобки и соберем все слагаемые в левой стороне
$3х^2-5х+2=0$
Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$
$x_1=1, x_2={2}/{3}$
В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=1, x_2={2}/{3}$
Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.
Чтобы решить иррациональное уравнение, необходимо:
- Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
- Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
- Решить полученное рациональное уравнение.
- Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.
Решение:
Обе части уравнение возведем в квадрат:
$√{4х-3}^2=х^2$
Получаем квадратное уравнение:
$4х-3=х^2$
Перенесем все слагаемые в левую часть уравнения:
${-х}^2+4х-3=0$
Решим данное квадратное уравнение устным способом, так как
$a+b+c=0$
$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$√{4·1-3}=1$
$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.
$√{4·(3)-3}=3$
$√9=3$
$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит
$х_1=1$ наименьший корень.
Ответ: $1$
Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
- Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$
Решить уравнение: $х-6=√{8-х}$
Возведем обе части уравнения в квадрат
$(х-6)^2=8-х$
В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение
$х^2-2·6·х+6^2=8-х$
$х^2-12х+36=8-х$
Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.
$х^2-12х+36-8+х=0$
Приводим подобные слагаемые:
$х^2-11х+28=0$
Найдем корни уравнения через дискриминант:
$D=b^2-4ac=121-4·28=121-112=9=3^2$
$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$
$x_1=7; x_2=4$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$x_1=7$
$7-6=√{8-7}$
$1=1$, получили верное равенство, следовательно, корень нам подходит.
$x_2=4$
$4-6=√{8-4}$
$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.
Ответ: $7$
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n⋅a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.
Решить уравнение $25·5^х=1$
Решение:
В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$
$5^2·5^х=5^0$
При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются
$5^{2+х}=5^0$
Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели
$2+х=0$
$х=-2$
Ответ: $-2$
Решить уравнение $2^{3х+2}-2^{3х-2}=30$
Решение:
Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель
$2^{3x+2}-2^{3x-2}=30$
$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$
$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$
$2^{3x-2}(2^4-1)=30$
$2^{3x-2}·15=30$
Разделим обе части уравнения на $15$
$2^{3х-2}=2$
$2^{3х-2}=2^1$
$3х-2=1$
$3х=3$
$х=1$
Ответ: $1$