Приведите пример четырёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Спрятать решение
Решение.
Пусть наше число имеет вид Тогда имеем
И так как число делится на 4,
делится на 4. Можно заметить, что если среди цифр есть хотя бы три единицы, то равенство невозможно, так как сумма будет больше произведения. Если единица только одна, то произведение будет слишком большое. Таким образом, среди цифр есть ровно две единицы. Рассмотрим двузначные числа, которые делятся на 4, две их последние цифры образуют число, делящееся на 4. Нельзя брать числа с нулём, так как в этом случае произведение будет равно нулю.
12: тогда одна из оставшихся цифр 1, а другая 4.
16: тогда одна из оставшихся цифр 1, а никакая другая не подойдёт.
24: значит, оставшиеся цифры — единицы.
Остальные числа будут давать слишком большое произведение или нечётную сумму.
Таким образом, искомые числа: 1412, 4112, 1124.
Ответ: 1124, или 1412, или 4112.
Каталог заданий
Версия для печати и копирования в MS Word
1
Тип 19 № 507010
Приведите пример четырёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Аналоги к заданию № 507010: 506362 506874 511623 511663 514752 522367 Все
Раздел кодификатора ФИПИ: Цифровая запись числа
Решение
·
·
Сообщить об ошибке · Помощь
501044 решу егэ математика профиль
Задание 10 № 508780
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:
Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:
Приведем решение Ирины Шраго.
Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей
Задание 10 № 508780
Задание 10 508780.
Math-ege. sdamgia. ru
08.11.2017 2:12:44
2017-11-08 02:12:44
Источники:
Https://math-ege. sdamgia. ru/problem? id=508780
14.05.2022 Пробный ЕГЭ 2022 профиль математика 3 варианта с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } 501044 решу егэ математика профиль
14.05.2022 Пробный ЕГЭ 2022 профиль математика 3 варианта с ответами
14.05.2022 Пробный ЕГЭ 2022 профиль математика 3 варианта с ответами
2)На олимпиаде по экономике 300 участников разместили в четырнадцати аудиториях. В первых тринадцати удалось разместить по 22 участника, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории? Ответ округлите до сотых.
3)В четырёхугольник ABCD вписана окружность, АВ = 19, ВС = 18 и CD = 32. Найдите длину четвёртой стороны четырёхугольника.
5)Площадь поверхности правильной треугольной призмы равна 70, а боковой – 62. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь поверхности отсечённой треугольной призмы.
6)На рисунке изображены график функции y = f(x) и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
8)Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
10)В ящике 14 красных и 12 синих фломастеров. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
13)В правильной четырёхугольной пирамиде SABCD точка К является серединой ребра SD, а точка L – серединой стороны ВС основания ABCD. Плоскость AKL пересекает ребро SC в точке N. а) Докажите, что SN : NC = 2 : 1. б) Найдите угол между плоскостями AKL и ABC, если АВ = 10, а высота пирамиды равна 20.
15)Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, – 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Задания с 2 варианта
2)На олимпиаде по экономике 355 участников разместили в шестнадцати аудиториях. В первых пятнадцати удалось разместить по 23 участника, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории? Ответ округлите до сотых.
3)В четырёхугольник ABCD вписана окружность, АВ = 18, ВС = 17 и CD = 33. Найдите длину четвёртой стороны четырёхугольника.
5)Площадь поверхности правильной треугольной призмы равна 102, а боковой – 78. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь поверхности отсечённой треугольной призмы.
8)Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 125 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
10)В ящике 7 красных и 9 синих фломастеров. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
13)В правильной четырёхугольной пирамиде SABCD точка К является серединой ребра SD, а точка L – серединой стороны ВС основания ABCD. Плоскость AKL пересекает ребро SC в точке N. а) Докажите, что SN : NC = 2 : 1. б) Найдите угол между плоскостями AKL и ABC, если АВ = 9, а высота пирамиды равна 15.
15)Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 600 рублей, а на заводе, расположенном во втором городе, – 300 рублей. Антон готов выделять 720 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Задания с 3 варианта
2)На олимпиаде по экономике 310 участников разместили в четырнадцати аудиториях. В первых тринадцати удалось разместить по 23 участника, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории? Ответ округлите до сотых.
3)В четырёхугольник ABCD вписана окружность, АВ = 17, ВС = 16 и CD = 34. Найдите длину четвёртой стороны четырёхугольника.
5)Площадь поверхности правильной треугольной призмы равна 88, а боковой – 72. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь поверхности отсечённой треугольной призмы.
8)Имеется два сплава. Первый содержит 5% никеля, второй — 40% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
10)В ящике 9 красных и 7 синих фломастеров. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
15)Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, – 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
05.2022 Пробный ЕГЭ 2022 профиль математика 3 варианта с ответами
2)На олимпиаде по экономике 300 участников разместили в четырнадцати аудиториях. В первых тринадцати удалось разместить по 22 участника, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории? Ответ округлите до сотых.
3)В четырёхугольник ABCD вписана окружность, АВ = 19, ВС = 18 и CD = 32. Найдите длину четвёртой стороны четырёхугольника.
5)Площадь поверхности правильной треугольной призмы равна 70, а боковой – 62. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь поверхности отсечённой треугольной призмы.
6)На рисунке изображены график функции y = f(x) и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
8)Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
10)В ящике 14 красных и 12 синих фломастеров. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
13)В правильной четырёхугольной пирамиде SABCD точка К является серединой ребра SD, а точка L – серединой стороны ВС основания ABCD. Плоскость AKL пересекает ребро SC в точке N. а) Докажите, что SN : NC = 2 : 1. б) Найдите угол между плоскостями AKL и ABC, если АВ = 10, а высота пирамиды равна 20.
15)Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, – 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
100ballnik. com
16.08.2018 13:09:57
2020-01-15 22:41:25
Источники:
Https://100ballnik. com/14-05-2022-%D0%BF%D1%80%D0%BE%D0%B1%D0%BD%D1%8B%D0%B9-%D0%B5%D0%B3%D1%8D-2022-%D0%BF%D1%80%D0%BE%D1%84%D0%B8%D0%BB%D1%8C-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0-3-%D0%B2%D0%B0/
Задание 4 решу ЕГЭ 2022 математика профильный уровень 100 заданий с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } 501044 решу егэ математика профиль
Задание 4 решу ЕГЭ 2022 математика профильный уровень 100 заданий с ответами
Задание 4 решу ЕГЭ 2022 математика профильный уровень 100 заданий с ответами
Более 100 тренировочных прототипов задания №4 решу ЕГЭ 2022 по математике 11 класс профильный уровень с ответами и решением для практики. Задание №4 профильного ЕГЭ по математике – вычисления и преобразования.
На ЕГЭ вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки.
Рациональные выражения ЕГЭ 2022 по математике профиль:
Иррациональные выражения ЕГЭ 2022 по математике профиль:
Степенные выражения ЕГЭ 2022 по математике профиль:
Логарифмические выражения ЕГЭ 2022 по математике профиль:
Тригонометрические выражения ЕГЭ 2022 по математике профиль:
1)Найдите значение выражения log 5 27⋅log 3 25.
2)Найдите значение выражения 14 sin225°+cos2205° .
3)Найдите значение выражения 5 cos233°+cos2123° .
4)Найдите значение выражения 18(sin216°−cos216°) cos32°
5)Найдите значение выражения (1−log318)(1−log618).
6)Найдите значение выражения log336 2+log34 .
7)Найдите значение выражения log2(log5625).
8)Найдите значение выражения 7log550 7log52 .
9)Найдите значение выражения log723 log4923 .
10)Найдите значение выражения 15cos19° cos341° .
11)Найдите значение выражения 3cos39° sin51° .
12)Найдите значение выражения 15√x−3 √x + 3√x x +2x−8 при x=3.
13)Найдите значение выражения f(x+3) f(x−3) , если f(x)=5x.
14)Найдите значение выражения (√23−√15)(√23+√15).
15)Найдите значение выражения 63√2+2·62√2 65√2−1 .
16)Найдите значение выражения 83√5−1⋅81−√5:82√5−1.
17)Найдите значение выражения 6x⋅(2×9)4:(4×12)3 при x=5.
18)Найдите значение выражения x⋅52x+1⋅25−x при x=3.
19)Найдите значение выражения 3sinβ+15cosβ−8 sinβ+5cosβ+2 , если tgβ=−5.
20)Найдите значение выражения −6√3 cos390°⋅sin(−750°) .
21)Найдите значение выражения 5√14⋅5√16 5√7 .
22)Найдите значение выражения log0,85⋅log51,25.
23)Найдите значение выражения 18 √6 tg π 3 ⋅sin π 4 .
24)Найдите значение выражения 12√6tg π 6 ⋅cos π 4 .
25)Найдите значение выражения 5tg125°⋅tg35°.
26)Найдите значение выражения 7tg27°⋅tg117°.
27)Найдите значение выражения a+7b+12 a+5b+10 , если a b =5.
28)Найдите значение выражения a b, если 5a+2b 2a+5b =3.
Рациональные выражения ЕГЭ 2022 по математике профиль:
1)Найдите значение выражения log 5 27⋅log 3 25.
2)Найдите значение выражения 14 sin225°+cos2205° .
3)Найдите значение выражения 5 cos233°+cos2123° .
4)Найдите значение выражения 18(sin216°−cos216°) cos32°
5)Найдите значение выражения (1−log318)(1−log618).
6)Найдите значение выражения log336 2+log34 .
7)Найдите значение выражения log2(log5625).
8)Найдите значение выражения 7log550 7log52 .
9)Найдите значение выражения log723 log4923 .
10)Найдите значение выражения 15cos19° cos341° .
11)Найдите значение выражения 3cos39° sin51° .
12)Найдите значение выражения 15√x−3 √x + 3√x x +2x−8 при x=3.
13)Найдите значение выражения f(x+3) f(x−3) , если f(x)=5x.
14)Найдите значение выражения (√23−√15)(√23+√15).
15)Найдите значение выражения 63√2+2·62√2 65√2−1 .
16)Найдите значение выражения 83√5−1⋅81−√5:82√5−1.
17)Найдите значение выражения 6x⋅(2×9)4:(4×12)3 при x=5.
18)Найдите значение выражения x⋅52x+1⋅25−x при x=3.
19)Найдите значение выражения 3sinβ+15cosβ−8 sinβ+5cosβ+2 , если tgβ=−5.
20)Найдите значение выражения −6√3 cos390°⋅sin(−750°) .
21)Найдите значение выражения 5√14⋅5√16 5√7 .
22)Найдите значение выражения log0,85⋅log51,25.
23)Найдите значение выражения 18 √6 tg π 3 ⋅sin π 4 .
24)Найдите значение выражения 12√6tg π 6 ⋅cos π 4 .
25)Найдите значение выражения 5tg125°⋅tg35°.
26)Найдите значение выражения 7tg27°⋅tg117°.
27)Найдите значение выражения a+7b+12 a+5b+10 , если a b =5.
28)Найдите значение выражения a b, если 5a+2b 2a+5b =3.
Иррациональные выражения ЕГЭ 2022 по математике профиль.
100ballnik. com
19.08.2017 20:35:50
2017-08-19 20:35:50
Источники:
Https://100ballnik. com/%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5-4-%D1%80%D0%B5%D1%88%D1%83-%D0%B5%D0%B3%D1%8D-2022-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0-%D0%BF%D1%80%D0%BE%D1%84%D0%B8%D0%BB%D1%8C/

В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки. Ответами к заданиям 1–22 являются последовательность цифр, число или слово (словосочетание). Ответы запишите в поля ответов в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ № 1 справа от номеров соответствующих заданий, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Скачать тренировочный вариант ЕГЭ: Скачать
Скачать ответы на тренировочный вариант ЕГЭ: Скачать
Задания:
1. Рассмотрите таблицу «Методы биологических исследований» и заполните ячейку, вписав соответствующий термин. Применяется для выявления геномных мутаций.
2. Исследователь добавлял в стакан коровьего молока желудочный сок собаки. Как спустя час в стакане изменится содержание дисахарида лактозы и животных жиров? Для каждой величины определите соответствующий характер её изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
3. Площадь земель, покрытых лесом, в России составляет примерно 1200 млн га. Известно, что 12 га леса связывают 18 тонн диоксида углерода в год. Сколько млн тонн углекислого газа может быть связано за год за счет российских лесов?
4. Определите вероятность (в %) гибели от анемии ребенка, родившегося в браке гомозиготных по рецессивному аллелю родителей, если эта форма анемии наследуется как аутосомный доминантный признак. В ответ запишите только соответствующее число.
5. Каким номером на рисунке обозначена структура, образующая спираль в сперматозоидах млекопитающих?
6. Установите соответствие между характеристиками и структурами, обозначенными на рисунке цифрами 1, 2, 3, 4: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
7. Выберите три признака, которые соответствуют описаниям селекции. Запишите в таблицу цифры, под которыми они указаны.
1) выведение новых штаммов микроорганизмов
2) получение новых семейств растений
3) получение генномодифицированных растений
4) выведение тритикале при скрещивании пшеницы и ржи
5) получение рекомбинантной плазмиды
6) выведение пород животных и сортов растений
8. Установите последовательность этапов ферментативного катализа. Запишите в таблицу соответствующую последовательность цифр.
1) образование нестабильного комплекса фермент-продукт
2) сближение фермента и субстрата
3) начало распада комплекса фермент-продукт
4) формирование фермент-субстратного комплекса
5) высвобождение продукта и фермента
9. Какой цифрой на рисунке обозначена вторичная полость тела?
10. Установите соответствие между характеристиками и структурами тела дождевого червя, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
11. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Для растения, изображенного на рисунке, характерно:
1) гаметофит обоеполый — содержит архегонии и антеридии
2) дихотомическое ветвление
3) заросток сердцевидной формы
4) споры созревают в сорусах
5) споры образуются в спороносных колосках
6) гаметофит формирует вайи
12. Установите последовательность систематических групп, начиная с самого низкого ранга. Запишите в таблицу соответствующую последовательность цифр.
1) Эукариоты
2) Членистоногие
3) Ежемухи
4) Ежемуха свирепая
5) Двукрылые
6) Животные
13. Какой цифрой на рисунке указан тип научения, который изучал К. Лоренц?
14. Установите соответствие между характеристиками и типами научения, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
15. Выберите три верно обозначенные подписи к рисунку «Строение уха». Запишите цифры, под которыми они указаны.
1) серная (церуминозная) железа
2) наружный слуховой проход
3) слуховая косточка
4) овальное окно
5) преддверно-улитковый нерв
6) улитка
16. Установите последовательность событий, происходящих при свертывании крови. Запишите в таблицу соответствующую последовательность цифр.
1) разрушение тромбоцитов у места повреждения
2) превращение протромбина в тромбин
3) уплотнение рыхлой пробки тромбоцитов фибриновыми нитями
4) превращение фибриногена в фибрин
5) выделение тромбопластина
6) образование тромба
17. Прочитайте текст. Выберите три предложения, в которых даны описания географического видообразования. Запишите цифры, под которыми они указаны. (1)Видообразование происходит в результате расширения ареала исходного вида или при попадании популяции в новые условия. (2)Такое видообразование называют аллопатрическим. (3)Примером видообразования служит формирование двух подвидов погремка большого на одном лугу. (4)Естественный отбор способствовал формированию двух рас севанской форели, нерестящихся в разное время. (5)Репродуктивная изоляция особей не является обязательным условием видообразования. (6)Результатом изоляции является формирование эндемичных островных видов животных.
18. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Примеры антропогенных факторов воздействия:
1) разрушение озонового слоя под действием фреонов
2) гибель сусликов из-за пандемии
3) нарушение режима рек под влиянием деятельности бобров
4) разрыхление почв дождевыми червями
5) эвтрофикация водоемов из-за смыва удобрений
6) металлизация атмосферы
19. Установите соответствие между типами взаимоотношений и организмами, между которыми они устанавливаются: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
20. Установите последовательность этапов эволюции животных, начиная с самых древних представителей. Запишите соответствующую последовательность цифр.
1) стегоцефал
2) зверозубый ящер
3) тушканчик
4) сеймурия
5) кистеперая рыба
21. Проанализируйте таблицу «Роль прокариотов в экосистемах». Заполните пустые ячейки таблицы, используя элементы, приведённые в списке. Для каждой ячейки, обозначенной буквой, выберите соответствующий элемент из предложенного списка. Список элементов:
1) Редуценты
2) Бактерии-хемосинтетики
3) Продуценты
4) Гетеротрофы
5) Бактерии-фотосинтетики
6) Денитрифицирующие
7) Автотрофы
Консументы
22. Проанализируйте диаграмму, отражающую содержание холестерола ЛПНП (липопротеинов низкой плотности) в плазме крови обследованных в лаборатории людей. Выберите все утверждения, которые можно сформулировать на основании анализа представленных данных. Запишите в ответе цифры, под которыми указаны выбранные утверждения.
1) Пятеро из обследованных людей имеют значение содержания холестерола-ЛПНП в интервале от 200 до 249 мг/дл.
2) Более 60% пациентов имеют чрезвычайно высокий риск развития атеросклероза.
3) Значение содержания холестерола-ЛПНП более 300 мг/дл смертельно.
4) Более 50% обследованных людей имеют от 75 до 149 мг/дл холестеролЛПНП в плазме крови.
5) В плазме крови 4% людей содержание холестерола-ЛПНП находится в пределах от 50 до 74 мг/дл.
23. Какая переменная в этом эксперименте будет зависимой (изменяющейся), а какая — независимой (задаваемой)? Объясните, как в данном эксперименте можно поставить отрицательный контроль. С какой целью необходимо такой контроль ставить? * Отрицательный контроль – это экспериментальный контроль, при котором изучаемый объект не подвергается экспериментальному воздействию при сохранении всех остальных условий.
24. Предположите, почему для обработки кукурузных полей используют 2,4- Д. Каким веществом по результату действия на двудольные растения является 2,4-дихлорфеноксиуксусная кислота?
25. Рассмотрите рисунок. Какие пары комплементарных азотистых оснований ДНК отмечены буквами А и Б? При содержании большего количества каких пар азотистых оснований молекула ДНК будет медленнее подвергаться денатурации при воздействии повышенной температуры? Ответ поясните.
26. Некоторые виды лишайников являются трехкомпонентными, то есть включают клетки трех видов организмов: гриба, зеленой водоросли и цианобактерии. Какие функции могут выполнять цианобактерии в составе такого лишайника? Назовите не менее двух. Какие преимущества имеет гриб в составе трехкомпонентного лишайника по сравнению с двухкомпонентным?
27. У животных существует несколько типов брачных отношений, например, моногамия – образование стойких супружеских пар, полигамия – спаривание особи одного пола со множеством партнеров противоположного пола. Большинство видов гнездовых птиц практикуют моногамные отношения, а большинство видов млекопитающих — полигамные. Объясните, почему для гнездовых птиц стратегия моногамного поведения наиболее выгодна. По каким причинам птицы, как правило, не могут практиковать полигамию, как это делают млекопитающие? Ответ поясните.
28. Какой хромосомный набор (n) характерен для клеток мегаспорангия и мегаспоры цветкового растения? Объясните, из каких исходных клеток и в результате какого деления образуются клетки мегаспорангия и мегаспора.
29. Существует два вида наследственной слепоты, каждый из которых определяется рецессивными аллелями генов (а или b). Оба аллеля находятся в различных парах гомологичных хромосом. Какова вероятность рождения слепой внучки в семье, в которой бабушки по материнской и отцовской линиям хорошо видят (не имеют рецессивных генов), а оба дедушки дигомозиготны и страдают различными видами слепоты? Составьте схему решения задачи. Определите генотипы и фенотипы бабушек и дедушек, их детей и возможных внуков.
Вам будет интересно:
ЕГЭ по биологии 11 класс 2023. Новый тренировочный вариант №6 — №221121 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
Решение и ответы заданий Варианта №5 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
Найдите корень уравнения sqrt{9-8x}=-x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Задание 2.
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.
Задание 3.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
Задание 4.
Найдите значение выражения frac{2^{log_{9}3}}{2^{log_{9}243}}.
Задание 5.
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.
Задание 6.
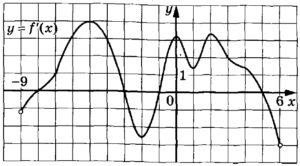
На рисунке изображён график у = f′(x) – производной функции f(x), определённой на интервале (–9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Задание 7.
Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону v=v_{0}cos frac{2pi t}{T}, где t – время с момента начала колебаний, Т = 2с – период колебаний, v0 = 1,6 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E=frac{mv^{2}}{2}, где m – масса груза в килограммах, v – скорость груза в м/с2. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Задание 8.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
Задание 9.
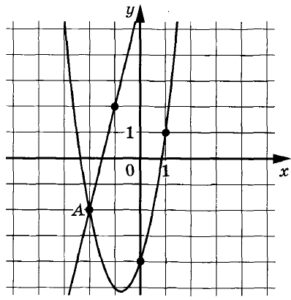
На рисунке изображены функций графики f(x) = ах2 + bх + с и g(x) = kx + d, которые пересекаются в точках А и В. Найдите абсциссу точки В.
Задание 10.
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Задание 11.
Найдите наибольшее значение функции у = х5 + 5х3 – 140х на отрезке [–8; –1].
Задание 12.
а) Решите уравнение sin2x + cos2x = 1.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi }{2}; –2pi].
Задание 13.
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно √3 , а сторона основания равна 2. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая l.
а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми l и СВ1.
Задание 14.
Решите неравенство 7^{log_{frac{1}{7}}log_{frac{1}{2}}(-x)}< 2^{log_{frac{1}{2}}log_{frac{1}{7}}(-x)}.
Задание 15.
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
– в январе 2026, 2027 и 2028 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
– в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.
Задание 16.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac{12}{49} площади трапеции ABCD.
Задание 17.
Найдите все такие значения а, при каждом из которых неравенство
–1 ≤ sinx(a – cos2x) ≤ 1
верно при всех действительных значениях х.
Задание 18.
Отношение трёхзначного натурального числа к сумме его цифр – целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
- ЕГЭ по математике профиль
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 6-7 | 27-33 | 3 |
| 8-9 | 39-45 | |
| 10-11-12 | 50-56-62 | 4 |
| 13-14-15 | 68-70-72 | 5 |
| 16-17-18 | 74-76-78 | |
| 19-20-21 | 80-82-84 | |
| 22-23-24 | 86-88-90 | |
| 25-26-27 | 92-94-96 | |
| 28-29-32 | 99-100 |
| Первичный балл | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тестовый балл | 27 | 33 | 39 | 45 | 50 | 56 | 62 | 68 | 70 | 72 | 74 | 76 | 78 |
| Итоговая оценка | 3 | 4 | 5 |
| Первичный балл | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30+ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тестовый балл | 80 | 82 | 84 | 86 | 88 | 90 | 92 | 94 | 96 | 98 | 99 | 100 |
| Итоговая оценка | 5 |
| Статистика | ||||
|---|---|---|---|---|
| 2020 | 17,6% | 38,3% | 37,5% | 6,6% |
| 2019 | 14,6% | 37,4% | 40,9% | 7,1% |
| 2017 / 2018 | 14,3% / 7% | 85,7% / 93% | ||
| 2016 | 15,3% | 55,7% | 25,2% | 3,8% |
| 2015 | 21,1% | 49,9% | 20,3% | 2,3% |
| не сдали | 27-59 | 60-79 | 80-100 |
Тренировочные варианты профильного ЕГЭ 2022 по математике с ответами.admin2022-04-17T20:59:36+03:00
Тренировочный вариант №172 профильного ЕГЭ (новый формат).
Тренировочный вариант №171 профильного ЕГЭ (новый формат).
Тренировочный вариант №170 профильного ЕГЭ (новый формат).
Тренировочный вариант №169 профильного ЕГЭ (новый формат).
Тренировочный вариант №168 профильного ЕГЭ (новый формат).
Тренировочный вариант №167 профильного ЕГЭ (новый формат).
Тренировочный вариант №166 профильного ЕГЭ (новый формат).
Тренировочный вариант №165 профильного ЕГЭ (новый формат).
Тренировочный вариант №164 профильного ЕГЭ (новый формат).
Тренировочный вариант №163 профильного ЕГЭ (новый формат).
Тренировочный вариант №162 профильного ЕГЭ (новый формат).
Тренировочный вариант №161 профильного ЕГЭ (новый формат).
Тренировочный вариант №160 профильного ЕГЭ (новый формат).
Тренировочный вариант №159 профильного ЕГЭ (новый формат).
Тренировочный вариант №158 профильного ЕГЭ (новый формат).
Тренировочный вариант №157 профильного ЕГЭ (новый формат).
Тренировочный вариант №156 профильного ЕГЭ (новый формат).
Тренировочный вариант №155 профильного ЕГЭ (новый формат).
Тренировочный вариант №154 профильного ЕГЭ (новый формат).
Тренировочный вариант №153 профильного ЕГЭ (новый формат).
Тренировочный вариант №152 профильного ЕГЭ (новый формат).
Тренировочный вариант №151 профильного ЕГЭ (новый формат).
Тренировочный вариант №150 профильного ЕГЭ (новый формат).
Тренировочный вариант №149 профильного ЕГЭ (новый формат).
Тренировочный вариант №148 профильного ЕГЭ (новый формат).
Тренировочный вариант №147 профильного ЕГЭ (новый формат).
Тренировочный вариант №146 профильного ЕГЭ (новый формат).
Тренировочный вариант №145 профильного ЕГЭ (новый формат).
Тренировочный вариант №144 профильного ЕГЭ (новый формат).
Тренировочный вариант №143 профильного ЕГЭ (новый формат).
Тренировочный вариант №142 профильного ЕГЭ (новый формат).
Тренировочный вариант №141 профильного ЕГЭ (новый формат).
Тренировочный вариант №140 профильного ЕГЭ (новый формат) (с видео-разбором).
Тренировочный вариант №139 профильного ЕГЭ.
Тренировочный вариант №138 профильного ЕГЭ.
Тренировочный вариант №137 профильного ЕГЭ.
Тренировочный вариант №136 профильного ЕГЭ.
Тренировочный вариант №135 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №134 профильного ЕГЭ.
Тренировочный вариант №133 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №132 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №131 профильного ЕГЭ.
Тренировочный вариант №130 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №129 профильного ЕГЭ.
Тренировочный вариант №128 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №127 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №126 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №125 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №124 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №123 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №122 профильного ЕГЭ (с видео-разбором).
Тренировочный вариант №121 профильного ЕГЭ.
Тренировочный вариант №120 профильного ЕГЭ.
Тренировочный вариант №119 профильного ЕГЭ.
Тренировочный вариант №118 профильного ЕГЭ.
Тренировочный вариант №117 профильного ЕГЭ.
Тренировочный вариант №116 профильного ЕГЭ.
Тренировочный вариант №115 профильного ЕГЭ.
Тренировочный вариант №114 профильного ЕГЭ.
Тренировочный вариант №113 профильного ЕГЭ.
Тренировочный вариант №112 профильного ЕГЭ.
Тренировочный вариант №111 профильного ЕГЭ.
Тренировочный вариант №110 профильного ЕГЭ.
Тренировочный вариант №109 профильного ЕГЭ.
Тренировочный вариант №108 профильного ЕГЭ.
Тренировочный вариант №107 профильного ЕГЭ.
Тренировочный вариант №106 профильного ЕГЭ.
Тренировочный вариант №105 профильного ЕГЭ.
Тренировочный вариант №104 профильного ЕГЭ.
Тренировочный вариант №103 профильного ЕГЭ.
Тренировочный вариант №102 профильного ЕГЭ.
Тренировочный вариант №101 профильного ЕГЭ.
Тренировочный вариант №100 профильного ЕГЭ.
Тренировочный вариант №99 профильного ЕГЭ.
Тренировочный вариант №98 профильного ЕГЭ.
Тренировочный вариант №97 профильного ЕГЭ.
Тренировочный вариант №96 профильного ЕГЭ.
Тренировочный вариант №95 профильного ЕГЭ.
Тренировочный вариант №94 профильного ЕГЭ.
Тренировочный вариант №93 профильного ЕГЭ.
Тренировочный вариант №92 профильного ЕГЭ.
Тренировочный вариант №91 профильного ЕГЭ.
Тренировочный вариант №90 профильного ЕГЭ.
Тренировочный вариант №89 профильного ЕГЭ.
Тренировочный вариант №88 профильного ЕГЭ.
Тренировочный вариант №87 профильного ЕГЭ.
Тренировочный вариант №86 профильного ЕГЭ.
Тренировочный вариант №85 профильного ЕГЭ.
Тренировочный вариант №84 профильного ЕГЭ.
Тренировочный вариант №83 профильного ЕГЭ.
Тренировочный вариант №82 профильного ЕГЭ.
Тренировочный вариант №81 профильного ЕГЭ.
Тренировочный вариант №80 профильного ЕГЭ.
Тренировочный вариант №79 профильного ЕГЭ.
Тренировочный вариант №78 профильного ЕГЭ.
Тренировочный вариант №77 профильного ЕГЭ.
Тренировочный вариант №76 профильного ЕГЭ.
Тренировочный вариант №75 профильного ЕГЭ.
Тренировочный вариант №74 профильного ЕГЭ.
Тренировочный вариант №73 профильного ЕГЭ.
Тренировочный вариант №72 профильного ЕГЭ.
Тренировочный вариант №71 профильного ЕГЭ.
Тренировочный вариант №70 профильного ЕГЭ.
Тренировочный вариант №69 профильного ЕГЭ.
Тренировочный вариант №68 профильного ЕГЭ.
Тренировочный вариант №67 профильного ЕГЭ.
Тренировочный вариант №66 профильного ЕГЭ.
Тренировочный вариант №65 профильного ЕГЭ.
Тренировочный вариант №64 профильного ЕГЭ.
Тренировочный вариант №63 профильного ЕГЭ.
Тренировочный вариант №62 профильного ЕГЭ.
Тренировочный вариант №61 профильного ЕГЭ.
Тренировочный вариант №60 профильного ЕГЭ.
Тренировочный вариант №59 профильного ЕГЭ.
Тренировочный вариант №58 профильного ЕГЭ.
Тренировочный вариант №57 профильного ЕГЭ.
Тренировочный вариант №56 профильного ЕГЭ.
Тренировочный вариант №55 профильного ЕГЭ.
Тренировочный вариант №54 профильного ЕГЭ.
Тренировочный вариант №53 профильного ЕГЭ.
Тренировочный вариант №52 профильного ЕГЭ.
Тренировочный вариант №51 профильного ЕГЭ.
Тренировочный вариант №50 профильного ЕГЭ.
Тренировочный вариант №49 профильного ЕГЭ.
Тренировочный вариант №48 профильного ЕГЭ.
Тренировочный вариант №47 профильного ЕГЭ.
Тренировочный вариант №46 профильного ЕГЭ.
Тренировочный вариант №45 профильного ЕГЭ.
Тренировочный вариант №44 профильного ЕГЭ.
Тренировочный вариант №43 профильного ЕГЭ.
Тренировочный вариант №42 профильного ЕГЭ.
Тренировочный вариант №41 профильного ЕГЭ.
Тренировочный вариант №40 профильного ЕГЭ.
Тренировочный вариант №39 профильного ЕГЭ.
Тренировочный вариант №38 профильного ЕГЭ.
Тренировочный вариант №37 профильного ЕГЭ.
Тренировочный вариант №36 профильного ЕГЭ.
Тренировочный вариант №35 профильного ЕГЭ.
Тренировочный вариант №34 профильного ЕГЭ.
Тренировочный вариант №33 профильного ЕГЭ.
Тренировочный вариант №32 профильного ЕГЭ.
Тренировочный вариант №31 профильного ЕГЭ.
Тренировочный вариант №30 профильного ЕГЭ.
Тренировочный вариант №29 профильного ЕГЭ.
Тренировочный вариант №28 профильного ЕГЭ.
Тренировочный вариант №27 профильного ЕГЭ.
Тренировочный вариант №26 профильного ЕГЭ.
Тренировочный вариант №25 профильного ЕГЭ.
Тренировочный вариант №24 профильного ЕГЭ.
Тренировочный вариант №23 профильного ЕГЭ.
Тренировочный вариант №22 профильного ЕГЭ.
Тренировочный вариант №21 профильного ЕГЭ.
Тренировочный вариант №20 профильного ЕГЭ.
Тренировочный вариант №19 профильного ЕГЭ.
Тренировочный вариант №18 профильного ЕГЭ.
Тренировочный вариант №17 профильного ЕГЭ.
Тренировочный вариант №16 профильного ЕГЭ.
Тренировочный вариант №15 профильного ЕГЭ.
Тренировочный вариант №14 профильного ЕГЭ.
Тренировочный вариант №13 профильного ЕГЭ.
Тренировочный вариант №12 профильного ЕГЭ.
Тренировочный вариант №11 профильного ЕГЭ.
Тренировочный вариант №10 профильного ЕГЭ.
Тренировочный вариант №9 профильного ЕГЭ.
Тренировочный вариант №8 профильного ЕГЭ.
Тренировочный вариант №7 профильного ЕГЭ.
Тренировочный вариант №6 профильного ЕГЭ.
Тренировочный вариант №5 профильного ЕГЭ.
Тренировочный вариант №4 профильного ЕГЭ.
Тренировочный вариант №3 профильного ЕГЭ.
Тренировочный вариант №2 профильного ЕГЭ.
Тренировочный вариант №1 профильного ЕГЭ.
Чтобы сдать профильное ЕГЭ по математике больше чем на 27 баллов, придётся усердно поработать. Важно не просто прорешать все возможные варианты с ФИПИ и Решу ЕГЭ, важно иметь полное системное представление о математике. Данные тренировочные варианты помогут вам проверить свои знания на практике, получить представление о трудностях на экзамене. Тренировочные варианты содержат задания разных уровней сложности:
1) 12 номеров с кратким вариантов ответа;
2) 7 номеров с развернутым вариантом ответа, из которых 2 последних задачи олимпиадного уровня.
На сайте math100.ru вы можете подготовиться к каждой теме, представленной в кодификаторе. Главное идти к цели — сдать не менее, чем на 100 баллов. И помни: «Математикой можно не заниматься только 2 дня в году: вчера и завтра».
Ресурс носит неофициальный информационно-справочный характер, персональные данные не собирает и не обрабатывает, на интеллектуальные права третьих лиц не претендует.
Все ссылки ведут напрямую на официальные сайты описываемых услуг.
Карта сайта
Тренировочная работа №4 статград по математике 11 класс ЕГЭ 2022, 12 тренировочных вариантов базового и профильного уровня МА2110401-МА2110412 с ответами и решением на все задания, официальная дата проведения работы статград 15 марта 2022 года.
Скачать варианты базового уровня
Скачать варианты профильного уровня
Скачать ответы и решения для вариантов
Решать варианты статград ЕГЭ 2022 по математике 11 класс база задания и ответы:
Решать варианты статград профильного уровня:
Сложные задания с варианта МА2110401:
2)Для ремонта требуется 63 рулона обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 6 рулонов?
3)Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) диаметр монеты Б) рост жирафа В) высота Эйфелевой башни Г) радиус Земли
- 1) 6400 км
- 2) 324 м
- 3) 20 мм
- 4) 5 м
4)Результаты соревнований по метанию молота представлены в таблице. Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Каков результат лучшей попытки (в метрах) спортсмена, занявшего четвёртое место?
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
6)Число больных гриппом в школе уменьшилось за месяц в десять раз. На сколько процентов уменьшилось число больных гриппом?
10)Квартира состоит из двух комнат, кухни, коридора и санузла (см. план). Первая комната имеет размеры 4 м×4,5 м, вторая — 4 м×4м , санузел имеет размеры 1,5 м ×1,5 м , длина коридора — 10,5 м. Найдите площадь кухни (в квадратных метрах).
11)У бабушки 10 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
12)Дмитрий Валентинович собирается в туристическую поездку на трое суток в некоторый город. В таблице дана информация о гостиницах в этом городе со свободными номерами на время его поездки. Дмитрий Валентинович хочет остановиться в гостинице, которая находится не далее чем в 2,5 км от центральной площади и рейтинг которой не ниже 8,5. Среди гостиниц, удовлетворяющих этим условиям, выберите гостиницу с наименьшей ценой номера за сутки. Сколько рублей стоит проживание в этой гостинице в течение трёх суток?
13)Ящик, имеющий форму куба с ребром 40 см без одной грани, нужно покрасить снаружи со всех сторон . Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
15)В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине B равен 115° . Найдите угол C. Ответ дайте в градусах.
16)Основанием четырёхугольной пирамиды является прямоугольник со сторонами 6 и 8. Найдите высоту этой пирамиды, если её объём равен 80.
18)Диагностика 30 машин в автосервисе показала, что у 5 машин нужно заменить тормозные колодки, а у 10 машин — заменить воздушный фильтр (колодки и фильтр требуют замены независимо друг от друга). Выберите утверждения, которые верны при указанных условиях вне зависимости от того, какие машины нуждаются в замене фильтра, а какие — в замене колодок.
- 1) Найдётся 6 машин, в которых нужно поменять и колодки, и фильтр.
- 2) Найдётся 9 машин, в которых не нужно менять ни колодки, ни фильтр.
- 3) Не найдётся 7 машин, в которых нужно менять и колодки, и фильтр.
- 4) Если в машине нужно менять колодки, то фильтр тоже нужно менять.
19)Найдите четырёхзначное натуральное число, кратное 36, произведение цифр которого больше 12, но меньше 18. В ответе укажите какое-нибудь одно такое число.
20)Расстояние между городами A и B равно 790 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 85 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 450 км от города A. Ответ дайте в км/ч.
21)Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 9 проводов. Сколько всего проводов протянуто между этими десятью столбами?
Сложные задания с варианта МА2110402:
2)Для ремонта требуется 66 рулонов обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 7 рулонов?
3)Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) высота вагона Б) рост восьмилетнего ребёнка В) высота Троицкой башни Кремля Г) длина реки Москвы
- 1) 134 см
- 2) 79,3 м
- 3) 370 см
- 4) 502 км
4)Результаты соревнований по метанию молота представлены в таблице. Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Каков результат лучшей попытки (в метрах) спортсмена, занявшего третье место?
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
6)Число больных гриппом в школе уменьшилось за месяц в двадцать раз. На сколько процентов уменьшилось число больных гриппом?
11)У бабушки 25 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
12)Дмитрий Валентинович собирается в туристическую поездку на трое суток в некоторый город. В таблице дана информация о гостиницах в этом городе со свободными номерами на время его поездки. Дмитрий Валентинович хочет остановиться в гостинице, которая находится не далее чем в 2,5 км от центральной площади и рейтинг которой не ниже 8,5. Среди гостиниц, удовлетворяющих этим условиям, выберите гостиницу с наименьшей ценой номера за сутки. Сколько рублей стоит проживание в этой гостинице в течение трёх суток?
13)Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить снаружи со всех сторон . Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
15)В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине B равен 142° . Найдите угол C. Ответ дайте в градусах.
16)Основанием четырёхугольной пирамиды является прямоугольник со сторонами 12 и 5. Найдите высоту этой пирамиды, если её объём равен 60.
18)Марусе на день рождения подарили 20 шариков, из которых 13 красных, а остальные синие. Маруся хочет на четырёх случайных шариках нарисовать рисунки маркером, чтобы подарить маме, папе, брату и сестре. Выберите утверждения, которые будут верны при указанных условиях независимо от того, на каких шариках Маруся нарисует рисунки. 1) Найдётся 4 красных шарика с рисунками. 2) Найдётся 2 синих шарика без рисунков. 3) Если шарик красный, то на нём есть рисунок. 4) Не найдётся 5 синих шариков с рисунками.
19)Найдите четырёхзначное натуральное число, кратное 12, произведение цифр которого больше 40, но меньше 45. В ответе укажите какое-нибудь одно такое число.
20)Расстояние между городами A и B равно 390 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 85 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 220 км от города A. Ответ дайте в км/ч.
21)Семь столбов соединены между собой проводами так, что от каждого столба отходит ровно 4 провода. Сколько всего проводов протянуто между этими восемью столбами?
Сложные задания с варианта МА2110409:
1)В сборнике билетов по физике всего 40 билетов, в 14 из них встречается вопрос по теме «Скорость». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Скорость».
4)Найдите − α 20cos2 , если sin α=−0,8 .
5)Объём куба равен 375√3 . Найдите его диагональ.
8)Товарный поезд каждую минуту проезжает на 450 метров меньше, чем скорый, и на путь в 630 км тратит времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
10)Первый игральный кубик обычный, а на гранях второго кубика числа 5 и 6 встречаются по три раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 5 и 6 очков. Какова вероятность того, что бросали второй кубик?
13)В правильной четырёхугольной пирамиде SABCD с основанием ABCD из точки B опущен перпендикуляр BH на плоскость SAD . а) Докажите, что ∠AHC = 90° . б) Найдите объём пирамиды, если HA = 2 и HC = 4.
15)В июле планируется взять в банке некоторую сумму в кредит на три года. Условия его возврата таковы: — каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года нужно внести платёж, равный 2,662 млн рублей. Сколько рублей было взято в банке, если известно, что долг был полностью погашен тремя равными платежами (то есть за три года)?
16)Из вершины тупого угла C треугольника ABC проведена высота CH . Окружность с центром H и радиусом HC второй раз пересекает стороны AC и BC в точках M и N соответственно, а прямая CH — эту окружность в точке D . а) Докажите, что угол MDN равен сумме углов A и B треугольника ABC . б) Найдите отношение MN к AB, если известно, что CM MA : 2 : 25 = и CN NB : 2:1 = .
18)У Вани есть несколько пакетов с вещами, каждый из которых весит целое число килограммов. Он хочет разложить все эти пакеты, не перекладывая их содержимое, по n имеющимся у него одинаковым рюкзакам. В каждый рюкзак можно положить любое число пакетов, суммарная масса которых не превосходит m килограммов. а) Сможет ли Ваня разложить таким образом семь пакетов, которые весят 3, 6, 9, 12, 15, 18 и 21 кг, если n = 3 и m = 29 ? б) Сможет ли Ваня разложить таким образом семь пакетов, которые весят 2, 5, 8, 11, 14, 17 и 20 кг, если n = 3 и m = 26 ? в) Какое наименьшее значение может принимать m , чтобы Ваня при n = 4 смог разложить таким образом девять пакетов, которые весят 3, 5, 7, 9, 11, 13, 15, 17 и 19 кг?
Сложные задания с варианта МА2110410:
1)В сборнике билетов по географии всего 25 билетов, в 15 из них встречается вопрос по теме «Реки и озёра». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Реки и озёра».
8)Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 560 км тратит времени на 4 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
10)Первый игральный кубик обычный, а на гранях второго кубика числа 1 и 2 встречаются по три раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 1 и 2 очка. Какова вероятность того, что бросали первый кубик?
15)В июле планируется взять в банке некоторую сумму в кредит на три года. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года нужно внести платёж, равный 2,592 млн рублей. Сколько рублей было взято в банке, если известно, что долг был полностью погашен тремя равными платежами (то есть за три года)?
18)У Вани есть несколько пакетов с вещами, каждый из которых весит целое число килограммов. Он хочет разложить все эти пакеты, не перекладывая их содержимое, по n имеющимся у него одинаковым рюкзакам. В каждый рюкзак можно положить любое число пакетов, суммарная масса которых не превосходит m килограммов. а) Сможет ли Ваня разложить таким образом семь пакетов, которые весят 3, 9, 12, 15, 18, 21 и 24 кг, если n = 3 и m = 35? б) Сможет ли Ваня разложить таким образом семь пакетов, которые весят 2, 8, 11, 14, 17, 20 и 23 кг, если n = 3 и m = 32 ? в) Какое наименьшее значение может принимать m , чтобы Ваня при n = 4 смог разложить таким образом девять пакетов, которые весят 3, 7, 9, 11, 13, 15, 17, 19 и 21 кг?
Сложные задания с варианта МА2110411:
1)В сборнике билетов по философии всего 50 билетов, в 6 из них встречается вопрос по теме «Пифагор». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме «Пифагор».
3)Диагонали четырёхугольника равны 34 и 38. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного четырёхугольника.
5)Основанием прямой призмы является ромб с диагоналями, равными 10 и 24. Найдите боковое ребро призмы, если площадь её поверхности равна 422.
8)Курага получается в процессе сушки абрикосов. Сколько килограммов абрикосов потребуется для получения 21 килограмма кураги, если абрикосы содержат 86 % воды, а курага содержит 18 % воды?
10)Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 5 очков в двух играх. Если команда выигрывает, она получает 4 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
15)В июле планируется взять в банке некоторую сумму в кредит на три года. Условия его возврата таковы: — каждый январь долг возрастает на 25 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года нужно внести платёж, равный 2,5 млн рублей. Сколько рублей было взято в банке, если известно, что долг был полностью погашен тремя равными платежами (то есть за три года)?
Другие работы статград по математике для 11 класса ЕГЭ 2022:
- Тренировочная работа статград №3 ЕГЭ по математике 11 класс
- Тренировочная работа статград №2 ЕГЭ 2022 по математике 11 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Цифровая запись числа
1. Задание 19 № 506263. Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9.
Пояснение.
Разложим число 20 на слагаемые различными способами:
20 = 9 + 9 + 2 = 9 + 8 + 3 = 9 + 7 + 4 = 9 + 6 + 5 = 8 + 8 + 4 = 8 + 7 + 5 = 8 + 6 + 6 = 7 + 7 + 6.
При разложении способами 1−4, 7 и 8 суммы квадратов чисел не кратны трём. При разложении пятым способом сумма квадратов кратна девяти. Разложение шестым способом удовлетворяет условиям задачи. Таким образом, условию задачи удовлетворяет любое число, записанное цифрами 5, 7 и 8, например, число 578.
2. Задание 19 № 507010. Приведите пример четырёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Пояснение.
Пусть наше число имеет вид . Тогда имеем
И так как число делится на 4,
делится на 4. Можно заметить, что если среди цифр есть хотя бы три единицы, то равенство невозможно, так как сумма будет больше произведения. То же самое, если единиц меньше, чем две. В этом случае произведение будет слишком большое. Таким образом, среди цифр есть ровно две единицы. Рассмотрим двузначные числа, которые делятся на 4, это концовка нашего числа. Нельзя брать числа с нулём, так как в этом случае произведение будет равно нулю, что плохо.
12: тогда одна из оставшихся цифр 1, а другая — 4.
16: тогда одна из оставшихся цифр 1, а другая никакая не подойдёт.
24: значит, оставшиеся цифры — единицы. Всё сходится.
Остальные числа будут давать слишком большое произведение или нечётную сумму.
Таким образом, исходные числа: 1412, 4112, 1124.
3. Задание 19 № 507052. Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 0 и делится на 24.
Пояснение.
Чтобы число делилось на 24 оно должно делится на 3 и на 8.
Число делится на 8, если три его последние цифры образуют число, делящееся на 8. Искомое число записывается только нулями и единицами, значит, оно заканчивается на 000.
Число делится на 3, если его сумма цифр числа делится на 3. Поскольку три послледние цифры числа нули, первые три должны быть единицами.
Таким образом, единственное число, удовлетворяющее условию задачи, это число 111 000.
Ответ: 111 000.
4. Задание 19 № 507053. Найдите наименьшее трёхзначное число, которое при делении на 2 даёт остаток 1, при делении на 3 даёт остаток 2, при делении на 5 даёт остаток 3 и которое записано тремя различными нечётными цифрами.
Пояснение.
Число при делении на 2 даёт остаток 1, следовательно, оно нечётное. При делении на 3 число даёт остаток 2, то есть число имеет вид При делении на 5 число даёт остаток 3, то есть число имеет вид
то есть число может оканчиваться либо на тройку, либо на восьмёрку. Число нечётное, следовательно, может оканчиваться только на тройку. Учитывая, что число оканчивается на 3:
Перебирая значения
что при
получаем число, удовлетворяющее условиям задачи. Это число 173.
Ответ: 173.
5. Задание 19 № 507054. Найдите четырёхзначное натуральное число, кратное 19, сумма цифр которого на 1 больше их произведения.
Пояснение.
Если хотя бы одна цифра в записи числа — нуль, то произведение цифр равно 0, а тогда их сумма равна 1. Единственное такое четырёхзначное число — 1000, но оно не кратно 19. Поэтому нулей среди цифр нет. Отсюда следует, что все цифры не меньше 1, и их сумма не меньше четырёх, а значит, произведение цифр не меньше трёх. Чтобы произведение было не меньше трёх хотя бы одна из цифр должна быть больше 1. Рассмотрим такие числа в порядке возрастания суммы их цифр.
Если сумма цифр равна 5, то число записывается одной двойкой и тремя единицами (это числа 1112, 1121, 1211, 2111). Произведение цифр равно 2, поэтому они не удовлетворяют условию.
Если сумма цифр равна 6, то число записывается одной тройкой и тремя единицами или двумя двойками и двумя единицами (это числа 1113, 1131, 1311, 3111, 1122, 1212, …). Произведение цифр равно 3 или 4 соответственно, поэтому такие числа не удовлетворяют условию.
Если сумма цифр равна 7, то произведение должно быть равно 6. Это выполнено для чисел, записываемых тройкой, двойкой и двумя единицами. Поскольку число 3211 кратно 19, оно и является искомым.
Ответ: 3211.
Примечание.
Четырёхзначное число, обладающее требуемыми свойствами, единственно. Покажем это, приведя другое решение.
Приведём решение Дмитрия Мухина (Москва).
Пусть a, b, c, d — цифры числа и пусть а самая большая из них (порядок цифр не важен). Покажем, что произведение меньших цифр не больше четырёх. Действительно, из равенства a + b + c + d= 1 + abcd, получаем 4a ≥ abcd + 1. Деля на наибольшую цифру a, получаем, что bcd < 4.
Рассмотрим теперь следующие случаи.
1. Пусть среди чисел b, c, d есть нуль, тогда поскольку a + b + c + d = 1, это число 1000, но оно на 19 не делится. Итак, все три меньшие цифры числа отличны от нуля.
2. Пусть все три меньшие цифры равны единице, тогда a + 3 = a + 1. Этот случай невозможен.
3. Пусть меньшие цифры это две единицы и двойка. Тогда a + 4 = 2a + 1, откуда a = 3. Перебирая 12 чисел, составленных из цифр 1, 1, 2, 3, находим, что из них кратно 19 только число 3211. Оно и является ответом.
4. Пусть меньшие цифры это две единицы и тройка. Тогда a + 5 = 3a + 1. Отсюда a = 2, но тогда aне наибольшая цифра. Противоречие.
Поскольку bcd < 4, других вариантов нет. Искомое число единственно, оно равно 3211.
6. Задание 19 № 507055. Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число делилось на 27. В ответе укажите получившееся число.
Пояснение.
Если число делится на 27, тогда оно делится на 3 и на 9. Число делится на 9, тогда и только тогда, когда сумма цифр числа делится на 9. Число делится на 3, тогда и только тогда, когда сумма цифр числа делится на 3. Заметим, что, если число делится на 9,то оно делится и на 3. Сумма цифр числа 123456 равна 1 + 2 + 3 + 4 + 5 + 6 = 21. Вычеркнув числа 2, 4 и 6 получим, число, сумма цифр которого равна девяти. Девять делится на девять.
Ответ: 135.
7. Задание 19 № 507056. Найдите наименьшее четырёхзначное число, кратное 11, у которого произведение его цифр равно 12.
В ответе укажите наименьшее такое число.
Пояснение.
Пусть число имеет вид Произведение цифр числа равно 12, то есть
откуда получаем, что
может быть набором цифр: 1, 2, 2, 3; 1, 1, 3, 4. Число делится на 11, если сумма цифр, стоящих на нечётных местах равна сумме цифр, стоящих на чётных местах. Наименьшее число, удовлетворяющее этому требованию и состоящее из имеющихся наборов цифр, — 1232.
Ответ: 1232.
8. Задание 19 № 507057. Найдите наименьшее трёхзначное натуральное число, которое при делении на 6 и на 11 даёт равные ненулевые остатки и у которого средняя цифра является средним арифметическим двух крайних цифр.
Пояснение.
По модулю 6 и 11 число имеет одинаковые остатки, следовательно, число имеет тот же остаток при делении на 66, причём этот остаток не равен нулю и меньше шести. Таким образом, искомое число может иметь вид:
При получаем: 67, 68, 69, 70, 71. Все эти числа не являются трёхзначными.
При получаем: 133, 134, 135, 136, 137. Число 135 удовлетворяет всем условиям задачи.
Ответ: 135.
9. Задание 19 № 507058. Сумма цифр трёхзначного натурального числа А делится на 12. Сумма цифр числа (А + 6) также делится на 12. Найдите наименьшее возможное число А.
Пояснение.
Пусть число имеет вид
Если
, то сумма цифр в новом числе будет на 6 больше, чем в исходном. Пусть
делится на 12, тогда
то есть число
не делится на 12. Аналогично, если число
делится на 12, то число
не делится на 12. Значит,
. Рассмотрим три случая:
1) Число
имеет вид:
, сумма цифр числа
на 3 меньше суммы цифр числа
2) Число
имеет вид:
, сумма цифр числа
на 12 меньше суммы цифр числа
3) Число
имеет вид:
, сумма цифр числа
на 21 меньше суммы цифр числа
Ясно, что условиям задачи удовлетворяют числа, рассмотренные в пункте 2). Подберём число так, чтобы сумма его цифр делилась на 12. Наименьшее возможное
удовлетворяющее условиям задачи, — 699.
Ответ: 699.
10. Задание 19 № 507059. Найдите наименьшее пятизначное число, кратное 55, произведение цифр которого больше 50, но меньше 75.
Пояснение.
Если число делится на 55, то оно делится на 5 и на 11. Если число делится на 5 то оно может оканчиваться на 0 или на 5. Если в записи числа есть ноль, то произведение цифр числа равно нулю, следовательно, запись числа должна оканчиваться на 5. Пусть число имеет вид Число делится на 11, если сумма цифр на нечётных местах равна сумме цифр на чётных местах:
Рассмотрим различные произведения
такие, что
Последняя цифра числа равна пяти, следовательно, возможные значения произведения
50, 55, 60, 65, 70. Разложим каждое число на простые множители:
Попытаемся удовлетворить уравнению Перебирая различные возможные значения, получим, что только число разложение числа 70 в виде
удовлетворяет уравнению:
Наименьшее число, удовлетворяющее условиям задачи — 11275.
Ответ: 11275.
11. Задание 19 № 507524. Сумма цифр трёхзначного числа A делится на 13. Сумма цифр числаA+5 также делится на 13. Найдите такое число A.
Пояснение.
Пусть число имеет вид
Если
, то сумма цифр в новом числе будет на 6 больше, чем в исходном. Пусть
делится на 12, тогда
то есть число
не делится на 13. Аналогично, если число
делится на 13, то число
не делится на 13. Значит,
. Рассмотрим 3 случая:
1) Число
имеет вид:
, сумма цифр числа
на 3 меньше суммы цифр числа
2) Число
имеет вид:
, сумма цифр числа
на 13 меньше суммы цифр числа
3) Число
имеет вид:
, сумма цифр числа
на 21 меньше суммы цифр числа
Ясно, что условиям задачи удовлетворяют числа, рассмотренные в пункте 2). Подберём число так, чтобы сумма его цифр делилась на 13. Наименьшее возможное
удовлетворяющее условиям задачи, — 899.
Ответ: 899.
12. Задание 19 № 507967. Вычеркните в числе 141565041 три цифры так, чтобы получившееся число делилось на 30. В ответе укажите ровно одно получившееся число.
Пояснение.
Если число делится на 30, то оно также делится на 3 и на 10. Поэтому в последнем разряде числа должен быть ноль. Тогда вычёркиваем 41. Остаётся 1415650. Для того, чтобы число делилось на три необходимо, чтобы сумма цифр была кратна трём, значит, нужно вычеркнуть цифру 1 или цифру 4. Таким образом, получаем числа 145650, 115650 и 415650
Ответ: 145650, 115650 или 415650.
13. Задание 19 № 508010. Вычеркните в числе 74513527 три цифры так, чтобы получившееся число делилось на 15. В ответе укажите ровно одно получившееся число.
Пояснение.
Если число делится на 15, то оно также делится на 3 и на 5. Поэтому в последнем разряде числа должен быть ноль или цифра пять. Тогда вычёркиваем 27. Остаётся 745135. Посчитаем сумму цифр — 25. Для того, чтобы число делилось на три необходимо, чтобы сумма цифр была кратна трём. В таком случае можно вычеркнуть цифру 1 и получить число 74535, цифру 4 и получить 75135 или вычеркнуть цифру 7 и получить число 45135.
Ответ: 74535, 75135 или 45135.
14. Задание 19 № 508051. Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите ровно одно получившееся число.
Пояснение.
Если число делится на 18, то оно также делится на 9 и на 2. Число должно быть чётным, для этого вычеркнем цифру 7, получим 8541762. Посчитаем сумму цифр — 33. Для того, чтобы число делилось на девять необходимо, чтобы сумма цифр была кратна девяти. Можно вычеркнуть цифры 5 и 1, получив число 84762, либо вычеркнуть цифры 4 и 2 и получить число 85176. Также возможно вычеркнуть цифры 7 и 8 и получить число 54162.
Ответ: 84762, 85176 или 54162.
15. Задание 19 № 508400. Найдите трехзначное натуральное число, большее 500, которое при делении на 4, на 5 и на 6 дает в остатке 2, и в записи которого есть только две различные цифры. В ответе укажите какое-нибудь одно такое число.
Пояснение.
При делении на 4 число даёт в остатке 2, следовательно, оно чётное. Поскольку число при делении на 5 даёт в остатке 2, то оно может оканчиваться на 2 или на 7. Таким образом, число обязательно должно заканчиваться цифрой 2.
Подбором находим, что условию задачи удовлетворяют числа 662 и 722.
Ответ: 662, 722.
16. Задание 19 № 508420. Найдите трехзначное натуральное число, большее 600, которое при делении на 4, на 5 и на 6 дает в остатке 3, и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь одно такое число.
Пояснение.
При делении на 4 число даёт в остатке 3, следовательно, оно нечётное. Поскольку число при делении на 5 даёт в остатке 2, то оно может оканчиваться на 2 или на 8. Таким образом, число обязательно должно заканчиваться цифрой 3.
Подбором находим, что условию задачи удовлетворяют числа 963 и 843.
Ответ: 963, 843.
17. Задание 19 № 509226. Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Пояснение.
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4. Из признака делимости на 4 следует, что число чётное — вычеркнем последнюю цифру. Теперь используем признак делимости на 3. Найдём сумму цифр в числе 1 + 8 + 1 + 6 + 1 + 5 + 1 + 2 = 25. Ближайшие суммы цифр — 24, 21, 18. Чтобы получить сумму цифр 18 вычеркнем из числа цифры 6 и 1. Получим число 181512. Это число делится и на 4, и на 3. Число 116112 также подходит для ответа.
Ответ: 181512, 116112.
18. Задание 19 № 509744. Найдите трёхзначное число A, обладающее всеми следующими свойствами:
· сумма цифр числа A делится на 8;
· сумма цифр числа A + 1 делится на 8;
· в числе A сумма крайних цифр кратна средней цифре.
В ответе укажите какое-нибудь одно такое число.
Пояснение.
Пусть число имеет вид , если
, то сумма цифр в новом числе будет на 1 больше, чем в исходном, и обе они не могут делиться на 8. Значит
. Рассмотрим теперь 2 случая:
1) Число перейдёт в
, сумма изменится на 8.
2) Число перейдёт в
, сумма изменится на 18.
Итак, условиям задачи удовлетворяют числа вида , где
кратно
. Одним из таких чисел является 349.
Ответ: 349.
19. Задание 19 № 509764. Найдите четырёхзначное число, кратное 88, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.
Пояснение.
Число делится на 88, если оно делится на 8 и на 11. Признак делимости на 8: число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на 8. Признак делимости на 11: число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо разность этих сумм делится на 11. Используя признак делимости на 8, и учитывая, что все цифры искомого числа должны быть чётны и различны получаем, что последними цифрами числа могут быть: 024, 048, 064, 208, 240, 264, 280, 408, 480, 608, 624, 640, 648, 680, 824, 840, 864. Используя признак делимости на 11 получим, что условию задачи удовлетворяют числа: 6248, 8624, 2640.
Ответ: 2640, 6248 или 8624.
Приведём идею другого решения.
Искомое число должно быть записано четырьмя из пяти цифр 0, 2, 4, 6 и 8, каждая из которых взята один раз. Причём сумма цифр в разрядах тысяч и десятков должна быть равна сумме цифр в разрядах сотен и единиц, а три последние цифры искомого числа должны образовывать трёхзначное число, кратное восьми. Пусть в разряде тысяч стоит 8, тогда в разряде десятков должна быть 2, а в разряде сотен и единиц — цифры 4 и 6. Заметим, что число 8624 удовлетворяет условию. Далее аналогично для чисел, начинающихся с 2, 4 и 6.
20. Задание 19 № 506312. Трёхзначное число при делении на 10 даёт в остатке 3. Если последнюю цифру числа перенести в начало его записи, то полученное число будет на 72 больше первоначального. Найдите исходное число.
Пояснение.
Пусть число имеет вид
Тогда условие записывается так:
Подставив значение в третье выражение и преобразовав его, получим, что
Подходит только пара .
Таким образом, условиям задачи удовлетворяет число 253.
21. Задание 19 № 506318. Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что его квадрат делится на 16.
Пояснение.
Разложим число 25 на слагаемые: 25 = 9 + 9 + 7 = 9 + 8 + 8.
Квадрат числа делится на 16, значит, само число делится на 4. Это значит, что оно как минимум заканчивается на чётную цифру. То есть первый набор отпадает, так как в нём таковых нет. Из второго мы можем составить числа 988 и 898. Первое число удовлетворяет условиям задачи.
22. Задание 19 № 506291. Приведите пример четырёхзначного числа А, обладающего следующими свойствами:
1) сумма цифр числа А делится на 8;
2) сумма цифр числа (А + 2) также делится на 8;
3) число А меньше 3000.
В ответе укажите ровно одно такое число.
Пояснение.
Пусть число имеет вид . Если
, то сумма цифр в новом числе будет на 2 больше, чем в исходном, и обе они не могут делиться на 8. Значит,
. Рассмотрим теперь 3 случая:
1) Число перейдёт в
, сумма изменится на 7.
2) Число перейдёт в
, сумма изменится на 16.
3) Число перейдёт в
, сумма изменится на 25.
Итак, условиям задачи удовлетворяют числа вида . Так как
, несложно выписать все варианты: 1698, 2598, 1599, 2499.
23. Задание 19 № 506342. Приведите пример шестизначного натурального числа, которое записывается только цифрами 1 и 2 и делится на 24. В ответе укажите ровно одно такое число.
Пояснение.
Если число делится на 24, то оно также делится на 3 и на 8.
Число делится на 8 тогда и только тогда, когда три его последние цифры образуют число, которое делится на 8. Перебрав трёхзначные числа из 1 и 2, получим, что только 112 делится на 8. Это число образует последние три цифры искомого числа.
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Последние три цифры 112 дают к сумме 4. Рассмотрим первые три цифры. Их сумма может быть от 3 до 6. Условиям задачи удовлетворяет сумма цифр, равная 5. Троек с данной суммой цифр три: 122, 212, 221.
Таким образом, подходят числа: 122112, 212112, 221112.
24. Задание 19 № 506482. Приведите пример шестизначного натурального числа, которое записывается только цифрами 2 и 0 и делится на 24. В ответе укажите ровно одно такое число.
Пояснение.
Если число делится на 24, то но делится на 3 и на 8.
Если число делится на 8, то число, образованное последними его тремя цифрами, тоже делится на 8. Трёхзначных чисел из 0 и 2, делящихся на 8, два: 000 и 200. Это окончания исходного числа.
Если число делится на 3, то сумма его цифр тоже делится на 3.
000 даёт к сумме 0, то есть сумма первых цифр должна равняться 6, то есть это 222.
200 даёт к сумме 2, то есть сумма первых цифр должна равняться 4, то есть 220 или 202 (022 не может быть, так как это первые цифры, а первая цифра в числе не может равняться 0).
Таким образом, искомые числа: 220200, 202200, 222000.
25. Задание 19 № 506585. Приведите пример шестизначного натурального числа, которое записывается только цифрами 1 и 2 и делится на 72. В ответе укажите ровно одно такое число.
Пояснение.
Если число делится на 72, то но делится на 8 и на 9.
Если число делится на 8, то число, образованное последними его тремя цифрами, тоже делится на 8. Шестизначных чисел из 1 и 2, делящиеся на 8 должны заканчиваться тройкой цифр 112.
Если число делится на 9, то сумма его цифр тоже делится на 9.
112 даёт к сумме 4, то есть сумма первых цифр должна равняться 5, то есть должна состоять из перестановок двух двоек и единицы.
Таким образом, искомые числа: 122112, 212112, 221112.
Ответ: 122112, 212112 или 221112.
26. Задание 19 № 506442. Приведите пример трёхзначного натурального числа, большего 500, которое при делении на 8 и на 5 даёт равные ненулевые остатки и первая слева цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.
Пояснение.
По модулю 5 и 8 число имеет одинаковые остатки. Оно будет иметь тот же остаток и при делении на 40. Этот остаток больше нуля и меньше пяти. Пусть наше число имеет вид , тогда имеем:
Заметим, также, что искомое число должно быть чётным. Переберём все варианты, их четыре: 564, 684.
Ответ: 564; 684.
27. Задание 19 № 506772. Приведите пример трёхзначного натурального числа, большего 600, которое при делении на 4, на 5 и на 6 даёт в остатке 3 и цифры которого расположены в порядке убывания слева направо. В ответе укажите ровно одно такое число.
Пояснение.
Так как число даёт одинаковый остаток по модулям 4, 5 и 6, то оно также даёт такой же остаток и по модулю 60. То есть число имеет вид Все такие числа: 603, 663, 723, 783, 843, 903, 963. Из них подходят под последнее условие только 843 и 963.
28. Задание 19 № 506645. Приведите пример трёхзначного натурального числа, большего 500, которое при делении на 3, на 4 и на 5 даёт в остатке 2 и в записи которого есть только две различные цифры. В ответе укажите ровно одно такое число.
Пояснение.
Раз число даёт один и тот же остаток по модулю 3, 4 и 5, то оно даёт такой же остаток и по модулю. А значит, число имеет вид
Все числа, удовлетворяющие этому неравенству: 542, 602, 662, 722, 782, 842, 902, 962. Из них удовлетворяют условию про две различные цифры: 662, 722.
29. Задание 19 № 506605. Приведите пример трёхзначного натурального числа, которое при делении на 3, на 5 и на 7 даёт в остатке 1 и цифры которого расположены в порядке убывания слева направо. В ответе укажите ровно одно такое число.
Пояснение.
Если число имеет одинаковые остатки по каким-то модулям, то оно имеет такой же остаток по модулю, являющемуся НОК этих модулей. То есть в данном случае по модулю 105. Тогда наше число . Переберём все возможные варианты: 106, 211, 316, 421, 526, 631, 736, 841, 946. Условиям задачи удовлетворяют числа 421, 631 и 841.
Ответ: 421; 631; 841.
30. Задание 19 № 506854. Приведите пример трёхзначного натурального числа, которое при делении на 3, на 5 и на 7 даёт в остатке 2 и в записи которого есть только две различные цифры. В ответе укажите ровно одно такое число.
Пояснение.
Так как число даёт одинаковые остатки по модулям 3, 5 и 7, то оно также даёт такой же остаток по модулю 105. То есть число имеет имеет вид . Все такие числа: 107, 212, 317, 422, 527, 632, 737, 842, 947. Под последнее условие подходят только числа 212, 422 и 737.
31. Задание 19 № 506462. Приведите пример трёхзначного натурального числа большего 500, которое при делении на 6 и на 5 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите ровно одно такое число.
Пояснение.
По модулю 5 и 6 число имеет одинаковые остатки. Оно будет иметь тот же остаток и при делении на 30. Этот остаток больше нуля и меньше пяти. Пусть наше число имеет вид , тогда имеем:
Переберём все варианты, их 10: 531, 543, 642, 654, 741, 753, 852, 864, 951, 963.
Из них имеют одинаковые остатки по модулям 5 и 6: 543, 753, 963.
32. Задание 19 № 506792. Приведите пример трёхзначного натурального числа, большего 500, которое при делении на 8 и на 5 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите ровно одно такое число.
Пояснение.
Число даёт одинаковые остатки при делении на 5 и 8. Значит, оно даёт такой же остаток и по модулю 40. То есть число имеет вид Первая цифра не меньше 5. Первая и последняя цифры в сумме дают чётное число. Разность числа и p делится на 40, то есть число, образованное первыми двумя цифрами, делится на 4. Теперь можно выписать все числа, которые подходят под эти условия: 642, 963.
33. Задание 19 № 506752. Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите ровно одно такое число.
Пояснение.
Если число даёт одинаковые остатки при делении на 4 и на 15, то оно даёт такой же остаток и при делении на 60. То есть теперь мы знаем, что на наше число имеет вид То есть разность нашего числа и
должна делиться на 60, то есть число, образованное первыми двумя цифрами, должно делиться на 6. А если число делится на 6, то оно также делится на 2 и на 3. А это значит, что последняя его цифра чётная, а сумма цифр делится на 3. Из условия на среднее арифметическое также следует, что сумма первой и последней цифры в исходном числе чётная. Переберём последнюю и вторую цифры, а по ним однозначно восстановим первую и получим числа: 123, 543, 963.
34. Задание 19 № 506727. Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и первая справа цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.
Пояснение.
Если число даёт одинаковые остатки при делении на 4 и на 15, то оно даёт такой же остаток и при делении на 60. То есть теперь мы знаем, что на наше число имеет вид То есть разность нашего числа и
должна делиться на 60, то есть число, образованное первыми двумя цифрами, должно делиться на 6. А если число делится на 6, то оно также делится на 2 и на 3. А это значит, что последняя его цифра чётная, а сумма цифр делится на 3. А из условия на среднее арифметическое следует, что сумма этих цифр также чётная. Под все эти условия подходят числа 24, 42 и 60. А соответствующие им исходные числа будут равны 243, 423 и 603.
35. Задание 19 № 506814. Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и первая справа цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.
Пояснение.
Если число даёт одинаковые остатки при делении на 4 и на 15, то оно даёт такой же остаток и при делении на 60. То есть теперь мы знаем, что на наше число имеет вид То есть разность нашего числа и
должна делиться на 60, то есть число, образованное первыми двумя цифрами, должно делиться на 6. А если число делится на 6, то оно также делится на 2 и на 3. А это значит, что последняя его цифра чётная, а сумма цифр делится на 3. А из условия на среднее арифметическое следует, что сумма этих цифр также чётная. Под все эти условия подходят числа 24, 42 и 60. А соответствующие им исходные числа будут равны 243, 423 и 603.
36. Задание 19 № 506874. Приведите пример трёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Пояснение. Можно заметить, что если среди цифр есть хотя бы две единицы, то равенство невозможно, так как сумма будет больше произведения. То же самое, если единиц нет вообще. В этом случае произведение будет слишком большое. Таким образом, среди цифр есть ровно одна единица. Число делится на 4, значит, последняя цифра чётная, а это значит, что произведение тоже чётное. А значит, и сумма. И так как последняя цифра чётная, то оставшиеся две цифры должны быть одной чётности. А так как мы выяснили, что среди цифр есть ровно одна единица, то эти числа нечётные. Под эти ограничения подходят числа: 132, 136, 152, 156, 172, 176, 192, 196, 312, 316, 512, 516, 712, 716, 912, 916, из которых удовлетворяют всем условиям только числа 132 и 312.
37. Задание 19 № 506502. Приведите пример четырёхзначного числа, кратного 12, произведение цифр которого больше 40, но меньше 45. В ответе укажите ровно одно такое число.
Пояснение. Если число делится на 12, то оно делится на 3 и на 4. Если число делится на 3, то сумма всех его цифр тоже делится на 3. Если число делится на 4, то число, образованное двумя последними его цифрами тоже делится на 4. Пусть наше число имеет вид , тогда условие записывается так:
В интервале находятся числа 41, 42, 43, 44. 41 и 43 — простые, а 44 делится на 11 — тоже простое. Таким образом, 41, 43 и 44 не подходят, потому что не могут быть представлены в виде произведения. То есть
Два набора цифр подходят как решение: (1, 2, 3, 7) и (1, 1, 6, 7). Но в первом наборе сумма цифр не кратна трём, так что он отпадает. Имеем (1,1,6,7). Последняя цифра в числе должна быть чётной, иначе число не будет делиться на 4.
Остальные цифры могут стоять в любом порядке. Выпишем искомые числа: 1176, 1716, 7116.
38. Задание 19 № 506834. Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из первого числа вычли второе и получили 1458. Приведите ровно один пример такого числа.
Пояснение.
Число делится на 5, значит, его последняя цифра или 0, или 5. Но так как при записи в обратном порядке цифры также образуют четырёхзначное число, то эта цифра 5, ибо число не может начинаться с 0. Пусть число имеет вид . Тогда условие можно записать так:
Второе слагаемое в левой части делится на 10. Значит, за разряд единиц в сумме отвечает только первое слагаемое. То есть Откуда
Подставив полученное значение в уравнение, получим, что
Перебрав все пары b и с, которые являются решением этого равенства, выпишем все числа, являющиеся ответом: 7065, 7175, 7285, 7395.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
t1∘=0∘Ct2∘−искомая температураL(t1∘)=L0(1+α⋅t1∘);L(t2∘)=L0(1+α⋅t2∘);мы ищем Δt=(t2−t1);L(t2∘)−L(t1∘)=L0(1+α⋅t2∘)−L0(1+α⋅t1∘); ΔL=L(t2∘)−L(t1∘)=9 мм;ΔL=L0+L0⋅α⋅t2∘−(L0+L0⋅α⋅t1∘);ΔL=L0+L0⋅α⋅t2∘−L0−L0⋅α⋅t1∘;ΔL=L0⋅α⋅t2∘−L0⋅α⋅t1∘;ΔL=L0⋅α⋅(t2∘−t1∘);ΔL=L0⋅α⋅Δt;ΔLL0⋅α=Δt;Δt=ΔLL0⋅α;t2−t1=ΔLL0⋅α;t2=ΔLL0⋅α;displaystyle
t^circ_1=0 ^circ C \
t^circ_2 — искомая температура \
L(t^circ_1 )=L_0(1+alphacdot t^circ_1 ); \
L(t^circ_2 )=L_0(1+alphacdot t^circ_2 ); \
мы ищем Delta t = (t_2 — t_1);\
L(t^circ_2 ) — L(t^circ_1 ) = L_0(1+alphacdot t^circ_2 ) — L_0(1+alphacdot t^circ_1 );\
Delta L = L(t^circ_2 ) — L(t^circ_1 ) = 9 мм;\
Delta L = L_0 + L_0 cdot alphacdot t^circ_2 — ( L_0+L_0cdot alphacdot t^circ_1 ); \
Delta L = L_0 + L_0 cdot alphacdot t^circ_2 — L_0-L_0cdot alphacdot t^circ_1 ; \
Delta L = L_0 cdot alphacdot t^circ_2 — L_0cdot alphacdot t^circ_1 ; \
Delta L = L_0 cdot alphacdot (t^circ_2 -t^circ_1) ; \
Delta L = L_0 cdot alphacdot Delta t ; \
frac{ Delta L} { L_0 cdot alpha} = Delta t ; \
Delta t = frac{ Delta L} { L_0 cdot alpha} ; \
t_2 — t_1 = frac{ Delta L} { L_0 cdot alpha} ; \
t_2 = frac{ Delta L} { L_0 cdot alpha} ;
тут надо разобраться с метрами и миллиметрами. Начальную длину рельса L0 = 10 м и удлинение 9 мм надо привести к одному размеру.
Мне нравятся метры. 1 метр = 1000 мм, 1 мм= 0,001 м, а 9 мм = 0,009 м подставляем!
t2=0,00910⋅1,2⋅10−5displaystyle{
t_2 =frac {0,009} {10 cdot 1,2cdot 10^{-5 }}
}
t2=0,009⋅10510⋅1,2displaystyle {
t_2 =frac {0,009 cdot 10^{5 }} {10 cdot 1,2}
}
t2=90012=75
displaystyle {
t_2 =frac {900 } {12} =75
}
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
Раскроем скобки.
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$
$х=-{17}/{5}$
$х = — 3,4$
Ответ: $- 3,4$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
$x = 0; ax + b = 0$
2. Решаем получившиеся уравнения каждое отдельно.
Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$
$4х^2 — 5х = 0$
Вынесем х как общий множитель за скобки:
$х (4х — 5) = 0$
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
$ax^2 + c = 0$
$ax^2 = — c$
$x_2 = {-c}/{a}$
При решении последнего уравнения возможны два случая:
если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$
если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.
$x^2 — 16 = 0$
$x^2 = 16$
$x = ±4$
Ответ: $х_1 = 4, х_2 = — 4$
Решение полного квадратного уравнения
Решение с помощью дискриминанта
Дискриминантом квадратного уравнения D называется выражение
$b^2 — 4ac$.
При решении уравнения с помощью дискриминанта возможны три случая:
1. $D > 0$. Тогда корни уравнения равны:
$x_{1,2}={-b±√D}/{2a}$
2. $D = 0$. В данном случае решение даёт два двукратных корня:
$x_{1}=x_{2}={-b}/{2a}$
3. $D < 0$. В этом случае уравнение не имеет корней.
$3х^2 — 11 = -8х$
Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней
$3х^2 + 8х — 11 = 0$
$a = 3 ,b = 8, c = — 11$
$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$
$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$
$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$
Ответ: $x_1=1, x_2=-3{2}/{3}$
Устные способы
Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$
$4х^2+ 3х — 7 = 0$
$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$
Ответ: $х_1= 1, х_2 = -{7}/{4}$
Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$
$5х^2+ 7х + 2 = 0$
$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$
Ответ: $х_1= -1, х_2 = -{2}/{5}$
Кубические уравнения
Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.
$(x — 3)^3 = 27$
Представим обе части как основания в третьей степени
$(x — 3)^3 = $33
Извлечем кубический корень из обеих частей
$х — 3 = 3$
Соберем известные слагаемые в правой части
$x = 6$
Ответ: $х = 6$
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
$4x + 1 — {3}/{x} = 0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x + 1 — {3}/{x}= 0¦· x$
$4x · x + 1 · x — {3·x}/{x} = 0$
3. решаем полученное уравнение
$4x^2 + x — 3 = 0$
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = {3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = {3}/{4}$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$
${3х-5}/{-2}={1}/{х}$
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х (3х — 5) = -2$
Раскроем скобки и соберем все слагаемые в левой части уравнения
$3х^2- 5х + 2 = 0$
Решим данное квадратное уравнение первым устным способом, т.к.
$a + b + c = 0$
$x_1 = 1, x_2 = {2}/{3}$
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1 = 1, x_2 = {2}/{3}$
Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.
Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.
Например,
${2}/{x}+5x=7$ – рациональное уравнение
$3x+√x=7$ — иррациональное уравнение (содержит корень)
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль общий знаменатель.
Решить уравнение: $4x+1-{3}/{x}=0$
Решение:
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x ≠ 0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x+1-{3}/{x}=0|·x$
$4x·x+1·x-{3·x}/{x}=0$
3. решаем полученное уравнение
$4x^2+x-3=0$
Решим вторым устным способом, т.к. $а+с=b$
Тогда, $x_1=-1, x_2=-{3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=-1, x_2=-{3}/{4}$
При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$
Решить уравнение ${3x-5}/{-2}={1}/{x}$
Решение:
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х(3х-5)=-2$
Раскроем скобки и соберем все слагаемые в левой стороне
$3х^2-5х+2=0$
Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$
$x_1=1, x_2={2}/{3}$
В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=1, x_2={2}/{3}$
Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.
Чтобы решить иррациональное уравнение, необходимо:
- Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
- Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
- Решить полученное рациональное уравнение.
- Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.
Решение:
Обе части уравнение возведем в квадрат:
$√{4х-3}^2=х^2$
Получаем квадратное уравнение:
$4х-3=х^2$
Перенесем все слагаемые в левую часть уравнения:
${-х}^2+4х-3=0$
Решим данное квадратное уравнение устным способом, так как
$a+b+c=0$
$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$√{4·1-3}=1$
$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.
$√{4·(3)-3}=3$
$√9=3$
$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит
$х_1=1$ наименьший корень.
Ответ: $1$
Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
- Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$
Решить уравнение: $х-6=√{8-х}$
Возведем обе части уравнения в квадрат
$(х-6)^2=8-х$
В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение
$х^2-2·6·х+6^2=8-х$
$х^2-12х+36=8-х$
Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.
$х^2-12х+36-8+х=0$
Приводим подобные слагаемые:
$х^2-11х+28=0$
Найдем корни уравнения через дискриминант:
$D=b^2-4ac=121-4·28=121-112=9=3^2$
$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$
$x_1=7; x_2=4$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$x_1=7$
$7-6=√{8-7}$
$1=1$, получили верное равенство, следовательно, корень нам подходит.
$x_2=4$
$4-6=√{8-4}$
$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.
Ответ: $7$
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n⋅a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.
Решить уравнение $25·5^х=1$
Решение:
В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$
$5^2·5^х=5^0$
При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются
$5^{2+х}=5^0$
Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели
$2+х=0$
$х=-2$
Ответ: $-2$
Решить уравнение $2^{3х+2}-2^{3х-2}=30$
Решение:
Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель
$2^{3x+2}-2^{3x-2}=30$
$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$
$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$
$2^{3x-2}(2^4-1)=30$
$2^{3x-2}·15=30$
Разделим обе части уравнения на $15$
$2^{3х-2}=2$
$2^{3х-2}=2^1$
$3х-2=1$
$3х=3$
$х=1$
Ответ: $1$