Дан выпуклый четырёхугольник ABCD.
а) Докажите, что отрезки LN и KM, соединяющие середины его противоположных сторон, делят друг друга пополам.
б) Найдите площадь четырёхугольника ABCD, если
Спрятать решение
Решение.
а) Пусть K, L, M и N — середины сторон AB, BC, CD и AD четырёхугольника ABCD соответственно. Тогда KL и MN — средние линии треугольников ABC и ADC. Значит,
и KL || AC || MN, поэтому KLMN — параллелограмм. Его диагонали KM и LN делят друг друга пополам, что и требовалось доказать.
б) В треугольнике KLM имеем:
Значит, KL = 9. Тогда поэтому треугольник KLM прямоугольный треугольник с прямым углом при вершине L. Четырёхугольник KLMN — прямоугольник, поэтому
Отрезок KL является средней линией треугольника ABC, поэтому Аналогично
Тогда, имеем:
Где S — искомая площадь четырёхугольника ABCD. Аналогично Поэтому
Следовательно,
Ответ:
Приведем решение пункта б) wladius w.
В треугольнике KLM имеем:
Значит, KL = 9. Тогда поэтому треугольник KLM прямоугольный, то есть
KL || AC, LM || BD, тогда
Следовательно,
Примечание.
Заметим, что четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника
(см. параллелограмм Вариньона). При решении данной задачи фактически доказана теорема Вариньона и следствие из нее.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б)
ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки |
2 |
| Имеется верное доказательство утверждения пункта а)
ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен |
1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-14

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html
На какие числа делится число онлайн калькулятор. Посчитать делители числа.
Какие числа делятся на 505389?
На число 505389 без остатка (нацело) делятся следующие числа: 505389, 1010778, 1516167, 2021556, 2526945, 3032334, 3537723, 4043112, 4548501, 5053890, 5559279, 6064668 и многие другие.
Какие четные числа делятся на 505389?
На число 505389 делятся следующие четные числа: 1010778, 2021556, 3032334, 4043112, 5053890, 6064668, 7075446, 8086224, 9097002, 10107780, 11118558, 12129336 и многие други.
Какие нечетные числа делятся на 505389?
На число 505389 делятся следующие нечетные числа: 505389, 1516167, 2526945, 3537723, 4548501, 5559279, 6570057, 7580835, 8591613, 9602391, 10613169, 11623947 и многие другие.
На какое наибольшее число делится число 505389 без остатка?
Наибольшее число на которое делится число 505389 есть само число 505389. т.е делиться на само себя без остатка.
На какое наибольшее число делится число 505389 без остатка, не считая числа 505389 и 1?
Наибольшим делителем числа 505389 не считая самого числа 505389 является число 168463.
Какое наименьшее натуральное число делится на 505389?
Наименьшее натуральное число которое делиться на число 505389 является само число 505389.
На какое наименьшее натуральное число делится число 505389?
Наименьшее натуральное число на которое можно разделить число 505389 — это число 1.
Делители числа 505389.
(что бы не забыть запишите все делители числа 505389 в блокнот.)На какие целые и(или) натуральные числа делится число 505389?
Число 505389 делится на следующие целые, натуральные числа (все делители числа 505389): 1, 3, 168463, 505389
На какие четные числа делится число 505389?
Таких чисел нет.
На какие нечетные числа делится число 505389?
Число 505389 делится на следующие нечетные числа (нечетные делители числа): 1, 3, 168463, 505389
Сколько делителей имеет число 505389?
Число 505389 имеет 4 делителя
Сколько четных делителей имеет число 505389?
Число 505389 имеет 0 четных делителей
Сколько нечетных делителей имеет число 505389?
Число 505389 имеет 4 нечетных делителя
Число 505389 прописью, словами.
— пятьсот пять тысяч триста восемьдесят девять
(что бы не забыть запишите число 505389 прописью в блокнот.)
Числа кратные 505389.
— кратные числа, числу 505389 : 1010778, 1516167, 2021556, 2526945, 3032334, 3537723, 4043112, 4548501, 5053890, 5559279, 6064668 и многие другие.
Простые множители числа 505389.
Простые множители числа 505389 = 3, 168463 (единица также является простым множителем числа 505389)
Сумма цифр числа 505389.
Сумма цифр числа 505389 равна 30
Произведение цифр числа 505389.
Произведение цифр числа 505389 равна 0
Квадрат числа 505389.
Квадрат числа 505389 равен 255418041321
Куб числа 505389.
Куб числа 505389 равен 129085468485178869
Квадратный корень числа 505389.
Квадратный корень числа 505389 равен 710.9071.
Число 505389 в двоичной системе счисления.
Запись числа 505389 в двоичной системе счисления выглядит так: 1111011011000101101
Количество значащих нулей в двоичной записи числа 505389 = 7
Количество едениц в двоичной записи числа 505389 = 12
(что бы не забыть запишите число 505389 в двоичной системе счисления в блокнот.)Число 505389 в шестнадцатеричной системе счисления.
Запись числа 505389 в шестнадцатеричной системе счисления выглядит так: 7b62d
(что бы не забыть запишите число 505389 в шестнадцатеричной системе счисления в блокнот.)Число 505389 в восьмеричной системе счисления.
Запись числа 505389 в восьмеричной системе счисления выглядит так: 1733055
(что бы не забыть запишите число 505389 в восьмеричной системе счисления в блокнот.)Число 505389 не является простым!
Корни числа 505389.
Корень 3 степени из 505389.
Корень 3 (третьей) степени из 505389 равен 79.654184381745
Корень 4 степени из 505389.
Корень 4 (четвертой) степени из 505389 равен 26.662842439157
Корень 5 степени из 505389.
Корень 5 (пятой) степени из 505389 равен 13.826910668821
Корень 6 степени из 505389.
Корень 6 (шестой) степени из 505389 равен 8.9249192927301
Корень 7 степени из 505389.
Корень 7 (седьмой) степени из 505389 равен 6.5283538133187
Корень 8 степени из 505389.
Корень 8 (восьмой) степени из 505389 равен 5.1636075024306
Корень 9 степени из 505389.
Корень 9 (девятой) степени из 505389 равен 4.3026517694579
Корень 10 степени из 505389.
Корень 10 (десятой) степени из 505389 равен 3.718455414392
Корень 11 степени из 505389.
Корень 11 (одиннадцатой) степени из 505389 равен 3.2999809667241
Корень 12 степени из 505389.
Корень 12 (двенадцатой) степени из 505389 равен 2.9874603416163
Корень 13 степени из 505389.
Корень 13 (тринадцатой) степени из 505389 равен 2.7462523717985
Корень 14 степени из 505389.
Корень 14 (четырнадцатой) степени из 505389 равен 2.5550643462188
Корень 15 степени из 505389.
Корень 15 (пятнадцатой) степени из 505389 равен 2.4001684296622
Степени числа 505389.
505389 в 3 степени.
505389 в 3 степени равно 129085468485178869.
505389 в 4 степени.
505389 в 4 степени равно 6.5238375832256E+22.
505389 в 5 степени.
505389 в 5 степени равно 3.2970757523488E+28.
505389 в 6 степени.
505389 в 6 степени равно 1.6663058174038E+34.
505389 в 7 степени.
505389 в 7 степени равно 8.4213263075189E+39.
505389 в 8 степени.
505389 в 8 степени равно 4.2560456812307E+45.
505389 в 9 степени.
505389 в 9 степени равно 2.1509586707915E+51.
505389 в 10 степени.
505389 в 10 степени равно 1.0870708516726E+57.
505389 в 11 степени.
505389 в 11 степени равно 5.4939365065599E+62.
505389 в 12 степени.
505389 в 12 степени равно 2.7765750771138E+68.
505389 в 13 степени.
505389 в 13 степени равно 1.4032505016475E+74.
505389 в 14 степени.
505389 в 14 степени равно 7.0918736777711E+79.
505389 в 15 степени.
505389 в 15 степени равно 3.584154946135E+85.
Какое число имеет такую же сумму цифр как и число 505389?Математика. Найти сумму цифр числа 505389.
Число 505389 состоит из следующих цифр — 5, 0, 5, 3, 8, 9.
Определить сумму цифр числа 505389 не так уж и сложно.
Сумма цифр шестизначного числа 505389 равна 5 + 0 + 5 + 3 + 8 + 9 = 30.
Числа сумма цифр которых равна 30.
Следующие числа имеют такую же сумму цифр как и число 505389 — 3999, 4899, 4989, 4998, 5799, 5889, 5898, 5979, 5988, 5997, 6699, 6789, 6798, 6879, 6888, 6897, 6969, 6978, 6987, 6996.
Четырехзначные числа сумма цифр которых равна 30 — 3999, 4899, 4989, 4998, 5799, 5889, 5898, 5979, 5988, 5997.
Пятизначные числа сумма цифр которых равна 30 — 12999, 13899, 13989, 13998, 14799, 14889, 14898, 14979, 14988, 14997.
Шестизначные числа сумма цифр которых равна 30 — 102999, 103899, 103989, 103998, 104799, 104889, 104898, 104979, 104988, 104997.
Квадрат суммы цифр числа 505389.
Квадрат суммы цифр шестизначного числа 505389 равен 5 + 0 + 5 + 3 + 8 + 9 = 30² = 900.
Сумма квадратов цифр шестизначного числа 505389.
Сумма квадратов цифр числа 505389 равна 5² + 0² + 5² + 3² + 8² + 9² = 25 + 0 + 25 + 9 + 64 + 81 = 204.
Сумма четных цифр числа 505389.
Сумма четных цифр шестизначного числа 505389 равна 8 = 8.
Квадрат суммы четных цифр шестизначного числа 505389.
Квадрат суммы четных цифр числа 505389 равна 8 = 8² = 64.
Сумма квадратов четных цифр шестизначного числа 505389.
Сумма квадратов четных цифр числа 505389 равна 8² = 64 = 64.
Сумма нечетных цифр числа 505389.
Сумма нечетных цифр шестизначного числа 505389 равна 5 + 5 + 3 + 9 = 22.
Квадрат суммы нечетных цифр шестизначного числа 505389.
Квадрат суммы нечетных цифр числа 505389 равна 5 + 5 + 3 + 9 = 22² = 484.
Сумма квадратов нечетных цифр шестизначного числа 505389.
Сумма квадратов нечетных цифр числа 505389 равна 5² + 5² + 3² + 9² = 25 + 25 + 9 + 81 = 140.
Произведение цифр числа 505389.
Какое число имеет такое же произведение цифр как и число 505389?Математика. Найти произведение цифр числа 505389.
Число 505389 состоит из следующих цифр — 5, 0, 5, 3, 8, 9.
Найти сумму цифр числа 505389 просто.
Решение:
Произведение цифр числа 505389 равно 5 * 0 * 5 * 3 * 8 * 9 = 0.
Числа произведение цифр которых равно 0.
Следующие числа имеют такое же произведение цифр как и число 505389 — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110.
Двухзначные числа произведение цифр которых равно 0 — 10, 20, 30, 40, 50, 60, 70, 80, 90.
Трехзначные числа произведение цифр которых равно 0 — 100, 101, 102, 103, 104, 105, 106, 107, 108, 109.
Четырехзначные числа произведение цифр которых равно 0 — 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009.
Пятизначные числа произведение цифр которых равно 0 — 10000, 10001, 10002, 10003, 10004, 10005, 10006, 10007, 10008, 10009.
Шестизначные числа произведение цифр которых равно 0 — 100000, 100001, 100002, 100003, 100004, 100005, 100006, 100007, 100008, 100009.
Квадрат произведения цифр числа 505389.
Квадрат произведения цифр шестизначного числа 505389 равен 5 * 0 * 5 * 3 * 8 * 9 = 0² = 0.
Произведение квадратов цифр шестизначного числа 505389.
Произведение квадратов цифр числа 505389 равна 5² * 0² * 5² * 3² * 8² * 9² = 25 * 0 * 25 * 9 * 64 * 81 = 0.
Произведение четных цифр числа 505389.
Произведение четных цифр шестизначного числа 505389 равно 8 = 8.
Квадрат произведения четных цифр шестизначного числа 505389.
Квадрат произведения четных цифр числа 505389 равен 8 = 8² = 64.
Произведение квадратов четных цифр шестизначного числа 505389.
Произведение квадратов четных цифр числа 505389 равно 8² = 64 = 64.
Запишите числа которые в сумме дают число 505389.
Задача: Данно число 505389.Какие 2(два) числа дают в сумме число 505389?Решение:
1) 36644 + 468745 = 505389
2) 196984 + 308405 = 505389
3) 159337 + 346052 = 505389
4) 143153 + 362236 = 505389
5) 199859 + 305530 = 505389
Какие 3(три) числа дают в сумме число 505389?Решение:
1) 41868 + 170636 + 292885 = 505389
2) 32591 + 85221 + 387577 = 505389
3) 64121 + 204743 + 236525 = 505389
4) 99262 + 35199 + 370928 = 505389
5) 126409 + 61856 + 317124 = 505389
Какие 4(четыре) числа дают в сумме число 505389?Решение:
1) 116841 + 48229 + 114578 + 225741 = 505389
2) 38972 + 17537 + 136311 + 312569 = 505389
3) 91533 + 89468 + 138085 + 186303 = 505389
4) 23206 + 45327 + 185377 + 251479 = 505389
5) 60239 + 58036 + 25382 + 361732 = 505389
Какие 5(пять) чисел дают в сумме число 505389?Решение:
1) 53343 + 48776 + 55661 + 152216 + 195393 = 505389
2) 64744 + 18098 + 80384 + 110097 + 232066 = 505389
3) 94078 + 10494 + 120685 + 105682 + 174450 = 505389
4) 2755 + 50770 + 4640 + 217839 + 229385 = 505389
5) 55451 + 52867 + 80269 + 29312 + 287490 = 505389
Задание 1
Решите уравнение $$sinfrac{pi(x+2)}{6}=frac{sqrt{3}}{2}.$$ В ответе укажите наибольший отрицательный корень.
Ответ: -10
Скрыть
$$sinfrac{pi(x+2)}{6}=frac{sqrt{3}}{2}$$
$$left[begin{matrix} frac{pi(x+2)}{6}=frac{pi}{3}+2pi n,nin Z\ frac{pi(x+2)}{6}=frac{2pi}{3}+2pi n end{matrix}right.Leftrightarrowleft[begin{matrix} x+2=2+12n,nin Z\ x+2=4+12n end{matrix}right.Leftrightarrowleft[begin{matrix} x=12n,nin Z\ x=2+12n end{matrix}right.$$
Пусть $$n=1$$: получим $$-12$$ и $$-10.$$ Пусть $$n=0$$: $$0$$ и $$2.$$
Тогда наибольший отрицательный $$-10$$
Задание 2
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Ответ: 0,32
Скрыть
Так как вероятности выигрыша и проигрыша равны по $$0,4,$$ то вероятность сыграть вничью, равна $$1-0,4-0,4=0,2.$$ Таким образом, футбольная команда может выйти в следующий круг при следующих несовместных исходах:
— выиграла первую игру и выиграла вторую игру;
— сыграла вничью первую игру и выиграла вторую игру;
— выиграла первую игру и сыграла вничью вторую игру.
Вероятность первого исхода равна $$P_1=0,4cdot0,4=0,16.$$ Вероятность второго исхода $$P_2=0,2cdot0,4=0,08.$$ Вероятность третьего исхода $$P_3=0,4cdot0,2=0,08.$$ Искомая вероятность выхода в следующий круг соревнований, равна сумме вероятностей этих трех независимых исходов:
$$P=P_1+P_2+P_3=0,16+0,08+0,08=0,32$$
Задание 3
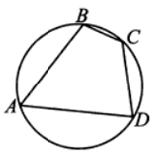
Точки А, В, С, D, расположенные на окружности, делят эту окружность на четыре дуги АВ, ВС, CD и AD, градусные величины которых относятся как 4:2:3:6. Найдите угол АВС. Ответ дайте в градусах.
Ответ: 108
Скрыть
Из рисунка видно, что угол A вписанный и опирается на дугу BD, следовательно, угол A равен половине градусной меры дуги BD. Найдем сначала градусные меры дуг BC и CD. Обозначим через x градусов единичную дугу, тогда можно записать, что
$$4x+2x+3x+6x=360^{circ}$$
откуда
$$15x=360^{circ}$$
$$x=24^{circ}$$
В результате, получаем, что дуга $$AD=6cdot24^{circ}=144^{circ},$$ дуга $$CD=3cdot24^{circ}=72^{circ}$$ и дуга
$$AC=AD+CD=144^{circ}+72^{circ}=216^{circ}$$
получаем, что угол $$ABC,$$ равен:
$$angle ABC=frac{AC}{2}=frac{216^{circ}}{2}=108^{circ}$$
Задание 4
Найдите значение выражения $$frac{log_2^214+log_2 14cdotlog_2 7-2log_2^2 7}{log_2 14+2log_2 7}$$
Ответ: 1
Скрыть
$$frac{log_2^214+log_2 14cdotlog_2 7-2log_2^2 7}{log_2 14+2log_2 7}=frac{log_2 14(log_2 14+log_2 7)-2log_2^2 7}{log_2 7+log_2 2+2log_2 7}=$$
$$=frac{(log_2 7+log_2 2)(log_2 7+log_2 2+log_2 7)-2log_2^2 7}{3log_2 7+1}=$$
$$=frac{(log_2 7+1)(2log_2 7+1)-2log_2^2 7}{3log_2 7+1}=frac{2log_2^2 7+log_2 7+2log_2 7+1-2log_2^2 7}{3log_2 7+1}=$$
$$=frac{3log_2 7+1}{3log_2 7+1}=1$$
Задание 5
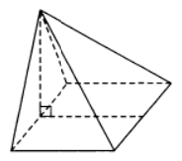
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 30°. Высота пирамиды равна 8. Найдите объём пирамиды.
Ответ: 1024
Скрыть
Из прямоугольного треугольника $$SAH$$:
$$AH=frac{8}{tg30^{circ}}=frac{24}{sqrt{3}}$$
Так как $$Delta SAB$$ — р/б, то $$AB=2AH=frac{48}{sqrt{3}}$$
$$AD=frac{8}{tg30^{circ}}=frac{24}{sqrt{3}}$$ – из прямоугольного треугольника $$SHM,$$ так как $$HM=AD$$
$$V=frac{1}{3}cdotfrac{24}{sqrt{3}}cdotfrac{48}{sqrt{3}}cdot8=1024$$
Задание 6
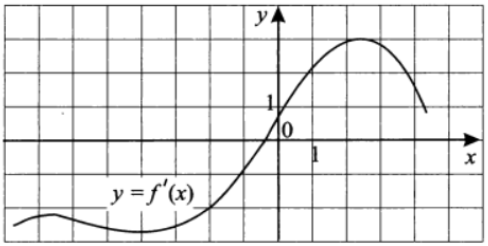
На рисунке изображен график функции $$y=f'(x)$$ — производной функции $$f(x).$$ Найдите абсциссу точки, в которой касательная к графику $$y=f(x)$$ параллельна прямой $$y=-2x+12$$ или совпадает с ней.
Ответ: -2
Скрыть
$$k_1=k_2$$
$$k_1=y'(x_0)=-2$$
$$k_2=f'(x_0)$$
$$f'(x_0)=-2$$
Задание 7
Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле $$l=sqrt{frac{Rh}{500}},$$ где R = 6400 км — радиус Земли. Человек, стоящий на пляже, видит 500 горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
Ответ: 1,4
Скрыть
Необходимо обеспечить значение $$l=6,4$$ километров, выбирая соответствующее значение $$h.$$ Найдем значение параметра $$h$$ при $$l=6,4,$$ получим:
$$l^2=frac{Rh}{500}Rightarrow h=frac{500l^2}{R}$$
Подставим числовые значения, имеем:
$$h=frac{500cdot6,4^2}{6400}=3,2$$
Изначально наблюдатель находится на высоте, при которой горизонт имеет значение $$l=4,8,$$ т.е. на высоте
$$h_0=frac{500cdot4,8^2}{6400}=1,8$$
Следовательно, ему нужно подняться на
$$3,2-1,8=1,4$$ метров.
Задание 8
Пешеход шел из деревни на станцию. Пройдя 3 км за час, он рассчитал, что опаздывает на 40 мин на поезд, если будет двигаться с той же скоростью. Поэтому он увеличил скорость до 4 км/час и пришел на станцию за 40 мин до отхода поезда. Найти расстояние (в км) между станцией и деревней.
Ответ: 19
Скрыть
$$40$$ мин $$= frac{2}{3}$$ ч
$$S-3$$ — оставшийся путь
$$t$$ — время до отправления поезд
$$frac{S-3}{3}=t+frac{2}{3}$$ — пешеход прошел оставшийся путь со скоростью 3 км/ч за $$t+frac{2}{3}$$ ч
$$t=frac{S-3-2}{3}=frac{4S-20}{12}$$
$$frac{S-3}{4}=t-frac{2}{3}$$ — пешеход прошел оставшийся путь со скоростью 4 км/ч за $$t-frac{2}{3}$$ ч
$$t=frac{S-3}{4}+frac{2}{3}=frac{3S-1}{12}$$
$$frac{4S-20}{12}=frac{3S-1}{12}$$
$$4S-3S=20-1$$
$$S=19$$
Задание 9
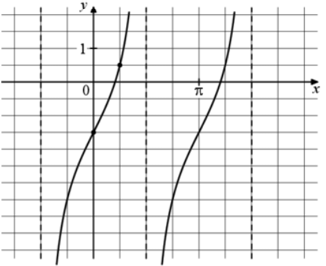
На рисунке изображен график функции $$f'(x)=acdot tg x+b.$$ Найдите $$a.$$
Ответ: 2
Скрыть
Точки $$(frac{pi}{4};frac{1}{2})$$ и $$(0;-frac{3}{2})$$ принадлежат графику функции. Тогда:
$$left{begin{matrix}
acdottgfrac{pi}{4}+b=frac{1}{2}\
acdottg0+b=-frac{3}{2}
end{matrix}right.Leftrightarrowleft{begin{matrix}
a-frac{3}{2}=frac{1}{2}\
b=-frac{3}{2}
end{matrix}right.Leftrightarrowleft{begin{matrix}
a=2\
b=-frac{3}{2}
end{matrix}right.$$
Задание 10
В таблице показано распределение случайной величины Х. Найдите математическое ожидание этой случайной величины.
| Значение x | -4 | 0 | 1 | 3 |
| Вероятности | 0,2 | 0,1 | 0,4 | 0,3 |
Ответ: 0,5
Скрыть
Математическое ожидание $$=-4cdot0,2+0cdot0,1+1cdot0,4+3cdot0,3=-0,8+0+0,4+0,9=0,1+0,4=0,5$$
Задание 11
Найдите точку минимума функции $$y=2x^2-5x+ln x-3.$$
Ответ: 1
Скрыть
1) $$D(y): x>0$$
2) $$y’=4x-5+frac{1}{x}$$
3) $$y’geq0$$
$$4x-5+frac{1}{x}geq0$$
$$frac{4x^2-5x+1}{x}geq0$$
$$frac{4(x-1)(x-frac{1}{4})}{x}geq0$$
$$x=1$$ и $$x=frac{1}{4}$$
$$x_{min}=1$$
Задание 12
А) Решите уравнение $$cos^2 3x+cos^2 4x+cos^2 5x=frac{3}{2}$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[frac{pi}{2};pi]$$
Ответ: А)$$frac{pi}{16}+frac{pi n}{8};pmfrac{pi}{3}+pi n,nin Z$$ Б)$$frac{9pi}{16};frac{2pi}{3};frac{11pi}{16};frac{13pi}{16};frac{15pi}{16}$$
Задание 13
В правильной четырёхугольной пирамиде SABCD точка К является серединой ребра SD, а точка L — серединой стороны ВС основания ABCD. Плоскость AKL пересекает ребро SC в точке N.
А) Докажите, что SN : NC=2 : 1.
Б) Найдите угол между плоскостями AKL и АВС, если АВ = 10, а высота пирамиды равна 20.
Ответ: $$arctgfrac{4}{sqrt{5}}$$
Задание 14
Решите неравенство: $$log_{frac{1}{2}}(log_2(log_{x-1}9))>0$$
Ответ: $$(4;10)$$
Задание 15
Евгений взял 15 января кредит на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы. Каждый месяц 1-го числа долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца. Со 2-го по 14-е число каждого месяца необходимо выплатить часть долга. Каждый месяц 15-го числа долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг, млн рублей | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найти наименьшее значение r, при котором общая сумма выплат будет составлять более 1,25 млн рублей.
Ответ: 6
Задание 16
В треугольнике АВС точка D лежит на стороне ВС. В треугольники ABD и ACD вписаны окружности, и к ним проведена общая внешняя касательная (отличная от ВС), пересекающая AD в точке К.
А) Докажите, что длина отрезка АК не зависит от положения точки D на ВС.
Б) Найдите длину отрезка АК, если периметр треугольника АВС равен 30, а длина стороны ВС равна 10.
Ответ: 5
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение
$$frac{x+2}{|x+2|}+|x|cdot(x^2-48)=a$$
имеет ровно три решения.
Ответ: $$-127;[-89;-87];1$$
Задание 18
Множество простых делителей числа n будем называть ДНК этого числа. Числа m и n, имеющие одинаковые ДНК, будем называть родственными. Например, числа 12 и 18 родственные, т.к. их ДНК= {2,3}.
Число m называется симметричным с числом n, если оно записано теми же цифрами, но в обратном порядке. При этом если последними цифрами числа n были нули, то в начале числа m они отбрасываются.
А) Пусть число n делится на 10. Может ли оно быть родственным со своим симметричным числом?
Б) Сумма первой и последней цифр натурального числа равна 13. Может ли оно быть родственным со своим симметричным числом?
В) Найдите минимальное и максимальное составное трёхзначное число, у которого нет трёхзначных родственных чисел.
Ответ: А) нет, Б) нет, В) 121;998