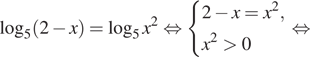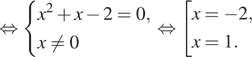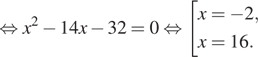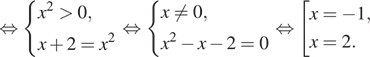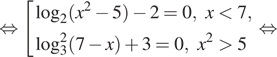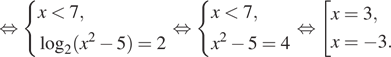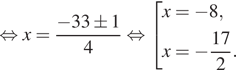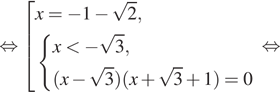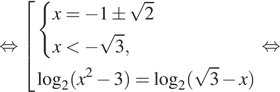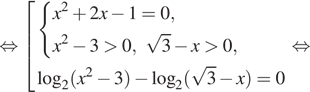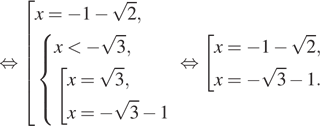Решу егэ математика 502053


Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

а)  Решите уравнение 1 плюс логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию левая круглая скобка корень из 2 правая круглая скобка корень из 8x в степени левая круглая скобка 4 правая круглая скобка плюс 14.

б)  Найдите все корни этого уравнения, принадлежащие отрезку левая квадратная скобка минус 1; дробь: числитель: 8, знаменатель: 9 конец дроби правая квадратная скобка .

Спрятать решение

Решение.

а)  Заметим, что уравнение определено при любом x. Запишем исходное уравнение в виде:

логарифм по основанию 2 левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию 2 левая круглая скобка 8x в степени 4 плюс 14 правая круглая скобка минус логарифм по основанию 2 2 равносильно логарифм по основанию 2 левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию 2 левая круглая скобка 4x в степени 4 плюс 7 правая круглая скобка равносильно равносильно 9x в квадрате плюс 5=4x в степени 4 плюс 7 равносильно 4x в степени 4 минус 9x в квадрате плюс 2=0 равносильно левая круглая скобка 4x в квадрате минус 1 правая круглая скобка левая круглая скобка x в квадрате минус 2 правая круглая скобка =0.

Значит, либо 4x в квадрате минус 1=0, откуда x= дробь: числитель: 1, знаменатель: 2 конец дроби или x= минус дробь: числитель: 1, знаменатель: 2 конец дроби , либо x в квадрате минус 2=0, откуда x= корень из 2 или x= минус корень из 2.

б)  Поскольку минус корень из 2 меньше минус 1 меньше минус дробь: числитель: 1, знаменатель: 2 конец дроби меньше дробь: числитель: 1, знаменатель: 2 конец дроби меньше дробь: числитель: 8, знаменатель: 9 конец дроби меньше корень из 2, отрезку левая квадратная скобка минус 1; дробь: числитель: 8, знаменатель: 9 конец дроби правая квадратная скобка принадлежат корни x= дробь: числитель: 1, знаменатель: 2 конец дроби и x= минус дробь: числитель: 1, знаменатель: 2 конец дроби .

Ответ: а) x=pm корень из 2,x=pm дробь: числитель: 1, знаменатель: 2 конец дроби ; б) pm дробь: числитель: 1, знаменатель: 2 конец дроби .

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания Баллы
Обоснованно получены верные ответы в обоих пунктах. 2
Обоснованно получен верный ответ в пункте а),

ИЛИ

получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б).

 1
Решение не соответствует ни одному из критериев, перечисленных выше. 0
Максимальный балл 2

Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 602., Задания 13 (С1) ЕГЭ 2013

Спрятать решение

·

·

Курс Д. Д. Гущина

·

Гость 19.01.2015 14:25

как разложить на множители ур-е приводимое к квадратному????

Александр Иванов

решить соответствующее квадратное

Ксения Sunny 12.02.2016 15:37

почему вы не искали одз для прологарифмированных выражений?

Источник

  • ЗАДАЧИ ЕГЭ С ОТВЕТАМИ

  • АНГЛИЙСКИЙ без ГРАНИЦ

2013-02-28

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

  • РубрикиРубрики
  • Задачи по номерам!

    №1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16

  • МЕТКИ

    БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие

  • ОСТЕОХОНДРОЗУ-НЕТ!

Источник

Решу егэ профиль математика 517739

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Задание 12 № 517747

Ответ а 3 и 27; б 3.

Ege. sdamgia. ru

12.01.2020 13:48:01

2020-01-12 13:48:01

Источники:

Https://ege. sdamgia. ru/test? likes=517739

Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Б Заметим, что Значит, указанному отрезку принадлежит корень 3.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Dankonoy. com

16.06.2020 6:45:22

2020-06-16 06:45:22

Источники:

Https://dankonoy. com/ege/ege11/archives/10087

Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Материал для подготовки к экзамену по математике 1 курс

Материал для подготовки к экзамену по математике 1 курс.

нажмите, чтобы узнать подробности

Материал для подготовки к экзамену по математике для 1 курса СПО.

Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»

Логарифмические уравнения

1. Задание 5 № 26646

Найдите корень уравнения

2. Задание 5 № 26647

Найдите корень уравнения

3. Задание 5 № 26648

Найдите корень уравнения

4. Задание 5 № 26649

Найдите корень уравнения

5. Задание 5 № 26657

Найдите корень уравнения

6. Задание 5 № 26658

Найдите корень уравнения

7. Задание 5 № 26659

Найдите корень уравнения

8. Задание 5 № 77380

Решите уравнение

9. Задание 5 № 77381

Решите уравнение

10. Задание 5 № 77382

Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

11. Задание 5 № 315120

Найдите корень уравнения

12. Задание 5 № 315535

Найдите корень уравнения

13. Задание 5 № 525399

Решите уравнение

Тригонометрические уравнения

1. Задание 5 № 26669

Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.


Значениям соответствуют положительные корни.

Если, то и

Если, то и

Значениям соответствуют меньшие значения корней.

Следовательно, наибольшим отрицательным корнем является число

2. Задание 5 № 77376

Решите уравнение В ответе напишите наибольший отрицательный корень.

Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.

3. Задание 5 № 77377

Решите уравнение В ответе напишите наименьший положительный корень.

Значениям соответствуют отрицательные корни.

Если, то и

Если, то и

Значениям соответствуют большие положительные корни.

Наименьшим положительным решением является 0,5.

Преобразования числовых логарифмических выражений

1. Задание 9 № 26843

Найдите значение выражения

2. Задание 9 № 26844

Найдите значение выражения

3. Задание 9 № 26845

Найдите значение выражения

4. Задание 9 № 26846

Найдите значение выражения

5. Задание 9 № 26847

Найдите значение выражения

6. Задание 9 № 26848

Найдите значение выражения

7. Задание 9 № 26849

Найдите значение выражения

8. Задание 9 № 26850

Найдите значение выражения

9. Задание 9 № 26851

Найдите значение выражения

10. Задание 9 № 26852

Найдите значение выражения

11. Задание 9 № 26853

Найдите значение выражения

12. Задание 9 № 26854

Найдите значение выражения

13. Задание 9 № 26855

Найдите значение выражения

14. Задание 9 № 26856

Найдите значение выражения

15. Задание 9 № 26857

Найдите значение выражения

16. Задание 9 № 26858

Найдите значение выражения

17. Задание 9 № 26859

Найдите значение выражения

18. Задание 9 № 26860

Найдите значение выражения

19. Задание 9 № 26861

Найдите значение выражения

20. Задание 9 № 26862

Найдите значение выражения

21. Задание 9 № 26882

Найдите значение выражения

22. Задание 9 № 26883

Найдите значение выражения

23. Задание 9 № 26885

Найдите значение выражения

24. Задание 9 № 26889

Найдите значение выражения

25. Задание 9 № 26892

Найдите значение выражения

26. Задание 9 № 26893

Найдите значение выражения

27. Задание 9 № 26894

Найдите значение выражения

28. Задание 9 № 26896

Найдите значение выражения

29. Задание 9 № 77418

Вычислите значение выражения:

30. Задание 9 № 505097

Найдите значение выражения

31. Задание 9 № 509086

Найдите значение выражения

32. Задание 9 № 510939

Найдите значение выражения

33. Задание 9 № 525403

Найдите значение выражения

Вычисление значений тригонометрических выражений

1. Задание 9 № 26775

Найдите, если и

2. Задание 9 № 26776

Найдите, если и

3. Задание 9 № 26777

Найдите, если и

4. Задание 9 № 26778

Найдите, если и

5. Задание 9 № 26779

Найдите, если

6. Задание 9 № 26780

Найдите, если

7. Задание 9 № 26783

Найдите значение выражения, если

8. Задание 9 № 26784

Найдите, если и

9. Задание 9 № 26785

Найдите, если и

10. Задание 9 № 26786

Найдите, если

11. Задание 9 № 26787

Найдите, если

12. Задание 9 № 26788

Найдите, если

13. Задание 9 № 26789

Найдите, если

14. Задание 9 № 26790

Найдите, если

15. Задание 9 № 26791

Найдите, если

16. Задание 9 № 26792

Найдите значение выражения, если

17. Задание 9 № 26793

Найдите значение выражения, если

18. Задание 9 № 26794

Найдите, если

19. Задание 9 № 316350

Найдите, если

20. Задание 9 № 501598

Найдите значение выражения

21. Задание 9 № 502014

Найдите значение выражения

22. Задание 9 № 502045

Найдите значение выражения

23. Задание 9 № 502106

Найдите значение выражения

24. Задание 9 № 502285

Найдите значение выражения

25. Задание 9 № 502305

Найдите значение выражения если и

26. Задание 9 № 504410

Найдите значение выражения:

27. Задание 9 № 504824

Найдите значение выражения

28. Задание 9 № 508966

Найдите если

29. Задание 9 № 510424

Найдите если и

30. Задание 9 № 549336

Найдите если и

Преобразования числовых тригонометрических выражений

1. Задание 9 № 26755

Найдите значение выражения

2. Задание 9 № 26756

Найдите значение выражения

3. Задание 9 № 26757

Найдите значение выражения

4. Задание 9 № 26758

Найдите значение выражения

5. Задание 9 № 26759

Найдите значение выражения

6. Задание 9 № 26760

Найдите значение выражения

7. Задание 9 № 26761

Найдите значение выражения

8. Задание 9 № 26762

Найдите значение выражения

9. Задание 9 № 26763

Найдите значение выражения

10. Задание 9 № 26764

Найдите значение выражения

11. Задание 9 № 26765

Найдите значение выражения

12. Задание 9 № 26766

Найдите значение выражения

13. Задание 9 № 26767

Найдите значение выражения

14. Задание 9 № 26769

Найдите значение выражения

15. Задание 9 № 26770

Найдите значение выражения

16. Задание 9 № 26771

Найдите значение выражения

17. Задание 9 № 26772

Найдите значение выражения

18. Задание 9 № 26773

Найдите значение выражения

19. Задание 9 № 26774

Найдите значение выражения

20. Задание 9 № 77412

Найдите значение выражения

21. Задание 9 № 77413

Найдите значение выражения

22. Задание 9 № 77414

Найдите значение выражения:

23. Задание 9 № 245169

Найдите значение выражения

24. Задание 9 № 245170

Найдите значение выражения

25. Задание 9 № 245171

Найдите значение выражения

26. Задание 9 № 245172

Найдите значение выражения

27. Задание 9 № 501701

Найдите значение выражения

28. Задание 9 № 502994

Найдите значение выражения

29. Задание 9 № 503310

Найдите значения выражения

30. Задание 9 № 510013

Найдите если и

31. Задание 9 № 510312

Найдите значение выражения

32. Задание 9 № 510386

Найдите значение выражения

33. Задание 9 № 510405

Найдите значение выражения

34. Задание 9 № 510824

Найдите значение выражения

35. Задание 9 № 510843

Найдите значение выражения

36. Задание 9 № 525113

Найдите значение выражения

37. Задание 9 № 526009

Найдите значение выражения

Ло­га­риф­ми­че­ские и по­ка­за­тель­ные уравнения

1. Задание 13 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

2. Задание 13 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

3. Задание 13 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

4. Задание 13 № 516760

А) Решите уравнение:

Б) Определите, какие из его корней принадлежат отрезку

5. Задание 13 № 514623

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

6. Задание 13 № 502053

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

7. Задание 13 № 525377

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

8. Задание 13 № 513605

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

9. Задание 13 № 503127

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

10. Задание 13 № 514081

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащего отрезку

11. Задание 13 № 502999

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].

12. Задание 13 № 528517

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

13. Задание 13 № 550261

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие промежутку

14. Задание 13 № 555265

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

15. Задание 13 № 555583

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

16. Задание 13 № 561853

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].

17. Задание 13 № 562032

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

18. Задание 13 № 562757

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение В ответе напишите наименьший положительный корень.

Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»

Б Укажите корни этого уравнения, принадлежащие отрезку.

Multiurok. ru

06.02.2020 18:29:01

2020-02-06 18:29:01

Источники:

Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html

Источник

Тема .

ЕГЭ Обществознание с HISTRUCTOR

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

егэ обществознание с histructor

.0117-20. Задания по тексту HIS

.0221. Анализ экономического графика HIS

.0322. Задание – задача

.0423. Задание по Конституции

.0524. План HIS

.0625. Причинно-следственные связи и примеры социальных явлений

.07тест

Решаем задачу:

Задание 24. Используя обществоведческие знания, составьте сложный план, позволяющий раскрыть по существу тему «Ценные бумаги». Сложный план должен содержать не менее трех пунктов, непосредственно раскрывающих тему по существу, из которых два или более детализированы в подпунктах. (4 балла)

Показать ответ и решение

1.Понятие ценной бумаги.

2.Свойства (признаки) ценных бумаг:
а) обращаемость;
б) доступность для гражданского оборота;
в) стандартность;
г) документарность;
д) регулируемость и признание государством;
е) рыночность;
ё) ликвидность;
ж) риск;
з) доходность и т.д.

3. Основные ценные бумаги:
а) акция (обыкновенная и привилегированная);
б) облигация;
в) вексель;
г) чек;
д) банковские сертификаты (депозитный и сберегательный сертификат);
е) инвестиционный пай;
ё) закладная;
ж) варрант;
з) коносамент и т.д.

4. Функции ценных бумаг:
а) информационная (характеризуют состояние экономики);
б) перераспределительная (перераспределение капитала между различными сферами экономики);
в) мобилизующая (аккумулирование, мобилизация временно свободных денежных сбережений);
г) регулирующая (регулирование денежного обращения);
д) расчётная (универсальный̆ кредитно- расчётный инструмент).

5. Фондовые биржи.

Обязательные пункты: 2, 3 и 4

Критерии оценки

24.1. Раскрытие темы по существу. 

Сложный план содержит не менее трёх пунктов, включая два пункта, наличие которых позволяет раскрыть данную тему по существу. Оба этих «обязательных» пункта детализированы в подпунктах, позволяющих раскрыть данную тему по существу. Количество подпунктов каждого пункта должно быть не менее трёх, за исключением случаев, когда с точки зрения общественных наук возможно только два подпункта — 3 балла

Сложный план содержит не менее трёх пунктов, из которых два или более детализированы в подпунктах, включая два пункта, наличие которых позволяет раскрыть данную тему по существу. Только один из этих «обязательных» пунктов детализирован в подпунктах, позволяющих раскрыть данную тему по существу. Количество подпунктов должно быть не менее трёх, за исключением случаев, когда с точки зрения общественных наук возможно только два подпункта. ИЛИ Сложный план содержит не менее трёх пунктов, включая два пункта, наличие которых позволяет раскрыть данную тему по существу. Оба этих «обязательных» пункта детализированы в подпунктах, позволяющих раскрыть данную тему по существу. Хотя бы один любой пункт (обязательный или нет) детализирован в подпунктах в количестве менее трёх, за исключением случаев, когда с точки зрения общественных наук возможно только два подпункта — 2 балла

Сложный план содержит не менее трёх пунктов, из которых два или более детализированы в подпунктах, включая только один пункт, наличие которого позволяет раскрыть данную тему по существу. Этот «обязательный» пункт детализирован в подпунктах, позволяющих раскрыть данную тему по существу. Количество подпунктов должно быть не менее трёх, за исключением случаев, когда с точки зрения общественных наук возможно только два подпункта — 1 балл 

Все иные ситуации, не предусмотренные правилами выставления 3, 2 и 1 балла. ИЛИ Случаи, когда ответ выпускника по форме не соответствует требованию задания (например, не является сложным планом / не оформлен в виде плана с выделением пунктов и подпунктов) — 0 баллов

24.2 Корректность формулировок пунктов и подпунктов плана

Формулировки пунктов и подпунктов плана корректны и не содержат ошибок, неточностей — 1 балл

Все иные ситуации — 0 баллов

Указания по оцениванию 1. Пункты/подпункты, имеющие абстрактно-формальный характер и не отражающие специфики темы, не засчитываются при оценивании. 2. 1 балл по критерию 24.2 может быть выставлен только в случае, если по критерию 24.1 выставлено 3 балла.

Источник

Логарифмические
уравнения из материалов ЕГЭ профильного уровня.

 (Для
всех уравнений делается проверка или находится ОДЗ).

1. а)  Решите уравнение логарифм по основанию 5 левая круглая скобка 2 минус x правая круглая скобка = логарифм по основанию левая круглая скобка 25 правая круглая скобка x в степени 4 .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка логарифм по основанию 9 дробь: числитель: 1, знаменатель: { конец дроби 82; логарифм по основанию 9 8 правая квадратная скобка .

Решение. а)  Запишем
исходное уравнение в виде:

логарифм по основанию 5 левая круглая скобка 2 минус x правая круглая скобка = логарифм по основанию 5 x в квадрате равносильно система выражений 2 минус x=x в квадрате ,x в квадрате больше 0 конец системы равносильно
равносильно система выражений x в квадрате плюс x минус 2=0,x не равно 0 конец системы . равносильно совокупность выражений x= минус 2,x=1. конец совокупности .

б)  Поскольку логарифм по основанию целая часть: 9, дробная часть: числитель: 1, знаменатель: 82 меньше минус 2 меньше логарифм по основанию 9 8 меньше 1,отрезку
левая квадратная скобка логарифм по основанию целая часть: 9, дробная часть: числитель: 1, знаменатель: 82 ; логарифм по основанию 9 8 правая квадратная скобка принадлежит
единственный корень −2.

Ответ: а) −2; 1, б) −2.

2. а)  Решите уравнение логарифм по основанию 2 левая круглая скобка x в квадрате минус 14x правая круглая скобка =5.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка логарифм по основанию 3 0,1; 5 корень из 10 правая квадратная скобка .

Решение. а)  Из
уравнения получаем:

логарифм по основанию 2 левая круглая скобка x в квадрате минус 14x правая круглая скобка =5 равносильно x в квадрате минус 14x=32 равносильно
равносильно x в квадрате минус 14x минус 32=0 равносильно совокупность выражений x= минус 2,x=16. конец совокупности .

б)  Заметим, что логарифм по основанию 3 0,1 меньше логарифм по основанию 3 дробь: числитель: 1, знаменатель: 9 конец дроби = минус 2 меньше 5 корень из 10= корень из 250 меньше корень из 256=16.Значит,
указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

3. а)  Решите уравнение 6 логарифм по основанию 8 в квадрате x минус 5 логарифм по основанию 8 x плюс 1=0.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка 2;2,5 правая квадратная скобка .

Решение. а)  Запишем
исходное уравнение в виде:

левая круглая скобка 3 логарифм по основанию 8 x минус 1 правая круглая скобка левая круглая скобка 2 логарифм по основанию 8 x минус 1 правая круглая скобка =0.

Значит, 3 логарифм по основанию 8 x=1,откуда
x=2,или 2 логарифм по основанию 8 x=1,откуда
x=2 корень из 2 .

б)  Заметим, что 2 меньше 2,5= корень из 6,25 меньше корень из 8 =2 корень из 2 .

Значит, указанному отрезку принадлежит корень 2.

Ответ: а) 2 и 2 корень из 2 ;б) 2.

4.  а)  Решите уравнение 1 плюс логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию левая круглая скобка корень из 2 правая круглая скобка корень из 8x в степени левая круглая скобка 4 правая круглая скобка плюс 14.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус 1; дробь: числитель: 8, знаменатель: 9 конец дроби правая квадратная скобка .

Решение. а)  Заметим,
что уравнение определено при любом x.Запишем исходное уравнение
в виде:

логарифм по основанию 2 левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию 2 левая круглая скобка 8x в степени 4 плюс 14 правая круглая скобка минус логарифм по основанию 2 2 равносильно
равносильно логарифм по основанию 2 левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию 2 левая круглая скобка 4x в степени 4 плюс 7 правая круглая скобка равносильно равносильно 9x в квадрате плюс 5=4x в степени 4 плюс 7 равносильно 4x в степени 4 минус 9x в квадрате плюс 2=0 равносильно
равносильно левая круглая скобка 4x в квадрате минус 1 правая круглая скобка левая круглая скобка x в квадрате минус 2 правая круглая скобка =0.

Значит, либо 4x в квадрате минус 1=0,откуда x= дробь: числитель: 1, знаменатель: 2 конец дроби или x= минус дробь: числитель: 1, знаменатель: 2 конец дроби , либо x в квадрате минус 2=0,откуда x= корень из 2или x= минус корень из 2.

б)  Поскольку минус корень из 2 меньше минус 1 меньше минус дробь: числитель: 1, знаменатель: 2 конец дроби меньше дробь: числитель: 1, знаменатель: 2 конец дроби меньше дробь: числитель: 8, знаменатель: 9 конец дроби меньше корень из 2, отрезку
левая квадратная скобка минус 1; дробь: числитель: 8, знаменатель: 9 конец дроби правая квадратная скобка принадлежат
корни x= дробь: числитель: 1, знаменатель: 2 конец дроби и x= минус дробь: числитель: 1, знаменатель: 2 конец дроби .

Ответ: а) x=pm корень из 2,x=pm дробь: числитель: 1, знаменатель: 2 конец дроби ; б)
pm дробь: числитель: 1, знаменатель: 2 конец дроби .

5.   а)  Решите уравнение логарифм по основанию 7 левая круглая скобка x плюс 2 правая круглая скобка = логарифм по основанию левая круглая скобка 49 правая круглая скобка левая круглая скобка x в степени 4 правая круглая скобка .

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка логарифм по основанию целая часть: 6, дробная часть: числитель: 1, знаменатель: 7 ; логарифм по основанию 6 35 правая квадратная скобка .

Решение. а)  Поскольку
логарифм по основанию левая круглая скобка 7 в квадрате правая круглая скобка x в степени 4 = логарифм по основанию 7 x в квадрате ,получаем:

логарифм по основанию 7 левая круглая скобка x плюс 2 правая круглая скобка = логарифм по основанию левая круглая скобка 49 правая круглая скобка x в степени 4 равносильно логарифм по основанию 7 левая круглая скобка x плюс 2 правая круглая скобка = логарифм по основанию 7 x в квадрате равносильно
равносильно система выражений x в квадрате больше 0,x плюс 2=x в квадрате конец системы . равносильно система выражений x не равно 0,x в квадрате минус x минус 2=0 конец системы . равносильно совокупность выражений x= минус 1,x=2. конец совокупности .

б)  В силу цепочки соотношений логарифм по основанию целая часть: 6, дробная часть: числитель: 1, знаменатель: 7 меньше логарифм по основанию целая часть: 6, дробная часть: числитель: 1, знаменатель: 6 = минус 1 меньше логарифм по основанию 6 35 меньше логарифм по основанию 6 36=2заданному
отрезку принадлежит только число −1.

Ответ: а) {−1, 2}, б) −1.

6. а)  Решите уравнение логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка умножить на логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка минус 6=
=0.

б)  Укажите корни этого уравнения, принадлежащие
промежутку левая квадратная скобка логарифм по основанию целая часть: 2, дробная часть: числитель: 1, знаменатель: 7 ; логарифм по основанию 2 9 правая квадратная скобка .

Решение. а)  Преобразуем
уравнение:

логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка умножить на логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка минус 6=0 равносильно

равносильно логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка умножить на левая круглая скобка логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 правая круглая скобка минус 2 левая круглая скобка логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 правая круглая скобка =0 равносильно

равносильно левая круглая скобка логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 правая круглая скобка левая круглая скобка логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 правая круглая скобка =0 равносильно
равносильно совокупность выражений логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 = 0, x меньше 7, логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 = 0, x в квадрате больше 5 конец совокупности . равносильно

равносильно система выражений x меньше 7, логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка = 2 конец системы . равносильно система выражений x меньше 7, x в квадрате минус 5 = 4 конец системы . равносильно совокупность выражений x=3,x= минус 3. конец совокупности .

б)  Заметим, что

минус 3 = логарифм по основанию целая часть: 2, дробная часть: числитель: 1, знаменатель: 8 меньше логарифм по основанию целая часть: 2, дробная часть: числитель: 1, знаменатель: 7 меньше 3 = логарифм по основанию 2 8 меньше логарифм по основанию 2 9,

поэтому в указанный промежуток попадает только корень x=3.

Ответ: а) {−3; 3} б) 3.

7. а)  Решите
уравнение логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка 2x в квадрате плюс 136 правая круглая скобка = дробь: числитель: 1, знаменатель: логарифм по основанию левая круглая скобка минус 33x правая круглая скобка левая круглая скобка левая круглая скобка 1 минус x правая круглая скобка левая круглая скобка x плюс 33 правая круглая скобка правая круглая скобка конец дроби .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус корень из 333; минус корень из 33 правая квадратная скобка .

Решение. а)  Заметим,
что уравнение имеет смысл при минус 33 меньше x меньше 0,x не равно минус дробь: числитель: 1, знаменатель: конец дроби 33,x не равно минус 16 минус 12 корень из 2 (⁎). Преобразуем его при
этих условиях:

логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка 2x в квадрате плюс 136 правая круглая скобка = дробь: числитель: 1, знаменатель: логарифм по основанию левая круглая скобка минус 33x правая круглая скобка левая круглая скобка левая круглая скобка 1 минус x правая круглая скобка левая круглая скобка x плюс 33 правая круглая скобка правая круглая скобка конец дроби равносильно

underset левая круглая скобка * правая круглая скобка mathop равносильно логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка 2x в квадрате плюс 136 правая круглая скобка = логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка минус 33x правая круглая скобка равносильно

underset левая круглая скобка * правая круглая скобка mathop равносильно 2x в квадрате плюс 136= минус 33x равносильно 2x в квадрате плюс 33x плюс 136=0 равносильно
равносильно x= дробь: числитель: минус 33pm1, знаменатель: 4 конец дроби равносильно совокупность выражений x= минус 8,x= минус дробь: числитель: 17, знаменатель: 2 конец дроби . конец совокупности .

б)  Заметим, что 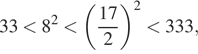33 меньше 8 в квадрате меньше левая круглая скобка дробь: числитель: 17, знаменатель: 2 конец дроби правая круглая скобка в квадрате меньше 333, поэтому
подходят оба корня.

Ответ: а) левая фигурная скобка минус 8; минус дробь: числитель: 17, знаменатель: 2 конец дроби правая фигурная скобка ; б)
минус 8, минус дробь: числитель: 17, знаменатель: 2 конец дроби .

8.     а)  Решите уравнение левая круглая скобка x в квадрате плюс 2x минус 1 правая круглая скобка левая круглая скобка логарифм по основанию 2 левая круглая скобка x в квадрате минус 3 правая круглая скобка плюс логарифм по основанию левая круглая скобка 0,5 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка правая круглая скобка =0.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку [−2,5; −1,5].

Решение. а)  Запишем
исходное уравнение в виде:

левая круглая скобка x в квадрате плюс 2x минус 1 правая круглая скобка левая круглая скобка логарифм по основанию 2 левая круглая скобка x в квадрате минус 3 правая круглая скобка плюс логарифм по основанию левая круглая скобка 0,5 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка правая круглая скобка =0 равносильно
равносильно совокупность выражений x = минус 1 минус корень из 2, система выражений x меньше минус корень из 3, левая круглая скобка x минус корень из 3 правая круглая скобка левая круглая скобка x плюс корень из 3 плюс 1 правая круглая скобка = 0 конец системы . конец совокупности . равносильно равносильно совокупность выражений система выражений x = минус 1 pm корень из 2x меньше минус корень из 3, конец системы логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка x в квадрате минус 3 правая круглая скобка = логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка конец совокупности . равносильно равносильно совокупность выражений система выражений x в квадрате плюс 2x минус 1 = 0,x в квадрате минус 3 больше 0, корень из 3 минус x больше 0, конец системы логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка x в квадрате минус 3 правая круглая скобка минус логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка = 0 конец совокупности . равносильно

равносильно совокупность выражений x = минус 1 минус корень из 2, система выражений x меньше минус корень из 3, совокупность выражений x = корень из 3,x = минус корень из 3 минус 1 конец системы . конец совокупности . конец совокупности . равносильно совокупность выражений x = минус 1 минус корень из 2,x = минус корень из 3 минус 1. конец совокупности .

б)  Проверим корни на отрезке левая квадратная скобка минус 2,5; минус 1,5 правая квадратная скобка :

минус дробь: числитель: 5, знаменатель: 2 конец дроби меньше минус 1 минус корень из 2 меньше минус дробь: числитель: 3, знаменатель: 2 конец дроби равносильно минус дробь: числитель: 3, знаменатель: 2 конец дроби меньше минус корень из 2 меньше минус дробь: числитель: 1, знаменатель: 2 конец дроби равносильно
равносильно дробь: числитель: 1, знаменатель: 2 конец дроби меньше корень из 2 меньше дробь: числитель: 3, знаменатель: 2 конец дроби равносильно 1 меньше 2 корень из 2 меньше 3 равносильно 1 меньше 8 меньше 9.

Поскольку конечное неравенство верное, значение минус 1 минус корень из 2подходит и войдет в ответ.

Проверим следующее значение x:

минус дробь: числитель: 5, знаменатель: 2 конец дроби меньше минус корень из 3 минус 1 меньше минус дробь: числитель: 3, знаменатель: 2 конец дроби равносильно минус дробь: числитель: 3, знаменатель: 2 конец дроби меньше минус корень из 3 меньше минус дробь: числитель: 1, знаменатель: 2 конец дроби равносильно
равносильно дробь: числитель: 1, знаменатель: 2 конец дроби меньше корень из 3 меньше дробь: числитель: 3, знаменатель: 2 конец дроби равносильно 1 меньше 12 меньше 9.

Так как второе значение минус корень из 3 минус 1не дает правильного конечного неравенства, оно
не войдет в ответ.

Ответ: а) левая фигурная скобка минус 1 минус корень из 2, минус 1 минус корень из 3 правая фигурная скобка ;б)
минус 1 минус корень из 2.

Скачано с www.znanio.ru

Источник

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания,
берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта
готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием
сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом
администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта
и представлены на сайте исключительно для ознакомления. Авторские права на материалы
принадлежат их законным авторам. Частичное или полное копирование материалов сайта без
письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой
зрения авторов.

Источник

9 марта 2023

В закладки

Обсудить

Жалоба

Теория и практика.

Содержание

1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой
8) Тригонометрические функции
9) Показательные функции
10) Логарифмические функции

10_zadacha.pdf

Источник: vk.com/profimatika

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Решу егэ математика 502045
  • Решу егэ математика 502014
  • Решу егэ математика 501944
  • Решу егэ математика 501724
  • Решу егэ математика 501693

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии