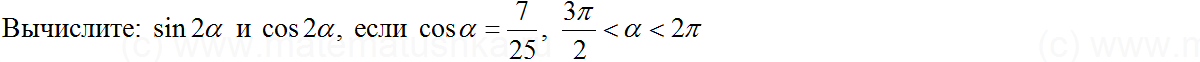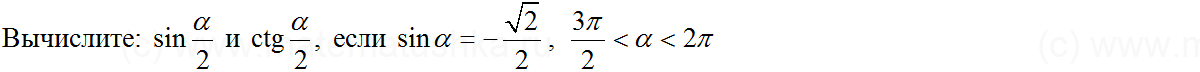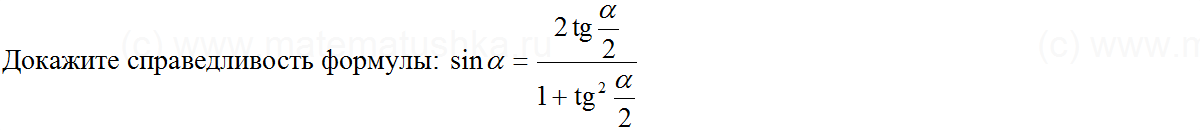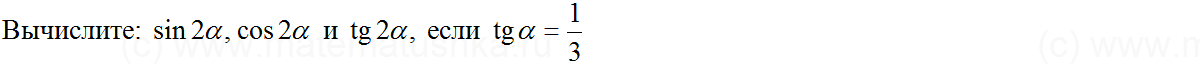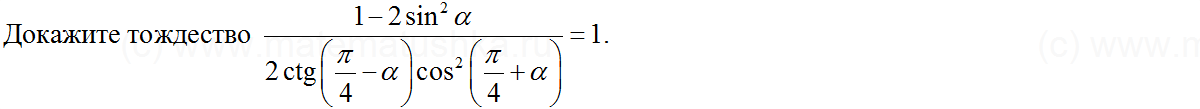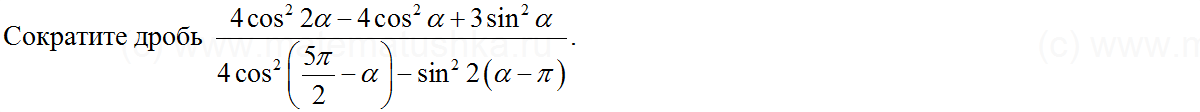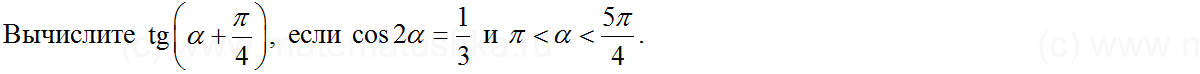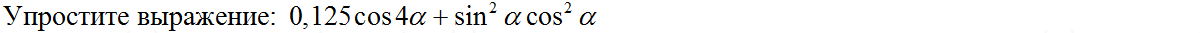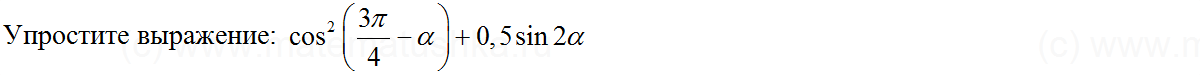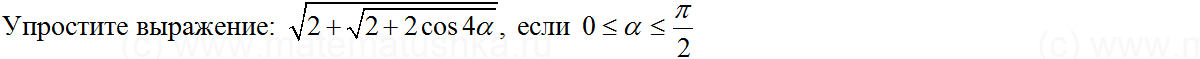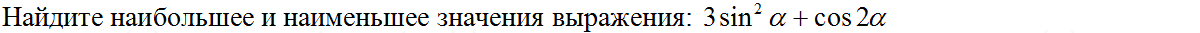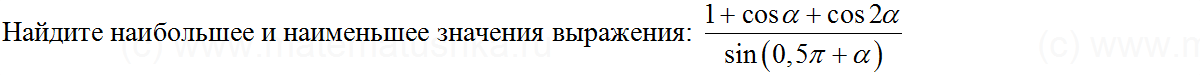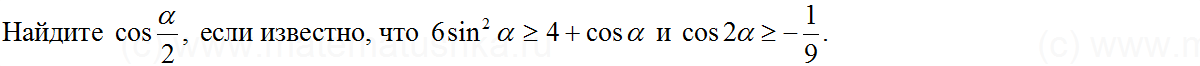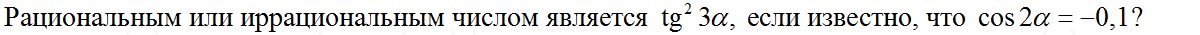Решу егэ формулы двойного аргумента - Помощь в подготовке к экзаменам и поступлению

Самостоятельная работа «Формулы двойного аргумента в заданиях егэ»

Формулы двойного аргумента в задания егэ

Формулы двойного аргумента в заданиях егэ

Вариант 1

Вычислите:

4) 2cos

Найдите: если

Упростите выражения:

1) 0,5 sin 2 ctg 

2) ) 4 sin  cos  cos 2

Решите уравнение

Вариант 2

4) 2cos

Найдите: если

Упростите выражения:

1) 2 sin2  + cos 2

2) sin2 3x – cos2 3x

Решите уравнение

Вариант 3

4) 2cos

Найдите: если

Упростите выражения:

1) sin 2t ctg t – 1

Решите уравнение

Вариант 4

4) 2cos

Найдите: если

Упростите выражения:

1) 1 + cos 2

Решите уравнение

Опубликовано 18.02.18 в 15:07

Размер файла: 18.55 Кбайт

Источник

Проверочная работа «Формулы двойного аргумента в задания егэ»

Формулы двойного аргумента в задания егэ

Формулы двойного аргумента в заданиях егэ

Вариант 1

Вычислите:

1)  































4) 2cos











Найдите:  если

  





   

Упростите выражения:

1) 0,5 sin 2 ctg 

2) ) 4 sin  cos  cos 2

Решите уравнение

 



  

Вариант 2

1)  































4) 2cos











Найдите:  если

  





   

Упростите выражения:

1) 2 sin

 + cos 2

2) sin

3x – cos

Решите уравнение

  





 

Вариант 3

1)  































4) 2cos











Найдите:  если

  





   





Упростите выражения:

1) sin 2t ctg t – 1

Решите уравнение

   







Вариант 4

1)  































4) 2cos











Найдите:  если

 











   

Упростите выражения:

1) 1 + cos 2

Решите уравнение

    





 

Источник

Примеры:

(2 sin⁡15^° cos⁡15^°=sin⁡(2·15^°)=sin⁡30^° =frac{1}{2})
(cos⁡6α=cos^2⁡3α-sin^2⁡3α)
(sin⁡α=2 sin⁡frac{α}{2}cos⁡frac{α}{2})
(2 cos^2⁡frac{π}{12}-1=cos⁡frac{2π}{12}=cos⁡frac{π}{6}=frac{sqrt{3}}{2})

Примеры решения задач из ЕГЭ на формулы двойного угла

Пример (ЕГЭ). Найдите значение выражения (frac{12 sin⁡11^° cdot, cos⁡11^°}{sin ⁡22^° }).
Решение. (frac{12 sin⁡11^° cdot, cos⁡11^°}{sin⁡22^°})(=)(frac{12 sin⁡11^° cdot,cos⁡11^°}{2 sin⁡11^° cdot, cos⁡11^° })(=)(frac{12}{2})(=6).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}).
Решение. (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}=sqrt{3}(cos^2frac{5π}{12}-sin^2frac{5π}{12})=sqrt{3}cos(2cdotfrac{5π}{12})=sqrt{3}cosfrac{5π}{6})

Вычислим (cos⁡frac{5π}{6}) с помощью тригонометрического круга. Сначала найдем (frac{5π}{6}) на круге:

(frac{5π}{6}=frac{6π-π}{6}=π-frac{π}{6})

Теперь видно, что (cos⁡frac{5π}{6}=-frac{sqrt{3}}{2})
(sqrt{3}cos⁡ frac{5π}{6}=sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{3}{2}=-1,5).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (frac{24(sin^2 17^°- cos^2⁡ 17^°)}{cos⁡34^°}).
Решение. (frac{24(sin^2 17^°- cos^2⁡ 17^°)}{cos⁡34^°})(=)(frac{-24(cos^2⁡ 17^°- sin^2 17^° )}{cos⁡34^°})(=)(frac{-24 cos⁡2cdot 17^°}{cos⁡34^° }) (=)(frac{-24 cos⁡34^° }{cos⁡34^° })(=-24).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (5sinfrac{11π}{12}cos⁡frac{11π}{12}).
Решение. (5 sinfrac{⁡11π}{12}cos⁡frac{11π}{12}=frac{5}{2}cdot2sin⁡frac{11π}{12}cos⁡frac{11π}{12}=frac{5}{2}sinfrac{⁡2cdot 11π}{12}=frac{5}{2} sin⁡frac{11π}{6}=frac{5}{2}sin⁡frac{12π-π}{6}=frac{5}{2}sin⁡(frac{12π}{6}-frac{π}{6})=)
(=frac{5}{2}sin⁡(2π-frac{π}{6})=frac{5}{2}sin⁡(-frac{π}{6})=-frac{5}{2}sin⁡frac{π}{6}=-frac{5}{2}cdot frac{1}{2}=-frac{5}{4}=-1,25).

Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{5sin⁡98^°}{sin⁡49^° sin⁡ 41^°}).

Решение:

(frac{5sin⁡98^°}{sin⁡49^° sin⁡ 41^°})		Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что (98^°)ровно в два раза больше (49^°). То есть, имеет смысл разложить синус в числителе по формуле двойного угла.
(frac{10sin⁡49^°cos49^°}{sin⁡49^° sin⁡ 41^°})		Одинаковые синусы можно сократить.
(frac{10cos49^°}{sin⁡ 41^°})		Теперь обратите внимание на то, что (49^°=90^°-41^°). Поэтому мы можем заменить (49^°) на (90^°-41^°).
(frac{10cos(90^°-41^°)}{sin⁡ 41^°})		Теперь применим к косинусу формулу приведения: ((90^°-41^°)) – это первая четверть, косинус в ней положителен. Значит, знак будет плюс; (90^°)- находится на «вертикали» — функция меняется на кофункцию. (cos⁡ (90^°-41^°)=sin⁡41^°)
(=frac{10 sin⁡41^° }{sin⁡41^°})( =10)

Ответ: (10).

Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrt{12}cos^2⁡frac{5π}{12}-sqrt{3}).

Решение:

(sqrt{12}cos^2⁡frac{5π}{12}-sqrt{3}=)		С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать (sqrt{12}). (sqrt{12}=sqrt{4cdot 3}=2sqrt{3}).
(=2sqrt{3}cos^2⁡frac{5π}{12}-sqrt{3}=)		Теперь можно вынести (sqrt{3}) за скобки.
(=sqrt{3}(2 cos^2⁡frac{5π}{12}-1)=)		Вот теперь видно, что перед нами формула косинуса двойного угла.
(=sqrt{3}cos(2cdotfrac{5π}{12})=)		Сокращаем (2) и (12).
(=sqrt{3}cos(frac{5π}{6})=)		Разложим (frac{5π}{6}): (frac{5π}{6}=frac{6π-π}{6}=frac{6π}{6}-frac{π}{6}=π-frac{π}{6})
(=sqrt{3}cos(π-frac{π}{6})=)		Теперь применим к косинусу формулу приведения: ((π-frac{π}{6})) – это вторая четверть, косинус в ней отрицателен. Значит, знак будет минус; (π) — находится на «горизонтали» — функция не меняется на кофункцию. (cos⁡(π-frac{π}{6})=-cos frac{π}{6})
(=-sqrt{3}cos⁡frac{π}{6}=-sqrt{3}cdotfrac{sqrt{3}}{2}=) (=-frac{3}{2}=-1,5.)

Ответ: (-1,5).

Смотрите также:
Формулы тригонометрии с примерами

Источник

Математушка

Наши выпускники
Оставить заявку
ЕГЭ
Статьи
Контакты
Цены
Заочное обучение

Войти

Показать решение

Источник

Задания Открытого банка ЕГЭ по математике.

Скачать:

Предварительный просмотр:

ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.

1. Вычислите: а) $frac{18sin174^circcdot cos 174^circ}{sin348^circ}.$ ; б); $frac{-17sin108^{circ}}{sin54^{circ}cdot sin36^{circ}}$

в) $frac{18sin158^{circ}}{cos79^{circ}cdot cos11^{circ}}$ ; г) $sin{frac{23pi}{12}}cdotcos{frac{23pi}{12}}$ ;

д) $frac{22({{sin }^{2}}{72}^circ -{{cos }^{2}}{72}^circ )}{cos {144}^circ }$ ; е); $sqrt{32}cos^2{frac{3pi}{8}}-sqrt{32}sin^2{frac{3pi}{8}}$

ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.

1. Вычислите: а) $frac{18sin174^circcdot cos 174^circ}{sin348^circ}.$ ; б); $frac{-17sin108^{circ}}{sin54^{circ}cdot sin36^{circ}}$

в) $frac{18sin158^{circ}}{cos79^{circ}cdot cos11^{circ}}$ ; г) $sin{frac{23pi}{12}}cdotcos{frac{23pi}{12}}$ ;

д) $frac{22({{sin }^{2}}{72}^circ -{{cos }^{2}}{72}^circ )}{cos {144}^circ }$ ; е); $sqrt{32}cos^2{frac{3pi}{8}}-sqrt{32}sin^2{frac{3pi}{8}}$

ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.

1. Вычислите: а) $frac{18sin174^circcdot cos 174^circ}{sin348^circ}.$ ; б); $frac{-17sin108^{circ}}{sin54^{circ}cdot sin36^{circ}}$

в) $frac{18sin158^{circ}}{cos79^{circ}cdot cos11^{circ}}$ ; г) $sin{frac{23pi}{12}}cdotcos{frac{23pi}{12}}$ ;

д) $frac{22({{sin }^{2}}{72}^circ -{{cos }^{2}}{72}^circ )}{cos {144}^circ }$ ; е); $sqrt{32}cos^2{frac{3pi}{8}}-sqrt{32}sin^2{frac{3pi}{8}}$

ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.

1. Вычислите: а) $frac{18sin174^circcdot cos 174^circ}{sin348^circ}.$ ; б); $frac{-17sin108^{circ}}{sin54^{circ}cdot sin36^{circ}}$

в) $frac{18sin158^{circ}}{cos79^{circ}cdot cos11^{circ}}$ ; г) $sin{frac{23pi}{12}}cdotcos{frac{23pi}{12}}$ ;

д) $frac{22({{sin }^{2}}{72}^circ -{{cos }^{2}}{72}^circ )}{cos {144}^circ }$ ; е); $sqrt{32}cos^2{frac{3pi}{8}}-sqrt{32}sin^2{frac{3pi}{8}}$

ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.

1. Вычислите: а) $frac{18sin174^circcdot cos 174^circ}{sin348^circ}.$ ; б); $frac{-17sin108^{circ}}{sin54^{circ}cdot sin36^{circ}}$

в) $frac{18sin158^{circ}}{cos79^{circ}cdot cos11^{circ}}$ ; г) $sin{frac{23pi}{12}}cdotcos{frac{23pi}{12}}$ ;

д) $frac{22({{sin }^{2}}{72}^circ -{{cos }^{2}}{72}^circ )}{cos {144}^circ }$ ; е); $sqrt{32}cos^2{frac{3pi}{8}}-sqrt{32}sin^2{frac{3pi}{8}}$

ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.

1. Вычислите: а) $frac{18sin174^circcdot cos 174^circ}{sin348^circ}.$ ; б); $frac{-17sin108^{circ}}{sin54^{circ}cdot sin36^{circ}}$

в) $frac{18sin158^{circ}}{cos79^{circ}cdot cos11^{circ}}$ ; г) $sin{frac{23pi}{12}}cdotcos{frac{23pi}{12}}$ ;

д) $frac{22({{sin }^{2}}{72}^circ -{{cos }^{2}}{72}^circ )}{cos {144}^circ }$ ; е); $sqrt{32}cos^2{frac{3pi}{8}}-sqrt{32}sin^2{frac{3pi}{8}}$

ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.

1. Вычислите: а) $frac{18sin174^circcdot cos 174^circ}{sin348^circ}.$ ; б); $frac{-17sin108^{circ}}{sin54^{circ}cdot sin36^{circ}}$

в) $frac{18sin158^{circ}}{cos79^{circ}cdot cos11^{circ}}$ ; г) $sin{frac{23pi}{12}}cdotcos{frac{23pi}{12}}$ ;

д) $frac{22({{sin }^{2}}{72}^circ -{{cos }^{2}}{72}^circ )}{cos {144}^circ }$ ; е); $sqrt{32}cos^2{frac{3pi}{8}}-sqrt{32}sin^2{frac{3pi}{8}}$

ж) $sqrt{108}cos^2{frac{23pi}{12}}-sqrt{27}$ ; з) $sqrt{32}-sqrt{128}sin^2{frac{3pi}{8}}$

и) Найдите , если .

к) Найдите $frac{2sin 4alpha }{5cos 2alpha }$ , если .

л) Найдите , если $cos alpha =frac{1}{2}$ .

ж) $sqrt{108}cos^2{frac{23pi}{12}}-sqrt{27}$ ; з) $sqrt{32}-sqrt{128}sin^2{frac{3pi}{8}}$

и) Найдите , если .

к) Найдите $frac{2sin 4alpha }{5cos 2alpha }$ , если .

л) Найдите , если $cos alpha =frac{1}{2}$ .

ж) $sqrt{108}cos^2{frac{23pi}{12}}-sqrt{27}$ ; з) $sqrt{32}-sqrt{128}sin^2{frac{3pi}{8}}$

и) Найдите , если .

к) Найдите $frac{2sin 4alpha }{5cos 2alpha }$ , если .

л) Найдите , если $cos alpha =frac{1}{2}$ .

ж) $sqrt{108}cos^2{frac{23pi}{12}}-sqrt{27}$ ; з) $sqrt{32}-sqrt{128}sin^2{frac{3pi}{8}}$

и) Найдите , если .

к) Найдите $frac{2sin 4alpha }{5cos 2alpha }$ , если .

л) Найдите , если $cos alpha =frac{1}{2}$ .

ж) $sqrt{108}cos^2{frac{23pi}{12}}-sqrt{27}$ ; з) $sqrt{32}-sqrt{128}sin^2{frac{3pi}{8}}$

и) Найдите , если .

к) Найдите $frac{2sin 4alpha }{5cos 2alpha }$ , если .

л) Найдите , если $cos alpha =frac{1}{2}$ .

ж) $sqrt{108}cos^2{frac{23pi}{12}}-sqrt{27}$ ; з) $sqrt{32}-sqrt{128}sin^2{frac{3pi}{8}}$

и) Найдите , если .

к) Найдите $frac{2sin 4alpha }{5cos 2alpha }$ , если .

л) Найдите , если $cos alpha =frac{1}{2}$ .

ж) $sqrt{108}cos^2{frac{23pi}{12}}-sqrt{27}$ ; з) $sqrt{32}-sqrt{128}sin^2{frac{3pi}{8}}$

и) Найдите , если .

к) Найдите $frac{2sin 4alpha }{5cos 2alpha }$ , если .

л) Найдите , если $cos alpha =frac{1}{2}$ .

По теме: методические разработки, презентации и конспекты

Урок «Формулы двойного угла»

Урок по теме «Формулы двойного угла».Цели урока:· формирование представлений о формулах двойного угла синуса, косинуса;· ф…

«Формулы двойного угла»

В рабочей программе тема “Формулы двойного угла” входит в раздел 1 “Алгебра и начала анализа” предмета “Математика”. В этой теме изучаются, систематизируются знания студентов об основных формулах триг…

Конспект урока в 10 классе «Формулы двойного угла»

Формирование навыков применения формул двойного углапри выполнении заданий, создание условий, в которых обучающиесямогли самостоятельно планировать и анализировать свои собственные действия, реально о…

Мне нравится

Источник

Самостоятельная работа «Формулы двойного аргумента в заданиях егэ»

Проверочная работа «Формулы двойного аргумента в задания егэ»

Примеры решения задач из ЕГЭ на формулы двойного угла

Задачи ЕГЭ по математике

Задача № 1

Задача № 2

Задача № 3

Задача № 4

Задача № 5

Задача № 6

Задача № 7

Задача № 8

Задача № 9

Задача № 10

Задача № 11

Задача № 12

Задача № 13

Задача № 14

Задача № 15

Задача № 16

Задача № 17

Задача № 18

Задача № 19

Задача № 20

Задача № 21

Задача № 22

Задача № 23

Задача № 24

Задача № 25

Задача № 26

Задача № 27

Задача № 28

Задача № 29

Задача № 30

Задача № 31

Задача № 32

Задача № 33

Задача № 34

Скачать:

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Урок «Формулы двойного угла»

«Формулы двойного угла»

Конспект урока в 10 классе «Формулы двойного угла»

Новое и интересное на сайте: