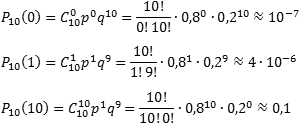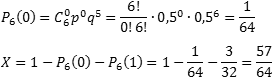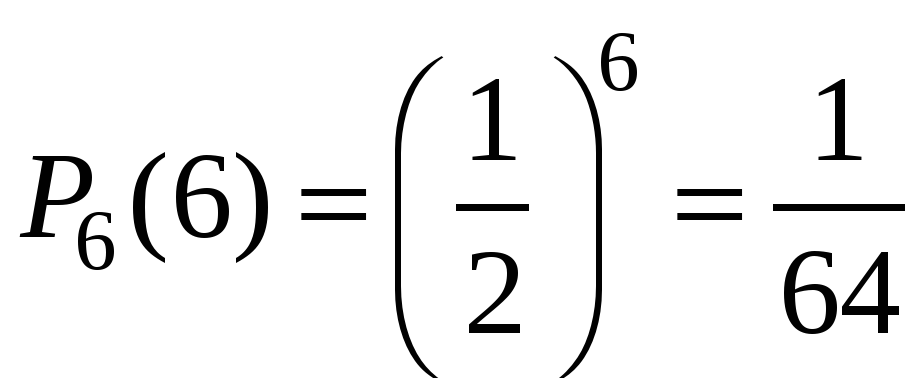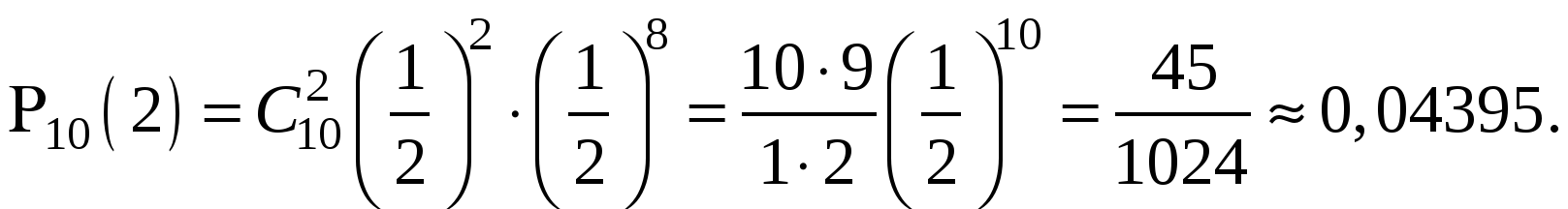Решу егэ формула бернулли

Алгебра и начала математического анализа, 11 класс

Урок №36. Формула Бернулли.

Перечень вопросов, рассматриваемых в теме:

• Формула Бернулли
• Суть задачи, решаемой с применением формулы Бернулли;
• Решение задач на вычисление вероятности;

Глоссарий по теме

Независимые события – такие события, вероятности наступления которых не зависит от появления друг друга.

Полная группа события – это система случайных событий, такая, что в результате произведенного случайного эксперимента непременно произойдет одно и только одно из них.

Рассмотрим важный частный случай: проводятся n одинаковых независимых испытаний с двумя исходами А или Ā. Вероятности P(А)=p и P(Ā)=1-p=q постоянны и не равны ни нулю, ни единице.

Вероятность того, что событие A наступит ровно k раз из n, равна P(k) = C_n^kp^kq^n-k, k=0, 1, 2 … n, C_n^k – число сочетаний из n по k.

Эта формула называется «формулой Бернулли», а модель, описывающая совокупный результат n независимых испытаний с двумя исходами (А или Ā) называется «схемой Бернулли».

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 197-203.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Попробуйте решить такую задачу:

Бросаем монетку десять раз. Какова вероятность того, что орёл выпадет ровно пять раз?

Ответ. 63/256

Достаточно часто возникает необходимость узнать вероятность появления определённого события в серии испытаний. Формулу для расчёта такой вероятности вывел выдающийся швейцарский математик Якоб Бернулли. В этом уроке мы познакомимся с формулой Бернулли и научимся её применять в решении задач.

Формула Бернулли

Рассмотрим важный частный случай: проводятся n одинаковых независимых испытаний с двумя исходами А или Ā. Вероятности P(А)=p и P(Ā)=1-p=q постоянны и не равны ни нулю, ни единице. Такие испытания иногда называют испытаниями Бернулли, исход А – успех, а исход Ā – неудача.

По теореме умножения вероятностей независимых событий для каждого элементарного события найдем вероятность, равную произведению вероятностей результатов отдельных испытаний: p^kq^n-k, где k– количество опытов, в которых произошло событие A, (n-k) – количество опытов, в которых произошло событие Ā.

Якоб Бернулли впервые доказал, что вероятность того, что событие A наступит ровно k раз из n, равна P(k) = C_n^kp^kq^n-k, k=0, 1, 2 … n, C_n^k– число сочетаний из n по k.

Эта формула называется «формулой Бернулли», а модель, описывающая совокупный результат n независимых испытаний с двумя исходами (А или Ā) называется «схемой Бернулли».

Примеры и разбор решения заданий тренировочного модуля

1. Охотник Джек попадает в мишень в среднем четыре раза из пяти. Последние четыре раза он попал. Какова вероятность, что он попадёт в следующий раз? Выделите цветом правильный ответ.

1. 0,8
2. 0,4
3. 0,2
4. 0,1

Решение:

Вероятность каждого успеха не зависит от результатов предыдущих испытаний и составляет 4/5 = 0,8.

Ответ: 1) 0,8

2. Подчеркните событие, которое более вероятно: выбросить шестёрку 3 раза, бросив кубик 6 раз, или вытянуть из колоды двух тузов, вытащив четыре карты.

Решение:

Вероятность выбросить шестёрку три раза за шесть бросков кубика

P₆(3) = C₆³·(1/6)³·(5/6)³ = 20·(1/216)·(125/216) ≈ 0,0536

Вероятность вытянуть двух тузов, вытащив четыре карты из колоды – сумма вероятностей шести событий в каждом из которых тузы выпадают на разных позициях: 1 и 2, 1 и 3, 1 и 4, 2 и 3, 2 и 4, 3 и 4. При этом вероятности этих шести событий равны между собой.

P = (4/36)·(3/35)·(32/34)·(31/33) + (4/36)·(32/35)·(3/34)·(31/33) + … = 6·(4·3·32·31)/(36·35·34·33) ≈ 0,0505.

В итоге оказывается, что вероятность выкинуть три шестёрки за шесть бросков кубика, чуть выше, чем вероятность вытянуть двух тузов, вытащив четыре карты.

Ответ: выбросить шестёрку 3 раза, бросив кубик 6 раз

Схема Бернулли. Примеры решения задач

5 июля 2011

Не будем долго размышлять о высоком — начнем сразу с определения.

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

1. A — появление события A с вероятностью p;
2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.

Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C_n^k — число сочетаний, q = 1 − p.

Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):

Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:

1. герб выпадет три раза;
2. герб выпадет один раз;
3. герб выпадет не менее двух раз.

Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.

Таким образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим вероятность того, что герб выпал три раза, т.е. k = 3:

Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:

Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P₆(2) + P₆(3) + … + P₆(6).

Заметим, что эта сумма также равна (1 − P₆(0) − P₆(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P₆(1) нам уже известно, осталось найти P₆(0):

Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?

Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.

Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.

Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3):

[begin{array}{l}{P_{20}}left( 2 right) = C_{20}^2{p^2}{q^{18}} = frac{{20!}}{{2!18!}} cdot {0,2^2} cdot {0,8^{18}} approx 0,137\{P_{20}}left( 3 right) = C_{20}^3{p^3}{q^{17}} = frac{{20!}}{{3!17!}} cdot {0,2^3} cdot {0,8^{17}} approx 0,41end{array}]

Очевидно, P₂₀(3) > P₂₀(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.

Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.

P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.

Смотрите также:

1. Локальная теорема Муавра — Лапласа
2. Формула полной вероятности
3. Тест к уроку «Сложение и вычитание дробей» (легкий)
4. Сводный тест по задачам B12 (2 вариант)
5. Как решать задачи про летающие камни?
6. Задача C1: тригонометрические уравнения и формула двойного угла

Калькуляторы на формулу Бернулли

Обратите внимание на следующие разделы, где разобраны типовые задачи на формулу Бернулли. Вы можете решить или проверить вычисления своих заданий с помощью онлайн-калькуляторов. Теорию по этой теме можно найти в онлайн-учебнике.

• Задача про партии в шахматы
• Задача про выстрелы
• Задача про мальчиков и девочек
• Задача про лотерейные билеты
• Задача о наивероятнейшем значении
• Формула Пуассона

Еще: решаем в Excel по формуле Бернулли.

Спасибо за ваши закладки и рекомендации

Схема Бернулли: решенные задачи

Задача 1. Из $n$ аккумуляторов за год хранения $k$ выходит из строя. Наудачу выбирают $m$ аккумуляторов. Определить вероятность того, что среди них $l$ исправных.
$n = 100, k = 7, m = 5, l = 3.$

Задача 2. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента;
б) не менее четырех элементов;
в) хотя бы один элемент.

Задача 3. Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?

Задача 5. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта.

Задача 6. Что более вероятно выиграть у равносильного противника: не менее двух партий из трёх или не более одной из двух?

Задача 7. а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4;
б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

Формула Пуассона: решенные задачи

Задача 4. С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия.

Задача 8. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено:
а) три ошибочно укомплектованных пакета;
б) не более трех пакетов.

Мы отлично умеем решать задачи по теории вероятностей

Решебник — когда задачи нужны быстро

Алгебра и начала математического анализа, 11 класс

Урок №36. Формула Бернулли.

Перечень вопросов, рассматриваемых в теме:

• Формула Бернулли
• Суть задачи, решаемой с применением формулы Бернулли;
• Решение задач на вычисление вероятности;

Глоссарий по теме

Независимые события – такие события, вероятности наступления которых не зависит от появления друг друга.

Полная группа события – это система случайных событий, такая, что в результате произведенного случайного эксперимента непременно произойдет одно и только одно из них.

Рассмотрим важный частный случай: проводятся n одинаковых независимых испытаний с двумя исходами А или Ā. Вероятности P(А)=p и P(Ā)=1-p=q постоянны и не равны ни нулю, ни единице.

Вероятность того, что событие A наступит ровно k раз из n, равна P(k) = C_n^kp^kq^n-k, k=0, 1, 2 … n, C_n^k – число сочетаний из n по k.

Эта формула называется «формулой Бернулли», а модель, описывающая совокупный результат n независимых испытаний с двумя исходами (А или Ā) называется «схемой Бернулли».

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 197-203.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Попробуйте решить такую задачу:

Бросаем монетку десять раз. Какова вероятность того, что орёл выпадет ровно пять раз?

Ответ. 63/256

Достаточно часто возникает необходимость узнать вероятность появления определённого события в серии испытаний. Формулу для расчёта такой вероятности вывел выдающийся швейцарский математик Якоб Бернулли. В этом уроке мы познакомимся с формулой Бернулли и научимся её применять в решении задач.

Формула Бернулли

Рассмотрим важный частный случай: проводятся n одинаковых независимых испытаний с двумя исходами А или Ā. Вероятности P(А)=p и P(Ā)=1-p=q постоянны и не равны ни нулю, ни единице. Такие испытания иногда называют испытаниями Бернулли, исход А – успех, а исход Ā – неудача.

По теореме умножения вероятностей независимых событий для каждого элементарного события найдем вероятность, равную произведению вероятностей результатов отдельных испытаний: p^kq^n-k, где k– количество опытов, в которых произошло событие A, (n-k) – количество опытов, в которых произошло событие Ā.

Якоб Бернулли впервые доказал, что вероятность того, что событие A наступит ровно k раз из n, равна P(k) = C_n^kp^kq^n-k, k=0, 1, 2 … n, C_n^k– число сочетаний из n по k.

Эта формула называется «формулой Бернулли», а модель, описывающая совокупный результат n независимых испытаний с двумя исходами (А или Ā) называется «схемой Бернулли».

Примеры и разбор решения заданий тренировочного модуля

1. Охотник Джек попадает в мишень в среднем четыре раза из пяти. Последние четыре раза он попал. Какова вероятность, что он попадёт в следующий раз? Выделите цветом правильный ответ.

1. 0,8
2. 0,4
3. 0,2
4. 0,1

Решение:

Вероятность каждого успеха не зависит от результатов предыдущих испытаний и составляет 4/5 = 0,8.

Ответ: 1) 0,8

2. Подчеркните событие, которое более вероятно: выбросить шестёрку 3 раза, бросив кубик 6 раз, или вытянуть из колоды двух тузов, вытащив четыре карты.

Решение:

Вероятность выбросить шестёрку три раза за шесть бросков кубика

P₆(3) = C₆³·(1/6)³·(5/6)³ = 20·(1/216)·(125/216) ≈ 0,0536

Вероятность вытянуть двух тузов, вытащив четыре карты из колоды – сумма вероятностей шести событий в каждом из которых тузы выпадают на разных позициях: 1 и 2, 1 и 3, 1 и 4, 2 и 3, 2 и 4, 3 и 4. При этом вероятности этих шести событий равны между собой.

P = (4/36)·(3/35)·(32/34)·(31/33) + (4/36)·(32/35)·(3/34)·(31/33) + … = 6·(4·3·32·31)/(36·35·34·33) ≈ 0,0505.

В итоге оказывается, что вероятность выкинуть три шестёрки за шесть бросков кубика, чуть выше, чем вероятность вытянуть двух тузов, вытащив четыре карты.

Ответ: выбросить шестёрку 3 раза, бросив кубик 6 раз

Урок по теории вероятностей для 11 класса по теме: «Схема Бернулли. Формула Бернулли»

Корнюшина Татьяна Анатольевна
учитель математики, МБОУ «Гимназия №4», г. Брянск

Цель:

-формирование вероятностно-статистическое мышление учащихся;

-мотивация учащихся к изучению тем теории вероятностей;

-ознакомление с применением формулы Бернулли при решении задач.

Задачи:

-закрепить знания и умения решать комбинаторные задачи;

— формировать навыки применения схемы Бернулли при решении задач,

-формировать навыки решения задач по формуле Бернулли,

-развивать основные мыслительные операции учащихся: умение сравнивать, анализировать.

Тип урока: изучение нового материала.

Формы работы: фронтальная, индивидуальная, групповая.

Оборудование: компьютер, презентация.

Ход урока:

Актуализация знаний.

Вспомним основные понятия и формулы комбинаторики.

1. Что называется факториалом числа n?

Это произведение первых натуральных n чисел от 1 до n.

2.Сколькими способами можно расставить 4 различные книги на полке?

3! = 3·2·1

Это число перестановок из 3 элементов.

3. Сколькими способами можно распределить I, II, III места между 7 участниками соревнования?

7·6·5=210

Это число размещений из 7 элементов по 3.

4. Сколькими способами можно составить график дежурства 3 учащихся из 5?

Презентация (слайд 1)

5. Сформулируйте классическое определение вероятности.

Презентация (слайд 2)

Презентация (слайд 3)

Организационный момент.

(Сообщение темы, целей и задач урока)

Презентация (слайд 4)

Изучение нового материала.

При практическом применении теории вероятностей и математической статистики часто приходится встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или не появиться событие A, причем нас интересует не результат каждого опыта, а общее число появлений события A в серии опытов. Например, если производится серия выстрелов по одной и той же цели, то нас, как правило, интересует не результат каждого отдельного выстрела, а общее число попаданий. При этом результаты предыдущих опытов никак не сказываются на последующих.

Такая стандартная схема часто встречается и в самой теории вероятностей. Она называется схемой независимых испытаний или схемой Бернулли. Швейцарский математик XVII в. Якоб Бернулли объединил примеры и вопросы такого типа в единую вероятностную задачу-схему (работа «Искусство предположений» опубликована в 1713 году).

Историческая справка. Якоб Бернулли (27.12.1654, Базель, — 16.8.1705, там же) — профессор математики Базельского университета (1687) был выходцем из Голландии.

Вам дома надо было вычислить вероятность выпадения 6 на игральном кубике.

(Ученики называют результаты. Вывод: результаты могут зависеть и от размера кубика. от силы бросания и т.п.)

Несколько опытов называются независимыми, если вероятность исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. Например, несколько последовательных бросаний монеты — это независимые опыты. Несколько последовательных выниманий карты из колоды — независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются. В противном случае — это зависимые опыты.

Презентация (слайд 5)

.

Примеры.

Монета бросается n раз.

Из колоды извлекается карта n раз, причём каждый раз карта возвращается, колода перемешивается.

Исследуется n изделий некоторого производства, наугад выбранные, на качество.

Стрелок стреляет по мишени n раз и т.д.

Задание.

№1. Объясните, почему следующие вопросы укладываются в схему Бернулли. Укажите, в чем состоит «успех» и чему равны n и k.

а) Какова вероятность трехкратного выпадения «двойки» при десяти бросаниях игрального кубика?

б) Какова вероятность того, что при ста бросаниях монеты «орел» появится 73 раза?

в) Двадцать раз подряд бросили пару игральных кубиков. Какова вероятность того, что сумма очков ни разу не была равна десяти?

г) Из колоды в 36 карт вытащили три карты, записали результат и возвратили их в колоду, затем карты перемешали. Так повторялось 4 раза. Какова вероятность того, что каждый раз среди вытащенных карт была дама пик?

Решение. Ответы учащихся с использованием слайда 5 (парная работа).

Схема Бернулли предполагает, что один и тот же эксперимент повторяется в неизменных условиях, независимо, n раз; мы наблюдаем за появлением («успеха») или непоявлением («неудача») в каждом эксперименте одного и того же события А, вероятность появления которого в каждом эксперименте постоянна и равна p. Подсчитываем, сколько раз в серии из n повторных экспериментов произойдет событие А; k – это число «успехов» в серии из n испытаний.

а) Эксперимент – бросание кубика, число повторений n = 10.

Событие А – «выпало 2 очка» (Р(А)=const); успех – появление события А (появление двойки), число успехов k=3.

б) Эксперимент – бросание монеты, число повторений n = 100, событие А – «выпал орел» (Р(А)==const), успех – появление события А (появление «орла»), число успехов k=73.

в) Эксперимент – бросание двух кубиков одновременно, число повторений n =20, событие А – «сумма выпавших очков равна 10» (Р(А)==const), успех – появление события А (сумма выпавших очков оказалась 10); число успехов k = 0.

г) Эксперимент – извлечение одновременно трех карт из колоды 36 карт, число повторений n= 4, событие А – «среди извлеченных карт есть дама пик» (Р(А)==const), успех – появление события А (появление дамы пик в наборе); число успехов k= 4.

Ответ: а) n = 10, k=3; б) n =100, k =73; в) n = 20, k = 0; г) n = 4, k = 4.

Замечание. При решении этой задачи учащимся не нужно вычислять Р(А), достаточно сказать, что событие А имеет одну и ту же вероятность при каждом повторении эксперимента.

Презентация (слайд 6)

Решение заданий

Пример 1. Монета бросается 6 раз. Какова вероятность выпадения герба 0, 1, …6 раз?

Решение. Число опытов n=6. Событие А – «успех» – выпадение герба. Тогда .

;

;

;

;

;

;

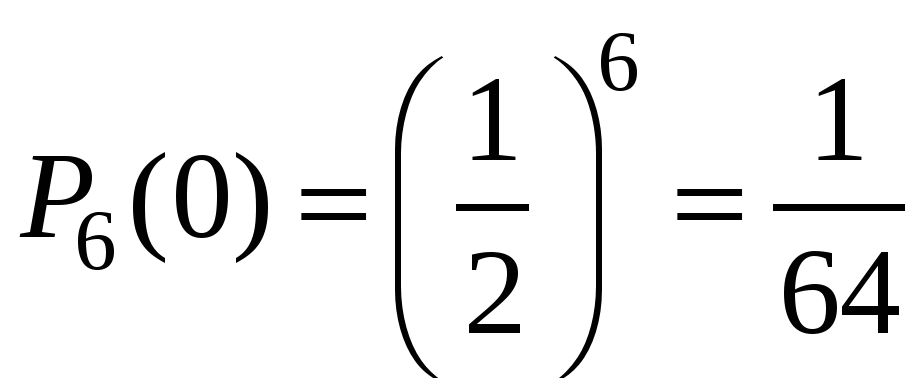
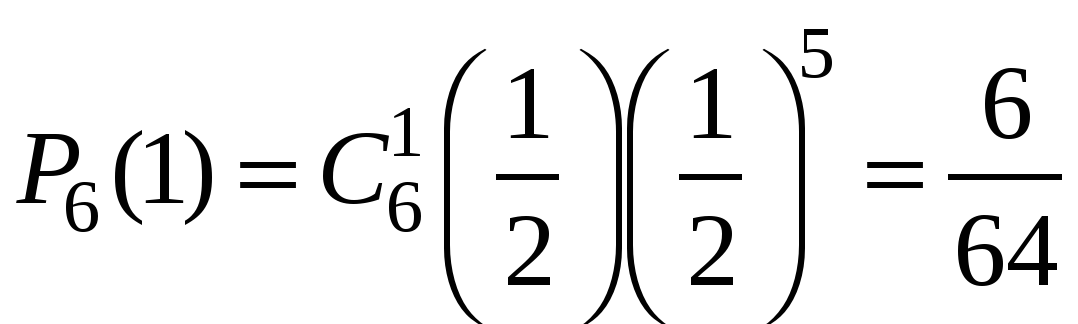
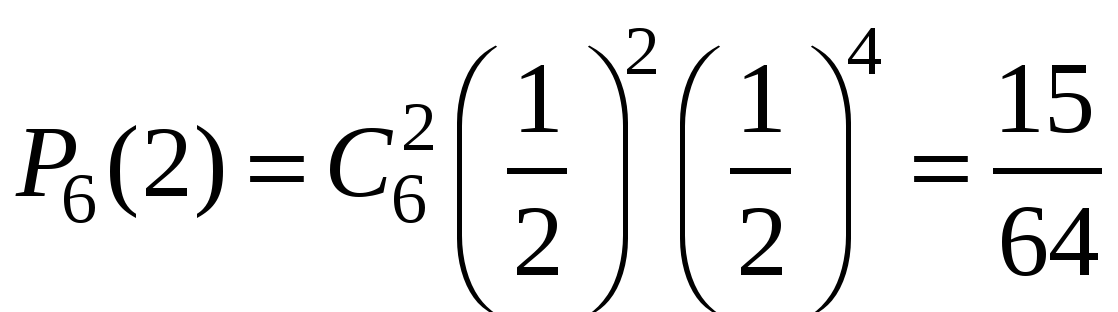
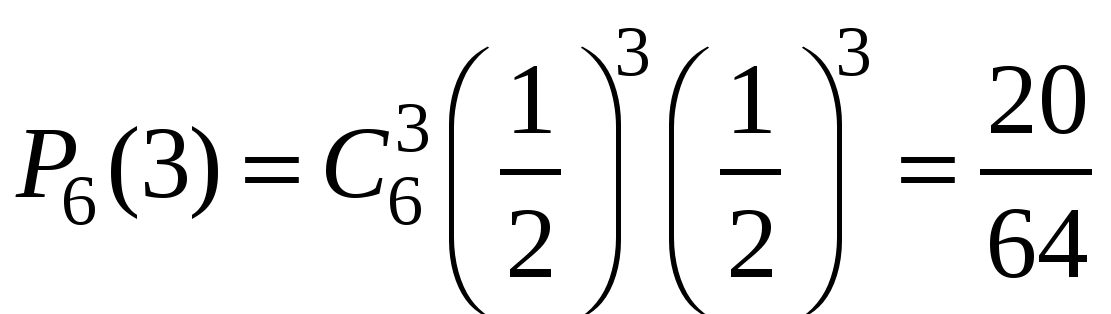
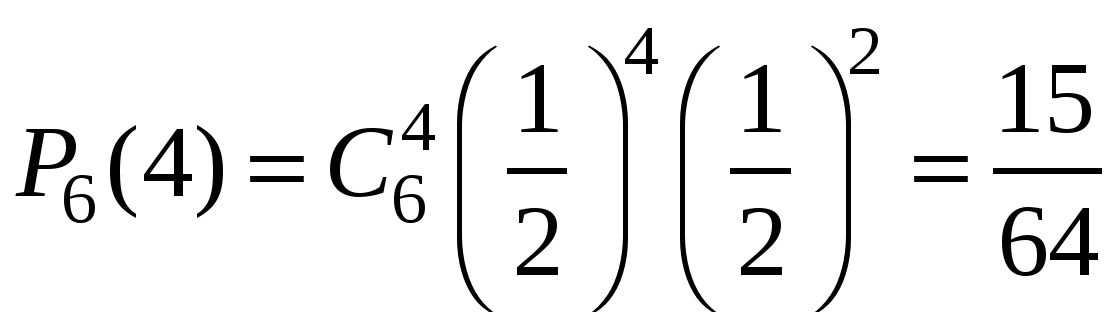
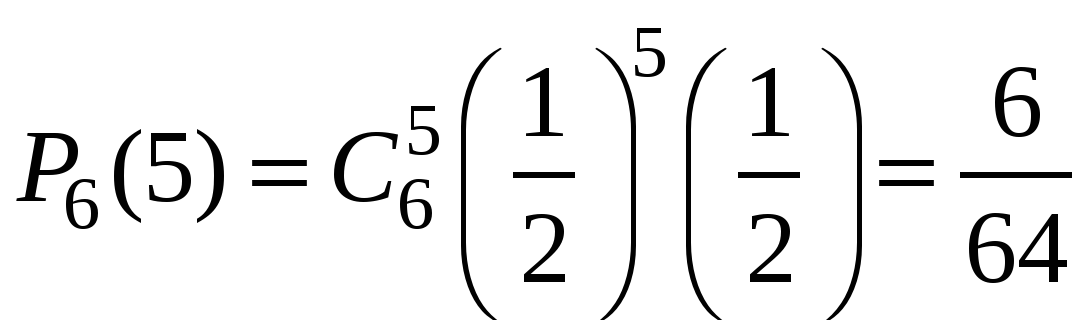
Очевидно, что наиболее вероятное число выпадений герба равно трём. Но далеко не каждый раз при шести бросаниях монеты герб выпадет ровно три раза! Вероятность говорит о том, что это будет происходить меньше, чем в трети случаях.

Пример 2. Монета бросается 10 раз. Какова вероятность двукратного появления герба?

Решение. Число опытов n=10, m= 2. Событие А – «успех» – выпадение герба. Тогда .

Ответ: 0,04395.

Пример 3. Вероятность того, что изделие не пройдет контроля, равна 0,125. Какова вероятность того, что среди 12 изделий не будет ни одного забракованного контролером?

Решение. Число опытов n=12, m=0. Событие А – «успех» – не будет ни одного забракованного. Тогда .

Ответ: 0,2514.

Домашнее задание

В следующих испытаниях найдите вероятности «успеха» и «неудачи».

а) Бросают пару различных монет. «Неудача» — выпадение двух «орлов».

б) Бросают игральный кубик. «Успех» — выпадение числа, кратного трем.

в) Бросают пару различных кубиков. «Неудача» — выпадение двух четных чисел.

г) Из 36 игральных карт берут 5. «Успех» — среди них нет дамы пик.

Решение.

а) Общее число исходов эксперимента n=2·2=4; вероятность «неудачи» ; вероятность «успеха» .

б) n=6; исходы, благоприятствующие «успеху» — выпадение 3 и 6 очков; ; вероятность «успеха» ; вероятность «неудачи» .

в) n=6·6=36; количество исходов, благоприятствующих «неудаче», (на каждом кубике 3 четные числа); вероятность «неудачи» ; вероятность «успеха» .

г) =376992; количество исходов, благоприятствующих «успеху», равно (выбираем карту из колоды без дамы пик);

вероятность «успеха» = = ,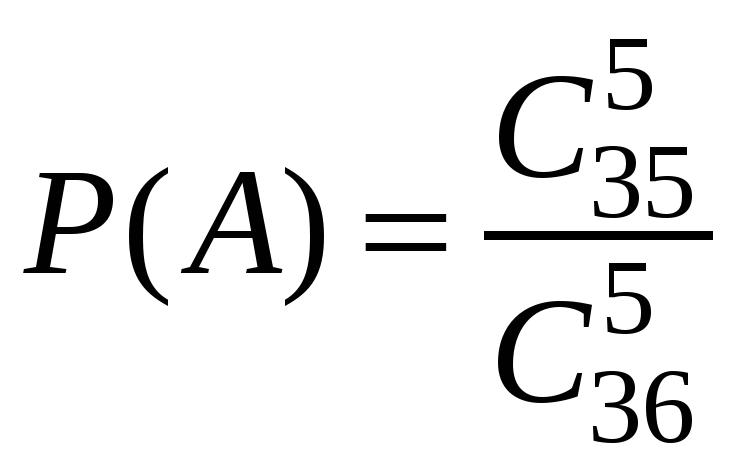

вероятность «неудачи» .

Подведение итогов

Примеры решений задач на формулу Бернулли

Калькуляторы на формулу Бернулли

Обратите внимание на следующие разделы, где разобраны типовые задачи на формулу Бернулли. Вы можете решить или проверить вычисления своих заданий с помощью онлайн-калькуляторов. Теорию по этой теме можно найти в онлайн-учебнике.

• Задача про партии в шахматы
• Задача про выстрелы
• Задача про мальчиков и девочек
• Задача про лотерейные билеты
• Задача о наивероятнейшем значении
• Формула Пуассона

Еще: решаем в Excel по формуле Бернулли.

Схема Бернулли: решенные задачи

Задача 1. Из $n$ аккумуляторов за год хранения $k$ выходит из строя. Наудачу выбирают $m$ аккумуляторов. Определить вероятность того, что среди них $l$ исправных.
$n = 100, k = 7, m = 5, l = 3.$

Задача 2. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента;
б) не менее четырех элементов;
в) хотя бы один элемент.

Задача 3. Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?

Задача 5. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта.

Задача 6. Что более вероятно выиграть у равносильного противника: не менее двух партий из трёх или не более одной из двух?

Задача 7. а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4;
б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

Формула Пуассона: решенные задачи

Задача 4. С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия.

Задача 8. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено:
а) три ошибочно укомплектованных пакета;
б) не более трех пакетов.

Решебник — когда задачи нужны быстро