Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Груз массой m на пружине, совершая свободные колебания, проходит положение равновесия со скоростью Через половину периода колебаний он проходит положение равновесия, двигаясь в противоположном направлении с такой же по модулю скоростью
Чему равен модуль изменения кинетической энергии груза за это время?
1)
2)
3)
4)
2
Камень массой 1 кг брошен вертикально вверх с начальной скоростью 4 м/с. На сколько увеличится потенциальная энергия камня от начала движения к тому времени, когда скорость камня уменьшится до 2 м/с? (Ответ дайте в джоулях.)
3
Растянутая на 2 см стальная пружина обладает потенциальной энергией упругой деформации 4 Дж. На сколько увеличится потенциальная энергия упругой деформации при растяжении этой пружины еще на 2 см? (Ответ дайте в джоулях.)
4
Мальчик столкнул санки с вершины горки. Сразу после толчка санки имели скорость 5 м/с. Высота горки 10 м. Трение санок о снег пренебрежимо мало. Какова скорость санок у подножия горки? (Ответ дайте в метрах в секунду.) Ускорение свободного падения считать равным 10 м/с2.
5
Мальчик столкнул санки с вершины горки. Сразу после толчка санки имели скорость а у подножия горки она равнялась
Трение санок о снег пренебрежимо мало. Какова высота горки? (Ответ дайте в метрах.) Ускорение свободного падения считать равным 10 м/с2.
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Мальчик столкнул санки с вершины горки. Сразу после толчка санки имели скорость 5 м/с. Высота горки 10 м. Трение санок о снег пренебрежимо мало. Какова скорость санок у подножия горки? (Ответ дайте в метрах в секунду.) Ускорение свободного падения считать равным 10 м/с2.
Мальчик столкнул санки с вершины горки. Сразу после толчка санки имели скорость а у подножия горки она равнялась
Трение санок о снег пренебрежимо мало. Какова высота горки? (Ответ дайте в метрах.) Ускорение свободного падения считать равным 10 м/с2.
Мальчик столкнул санки с вершины горки. Высота горки 10 м, у ее подножия скорость санок равнялась Трение санок о снег пренебрежимо мало. Какой была скорость санок сразу после толчка? (Ответ дайте в метрах в секунду.) Ускорение свободного падения считать равным 10 м/с2.
Задания Д28 C1 № 3279
Определите начальную скорость бруска, если известно, что после того, как он проехал 0,5 м вниз по наклонной плоскости с углом наклона 30° к горизонту, его скорость стала равна 3 м/с. Трением пренебречь. Ответ приведите в метрах в секунду.
На горизонтальной шероховатой плоскости (коэффициент трения равен μ) покоятся два одинаковых груза массой m на расстоянии L друг от друга, один из которых соединён со стенкой лёгкой нерастянутой горизонтальной пружиной жёсткостью k (см. рис.). Левому грузу сообщили в некоторый момент начальную скорость V0 в направлении правого, после чего грузы испытали абсолютно упругое лобовое столкновение. На какое расстояние l сместится после столкновения правый груз?
Какие законы Вы использовали для описания взаимодействия грузов? Обоснуйте их применение к данному случаю.
На горизонтальном гладком столе лежит длинная доска массой M = 10 кг, а на её левом конце — деревянный брусок массой m = 1 кг (см. рис.). В брусок попадает и прилипает к нему пластилиновый снаряд массой m0 = 200 г, летевший горизонтально по направлению вдоль доски со скоростью V0 = 10 м/с, после чего брусок скользит до остановки по шероховатой доске, не сваливаясь с неё. Какое количество теплоты Q выделится в этой системе в течение всего процесса?
Снаряд, движущийся со скоростью разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна
Найдите массу m осколка.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 2.
Снаряд в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Модуль скорости осколка, движущегося по направлению движения снаряда, равен а модуль скорости второго осколка равен
Найдите массу снаряда.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3.
Снаряд массой 2m, движущийся со скоростью разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося по направлению движения снаряда, равна
Найдите ΔЕ.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 4.
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Какие законы Вы используете для описания неупругого столкновения брусков? Обоснуйте их применение к данному случаю.
На горизонтальном гладком столе лежит длинная доска массой M = 10 кг, а на её левом конце — деревянный брусок массой m = 1 кг (см. рис.). В брусок попадает и прилипает к нему пластилиновый снаряд массой m0 = 200 г, летевший горизонтально по направлению вдоль доски со скоростью V0 = 10 м/с, после чего брусок скользит до остановки по шероховатой доске, не сваливаясь с неё. Какое количество теплоты Q выделится в этой системе в течение всего процесса?
Какие законы Вы используете для описания взаимодействия бруска, доски и пули? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 23.03.2018, вариант ФИ10401
Задания Д29 C2 № 4824
Снаряд в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Модуль скорости осколка, движущегося по направлению движения снаряда, равен а модуль скорости второго осколка равен
Найдите массу снаряда.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3.
Задания Д29 C2 № 7160
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Модуль скорости осколка, движущегося по направлению движения снаряда, равен а модуль скорости второго осколка равен
Найдите ΔЕ.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 4.
Снаряд массой 4 кг, летящий со скоростью 400 м/с в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ = 0,5 МДж. Найдите модуль скорости осколка, движущегося по направлению движения снаряда.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 2018. Часть С (ДВ)
Брусок скользит по наклонной плоскости вниз без трения. Что происходит при этом с его скоростью, потенциальной энергией, силой реакции наклонной плоскости?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость бруска | Потенциальная энергия
бруска |
Сила реакции наклонной
плоскости |
Задания Д29 C2 № 4789
Снаряд, движущийся со скоростью разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна
Найдите массу m осколка.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 2.
Снаряд массой 4 кг, летящий со скоростью 400 м/с в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ = 0,5 МДж. Найдите модуль скорости осколка, движущегося по направлению движения снаряда.
Источник: ЕГЭ по физике 2018. Часть С (ДВ)
На горизонтальной шероховатой плоскости (коэффициент трения равен μ) покоятся два одинаковых груза массой m на расстоянии L друг от друга, один из которых соединён со стенкой лёгкой нерастянутой горизонтальной пружиной жёсткостью k (см. рис.). Левому грузу сообщили в некоторый момент начальную скорость V0 в направлении правого, после чего грузы испытали абсолютно упругое лобовое столкновение. На какое расстояние l сместится после столкновения правый груз?
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?
Какие законы Вы используете для описания характера изменения энергии тела? Обоснуйте их применимость к данному случаю.
Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 4 № 64
Модуль скорости движения v1 первого тела массой m1 в два раза больше модуля скорости движения v2 второго тела массой m2. Если кинетические энергии этих тел равны (Ek1 = Ek2), то отношение массы второго тела к массе первого тела равно:
1)
2) 1
3)
4) 2
5) 4
Источник: Централизованное тестирование по физике, 2016
2
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии a = 70 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0|=200 пКл) шарик массой m = 630 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет = 36,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 400 кВ/м, то период T ударов шарика об одну из пластин равен … мс.
Источник: Централизованное тестирование по физике, 2015
3
На рисунке изображены три положения груза пружинного маятника, совершающего свободные незатухающие колебания с амплитудой x0. Если в положении В полная механическая энергия маятника W = 8,0 Дж, то в положении Б она равна:
1) 0 Дж
2) 2,0 Дж
3) 4,0 Дж
4) 6,0 Дж
5) 8,0 Дж
Источник: Централизованное тестирование по физике, 2015
4
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 80 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 500 пКл) шарик массой m = 380 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет = 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 250 кВ/м, то период T ударов шарика об одну из пластин равен … мс.
Источник: Централизованное тестирование по физике, 2015
5
Масса m1 первого тела в два раза больше массы m2 второго тела. Если модули скоростей этих тел равны (v1 = v2), то отношение кинетической энергии первого тела к кинетической энергии второго тела равно:
1) 1,0
2)
3) 2,0
4) 4,0
5) 8,0
Источник: Централизованное тестирование по физике, 2016
Пройти тестирование по этим заданиям
Опубликовано 24.01.2023 — 19:16 — Тимофеева Татьяна Сергеевна
Подборка из 21 расчетной задачи , в которых рассматриваются типовые ситуации связанные с темой «Закон сохранения энергии в механике».
Скачать:
| Вложение | Размер |
|---|---|
| 1.52 МБ |
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
РАБОТА. МОЩНОСТЬ. ЭНЕРГИЯ.ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ.
Презентация к уроку…
лабораторная работа №5 изучение закона сохранения энергии
Презентация к лабораторной работе изучение закона сохранения энергии для 10 класса…
Урок- практикум по решению задач (10 класс) Тема : Энергия. Закон сохранения энергии.
Урок- практикум по решению задач 10 класс «Энергия.Закон сохранения энергиии»…
9,10 класс. Закон сохранения энергии.Решение задач.
Урок-перезентация на тему » Решение задач по теме законы сохранения энергии». Обобщение по теме в виде решения задач….
План урока 9 Г класс (четверг) Тема «Полная механическая энергия. Закон сохранения и изменения полной механической энергии. Общефизический закон сохранения энергии»
В рамках дистанционного обучения возникает необходимость разработки подробного плана занятий для школьников в соответствии со школной программой и поурочным планированием….
Контрольная работа по теме «Динамика и законы сохранения энергии и импульса»
Задачи в контрольной работе рассчитаны на учащихся физико-математических и общеобразовательных классов и расположены по возрастанию сложности начиная со среднего уровня. Для общеобразовательных классо…
Конспект урока по физике в 7 классе «Закон сохранения энергии»
Конспект урока по физике в 7 классе «Закон сохранения энергии»…
- Мне нравится
Разделы сайта
Рекомендую
Законы сохранения энергии
Олимпиадная подготовка по динамике — 6

Хорошие, интересные задачи по динамике, решений многих из которых в сети нет.
Задача 4.
Шарнирная конструкция, состоящая из четырёх лёгких одинаковых стержней, удерживается нитью, привязанной к потолку, и опирается на гладкую горизонтальную поверхность, как показано на рисунке. Если к шарнирам, соединяющим центры стержней, подвесить грузы…
Олимпиадная подготовка по динамике — 5

Хорошие, интересные задачи по динамике, решений многих из которых в сети нет.
Задача 1.
На столе один на другом лежат три одинаковых длинных бруска. Их поверхности обработаны так, что коэффициенты трения скольжения между ними равны соответственно …
08.06.2022 05:33:30 | Автор: Анна
|
|
Задачи о бруске и шайбе

Пара интересных задач на трение. Из задачника 3800 задач Турчиной.
Задача 1.
На наклонной плоскости лежит брусок, соединенный пружиной с неподвижной опорой. Из положения, когда пружина недеформирована, брусок без начальной скорости отпускают, и он начинает скользить вниз. Определить максимальное растяжение пружины. Масса бруска
08.03.2022 08:04:07 | Автор: Анна
|
|
Законы сохранения — 6

Снова представляю решения задач, которые мы разбирали на групповых занятиях летом с ребятами, желающими участвовать в олимпиадах. Задача о двух шайбах.
Задача 11.
На горизонтальной шероховатой поверхности покоятся две одинаковые маленькие шайбы. По одной из них наносят удар клюшкой, после чего она налетает на вторую…
17.02.2022 05:38:20 | Автор: Анна
|
|
Законы сохранения — 5

Снова представляю решения задач, которые мы разбирали на групповых занятиях летом с ребятами, желающими участвовать в олимпиадах.
Задача 9.
Два одинаковых маленьких шарика, соединенных невесомым твердым стержнем длиной , падают на гладкую, абсолютно упругую горизонтальную плоскость. Непосредственно перед ударом…
15.02.2022 05:54:00 | Автор: Анна
|
|
Законы сохранения — 4

Снова представляю решения задач, которые мы разбирали на групповых занятиях летом с ребятами, желающими участвовать в олимпиадах. Продолжаем решать задачи на законы сохранения.
Задача 7.
Какую работу необходимо совершить, чтобы достаточно медленно переместить небольшой ящик массой из точки…
10.02.2022 05:53:31 | Автор: Анна
|
|
Законы сохранения — 3
Снова представляю решения задач, которые мы разбирали на групповых занятиях летом с ребятами, желающими участвовать в олимпиадах. В данной статье единственная, но сложная задача про акробата.
Задача 6.
По льду ледового цирка со скоростью едет диск массой
08.02.2022 11:11:32 | Автор: Анна
|
|
Законы сохранения — 2

Снова представляю решения задач, которые мы разбирали на групповых занятиях летом с ребятами, желающими участвовать в олимпиадах. Разбираем задачи на сохранение энергии.
Задача 4.
На горизонтальном столе покоится шар массой . С шаром упруго сталкивается клин, движущийся углом вперед…
03.02.2022 05:52:43 | Автор: Анна
|
|
Законы сохранения — 1

Снова представляю решения задач, которые мы разбирали на групповых занятиях летом с ребятами, желающими участвовать в олимпиадах. Здесь — серия задач на законы сохранения.
Задача 1.
Обруч массой катится без проскальзывания по горизонтальной поверхности. Скорость центра обруча равна…
01.02.2022 05:52:23 | Автор: Анна
|
|
Сохранение импульса и энергии

Задачи пришли из хорошего лицея с учеником (впрочем, как обычно). Все задачи решались «энергетически».
Задача 1.
Движение материальной точки массой 3 кг описывается уравнением .
Найдите модуль изменения кинетической энергии за первые 8 с от начала наблюдения за движением. Найдите…
13.07.2021 07:33:40 | Автор: Анна
|
|
Законы сохранения: готовимся к олимпиадам. 9 класс

Представляю вам «крепкие» задачки, комбинированные — на законы сохранения импульса и энергии одновременно.
Задача 1.
На гладком столе стоит куб массой , около которого находится лёгкая штанга длиной
28.05.2020 07:39:11 | Автор: Анна
|
|
Законы сохранения. 10 класс.

В статье содержатся несколько задач на законы сохранения энергии. Эти задачи ориентированы на подготовку к олимпиадам и рассчитаны на ребят 10 класса.
Задача 1.
Шарик на натянутой тонкой нерастяжимой, легкой нити первоначально находится в горизонтальном положении. Длина нити маятника
19.02.2019 15:47:03 | Автор: Анна
|
|
Тележка и мертвая петля

И снова сохранение энергии. Запустим тележку в «мертвую петлю»!
Задача. Небольшая тележка совершает мертвую петлю радиуса 2 м, скатываясь с минимальной высоты, обеспечивающей прохождение всей петли. На какой высоте сила давления на рельсы равна 1,5 силы тяжести тележки? Принять…
09.10.2018 06:29:19 | Автор: Анна
|
|
Шайба и горки

Две задачи похожие и в то же время разные про шайбу и горки на тему закона сохранения импульса предлагаю я сегодня вашему вниманию. У нас, репетиторов «вижу задачу – теряю волю, бросаюсь решать» — это обычная «болезнь».
Задача 1.
На гладком горизонтальном столе лежат две…
02.10.2018 07:01:37 | Автор: Анна
|
|
Сохранение импульса при нецентральном ударе

Две не очень простые задачи принесла ученица, на тему закона сохранения импульса. А у нас, репетиторов «вижу задачу – теряю волю, бросаюсь решать» — это обычная «болезнь».
Задача 1.
На покоящийся шар налетает шар такой же массы. Найдите угол разлета шаров после упругого нецентрального удара.
28.09.2018 19:43:44 | Автор: Анна
|
|
Механическая работа: поднимаем ведра и бросаемся льдинками
Задачи на работу неразрывно связаны с задачами на закон сохранения энергии. Потому что энергия тратится на работу и наоборот, тело приобретает энергию в результате выполнения кем-то или чем-то работы.
Задача 1.
Ведро с водой массой 10 кг поднимают на высоту 10 м, прикладывая постоянную силу…
19.08.2018 11:26:59 | Автор: Анна
|
|
Работа. Законы сохранения.
Самые хорошие и интересные задачи приносят ученики. Часто в этих задачах бывают нестыковки в условии: вместе разбираемся, исправляем условие так, чтобы задача была корректной. Так и с этими произошло.
Задача 1.
Пуля, летевшая горизонтально со скоростью 400 м/с, попадает в брусок, висящий на нити длиной…
17.08.2018 11:18:18 | Автор: Анна
|
|
Механическая работа. Закон сохранения энергии.

Задачи на работу неразрывно связаны с задачами на закон сохранения энергии. Потому что энергия тратится на работу и наоборот, тело приобретает энергию в результате выполнения кем-то или чем-то работы.
Задача 1.
Какая работа совершается при подъеме на крышу веревки массой 6 кг длиной 50 м?…
15.08.2018 11:10:50 | Автор: Анна
|
|
Подготовка в СУНЦ МГУ — динамика-2. Экзамен в 11 класс.

Наиболее трудными зачастую для абитуриентов оказываются задачи на динамику. Часто такие задачи требуют применения законов сохранения, а также знания кинематики, особенно большие трудности вызывает тема «относительность движения» и необходимость переходить в ту или иную систему отсчета.
Задача 1.
Маленький шарик находится на гладком горизонтальном столе и…
01.01.2018 12:15:37 | Автор: Анна
|
|
Подготовка в СУНЦ МГУ — динамика-1. Экзамен в 11 класс.

Наиболее трудными зачастую для абитуриентов оказываются задачи на динамику. Часто такие задачи требуют применения законов сохранения, а также знания кинематики, особенно большие трудности вызывает тема «относительность движения» и необходимость переходить в ту или иную систему отсчета.
Задача 1. Брусок массой
30.12.2017 07:26:15 | Автор: Анна
|
|
Сохранение энергии: задачи заочной школы МФТИ
Сложные, интересные задачи, после решения которых вы будете чувствовать себя гуру закона сохранения энергии)))
Задача 1.
Космический корабль (КК) движется по околоземной орбите. Чему равна работа силы земного тяготения за время половины одного оборота КК вокруг Земли?
Так как энергия корабля осталась неизменной, то и работа,…
27.09.2017 10:24:51 | Автор: Анна
|
|
Подготовка в СУНЦ МГУ: законы сохранения — 4
Задач на сохранение энергии и импульса в экзаменах прошлых лет встречается больше всего. В том числе довольно сложные. Именно этим объясняется, что больше всего статей я подготовила для вас на эту тему.
Задача 1.
Горизонтально летящая пуля массой
12.07.2017 10:48:08 | Автор: Анна
|
|
Подготовка в СУНЦ МГУ: законы сохранения — 3
Задач на сохранение энергии и импульса в экзаменах прошлых лет встречается больше всего. В том числе довольно сложные. Именно этим объясняется, что больше всего статей я подготовила для вас на эту тему.
Задача 1.
Пуля массой
10.07.2017 09:38:32 | Автор: Анна
|
|
Подготовка в СУНЦ МГУ: законы сохранения — 2
Я объединила задачи по законам сохранения в одно целое, потому что часто, чтобы определить энергию, нужно определить скорость с помощью закона сохранения импульса, и наоборот, требуется закон сохранения энергии, чтобы определить скорости тел.
Задача 1.
Тело массой
06.07.2017 13:59:02 | Автор: Анна
|
|
Подготовка в СУНЦ МГУ: законы сохранения
Я объединила задачи по законам сохранения в одно целое, потому что часто, чтобы определить энергию, нужно определить скорость с помощью закона сохранения импульса, и наоборот, требуется закон сохранения энергии, чтобы определить скорости тел.
Задача 1. Два тела массами
04.07.2017 09:41:49 | Автор: Анна
|
|
Fatal error: Uncaught PDOException: SQLSTATE[42000]: Syntax error or access violation: 1064 You have an error in your SQL syntax; check the manual that corresponds to your MySQL server version for the right syntax to use near » at line 1 in /home/elektrolad/domains/easy-physic.ru/public_html/modules/mod_obrabotka.php:178
Stack trace:
#0 /home/elektrolad/domains/easy-physic.ru/public_html/modules/mod_obrabotka.php(178): PDO->query(‘SELECT post_tit…’)
#1 /home/elektrolad/domains/easy-physic.ru/public_html/modules/mod_articles.php(28): require(‘/home/elektrola…’)
#2 /home/elektrolad/domains/easy-physic.ru/public_html/modules/mod_catalog.php(29): require(‘/home/elektrola…’)
#3 /home/elektrolad/domains/easy-physic.ru/public_html/router/rout.php(33): include(‘/home/elektrola…’)
#4 /home/elektrolad/domains/easy-physic.ru/public_html/index.php(117): require(‘/home/elektrola…’)
#5 {main}
thrown in /home/elektrolad/domains/easy-physic.ru/public_html/modules/mod_obrabotka.php on line 178
24 примера с решением.
zakoni-soh.ppt
zakoni-soh.pdf
Мальчик догоняет тележку (бежит навстречу тележке) и запрыгивает на нее. Дальше они двигаются вместе. Масса мальчика m1, масса тележки m2. Скорость мальчика V1 , скорость тележки V2.
На вагонетку массой 800 кг, катящуюся по горизонтальному пути со скоростью 0,2 м/с, насыпали сверху 200 кг щебня. На сколько уменьшилась скорость вагонетки?
Рыбак массой 60 кг переходит с носа на корму лодки. На сколько переместится лодка длиной 3 м и массой 120 кг относительно воды?
Охотник стреляет с легкой надувной лодки. Какую скорость приобретает лодка в момент выстрела, если масса охотника с лодкой равна 70 кг, масса дроби 35 г и средняя начальная скорость дроби 320 м/с? Ствол ружья во время выстрела образует угол 60° к горизонту.
Граната, летевшая в горизонтальном направлении со скоростью 10 м/с, разорвалась на два осколка массами 1 кг и 1,5 кг. Скорость большого осколка после разрыва горизонтально возросла до 25 м/с. Определите скорость и направление движения меньшего осколка.
Пуля летит горизонтально со скоростью 400м/с пробивает стоящий на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью ¾ V0. Масса коробки в 40 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью М= 0,15. На какое расстояние переместилась коробка к моменту, когда ее скорость уменьшится на 20%.
Тело массой 3 кг, свободно падает с высоты 5 м. Найти потенциальную и кинетическую энергию тела на расстоянии 2 м от поверхности земли.
Камень подброшен вертикально вверх с начальной скоростью 10 м/с. На какой высоте h кинетическая энергия камня равна его потенциальной энергии?
Груз массой 25 кг висит на шнуре длиной 2,5 м. На какую наибольшую высоту можно отвести в сторону груз, чтобы при дальнейших свободных качаниях шнур не оборвался? Максимальная сила натяжения, которую выдерживает шнур не обрываясь, равна 550 Н.
Цирковой артист массой 60 кг падает в натянутую сетку с высоты 4 м. С какой силой действует на артиста сетка, если она прогибается при этом на 1 м?
Маятник массой m отклонен на угол α от вертикали. Какова сила натяжения нити при прохождении маятником положения равновесия?
С поверхности земли со скоростью 8 м/с брошено тело под углом 60° к горизонту. Найти величину его скорости на высоте 1,95 м.
Тело скользит без трения по гладкой горизонтальной поверхности со скоростью 5 м/с и въезжает подвижную горку высотой H=1,2 м. На какую высоту поднимается тело по горке, если масса горки в 5 раз больше массы тела?
Два тела массой по 1/18 кг движутся навстречу друг другу. Скорость первого тела 4 м/с, второго — 8 м/с. Какое количество теплоты выделится в результате абсолютно неупругого удара тел?
На некоторой высоте планер имел скорость 10 м/с. Определить величину скорости планера при его снижении на 40 метров. Сопротивлением воздуха пренебречь
Два тела массы m1 и m2 прикреплены к нитям одинаковой длины с общей точкой подвеса и отклонены – одно влево, другое вправо – на один и тот же угол. Тела одновременно отпускают. При ударе друг о друга они слипаются. Определите отношение высоты, на которую тела поднимутся после слипания, к высоте, с которой они начали свое движение вниз.
Тяжелый шарик соскальзывает без трения по наклонному желобу, образующему «мертвую петлю» радиусом R. С какой высоты шарик должен начать движение, чтобы не оторваться от желоба в верхней точке траектории?
На гладком горизонтальном столе лежит шар массой М=240 г, прикрепленный к пружине жесткостью k=40 кН/м. Другой конец пружины закреплен. В шар попадает пуля массой m=10 г, имеющая в момент удара начальная скорость 400 м/с, направленную вдоль оси пружины. Пуля застревает в шаре. Определите амплитуду колебаний шара после удара.
Начальная скорость снаряда, выпущенного вертикально вверх, равна 160 м/с. В точке максимального подъема снаряд разорвался на 2 осколка, массы которых относятся как 1:4. Осколки разлетелись в вертикальных направлениях, причем меньший осколок полетел вниз и упал на землю со скоростью 200 м/с. Определите скорость, которую имел в момент удара о землю больший осколок. Сопротивлением воздуха пренебречь.
Алгоритм решения задач по теме «Законы сохранения»
1) Внимательно изучите условие задачи, поймите физическую сущность явлений и процессов, рассматриваемых в задаче, уясните основной вопрос задачи.
2) Мысленно представьте ситуацию, описанную в задаче, выясните цель решения, четко выделите данные и неизвестные величины.
3) Запишите краткое условие задачи. Одновременно выразите все величины в единицах СИ.
4) Сделайте чертеж, на котором отобразите ситуацию до и после события.
5) Запишите закон сохранения импульса (в проекции на выбранную ось) проверив систему на замкнутость или (и) закон сохранения энергии в соответствии с тем, что отобразили на чертеже (с одной стороны равенства что было «до», с другой что «после»). Выберите нулевой уровень потенциальной энергии.
6) Решите уравнение или систему уравнений относительно неизвестной величины, т.е. решите задачу в общем виде.
7) Если не все величины известны, то для нахождения их можете применить алгоритм решения задач по теме «Динамика».

9) Определите единицу величины. Проверьте, подходит ли она по смыслу.
10) Рассчитайте число.
11) Проверьте ответ на «глупость» и запишите его.
28. Механика (Расчетная задача).
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Законы сохранения в механике
Камень массой (m_1=3sqrt{3}) кг бросают вертикально вверх с начальной скоростью (v_0= 50) м/с, после трех секунд полета в него влетает снаряд массой (m_2=0,3) кг летящий горизонтально со скоростью (v_2=200) м/c, и застревает в нем,. Найдите угол отклонения от первоначальной траектории полета камня.
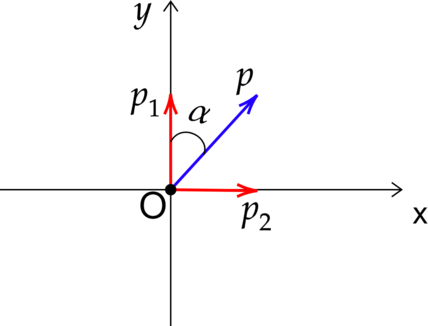
Сделаем рисунок системы “камень+снаряд” после столкновения.
Где (p_1) – импульс камня до столкновения, (p_2) – импульс снаряда до столкновения, О – точка столкновения камня и снаряда, (p) – суммарный импульс системы после столкновения, а угол (alpha) – угол отклонения от первоначальной траектории.
Камень, летящий вверх, движется равнозамедленно. Найдем скорость камня в момент столкновения по формуле: [v_1= v_0-gt]
Где (t) – время полета камня. Скорость камня в момент столкновения равна [v_1=50text{ м/с}-10text{ м/c$^2$}hspace{5 mm}2text{ с}=30text{ м/c}]
Так как система замкнутая, то выполняется закон сохранения импульса. [vec{p_1}+vec{p_2}=vec{p}]
Импульсы тел до столкновения найдем по формулам: (p_1=m_1v_1) и (p_2=m_2v_2)
Тогда (p_1=3sqrt{3}text{ кг}hspace{5 mm}20text{ м/c}=60sqrt{3} dfrac{text{ кг м}}{text{ с}}), а (p_2=0,3text{кг}hspace{5 mm} 200text{ м/c}=60dfrac{text{ кг м}}{text{ с}})
Спроецируем закон сохранения импульса на оси (Oy) и (Ox) и запишем полученные уравнения
[begin{cases}
Ox: & p_1=pcosalpha \
Oy: & p_2=psinalpha \
end{cases}]
Выразим (p) из каждого уравнения
[begin{cases}
Ox: & p=dfrac{p_1}{cosalpha}quad (1) \
Oy: & p=dfrac{p_2}{sinalpha}quad(2) \
end{cases}]
Приравняем (1) и (2) [dfrac{p_1}{cosalpha}=dfrac{p_2}{sinalpha}Rightarrow p_1sinalpha=p_2cosalpha] [60sqrt{3}sinalpha=60cosalpha]
Поделим уравнение на (dfrac{60}{cosalpha}) [sqrt{3}tgalpha=1Rightarrow tgalpha=dfrac{1}{sqrt{3}}]
Следовательно, угол отклонения составил 30 градусов
Ответ: 30
Шарик массой (m=2) кг падает с высоты (h=5) м, без начальной скорости, в результате его удара об пол выделилась количество теплоты (Q=20) Дж. Найдите максимальную высоту подъема шарика после удара о землю.
Так как шарик падает без начальной скорости, то кинетическая энергия вначале полета равна 0, аналогично с кинетической энергией на максимальной высоте после удара шарика об землю, следовательно, закон сохранения энергии можно переписать в виде: [E_text{ пот1}=E_text{ пот2}+Q quad (1)]
Где (E_text{ пот1}) – потенциальная энергия на высоте (h), (E_text{ пот2}) – потенциальная энергия на максимальной высоте после удара. Они находятся по формулам: [E_text{ пот1}=mgh quad (2)] [E_text{ пот2}=mgHquad (3)]
(H) – максимальная высота подъема камня после удара о землю. Подставим (2) и (3) в (1) [mgh=mgH+Q]
Выразим (H) [H=dfrac{mgh-Q}{mg}]
Подставим числа из условия [H=dfrac{2text{ кг}hspace{5 mm} 10text{ Н/кг}hspace{5 mm}5text{ м} — 20text{ Дж}}{2text{ кг}hspace{5 mm}10text{ Н/кг}}=4text{ м}]
Ответ: 4
Снаряд массой (m=2) кг разрывается на два равных осколка, один летит под углом 90 градусов к первоначальному направлению движения, другой пол углом 30 градусов, скорость первого осколка (v_1=10) м/c. Найдите импульс снаряда до разрыва. Ответ округлите до целых.
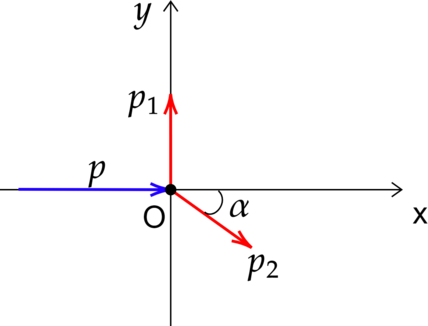
Сделаем рисунок
Где (p) – импульс снаряда, (p_1) – импульс первого осколка, (p_2) – импульс второго осколка.
По закону сохранения импульса [vec{p}=vec{p_1}+vec{p_2}]
Спроецируем закон сохранения импульса на оси (Oy) и (Ox) и запишем полученные уравнения
[begin{cases}
Ox: & p=p_2cosalpha quad(1) \
Oy: & 0=p_1+p_2sinalpha quad(2) \
end{cases}]
Выразим из (2) (p_2) [p_2=dfrac{p_1}{sinalpha} quad (3)]
Затем подставим (3) в (1) [p=dfrac{p_1cosalpha}{sinalpha} quad (4)]
Импульс первого осколка находится по формуле: [p_1=dfrac{mv_1}{2} quad (5)]
Подставим (5) в (4) [p=dfrac{mv_1cosalpha}{2sinalpha}=dfrac{dfrac{2text{ кг}hspace{5 mm} 10text{ м/c}hspace{5 mm}sqrt{3}}{2}}{dfrac{2}{2}}approx 17dfrac{text{ кг м }}{text{с }}]
Ответ: 17
Камень массой (m=2) кг брошен под углом 30(^circ). Начальный модуль импульса тела равен (p_0=4) (dfrac{text{кг м}}{text{с}}). Чему равна кинетическая энергия камня в верхней точке траектории его движения?
Во время подъема вертикальная составляющая импульса будет уменьшаться, пока не достигнет нуля, а горизонтальная будет неизменна и она находится по формуле: [p_x=p_ocos60= p_x=m v_0 cos30 quad (1)]
Кинетическая энергия камня в верхней точке находится по формуле: [E_k=dfrac{mv_0^2}{2}Rightarrow E_k=dfrac{m^2 v_0^2}{2m}quad (2)]
Подставим (1) в (2) [E_k=dfrac{p_x^2}{2m}=dfrac{p_0^2cos^2 30}{2m}=dfrac{4^2 text{кг$^2$ м$^2$/c$^2$}hspace{5 mm} 3}{4hspace{5 mm}2hspace{5 mm}2text{ кг}}=dfrac{48text{ кг м$^2$/c$^2$}}{16text{ кг}}=3text{ Дж}]
Ответ: 3
Шар массой (m_1=5) кг со скоростью (v_1=3) м/с врезается в неподвижный шар массой (m_2=10) кг. В результате их упругого столкновения второй шар приобрел скорость, а второй отскочил в обратном направлении. Найдите кинетическую энергию первого шара после столкновения.
Запишем систему, состоящую из закона сохранения импульса и закона сохранения энергии
[begin{cases}
vec{p_1}=vec{p_{k1}}+vec{p_{k2}}\
E_1=E_{k1}+E_{k2}\
end{cases}]
Запишем систему с учетом проекций векторов
[begin{cases}
p_1=-p_{k1}+p_{k2}\
E_1=E_{k1}+E_{k2}\
end{cases}]
Где (p_1 ) и (E_1) – импульс и кинетическая энергия первого шара до столкновения, (p_{k1}) и (E_{k1}) – импульс и кинетическая энергия первого шара после столкновения, а (p_{k2}) и (E_{k2}) – импульс и кинетическая энергия второго шара после столкновения. Импульс находится по формуле: [p=mv quad (1)]
А кинетическая энергия тела: [E=dfrac{mv^2}{2}quad (2)]
Подставим (1) и (2) в систему с учетом индексов
[begin{cases}
m_1 v_1 = -m_1v_{k1}+m_2v_{k2}\
dfrac{m_1v_1^2}{2}=dfrac{m_1v_{k1}^2}{2}+dfrac{m_2v_{k2}^2}{2} \
end{cases}]
Умножим на 2 второе уравнение
[begin{cases}
m_1 v_1 = -m_1v_{k1}+m_2v_{k2}\
m_1v_1^2=m_1v_{k1}^2+m_2v_{k2}^2 \
end{cases}]
Перенесем с (m_1) в одну сторону, а с (m_2) в другую и вынесем массы за скобку
[begin{cases}
m_1 (v_1+ v_{k1}) =m_2v_{k2}\
m_1(v_1^2-v_{k1}^2)=m_2v_{k2}^2 \
end{cases}]
Во втором уравнении преобразуем разность квадратов
[begin{cases}
m_1 (v_1+ v_{k1}) =m_2v_{k2} quad (1)\
m_1((v_1-v_{k1})(v_1+v_{k1}))=m_2v_{k2}^2 quad (2)\
end{cases}]
Поделим (2) на (1)
[dfrac{m_1((v_1-v_{k1})(v_1+v_{k1}))}{m_1 (v_1+ v_{k1})}=dfrac{m_2v_{k2}^2}{m_2v_{k2}}Rightarrow v_{k2}=v_1-v_{k1}quad(3)]
Подставим (3) в (1) и выразим (v_{k1})
[m_1(v_1+v_{k1})=m_2(v_1-v_{k1})Rightarrow v_{k1}=dfrac{v_1(m_1-m_2)}{m_2+m_1}quad(4)]
Подставим (4) в формулу для нахождения кинетической энергии первого шара после столкновения [E_{k1}=dfrac{m_1v_1^2 (m_2-m_1)^2}{2(m_2+m_1)^2}=dfrac{5text{ кг}hspace{5 mm}9text{ м$^2$/c$^2$ }(10text{ кг}-5text{ кг})}{2( 10text{ кг}+5text{ кг})}= 7,5text{ Дж}]
Ответ: 7,5
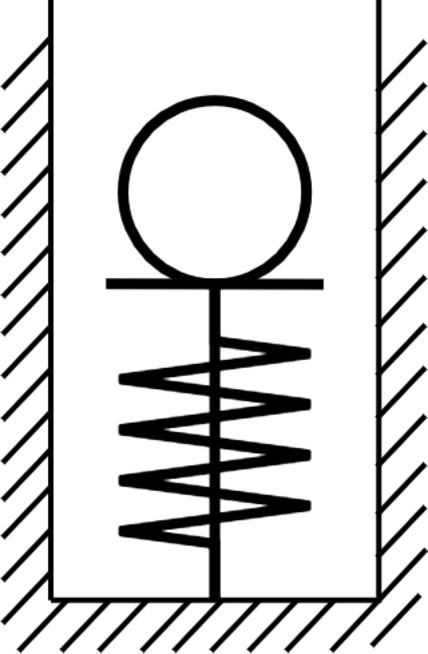
При разрыве нити, удерживающей пружину в сжатом на 1 см состоянии (см. рисунок), шарик приобретает скорость 10 м/с. Жесткость пружины 2кН/м. Какова масса шарика. Колебаниями пружины после отрыва шарика пренебречь.
Потенциальная энергия пружины переходит в кинетическую энергию мяча. [dfrac{kx^2}{2}=dfrac{mv^2}{2}] где (k) – жесткость пружины, (x) – сжатие, (m) – масса шарика, (v) – скорость шарика.
Отсюда масса шарика [m=dfrac{kx^2}{v^2}=dfrac{2cdot 10^3text{ Н/м}cdot 10^-4text{ м$^2$}}{10^2text{ м$^2$/с$^2$}}=2cdot 10^{-3}text{ кг}=0,002text{ кг}]
Ответ: 0,002
Человек на санках спустился без трения с горки высотой 6 м. При его движении по горизонтальной поверхности сила трения составила 160 Н. Какое расстояние проехал человек до полной остановки? Масса человека и санок равна 100 кг.
Потенциальная энергия на высоте (h=6) м перейдет в кинетическую энергию у подножья горки, которая впоследствии перейдет в работу сил трения, то есть [E_n=E_k=A] Или [mgh=FS] где (m) – масса человека и санок, (F) – сила трения, (S) – расстояние движения по горизонтали.
Откуда (S) равно [S=dfrac{mgh}{F}=dfrac{100text{ кг}cdot 10text{ Н/кг}cdot 6text{ м} }{160text{ Н}}=37,5text{ м}]
Ответ: 37,5

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ