Решу егэ физика задание 111 - Помощь в подготовке к экзаменам и поступлению

Образовательный портал для подготовки к экзаменам

Физика

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид:

Чему равна скорость тела в момент времени t  =  2 c при таком движении? (Ответ дайте в метрах в секунду.)

Спрятать решение

Решение.

При равноускоренном движении зависимость пройденного телом пути от времени в общем виде имеет вид

Сравнивая с выражением, данным в условии, заключаем, что оно укладывается в это общее правило, а значит, тело двигалось равноускоренно. Сопоставляя конкретные члены в выражениях получаем, что начальная скорость равна а ускорение Таким образом, скорость тела в момент времени t=2с равна :

Ответ: 8.

Спрятать решение

Гость 30.04.2012 18:33

Почему 8 м/с ?

s=vt

vt=v0t + (a(t)в кв)/2

vt=t(v0 +(at)/2) делим обе части на t

v=v0 +(at)/2

v=4 + (2*2)/2

v=4+2=6 м/с

Гость

Добрый день!

У Вас ошибка в первой формуле

s=vt — это формула для равномерного движения, можно ее с натяжкой использовать и для равноускоренного движения, но тогда под v надо понимать среднее арифметическое начальной и конечной скоростей (или значение скорости в середине исследуемого промежутка времени). В нашем случае, Вы таким образом получаете скорость в момент времени 1 с.

Лучше всего, запомните закон изменения скорости при равноускоренном движении

Гость 30.04.2012 21:36

А правильно ли будет решить математическим способом:найти производную,а потом подставить вместо t=2?

Гость

Добрый вечер!

Дифференциальный анализ придумали физики, чтобы решать приблизительно вот такие вот задачи. Так что спокойно можете использовать свои знания и умения, если Вы уверены в них. Главное — это получить правильный результат, способ его получения не столь важен.

Гость

Не за что, обращайтесь

Гость 02.06.2012 15:30

в задаче говорится про прямолинейное движение, а вы описываете равноускоренное…это правильно? объясните пж)

Гость

Добрый день!

Слово «прямолинейное» означает лишь, что траектория — прямая линия. Двигаться вдоль этой прямой тело может абсолютно произвольно. В данном случае движение равноускоренное.

Гость 15.10.2012 18:42

Спасибо,рассматривая следующую задачу поняла методику их решения

Гость 18.10.2012 15:01

Здравствуйте, а можно ли эту задачу решить, применяя производную?

т.е. S = 4t + t^2

V = S’ = 4 + 2t

V = 4 + 2*2 = 8

ответ 2

Никита Пасько 17.10.2016 20:34

Здравствуйте, скажите, как нашли a=2 м/с^2?

Антон

— общий вид,

— по условию,

значит, v_0=4, a=2.

Никита Пасько 18.10.2016 19:25

Источник

Новый тренировочный вариант 220912 решу ЕГЭ 2023 по физике 11 класс формата сложности ЕГЭ на 100 баллов с ответами для всех заданий. Данный вариант вы можете скачать или решать онлайн на сайте.

Скачать вариант с ответами и решением

решу-220912-физика-егэ2023

Для выполнения экзаменационной работы по физике отводится 3 часа 55 минут (235 минут). Работа состоит из двух частей, включающих в себя 30 заданий. В заданиях 1–3, 7–9, 12–14 и 18 ответом является целое число или конечная десятичная дробь.

Ответ запишите в поле ответа в тексте работы, а затем перенесите по приведённому ниже образцу в бланк ответа № 1. Единицы измерения физических величин писать не нужно.

Задания и ответы

Задание 1. Чему равна проекция ускорения тела на ось X в интервале времени от 20 до 25 с, если зависимость проекции скорости от времени на ту же ось задается следующим графиком?

Ответ: 3

Задание 2. На тело действуют две силы. На рисунке изображена одна сила 𝐹1⃗⃗⃗ и равнодействующая сила 𝐹 . Найдите модуль второй силы.

Ответ: 5

Задание 3. Бутылку с подсолнечным маслом, закрытую пробкой, перевернули. Определите силу, с которой действует масло на пробку площадью 5 см2 , если расстояние от уровня масла в сосуде до пробки равно 20 см.

Ответ: 0, 9

Задание 4. Человек наблюдал процесс свободного падения яблока и описал процесс его движения. Из приведенного ниже списка выберите все верные утверждения.

1) Движение яблока равноускоренное.
2) Ускорение яблока изменяется от максимального значения до нуля в момент падения.
3) Скорость яблока изменяется от максимального значения до нуля в момент падения.
4) Потенциальная энергия яблока изменяется от максимального значения до нуля.
5) Полная энергия яблока уменьшается.

Ответ: 14

Задание 5. В лаборатории на демонстрационном столе стоят камертон на 440 Гц и аквариум с водой. По ножке камертона ударили молоточком. Как изменятся скорость звуковой волны и частота колебаний при переходе звука из воздуха в воду? Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменится

Ответ: 13

Задание 6. Два пластилиновых бруска имеют массы m1 = m и m2 = 3m, второй скользит по гладкой горизонтальной поверхности навстречу первому со скоростью v2 = 2v. При этом v1 = 0. Установите соответствие между физическими величинами, характеризующими движение брусков после абсолютно неупругого столкновения, и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Ответ: 21

Задание 7. Какое изменение температуры ∆t (в градусах Цельсия) соответствует нагреву на 27 К?

Ответ: 27

Задание 8. На p–T диаграмме представлен процесс изменения состояния идеального одноатомного газа постоянной массы. В этом процессе газ получил 20 кДж теплоты. Определите работу газа в этом процессе.

Ответ: 0

Задание 9. Сосуд с поршнем содержит воздух, относительная влажность которого 40%. Какой станет относительная влажность, если с помощью поршня сжать воздух так, чтобы его объем уменьшился в 3 раза (температура не меняется)?

Ответ: 100

Задание 10. Вещество при температуре 160℃, находящееся в газообразном состоянии, охлаждают при постоянной мощности. В таблице приведены результаты измерений температуры вещества с течением времени. Выберите из предложенного перечня все верные утверждения:

1) Удельная теплоёмкость вещества в жидком и газообразном состояниях одинакова.
2) Температура кипения вещества в данных условиях составляет 124°С.
3) Процесс конденсации вещества занял более 10 мин.
4) Температура кипения вещества в данных условиях составляет 106°С.
5) Через 20 мин. после начала измерений вещество находилось только в жидком состоянии.

Ответ: 34

Задание 11. Некоторое количество идеального газа находится в сосуде при атмосферном давлении. Как изменятся давление и концентрация частиц, если в сосуде проделать небольшое отверстие и при постоянной температуре медленно уменьшать его объем? Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменится

Ответ: 33

Задание 12. По проводнику течет постоянный ток. Какой заряд пройдет по нему за 20 минут, если сила тока равна 0,5 А?

Ответ: 600

Задание 13. При равномерном уменьшении силы тока в катушке индуктивностью 0,4 Гн за 0,05 с в ней возникает ЭДС самоиндукции, равная 80 В. На сколько уменьшилась сила тока в катушке?

Ответ: 10

Задание 14. Угол падения составляет 30°. Определите угол γ между отраженным и падающим лучами при условии, что зеркало повернули на 10° относительно начального положения (см. рисунок).

Ответ: 80

Задание 15. Изначально два стеклянных кубика (1 и 2, верхняя часть рисунка) незаряжены, стоят по отдельности; их привели в соприкосновение и внесли в электрическое поле. Направление его напряженности – горизонтально вправо – показано на рисунке. Затем, как показано на нижней части рисунка, кубики разделили и только после этого выключили электрическое поле. Из приведённого ниже списка выберите все верные утверждения, которые соответствуют результатам проведённых экспериментальных исследований. Запишите цифры, под которыми они указаны.

1) После того как кубики раздвинули, заряд первого кубика оказался отрицателен, заряд второго – положителен.
2) После помещения в электрическое поле электроны из первого кубика стали переходить во второй.
3) После того как кубики раздвинули, заряды обоих кубиков оказались равными нулю.
4) До разделения кубиков в электрическом поле левая поверхность 1-ого кубика была заряжена отрицательно.
5) До разделения кубиков в электрическом поле правая поверхность 2-ого кубика была заряжена отрицательно.

Ответ: 34

Задание 16. По катушке индуктивности в течение времени t0 пропускают ток, сила которого линейно растет со временем. Затем этот опыт повторяют, предварительно вставив в катушку железный сердечник Зависимость силы тока от времени одинакова. Определите, как изменяются по отношению к первому опыту следующие физические величины. Для каждой величины определите соответствующий характер изменения:

1) увеличится
2) уменьшится
3) не изменится

Ответ: 111

Задание 17. Участок цепи постоянного тока содержит резистор. Установите соответствие между формулами для вычисления физических величин и названиями этих величин. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Ответ: 31

Задание 18. Частота оранжевого света примерно в 1,3 раза меньше частоты синего света. Во сколько раз энергия фотона синего света больше энергии фотона оранжевого света?

Ответ: 12

Задание 19. Большое число N радиоактивных ядер 80𝐻𝑔 203 распадается, образуя стабильные дочерние ядра 𝑇𝑙 81 203 . Период полураспада равен 46,6 суток. Какое количество исходных ядер останется через 93,2 суток, а дочерних появится за 139,8 суток после начала наблюдений? Установите соответствие между величинами и их значениями. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Ответ: 24

Задание 20. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.

1) При любом равномерном движении тело за каждую секунду совершает одинаковые перемещения.
2) Скорость диффузии жидкостей повышается с повышением температуры.
3) Общее сопротивление системы параллельно соединённых резисторов равно сумме сопротивлений всех резисторов.
4) Электромагнитные волны ультрафиолетового диапазона имеют большую длину волны, чем радиоволны.
5) Атомы изотопов одного элемента различаются число нейтронов в ядре и занимают одну и ту же клеточку в Периодической таблице Д.И. Менделеева.

Ответ: 5

Задание 21. Даны следующие зависимости величин: А) зависимость периода малых свободных колебаний математического маятника от длины нити маятника; Б) зависимость количества теплоты, выделяющегося при конденсации пара, от его массы; В) зависимость силы тока через участок цепи, содержащий резистор, от сопротивления резистора при постоянном напряжении на концах участка. Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами.

Ответ: 11

Задание 22. В мензурку для проведения опыта налита вода. Чему равен её объем, если градуировка шкалы выполнена в миллилитрах? Погрешность измерения принять равной половине цены деления шкалы?

Ответ: 1501

Задание 23. Необходимо обнаружить зависимость частоты свободных электромагнитных колебаний в колебательном контуре от электроёмкости конденсатора. Какие два колебательных контура надо выбрать для проведения такого опыта?

Задание 24. В цепи, изображенной на рисунке, сопротивление диода в прямом направлении пренебрежимо мало, а в обратном многократно превышает сопротивление резисторов. Все резисторы имеют одинаковое сопротивление, равное внутреннему сопротивлению источника тока. Во внешней цепи выделяется мощность P. Как изменится мощность, выделяющаяся во внешней цепи, при другой полярности подключения источника тока? Ответ поясните, опираясь на законы электродинамики.

Задание 25. Груз массой 120 кг удерживают с помощью рычага, приложив к его концу вертикально направленную силу величиной 300 Н (см. рисунок). Рычаг состоит из шарнира без трения и длинного однородного стержня массой 30 кг. Расстояние от оси шарнира до точки подвеса груза равно 1 м. Определите длину стержня.

Задание 26. На сетчатку глаза человека падает 135 фотонов за 3 с. Мощность поглощённого сетчаткой света равна 1,98 10-17 Вт. Определите длину волны света.

Задание 27. В сосуде объёмом V = 0,02 м3 с жёсткими стенками находится одноатомный газ при атмосферном давлении. В крышке сосуда имеется отверстие площадью s, заткнутое пробкой. Максимальная сила трения покоя F пробки о края отверстия равна 100 Н. Пробка выскакивает, если газу передать количество теплоты не менее 15 кДж. Определите значение s, полагая газ идеальным. Массой пробки пренебречь.

Задание 28. Колебательный контур радиоприемника настроен на длину волны λ=500 м. Индуктивность катушки контура L = 3 мкГн. В контуре используется плоский воздушный конденсатор, расстояние между пластинами которого d = 1 мм. Максимальная напряженность электрического поля конденсатора в ходе колебаний Emax = 3 В/м. Каков максимальный ток в катушке индуктивности?

Задание 29. Металлическую пластину освещают монохроматическим светом с длиной волны 500 нм. Определите максимальную скорость фотоэлектронов, вылетающих с поверхности пластины, если работа выхода электронов из данного металла составляет 1,4 эВ?

Задание 30. Свинцовый шар массой 4 кг подвешен на нити и полностью погружен в воду (см. рисунок). Нить образует с вертикалью угол α = 30°. Определите силу, с которой нить действует на шар. Плотность свинца ρ = 11 300 кг/м 3 . Трением шара о стенку пренебречь. Сделайте схематический рисунок с указанием сил, действующих на шар. Обоснуйте их применимость к данному случаю.

Демидова ЕГЭ 2023 физика сборник 30 тренировочных вариантов

Демидова ЕГЭ 2023 физика сборник 30 тренировочных вариантов

Источник

27 февраля 2023 Пробник ЕГЭ 2023 по физике 11 класс вариант 111 и ответы

Пробник ЕГЭ 2023 по физике 11 класс тренировочный вариант №111 в новом формате реального экзамена ЕГЭ 2023 года ФИПИ от easy-physi, задания, ответы и решения для подготовки. А также видео разбор варианта.

Пробник ЕГЭ 2023 по физике вариант 111

Задание 1. Тело, движущееся равноускоренно с начальной скоростью 7 м/с, пройдя некоторое расстояние, приобретает скорость 17 м/с. Какова была скорость тела в тот момент времени, когда оно прошло половину расстояния?

Задание 2. Однородная цепочка длиной 2 м лежит на столе. Когда часть цепочки длиной 0,2 м опускают со стола, она начинает скользить вниз. Масса цепочки 5 кг, а сила трения между столом и цепочкой составляет 0,1 веса цепочки. Какая работа против силы трения совершается при соскальзывании цепочки?

Задание 3. Имеются три математических маятника с периодами 2, 6 и 9 с. Нити этих маятников соединили, получив из трех один маятник. Каков период его колебаний?

Задание 4. Груз, подвешенный на лёгкой пружине жёсткостью 100 Н/м, совершает вертикальные колебания. На рисунке изображены графики зависимости смещения груза x и проекции скорости груза Vx от времени t. На основании анализа приведённых графиков, выберите все верные утверждения и укажите в ответе их номера.

1) Круговая частота ω колебаний груза равна 10 рад/с.
2) Период колебаний груза равен (0,2π) с.
3) Максимальное ускорение груза равно по модулю 800 см/с2 .
4) Масса груза равна 1 кг.
5) Максимальная потенциальная энергия упругой деформации пружины равна 4 кДж.

Задание 5. Пробковый шар объемом �� привязан ко дну конического сосуда с водой так, что нить вертикальна, а шар касается гладкой стенки сосуда. Угол между горизонтальным дном и стенкой сосуда ��. Плотности воды и пробки �� и ��1. Как изменится сила Архимеда, действующая на шар, и сила натяжения нити, если неподвижный сосуд начать двигать с постоянным горизонтальным ускорением ��? Для каждой величины определите соответствующий характер её изменения:

1) увеличивается
2) уменьшается
3) не изменяется

Задание 7. Резервуар объема ��1 = 50 л соединили с резервуаром объема ��2 = 15 л с помощью короткой трубки, в которой имеется специальный клапан давления, позволяющий газу просачиваться из большого резервуара в малый, если давление в большом резервуаре превышает давление в малом на ∆�� = 88 мм рт. ст. Сначала при ��0 = 290 К большой резервуар содержит газ при нормальном атмосферном давлении, а меньший – откачан до состояния вакуума. Каким будет давление ��2 в малом резервуаре, если всю систему нагреть до ��1 = 162℃? Ответ округлить до целых кПа.

Задание 8. На рисунке представлены два термометра, используемые для определения относительной влажности воздуха с помощью психрометрической таблицы (на рисунке слева), в которой влажность воздуха указана в процентах. Каковы показания влажного термометра, если разность показаний сухого и влажного термометров составила 4℃, и достоверно известно, что влажность в помещении 61%?

Задание 9. График циклического процесса, происходящего с идеальным одноатомным газом, изображен на рисунке. Определите работу ��, совершенную газом в этом процессе, если количество газа �� = 3 моль, ��1 = 400 К, ��2 = 800 К, ��4 = 1200 К. Ответ дать в кДж, округлив до целых.

Задание 10. С одним молем идеального одноатомного газа совершают циклический процесс 1—2—3—4— 1 (см. рис.). Выберите все верные утверждения относительно этого процесса:

1) КПД данного цикла меньше, чем КПД идеальной тепловой машины, работающей при тех же максимальной и минимальной температурах, в 8 раз.
2) КПД данного цикла меньше, чем КПД идеальной тепловой машины, работающей при тех же максимальной и минимальной температурах, в 10 раз.
3) КПД идеальной тепловой машины, работающей при тех же максимальной и минимальной температурах, равен 23 24 .
4) КПД идеальной тепловой машины, работающей при тех же максимальной и минимальной температурах, равен 24 25 .
5) Работа газа в процессе 12 больше, чем в процессе 23.

Задание 11. Одноатомный идеальный газ неизменной массы в изотермическом процессе совершает работу �� < 0. Как изменятся в этом процессе объем, давление и внутренняя энергия газа? К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Задание 12. Значения сопротивлений резисторов, из которых собран участок цепи, приведены в омах, сопротивление перемычки АВ пренебрежимо мало. Найти ток во внешней цепи, если через перемычку АВ протекает ток 3 А.

Задание 13. Определить индуктивность соленоида, в котором при равномерном увеличении тока на ∆�� = 2 А энергия магнитного поля увеличивается на ∆�� = 10−2 Дж. Средняя сила тока в цепи 5 А. Ответ дать в мГн.

Задание 14. Луч света падает на горизонтально расположенное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если, не меняя положения источника света, повернуть зеркало на 10°, как показано на рисунке? Ответ дайте в градусах.

Задание 15. В вершинах правильного шестиугольника со стороной �� помещаются точечные заряды одинаковой величины ��. Выберите все верные утверждения.

1) Потенциал в центре шестиугольника при условии, что знак всех зарядов одинаков, отличен от нуля.
2) Потенциал в центре шестиугольника при условии, что знаки соседних зарядов противоположны, отличен от нуля.
3) Напряженность поля в центре шестиугольника при условии, что знак всех зарядов одинаков, отлична от нуля.
4) Напряженность поля в центре шестиугольника при условии, что знаки соседних зарядов противоположны, отлична от нуля
5) Напряженность поля в центре шестиугольника и при условии, что знаки соседних зарядов одноименны, и при условии, что знаки соседних зарядов противоположны, равна нулю.

Задание 16. Металлическое кольцо находится в однородном магнитном поле, линии индукции которого перпендикулярны плоскости кольца. Проводя первый опыт, модуль индукции магнитного поля равномерно уменьшают от начального значения B0 до нуля за некоторое время. Во втором опыте модуль индукции магнитного поля снова равномерно уменьшают от B0 до нуля, но в два раза быстрее. Как изменятся во втором опыте по сравнению с первым возникающая в кольце ЭДС индукции и протёкший по кольцу электрический заряд? Для каждой величины определите соответствующий характер изменения:

1) увеличится
2) уменьшится
3) не изменится

Задание 17. На рис. 1 изображена электрическая схема идеального колебательного контура, состоящего из конденсатора ёмкостью C, катушки индуктивностью L и ключа. Конденсатор заряжают до некоторого начального напряжения U0, а затем в момент времени t0 = 0 замыкают ключ. На рис. 2 показан график зависимости заряда q левой обкладки этого конденсатора от времени t.

Задание 18. Образец радиоактивного полония 84�� 218 находится в закрытом сосуде, из которого откачан воздух. Ядра полония испытывают ��-распад с периодом полураспада 3 мин. Определите число моль полония-218 в сосуде через 9 мин., если образец в момент его помещения в сосуд имел в своём составе 2,4 ∙ 1023 атомов полония-218. Ответ дайте в молях.

Задание 19. Энергия протона, который движется в ускорителе уменьшилась на некоторую величину. Как в результате этого изменятся следующие две величины: скорость протона, кинетическая энергия протона? Для каждой величины определите соответствующий характер изменения:

1) увеличится
2) уменьшится
3) не изменится

1) Работа силы тяжести по перемещению тела между двумя заданными точками зависит от соединяющей их траектории.
2) В ходе процесса кипения жидкости её температура не меняется, а внутренняя энергия системы «жидкость и её пар» уменьшается.
3) Модуль сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорционален модулю каждого из зарядов.
4) Энергия магнитного поля катушки индуктивностью L увеличивается прямо пропорционально увеличению силы тока в катушке.
5) Атом излучает свет при переходе из стационарного состояния с большей энергией в стационарное состояние с меньшей энергией.

Задание 21. Даны следующие зависимости физических величин: А) зависимость модуля скорости тела от его кинетической энергии; Б) зависимость давления идеального газа от времени при медленном изобарическом нагревании газа; В) зависимость максимальной кинетической энергии фотоэлектрона от частоты падающего на металл света.

Задание 22. В мерный стакан налита вода. Укажите объём воды (в мл) с учётом погрешности измерения, учитывая, что погрешность составляет половину цены деления мерного стакана. В ответе запишите значение и погрешность слитно без пробела.

Задание 23. Нужно провести лабораторную работу с целью обнаружения зависимости сопротивления цилиндрического проводника от площади его поперечного сечения. Какие два проводника из перечисленных в таблице необходимо выбрать, чтобы провести такое исследование?

Задание 24. Четверо ребят на двух санях перевезли по одному и тому же пути металлолом. Веревки они натягивали с одинаковой силой, но ребята одной пары шли рядом, а другой пары – поодаль друг от друга. Которая из пар совершила большую работу? Ответ обоснуйте.

Задание 25. Газ находится в вертикальном цилиндре с площадью основания 0,1 м2 при температуре 0℃. На расстоянии 0,8 м от дна цилиндра находится поршень массой 15 кг. Атмосферное давление нормальное. Какую работу совершит газ при его нагревании на 25℃?

Задание 27. В длинной гладкой теплоизолированной трубе находятся теплоизолированные поршни массами ��1и ��2, между которыми в объеме ��0 находится одноатомный газ при давлении ��0. Поршни отпускают. Определите их максимальные скорости, если масса газа много меньше массы каждого поршня

Задание 28. Замкнутый контур из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. Площадь контура �� = 2 ∙ 10−3 м 2 . В контуре возникают колебания тока с амплитудой �� = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой �� = �� (��), где �� = 6 ∙ 10−3 Тл, �� = 3500 c -1 . Чему равно электрическое сопротивление контура ��?

Задание 29. Две плоско-выпуклые тонкие стеклянные линзы соприкасаются своими сферическими поверхностями. Найти оптическую силу такой системы, если в отраженном свете с �� = 0,6 мкм диаметр пятого светлого кольца �� = 1,5 мм.

Задание 30. На рисунке изображена система из трёх брусков, имеющих форму прямоугольных параллелепипедов, соединённых с помощью двух блоков и нерастяжимой натянутой нити. Массы брусков ��1 = 5��, ��2 = �� и ��3 = 3��. Блоки сначала удерживают неподвижно на горизонтальной поверхности, затем аккуратно отпускают. Все поверхности гладкие. С каким по величине ускорением начнёт движение брусок 1? Ответ выразите в м/с2 , округлив до сотых. Ускорение свободного падения считайте равным �� = 9,8 м/с2 .

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Условие:

Тело движется прямолинейно с постоянным ускорением.

7 1

Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

7 2

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) импульс тела
2) равнодействующая сила
3) кинетическая энергия тела
4) ускорение тела

Решение:

Прямолинейно с постоянным ускорением необходимо установить соответствие между графиками и физическими величинами зависимости которых от времени эти графики Могут представлять каждой позиции первого столбца подбери подобрать соответствующую позицию второго записать в таблицу выбранные цифры под соответствующими буквами рассматривая график зависимости движения данного тела мы замечаем что скорость у нас совпадают по направлению с ускорением так как ускорение у нас сонаправлена с движением данного тела Следовательно тело движется равноускоренно а следовательно его ускорение у нас больше нуля графики зависимости А и Б представлены в виде прямой и параболы рассматривая Что такое импульс тела и импульс это произведение массы на его скорость в первом графики физическая величина у нас увеличивается так как тело движется с постоянным ускорением Следовательно его скорость также увеличивается а график а соответствует данному значению поэтому под А у нас импульс тела ответ номер один вспоминаем Что такое равнодействующая сила равнодействующая сила равна произведение массы на ускорение так как ускорение есть величина постоянная и больше нуля Следовательно графикам зависимости F будет являться прямая которая будет параллельно оси T лежащие выше оси T данный график не соответствует данной величине поэтому 2 ответ у нас не подходит 4 график также не подходит так как у нас ускорение есть величина постоянная а следовательно графикам зависимости а а т является прямая лежащая выше Осетия остаётся ответ номер три вспоминаем Что такое кинетическая энергия кинетическая энергия равна м в квадрате деленное на 2 так как скорость стоит в квадрате это квадратичная функция а графиком квадратичной функции является Парабола Следовательно в данном случае под у нас цифра 3 так Ответ 13

Источник: ЕГЭ-2020 Физика (20 экзаменационных вариантов) «Экзаменационный тренажер к новой официальной экзаменационной версии ЕГЭ». С.Б. Бобошина

Разбор решения. (Видео)

Источник

За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 69.1%
Ответом к заданию 1 по физике может быть целое число или конечная десятичная дробь.

Алгоритм решения задания 1:

Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
Выбирайте наиболее подходящую для решения формулу.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Уравнение движения тела имеет вид x = 2t + 0,5t². Найдите, с каким ускорением двигалось тело. Ответ выразите в (м/с²).

Решение

Дано:

$x=2t+0.5t^2$

$a-?$

Решение:

Запишем уравнение движения в общем виде и сравнив с имеющимся: $x=2t+0.5t^2; x=υ_0t+{at^2}/{2}$, тогда ${at^2}/{2}=0.5t^2; a=0.5·2$ или $a=1м/с^2$.

Ответ: 1

Задача 2

Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ выразите в (км/ч).

Решение

Дано:

$υ_1=60$км/ч

$S_1={1}/{4}S$

$S_2={3S}/{4}$

$υ_{ср}=40$км/ч

$υ_2-?$

Решение:

Средняя скорость определяется выражением: $υ_{ср}={S_{общ}}/{t_{общ}}$(1), где $S_{общ}=S_1+S_2={S}/{4}+{3S}/{4}={4S}/{4}=S$(2), $t_{общ}=t_1+t_2={S_1}/{υ_1}+{S_2}/{υ_2}={S}/{4υ_1}+{3S}/{4υ_2}={Sυ_2+3Sυ_1}/{4υ_1υ_2}$(3).

Подставим выражения (2) и (3) в (1), получим: $υ_{ср}={S}/{1}:{S(3υ_1+υ_2)}/{4υ_1υ_2}={S}/{1}·{4υ_1υ_2}/{S(3υ_1+υ_2)}={4υ_1υ_2}/{(3υ_1+υ_2)}$(4). Из (4) выразим скорость $υ_2$: $υ_{ср}(3υ_1+υ_2)=4υ_1υ_2⇒3υ_1υ_{ср}+υ_{ср}υ_2=4υ_1υ_2⇒4υ_1υ_2-υ_{ср}υ_2=3υ_1υ_{ср}⇒υ_2(4υ_1-υ_{ср})=3υ_1υ_{ср}⇒υ_2={3υ_1υ_{ср}}/{(4υ_1-υ_{ср})}$(5). Подставим числовые значения в (5): $υ_2={3·60·40}/{4·60-40}={7200}/{200}=36км/ч$.

Ответ: 36

Задача 3

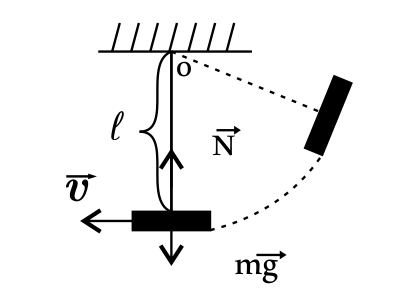
Цирковая гимнастка массой 50 кг качается на качелях с длиной верёвок 5 м. С какой силой она давит на сиденье при прохождении положения равновесия со скоростью 6 м/с? Ответ выразите в (Н). Ускорение свободного падения считать равным 10 м/с^2

Решение

Дано:

$m=50$кг

$g=10м/с^2$

$l=5$м

$υ=6$м/c

$N-?$

Решение:

При прохождении качелями среднего положения второй закон Ньютона в проекции на вертикальное направление иммет вид: $ma=N-mg$(1), здесь $a$ — ускорение гимнастики, совпадающее с центростремительным, $m$ — масса гимнастики, $N$ — сила реакции опоры (сиденья), равная по модулю, согласно третьему закону Ньютона, силе, с которой мальчик давит на сиденье. Так как центростремительное ускорение равно $a_{ц.с.}={υ^2}/{l}$(2), то сила, действующая на сиденье, равна: $N=ma+mg=m(a+g)=m({υ^2}/{l}+g)$(3). Подставим числовые значения в (3): $N=50·({36}/{5}+10)=50·17=860H$.

Ответ: 860

Задача 4

Из начала координат одновременно начинают движение две точки. Первая движется вдоль оси Ox со скоростью 3 м/с, а вторая — вдоль оси Oy со скоростью 4 м/с. (Оси перпендикулярны). С какой скоростью они будут удаляться друг от друга? Ответ выразите в (м/с).

Решение

Дано:

$υ_1=3$м/с

$υ_2=4$м/с

$υ_{отн}-?$

Решение:

Вектор относительной скорости $υ_{отн}$ есть разность векторов скоростей двух точек. По правилу вычитания векторов, вектор относительной скорости будет ижти от конца вектора скорости одной точки к концу векторая скорости другой точки. Так как скорости точек направлены перпендикулярно, длина вектора относительной скорости является гипотенузой прямоугольного треугольника и находится по теореме Пифагора: $υ_{отн}=√{υ_1^2+υ_2^2}=√{(3)^2+(4)^2}=√{9+16}=√{25}=5$м/с.

Ответ: 5

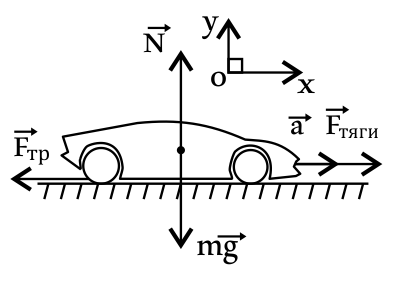
Задача 5

Автобус, масса которого 15 т, движется с ускорением 0,7 м/с². Чему равна сила тяги двигателя, если коэффициент сопротивления движению равен 0,03? Ответ выразите в (кН).

Решение

Дано:

$m=15·10^3$кг

$a=0.7м/с^2$

$μ=0.03$

$F_{тяги}-?$

Решение:

На автомобиль действуют силы: тяги, трения, тяжести и силы реакции опоры. Запишем второй закон Ньютона: $ma↖{→}={F_{тяги}}↖{→}+{F_{тр}}↖{→}+mg↖{→}+N↖{→}$(1).

В проекциях на оси координат имеем: $Ox:ma=F_{тяги}-F_{тр}$(2), откуда $F_{тяги}=ma+F_{тр}$(3). $Oy:O=N-mg$(4), откуда $N=mg$(5). Учитывая, что сила трения $F_{тр}=μN$, то с учетом (5) получим: $F_{тр}=μmg$(6). Подставим (6) в (3) и найдем $F_{тяги}:F_{тяги}=ma+μmg=m(a+μg)$(7), где $g≈10м/с^2$ — ускорение свободного падения.

Подставим числовые значения в (7), получим: $F_{тяги}=15·10^3·(0.7+0.03·10)=15·10^3·(0.7+0.3)=15·10^3·1=15·10^3=15$кН.

Ответ: 15

Задача 6

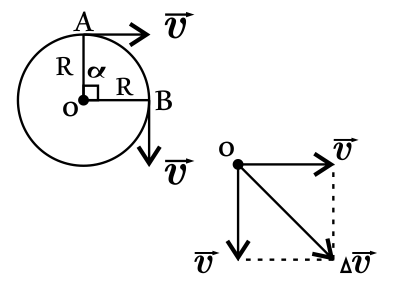
Тело движется по окружности равномерно. Радиус окружности 1 м. Найдите изменение вектора скорости при перемещении тела на угол 90◦. Период обращения 3,14 с. Ответ округлите до десятых. Ответ выразите в (м/с). Число ${π}$ принять равным 3,14

Решение

Дано:

$R=1$м

$α=90°$

$T=3.14$c

$∆υ-?$

Решение:

Изменение вектора скорости при перемещении тела на угол $90°$ равно по теореме Пифагора: $∆υ=√{υ^2+υ^2}=√{2υ^2}=√{2}υ$(1).

Найдем величину скорости $υ$: $υ={S}/{t}={2πR}/{T}={3.14·2·1}/{3.14}=2$м/с(2).

Подставим числовые значения в (1), получим: $∆υ=√2·υ=1.41·2=2.82=2.8$м/с.

Ответ: 2.8

Задача 7

Тело движется вдоль оси Ox. Чему равна проекция скорости тела v_x, координата x которого меняется с течением времени по закону x = 3 − 2t, где все величины выражены в системе СИ? Ответ выразите в (м/c).

Решение

Дано:

$x=3-2t$

$υ_х-?$

Решение:

Известно, что $υ_x=x'(t)$, тогда $x'(t)=-2·1=-2$.

Ответ: -2

Задача 8

Подъёмный кран поднимает груз вверх со скоростью 3 м/с. В некоторый момент времени трос обрывается и груз начинает падать вниз. Определите скорость груза в момент падения на землю, если время падения составляет 4 с. Ответ выразить в (м/с). Ускорение свободного падения принять равным $10м/с^2$

Решение

Дано:

$υ=3$м/с

$t=4$c

$υ_к-?$

Решение:

На тело действует сила тяжести и ускорение свободного падения $g=const=10м/с^2$

$g={υ_к-(-υ_0)}/{t}$, т.к. ускорение $g$ и $υ_0$ разнонаправлены. $υ_к=gt-υ_0=10·4-3=37$м/с.

Ответ: 37

Задача 9

Тело движется вдоль оси Ox. Чему равно перемещение тела за 10 с, координата x которого меняется с течением времени по закону x = 3 − 2t + t², где все величины выражены в системе СИ? Ответ выразить в (м).

Решение

Дано:

$t=10$c

$x=3-2t+t^2$

$x_0=3$

$r-?$

Решение:

$x=-20+100=80+3=83$

$r=x-x_0=83-3=80$м, т.к. изначально тело уже прошло 3м.

Ответ: 80

Задача 10

Планета имеет радиус в 2 раза меньший радиуса Земли. Найдите массу этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как и на Земле. Масса Земли 6 · 10²⁴ кг. Ответ выразить в (·10²⁴ кг).

Решение

Дано:

$R_n={R_3}/{2}$

$M_n-?$

$g_n=g_3$

$M_3=6·10^{24}$м

Решение:

${tableg_n=G{M_n}/{R_r^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{R_n^2}={M_3}/{R_3^2}; M_n=M_3·{R_n^2}/{R_3^2}=6·10^{24}·{1}/{4}=1.5·10^{24}$кг

Ответ: 1.5

Задача 11

Материальная точка движется по окружности радиусом ${1.5}/{π}$ м. Найдите перемещение точки за 2 полных оборота. Ответ выразить в (м).

Решение

Дано:

$R={1.5}{π}$

Решение:

Точка делает 2 полных оборота и возвращается в начальную точку, ее перемещение равно 0.

Ответ: 0

Задача 12

Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 10⁶ м. Ответ выразите в (км).

Решение

Дано:

$M_n={M_3}/{4}$

$R_n-?$

$g_n=g_3$

$R_3=6.4·10^6$м

Решение:

${tableg_n=G{M_n}/{R_n^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{M_3}={R_n^2}/{R_3^2}; {1}/{2}={R_n}/{R_3}$

$R_n=3200$км

Ответ: 3200

Задача 13

Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с²).

Решение

Дано:

$g_n-?$

$T_n=1.41$с

$T_3=1c$

Решение:

${tableT_n=2π√{{l}/{g_n}}; T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$

$g_n=5м/с^2$

Ответ: 5

Задача 14

Мяч массой 800 г брошен под углом 90◦ к горизонту с начальной скоростью 5 м/с. Найдите модуль силы тяжести, действующей на мяч сразу после броска. Ответ выразите в (Н).

Решение

Дано:

$m=0.8$кг

$υ=5$м/с

$F_{тяж}-?$

Решение:

Модуль силы тяжести, равна: $m·g=0.8·10=8H$

Ответ: 8

Задача 15

Найдите значение ускорения свободного падения на некоторой планете, плотность которой в два раза меньше плотности Земли, если радиусы планет одинаковы. Ответ выразите в (м/с²). Ускорение свободного падения на Земле принять равным 10 м/с^2

Решение

Дано:

$R_n=R_3$

${ρ_3}/{2}=ρ_n$

$ρ_n-?$

Решение:

${tableg^3=G{M_3}/{r^2}; g_n=G{M_n}/{r_n^2};$

а $V={4}/{3}π·R^3$, то и $V_n=V_3$.

${g_3}/{g_n}={ρ_3·V_3·r_n^2}/{ρ_n·V_n·r_3^2}⇒g_3=2·g_n; g_n=5м/с^2$.

Ответ: 5

Задача 16

Висящий на пружинке груз массой 400 г растягивает её на 10 см. На сколько сантиметров растянется пружина, если груз заменить на другой, массой 300 г? Ускорение свободного падения принять равным $10 м/{с^2}$. Ответ выразите в (см).

Решение

Дано:

$m_1=0.4$кг

$m_2=0.3$кг

$x_1=10^{-1}$ м=10 см

$x_2-?$

Решение:

${tablem_1g=kx_1; m_2g=kx_2;$ $⇒x_2={m_2g}/{m_1g}·x_1={0.3}/{0.4}·10см=7.5$

Ответ: 7.5

Задача 17

Велосипедист за 30 мин проехал 4 км, затем полчаса отдыхал, а затем проехал ещё 4 км за 15 мин. Какой была его средняя скорость на всём пути? Ответ выразите в (км/ч).

Решение

Известно, $υ_{ср}={∆S}/{∆t}={4+0+4}/{30+30+15}={8}/{1.25}=6.4{км}/ч$.

Ответ: 6.4

Задача 18

Найдите жёсткость пружины, если под действием силы 2 Н она растянулась на 4 см. Ответ выразите в (Н/м).

Решение

Дано:

$А=2·H$

$∆x=4·10^{-2}$

$K-?$

Решение:

По закону Гука $K={F}/{∆x}={2}/{4·10^{-2}}=50Н/м$.

Ответ: 50

Задача 19

Материальная точка равномерно движется по окружности. Найдите отношение пути к модулю перемещения за половину периода. Ответ округлить до сотых.

Решение

Дано:

${L}/{|S↖{→}|}-?$

$t={T}/{2}$

Решение:

1) За полпериода тело проходит половину окружности, поэтому пройденный путь равен половине дуги окружности: $L=π·R$
2) Модуль перемещения равен длине прямой, соединяющей начальную и конечную точки: $|S↖{→}|=2·R$

3) ${L}/{|S↖{→}|}={π·R}/{2·R}=1.57$

Ответ: 1.57

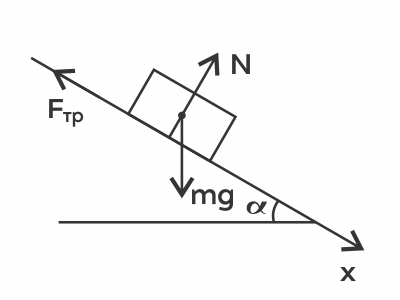
Задача 20

Брусок массой 2 кг покоится на наклонной плоскости с углом наклона 30◦ к горизонту. Определите силу трения, действующую на брусок, если коэффициент трения равен 0,7. Ответ выразите в (H). Ускорение свободного падения считать равным 10 $м/с^2$.

Решение

Дано:

$m=2$кг

$α=30°$

$μ=0.7$

Найти:$F_{тр}-?$

Решение:

Запишем 2-й закон Ньютона для тела: $ma↖{→}=mg↖{→}+N↖{→}+F_{тр}↖{→}=0$ (т.к. брусок покоится)

Направим ось х параллельно плоскости. 2-й закон Ньютона в проекции на ось х: $mg·sinα-F_{тр}=0⇒$

$F_{тр}=mgsinα=2·10·{1}/{2}=10Н$

Внимание! Многие при решении этой задачи используют неверную формулу $F_{тр}=μmgcosα$ — эта формула не может быть использована в этой задаче, потому что она описывает максимальную(!) силу трения покоя или силу трения скольжения. А в данной задаче тело покоится под действием силы трения, поэтому применять нужно формулы, указанные выше в решении.

Ответ: 10

Задания и ответы

Демидова ЕГЭ 2023 физика сборник 30 тренировочных вариантов

27 февраля 2023 Пробник ЕГЭ 2023 по физике 11 класс вариант 111 и ответы

Пробник ЕГЭ 2023 по физике вариант 111

Условие:

Разбор решения. (Видео)

Алгоритм решения задания 1:

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Задача 12

Решение

Задача 13

Решение

Задача 14

Решение

Задача 15

Решение

Задача 16

Решение

Задача 17

Решение

Задача 18

Решение

Задача 19

Решение

Задача 20

Решение

Рекомендуемые курсы подготовки

Новое и интересное на сайте: