Решу егэ физика ядерные реакции

Каталог заданий.
Ядерная физика


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Задания Д32 C3 № 3035

Пи -мезон массой 2,4 умножить на 10 в степени левая круглая скобка минус 28 правая круглая скобка кг распадается на два гамма -кванта. Найдите модуль импульса одного из образовавшихся гамма -квантов в системе отсчета, где первичный Пи в степени 0 -мезон покоится.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.1.2 Фотоны. Энергия фотона. Импульс фотона

Решение

·

·

Сообщить об ошибке · Помощь

2

Задания Д32 C3 № 3050

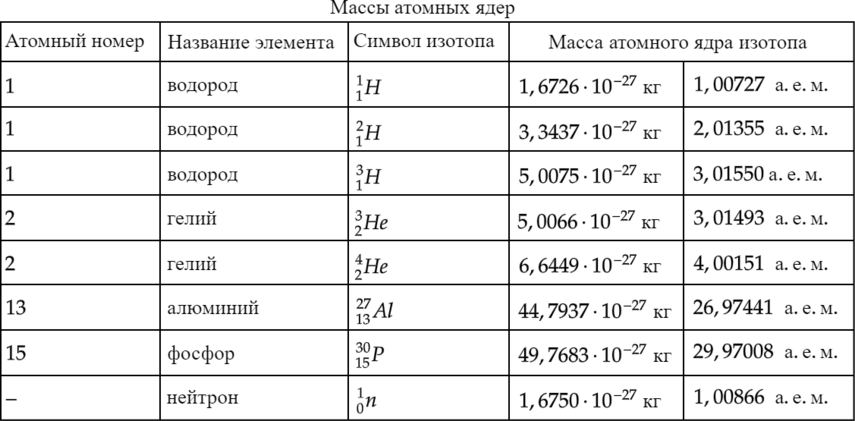
Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при синтезе 1 кг гелия из изотопов водорода  — дейтерия и трития: _1 в квадрате H плюс _1 в кубе Hto _2 в степени левая круглая скобка 4 правая круглая скобка He плюс _0 в степени левая круглая скобка 1 правая круглая скобка n.

Массы атомных ядер

Атомный номер Название элемента Символ изотопа Масса атомного ядра изотопа
1 водород _1 в степени левая круглая скобка 1 правая круглая скобка H 1,6726 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 1,00727а. е. м.
1 водород _1 в квадрате H 3,3437 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 2,01355а. е. м.
1 водород _1 в кубе H 5,0075 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01550а. е. м.
2 гелий _2 в кубе He 5,0066 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01493а. е. м.
2 гелий _2 в степени левая круглая скобка 4 правая круглая скобка He 6,6449 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 4,00151а. е. м.
13 алюминий _13 в степени левая круглая скобка 27 правая круглая скобка Al 44,7937 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 26,97441а. е. м.
15 фосфор _15 в степени левая круглая скобка 30 правая круглая скобка Р 49,7683 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 29,97008а. е. м.
— нейтрон _0 в степени левая круглая скобка 1 правая круглая скобка n 1,6750 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 1,00866а. е. м.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.3.2 Энергия связи нуклонов в ядре. Ядерные силы, 5.3.6 Ядерные реакции. Деление и синтез ядер

Решение

·

·

1 комментарий · Сообщить об ошибке · Помощь

3

Задания Д32 C3 № 3051

Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при осуществлении ядерной реакции:

_13 в степени левая круглая скобка 27 правая круглая скобка Al плюс _2 в степени левая круглая скобка 4 правая круглая скобка Heto_15 в степени левая круглая скобка 30 правая круглая скобка P плюс _0 в степени левая круглая скобка 1 правая круглая скобка n.

Массы атомных ядер

Атомный номер Название элемента Символ изотопа Масса атомного ядра изотопа
— нейтрон _0 в степени левая круглая скобка 1 правая круглая скобка n 1,6750 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 1,00866а. е. м.
1 водород _1 в степени левая круглая скобка 1 правая круглая скобка H 1,6726 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 1,00727а. е. м.
1 водород _1 в квадрате H 3,3437 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 2,01355а. е. м.
1 водород _1 в кубе H 5,0075 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01550а. е. м.
2 гелий _2 в кубе He 5,0066 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01493а. е. м.
2 гелий _2 в степени левая круглая скобка 4 правая круглая скобка He 6,6449 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 4,00151а. е. м.
13 алюминий _13 в степени левая круглая скобка 27 правая круглая скобка Al 44,7937 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 26,97441а. е. м.
15 фосфор _15 в степени левая круглая скобка 30 правая круглая скобка Р 49,7683 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 29,97008а. е. м.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.3.2 Энергия связи нуклонов в ядре. Ядерные силы, 5.3.6 Ядерные реакции. Деление и синтез ядер

Решение

·

·

Сообщить об ошибке · Помощь

4

Задания Д32 C3 № 3052

Определите, ядро какого изотопа X освобождается при осуществлении ядерной реакции:

_2 в кубе He плюс _2 в кубе Heto _2 в степени левая круглая скобка 4 правая круглая скобка He плюс _1 в степени левая круглая скобка 1 правая круглая скобка H плюс X.

Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при осуществлении этой ядерной реакции.

Атомный номер Название элемента Символ изотопа Масса атомного ядра изотопа
1 водород _1 в степени левая круглая скобка 1 правая круглая скобка H 1,6726 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 1,00727а. е. м.
1 водород _1 в квадрате H 3,3437 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 2,01355а. е. м.
1 водород _1 в кубе H 5,0075 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01550а. е. м.
2 гелий _2 в кубе He 5,0066 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01493а. е. м.
2 гелий _2 в степени левая круглая скобка 4 правая круглая скобка He 6,6449 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 4,00151а. е. м.
13 алюминий _13 в степени левая круглая скобка 27 правая круглая скобка Al 44,7937 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 26,97441а. е. м.
15 фосфор _15 в степени левая круглая скобка 30 правая круглая скобка Р 49,7683 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 29,97008а. е. м.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.3.2 Энергия связи нуклонов в ядре. Ядерные силы, 5.3.6 Ядерные реакции. Деление и синтез ядер

Решение

·

·

Сообщить об ошибке · Помощь

5

Задания Д32 C3 № 3053

Определите, какая частица X образуется при осуществлении ядерной реакции: _1 в степени левая круглая скобка 1 правая круглая скобка H плюс _1 в квадрате Hto _2 в кубе He плюс X. Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при осуществлении этой ядерной реакции.

Массы атомных ядер

Атомный номер Название элемента Символ изотопа Масса атомного ядра изотопа
1 водород _1 в степени левая круглая скобка 1 правая круглая скобка H 1,6726 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 1,00727а. е. м.
1 водород _1 в квадрате H 3,3437 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 2,01355а. е. м.
1 водород _1 в кубе H 5,0075 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01550а. е. м.
2 гелий _2 в кубе He 5,0066 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 3,01493а. е. м.
2 гелий _2 в степени левая круглая скобка 4 правая круглая скобка He 6,6449 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 4,00151а. е. м.
13 алюминий _13 в степени левая круглая скобка 27 правая круглая скобка Al 44,7937 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 26,97441а. е. м.
15 фосфор _15 в степени левая круглая скобка 30 правая круглая скобка Р 49,7683 умножить на 10 в степени левая круглая скобка минус 27 правая круглая скобка кг 29,97008а. е. м.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.3.2 Энергия связи нуклонов в ядре. Ядерные силы, 5.3.6 Ядерные реакции. Деление и синтез ядер

Решение

·

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Всего: 37    1–20 | 21–37

Добавить в вариант

Задания Д32 C3 № 3050

Задания Д32 C3 № 3057

Вычислите массу радиоактивных продуктов деления ядер урана, накапливающихся в ядерном реакторе тепловой мощностью 3 умножить на 10 в степени левая круглая скобка 9 правая круглая скобка Вт за сутки, принимая выделение энергии при делении ядра урана 235 равным 200 МэВ.

Задания Д32 C3 № 3051

Задания Д32 C3 № 3052

Задания Д32 C3 № 3053

В результате реакции синтеза ядра дейтерия с ядром _Y в степени левая круглая скобка X правая круглая скобка Z образуется ядро бора и нейтрон в соответствии с реакцией:

_1 в квадрате H плюс _Y в степени левая круглая скобка X правая круглая скобка Z to _5 в степени левая круглая скобка 10 правая круглая скобка B плюс _0 в степени левая круглая скобка 1 правая круглая скобка n.

Каковы массовое число X и заряд Y (в единицах элементарного заряда) ядра, вступившего в реакцию с дейтерием?

X Y
   

Реакция деления ядра урана тепловыми нейтронами описывается уравнением:

x умножить на в степени 1 _0n плюс в степени левая круглая скобка 235 правая круглая скобка _92U arrow в степени левая круглая скобка 144 правая круглая скобка _56Ba плюс в степени левая круглая скобка 89 правая круглая скобка _36Kr плюс y умножить на в степени 1 _0n.

Определите минимальное число нейтронов x, вступающих в реакцию, и число нейтронов y, образующихся в качестве продуктов этой реакции. Ответ дайте в виде двух чисел, записав каждое в соответствующий столбец таблицы.

Минимальное число нейтронов x, вступающих в реакцию Число нейтронов y, образующихся в качестве продуктов реакции

Каково массовое число ядра Х в реакции _95 в степени левая круглая скобка 241 правая круглая скобка Am плюс в степени левая круглая скобка 4 правая круглая скобка _2Helongrightarrow X плюс 2 в степени 1 _0n?

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 5.

Ядро бора может захватить альфа-частицу, в результате чего происходит ядерная реакция в степени левая круглая скобка 4 правая круглая скобка _2He плюс в степени левая круглая скобка 11 правая круглая скобка _5B arrow в степени левая круглая скобка A правая круглая скобка _ZX плюс в степени левая круглая скобка 1 правая круглая скобка _0n с образованием ядра химического элемента в степени левая круглая скобка A правая круглая скобка _ZX. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

В ответе запишите числа слитно без пробела.

Заряд ядра Z Массовое число ядра A

Источник: Демонстрационная версия ЕГЭ−2019 по физике

В результате ядерной реакции синтеза в квадрате _1$H плюс _1 в квадрате $H to$ _Z в степени A $X плюс _1 в степени 1 $p образуется ядро химического элемента в степени A _Z$X. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

Заряд ядра Z Массовое число ядра A

Источник: Демонстрационная версия ЕГЭ—2021 по физике

Каково массовое число ядра Х в реакции деления урана _0 в степени 1 n плюс в степени левая круглая скобка 235 правая круглая скобка _92U longrightarrow в степени левая круглая скобка 141 правая круглая скобка _56Ba плюс X плюс 3 в степени 1 _0n?

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 4.

В результате ядерной реакции ядро X превращается в ядро Y. Установите соответствие между ядерной реакцией и изменениями в этой реакции зарядового и массового числа ядра Y по сравнению с ядром X. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ЯДЕРНАЯ РЕАКЦИЯ

А)  X плюс $ в степени левая круглая скобка 4 правая круглая скобка _2$He $arrow$ Y плюс $ в степени левая круглая скобка 1 правая круглая скобка _0$n

Б)  X плюс $ в степени левая круглая скобка 4 правая круглая скобка _2$He $arrow$ Y плюс $ в степени левая круглая скобка 1 правая круглая скобка _1$p

ИЗМЕНЕНИЕ ЗАРЯДОВОГО И МАССОВОГО ЧИСЛА ЯДРА Y ПО СРАВНЕНИЮ С ЯДРОМ Х

1)  зарядовое число увеличивается на 1, массовое число увеличивается на 3

2)  зарядовое число уменьшается на 3, массовое число уменьшается на 2

3)  зарядовое число увеличивается на 2, массовое число увеличивается на 3

4)  зарядовое число увеличивается на 2, массовое число увеличивается на 1

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

В настоящее время принято считать, что одним из источников энергии Солнца служит так называемый углеродный цикл синтеза гелия в степени левая круглая скобка 4 правая круглая скобка _2He. Этот цикл начинается с ядра углерода в степени левая круглая скобка 12 правая круглая скобка _6C . В результате нескольких последовательных поглощений ядром протонов и испускания позитронов (при этом образуются ядра промежуточных элементов, а также нейтрино и гамма-кванты) вновь образуется прежнее ядро в степени левая круглая скобка 12 правая круглая скобка _6C и синтезируется ядро гелия в степени левая круглая скобка 4 правая круглая скобка _2He:

в степени левая круглая скобка 12 правая круглая скобка _6C плюс x умножить на в степени левая круглая скобка 1 правая круглая скобка _1p arrow в степени левая круглая скобка 12 правая круглая скобка _6C плюс в степени левая круглая скобка 4 правая круглая скобка _2He плюс y умножить на в степени левая круглая скобка 0 правая круглая скобка _1e.

Сколько протонов поглощается и сколько позитронов испускается в ходе такого углеродного цикла? В ответе запишите число протонов и позитронов без пробелов и запятых.

Число поглощаемых протонов, х Число испускаемых позитронов, у
   

В результате реакции синтеза ядра дейтерия с ядром в степени левая круглая скобка A правая круглая скобка _Z$X образуется ядро бора и нейтрон: в квадрате _1$H плюс _Z в степени A $X to$ _5 в степени левая круглая скобка 10 правая круглая скобка $B плюс _0 в степени 1 $n. Определите массовое число и зарядовое число ядра в степени левая круглая скобка A правая круглая скобка _Z$X.

Массовое число A Зарядовое число Z

Источник: ЕГЭ по физике 2021. Досрочная волна. Вариант 1

В результате бомбардировки ядра X некоторого атома нейтронами в результате ядерной реакции получается ядро Y другого атома. Установите характер изменения массового числа и зарядового числа атома в результате такой реакции.

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Массовое число ядра Зарядовое число ядра
   

Ядро некоторого элемента бомбардируется протонами. В результате ядерной реакции поглощаются протоны и образуются α-частицы и ядро нового элемента. У образовавшегося ядра массовое число меньше массового числа исходного ядра на 3, а зарядовое число больше зарядового числа исходного ядра на 5. Определите минимальное число протонов и минимальное число α-частиц, участвующих в этой ядерной реакции.

Минимальное число протонов Минимальное число α-частиц
   

Ядро бора может захватить нейтрон, в результате чего происходит ядерная реакция в степени левая круглая скобка 10 правая круглая скобка _5 $B$ плюс в степени 1 _0 n arrow в степени A _Z $X$ плюс в степени 4 _2 $He$ с образованием ядра химического элемента в степени A _Z$X$. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

Заряд ядра Z Массовое число ядра A

Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1

Всего: 37    1–20 | 21–37

Источник

Всего: 103    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Задания Д32 C3 № 3052

Задания Д32 C3 № 3053

Задания Д32 C3 № 3051

Ядро бора может захватить альфа-частицу, в результате чего происходит ядерная реакция в степени левая круглая скобка 4 правая круглая скобка _2He плюс в степени левая круглая скобка 11 правая круглая скобка _5B arrow в степени левая круглая скобка A правая круглая скобка _ZX плюс в степени левая круглая скобка 1 правая круглая скобка _0n с образованием ядра химического элемента в степени левая круглая скобка A правая круглая скобка _ZX. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

В ответе запишите числа слитно без пробела.

Заряд ядра Z Массовое число ядра A

Источник: Демонстрационная версия ЕГЭ−2019 по физике

В результате ядерной реакции ядро X превращается в ядро Y. Установите соответствие между ядерной реакцией и изменениями в этой реакции зарядового и массового числа ядра Y по сравнению с ядром X. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ЯДЕРНАЯ РЕАКЦИЯ

А)  X плюс $ в степени левая круглая скобка 4 правая круглая скобка _2$He $arrow$ Y плюс $ в степени левая круглая скобка 1 правая круглая скобка _0$n

Б)  X плюс $ в степени левая круглая скобка 4 правая круглая скобка _2$He $arrow$ Y плюс $ в степени левая круглая скобка 1 правая круглая скобка _1$p

ИЗМЕНЕНИЕ ЗАРЯДОВОГО И МАССОВОГО ЧИСЛА ЯДРА Y ПО СРАВНЕНИЮ С ЯДРОМ Х

1)  зарядовое число увеличивается на 1, массовое число увеличивается на 3

2)  зарядовое число уменьшается на 3, массовое число уменьшается на 2

3)  зарядовое число увеличивается на 2, массовое число увеличивается на 3

4)  зарядовое число увеличивается на 2, массовое число увеличивается на 1

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Ядро некоторого элемента бомбардируется протонами. В результате ядерной реакции поглощаются протоны и образуются α-частицы и ядро нового элемента. У образовавшегося ядра массовое число меньше массового числа исходного ядра на 3, а зарядовое число больше зарядового числа исходного ядра на 5. Определите минимальное число протонов и минимальное число α-частиц, участвующих в этой ядерной реакции.

Минимальное число протонов Минимальное число α-частиц
   

В результате бомбардировки ядра X некоторого атома нейтронами в результате ядерной реакции получается ядро Y другого атома. Установите характер изменения массового числа и зарядового числа атома в результате такой реакции.

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Массовое число ядра Зарядовое число ядра
   

Определите число протонов и нейтронов в атомном ядре неизвестного элемента X, участвующего в ядерной реакции в степени левая круглая скобка A правая круглая скобка _ZX плюс в степени левая круглая скобка 1 правая круглая скобка _1H arrow в кубе _2He плюс в степени левая круглая скобка 4 правая круглая скобка _2He. В ответе запишите число протонов и число нейтронов слитно без знаков препинания между ними.

Число протонов Число нейтронов

Ядро бора может захватить нейтрон, в результате чего происходит ядерная реакция в степени левая круглая скобка 1 правая круглая скобка _0n плюс в степени левая круглая скобка 10 правая круглая скобка _5B arrow в степени левая круглая скобка A правая круглая скобка _ZX плюс в степени левая круглая скобка 4 правая круглая скобка _2He с образованием ядра химического элемента в степени левая круглая скобка A правая круглая скобка _ZX. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

Заряд ядра Z Массовое число ядра A

Источник: ЕГЭ по физике. Вариант 114

Ядро бора может захватить нейтрон, в результате чего происходит ядерная реакция в степени левая круглая скобка 10 правая круглая скобка _5 $B$ плюс в степени 1 _0 n arrow в степени A _Z $X$ плюс в степени 4 _2 $He$ с образованием ядра химического элемента в степени A _Z$X$. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

Заряд ядра Z Массовое число ядра A

Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1

В результате ядерной реакции синтеза в квадрате _1$H плюс _1 в квадрате $H to$ _Z в степени A $X плюс _1 в степени 1 $p образуется ядро химического элемента в степени A _Z$X. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

Заряд ядра Z Массовое число ядра A

Источник: Демонстрационная версия ЕГЭ—2021 по физике

В результате реакции синтеза ядра дейтерия с ядром _Y в степени левая круглая скобка X правая круглая скобка Z образуется ядро бора и нейтрон в соответствии с реакцией:

_1 в квадрате H плюс _Y в степени левая круглая скобка X правая круглая скобка Z to _5 в степени левая круглая скобка 10 правая круглая скобка B плюс _0 в степени левая круглая скобка 1 правая круглая скобка n.

Каковы массовое число X и заряд Y (в единицах элементарного заряда) ядра, вступившего в реакцию с дейтерием?

X Y
   

Каково массовое число ядра Х в реакции _95 в степени левая круглая скобка 241 правая круглая скобка Am плюс в степени левая круглая скобка 4 правая круглая скобка _2Helongrightarrow X плюс 2 в степени 1 _0n?

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 5.

Каково массовое число ядра Х в реакции деления урана _0 в степени 1 n плюс в степени левая круглая скобка 235 правая круглая скобка _92U longrightarrow в степени левая круглая скобка 141 правая круглая скобка _56Ba плюс X плюс 3 в степени 1 _0n?

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 4.

Реакция деления ядра урана тепловыми нейтронами описывается уравнением:

x умножить на в степени 1 _0n плюс в степени левая круглая скобка 235 правая круглая скобка _92U arrow в степени левая круглая скобка 144 правая круглая скобка _56Ba плюс в степени левая круглая скобка 89 правая круглая скобка _36Kr плюс y умножить на в степени 1 _0n.

Определите минимальное число нейтронов x, вступающих в реакцию, и число нейтронов y, образующихся в качестве продуктов этой реакции. Ответ дайте в виде двух чисел, записав каждое в соответствующий столбец таблицы.

Минимальное число нейтронов x, вступающих в реакцию Число нейтронов y, образующихся в качестве продуктов реакции

Задания Д32 C3 № 3057

Вычислите массу радиоактивных продуктов деления ядер урана, накапливающихся в ядерном реакторе тепловой мощностью 3 умножить на 10 в степени левая круглая скобка 9 правая круглая скобка Вт за сутки, принимая выделение энергии при делении ядра урана 235 равным 200 МэВ.

В результате реакции в степени левая круглая скобка 27 правая круглая скобка _13$Al плюс в степени 1 _0$narrow в степени A _Z$X плюс в степени 4 _2$He образуется некоторое ядро X. Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

Заряд ядра Z Массовое число ядра A
   

Всего: 103    1–20 | 21–40 | 41–60 | 61–80 …

Источник

Версия для печати и копирования в MS Word

1

Если ядро радиоактивного изотопа _9 в степени левая круглая скобка 18 правая круглая скобка F испускает протон, то массовое число A нового элемента равно:

1) 82) 93) 164) 175) 19

2

Число нейтронов в ядре атоме лития в степени 7 _3Li равно:

1) 32) 43) 54) 75) 10

3

Число электронов в нейтральном атоме бора в степени левая круглая скобка 11 правая круглая скобка _5B равно:

1) 52) 63) 84) 115) 16

4

Число нейтронов в ядре атоме бериллия в степени левая круглая скобка 9 правая круглая скобка _4Be равно:

1) 132) 93) 64) 55) 4

5

Число электронов в нейтральном атоме натрия в степени левая круглая скобка 23 правая круглая скобка _11Na равно:

1) 342) 233) 174) 125) 11

6

Число нейтронов в ядре атоме алюминия в степени левая круглая скобка 27 правая круглая скобка _13Al равно:

1) 402) 273) 154) 145) 13

7

8

9

10

Ядро изотопа бария в степени левая круглая скобка 137 правая круглая скобка _56Ba состоит из:

1) 56 протонов и 81 нейтрона2) 137 протонов и 137 нейтронов3) 56 протонов и 137 нейтронов4) 137 протонов и 56 нейтронов5) 28 протонов и 28 нейтронов

11

12

13

Ядро изотопа брома в степени левая круглая скобка 78 правая круглая скобка _35Br состоит из:

1) 78 протонов и 78 нейтрона2) 35 протонов и 43 нейтронов3) 35 протонов и 35 нейтронов4) 43 протонов и 35 нейтронов5) 17 протонов и 18 нейтронов

14

Число нейтронов в ядре одного из изотопов кобальта N = 31, а удельная энергия связи ε = 8,07 МэВ/нуклон. Если энергия связи нуклонов в ядре этого изотопа Eсв = 468 МэВ, то его атомный номер Z равен:

1) 122) 163) 274) 325) 42

15

Ядро изотопа берклия в степени левая круглая скобка 249 правая круглая скобка _97Bk состоит из:

1) 249 протонов и 249 нейтрона2) 97 протонов и 97 нейтронов3) 249 протонов и 97 нейтронов4) 249 протонов и 152 нейтронов5) 97 протонов и 152 нейтронов

16

Ядро изотопа йода в степени левая круглая скобка 127 правая круглая скобка _53I состоит из:

1) 53 протонов и 53 нейтрона2) 74 протонов и 74 нейтронов3) 74 протонов и 53 нейтронов4) 53 протонов и 74 нейтронов5) 36 протонов и 36 нейтронов

17

Ядро изотопа ванадия в степени левая круглая скобка 51 правая круглая скобка _23Bk состоит из:

1) 51 протона и 51 нейтрона2) 23 протонов и 23 нейтронов3) 23 протонов и 28 нейтронов4) 28 протонов и 23 нейтронов5) 14 протонов и 14 нейтронов

18

Если удельная энергия связи нуклонов в ядре изотопа железа _26 в степени левая круглая скобка 56 правая круглая скобка Fe составляет ε = 8,79 МэВ/нуклон, то энергия связи Eсв этого ядра равна:

1) 136 МэВ2) 228 МэВ3) 264 МэВ4) 492 МэВ5) 652 МэВ

19

Атомный номер мышьяка Z = 33, а удельная энергия связи одного из его изотопов ε = 8,7 МэВ/нуклон. Если энергия связи нуклонов в ядре этого изотопа Eсв = 653 МэВ, то число нейтронов N в ядре равно:

1) 122) 163) 274) 325) 42

20

Атомный номер железа Z = 26, а удельная энергия связи одного из его изотопов ε = 8,79 МэВ/нуклон. Если энергия связи нуклонов в ядре этого изотопа Eсв = 510 МэВ, то число нейтронов N в ядре равно:

1) 122) 163) 274) 325) 42

21

Число нейтронов в ядре одного из изотопов кремния N = 16, а удельная энергия связи ε = 8,51 МэВ/нуклон. Если энергия связи нуклонов в ядре этого изотопа Eсв = 256 МэВ, то его атомный номер Z равен:

1) 112) 143) 274) 325) 42

22

Заряд q = 4,32·10−18 Кл имеет ядро атома:

1) $ в степени левая круглая скобка 55 правая круглая скобка _25 $Mn2) $ в степени левая круглая скобка 56 правая круглая скобка _26 $Fe3) $ в степени левая круглая скобка 59 правая круглая скобка _28 $Ni4) $ в степени левая круглая скобка 59 правая круглая скобка _27 $Co5) $ в степени левая круглая скобка 65 правая круглая скобка _30 $Zn

23

Заряд q = 4,8·10−18 Кл имеет ядро атома:

1) $ в степени левая круглая скобка 55 правая круглая скобка _25 $Mn2) $ в степени левая круглая скобка 56 правая круглая скобка _26 $Fe3) $ в степени левая круглая скобка 59 правая круглая скобка _28 $Ni4) $ в степени левая круглая скобка 59 правая круглая скобка _27 $Co5) $ в степени левая круглая скобка 65 правая круглая скобка _30 $Zn

24

Заряд q = 4,0·10−18 Кл имеет ядро атома:

1) $ в степени левая круглая скобка 55 правая круглая скобка _25 $Mn2) $ в степени левая круглая скобка 56 правая круглая скобка _26 $Fe3) $ в степени левая круглая скобка 59 правая круглая скобка _28 $Ni4) $ в степени левая круглая скобка 59 правая круглая скобка _27 $Co5) $ в степени левая круглая скобка 65 правая круглая скобка _30 $Zn

25

26

1) протон2) электрон3) альфа -частица4) позитрон5) нейтрон

27

Число электронов в электронейтральном атоме родия равно:

1) 452) 573) 584) 1025) 103

28

Число электронов в электронейтральном атоме палладия равно:

1) 1072) 1063) 604) 465) 23

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

Ядерные реакции

  • Темы кодификатора ЕГЭ: ядерные реакции, деление и синтез ядер.

  • Энергетический выход ядерной реакции

  • Деление ядер

  • Цепная ядерная реакция

  • Термоядерная реакция

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: ядерные реакции, деление и синтез ядер.

В предыдущем листке мы неоднократно говорили о расщеплении атомного ядра на составные части. Но как этого добиться в действительности? В результате каких физических процессов можно разбить ядро?

Наблюдения радиоактивного распада в изменяющихся внешних условиях — а именно, при различных давлениях и температурах, в электрических и магнитных полях — показали, что скорость радиоактивного распада от этих условий не зависит. Никаких превращений химических элементов друг в друга все эти факторы вызвать не способны. Очевидно, изменения энергии тут слишком малы, чтобы повлиять на атомное ядро — так ветер, обдувающий кирпичный дом, не в состоянии его разрушить.

Но разрушить дом можно артиллерийским снарядом. И Резерфорд в 1919 году решил воспользоваться наиболее мощными «снарядами», которые имелись тогда в распоряжении. Это были alpha-частицы, вылетающие с энергией около 5 МэВ при радиоактивном распаде урана. (Как вы помните, это те самые снаряды, которыми он восемь лет назад бомбардировал лист золотой фольги в своих знаменитых опытах, породивших планетарную модель атома.)

Правда, превращений золота в другие химические элементы в тех экспериментах не наблюдалось. Ядро золота ^{197}_{phantom{1} 79}rm{Au} само по себе весьма прочное, да и к тому же содержит довольно много протонов; они создают сильное кулоновское поле, отталкивающее alpha-частицу и не подпускающее её слишком близко к ядру. А ведь для разбивания ядра alpha-снаряд должен сблизиться с ядром настолько, чтобы включились ядерные силы! Что ж, раз большое количество протонов мешает — может, взять ядро полегче, где протонов мало?

Резерфорд подверг бомбардировке ядра азота ^{14}_{phantom{1} 7}rm{N} и в результате осуществил первую в истории физики ядерную реакцию:

^{14}_{vphantom{1}7}rm{N} + vphantom{1} ^{4}_{2}rm{He} rightarrow vphantom{1}^{17}_{phantom{1}8}rm{O} + vphantom{1}^{1}_{1}rm{H}. (1)

В правой части (1) мы видим продукты реакции — изотоп кислорода и протон.

Стало ясно, что для изучения ядерных реакций нужно располагать частицами-снарядами высоких энергий. Такую возможность дают ускорители элементарных частиц. Ускорители имеют два серьёзных преимущества перед естественными «радиоактивными пушками».

1. В ускорителях можно разгонять любые заряженные частицы. В особенности это касается протонов, которые при естественном распаде ядер не появляются. Протоны хороши тем, что несут минимальный заряд, а значит — испытывают наименьшее кулоновское отталкивание со стороны ядер-мишеней.

2. Ускорители позволяют достичь энергий, на несколько порядков превышающие энергию α-частиц при радиоактивном распаде. Например, в Большом адронном коллайдере протоны разгоняются до энергий в несколько ТэВ; это в миллион раз больше, чем 5 МэВ у alpha-частиц в реакции (1), осуществлённой Резерфордом.

Так, с помощью протонов, прошедших через ускоритель, в 1932 году удалось разбить ядро лития (получив при этом две alpha-частицы):

^{7}_{3}rm{Li} + vphantom{1}^{1}_{1}rm{H} rightarrow vphantom{1}^{4}_{2}rm{He} + vphantom{1}^{4}_{2}rm{He}. (2)

Ядерные реакции дали возможность искусственного превращения химических элементов.

Кроме того, в продуктах реакций стали обнаруживаться новые, не известные ранее частицы. Например, при облучении бериллия alpha-частицами в том же 1932 году был открыт нейтрон:

^{9}_{4}rm{Be} + vphantom{1}^{4}_{2}rm{He} rightarrow vphantom{1}^{12}_{phantom{1} 6}rm{O} + vphantom{1}^{1}_{0}rm{n}. (3)

Нейтроны замечательно подходят для раскалывания ядер: не имея электрического заряда, они беспрепятственно проникают внутрь ядра. (При этом ускорять нейтроны не надо — медленные нейтроны легче проникают в ядра. Нейтроны, оказывается, нужно даже замедлять, и делается это пропусканием нейтронов через обычную воду.) Так, при облучении азота нейтронами протекает следующая реакция:

^{14}_{phantom{1} 7}rm{N} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{11}_{phantom{1} 5}rm{B} + vphantom{1}^{4}_{2}rm{He}. (4)

к оглавлению ▴

Энергетический выход ядерной реакции

Обсуждая энергию связи, мы видели, что в результате ядерных процессов масса системы частиц не остаётся постоянной. Это, в свою очередь, приводит к тому, что кинетическая энергия продуктов ядерной реакции отличается от кинетической энергии исходных частиц.

Прежде всего напомним, что полная энергия E частицы массы m складывается из её энергии покоя mc^2 и кинетической энергии K:

E = mc^2 + K.

Пусть в результате столкновения частиц A и B происходит ядерная реакция, продуктами которой служат частицы X и Y:

A + B rightarrow X + Y. (5)

Полная энергия системы частиц сохраняется:

E_A + E_B = E_X + E_Y,

то есть

(m_Ac^2 + K_A) + (m_Bc^2 + K_B) = (m_Xc^2 + K_X) + (m_Y c^2 + K_Y ). (6)

Кинетическая энергия исходных частиц равна K_A + K_B. Кинетическая энергия продуктов реакции равна K_X + K_Y. Энергетический выход Q ядерной реакции — это разность кинетических энергий продуктов реакции и исходных частиц:

Q = (K_X + K_Y) - (K_A + K_B).

Из (6) легко получаем:

Q = (m_A + m_B - m_X - m_Y)c^2. (7)

Если Q > 0, то говорят, что реакция идёт с выделением энергии: кинетическая энергия продуктов реакции больше кинетической энергии исходных частиц. Из (7) мы видим, что в этом случае суммарная масса продуктов реакции меньше суммарной массы исходных частиц.

Если же Q < 0, то реакция идёт с поглощением энергии: кинетическая энергия продуктов реакции меньше кинетической энергии исходных частиц. Суммарная масса продуктов реакции в этом случае больше суммарной массы исходных частиц.

Таким образом, термины «выделение» и «поглощение» энергии не должны вызывать недоумение: они относятся только к кинетической энергии частиц. Полная энергия системы частиц, разумеется, в любой реакции остаётся неизменной.

Чтобы посчитать энергетический выход Q ядерной реакции (5), действуем по следующему алгоритму.

1. С помощью таблицы масс нейтральных атомов находим m_A, m_B, m_X и m_Y, выраженные в а. е. м. (для нахождения массы ядра не забываем вычесть из массы нейтрального атома массу электронов).

2. Вычисляем массу m_1 = m_A + m_B исходных частиц, массу m_2 = m_X + m_Y продуктов реакции и находим разность масс Delta m = m_1 - m_2.

3. Умножаем Delta m на 931,5 и получаем величину Q, выраженную в МэВ.

Мы сейчас подробно рассмотрим вычисление энергетического выхода Q на двух примерах бомбардировки ядер лития ^{7}_{3}rm{Li}: сначала — протонами, затем — alpha-частицами.

В первом случае имеем уже упоминавшуюся выше реакцию (2):

vphantom{1}^{7}_{3}rm{Li} + vphantom{1}^{1}_{1}rm{H} rightarrow vphantom{1}^{4}_{2}rm{He} + vphantom{1}^{4}_{2}rm{He}.

Масса атома лития ^{7}_{3}rm{Li} равна 7,01601 а. е. м. Масса электрона равна 0,000548 а. е. м. Вычитая из массы атома массу трёх его электронов, получаем массу ядра лития ^{7}_{3}rm{Li}:

7,01601 - 3 cdot 0,000548 = 7,01437 а. е. м.

Масса протона равна 1,00728 а. е. м., так что масса исходных частиц:

m_1 = 7,01437 + 1,00728 = 8,02165 а. е. м.

Переходим к продуктам реакции. Масса атома гелия равна 4,00260 а. е. м. Вычитаем массу электронов и находим массу ядра гелия vphantom{1}^{4}_{2}rm{He}:

4,00260 - 2 cdot 0,000548 = 4,00150 а. е. м.

Умножая на 2, получаем массу продуктов реакции:

m_2 = 2 cdot 4,00150 = 8,00300 а. е. м.

Масса, как видим, уменьшилась (m_2 < m_1); это означает, что наша реакция идёт с выделением энергии. Разность масс:

Delta m = m_1 - m_2 = 8,02165 - 8,00300 = 0,01865 а. е. м.

Выделившаяся энергия:

Q = 0,01865 cdot 931,5 = 17,4 МэВ.

Теперь рассмотрим второй пример. При бомбардировке ядер лития alpha-частицами происходит реакция:

vphantom{1}^{7}_{3}rm{Li} + vphantom{1}^{4}_{2}rm{He} rightarrow vphantom{1}^{10}_{phantom{1} 5}rm{B} + vphantom{1}^{1}_{0}rm{n}. (8)

Массы исходных ядер нам уже известны; остаётся сосчитать их суммарную массу:

m_1 = 7,01437 + 4,00150 = 11,01587 а. е. м.

Из таблицы берём массу атома бора vphantom{1}^{10}_{phantom{1} 5}rm{B} (она равна 10,01294 а. е. м.); вычитаем массу пяти электронов и получаем массу ядра атома бора:

10,01294 - 5 cdot 0,000548 = 10,01020 а. е. м.

Масса нейтрона равна 1,00867 а. е. м. Находим массу продуктов реакции:

m_2 = 10,01020 + 1,00867 = 11,01887 а. е. м.

На сей раз масса увеличилась (m_2 > m_1), то есть реакция идёт с поглощением энергии.

Разность масс равна:

Delta m = m_1 - m_2 = -0,0030 а. е. м.

Энергетический выход реакции:

Q = -0,0030 cdot 931,5 = -2,8 МэВ.

Таким образом, в реакции (8) поглощается энергия 2,8 МэВ. Это означает, что суммарная кинетическая энергия продуктов реакции (ядра бора и нейтрона) на 2,8 МэВ меньше, чем суммарная кинетическая энергия исходных частиц (ядра лития и alpha-частицы). Поэтому чтобы данная реакция в принципе осуществилась, энергия исходных частиц должна быть не меньше 2,8 МэВ.

к оглавлению ▴

Деление ядер

Бомбардируя ядра урана медленным нейтронами, немецкие физики Ган и Штрассман обнаружили появление элементов средней части периодической системы: бария, криптона, стронция, рубидия, цезия и т. д. Так было открыто деление ядер урана.

На рис. 1 мы видим процесс деления ядра (изображение с сайта oup.co.uk.). Захватывая нейтрон, ядро урана делится на два осколка, и при этом освобождаются два-три нейтрона.

Рис. 1. Деление ядра урана

Осколки являются ядрами радиоактивных изотопов элементов середины таблицы Менделеева. Обычно один из осколков больше другого. Например, при бомбардировке урана vphantom{1}^{235}_{phantom{1} 92}rm{U} могут встречаться такие комбинации осколков (как говорят, реакция идёт по следующим каналам).

• Барий и криптон: vphantom{1}^{235}_{phantom{1} 92}rm{U} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{144}_{phantom{1} 56}rm{Ba} + vphantom{1}^{89}_{36}rm{Kr} + 3 vphantom{1}^{1}_{0}rm{n}.

• Цезий и рубидий: vphantom{1}^{235}_{phantom{1} 92}rm{U} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{140}_{phantom{1} 55}rm{Cs} + 2vphantom{1}^{1}_{0}rm{n}.

• Ксенон и стронций: vphantom{1}^{235}_{phantom{1} 92}rm{U} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{140}_{phantom{1} 54}rm{Xe} + vphantom{1}^{94}_{38}rm{Sr} + 2vphantom{1}^{1}_{0}rm{n}.

В каждой из этих реакций выделяется очень большая энергия — порядка 200 МэВ. Сравните эту величину с найденным выше энергетическим выходом реакции (2), равным 17,4 МэВ! Откуда берётся такое количество энергии?

Начнём с того, что из-за большого числа протонов (92 штуки), упакованных в ядре урана, кулоновские силы отталкивания, распирающие ядро, очень велики. Ядерные силы, конечно, ещё в состоянии удерживать ядро от распада, но могучий кулоновский фактор готов сказать своё слово в любой момент. И такой момент настаёт, когда в ядре застревает нейтрон (рис. 2 — изображение с сайта investingreenenergy.com).

Рис. 2. Деформация, колебания и разрыв ядра

Застрявший нейтрон вызывает деформацию ядра. Начнутся колебания формы ядра, которые могут стать столь интенсивными, что ядро вытянется в «гантельку». Короткодействующие ядерные силы, скрепляющие небольшое число соседних нуклонов перешейка, не справятся с силами электрического отталкивания половинок гантельки, и в результате ядро разорвётся.

Осколки разлетятся с огромной скоростью — около 1/30 скорости света. Они и уносят большую часть высвобождающейся энергии (около 170 МэВ из 200).

Деление тяжёлых ядер можно истолковать с точки зрения уже известного нам графика зависимости удельной энергии связи ядра от его массового числа (рис. 3).

Рис. 3. Деление тяжёлых ядер энергетически выгодно

Цветом выделена область 50 leqslant A leqslant 90, в которой удельная энергия связи достигает наибольшего значения 8,7 МэВ/нуклон. Это область наиболее устойчивых ядер. Справа от этой области удельная энергия связи плавно уменьшается до 7,6 МэВ/нуклон у ядра урана.

Процесс превращения менее устойчивых ядер в более устойчивые является энергетически выгодным и сопровождается выделением энергии. При делении ядра урана, как видим, удельная энергия связи повышается примерно на 1 МэВ/нуклон; эта энергия как раз и выделяется в процессе деления. Умножив это на число нуклонов в ядре урана, получим приблизительно те самые 200 МэВ энергетического выхода, о которых говорилось выше.

к оглавлению ▴

Цепная ядерная реакция

Появление двух-трёх нейтронов в процессе деления ядра урана — важнейший факт. Эти нейтроны «первого поколения» могут попасть в новые ядра и вызвать их деление; в результате деления новых ядер возникнут нейтроны «второго поколения», которые попадут в следующие ядра и вызовут их деление; возникнут нейтроны «третьего поколения», которые приведут к делению очередных ядер и т. д. Так идёт цепная ядерная реакция, в ходе которой высвобождается колоссальное количество энергии.

Для протекания цепной ядерной реакции необходимо, чтобы число N_i высвободившихся нейтронов в очередном поколении было не меньше числа N_{i-1} нейтронов в предыдущем поколении. Величина

k = frac{displaystyle N_i}{displaystyle N_{i-1} vphantom{1^a}}

называеся коэффициентом размножения нейтронов. Таким образом, цепная реакция идёт при условии k > 1. Если k < 1, то цепная реакция не возникает.

В случае k > 1 происходит лавинообразное нарастание числа освобождающихся нейтронов, и цепная реакция становится неуправляемой. Так происходит взрыв атомной бомбы.

В ядерных реакторах происходит управляемая цепная реакция деления с коэффициентом размножения k = 1. Стационарное течение управляемой цепной реакции обеспечивается введением в активную зону реактора (то есть в ту область, где протекает реакция) специальных управляющих стержней, поглощающих нейтроны. При полностью введённых стержнях поглощение ими нейтронов настолько велико, что k < 1 и реакция не идёт. В процессе запуска реактора стержни постепенно выводят из активной зоны, пока выделяемая мощность не достигнет требуемого уровня. Этот уровень тщательно контролируется, и при его превышении включаются устройства, вводящие управляющие стержни назад в активную зону.

к оглавлению ▴

Термоядерная реакция

Наряду с реакцией деления тяжёлых ядер энергетически возможным оказывается и обратный в некотором смысле процесс — синтез лёгких ядер, то есть слияние ядер лёгких элементов (расположенных в начале периодической таблицы) с образованием более тяжёлого ядра.

Чтобы началось слияние ядер, их нужно сблизить вплотную — чтобы вступили в действие ядерные силы. Для такого сближения нужно преодолеть кулоновское отталкивание ядер, резко возрастающее с уменьшением расстояния между ними. Это возможно лишь при очень большой кинетической энергии ядер, а значит — при очень высокой температуре (в десятки и сотни миллионов градусов). Поэтому реакция ядерного синтеза называется термоядерной реакцией.

В качестве примера термоядерной реакции приведём реакцию слияния ядер дейтерия и трития (тяжёлого и сверхтяжёлого изотопов водорода), в результате которой образуется ядро гелия и нейтрон:

vphantom{1}^{2}_{1}rm{H} + vphantom{1}^{3}_{1}rm{H} rightarrow vphantom{1}^{4}_{2}rm{He} + vphantom{1}^{1}_{0}rm{n}. (9)

Эта реакция идёт с выделением энергии, равной 17,6 МэВ (попробуйте сами провести расчёты и получить данную величину). Это очень много, если учесть, что в реакции участвуют всего 5 нуклонов! В самом деле, в расчёте на один нуклон в реакции (9) выделяется энергия примерно 3,5 МэВ, в то время как при делении ядра урана выделяется «всего» 1 МэВ на нуклон.

Таким образом, термоядерные реакции служат источником ещё большего количества энергии, чем реакции деления ядер. С физической точки зрения это понятно: энергия реакции 6 ядерного деления есть в основном кинетическая энергия осколков, разогнанных электрическими силами отталкивания, а при ядерном синтезе энергия высвобождается в результате разгона нуклонов навстречу друг другу под действием куда более мощных ядерных сил притяжения.

Проще говоря, при делении ядер высвобождается энергия электрического взаимодействия, а при синтезе ядер — энергия сильного (ядерного) взаимодействия.

В недрах звёзд достигаются температуры, подходящие для синтеза ядер. Свет Солнца и далёких звёзд несёт энергию, выделяющуяся в термоядерных реакциях — при слиянии ядер водорода в ядра гелия и последующем слиянии ядер гелия в ядра более тяжёлых элементов, расположенных в средней части периодической системы. Направление термоядерного синтеза показано на рис. 4; синтез лёгких ядер энергетически выгоден, так как направлен в сторону увеличения удельной энергии связи ядра.

Рис. 4. Синтез лёгких ядер энергетически выгоден

Неуправляемая термоядерная реакция осуществляется при взрыве водородной бомбы. Сначала взрывается встроенная атомная бомба — это нужно для создания высокой температуры на первой ступени термоядерного взрыва. При достижении необходимой температуры в термоядерном горючем бомбы начинаются реакции синтеза, и происходит взрыв собственно водородной бомбы.

Осуществление управляемой термоядерной реакции остаётся пока нерешённой проблемой, над которой физики работают уже более полувека. Если удастся добиться управляемого течения термоядерного синтеза, то человечество получит в своё распоряжение фактически неограниченный источник энергии. Это чрезвычайно важная задача, стоящая перед нынешним и будущими поколениями — в свете угрожающей перспективы истощения нефтегазовых ресурсов нашей планеты.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Ядерные реакции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Атомная физика на ОГЭ. Вся теория и разбор заданий от преподавателя MAXIMUM

06.02.2021
17435

Атомная физика — один из труднейших разделов экзамена, а задания по этой теме кочуют из варианта в вариант каждый год. Не пугаемся! Для решения заданий ОГЭ на радиоактивность, распады и ядерные реакции нужно знать лишь самые базовые понятия. Из этой статьи вы узнаете все необходимое — атомная физика на ОГЭ обязательно вам покорится!

атомная физика огэ

Чтобы перейти к практике и научиться решать хитрые задания, сначала нужно вспомнить теорию, связанную с ними.

Таблица основных частиц, которые встречаются в каждом варианте ОГЭ

Вспомним, что химические элементы обозначаются в виде ,  где

  • X – название химического элемента
  • А – массовое число, равное сумме протонов и нейтронов
  • Z – зарядовое число, равное числу протонов в ядре

Давайте раз и навсегда узнаем, что скрывается за числами рядом с названием каждого элемента. Рассмотрим пример углерода:

  • 6 — это порядковый номер и зарядовое число Z. Таким образом, в ядре атома углерода 6 протонов. Z=6.
  • 12,011 — это атомная масса. Мы будем его округлять до 12 и называть массовым числом A, то есть суммой протонов и нейтронов. A=12.
  • Получается, в ядре атома углерода 6 протонов и 6 нейтронов.

Какие ядерные распады нужно знать?

На ОГЭ часто встречаются три типа распадов: альфа, бета и гамма.

Альфа-распад

α-распад — испускание ядром альфа-частицы. Что это такое? Все просто — так называют ядро атома гелия, то есть частицу из двух протонов и двух нейтронов.

  • У нас был элемент X с массовым числом A и с зарядовым числом Z
  • Атом испускает альфа-частицу с массовым числом=4 и зарядовым числом=2
  • Мы получаем новый элемент с массовым числом=A-4 и зарядовым числом=Z-2

В α-распаде заряд уменьшается на 2, а масса уменьшается на 4.

Самостоятельно подготовиться к ОГЭ непросто. На то, чтобы разобраться со всеми темами, понадобится много времени. Но и это не решит проблему! Например, если вы запомнили какое-то решение из интернета, а оно оказалось неправильным, можно на пустом месте потерять баллы. Если хотите научиться решать все задания ОГЭ по физике, обратите внимание на онлайн-курсы MAXIMUM! Наши специалисты уже проанализировали сотни вариантов ОГЭ и подготовили для вас вас максимально полезные занятия.

Приходите к нам на пробный урок! Вы узнаете всю структуру ОГЭ-2021, разберете сложные задания из первой части, получите полезные рекомендации и узнаете, как устроена подготовка к экзаменам в MAXIMUM. Все это абсолютно бесплатно!

Задача №1

Используя фрагмент Периодической системы элементов Д.И. Менделеева, представленный на рисунке, определите, какое ядро образуется в результате α-распада ядра нептуния-237. 

Разбор

  • Как мы говорили чуть выше, порядковый номер элемента — это, по совместительству, зарядовое число. То есть, количество протонов. Получается, в Нептунии 93 протона.
  • У α-частицы количество протонов = 2.
  • Посчитаем, чему равно зарядовое число нашего нового элемента: зарядовое число = 93-2 = 91. Взглянув на табличку, находим элемент под номером 91 — Протактиний.

Ответ: 1) Ядро протактиния

Изотопы

Теперь давай обратим внимание на массовые числа нептуния и протактиния. Отличаются ли они на массовое число альфа-частицы — на 4?

237-231=6

Время бить тревогу! Неужели мы что-то напутали и решили задачу неверно? Но нет, оказывается, мы все сделали правильно — ведь у протактиния более 15 изотопов.

Изотопы — это разновидности атомов (и ядер) какого-либо химического элемента, которые имеют одинаковое зарядовое число, но разные массовые числа. 

Например, изотопы азота:

и

Задача №2

Ядро тория   превратилось в ядро радия . Какую частицу испустило при этом ядро тория?

  1. нейтрон
  2. протон
  3. альфа-частицу
  4. бета-частицу

Разбор

  • Сверху находится массовое число — масса частицы. Вычтем из массы Тория массу Радия: 230-226=4. Получили массу неизвестной частицы.
  • Снизу находится зарядовое число — это заряд не­из­вест­ной частицы. Вычтем из заряда Тория заряд Радия: 90-88=2. Получили заряд неизвестной частицы.
  • Итого: массовое число = 4. Зарядовое число = 2
  • Взглянем на табличку самых распространенных частиц. 

Вуаля! Наша незнакомка — это альфа-частица — частица с двумя протонами и двумя нейтронами.

Ответ: 3) альфа-частица

Бета-распад

β-распад — испускание ядром бета-частицы. Бета-частицей называют электрон. Посмотрим в списке основных частиц наверху, чему равны массовое и зарядовое число бета-частицы (электрона).

  • У нас был элемент X с массовым числом A и с зарядовым числом Z
  • Атом испускает бета-частицу с массовым числом=0 и зарядовым числом=-1
  • Мы получаем новый элемент с прежним массовым числом=A и зарядовым числом=Z+1

В β-распаде заряд увеличивается на 1, а масса не меняется.

Задача №3

Изо­топ крип­то­на в ре­зуль­та­те серии рас­па­дов пре­вра­тил­ся изо­топ мо­либ­де­на . Сколь­ко β-частиц было ис­пу­ще­но в этой серии рас­па­дов?

Разбор

  • Обозначим количество испущенных β-частиц за N
  • Зарядовое число криптона до серии β-распадов равнялось 36
  • Зарядовое число молибдена после серии β-распадов 42
  • Тогда 42-36=6 β распадов

Ответ: было испущено 6 β распадов

Задача №4

Радиоактивный атом превратился в атом в результате цепочки альфа- и бета-распадов. Чему было равно число альфа- и бета-распадов?

Разбор

Эта задача требует максимальной концентрации — многие школьники ее решают неверно. Давайте разберем правильный подход к этой задаче.

  • Для начала рассмотрим альфа-распады 

  • Добьемся, чтобы массовое число изменилось с 232 до 208. Для этого производим альфа-распады, вычитая 4 из массового числа и 2 из зарядового числа.

  • Получили элемент с массовым числом=208 и зарядовым числом=78. Для этого мы произвели 6 альфа распадов.
  • Теперь перейдем к бета-распадам. Бета-распады влияют только на зарядовое число.

  • Добьемся того, чтобы зарядовое число изменилось с 78 до 82.

  • Получили элемент с массовым числом = 208 и зарядовым числом = 82. Для этого мы произвели 4 бета распада.

Ответ: 6 альфа распадов и 4 бета распада.

Гамма-распад

?-частицы — это излучение, а ?-распад — испускание ядром гамма-излучения. Пожалуй, это самый простой распад, потому что он ничего не меняет.

Элемент X до распада и элемент Y  после распада — это одно и то же.

Внимание! На ОГЭ ученики часто попадают в ловушки экзамена, считая, что ? излучение меняет элемент. Но это совсем не так! Какой элемент был до гамма-распада, такой и останется.

При ?-распаде заряд и масса не меняются.

Ядерные реакции

Атомная физика на ОГЭ включает в себя не только распады, но и ядерные реакции. Ядерные реакции происходят при столкновении ядер или элементарных частиц с другими ядрами. В результате изменяется массовое и зарядовое число элементов, появляются новые частицы.

Во всех ядерных реакциях работает очень простой лайфхак: при протекании ядерной реакции сохраняется суммарное массовое число  и суммарный заряд.

Сумма масс слева равна сумме масс справа: A1+A2=A3+A4.

Сумма зарядов слева равна сумме зарядов справа: Z1+Z2=Z3+Z4.

Сразу же закрепим эти правила на практике.

Задача 5

В результате столкновения ядра урана с частицей X произошло деление урана, описываемое реакцией:

Определите зарядовое и массовое числа частицы X, с которой столкнулось ядро урана.

Разбор

  • Сначала разберемся с массовым числом. Используем лайфхак: то, что слева, равно тому, что справа.
  • Также заметим, что у нас 3 нейтрона. Получается, нам нужно умножить массовое число нейтрона на 3.
  • С гамма-частицей разобраться легко — как мы показали ранее, она ни на что не влияет.

A+235 = 133+139+3*1

Отсюда A=133+139+3-235=40

  • Теперь настал черед зарядового числа.

Z+92 = 36+56+3*0

Отсюда Z=36+56+0-92=0

Ответ: получили элемент X c массовым числом 40 и зарядовым числом 0.

Атомная физика на ОГЭ: что нужно запомнить?

  • В α-распаде заряд уменьшается на 2, а масса уменьшается на 4.
  • α-частица — это ядро атома гелия. α-частица состоит из двух протонов и двух нейтронов.
  • В β-распаде заряд увеличивается на 1, а масса не меняется.
  • β-частица — это электрон.
  • В ?-распаде заряд и масса не меняются.
  • ?-частица — это порция электромагнитного излучения.
  • Изотопы — это разновидности атомов (и ядер) какого либо химического элемента, которые имеют одинаковое зарядовое число, но разные массовые числа. 
  • В ядерных реакциях сохраняется суммарное массовое число и суммарный заряд.

Теперь вы знаете, как решать задания на ядерные распады и реакции! Надеюсь, атомная физика на ОГЭ стала для вас намного понятнее. Если хотите разобраться в остальных темах по физике и не только, обратите внимание на наши онлайн-курсы. Уже более 150 тысяч выпускников подготовились с нами к ОГЭ и ЕГЭ. Кстати, у меня на курсах MAXIMUM тоже можно поучиться! Приходите на бесплатный пробный урок, чтобы познакомиться с нашей образовательной системой и узнать массу полезного про ОГЭ.

Лайфхаки экзамена

К рубрике

Источник

32. Электродинамика. Квантовая физика (расчетная задача)


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Ядерные реакции. Энергия связи

Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при синтезе 1 кг гелия из изотопов водорода — дейтерия и трития: [^2_1H+^3_1Hrightarrow ^4_2He+^1_0n]
Ответ дайте разделив его на (10^{14})

Выход (Delta E) ядерной реакции синтеза ядер гелия из ядер дейтерия и трития вычислим по формуле деффекта массы: [Delta E=Delta mc^2] [Delta m=m_{_1^2H}+m_{_1^3H}-m_{_1^4H}-m_n]
Найдем деффект массы (Delta m) ядерной реакции: [Delta m=2,01355+3,01550-4,00151-1,00866=0,01888text{ a.e. м}]
или: [Delta m=(3,3437+5,0075-6,6449-1,6750)cdot 10^{-27}text{ кг}=3,13cdot 10^{-29}text{ кг}]
Используя переводной коэффициент получим энергетический выход ядерной реакции: [Delta E=0,01888 cdot 931,5text{ МэВ}approx=17,6text{ МэВ}]
Или Умножим массу на вкадрат скорости света, получим энергетический выход ядерной реакции: [Delta E=3,13cdot 10^{-29}cdot 9cdot 10^{16}text{ Дж}=2,817cdot 10^{-12}text{ Дж}]
Найдем число (N) ядер в 1 кг гелия: [N=dfrac{m}{m_{He}}=dfrac{1text{ кг}}{6,6449cdot 10^{-27}text{ кг}}=approx 1,5cdot 10^{26}]
Количество энергии освободившееся при синтезе: [E=Delta Ecdot Napprox17,6cdot 1,6cdot 10^{-13}cdot 1,5 cdot 20^{26}approx 4,2cdot 10^{14}text{ Дж}]
или [E=Delta Ecdot Napprox 2,817cdot 10^{-12}cdot 1,5cdot 20^{26}approx 4,2cdot 10^{14}text{ Дж}]

Ответ: 4,2

При взрыве атомной бомбы освобождается энергия (8,3cdot10^{16}) Дж. Эта энергия получается в основном за счет деления ядер урана 238. При делении одного ядра урана 238 освобождается 200 МэВ, масса ядра равна примерно 238 а. е. м. Вычислите массу ядер урана, испытавших деление при взрыве, и суммарный дефект массы.

Масса (m) ядер урана, испытавших деление при взрыве: [m=Nm_0]
Число (N) ядер равно: [N=dfrac{E}{Delta E}]
Тогда значение массы: [m=Nm_0=dfrac{Ecdot M_0}{Delta E}=] [=dfrac{8,3cdot10^{16} cdot 238 cdot 1,66 cdot 10^{-27}}{200cdot 1,6 cdot 10^{-13} }approx 10^3text{ кг}]
Найдем деффект массы (Delta m) ядерной реакции: [Delta E=Delta mc^2]
выразим (Delta m): [Delta m=dfrac{E}{c^2}] [Delta m=dfrac{8,3cdot 10^{16}}{9cdot 10^{16}}approx 0,92text{ кг}]

Ответ: 0,92

Находящееся в однородном магнитном поле с индукцией (B = 5) Тл ядро покоящегося нейтрального атома испытывает (alpha)-распад, в результате которого рождается ион нового элемента массой (M = 50) а.е.м. Его траектория лежит в плоскости, перпендикулярной направлению магнитного поля, и представляет собой дугу окружности радиуса (R = 5) см. Найти выделившуюся при (alpha)-распаде энергию (Delta E), считая, что она целиком переходит в кинетическую энергию продуктов реакции. Ответ дайте, разделив его на (10^(-13)).

Поскольку исходный атом неподвижен и выделившаяся при реакции энергия (Delta E) целиком переходит в кинетическую энергию продуктов реакции, то из законов сохранения импульса и энергии следуют равенства [mupsilon=MV,] [dfrac{mupsilon^2}{2}+dfrac{MV^2}{2}=Delta E,]
Где (upsilon) и (V)–скорости (alpha)–частицы и иона после распада.
Исключая из этих равенств (upsilon), получаем, что [Delta E=dfrac{M(M+m)}{2m}cdot V^2.]
Из закона сохранения заряда следует, что модуль заряда иона равен заряду (alpha)–частицы. По второму закону Ньютона уранвение движения иона с магнитном поле под действием силы Лоренца имеет вид [dfrac{MV^2}{R}=qVB]
Подставляя (V=dfrac{qBR}{M}) в найденное выражение для (Delta E), получаем [Delta E=dfrac{(qBR)^2(M+m)}{2Mm}approx 5,2cdot 10^{-13}text{ Дж}]

Ответ: 5,2

При радиоактивном распаде ядра (^{226}_{88}Ra) вылетает (alpha)-частица. Известно, что в образце радия массой 1 мг каждую секунду распадаются (3,7 cdot 10^7) ядер. (alpha)-частицы вылетающие из этого образца за 2 часа, имеют суммарную энергию 205 мДж. Какую энергию имеет каждая (alpha)-частица? Ответ приведите в кэВ с точностью (pm100)кэВ.

Пусть (E_0) – энергия одной (alpha)-частицы, (N) – число распадов ядер в секунду, а, значит, и число (alpha)-частиц, вылетающих из образца за одну секунду. Суммарная энергия вылетевших (alpha)-частиц: [E=E_0 N t] [E_0=frac{E}{Nt}=frac{205cdot10^{-3}}{3,7 cdot 10^7cdot7200}=0,77 cdot10^{-12}text{ Дж}=4800 text{ кэВ}]

Ответ: 4800

Пренебрегая кинетическими энергиями и суммарным импульсом бериллия и гелия в ядерной реакции [^9_4Be+^4_2Herightarrow ^{12}_6C+_0^1n] определить кинетические энергии (E_C) и (E_n) углерода и нейтрона, считая, что вся выделяющаяся в реакции энергия (Delta E) практически равна (E_C +E_n.)
В ответ запишите разность между полученными значениями, разделив, на (10^{-14})

В соответсвии с закономи сохранении энергии сумма масс до реакции равна сумме масс после реакции плюс дефект массы (Delta m), связанный с выделяющейся или поглощающейся энергией (Delta E) соотношением [Delta E=|Delta m|cdot c^2]
Используя данные таблицы, получим: [Delta m=m_{Be}+m_{alpha}-m_{C}-m_{n}=9,01219+4,00260-12,00000-1,00867=0,00612text{ а.е. м.},]
где (m_{alpha})– масса образовавшейся (alpha)–частицы (ядра (_2^4He)). Поскольку (delta m)>0, в реакции происходит выделение энергии [Delta E=(m_{Be}+m_{alpha}-m_{C}-m_{n})cdot c^2.]
По условию суммарный импульс бериллия и гелия равен нулю, поэтому суммарный импульс углерода и нейтрона [p_C+p_n=0.]
Суммарная кинетическая энергия бериллия и гелия по условию также равна нулю, следовательно, вся выделяющаяся в реакции энергия [Delta E=E_C+E_n,] где [E_C=p^2_C/2m_Ctext{ и } E_n=p^2_n/2m_n]
–кинетическая энергия углерода и нейтрона
Отсюда получаем : [E_n=dfrac{m_n(m_{Be}+m_{alpha}-m_{C}-m_{n})cdot c^2}{m_C+m_n}=dfrac{1,00867cdot 0,00612}{12,00000+1,00867}cdot 1,66cdot 10^{-27}cdot(3cdot10^8)^2approx7cdot 10^{-14}text{ Дж}] [E_C=dfrac{m_c(m_{Be}+m_{alpha}-m_{C}-m_{n})cdot c^2}{m_C+m_n}=dfrac{12cdot 0,00612}{12,00000+1,00867}cdot 1,66cdot 10^{-27}cdot(3cdot10^8)^2approx 8,4cdot 10^{-13} text{ Дж}] [84-7=77]

Ответ: 77

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Решу егэ физика электростатика
  • Решу егэ физика электромагнитная индукция
  • Решу егэ физика электрические схемы
  • Решу егэ физика цикл карно
  • Решу егэ физика фотоэффект задачи

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии