Решу егэ физика оптика задачи с решениями - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На экране наблюдается спектр с помощью дифракционной решетки, имеющей 500 штрихов на миллиметр. Расстояние от решетки до экрана Спектральная линия в спектре первого порядка находится на расстоянии от центра экрана. Определите длину волны наблюдаемой спектральной линии.

Масляная пленка на воде при наблюдении вертикально к поверхности кажется оранжевой. Каково минимальное возможное значение толщины пленки? Показатель преломления воды 1,33, масла  — 1,47. Длина световой волны Учтите, что отражение света от оптически более плотной среды происходит с потерей полуволны, а от оптически менее плотной среды без потери полуволны.

Для наблюдения явления интерференции света используется точечный источник света и небольшой экран с двумя малыми отверстиями у глаза наблюдателя. Оцените максимальное расстояние d между малыми отверстиями в экране, при котором может наблюдаться явление интерференции света. Разрешающая способность глаза равна 1', длина световой волны

Человек читает книгу, держа ее на расстоянии 50 см от глаз. Если это для него расстояние наилучшего видения, то какой оптической силы очки позволят ему читать книгу на расстоянии 25 см?

Бассейн глубиной 4 м заполнен водой, относительный показатель преломления на границе воздух-вода 1,33. Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?

Пройти тестирование по этим заданиям

Источник

Всего: 22 1–20 | 21–22

Добавить в вариант

Луч света падает на горизонтально расположенное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если, не меняя положения источника света, повернуть зеркало на 10°, как показано на рисунке?

Ответ дайте в градусах.

Источник: ЕГЭ по физике 2022. Досрочная волна

Луч света падает на плоское зеркало. Угол между падающим и отражённым лучами равен Чему равен угол между отражённым лучом и зеркалом?

Угол между зеркалом и отражённым от него лучом равен 20° (см. рис.). Определите угол падения.

Источник: ЕГЭ по физике 2022. Досрочная волна. Вариант 2

Угол падения света на горизонтальное плоское зеркало равен 30°. Каким будет угол образованный падающим и отражённым лучами, если, не меняя положение источника света, повернуть зеркало на 10° так, как показано на рисунке? Ответ дайте в градусах.

Источник: ЕГЭ по физике 02.04.2016. Досрочная волна, ЕГЭ по физике 2022. Досрочная волна. Вариант 2

Луч света падает на плоское зеркало. Угол между падающим лучом и зеркалом равен 50°. Каков угол γ между падающим и отражённым лучами (см. рис.)?

Источник: ЕГЭ по физике. Вариант 114

На столе стоит сосуд с зеркальным дном и матовыми стенками. На дно пустого сосуда падает луч света На стенке CD сосуда при этом можно наблюдать «зайчик»  — блик отражённого луча. В сосуд наливают некоторое количество воды. Как при этом изменяются следующие физические величины: угол падения луча на дно, высота точки нахождения «зайчика», расстояние от точки отражения луча от дна сосуда до стенки CD? Отражением луча от поверхности жидкости пренебречь.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

A)  Угол падения луча на дно

Б)  Высота точки нахождения «зайчика»

B)  Расстояние от точки отражения луча от дна до стенки CD

ИХ ИЗМЕНЕНИЕ

1)  Увеличится

2)  Уменьшится

3)  Не изменится

Луч света падает на плоское зеркало. Угол между падающим и отраженным лучами равен 30°. Чему равен угол между отраженным лучом и зеркалом? (Ответ дать в градусах.)

Луч света падает на плоское зеркало. Угол отражения равен 12°. Сколько градусов угол между падающим лучом и зеркалом?

Два плоских зеркала З1 и З2 составляют друг с другом двугранный угол ° (см. рис.). Линия стыка зеркал перпендикулярна плоскости рисунка. Луч света падает на зеркало З1, распространяясь в плоскости рисунка параллельно поверхности зеркала З2. Определите угол падения этого луча на поверхность зеркала З2 после отражения от зеркала З1.

Два плоских зеркала образуют прямой двугранный угол, перпендикулярно биссектрисе которого расположена небольшая собирающая линза Л, а её фокус F находится в вершине угла (см.

рисунок). В плоскости линзы рядом с ней находится небольшой предмет П. Постройте изображение предмета, которое получится в результате двух отражений от зеркал и последующего преломления света линзой. На каком расстоянии от предмета будет находиться его изображение?

Луч света 1 падает на поверхность горизонтального зеркала А под углом = 20° (см. рис. слева). Отражаясь от зеркала А, луч света попадает на следующие два зеркала  — В и С. Сначала зеркала В и С расположены горизонтально. Затем их поворачивают: зеркало В на угол против часовой стрелки, а зеркало С устанавливают вертикально (как показано на рисунке справа).

Определите характер изменения угла отражения падающего луча 1 при отражении его от зеркал В и С.

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Угол отражения от зеркала В	Угол отражения от зеркала C

Оптическая система состоит из двух зеркал З₁ и З₂, способных вращаться вокруг горизонтальных осей, которые проходят через точки O₁ и O₂ соответственно. Изначально зеркала установлены горизонтально. Из точки A , лежащей в плоскости зеркала З₂, на зеркало З₁ направлен луч света, идущий в плоскости рисунка. Угол падения луча света на зеркало З₁ равен 30° (см. рис. 1).

Рис. 1

Рис. 2

Затем зеркало З₁ поворачивают на угол 10° по часовой стрелке (рис. 2). При этом отражённый от зеркала З₁ луч попадает в точку O₂ зеркала З₂. На какой угол требуется повернуть зеркало З₂, чтобы отражённый от него луч, минуя отражение от зеркала З₁, сразу попал обратно в точку A ? Ответ приведите в градусах.

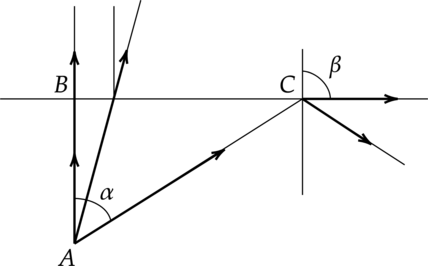
На рисунке изображён ход светового луча 1, падающего из среды с показателем преломления n₁ на плоскую поверхность среды с показателем преломления n₂. На рисунке также показаны отражённый и преломлённый лучи.

Из приведённого ниже списка выберите все верные утверждения. Запишите цифры, под которыми они указаны.

1)  Угол падения луча на границу раздела сред равен 60 °.

2)  Угол отражения луча равен 150 °.

3)  Угол между отражённым и преломлённым лучами равен 90 °.

4)  Показатель преломления среды 1 меньше показателя преломления среды 2.

5)  Скорость распространения света в среде 1 меньше скорости распространения света в среде 2.

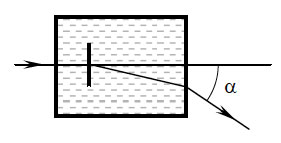
Верхняя грань AB прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина Луч света падает из воздуха на клин перпендикулярно грани АС, преломляется и выходит в воздух через другую грань под углом к её нормали. Определите показатель преломления материала клина.

Сделайте рисунок, поясняющий ход луча в клине.

Источник: ЕГЭ по физике 2022. Досрочная волна

На поверхность плоского зеркала, перпендикулярного оси OY, падает луч света под углом α. Отражаясь от зеркала, луч попадает на поверхность плоско-параллельной стеклянной пластины толщиной d (см. рис.).

Не изменяя угол падения луча на поверхность зеркала, пластину заменяют на другую пластину, показатель преломления которой больше, а толщина прежняя. Как в результате этого изменятся угол преломления луча при входе в пластину и расстояние вдоль оси OY между точками входа луча в пластину и выхода из неё?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Угол преломления луча при входе в пластину	Расстояние вдоль оси OY между точками входа луча в пластину и выхода из неё

Из приведённого ниже списка выберите все верные утверждения. Запишите цифры, под которыми они указаны.

1)  Угол падения луча на границу раздела сред равен 60°.

2)  Угол отражения луча равен 120°.

3)  Угол преломления луча равен 30°.

4)  Показатель преломления среды 1 больше показателя преломления среды 2.

5)  Скорость распространения света в среде 1 больше скорости распространения света в среде 2.

На рисунке слева изображены два плоских зеркала (З1 и З2) и луч, горизонтально падающий на зеркало 1. Зеркало 2 поворачивают относительно горизонтальной оси, проходящей через точку О, на угол 15º (рисунок справа). Под каким углом к горизонту будет распространяться луч, отражённый от зеркала 2?

Угол падения луча на поверхность равен 40º. Найдите угол между падающим и отраженным лучом.

Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1

Всего: 22 1–20 | 21–22

Источник

Задачи из ДЕМОВАРИАНТОВ (с решениями)

1. В дно водоема глубиной 3 м вертикально
вбита свая, скрытая под водой. Высота сваи 2 м. Свая отбрасывает
на дне водоема тень длиной 0,75 м. Определите угол падения
солнечных лучей на поверхность воды. Показатель преломления
воды n = 4/3.
Образец возможного решения

2. На экране с помощью тонкой линзы получено
изображение предмета с пятикратным увеличением. Экран передвинули
на 30 см вдоль главной оптической оси линзы. Затем при неизменном
положении линзы передвинули предмет, чтобы изображение снова
стало резким. В этом случае получилось изображение с трехкратным
увеличением. На каком расстоянии от линзы находилось изображение
предмета в первом случае?
Образец возможного решения

3. На поверхности
воды плавает надувной плот шириной 4 м и длиной 6 м. Небо затянуто
сплошным облачным покровом, полностью рассеивающим солнечный
свет. Определите глубину тени под плотом. Глубиной погружения
плота и рассеиванием света водой пренебречь. Показатель преломления
воды относительно воздуха принять равным 4/3.
Образец возможного решения

4. Объектив проекционного аппарата имеет
оптическую силу 5,4 дптр. Экран расположен на расстоянии 4
м от объектива. Определите размеры экрана, на котором должно
уместиться изображение диапозитива размером 6×9 см.
Образец возможного решения

5. Небольшой
груз, подвешенный на нити длиной 2,5 м, совершает гармонические
колебания, при которых его максимальная скорость достигает 0,2
м/с. При помощи собирающей линзы с фокусным расстоянием 0,2
м изображение колеблющегося груза проецируется на экран, расположенный
на расстоянии 0,5 м от линзы. Главная оптическая ось линзы перпендикулярна
плоскости колебаний маятника и плоскости экрана. Определите
максимальное смещение изображения груза на экране от положения
равновесия.
Образец возможного решения

6. На дифракционную решетку с периодом d
= 0,01 мм нормально к поверхности решетки падает параллельный
пучок монохроматического света с длиной волны λ = 600
нм. За решеткой, параллельно ее плоскости, расположена тонкая
собирающая линза с фокусным расстоянием f = 5 см.
Чему равно расстояние между максимумами первого и второго
порядков на экране, расположенном в фокальной плоскости линзы?
Образец возможного решения

Избранные задачи прошлых лет (с ответами)

7. Под медленно
движущимся кораблем с вертикальными бортами плывет разведчик
в легком водолазном костюме. Ширина корабля 4 м, глубина погружения
его днища 1,5 м. Небо затянуто сплошным облачным покровом, полностью
рассеивающим солнечный свет. На каком максимальном расстоянии
от днища корабля должен держаться разведчик, чтобы его не могли
увидеть находящиеся вокруг другие водолазы? Рассеиванием света
водой и размерами разведчика пренебречь. Показатель преломления
воды относительно воздуха принять равным 4/3.

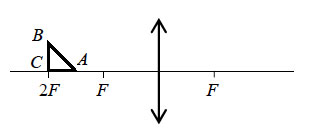
8. Равнобедренный
прямоугольный треугольник АВС площадью 50 см² расположен
перед тонкой собирающей линзой так, что его катет АС лежит на
главной оптической оси линзы. Фокусное расстояние линзы 50 см.
Вершина прямого угла С лежит дальше от центра линзы, чем вершина
острого угла А. Расстояние от центра линзы до точки С равно
удвоенному фокусному расстоянию линзы (см. рисунок). Постройте
изображение треугольника АВС и найдите площадь получившейся
фигуры.

9. На оси
ОХ в точке x₁ = 0 находится тонкая рассеивающая
линза с фокусным расстоянием f₁ = — 20 см,
а в точке x₂ = 20 см — тонкая собирающая
линза с фокусным расстоянием f₂ = 30 см.
Главные оптические оси обеих линз лежат на оси ОХ. Свет от точечного
источника S, расположенного в точке x < 0, пройдя данную
оптическую систему, распространяется параллельным пучком. Найдите
координату x (в см) точечного источника S.

10. Условимся
считать изображение на пленке фотоаппарата резким, если вместо
идеального изображения в виде точки на пленке получается изображение
пятна диаметром не более некоторого предельного значения. Поэтому,
если объектив находится на фокусном расстоянии от пленки, то
резкими считаются не только бесконечно удаленные предметы, но
и все предметы, находящиеся дальше некоторого расстояния d.
Оцените предельный размер пятна, если при фокусном расстоянии
объектива 50 мм и диаметре входного отверстия 5 мм резкими оказались
все предметы далее 5 м.

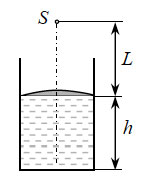
11. В сосуде на поверхности
воды плавает тонкая легкая плосковыпуклая линза выпуклой стороной
вверх (см. рисунок). Фокусное расстояние линзы в воздухе F.
Высота уровня воды в сосуде h. Изображение точечного
источника света S, расположенного на расстоянии L от
линзы на ее главной оптической оси, находится на дне сосуда.
Найти показатель преломления воды. Считать, что L >
F.

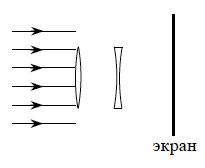
12. Параллельный световой
пучок падает нормально на тонкую собирающую линзу. На расстоянии
20 см от нее находится рассеивающая линза (см. рисунок). Оптическая
сила собирающей линзы 2,5 дптр, а у рассеивающей она равна -5
дптр. Диаметр линз равен 8 см. Экран расположен на расстоянии
L = 30 см от рассеивающей линзы. Каков диаметр светлого
пятна, создаваемого линзами на экране?

13. Дифракционная
решетка, имеющая 200 штрихов на 1 мм, расположена параллельно
экрану на расстоянии 1,25 м от него и освещается нормально падающим
пучком света длиной волны 500 нм. Определите расстояние между
вторыми дифракционными максимумами справа и слева от центрального
(нулевого). Считать, что tgα ≈ sinα.

14. Дифракционная решетка
имеет расстояние между штрихами 1 мкм. Она находится в прямоугольной
кювете, заполненной водой, и располагается параллельно боковой
стенке кюветы. Луч света, длина волны которого 0,5 мкм, падает
перпендикулярно стенке кюветы, проходит через решетку и выходит
из кюветы. Под каким углом α выходит луч, образующий первый
дифракционный максимум?

15. Между краями двух
хорошо отшлифованных тонких плоских стеклянных пластинок помещена
тонкая проволочка, противоположные концы пластинок плотно прижаты
друг к другу (см. рисунок). На верхнюю пластинку нормально к
ее поверхности падает монохроматический пучок света длиной волны
600 нм. Определите угол α который образуют пластинки, если
расстояние между наблюдаемыми интерференционными полосами равно
0,6 мм. Считать tgα ≈ α.

16. Мыльная пленка представляет
собой тонкий слой воды, на поверхности которой находятся молекулы
мыла, обеспечивающие механическую устойчивость и не влияющие
на оптические свойства пленки. Мыльная пленка натянута на квадратную
рамку со стороной d = 2,5 см. Две стороны рамки расположены
горизонтально, а две другие — вертикально. Под действием силы
тяжести пленка приняла форму клина (см. рисунок), утолщенного
внизу, с углом при вершине α = 2•10^-4
рад. При освещении квадрата параллельным пучком света лазера,
падающим перпендикулярно пленке, часть света отражается от нее,
образуя на ее поверхности интерференционную картину, состоящую
из 20 горизонтальных полос. Чему равна длина волны излучения
лазера в воздухе, если показатель преломления воды равен 4/3?

17. Вы светите
лазерной указкой на стену противоположного дома. Оцените расстояние
до дома, если диаметр пятна на стене D = 20 см (границы
пятна оцениваются из условия, что в области пятна лучи, идущие
от различных участков источника, не «гасят» друг друга), диаметр
выходного пучка лазера d = 3 мм, а длина волны λ
= 600 нм.

Ответы к избранным
задачам прошлых лет

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

32. Электродинамика. Квантовая физика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Геометрическая оптика

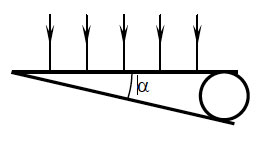
Бассейн глубиной (H = 3) м заполнен водой, показатель преломления которой (n = 4/3.) Каков радиус светового круга на поверхности воды от электрической лампы на дне бассейна?

Рассмотрим ход лучей

Полное внутреннее отражение происходит начиная с такого значения угла падения (alpha), при котором (beta = 90^circ). По закону преломления [dfrac{sin beta}{sin alpha }= n Rightarrow sin alpha = dfrac{1}{n}] Искомая величина (BC) равна [BC= ABcdot tg alpha =dfrac{AB}{sqrt{n^2-1}}=dfrac{3text{ м}}{sqrt{dfrac{16}{9}-1}}approx 3,4 text{ м}]

Ответ: 3,4

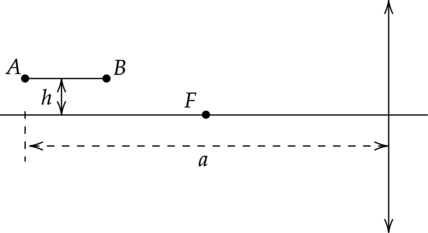
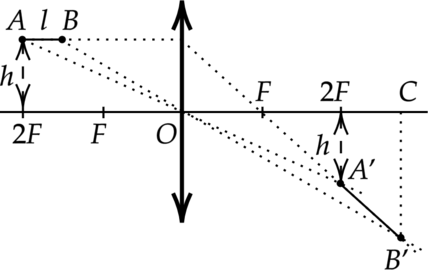
Тонкая палочка АВ длиной (l) = 10 см расположена параллельно главной оптической оси тонкой собирающей линзы на расстоянии (h) = 15 см от неё (см. рисунок). Конец А палочки располагается на расстоянии (a) = 40 см от линзы. Постройте изображение палочки в линзе и определите его длину (L). Фокусное расстояние линзы (F) = 20 cм.

“Демоверсия 2017”

1. Построение изображения (A’B’) предмета (AB) в линзе показано на рисунке.

2. Так как точка (A) находится на расстоянии (2F) от линзы, то её изображение (A’) также находится на расстоянии (2F) от линзы, и расстояние от точки (A’) до главной оптической оси равно (h).
3. Длина изображения (A’B’) [L=sqrt{(OC-2F)^2+(B’C-h)^2}] 4. Из формулы тонкой линзы [dfrac{1}{F}=dfrac{1}{2F-l}+dfrac{1}{OC}] следует [OC=dfrac{F(2F-l)}{F-l}=60text{ см}] 5. (dfrac{B’C}{h}=dfrac{OC}{2F-l}), откуда (B’C= hdfrac{OC}{2F-l}=30text{ см}) 6. Окончательные вычисления [L=sqrt{400+225}=25text{ см}]

Ответ: 25

Точечный источник находится на главной оптической оси собирающей линзы с фокусным расстоянием 8 см на расстоянии 6 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в направлении, перпендикулярном оптической оси. С какой скоростью (в мм/с) движется изображение источника?

Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}+frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f=frac{Fd}{F-d}] [Gamma=frac{f}{d}=frac{F}{F-d}=frac{8}{2}=4]
(v) – скорость предмета относительно линзы
(u) – скорость изображения источника [u=vGamma=12 text{ мм/с}]

Ответ: 12

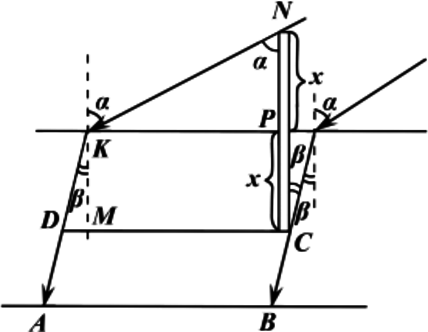
Палка, наполовину погружённая в вертикальном положении в воду, отбрасывает на дно бассейна тень длиной (l = 0, 5) м. Определите длину выступающей над водой части палки, если глубина воды равна (h = 3) м, а угол падения солнечных лучей равен (alpha = 30^circ ) (Показатель преломления воды – 4/3.) Ответ дайте в метрах и округлите до десятых

Построим ход лучей:

Закон преломления:

[sin alpha=n sin beta] (n=4 / 3) (по условию), тогда: [tg=frac{sin beta}{cos beta}=frac{sin beta}{sqrt{1-sin ^{2} beta}}=frac{frac{sin alpha}{n}}{sqrt{1-frac{sin ^{2} alpha}{n^{2}}}}=frac{sin alpha}{sqrt{n^{2}-sin ^{2} alpha}}=frac{1 / 2}{sqrt{(4 / 3)^{2}-(1 / 2)^{2}}}=frac{1 / 2}{sqrt{55 / 36}}=frac{3}{sqrt{55}}] Пусть (x) – длина надводной части палки. Палка погружена наполовину, следовательно, длина подводной части – (x .) Тогда [begin{array}{c}
l=|A B|=|C D|=|P K|+|K M| tg alpha=|P N| tg alpha+x tg beta=x tg alpha+x tg beta
x=frac{l}{tg alpha+tg beta}=frac{0,5}{frac{3}{sqrt{55}}+frac{1}{sqrt{3}}} approx 0,51 text{ м}
end{array}]

Ответ: 0,5

Бассейн глубиной (H=4) м заполнен водой, относительный показатель преломления на границе воздух-вода (n=4/3). Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?

Пусть (h) – кажущаяся высота.
По закону Снеллиуса [dfrac{sin beta}{sin alpha}= n] Рассмотрим ход лучей

Тогда [h=dfrac{tg alpha}{tg beta} H] Так как углы малые: [happrox dfrac{sin alpha}{sin beta} H approx dfrac{H}{n}=dfrac{4text{ м}}{4/3}approx 3 text{ м}]

Ответ: 3

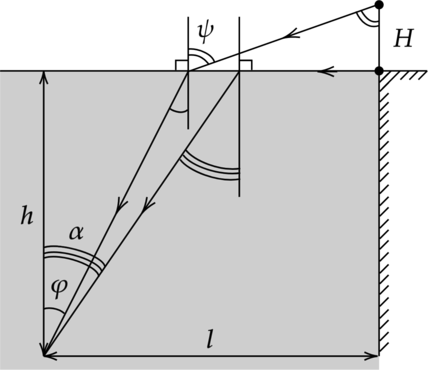
В горизонтальное дно водоема глубиной 3 м вертикально вбита свая, полностью скрытая под водой. При угле падения солнечных лучей на поверхность воды, равном 300, свая отбрасывает на дно водоёма тень длиной 0,8 м. Определите высоту сваи. Показатель преломления воды составляет (n = 4/3.) Ответ дайте в метрах и округлите до сотых.

Рассмотрим ход лучей

Из закона преломления, луч идущий горизонтально от ног тренера (угол падения равен 90(^circ)) следует по закону полного внутреннего отражения: [sin alpha = dfrac{1}{n} Rightarrow alpha = arcsin dfrac{3}{4}] Аналогично распишем закон преломления для луча идущего от головы тренера: [dfrac{sin psi}{sin varphi}= n Rightarrow sin psi = n sin varphi =dfrac{4}{3}cdot dfrac{1}{2}=dfrac{2}{3}] Из рисунка [H=(l-hcdot tg varphi)ctg psi =(l-h cdot tg varphi) dfrac{cos phi}{sin psi}= (l-h cdot tg varphi)=(l-h cdot tg varphi)dfrac{sqrt{1-sin^2 psi}}{sin psi}=dfrac{sqrt{1-n^2sin^2varphi^2}}{nsin varphi}] Подставляя числа из условий, получим [H= left(3-2,5cdot dfrac{sqrt{3}}{3}right)cdot dfrac{sqrt{5}}{2}approx 1,74text{ м}.]

Ответ: 1,74

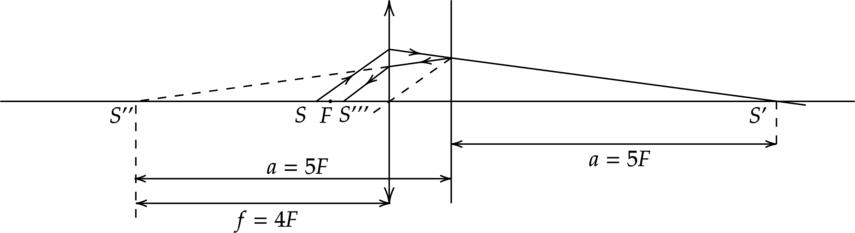
Точечный источник света находится на расстоянии 12 см от собирающей линзы с фокусным расстоянием 10 см. За линзой на расстоянии 10 см установлено плоское зеркало, перпендикулярное главной оптической оси линзы. На каком расстоянии (в см) от линзы находится изображение, образованное лучами, прошедшими через линзу после отражения от зеркала?

Формула тонкой линзы для собирающей линзы(без участия зеркала): [frac{1}{F}=frac{1}{d_1}+frac{1}{f_1}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f_1=frac{Fd_1}{d_1-F}=frac{10cdot12}{12-10}=60 text{ см}] Отразим лучи в зеркале после прохождения линзы один раз, получаем (S») – мнимый предмет, расстояние (d_2=40) см
Формула тонкой линзы для собирающей линзы (предмет S”, изображение S”’): [frac{1}{F}=-frac{1}{d_2}+frac{1}{f_2}] [f_2=frac{Fd_2}{F+d_2}=frac{10text{ см}cdot40text{ см}}{50text{ см}}=8 text{ см}]

Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

«Система подготовки учащихся к ЕГЭ.

Разбор проблемных задач

из КИМов ЕГЭ-2010»

(практикум)

1. При коротком замыкании выводов аккумулятора сила тока в цепи равна 12 А. При подключении к выводам аккумулятора электрической лампы электрическим сопротивлением 5 Ом сила тока в цепи равна 2 А. По результатам этих экспериментов определите внутреннее сопротивление аккумулятора.

Дано: Решение:

I к.з. = 12 А I к.з. = ε / r I = ε /( R+r)

R = 5 Ом ε = I к . з . ∙r ε = I ( R + r )

I = 2 А I к . з . ∙r = I ( R + r )

I к . з . ∙r = I∙R + I∙r

r — ? I к . з . ∙r — I∙r = I∙R

r ( I к . з . – I ) = I∙R

r = IR /( I к.з. — I )

r = 2 А∙5 Ом/(12А — 2А) =1 Ом

Ответ: 1 Ом

2. Найти внутреннее сопротивление и ЭДС источника тока, если при силе тока 30 А мощность во внешней цепи равна 180 Вт, а при силе тока 10 А эта мощность равна 100 Вт.

Дано: Решение:

Р 1 = 180 Вт Р 1 = I 1 2 R 1 Р 2 = I 2 2 R 2 R 1 ≠ R 2

I 1 = 30 А R 1 = Р 1 / I 1 2 R 2 = Р 2 / I 2 2

P 2 = 100 Вт ε = I 1 (R 1 + r) ε = I 2 (R 2 + r)

I 2 = 10 А ε = I 1 ( Р 1 / I 1 2 + r) ε = I 2 ( Р 2 / I 2 2 + r)

ε — ? r — ? I 1 ( Р 1 / I 1 2 + r) = I 2 ( Р 2 / I 2 2 + r )

Р 1 / I 1 + I 1 ∙ r = Р 2 / I 2 + I 2 ∙r

I 1 ∙ r – I 2 ∙ r = Р 2 / I 2 — Р 1 / I 1

r (I 1 – I 2 ) = Р 2 / I 2 — Р 1 / I 1

r (I 1 – I 2 ) = (I 1 P 2 -I 2 P 1 ) / I 1 I 2 r = (I 1 P 2 -I 2 P 1 ) / I 1 I 2 (I 1 – I 2 )

r = 0,2 Ом

ε = Р 1 / I 1 + I 1 ∙ r ε = 12 В

Ответ: 12 В; 0,2 Ом

3. Батарея состоит из 100 источников тока с ЭДС, равным 1 В и внутренним сопротивлением 0,1 Ом каждый. Источники соединили в группы по 5 штук последовательно, а эти группы соединили параллельно. Какая максимальная полезная мощность может выделяться в нагрузочном сопротивлении этой батареи?

Дано: Решение:

ε = 1 В ε – ЭДС 1 элемента, 5ε – ЭДС одной группы

r = 0,1 Ом и всей батареи

n = 5 r – внутреннее сопротивление элемента, 5 r – группы,

N = 100 5 r /20 = r /4 – внутреннее сопротивление батареи.

Р -? Максимальная мощность Р m будет при условии

равенства внутреннего и внешнего сопротивлений

R = r /4.

Через нагрузочное сопротивление идёт ток

I = 5 ε / (R + r /4) = 5 ε / (r /4 + r /4) = 5 ε∙ 4/2 r = 10 ε / r

P m = I 2 R = 100 ε 2 / r 2 ∙ r /4 = 25 ε 2 / r

P m = 250 Вт

Ответ : 250 Вт

Источник

32. Электродинамика. Квантовая физика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Геометрическая оптика

Рассмотрим ход лучей

Ответ: 3,4

“Демоверсия 2017”

1. Построение изображения (A’B’) предмета (AB) в линзе показано на рисунке.

Ответ: 25

Ответ: 12

Построим ход лучей:

Закон преломления:

[sin alpha=n sin beta] (n=4 / 3) (по условию), тогда: [tg=frac{sin beta}{cos beta}=frac{sin beta}{sqrt{1-sin ^{2} beta}}=frac{frac{sin alpha}{n}}{sqrt{1-frac{sin ^{2} alpha}{n^{2}}}}=frac{sin alpha}{sqrt{n^{2}-sin ^{2} alpha}}=frac{1 / 2}{sqrt{(4 / 3)^{2}-(1 / 2)^{2}}}=frac{1 / 2}{sqrt{55 / 36}}=frac{3}{sqrt{55}}] Пусть (x) – длина надводной части палки. Палка погружена наполовину, следовательно, длина подводной части – (x .) Тогда [begin{array}{c}
l=|A B|=|C D|=|P K|+|K M| tg alpha=|P N| tg alpha+x tg beta=x tg alpha+x tg beta \
x=frac{l}{tg alpha+tg beta}=frac{0,5}{frac{3}{sqrt{55}}+frac{1}{sqrt{3}}} approx 0,51 text{ м}
end{array}]

Ответ: 0,5

Пусть (h) – кажущаяся высота.
По закону Снеллиуса [dfrac{sin beta}{sin alpha}= n] Рассмотрим ход лучей

Тогда [h=dfrac{tg alpha}{tg beta} H] Так как углы малые: [happrox dfrac{sin alpha}{sin beta} H approx dfrac{H}{n}=dfrac{4text{ м}}{4/3}approx 3 text{ м}]

Ответ: 3

Рассмотрим ход лучей

Ответ: 1,74

Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Предлагаем разобрать три задачи, приведенные ниже. Это варианты задания №27 из ЕГЭ прошлых лет, рекомендованные как тренировочные.

Задача № 1

Коллекционер разглядывает при помощи лупы элемент марки, имеющий размер 0,2 мм, и видит его мнимое изображение, увеличенное до 1,2 мм. Рассматриваемый элемент расположен на расстоянии 7 мм от лупы. На каком расстоянии от лупы находится изображение? Ответ приведите в миллиметрах.

Решение

Составим чертеж, согласно условию задачи (Рис. 1):

Рис. 1

Лупа представляет собой собирающую линзу. Чтобы получать в ней неперевернутые увеличенные изображения, необходимо размещать предмет ближе фокусного расстояния. При этом изображение будет мнимым.

Из рисунка (Рис. 1) видно, что в силу подобия треугольников расстояние от предмета до лупы «d», расстояние от лупы до изображения «f», размер предмета «h» и размер изображения «H» связаны соотношением:

Выразим из этой формулы «f»:

f =

Подставим числовые значения:

f = = 42

Таким образом, изображение находится от лупы на расстоянии 42 мм.

Ответ: 42 мм.

Задача № 2

Линза с фокусным расстоянием F = 0,1 м даёт на экране изображение предмета, увеличенное в 6 раз. Каково расстояние от линзы до изображения? Ответ приведите в метрах.

Решение

Фокусное расстояние связано с расстоянием от предмета до линзы и расстоянием от линзы до изображения формулой линзы:

= +

Увеличение линзы равно отношению высоты изображения к высоте объекта:

Г =

Из геометрического построения найдем, что:

Г =

Тогда получим:

= 6 => = + = => f = 7F = 7 · 0,1 = 0,7 м

Ответ: 0,7 м.

Задача № 3

Линза с фокусным расстоянием F = 0,3 м даёт на экране изображение предмета, увеличенное в 3 раза. Каково расстояние от линзы до изображения? Ответ приведите в метрах.

Решение

= +

Увеличение линзы равно отношению высоты изображения к высоте объекта:

Г =

Из геометрического построения найдем, что:

Г =

Тогда получим:

= 3 => f = 3d=> = + = => f = 4F = 4 · 0,3 = 1,2 м

Ответ:1, 2 м.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Источник

Задачи по оптике с решениями

Отражение света

10.1.1 На какой угол повернется отраженный от зеркала солнечный луч при повороте зеркала
10.1.2 Предмет находился на расстоянии 20 см от плоского зеркала. Затем его отодвинули на 10 см
10.1.3 В плоскости экрана находится источник света, испускающий узкий пучок лучей под углом
10.1.4 От подъемного крана, освещенного солнцем, падает тень длиной 75 м, а тень от вертикально
10.1.5 Луч света падает на систему двух взаимно перпендикулярных зеркал. Угол падения
10.1.6 Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа
10.1.7 Высота Солнца над горизонтом 38°. Под каким углом к горизонту надо расположить
10.1.8 Солнечный луч, проходящий через отверстие в ставне, составляет с поверхностью стола
10.1.9 Небольшой предмет расположен между двумя плоскими зеркалами, образующими угол
10.1.10 На какой высоте находится аэростат, если с башни высотой 20 м он виден под углом 45°
10.1.11 Какова должна быть минимальная высота вертикального зеркала, в котором человек
10.1.12 Предмет помещен между двумя взаимно перпендикулярными зеркалами. Сколько
10.1.13 Под каким углом к поверхности стола надо расположить плоское зеркало, чтобы получить
10.1.14 Человек, стоящий на берегу озера, видит на гладкой поверхности воды изображение солнца
10.1.15 Светящаяся точка приближается к плоскому зеркалу со скоростью 4 м/с. С какой скоростью
10.1.16 Предмет находится от плоского зеркала на расстоянии 30 см. На каком расстоянии
10.1.17 Точечный источник света освещает тонкий диск диаметром 0,2 м. При этом на экране
10.1.18 На каком из приведенных ниже рисунков правильно построено изображение И предмета П
10.1.19 Горизонтальный луч падает на плоское вертикально расположенное зеркало. На какой
10.1.20 Вертикально стоящий шест высотой 1,1 м, освещенный Солнцем, отбрасывает
10.1.21 На горизонтальном столе по прямой движется шарик. Под каким углом к плоскости стола
10.1.22 Плоское зеркало AB движется поступательно со скоростью v1=2 м/с, а точка S движется
10.1.23 Светящаяся точка равномерно движется по прямой, образующей угол 30° с плоскостью

Показатель преломления и скорость света

10.2.1 Показатель преломления воды для света с длиной волны в вакууме λ₁=0,76 мкм
10.2.2 Как велика скорость света в алмазе?
10.2.3 На поверхность воды падает красный свет с длиной волны 0,7 мкм и далее распространяется
10.2.4 Во сколько раз изменится длина волны света при переходе из среды с абсолютным
10.2.5 Монохроматический свет с частотой 1,5·10¹⁵ Гц распространяется в пластинке
10.2.6 Длина световой волны в стекле 450 нм. Свет в стекле распространяется со скоростью
10.2.7 Световой луч проходит в вакууме расстояние 30 см, а в прозрачной жидкости за то же
10.2.8 Абсолютный показатель преломления алмаза равен 2,42, стекла – 1,5. Каково должно быть
10.2.9 Свет идет по кратчайшему пути из одной среды в другую. Каков показатель преломления
10.2.10 Показатель преломления света относительно воды равен 1,16. Найти скорость света в воде
10.2.11 При падении света на поверхность скипидара из вакуума угол падения равен 45°

Преломление света

10.3.1 Угол падения луча света на границу стекло-воздух равен 30°. Каков угол преломления?
10.3.2 Под каким углом следует направить луч на поверхность стекла, чтобы угол преломления
10.3.3 Определить скорость света внутри льда, если при угле падения луча на лед, равном
10.3.4 Луч света переходит из воды в стекло. Угол падения 38°. Найти угол преломления.
10.3.5 Скорость распространения света в некоторой жидкости равна 2,4·10^8 м/с. На поверхность
10.3.6 Определить абсолютный показатель преломления и скорость распространения света в слюде
10.3.7 Луч света при переходе изо льда в воздух падает на поверхность льда под углом 15
10.3.8 На горизонтальном дне водоема глубиной 1,2 м лежит плоское зеркало. На каком
10.3.9 Два взаимно перпендикулярных луча падают на поверхность воды. Угол падения
10.3.10 Водолазу, находящемуся под водой, кажется, что солнечные лучи падают под углом 60
10.3.11 Взаимно перпендикулярные лучи идут из воздуха в жидкость. Каков показатель преломления
10.3.12 Палка с изломом посередине погружена в пруд так, что наблюдателю, находящемуся
10.3.13 Под каким углом должен падать луч на поверхность стекла, чтобы угол преломления был
10.3.14 Найти угол падения луча на поверхность воды, если известно, что он больше угла
10.3.15 Луч белого света падает на поверхность воды под углом 60°. Чему равен угол
10.3.16 Определить на какой угол отклоняется узкий световой пучок от своего первоначального
10.3.17 На стеклянную пластинку падает луч света. Каков угол падения луча, если угол между
10.3.18 Луч света, падая из воздуха на поверхность воды, частично отражается и частично
10.3.19 Под каким углом должен падать луч света на плоскую поверхность льда, чтобы
10.3.20 Световой луч падает под углом 60° на пластинку с показателем преломления 1,73
10.3.21 Луч падает на границу раздела сред под углом 30°. Показатель преломления первой
10.3.22 Определить угол преломления луча, если при переходе из воздуха в этиловый спирт
10.3.23 В дно пруда вертикально вбита свая так, что она целиком находится под водой. Определите
10.3.24 В дно водоема глубиной 2 м вбита свая, выступающая из воды на 0,5 м. Найти длину тени
10.3.25 Высота солнца над горизонтом 60°. Высота непрозрачного сосуда 25 см. На сколько
10.3.26 Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя
10.3.27 На поверхности водоема глубиной 5,3 м плавает круг радиусом 1 м, над центром которого
10.3.28 Луч света падает на стеклянную пластинку толщиной 3 см под углом 60°. Определить
10.3.29 Луч света падает под углом 40° на систему из трех плоскопараллельных стеклянных
10.3.30 Поверх стеклянной горизонтально расположенной пластины налит тонкий слой воды
10.3.31 На плоскопараллельную стеклянную пластинку толщиной 2 см под углом 60° падает луч
10.3.32 На какое расстояние сместится луч, пройдя плоскопараллельную стеклянную пластинку
10.3.33 Определить смещение светового луча при прохождении его через стеклянную пластинку
10.3.34 Луч света падает под углом 30° на плоскопараллельную стеклянную пластинку
10.3.35 Луч света падает перпендикулярно на вертикальную грань прозрачной призмы
10.3.36 Показатель преломления стекла призмы для красных лучей равен 1,483. Преломляющий
10.3.37 Сечение стеклянной призмы имеет вид равностороннего треугольника. Луч света падает
10.3.38 Определить угол отклонения луча призмой. Преломляющий угол призмы равен 60°
10.3.39 Луч света входит в стеклянную призму под углом π/6 и выходит из призмы в воздух
10.3.40 Какова глубина бассейна, если человек, глядя под углом 30° к поверхности воды
10.3.41 Какова истинная глубина водоема, если камень, лежащий на дне его, при рассматривании
10.3.42 Кажущаяся глубина водоема h=4 м. Определить истинную глубину h0 водоема, если
10.3.43 На расстоянии 1,5 м от поверхности воды в воздухе находится точечный источник света
10.3.44 Угол падения луча на пластинку толщиной 6 мм и показателем преломления, равным

Полное внутреннее отражение

10.4.1 Предельный угол полного внутреннего отражения для воздуха и стекла 34°
10.4.2 Найти предельный угол падения луча на границу раздела стекла и воды
10.4.3 Определить угол полного внутреннего отражения для алмаза, погруженного в воду
10.4.4 Предельный угол полного внутреннего отражения для льда равен 50°. Определить
10.4.5 В системах бензин-воздух и стекло-воздух предельные углы полного внутреннего отражения
10.4.6 В алмазе свет распространяется со скоростью 1,22·10^8 м/с. Определить
10.4.7 Предельный угол полного внутреннего отражения для стекла 45°. Найти скорость
10.4.8 Предельный угол полного отражения в системе стекло-воздух равен 42°. Чему равна
10.4.9 Предельный угол полного отражения для алмаза 24°. Чему равна скорость
10.4.10 Предельный угол полного внутреннего отражения для бензола 45°. Определить
10.4.11 Чему равен предельный угол полного внутреннего отражения светового луча на границе
10.4.12 Предельный угол полного внутреннего отражения в системе скипидар-воздух равен 45°
10.4.13 На дне сосуда, заполненного водой до высоты 0,40 м, находится точечный источник света
10.4.14 Точечный источник света находится на дне сосуда с жидкостью с показателем преломления
10.4.15 Преломляющий угол трехгранной призмы равен 60°. Найти угол падения луча света
10.4.16 В водоем на некоторую глубину помещают источник белого света. Показатели преломления
10.4.17 Луч света переходит из воды в воздух. Угол падения луча 52°. Определить угол
10.4.18 Предельный угол полного внутреннего отражения для воздуха и стекла 34°. Определить
10.4.19 В алмазе свет распространяется со скоростью 1,22·10^8 м/с. Определить предельный
10.4.20 Световой луч падает на стеклянную пластинку квадратного сечения. Каким должен быть

Линзы

10.5.1 Найти оптическую силу собирающей линзы, если изображение предмета, помещенного
10.5.2 На расстоянии 25 см от двояковыпуклой линзы, оптическая сила которой 5 дптр
10.5.3 Предмет находится на расстоянии 8 см от переднего фокуса линзы, а его изображение
10.5.4 На каком расстоянии от собирающей линзы с фокусным расстоянием 20 см получится
10.5.5 Собирающая линза дает прямое изображение предмета с увеличением Γ=2
10.5.6 На каком расстоянии от выпуклой линзы с фокусным расстоянием 32 см следует поместить
10.5.7 Линза дает увеличение предмета в три раза, если предмет находится на расстоянии 10 см
10.5.8 Предмет помещен на расстоянии 25 см перед передним фокусом собирающей линзы
10.5.9 Светящийся предмет находится на расстоянии 3 м от экрана. На каком минимальном
10.5.10 Расстояние между лампой и экраном 3,2 м. Фокусное расстояние линзы 0,6 м. Определить
10.5.11 Предмет находится на расстоянии 12 см от двояковогнутой линзы, фокусное расстояние
10.5.12 Фокусное расстояние собирающей линзы равно 0,15 м. Определить высоту предмета
10.5.13 Оптическая сила тонкой линзы 5 дптр. Предмет поместили на расстоянии 60 см
10.5.14 Предмет находится на расстоянии 4F от собирающей линзы. Найдите коэффициент увеличения
10.5.15 На каком расстоянии от линзы с оптической силой 5 дптр необходимо поставить предмет
10.5.16 Фокусное расстояние собирающей линзы 0,2 м. На каком расстоянии от линзы следует
10.5.17 Когда предмет поместили на расстоянии 20 см от линзы, изображение получилось
10.5.18 Предмет находится на расстоянии 0,7 м от тонкой собирающей линзы. На каком
10.5.19 Каково главное фокусное расстояние линзы, если для получения изображения
10.5.20 Предмет и его прямое изображение, создаваемое тонкой собирающей линзой
10.5.21 Расстояние от предмета до экрана 5 м. Какой оптической силы надо взять линзу
10.5.22 Линза дает действительное изображение предмета с увеличением 3. Какое увеличение
10.5.23 Предмет находится на расстоянии 0,1 м от переднего фокуса собирающей линзы
10.5.24 Точечный источник света находится на расстоянии 50 см от собирающей линзы
10.5.25 Расстояние между предметом и экраном равно 120 см. На каком максимальном расстоянии
10.5.26 Изображение миллиметрового деления шкалы, расположенной перед линзой
10.5.27 Расстояние между лампой и экраном 3,2 м. Фокусное расстояние линзы 0,6 м.
10.5.28 Определить наименьшее возможное расстояние между светящимся предметом и его
10.5.29 Расстояние от предмета до экрана 90 см. Где нужно поместить между ними линзу
10.5.30 Светящийся предмет находится на расстоянии 420 см от экрана. На каком расстоянии
10.5.31 Расстояние от предмета до двояковыпуклой линзы d=kF, где F – фокусное расстояние
10.5.32 Найти наименьшее возможное расстояние между светящимся предметом и его
10.5.33 Расстояние между предметом и его равным, действительным изображением равно 2 м
10.5.34 С помощью линзы на экране получено изображение в 4 раза по площади больше самого
10.5.35 Перед собирающей линзой с оптической силой 2,5 дптр на расстоянии 30 см находится
10.5.36 Фокусное расстояние собирающей линзы 10 см, расстояние от переднего фокуса 5 см
10.5.37 Фокусное расстояние собирающей линзы равно 10 см, расстояние от предмета до фокуса
10.5.38 Мнимое изображение предмета находится на расстоянии 1 м от собирающей линзы
10.5.39 Величина прямого изображения предмета вдвое больше самого предмета. Расстояние
10.5.40 Линзой с оптической силой 4 дптр надо получить увеличенное в 5 раз мнимое изображение
10.5.41 Мнимое изображение предмета, получаемое с помощью линзы, в 4,5 раза больше
10.5.42 Предмет находится на расстоянии 1,5F от линзы. Его приблизили к линзе на расстояние 0,7F
10.5.43 Определить главное фокусное расстояние рассеивающей линзы, если известно, что
10.5.44 Предмет расположен на расстоянии 0,5F от рассеивающей линзы с фокусным расстоянием
10.5.45 Главное фокусное расстояние рассеивающей линзы 12 см. Изображение предмета
10.5.46 Предмет находится перед рассеивающей линзой на расстоянии 2 м. На каком расстоянии
10.5.47 Тонкая рассеивающая линза создает изображение предмета, находящегося в ее фокальной
10.5.48 Определите оптическую силу линзы, если изображение предмета, помещенного перед
10.5.49 Пучок лучей, параллельный главной оптической оси, после преломления в линзе
10.5.50 Расстояние от освещенного предмета до экрана 100 см. Линза, помещенная между ними
10.5.51 Высота пламени свечи 5 см. Линза дает на экране изображение этого пламени высотой
10.5.52 Предмет расположен на расстоянии 1,6F от линзы. Его переместили к линзе на расстояние
10.5.53 Собирающая линза дает изображение предмета, увеличенное в 5 раз. Экран придвинули
10.5.54 Собирающая линза дает двукратное изображение предмета. Когда линзу придвинули
10.5.55 Расстояние от предмета до линзы и от линзы до изображения предмета одинаковы
10.5.56 От предмета высотой 20 см при помощи линзы получили действительное изображение
10.5.57 Предмет расположен перпендикулярно оптической оси собирающей линзы. На сколько
10.5.58 Точечный источник света находится на расстоянии 40 см от собирающей линзы
10.5.59 На каком расстоянии от рассеивающей линзы с фокусным расстоянием 10 см находится
10.5.60 Изображение светящейся точки в рассеивающей линзе с оптической силой D=-5 дптр
10.5.61 Светящаяся точка находится в фокусе рассеивающей линзы. На каком расстоянии от линзы
10.5.62 Середина стержня, имеющего длину 10 мм, находится на расстоянии 18 см от собирающей
10.5.63 Точечный источник света находится на расстоянии 40 см от собирающей линзы с фокусным
10.5.64 На расстоянии 60 см от собирающей линзы с фокусным расстоянием 50 см находится
10.5.65 Какое линейное увеличение можно получить при помощи проекционного аппарата
10.5.66 Фотоаппаратом с расстояния 500 м сделан снимок телебашни. Фокусное расстояние
10.5.67 Линзой пользуются как лупой. Первоначально изображение было в 4 раза больше
10.5.68 С самолета, летящего на высоте 12 км, сфотографирована местность в масштабе 1:16000
10.5.69 При фотографировании предмета с расстояния 1 м высота изображения равна 6 см
10.5.70 Светящаяся точка приближается к собирающей линзе вдоль ее главной оптической оси
10.5.71 Небольшому шарику, который находится на поверхности горизонтально расположенной
10.5.72 Точечный предмет движется по окружности со скоростью 0,04 м/с вокруг главной
10.5.73 Укажите номер рисунка, на котором правильно изображен ход светового луча

Интерференция света

10.6.1 Разность хода двух волн, полученных от когерентных источников до данной точки равна
10.6.2 Разность хода двух интерферирующих лучей монохроматического света равна λ/4
10.6.3 Два когерентных источника звука колеблются в одинаковой фазе. В точке, отстоящей
10.6.4 Разность хода двух интерферирующих лучей монохроматического света равно четверти
10.6.5 Разность фаз двух интерферирующих световых волн равна 5π, разность хода между ними
10.6.6 Тонкая мыльная пленка освещается светом с длиной волны 0,6 мкм. Чему равна

Дифракция света

10.7.1 Определить угол отклонения лучей монохроматического света с длиной волны 0,55 мкм
10.7.2 Один миллиметр дифракционной решетки содержит 20 штрихов. На какой угол отклоняются
10.7.3 Дифракционная решетка имеет 250 штрихов на миллиметр. Под каким углом виден максимум
10.7.4 Определить число штрихов на 1 мм дифракционной решетки, если углу дифракции 30°
10.7.5 Сколько штрихов на 1 мм должна иметь дифракционная решетка, чтобы зеленая линия
10.7.6 Сколько штрихов на 1 мм должна иметь дифракционная решетка для того, чтобы второй
10.7.7 Период дифракционной решетки в два раза больше длины световой волны
10.7.8 На дифракционную решетку нормально падает монохроматический свет с длиной волны
10.7.9 На дифракционную решетку с периодом 6 мкм падает монохроматическая волна
10.7.10 Период дифракционной решетки 3 мкм. Найдите наибольший порядок спектра для желтого
10.7.11 На дифракционную решетку нормально падает монохроматический свет с длиной волны
10.7.12 Какой наибольший порядок спектра можно наблюдать с помощью дифракционной решетки
10.7.13 Период дифракционной решетки 3 мкм. Найдите наибольший порядок спектра
10.7.14 На дифракционную решетку нормально падает монохроматический свет с длиной
10.7.15 Какой наибольший порядок спектра можно наблюдать с помощью дифракционной
10.7.16 Вычислите максимальный порядок спектра дифракционной решетки с периодом 2 мкм
10.7.17 Найти наибольший порядок спектра для света с длиной волны 700 нм, если постоянная
10.7.18 Дифракционная линия для волны 546,1 нм в спектре первого порядка наблюдается под углом
10.7.19 Сколько максимумов можно будет увидеть на экране, если на дифракционную решетку
10.7.20 Постоянная дифракционной решетки в 3,7 раза больше длины световой волны, нормально
10.7.21 Определить длину волны для линии в дифракционном спектре третьего порядка
10.7.22 Определить длину волны для линии в дифракционном спектре второго порядка
10.7.23 На дифракционную решетку нормально падает пучок света от разрядной трубки. Какова
10.7.24 Период дифракционной решетки равен 1,5 мкм. Чему равна ширина прозрачных щелей
10.7.25 Определите оптическую разность хода волн длиной 540 нм, падающих на дифракционную
10.7.26 Дифракционная решетка, имеющая 100 штрихов на 1 мм, находится на расстоянии 1 м
10.7.27 На дифракционную решетку с периодом 4 мкм падает нормально монохроматическая волна
10.7.28 При помощи дифракционной решетки с периодом 0,02 мм получено первое дифракционное
10.7.29 На каком расстоянии от дифракционной решетки надо поставить экран, чтобы расстояние
10.7.30 Для измерения длины световой волны применена дифракционная решетка, имеющая
10.7.31 Определить длину волны, падающей на дифракционную решетку, имеющую 400 штрихов
10.7.32 Найти период решетки, если дифракционный максимум 1-го порядка для волны 486 нм
10.7.33 Найдите наибольший порядок спектра для длины волны, равной 600 нм, если период
10.7.34 На дифракционную решетку с периодом 1 мкм падает нормально монохроматический свет
10.7.35 Дифракционная решетка длины 2 см имеет 10000 штрихов. Под каким углом наблюдается
10.7.36 На дифракционную решетку нормально падает пучок света от разрядной трубки
10.7.37 При нормальном падении белого света на дифракционную решетку зеленая линия

( 111 оценок, среднее 4.95 из 5 )

Источник

Задачи из ДЕМОВАРИАНТОВ (с решениями)

Избранные задачи прошлых лет (с ответами)

Геометрическая оптика

Геометрическая оптика

Задача № 1

Задача № 2

Задача № 3

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задачи по оптике с решениями

Отражение света

Показатель преломления и скорость света

Преломление света

Полное внутреннее отражение

Линзы

Интерференция света

Дифракция света

Новое и интересное на сайте: