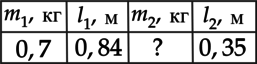Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода? (Ответ дайте в ньютонах.) Трение в осях блоков мало. Блоки и нити считайте невесомыми.
Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.
2
К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рис.).
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии? (Ответ дайте в килограммах.)
3
На рычаг действуют две силы. Момент первой силы относительно оси вращения рычага равен 50 Н · м. Какова величина второй силы, если её плечо относительно этой же оси равно 0,5 м и рычаг при этом находится в равновесии?
Ответ дайте в Ньютонах.
Источник: Демонстрационная версия ЕГЭ—2022 по физике
4
Под действием веса груза mg и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, а груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 240 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
5
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.).
Чему равна масса груза, который надо подвесить ко второму делению левого плеча рычага для достижения равновесия? (Ответ дайте в килограммах.)
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 544 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 …
Добавить в вариант
Два небольших шара массами m1 = 0,2 кг и m2 = 0,3 кг закреплены на концах невесомого стержня AB, расположенного горизонтально на опорах C и D (см. рис.). Расстояние между опорами l = 0,6 м, а расстояние AC равно 0,2 м. Чему равна длина стержня L, если сила давления стержня на опору D в 2 раза больше, чем на опору C? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень — шары».
Какие законы Вы используете для описания равновесия тела? Обоснуйте их применение к данному случаю.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
Однородная лестница массой 20 кг прислонена к гладкой вертикальной стене, составляя с ней угол 60о. Пол шероховатый. Чему равен модуль силы реакции, действующей на верхний конец лестницы? Ответ дайте в ньютонах и округлите до целого числа.
Однородная лестница массой 20 кг прислонена к гладкой вертикальной стене, составляя с ней угол 30о. Пол шероховатый. Чему равен модуль силы реакции, действующей на верхний конец лестницы? Ответ дайте в ньютонах, округлите до целого числа.
К горизонтальной лёгкой рейке, лежащей на двух опорах А и В, в точке О прикреплён груз массой 10 кг. Длина отрезка ОА равна 4 м, длина отрезка ОВ равна 1 м. Определите модуль силы, с которой действует на рейку опора В.
К горизонтальной лёгкой рейке, лежащей на двух опорах А и В, в точке О прикреплён груз массой 10 кг. Длина отрезка ОА равна 4 м, длина отрезка ОВ равна 1 м. Определите модуль силы, с которой действует на рейку опора А.
К лёгкой рейке подвешено на нити тело массой 7 кг (см. рис.). Рейка уравновешена на шероховатой опоре в горизонтальном положении с помощью силы приложенной к концу рейки и направленной под углом α = 30° к горизонту. Определите модуль вертикальной составляющей силы реакции опоры, действующей на рейку в точке O.
На рисунке изображен невесомый стержень длиной 3 м, расположенный в стакане под углом 45°. На расстоянии 1 м от нижнего угла подвешен шарик массой 3 кг. Найдите силу, с которой стержень давит на стенку стакана.
Источник: ЕГЭ по физике 13.07.2020. Основная волна. ЦФО. Часть C. Вариант 2
Задания Д29 C2 № 4367
На зиму в подмосковном яхт-клубе катера и яхты вытаскивают на берег по бетонному «слипу», то есть наклонной плоскости, уходящей под воду. Под плавающее судно помещают под водой лёгкую тележку, которая практически без трения может кататься по слипу, и при помощи лебёдки и системы блоков вытаскивают судно, поднимая его над уровнем воды.
Найдите максимальное водоизмещение судна, которое можно медленно вытащить из воды при помощи показанной на рисунке системы простых механизмов, если лебёдка даёт выигрыш в силе в раз, к её ручке прикладывают максимальную силу
а угол наклона слипа к горизонту равен
рад. Трением можно пренебречь.
Примечания: водоизмещением называется масса воды, вытесняемой судном (измеряется обычно в тоннах); при углах рад можно считать
Источник: Демонстрационная версия ЕГЭ—2022 по физике
Человек несёт груз на лёгкой палке (см. рис.). Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA? Ответ дайте в сантиметрах.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рис.).
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии? (Ответ дайте в килограммах.)
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.).
Чему равна масса груза, который надо подвесить ко второму делению левого плеча рычага для достижения равновесия? (Ответ дайте в килограммах.)
Велосипедное колесо, у которого вместо металлических спиц обод удерживают натянутые резинки, установлено в вертикальной плоскости и может свободно вращаться вокруг своей горизонтальной оси, зажатой в штативе. К неподвижному колесу подносят слева мощную лампу и начинают нагревать резиновые «спицы» (см. рис.). Резина, в отличие от металла, при нагревании не расширяется, а сжимается. Опишите, опираясь на известные физические законы, что будет происходить с резинками, и как колесо будет двигаться.
Ступенчатый блок имеет внутренний шкив радиусом 6 см. К нитям, намотанным на внешний и внутренний шкивы, подвешены грузы так, как показано на рисунке. Трение в оси блока отсутствует. Чему равен радиус внешнего шкива блока, если система находится в равновесии? Ответ выразите в сантиметрах.
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания
Тело массой 0,3 кг подвешено к правому плечу невесомого рычага (см. рис.). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия? Ответ приведите в килограммах.
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Источник: Демонстрационная версия ЕГЭ—2018 по физике
В постоянном однородном магнитном поле с индукцией B = 0,2 Тл находится прямоугольная проволочная рамка, сделанная из проволоки длиной 8 см, по которой пропускают ток силой I = 20 мА. Какое максимальное значение может иметь действующий на эту рамку момент сил Ампера?
Многовитковая катушка гальванометра намотана тонким проводом на плоский прямоугольный каркас с размерами a = 2 см и b = 3 см и подвешена на проводах в однородном горизонтальном магнитном поле с индукцией B = 0,05 Тл так, что более длинная сторона катушки вертикальна, а её плоскость составляет угол с вектором
Когда по катушке пустили ток I = 200 нА, на неё стал действовать момент сил M = 1,2 · 10 − 9 Н · м. Каково число N витков провода в катушке?
В некоторый момент времени скорость
электрона
движущегося в магнитном поле, направлена вдоль оси х (см. рис.). Как направлен вектор магнитной индукции
если в этот момент сила Лоренца, действующая на электрон, направлена вдоль оси у?
1) из плоскости чертежа от нас
2) в отрицательном направлении оси х
3) в положительном направлении оси х
4) из плоскости чертежа к нам
Всего: 544 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 …
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 544 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Легкая рейка прикреплена к вертикальной стене в точке O (см. рис.). Длины отрезков OA, AB и BC одинаковы. В точке B к рейке прикреплен груз массой m. В точке C к рейке прикреплена легкая вертикальная нерастяжимая нить, второй конец которой привязан к потолку. Система находится в равновесии.
Нить перемещают так, что она, сохраняя вертикальное положение, оказывается прикрепленной к рейке в точке A. Как изменяются при этом следующие физические величины: сила натяжения нити; момент действующей на груз силы тяжести относительно точки O; момент силы натяжения нити относительно точки O?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Сила натяжения нити
Б) Момент действующей на груз силы тяжести относительно точки O
В) Момент силы натяжения нити относительно точки O
ИХ ИЗМЕНЕНИЕ
1) Увеличивается
2) Уменьшается
3) Не изменяется
Легкая рейка прикреплена к вертикальной стене на шарнире в точке O (см. рис.). Длины отрезков OA, AB и BC одинаковы. В точке C к рейке прикреплен груз массой m. В точке B к рейке прикреплена легкая вертикальная нерастяжимая нить, второй конец которой привязан к потолку. Система находится в равновесии.
Груз перевешивают, прикрепив его к рейке в точке A. Как изменяются при этом следующие физические величины: сила натяжения нити; момент действующей на груз силы тяжести относительно точки O; момент силы натяжения нити относительно точки O?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Сила натяжения нити
Б) Момент действующей на груз силы тяжести относительно точки O
В) Момент силы натяжения нити относительно точки O
ИХ ИЗМЕНЕНИЕ
1) Увеличивается
2) Уменьшается
3) Не изменяется
Из лёгкого жёсткого стержня сделан горизонтальный рычаг с длинами плеч 40 см и 200 см. К короткому концу рычага на нити подвешен груз массой m, а к длинному концу рычага для уравновешивания приложена некоторая сила. Человек начинает медленно опускать длинный конец рычага, прикладывая к нему вертикально вниз силу (см. рис.). На графике показана зависимость момента M силы тяжести груза m (относительно точки опоры рычага) от угла α между рычагом и горизонтом.
Из приведённого ниже списка выберите все правильные утверждения на основании анализа графика.
1) При повороте рычага плечо действующей на груз силы тяжести не изменяется.
2) Когда уравновешенный рычаг горизонтален, модуль приложенной к его длинному концу силы равен 0,5 Н.
3) Масса груза m равна 250 г.
4) При увеличении угла α момент силы относительно точки опоры рычага уменьшается.
5) Момент силы относительно точки опоры рычага всё время больше 1 Н·м.
Из лёгкого жёсткого стержня сделан горизонтальный рычаг с длинами плеч 50 см и 200 см. К короткому концу рычага на нити подвешен груз массой m, а к длинному концу рычага для уравновешивания приложена некоторая сила. Человек начинает медленно опускать длинный конец рычага, прикладывая к нему вертикально вниз силу (см. рис.). На графике показана зависимость момента M силы тяжести груза m (относительно точки опоры рычага) от угла α между рычагом и горизонтом.
Из приведённого ниже списка выберите все правильные утверждения на основании анализа графика.
1) При повороте рычага плечо действующей на груз силы тяжести не изменяется.
2) Когда уравновешенный рычаг горизонтален, модуль приложенной к его длинному концу силы равен 0,5 Н.
3) Масса груза m равна 250 г.
4) При увеличении угла α сила давления рычага на опору уменьшается.
5) Момент силы относительно точки опоры рычага всё время не превышает 1 Н·м.
Тонкий однородный стержень, частично погружённый в воду, удерживается в состоянии равновесия с помощью невесомой нерастяжимой нити (см. рис.). Длина отрезка АВ в два раза меньше длины отрезка ОА.
Выберите все верные утверждения.
1) Модуль силы натяжения нити больше модуля действующей на стержень силы тяжести.
2) Сумма модулей силы натяжения нити и силы Архимеда меньше модуля действующей на стержень силы тяжести.
3) Относительно оси, проходящей через точку О, отношение плеча действующей на стержень силы тяжести к плечу силы натяжения нити равно 0,5.
4) Относительно оси, проходящей через точку О, плечо силы Архимеда больше плеча действующей на стержень силы тяжести.
5) Относительно оси, проходящей через точку О, момент силы Архимеда равен моменту силы тяжести.
Насаженное на ось колесо начинают раскручивать из состояния покоя, прикладывая к ободу колеса постоянную по модулю силу. Затем модуль силы увеличивают, не изменяя её направления, и начинают раскручивать колесо из состояния покоя заново. Как в результате этого изменятся следующие физические величины: момент силы относительно оси колеса модуль угловой скорости колеса через 1 секунду после начала раскручивания?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
| Момент силы
относительно оси колеса |
Модуль угловой
скорости колеса через 1 секунду после начала раскручивания |
Насаженное на ось колесо начинают раскручивать из состояния покоя, прикладывая к ободу колеса постоянную по модулю силу. Затем модуль силы уменьшают, не изменяя её направления, и начинают раскручивать колесо из состояния покоя заново. Как в результате этого изменятся следующие физические величины: момент силы относительно оси колеса модуль угловой скорости колеса через 1 секунду после начала раскручивания?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
| Момент силы
относительно оси колеса |
Модуль угловой
скорости колеса через 1 секунду после начала раскручивания |
Максимальный угол наклона к вертикали, под которым может стоять лестница массой m, прислонённая к вертикальной гладкой стене и опирающаяся на горизонтальный шероховатый пол, равен
Коэффициент трения между ножками лестницы и полом равен
Лестницу установили, наклонив её именно под углом
Из приведённого ниже списка выберите два правильных утверждения.
1) Модуль силы реакции со стороны стены равен модулю силы трения между ножками лестницы и полом.
2) Модуль силы трения между лестницей и полом равен произведению коэффициента трения μ на модуль суммы сил реакции пола и стены.
3) Модуль силы трения между лестницей и полом больше произведения коэффициента трения на модуль силы тяжести.
4) Модуль силы тяжести равен модулю силы реакции со стороны пола.
5) Момент силы трения относительно оси, проходящей через точку А, по модулю больше момента силы тяжести, относительно этой же оси.
Многовитковая катушка гальванометра намотана тонким проводом на плоский прямоугольный каркас с размерами a = 2 см и b = 3 см и подвешена на проводах в однородном горизонтальном магнитном поле с индукцией B = 0,1 Тл так, что более длинная сторона катушки вертикальна, а её плоскость составляет угол с вектором
Когда по катушке пустили ток I = 0,1 мкА, на неё стал действовать момент сил M = 0,9 · 10 − 9 Н · м. Каково число N витков провода в катушке?
Лёгкая рейка может вращаться вокруг неподвижной горизонтальной оси, проходящей через точку О. Рейка уравновешена при помощи двух грузов, которые прикреплены к рейке лёгкими нитями, перекинутыми через идеальные блоки так, как показано на рисунке. Груз 1 имеет массу 4 кг.
Установите соответствие между физическими величинами и их значениями в единицах СИ. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) масса груза 2
Б) момент силы натяжения нити, прикреплённой в точке B, относительно оси, проходящей через точку О
Твёрдое тело может вращаться вокруг жёсткой оси O. На расстоянии L от оси к телу приложена сила
лежащая в плоскости, перпендикулярной оси (см. рис. — вид со стороны оси). Установите соответствие между физическими величинами и формулами, при помощи которых их можно найти. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) плечо силы относительно оси O
Б) момент силы относительно оси O
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Твёрдое тело неподвижно закреплено на вертикальной оси O и не может вращаться вокруг неё. К точке A тела на расстоянии R от оси приложена сила
направленная горизонтально. Вектор этой силы составляет угол α с отрезком OA (на рисунке показан вид сверху).
Установите соответствие между физическими величинами и графиками зависимостей от угла α.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Модуль момента силы
Б) Модуль силы реакции оси
ГРАФИКИ
Твёрдое тело неподвижно закреплено на вертикальной оси O и не может вращаться вокруг неё. К точке A тела на расстоянии R от оси приложена сила
направленная горизонтально. Вектор этой силы составляет угол α с отрезком OA (на рисунке показан вид сверху).
Установите соответствие между физическими величинами и графиками зависимостей от расстояния R.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Модуль момента силы
Б) Модуль силы реакции оси
ГРАФИКИ
Тяжёлая однородная рейка может вращаться вокруг горизонтальной оси, проходящей через точку О (см. рис.).
В рейке проделаны небольшие отверстия (они показаны на рисунке чёрными точками). Расстояние между соседними отверстиями 8 см. С помощью силы F = 10 Н, приложенной в точке А и направленной под углом к рейке, она удерживается в равновесии. Чему равен модуль момента силы F относительно горизонтальной оси, проходящей через точку B? Ответ дайте в ньютон-метрах
Тяжёлая однородная рейка может вращаться вокруг горизонтальной оси, проходящей через точку О (см. рис.).
В рейке проделаны небольшие отверстия (они показаны на рисунке чёрными точками). Расстояние между соседними отверстиями 20 см. С помощью силы F = 10 Н, приложенной в точке А и направленной под углом к рейке, она удерживается в равновесии. Чему равен модуль момента силы F относительно горизонтальной оси, проходящей через точку С?
Ответ дайте в ньютон-метрах.
Максимальный угол наклона к вертикали, под которым может стоять лестница массой m, прислонённая к вертикальной гладкой стене и опирающаяся на горизонтальный шероховатый пол, равен
Коэффициент трения между ножками лестницы и полом равен
Лестницу установили, наклонив её именно под углом
Из приведённого ниже списка выберите все правильные утверждения.
1) Модуль силы реакции со стороны стены равен модулю силы трения между ножками лестницы и полом.
2) Модуль силы трения между лестницей и полом равен произведению коэффициента трения на модуль силы реакции со стороны стены.
3) Модуль силы трения между лестницей и полом равен произведению коэффициента трения на модуль силы тяжести.
4) Модуль силы тяжести меньше модуля силы реакции со стороны пола.
5) Момент силы трения относительно оси, проходящей через точку А, равен нулю.
Лёгкий стержень подвешен в горизонтальном положении при помощи вертикальных нитей, привязанных к его концам. К середине стержня подвешен груз. Груз перевешивают ближе к концу
стержня. Как в результате изменяются следующие физические величины: модуль силы натяжения левой нити, модуль силы натяжения правой нити, момент действующей на груз силы тяжести относительно точки
?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) Модуль силы натяжения левой нити
Б) Модуль силы натяжения правой нити
B) Момент действующей на груз силы тяжести относительно точки
ИХ ИЗМЕНЕНИЕ
1) Увеличивается
2) Уменьшается
3) Не изменяется
Лёгкий стержень AB подвешен в горизонтальном положении при помощи вертикальных нитей, привязанных к его концам. К середине стержня подвешен груз. Груз перевешивают ближе к концу B стержня. Как в результате изменяются следующие физические величины: модуль силы натяжения левой нити, модуль силы натяжения правой нити, момент действующей на груз силы тяжести относительно точки B?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) Модуль силы натяжения левой нити
Б) Модуль силы натяжения правой нити
B) Момент действующей на груз силы тяжести относительно точки B
ИХ ИЗМЕНЕНИЕ
1) Увеличивается
2) Уменьшается
3) Не изменяется
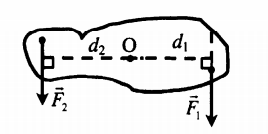
Очень лёгкая рейка закреплена на горизонтальной оси O, перпендикулярной плоскости рисунка, и может вращаться вокруг неё без трения. К рейке приложены четыре силы, изображённые на рисунке.
Из приведённого ниже списка выберите все правильные утверждения.
1) Относительно оси O минимальное плечо имеет сила F1.
2) Относительно оси O максимальное плечо имеет сила F4.
3) Относительно оси O минимальным будет момент, создаваемый силой F1.
4) Относительно оси O максимальным будет момент, создаваемый силой F4.
5) Под действием всех изображённых на рисунке сил рейка вращаться не будет.
Очень лёгкая рейка закреплена на горизонтальной оси O, перпендикулярной плоскости рисунка, и может вращаться вокруг неё без трения. К рейке приложены четыре силы, изображённые на рисунке.
Из приведённого ниже списка выберите все правильные утверждения.
1) Относительно оси O минимальное плечо имеет сила F2.
2) Относительно оси O максимальное плечо имеет сила F3.
3) Относительно оси O минимальным будет момент, создаваемый силой F1.
4) Относительно оси O максимальным будет момент, создаваемый силой F3.
5) Под действием всех изображённых на рисунке сил рейка будет вращаться.
Всего: 544 1–20 | 21–40 | 41–60 | 61–80 …
Данная тема посвящена решению задач
на тему «Момент силы. Условия равновесия твердого тела».
Задача 1. Однородный сплошной кубик установлен так, что
одним своим ребром он опирается на вертикальную стену, а другим ребром
— на горизонтальный пол. Кубик находится в равновесии. На рисунке
показаны силы, которые действуют на кубик. Относительно каких точек,
обозначенных на рисунке, момент силы трения кубика о пол равен нулю?
РЕШЕНИЕ
Момент силы относительно некоторой точки определяется,
как произведение модуля этой силы на ее плечо.
Плечо — это длина перпендикуляра, опущенного
из рассматриваемой точки, на линию действия силы.
Модуль силы трения отличен
от нуля. Поэтому момент этой силы равен нулю только относительно таких
точек, относительно которых ее плечо равно нулю. То есть нас интересуют
только точки, лежащие на линии действия силы. А таких точек две — это точки
В и С.
ОТВЕТ: относительно точек В и С.
Задача 2. На поверхности земли находится две опоры на
расстоянии 5 м друг от друга. На эти опоры кладут горизонтальную балку массой
150 кг и длиной 8 м так, что 3 м балки выступают за правую опору. Определите
силу давления балки на эту опору.
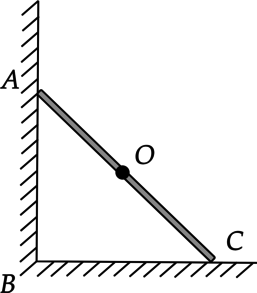
Задача 3. Определите все силы, действующие на лестницу,
прислоненную к вертикальной стене. Масса лестницы m, а ее
центр тяжести располагается ровно посередине. При какой величине угла лестница
начнет скользить, если коэффициенты трения о пол и о стену одинаковы и равны μ?
«Ничто не мешает
человеку завтра
стать умнее, чем он
был вчера»
П.Л. Капица
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Момент силы, механическое равновесие тела
При одновременном действии на одно тело нескольких сил тело движется с ускорением.
Линия действия силы — прямая, проходящая через вектор силы. Если силы действуют параллельно друг другу, то точки приложения результирующей силы нет.
Момент силы относительно оси вращения — это произведение силы на плечо. [vec{M}=vec{F}vec{l}]
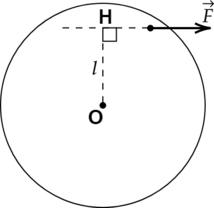
Плечо силы — это расстояние от оси вращения до линия действия силы. В качестве примера на рисунке изображён некий диск, к которому приложена сила (vec{F}). Ось вращения перпендикулярна плоскости чертежа и проходит через точку O. Плечом силы является величина (l = OH), где (displaystyle H) — основание перпендикуляра, опущенного из точки O на линию действия силы.
Момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил равна нулю.
Условия равновесия тела:
1) Силы уравновешены вдоль любой оси.
2) Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.
Также условия равновесия тела можно сформулировать следующим образом:
1) Равна нулю векторная сумма всех сил, приложенных к телу.
2) Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.
Центр тяжести тела — центр параллельных сил тяжести элементарных частей этого тела.
1) Если однородное тело имеет ось симметрии, то центр тяжести находится на этой оси.
2) Если однородное тело имеет плоскость симметрии, то центр тяжести находится в этой плоскости.
3) Если однородное тело имеет центр симметрии, то центр тяжести находится в этой точке.
Виды равновесия
Равновесие называется устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия.
Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия.
Равновесие называется безразличным, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил равна нулю.
Сила, приложенная к рычагу слева равна 300 Н. Какой длины должно быть ее плечо, чтобы рычаг находился в равновесии, если момент силы, действующей на него справа, равен 90 Н(cdot)м? (Ответ дайте в сантиметрах.)
Пусть (M_1) – момент силы, приложенной к рычагу справа, а (M_2) – слева. Чтобы рычаг находился в равновесии, моменты сил, действующих на него слева и справа, должны быть равны: [M_1 = M_2] В то же время момент силы (M_2) по определению равен произведению силы на ее плечо: [M_2 = Fcdot{l},] где (F) – величина силы, приложенной слева; (l) – длина плеча слева. Исходя из этого получаем, что: [M_1 = Fcdot{l}] Отсюда выразим (l): [l = frac{M_1}{F}] [l = frac{90text{ Н}cdot{text{м}}}{300text{ Н}} = 0,3text{ м} = 30text{ см }]
Ответ: 30
Тело массой 1 кг подвешено к правому плечу невесомого рычага (см. рисунок). К какому делению левого плеча рычага нужно подвесить груз массой 3,5 кг для достижения равновесия?
Пусть масса правого груза (m_1), а левого – (m_2).
Обозначим длину одного деления за (l). Тогда, исходя из рисунка, длина правого плеча равна (l_1 = 7l), а длина левого плеча равна (l_2 = nl), где (n) – количество делений.
Чтобы рычаг достиг равновесия, моменты сил, действующих на него справа и слева, должны быть равны: (M_1 = M_2).
В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] Отсюда получаем: (F_1l_1 = F_2l_2)
Выразим длину левого плеча рычага: (displaystyle{l_2 = frac{F_1l_1}{F_2}})
На оба груза действует единственная сила – сила тяжести, поэтому: [F_1 = m_1g] [F_2 = m_2g] С учетом этого: [l_2 = displaystyle{frac{m_1gcdot{l_1}}{m_2g}} = frac{m_1l_1}{m_2}] [displaystyle{l_2 = frac{1text{ кг}cdot{7l}}{3,5text{ кг}} = 2l}Rightarrow nl = 2l Rightarrow n = 2]
Ответ: 2
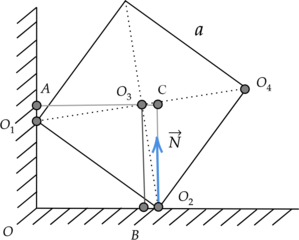
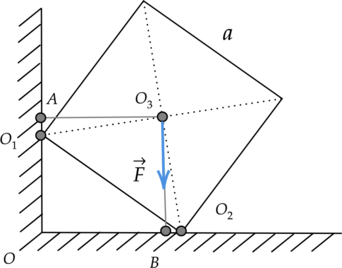
Две вершины однородного железного куба объемом (V = 512) см(^3) опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равно плечо силы реакции опоры относительно оси, перпендикулярной плоскости чертежа и проходящей через точку (O_3)? (O_2C = sqrt{7}) см (Ответ дайте в метрах.)
Плечо – это кратчайшее расстояние между осью вращения и линией действия силы. Мысленно продолжим линию действия силы реакции опоры (N) и перпендикуляром соединим ее с прямой, проходящей через точку (O_3). Получаем, что плечом этой силы является отрезок (O_3C).
Воспользуемся геометрией, чтобы найти отрезок (O_3C).
Рассмотрим треугольник (Delta O_1O_2O_4) с прямым углом (O_2): [O_1O_4^2 = O_1O_2^2 + O_4O_2^2] [O_1O_2 = O_2O_4 = a] [displaystyle{O_1O_4 = sqrt{2a^2} = asqrt{2}}] Далее найдем отрезок (O_2O_3): [displaystyle{O_2O_3 = frac{1}{2}O_1O_4} = frac{asqrt{2}}{2}] Рассмотрим треугольник (Delta O_3O_2C) с прямым углом (C): [O_3O_2^2 = O_3C^2 + O_2C^2] [displaystyle{O_3C = {sqrt{O_3O_2^2 — O_2C^2 }}}] [displaystyle{O_3C = {sqrt{left(frac{asqrt{2}}{2}right)^2 — O_2C^2 }}}] Зная объем куба, можно найти его сторону (a): [V = a^3 Rightarrow a = sqrt[3]{V} = sqrt[3]{512text{ см}^3} = 8 text{ см }] Тогда: [displaystyle{O_3C = {sqrt{left(frac{8text{ см}cdotsqrt{2}}{2}right)^2 — (sqrt{7}text{ см})^2 }} = 5 text{ см} = 0,05text{ м }}]
Ответ: 0,05
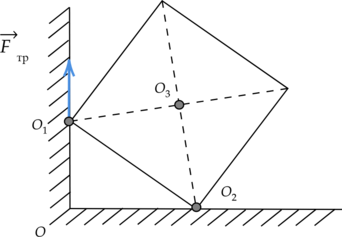
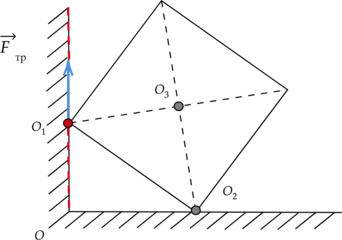
Две вершины однородного медного куба опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равен момент силы трения относительно оси, проходящей через точку (O_1) перпендикулярно плоскости рисунка, если масса куба равна 0,7 кг? (OO_2 = 0,4) м (Ответ дайте в Н(cdot)м)
Момент силы трения (M) равен произведению модуля силы трения (F_text{тр}) на ее плечо (l): [M = F_text{тр}cdot{l}] Прямая (OO_1) – линия действия силы трения. По рисунку видно, что длина плеча силы трения (l) относительно точки (O_1) равна нулю (так как ось вращения, проходящая через точку (O_1), перпендикулярна линии действия силы трения).
Следовательно, и момент силы трения (M) так же равен нулю: [M = F_text{тр}cdot{0}text{ м} = 0text{ Н}cdot{text{м }}]
Ответ: 0
Две вершины однородного деревянного куба со стороной (a = 5sqrt{2}) м опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равен момент силы тяжести относительно оси, перпендикулярной плоскости чертежа и проходящей через точку (A)? (AO_1 = 3) м (Ответ дайте в МН(cdot)м и округлите до десятых.)
Момент силы тяжести M равен произведению модуля силы тяжести (F) на ее плечо (l): [M = Fcdot{l}] Плечо – это кратчайшее расстояние между осью вращения и линией действия силы. Мысленно продолжим линию действия силы тяжести (F) и перпендикуляром соединим ее с прямой, проходящей через точку (A). Получаем, что плечом силы тяжести является отрезок (AO_3).
Воспользуемся геометрией, чтобы найти отрезок (AO_3).
Рассмотрим треугольник (Delta O_1O_2O_3) с прямым углом (O_3): [O_1O_2^2 = O_1O_3^2 + O_2O_3^2] [O_1O_3 = O_2O_3] [O_1O_2^2 = 2O_1O_3^2] [displaystyle{O_1O_3 = frac{O_1O_2}{sqrt{2}}}] [displaystyle{O_1O_3 = frac{5sqrt{2}}{sqrt{2}}} = 5text{ м }] Рассмотрим треугольник (Delta O_1AO_3) с прямым углом A: [O_1O_3^2 = AO_3^2 + AO_1^2] [AO_3 = sqrt{O_1O_3^2 — AO_1^2}] [AO_3 = sqrt{(5text{ м})^2 — (3text{ м})^2} = 4text{ м }] Сила тяжести равна произведению массы куба (m) на ускорение свободного падения (g): [F = mg] Подставим это значение в исходную формулу: [M = mgcdot{AO_3}] Зная плотность и объем куба, можно найти его массу: [displaystyle{rho =frac{m}{V}},text{ где }V = a^3] [m = rho V = rho a^3] Подставим это значение в предыдущую формулу и найдем искомую величину: [M = rho a^3gcdot{AO_3}] [displaystyle{M = 400text{ }frac{text{кг}}{text{м}^3}cdot{(5sqrt{2}text{ м})}^3cdot{10frac{text{м}}{text{с}^2}}cdot{4}text{ м} approx 5,7text{ М,Н$cdot$м }}]
Ответ: 5,7
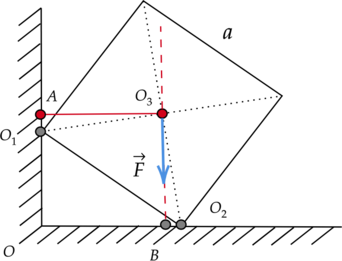
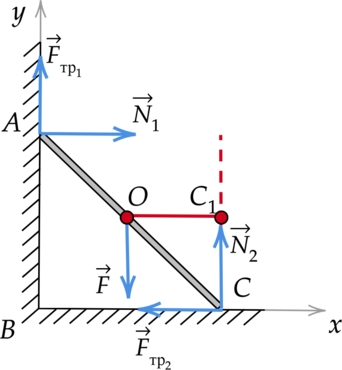
На прут массой 1 кг со стороны вертикальной поверхности действует сила трения, равная 3 Н. Найдите момент силы реакции опоры, действующей на него со стороны горизонтальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, если (AB = 6,5) м, а (AC = 9,7) м. (Ответ дайте в Н(cdot)м и округлите до целого числа.)
Момент действующей на горизонтальную стенку силы реакции опоры относительно оси, перпендикулярной плоскости рисунка и проходящей через точку (O), равен: [M = N_2l,] где (l) – плечо силы. Мысленно продолжим линию действия силы рекции опоры (N_2) и перпендикуляром соединим ее с прямой, проходящей через точку (O). Получаем, что плечом силы (N_2) является отрезок (OC_1), равный: [displaystyle{OC_1 = frac{BC}{2}} = frac{sqrt{AC^2 — AB^2}}{2}] [OC_1 = frac{sqrt{9,7text{ м}^2 — 6,5text{ м}^2}}{2} = 3,6text{ м }] Чтобы найти неизвестную величину (N_2), укажем все силы, действующие на прут, и запишем второй закон Ньютона с учетом того, что тело находится в равновесии: [vec{F}_{text{тр}1} + vec{N}_1 + vec{F} + vec{N}_2 + vec{F}_{text{тр}2} = 0] Введем оси (OX) и (OY), спроецируем на них все силы. [OX: N_1 — F_{text{тр}2} = 0] [OY: F_{text{тр}1} + N_2 — F = 0] Выразим силу реакции опоры (N_2), действующую на горизонтальную стенку: [N_2 = F — F_{text{тр}1}] Сила тяжести (F) по определению равна: (F = mg), поэтому: [N_2 = mg — F_{text{тр}1}] [N_2 = 1text{ кг}cdot{10text{ }frac{text{м}}{text{c}}^2} — 3text{ H} = 7text{ H }] Подставим найденные значения в начальную формулу: [M = 7{text{ Н}cdot{3,6}text{ м}} = 25,2text{ Н}cdot{text{м}}approx{25}text{ Н}cdot{text{м }}]
Ответ: 25
Группа школьников проводила лабораторную работу, исследуя основные условия равновесия легкого рычага, плечи сил которого равны (l_1) и (l_2). К рычагу с двух сторон ребята подвесили грузы массой (m_1) и (m_2).
Результаты эксперимента были занесены в следующую таблицу:
Чему равна масса груза (m_2), если рычаг находился в равновесии? (Ответ дайте в килограммах и округлите до десятых.)
Так как рычаг находился в равновесии, то моменты сил, действующих на него справа и слева, должны быть равны: (M_1 = M_2).
В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] Отсюда получаем: (F_1l_1 = F_2l_2)
На оба груза действует единственная сила – сила тяжести, поэтому: [F_1 = m_1g] [F_2 = m_2g] С учетом этого: (M_1 = m_1gcdot{l_1}) и (M_2 = m_2gcdot{l_2}). Приравняв (M_1) и (M_2), получаем, что: [m_1gcdot{l_1} = m_2gcdot{l_2}] [m_1l_1 = m_2l_2] Выразим массу второго груза (m_2): [displaystyle{m_2 = frac{m_1l_1}{l_2}}] [displaystyle{m_2 = frac{0,7text{ кг}cdot{0,84text{ м}}}{0,35text{ м}}} approx 1,7text{ кг }]
Ответ: 1,7

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Статика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
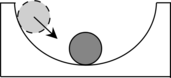
Устойчивое равновесие |
|
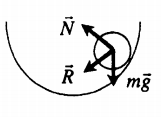 |
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). |
Неустойчивое равновесие |
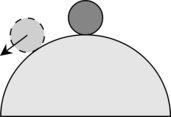
|
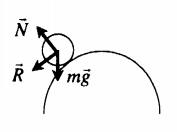 |
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). |
Безразличное равновесие |
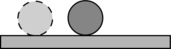
|
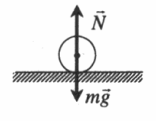 |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. |
Момент силы
Определение
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
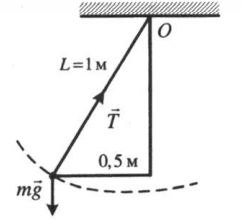
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
Момент силы может быть положительным и отрицательным.
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1d1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: |
∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: |
∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) |
∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
Определение
Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость |
|
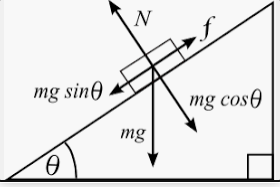 |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg |
Рычаг |
|
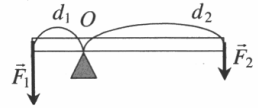 |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1 |
Неподвижный блок |
|
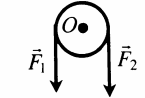 |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 |
Подвижный блок |
|
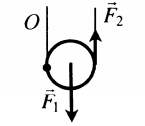 |
Дает выигрыш в силе в 2 раза:
d1 = R d2 = 2R F1 = 2F2 |
Клин |
|
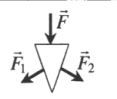 |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
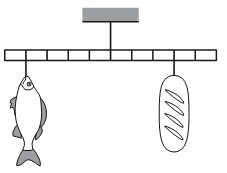
Задание EF22660
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор | оценить
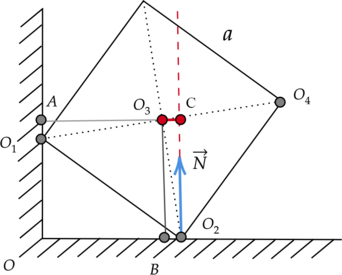
Задание EF18706
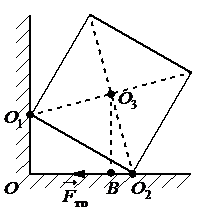
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 8.9k