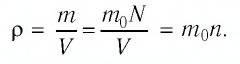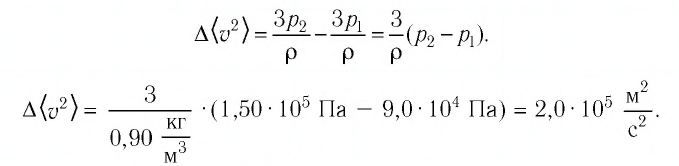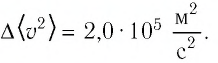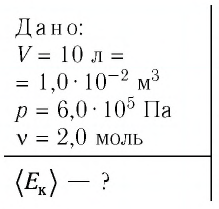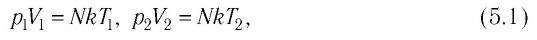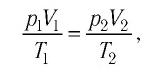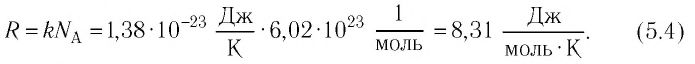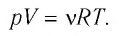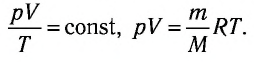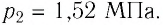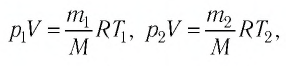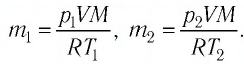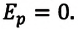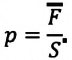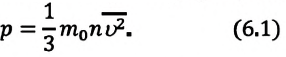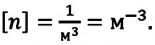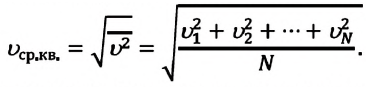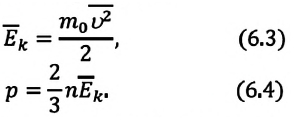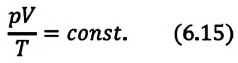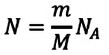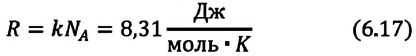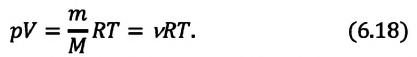Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д5 B8 № 3140
В сосуде неизменного объема находилась при комнатной температуре смесь двух идеальных газов, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль первого газа. Как изменились в результате парци-альные давления газов и их суммарное давление, если температура газов в сосуде поддерживалась неизменной? Для каждой величины определите соответствующий характер изменения:
1) увеличилось;
2) уменьшилось;
3) не изменилось.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Парциальное давление
первого газа |
Парциальное давление
второго газа |
Давление смеси газов
в сосуде |
2
Задания Д5 B8 № 3508
Каково будет изменение температуры идеального газа, если в ходе процесса его объем уменьшился в 2 раза?
1) увеличится в 2 раза
2) уменьшится в 2 раза
3) не изменится
4) увеличится в 4 раза
3
Задания Д5 B8 № 3509
Какой график соответствует изохорическому нагреванию трех газов — кислорода, гелия и углекислого газа, имеющих одинаковые массы и занимающих одинаковые объемы?
1) 1 — гелий, 2 — кислород, 3 — углекислый газ
2) 1 — углекислый газ, 2 — кислород, 3 — гелий
3) 1 — гелий, 2 — углекислый газ, 3 — кислород
4) 1 — кислород, 2 — гелий, 3 — углекислый газ
4
Задания Д5 B8 № 3586
На рисунке изображены: пунктирной линией — график зависимости давления p насыщенных паров воды от температуры T, и сплошной линией — процесс 1-2 изменения парциального давления паров воды.
По мере такого изменения парциального давления паров воды абсолютная влажность воздуха
1) увеличивается
2) уменьшается
3) не изменяется
4) может как увеличиваться, так и уменьшаться
5
Задания Д5 B8 № 3707
В каком из четырех состояний, показанных для некоторой массы идеального газа точками на pV–диаграмме, идеальный газ обладает максимальной внутренней энергией?
1) 1
2) 2
3) 3
4) 4
Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 788 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
Добавить в вариант
В закрытом сосуде с жёсткими стенками содержится идеальный газ при температуре 27 °C. Температуру газа повысили до 87 °C. Во сколько раз изменилось давление этого газа? Ответ округлите до десятых долей.
Идеальный газ изохорно нагревают так, что его температура изменяется на а давление — в 1,6 раза. Масса газа постоянна. Какова начальная температура газа по шкале Кельвина?
Идеальный газ изобарно нагревают так, что его температура изменяется на а объём — в 1,4 раза. Масса газа постоянна. Какова начальная температура газа по шкале Кельвина?
На рисунке изображены графики двух процессов, проведённых с идеальным газом при одном и том же давлении. Графики процессов представлены на рисунке. Почему изобара I лежит выше изобары II? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 2., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 4.
На рисунке изображены графики двух процессов, проведённых с идеальным газом при одном и том же давлении. Графики процессов представлены на рисунке. Почему изобара I лежит выше изобары II? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 5.
При понижении абсолютной температуры идеального газа его средняя кинетическая энергия уменьшилась в два раза. Если начальная температура составляла 600 К, то чему будет равна температура газа при новых условиях?
Источник: ЕГЭ по физике 07.06.2017. Основная волна
Идеальный газ находится в закрытом сосуде при нормальном атмосферном давлении. При неизменной концентрации молекул средняя кинетическая энергия хаотического теплового движения молекул уменьшается на 2%. Определите конечное давление газа. Ответ выразите в килопаскалях.
Идеальный газ находится в закрытом сосуде при нормальном атмосферном давлении. При неизменной концентрации молекул средняя кинетическая энергия хаотического теплового движения молекул увеличивается на 2%. Определите конечное давление газа. Ответ дайте в кПа.
В результате нагревания идеального газа средняя кинетическая энергия теплового движения его молекул увеличилась в 4 раза. Во сколько раз изменилась абсолютная температура газа?
Установите соответствие между процессами в идеальном газе и формулами, которыми они описываются (N — число частиц, p — давление, V — объём, T — абсолютная температура, Q — количество теплоты.)
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) Изохорный процесс при N = const
Б) Изотермический процесс при N = const
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Во сколько раз уменьшится средняя кинетическая энергия движения молекул идеального газа, если давление увеличится в 2 раза, а концентрация молекул увеличится в 6 раз?
Источник: ЕГЭ по физике 07.06.2017. Основная волна
Имеется два сосуда, заполненных идеальными газами: в первом сосуде находится кислород при температуре 47 °C, во втором — азот при температуре 164,5 °C. Определите, на какую величину среднеквадратичная скорость хаотического движения молекул азота больше среднеквадратичной скорости хаотического движения молекул кислорода. Ответ выразите в метрах в секунду и округлите до целого числа.
Установите соответствие между уравнениями процессов, в которых участвует постоянное количество идеального газа, и графиками процессов, изображёнными на диаграммах (p — давление, V — объём, T — абсолютная температура, ρ — плотность).
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
УРАВНЕНИЕ ПРОЦЕССА
А) T/p = const
Б) p/ρ = const
ГРАФИК ПРОЦЕССА
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
При построении температурной шкалы Реомюра принимается, что при нормальном атмосферном давлении лёд тает при температуре 0 градусов Реомюра (°R), а вода кипит при температуре 80 °R. Найдите, чему равна средняя кинетическая энергия поступательного теплового движения частицы идеального газа при температуре 91 °R. Ответ выразите в электрон-вольтах и округлите до сотых долей.
При построении температурной шкалы Реомюра принимается, что при нормальном атмосферном давлении лёд тает при температуре 0 градусов Реомюра (°R), а вода кипит при температуре 80 °R. Найдите, чему равна средняя кинетическая энергия поступательного теплового движения частицы идеального газа при температуре 29 °R. Ответ выразите в электрон-вольтах и округлите до сотых долей.
Источник: Тренировочная работа по физике 13.12.2017, вариант ФИ10204
На pV-диаграмме представлен цикл идеальной тепловой машины (цикл Карно), совершаемый с постоянным количеством идеального газа.
Из приведённого ниже списка выберите все правильные утверждения.
1) Процессы 2–3 и 4–1 являются изотермическими.
2) Процессы 2–3 и 4–1 являются адиабатическими.
3) В процессе 3–4 газ не совершает работы.
4) В процессе 2–3 газ отдает некоторое количество теплоты.
5) В процессе 1–2 газ получает некоторое количество теплоты.
Два моля одноатомного идеального газа участвуют в циклическом процессе, график которого изображён на UV-диаграмме (U — внутренняя энергия газа, V — его объём).
Выберите все верные утверждения на основании анализа представленного графика.
1) В процессе 1–2 газ изобарно нагревается.
2) В процессе 2–3 температура газа увеличивается.
3) В процессе 3–4 газ отдаёт некоторое количество теплоты.
4) В процессе 4–1 работа газа отрицательная.
5) В процессе 1–2 газ совершает работу 200 Дж.
На pV-диаграмме показан циклический процесс, состоящий из двух изохор и двух адиабат. В качестве рабочего вещества используется одноатомный идеальный газ.
Из приведённого ниже списка выберите все правильные утверждения.
1) Данный цикл соответствует циклу идеальной тепловой машины (циклу Карно).
2) В процессе 4–1 газ получил количество теплоты 450 Дж.
3) В процессе 2–3 газ отдал в 4 раза большее количество теплоты, чем получил в процессе 4–1.
4) Внутренняя энергия газа в процессе 1–2 уменьшается.
5) В процессах 1–2 и 3–4 газ не совершает работы.
На рисунке показана зависимость давления газа p от его плотности ρ в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности. На основании анализа этого циклического процесса выберите все верные утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
Источник: Демонстрационная версия ЕГЭ−2017 по физике, ЕГЭ по физике 2022. Досрочная волна. Вариант 2
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах р–Т, где р — давление газа, Т — абсолютная температура газа. Количество вещества газа постоянно.
Из приведённого ниже списка выберите все правильные утверждения, характеризующих процессы на графике, и укажите их номера.
1) Газ за цикл совершает положительную работу.
2) В процессе АВ газ получает положительное количество теплоты.
3) В процессе ВС внутренняя энергия газа уменьшается.
4) В процессе СD над газом совершают работу внешние силы.
5) В процессе DA газ изотермически расширяется.
Источник: Демонстрационная версия ЕГЭ—2018 по физике
Всего: 788 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
←Применяем первый закон термодинамики к различным процессам
Задача 1:
На высоте 200км давление воздуха составляет примерно 10-9 от нормального давления, а температура воздуха примерно 1200К. Оцените плотность воздуха на этой высоте. Ответ дайте 10-10 , округлите до десятых
Начнем! Сначала преобразуем уравнение Менделеева-Клайперона для данного конкретного случая:
PV = νRT
Заменим m = ρV, получим
Очевидно, что можно разделить все уравнение на V, получим
Выделяем из этого уравнения плотность, получим
= 291· 10-12≈ 2,9· 10-10
Ответ: 2,9
Задача 2:

Посмотрим, что мы имеем в относительных величинах, используем приложенный график:
V2 = 3V1 ,
p2 = 2p1 ,
Т2 = 2Т1 — по условию задачи.
Обозначим искомое отношение буквой / Тогда N2 = k N1 . Массу газа в поршне можно представить, как m = N· m0 . Тогда, учитывая, что газ не менялся, массы вначале и в конце опыта будут тоже соответствовать условию m2 = k m1 .
В уравнении постоянными будут только молярная масса М и газовая постоянная R. Преобразуем это уравнение, перенеся постоянные величины влево, а меняющиеся — вправо
То есть = const, а значи, мы можем составить уравнение
Подставляем все значения
Сокращаем и получаем k = 3
Ответ: 3
Задача 3:
При постоянном давлении газообразный гелий нагрели на 20ºК. Какое количество теплоты получил гелий в этом процессе, если масса гелия равна 40г?
Используем измененную формулу первого закона термодинамики, учитывая,что гелий нагревали, значит тепло передавали газу, газ увеличивал объем и нагревался. Значит, везде берем знак «+»
Q = A + ΔU,
Так как нам известно, что давление постоянное, мы можем воспользоваться формулой
Q = ν R ΔT ( 1 + )
В нашем случае газ гелий одноатомный, следовательно, i = 3.
Q = R ΔT
Q = = 4155
Ответ: 4155 Дж
Задача 4:
Идеальный одноатомный газ в количестве ν = 0,09 моль находится в равновесии в вертикальном гладком цилиндре под массивным поршнем с площадью S = 25 см². Внешнее атмосферное давление p0 = 105 Па. В результате охлаждения газа поршень опустился на высоту Δh = 4 см, а температура газа понизилась на ΔТ = 16 К. Какова масса поршня?
Для того,чтобы найти массу поршня, мы должны понять, где она здесь есть. а она — составляющая силы тяжести
F = mg

F0д = p0· S ,
F1д = p1· S
Получаем уравнение:
p0· S + mg = p1· S
Отсюда
m =
Осталось разобраться с давлением p1 . В процессе охлаждения газа внешнее давление не менялось, масса поршня тоже оставалась прежней, а значит, давление внутри, под поршнем было постоянным. Ура! У нас изобарный процесс! А значит, пользуемся удобными формулами!
Можно воспользоваться уравнением Менделеева-Клайперона
р1 V = νRT,
учитывая, что мы имеем дело с изменением температуры в правой части уравнения, а в левой измениться может только объем — у нас же изотермический процесс!
р1 ·ΔV = νR·ΔT

р1 S·Δh = νR·ΔT
р1 =
m = =
—
m = —
= 29,916 — 25 = 4,916
Округляем ответ до целых, получаем m = 5 кг.
Ответ: 5 кг
←Применяем первый закон термодинамики к различным процессам
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Газовые законы
1 моль гелия изохорно нагревают на 154 К, при этом давление газа увеличивается в 2,1 раза. До какой температуры нагрели газ? Ответ дайте в кельвинах.
Процесс изохорный, т.е. объём не меняется. Запишем закон Шарля: [hspace{ 5 mm} dfrac{p_1}{T_1}=dfrac{p_2}{T_2} hspace{ 5 mm} (1)] Изменение температуры есть разница конечной и начальной температуры газа: [hspace{ 5 mm} Delta T = T_2 — T_1 hspace{3 mm} Rightarrow hspace{3 mm} T_1 = T_2 — Delta T hspace{ 5 mm} (2)] По условию давление газа увеличивается в 2,1 раза: [hspace{ 5 mm}p_2 = 2,1 p_1hspace{ 5 mm} (3)] Подставим (2), (3) в (1) и выразим температуру, до которой нагрели газ: [dfrac{p_1}{T_2 — Delta T}=dfrac{2,1 p_1}{T_2}] [T_2 = dfrac{2,1 p_1 Delta T}{2,1p_1 — p_1} = dfrac{2,1 Delta T}{1,1} = dfrac{2,1 cdot 154text{ K}}{1,1} = 294 text{ K}]
Ответ: 294
Воздух при температуре 27(^{circ})C и давлении 202,65 кПа занимает объём 0,3 м(^3). Газ изобарно нагрели, причём объём газа увеличился до 0,5 м(^3). Найдите конечную температуру воздуха. Ответ дайте в кельвинах.
Т.к. процесс изобарный ((p=const)), используем закон Гей – Люссака: [dfrac{V_1}{T_1}=dfrac{V_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_2=dfrac{T_1 cdot V_2}{V_1}] Переведём (T_1) в кельвины: 27(^{circ})С + 273 = 300 К. [T_2=dfrac{300 text{ К} cdot 0,5 text{ м$^3$}}{0,3text{ м$^3$}}=500 text{ К}]
Ответ: 500
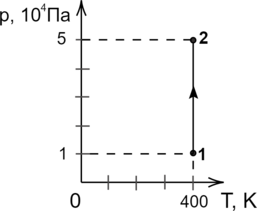
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 1 равна 56(^{circ})C. Какова температура аргона в состоянии 2? Ответ дайте в кельвинах.
Из графика видно, что процесс 1–2 — изобарный ((p=const)). Воспользуемся законом Гей – Люссака: [dfrac{V_1}{T_1}=dfrac{V_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_2=dfrac{T_1 cdot V_2}{V_1}] Переведём (T_1) в кельвины: 56(^{circ})С + 273 = 329 К. [T_2=dfrac{329text{ К} cdot 14text{ м$^3$}}{7text{ м$^3$}} = 658 text{ К}]
Ответ: 658
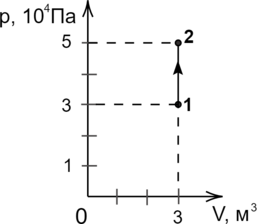
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 2 равна 212(^{circ})C. Какова температура аргона в состоянии 1? Ответ дайте в кельвинах.
Из графика видно, что процесс 1–2 — изохорный ((V=const)). Воспользуемся законом Шарля: [dfrac{p_1}{T_1}=dfrac{p_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_1=dfrac{p_1 cdot T_2}{p_2}] Переведём (T_2) в кельвины: 212(^{circ})С + 273 = 485 К. [T_1=dfrac{3cdot 10^4 text{ Па} cdot 485text{ К}}{5 cdot 10^4text{ Па}} = 291 text{ К}]
Ответ: 291
Давление газа при температуре 306 К равно 159 кПа. Газ нагрели до температуры (T_2), при этом объём газа не изменился. После нагревания давление газа стало равно 212 кПа. Найдите, до какой температуры (T_2) нагрели газ. Ответ дайте в кельвинах.
По условию процесс изохорный ((V=const)).
Согласно закону Шарля: [dfrac{p_1}{T_1} = dfrac{p_2}{T_2}hspace{3 mm}Rightarrowhspace{3 mm} T_2 = dfrac{T_1 p_2}{p_1}] [T_2 = dfrac{306 text{ K} cdot 212 cdot 10^3 text{ Па}}{159 cdot 10^3 text{ Па}} = 408 text{ K}]
Ответ: 408
Газ занимает объём 0,03 м(^3) при температуре 418 К. Какой объём займёт этот же газ, если его температура понизится до 209 К? Давление и масса газа не меняются. Ответ дайте в м(^3).
По условию процесс изобарный ((p=const)). По закону Гей – Люссака: [dfrac{V_1}{T_1} = dfrac{V_2}{T_2}hspace{3 mm}Rightarrowhspace{3 mm} V_2 = dfrac{V_1T_2}{T_1}] [V_2 = dfrac{0,03 text{ м$^3$} cdot 209 text{ К}}{418 text{ К}} = 0,015 text{ м$^3$}]
Ответ: 0,015
На рисунке представлен график зависимости давления от температуры газа. Объём газа в состоянии 2 равен 6 л. Какой объём занимает газ в состоянии 1? Масса газа не меняется. Ответ дайте в м(^3).
По графику видно, что процесс 1–2 — изотермический ((T=const)). По закону Бойля – Мариотта: [p_1V_1 = p_2V_2hspace{3 mm}Rightarrowhspace{3 mm} V_1 = dfrac{p_2V_2}{p_1}] Переведём объём газа в м(^3): (; 
Ответ: 0,03

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
С одноатомным идеальном газом проводят циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя? Количество вещества газа в ходе процесса остаётся неизменным.
Одноатомный идеальный газ в количестве 10 моль сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2–3?
Задача 17
Давление насыщенного водяного пара при температуре 40 °С приблизительно равно 6 кПа. Каково парциальное давление водяного пара
в комнате при этой температуре при относительной влажности 30%?
Дано
Pн=6 кПа ф=30% P- ?
Ф=P*100%/Pн
P=Pн*30%/100%=6*0,3=1,8 кПа
Ответ P=1,8кПа
Задача 18
Для определения удельной теплоты плавления в сосуд с водой массой 300 г и температурой 20°С стали бросать кусочки тающего льда при непрерывном помешивании. К моменту времени, когда
лед перестал таять, масса воды увеличилась на 84 г. Определите по данным опыта удельную теплоту плавления льда. Ответ выразите в кДж/кг.
Уравнения количества теплоты Q(воды)=c(воды)*m(воды)*на дельта t и Q(льда)=лямбда(удельная теплота плав. льда)*m(льда). Приравниваем их получаем 4200*0.3*20=Лямбда*0.084, выражаешь лямбда=4200*0.3*20/0.084=300000=300кДж
Задача 19
В одном сосуде находится аргон, а в другом — неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Температура — это мера средней кинетической энергии молекул идеального газа а значит, оба газа находятся при одинаковой температуре. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения)
где
— концентрация молекул газа.
Тогда отношение концентрации молекул аргона к концентрации молекул неона принимает значение:
Задача 20
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной d = 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз и нагрели на = 60 К. При этом объем, занимаемый воздухом, не изменился. Атмосферное давление
= 750 мм рт.ст. Определите температуру воздуха
в лаборатории.
Условие равновесия столбика ртути определяет давление воздуха в вертикальной трубке: , где
— атмосферное давление. Здесь Н = 750 мм,
— плотность ртути.
Поскольку нагрев воздуха в трубке происходит до температуры и объем, занимаемый воздухом, не изменился, то, согласно уравнению Клапейрона-Менделеева:
Окончательно получаем:К.
Задача 21
В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.
1. Когда трубка расположена горизонтально, объём воздуха и его давление равны, соответственно: , где S — площадь сечения трубки;
, что вытекает из условия равновесия столбика ртути.
2. Когда трубка расположена вертикально отверстием вверх, объём закрытой части трубки и давление воздуха в ней равны, соответственно:
,
где ρ — плотность ртути.
3. Так как T = const, получаем: .
, откуда (с учетом того, что 750 мм рт. ст. = 100 000 Па):

Задача 22
В горизонтальном цилиндре с гладкими стенками под массивным поршнем с площадью S находится одноатомный идеальный газ. Поршень соединён с основанием цилиндра пружиной. В начальном состоянии расстояние между поршнем и основанием цилиндра равно L, а давление газа в цилиндре равно внешнему атмосферному давлению p0 (см. рисунок).
Затем газу было передано количество теплоты Q, и в результате поршень медленно переместился вправо на расстояние b. Чему равна жёсткость пружины k?

Тепло, переданное газу, идёт на изменение его внутренней энергии и на совершением им работы:
В начальном состоянии давление и объём газа равны и
в конечном состоянии —
и
Используя уравнение Менделеева — Клапейрона
для изменения внутренней энергии получаем:
Чтобы рассчитать работу, заметим, что в каждый момент времени, когда поршень сдвинут на от начального положения давление равно
т. е. давление линейно зависит от объёма. Значит, на pV-диаграмме процесс расширения будет изображён отрезком прямой, а фигура под графиком будет являться трапецией, площадь которой равна
Заметим, что этот результат можно получить, посчитав работу газа как минус сумму работ пружины и внешней атмосферы
В итоге
Одноатомный идеальный газ участвует в процессе, для которого внутренняя энергия газа пропорциональна квадрату его объема где α — постоянная. Найдите работу A, совершенную газом в таком процессе, если известно количество теплоты Q = 800 Дж, сообщенное при этом газу.
Спрятать решение
Решение.
Внутренняя энергия одноатомного газа
Но
Тогда, учитывая данную в условии задачи зависимость внутренней энергии газа от объема
запишем
И уравнение данного процесса перепишем в виде то есть в заданном процессе давление газа линейно зависит от его объема. Работа, совершаемая газом при его расширении, равна площади под прямой, изображающей процесс на РV-диаграмме. Тогда
Изменение внутренней энергии Значит,
Из (2) Тогда, подставив в (1), получим
Ответ:
Классификатор: МКТ и термодинамика. Первый закон термодинамики
Содержание:
Идеальный газ:
Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644).
Макро- и микропараметры:
При изучении механики в 9-м классе вы познакомились с понятием «состояние механической системы тел». Параметрами этого состояния являются координаты, скорости или импульсы тел. В тепловых процессах основными физическими величинами, характеризующими состояние макроскопических тел без учёта их молекулярного строения, являются давление
Одна из важнейших задач молекулярно-кпнетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.
Идеальный газ
Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.
Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.
Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.
Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.
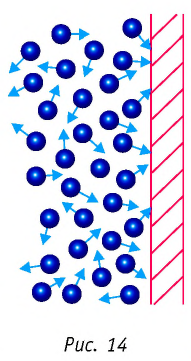
Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р идеального газа через массу 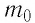
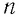
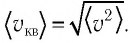
Зависимость давления газа от среднего значения квадрата скорости 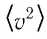
Обозначим через 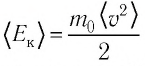
Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.
Пример №1
Баллон электрической лампы наполнен газом, плотность которого 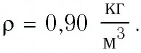
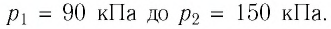
Решение. Покажем, что между плотностью р газа и концентрацией 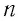
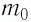
Тогда основное уравнение молекулярно-кинетической теории можно записать в виде: 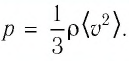
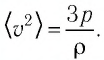
Ответ:
Пример №2
В сосуде вместимостью 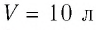
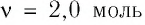
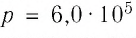
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде 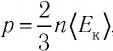
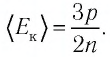
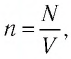
Ответ:
Уравнение состояния идеального газа
Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, масса 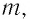
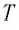
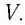
Если при переходе идеального газа из одного состояния в другое число его т
молекул 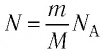
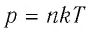
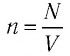
где 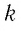
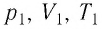
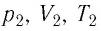
или
При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.
Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.
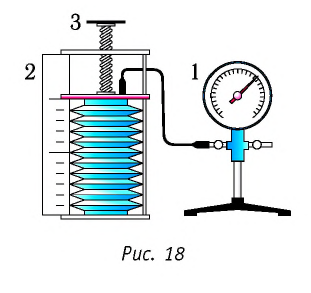
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
Измерив параметры газа 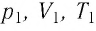
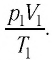
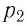
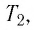
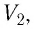
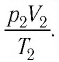
Уравнение состояния (5.2) можно применять для газов при следующих условиях:
- не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);
- не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
Поскольку число частиц 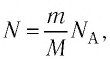
Величину, равную произведению постоянной Больцмана 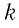
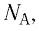
С учётом выражения (5.4) уравнение (5.3) примет вид:
Поскольку количество вещества 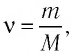
Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона—Менделеева.
Отметим, что уравнение Клапейрона—Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона-Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Давление смеси газов
В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота, кислорода, инертных газов и водорода, а также некоторых других газов.
Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.
Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Смесь идеальных газов принимают за идеальный газ.
Из истории физики:
Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766-1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801-1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778-1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.
При постоянных массе и молярной массе отношение произведения давления идеального газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Пример №3
Баллон с газом, давление которого 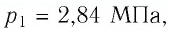
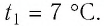
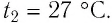
Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона—Менделеева для начального и конечного состоянии газа, считая его идеальным:
откуда
Тогда
Ответ:
Основное уравнение молекулярно-кинетической теории идеального газа
В молекулярной физике изучаются свойства вещества во всех агрегатных состояниях, в том числе и газообразном. В природе почти нет отдельно взятого газа, реальный газ атмосферы представляют собой сложную систему разных газов.
Основная задача молекулярно-кинетической теории — установление связи между макроскопическими и микроскопическими параметрами, характеризующими свойства этой сложной системы. С этой целью реальный газ сложного состава заменяется упрощенной, идеализированной моделью.
Идеальный газ:
Первый шаг в создании любой физической теории состоит в построении идеализированной модели реального объекта. Такая модель всегда имеет упрощенный вид действительности, и с ее помощью изучаются количественные и качественные закономерности и свойства реального объекта с учетом определенных ограничений.
Для изучения свойств газов в молекулярно-кинетической теории применяется идеализированная модель — «идеальный газ».
Идеальный газ — это газ, удовлетворяющий следующим условиям:
- — линейные размеры молекул во много раз меньше расстояний между ними и не принимаются во внимание. Поэтому можно сказать, что молекулы идеального газа не взаимодействуют друг с другом, то есть потенциальная энергия взаимодействия молекул идеального газа равна нулю:
Поэтому идеальный газ можно сколько угодно сжимать; —только при соударении молекул друг с другом или со стенками сосуда между ними возникают силы отталкивания;
- — соударения молекул абсолютно упругие;
- — скорость молекул может иметь произвольные значения, движение каждой молекулы подчиняется законам классической механики.
Свойства идеального газа характеризуются микроскопическими и макроскопическими параметрами и связями между ними.
Микроскопические параметры газа — это параметры, характеризующие движение молекул газа. К ним относятся масса молекулы, его скорость, импульс и кинетическая энергия поступательного движения молекулы.
Макроскопическими являются такие параметры газа, как ее давление, объем и температура, определяющие свойства газа в целом.
Основной задачей молекулярно-кинетической теории является установление взаимной связи между микроскопическими параметрами, характеризующими молекулы газа, и макроскопическими (измеряемыми) величинами, характеризующими газ.
Основное уравнение молекулярно-кинетической теории идеального газа:
Известно, что давление газа возникает в результате многочисленных непрерывных и беспорядочных соударений молекул газа о стенки сосуда, в котором он находится. Это давление равно среднему значению модуля равнодействующей силы, приходящейся на единицу площади:
В 1857 г. немецкий физик Рудольф Клаузиус (1822-1888), используя модель идеального газа, определил уравнение для давления газа, называемое основным уравнением молекулярно-кинетической теории идеального газа.
Основное уравнение молекулярно-кинетической теории идеального газа — это уравнение, связывающее макроскопический параметр газа — его давление, с микроскопическими параметрами, характеризующими молекулы газа:
Где 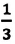
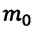
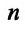
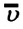
Концентрация молекул — это число молекул в единице объема:
Единица концентрации в СИ:
Средняя квадратичная скорость молекул равна корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул:
Так как среднее значение квадрата скорости молекул связано со средним значением кинетической энергии их поступательного движения, то, следовательно, и давление идеального газа зависит от среднего значения кинетической энергии молекул:
Давление идеального газа прямо пропорционально концентрации молекул и среднему значению кинетической энергии молекул.
Если принять во внимание, что плотность газа 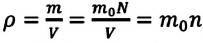
Вы исследовали идеальный газ с позиций MKT и определили связь между его макроскопическими и микроскопическими параметрами.
Уравнение Клапейрона
Связь между тремя макроскопическими параметрами (давление, объем и температура), характеризующими состояние идеального газа, определяет уравнение состояние идеального газа.
Уравнение состояния идеального газа — это уравнение, описывающее состояние газа и устанавливающее связь между параметрами его начального и конечного состояний.
Если число молекул идеального газа остается постоянным, то есть масса и молярная масса не меняются, то при переходе идеального газа из одного состояния в другое, из формул (6.2) и (6.9) имеем для этих состояний:
Где 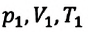
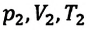
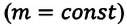
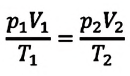
Это уравнение (6.15), характеризующее состояние идеального газа, впервые в 1834 году получил французский физик Бенуа Клапейрон (1799-1864), поэтому его назвали уравнением Клапейрона.
Отношение произведения давления идеального газа данной массы на его объем к абсолютной температуре является постоянной величиной.
Уравнение Менделеева-Клапейрона:
Приняв во внимание формулу, связывающую число частичек вещества, общую массу вещества, молярную массу и число Авогадро,
в формуле (6.14), получим:
Произведение постоянной Больцмана на постоянную Авогадро также является постоянной величиной. Оно называется универсальной газовой постоянной, обозначается буквой 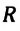
Приняв во внимание выражение (6.17) в (6.16), получаем выражение, характеризующее состояние идеального газа и называемое уравнением Менделеева-Клапейрона.
Физический смысл универсальной газовой постоянной определяется из последнего выражения.
Универсальная газовая постоянная равна отношению произведения давления и объема к абсолютной температуре одного моля любого газа.
Уравнение Менделеева-Клапейрона можно записать и в таком виде:
Где 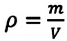
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Зависимость веса тела от вида движения
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов