Решу егэ физика геометрическая оптика

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На экране наблюдается спектр с помощью дифракционной решетки, имеющей 500 штрихов на миллиметр. Расстояние от решетки до экрана Спектральная линия в спектре первого порядка находится на расстоянии от центра экрана. Определите длину волны наблюдаемой спектральной линии.

Масляная пленка на воде при наблюдении вертикально к поверхности кажется оранжевой. Каково минимальное возможное значение толщины пленки? Показатель преломления воды 1,33, масла  — 1,47. Длина световой волны Учтите, что отражение света от оптически более плотной среды происходит с потерей полуволны, а от оптически менее плотной среды без потери полуволны.

Для наблюдения явления интерференции света используется точечный источник света и небольшой экран с двумя малыми отверстиями у глаза наблюдателя. Оцените максимальное расстояние d между малыми отверстиями в экране, при котором может наблюдаться явление интерференции света. Разрешающая способность глаза равна 1', длина световой волны

Человек читает книгу, держа ее на расстоянии 50 см от глаз. Если это для него расстояние наилучшего видения, то какой оптической силы очки позволят ему читать книгу на расстоянии 25 см?

Бассейн глубиной 4 м заполнен водой, относительный показатель преломления на границе воздух-вода 1,33. Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?

Пройти тестирование по этим заданиям

Источник

Всего: 22 1–20 | 21–22

Добавить в вариант

Луч света падает на горизонтально расположенное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если, не меняя положения источника света, повернуть зеркало на 10°, как показано на рисунке?

Ответ дайте в градусах.

Источник: ЕГЭ по физике 2022. Досрочная волна

Луч света падает на плоское зеркало. Угол между падающим и отражённым лучами равен Чему равен угол между отражённым лучом и зеркалом?

Угол между зеркалом и отражённым от него лучом равен 20° (см. рис.). Определите угол падения.

Источник: ЕГЭ по физике 2022. Досрочная волна. Вариант 2

Угол падения света на горизонтальное плоское зеркало равен 30°. Каким будет угол образованный падающим и отражённым лучами, если, не меняя положение источника света, повернуть зеркало на 10° так, как показано на рисунке? Ответ дайте в градусах.

Источник: ЕГЭ по физике 02.04.2016. Досрочная волна, ЕГЭ по физике 2022. Досрочная волна. Вариант 2

Луч света падает на плоское зеркало. Угол между падающим лучом и зеркалом равен 50°. Каков угол γ между падающим и отражённым лучами (см. рис.)?

Источник: ЕГЭ по физике. Вариант 114

На столе стоит сосуд с зеркальным дном и матовыми стенками. На дно пустого сосуда падает луч света На стенке CD сосуда при этом можно наблюдать «зайчик»  — блик отражённого луча. В сосуд наливают некоторое количество воды. Как при этом изменяются следующие физические величины: угол падения луча на дно, высота точки нахождения «зайчика», расстояние от точки отражения луча от дна сосуда до стенки CD? Отражением луча от поверхности жидкости пренебречь.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

A)  Угол падения луча на дно

Б)  Высота точки нахождения «зайчика»

B)  Расстояние от точки отражения луча от дна до стенки CD

ИХ ИЗМЕНЕНИЕ

1)  Увеличится

2)  Уменьшится

3)  Не изменится

Луч света падает на плоское зеркало. Угол между падающим и отраженным лучами равен 30°. Чему равен угол между отраженным лучом и зеркалом? (Ответ дать в градусах.)

Луч света падает на плоское зеркало. Угол отражения равен 12°. Сколько градусов угол между падающим лучом и зеркалом?

Два плоских зеркала З1 и З2 составляют друг с другом двугранный угол ° (см. рис.). Линия стыка зеркал перпендикулярна плоскости рисунка. Луч света падает на зеркало З1, распространяясь в плоскости рисунка параллельно поверхности зеркала З2. Определите угол падения этого луча на поверхность зеркала З2 после отражения от зеркала З1.

Два плоских зеркала образуют прямой двугранный угол, перпендикулярно биссектрисе которого расположена небольшая собирающая линза Л, а её фокус F находится в вершине угла (см.

рисунок). В плоскости линзы рядом с ней находится небольшой предмет П. Постройте изображение предмета, которое получится в результате двух отражений от зеркал и последующего преломления света линзой. На каком расстоянии от предмета будет находиться его изображение?

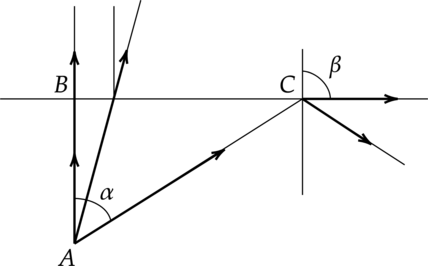
Луч света 1 падает на поверхность горизонтального зеркала А под углом = 20° (см. рис. слева). Отражаясь от зеркала А, луч света попадает на следующие два зеркала  — В и С. Сначала зеркала В и С расположены горизонтально. Затем их поворачивают: зеркало В на угол против часовой стрелки, а зеркало С устанавливают вертикально (как показано на рисунке справа).

Определите характер изменения угла отражения падающего луча 1 при отражении его от зеркал В и С.

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Угол отражения от зеркала В	Угол отражения от зеркала C

Оптическая система состоит из двух зеркал З₁ и З₂, способных вращаться вокруг горизонтальных осей, которые проходят через точки O₁ и O₂ соответственно. Изначально зеркала установлены горизонтально. Из точки A , лежащей в плоскости зеркала З₂, на зеркало З₁ направлен луч света, идущий в плоскости рисунка. Угол падения луча света на зеркало З₁ равен 30° (см. рис. 1).

Рис. 1

Рис. 2

Затем зеркало З₁ поворачивают на угол 10° по часовой стрелке (рис. 2). При этом отражённый от зеркала З₁ луч попадает в точку O₂ зеркала З₂. На какой угол требуется повернуть зеркало З₂, чтобы отражённый от него луч, минуя отражение от зеркала З₁, сразу попал обратно в точку A ? Ответ приведите в градусах.

На рисунке изображён ход светового луча 1, падающего из среды с показателем преломления n₁ на плоскую поверхность среды с показателем преломления n₂. На рисунке также показаны отражённый и преломлённый лучи.

Из приведённого ниже списка выберите все верные утверждения. Запишите цифры, под которыми они указаны.

1)  Угол падения луча на границу раздела сред равен 60 °.

2)  Угол отражения луча равен 150 °.

3)  Угол между отражённым и преломлённым лучами равен 90 °.

4)  Показатель преломления среды 1 меньше показателя преломления среды 2.

5)  Скорость распространения света в среде 1 меньше скорости распространения света в среде 2.

Верхняя грань AB прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина Луч света падает из воздуха на клин перпендикулярно грани АС, преломляется и выходит в воздух через другую грань под углом к её нормали. Определите показатель преломления материала клина.

Сделайте рисунок, поясняющий ход луча в клине.

Источник: ЕГЭ по физике 2022. Досрочная волна

На поверхность плоского зеркала, перпендикулярного оси OY, падает луч света под углом α. Отражаясь от зеркала, луч попадает на поверхность плоско-параллельной стеклянной пластины толщиной d (см. рис.).

Не изменяя угол падения луча на поверхность зеркала, пластину заменяют на другую пластину, показатель преломления которой больше, а толщина прежняя. Как в результате этого изменятся угол преломления луча при входе в пластину и расстояние вдоль оси OY между точками входа луча в пластину и выхода из неё?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Угол преломления луча при входе в пластину	Расстояние вдоль оси OY между точками входа луча в пластину и выхода из неё

Из приведённого ниже списка выберите все верные утверждения. Запишите цифры, под которыми они указаны.

1)  Угол падения луча на границу раздела сред равен 60°.

2)  Угол отражения луча равен 120°.

3)  Угол преломления луча равен 30°.

4)  Показатель преломления среды 1 больше показателя преломления среды 2.

5)  Скорость распространения света в среде 1 больше скорости распространения света в среде 2.

На рисунке слева изображены два плоских зеркала (З1 и З2) и луч, горизонтально падающий на зеркало 1. Зеркало 2 поворачивают относительно горизонтальной оси, проходящей через точку О, на угол 15º (рисунок справа). Под каким углом к горизонту будет распространяться луч, отражённый от зеркала 2?

Угол падения луча на поверхность равен 40º. Найдите угол между падающим и отраженным лучом.

Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1

Всего: 22 1–20 | 21–22

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

32. Электродинамика. Квантовая физика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Геометрическая оптика

Бассейн глубиной (H = 3) м заполнен водой, показатель преломления которой (n = 4/3.) Каков радиус светового круга на поверхности воды от электрической лампы на дне бассейна?

Рассмотрим ход лучей

Полное внутреннее отражение происходит начиная с такого значения угла падения (alpha), при котором (beta = 90^circ). По закону преломления [dfrac{sin beta}{sin alpha }= n Rightarrow sin alpha = dfrac{1}{n}] Искомая величина (BC) равна [BC= ABcdot tg alpha =dfrac{AB}{sqrt{n^2-1}}=dfrac{3text{ м}}{sqrt{dfrac{16}{9}-1}}approx 3,4 text{ м}]

Ответ: 3,4

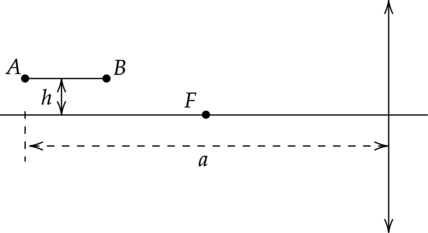
Тонкая палочка АВ длиной (l) = 10 см расположена параллельно главной оптической оси тонкой собирающей линзы на расстоянии (h) = 15 см от неё (см. рисунок). Конец А палочки располагается на расстоянии (a) = 40 см от линзы. Постройте изображение палочки в линзе и определите его длину (L). Фокусное расстояние линзы (F) = 20 cм.

“Демоверсия 2017”

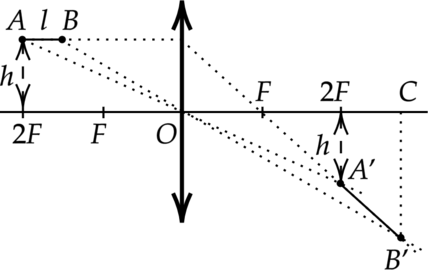
1. Построение изображения (A’B’) предмета (AB) в линзе показано на рисунке.

2. Так как точка (A) находится на расстоянии (2F) от линзы, то её изображение (A’) также находится на расстоянии (2F) от линзы, и расстояние от точки (A’) до главной оптической оси равно (h).
3. Длина изображения (A’B’) [L=sqrt{(OC-2F)^2+(B’C-h)^2}] 4. Из формулы тонкой линзы [dfrac{1}{F}=dfrac{1}{2F-l}+dfrac{1}{OC}] следует [OC=dfrac{F(2F-l)}{F-l}=60text{ см}] 5. (dfrac{B’C}{h}=dfrac{OC}{2F-l}), откуда (B’C= hdfrac{OC}{2F-l}=30text{ см}) 6. Окончательные вычисления [L=sqrt{400+225}=25text{ см}]

Ответ: 25

Точечный источник находится на главной оптической оси собирающей линзы с фокусным расстоянием 8 см на расстоянии 6 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в направлении, перпендикулярном оптической оси. С какой скоростью (в мм/с) движется изображение источника?

Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}+frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f=frac{Fd}{F-d}] [Gamma=frac{f}{d}=frac{F}{F-d}=frac{8}{2}=4]
(v) – скорость предмета относительно линзы
(u) – скорость изображения источника [u=vGamma=12 text{ мм/с}]

Ответ: 12

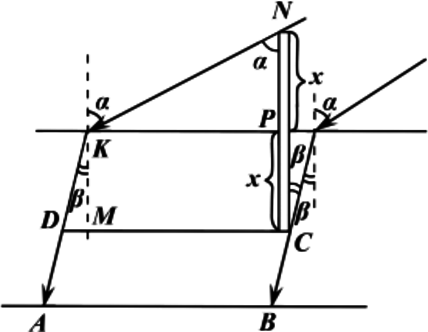
Палка, наполовину погружённая в вертикальном положении в воду, отбрасывает на дно бассейна тень длиной (l = 0, 5) м. Определите длину выступающей над водой части палки, если глубина воды равна (h = 3) м, а угол падения солнечных лучей равен (alpha = 30^circ ) (Показатель преломления воды – 4/3.) Ответ дайте в метрах и округлите до десятых

Построим ход лучей:

Закон преломления:

[sin alpha=n sin beta] (n=4 / 3) (по условию), тогда: [tg=frac{sin beta}{cos beta}=frac{sin beta}{sqrt{1-sin ^{2} beta}}=frac{frac{sin alpha}{n}}{sqrt{1-frac{sin ^{2} alpha}{n^{2}}}}=frac{sin alpha}{sqrt{n^{2}-sin ^{2} alpha}}=frac{1 / 2}{sqrt{(4 / 3)^{2}-(1 / 2)^{2}}}=frac{1 / 2}{sqrt{55 / 36}}=frac{3}{sqrt{55}}] Пусть (x) – длина надводной части палки. Палка погружена наполовину, следовательно, длина подводной части – (x .) Тогда [begin{array}{c}
l=|A B|=|C D|=|P K|+|K M| tg alpha=|P N| tg alpha+x tg beta=x tg alpha+x tg beta
x=frac{l}{tg alpha+tg beta}=frac{0,5}{frac{3}{sqrt{55}}+frac{1}{sqrt{3}}} approx 0,51 text{ м}
end{array}]

Ответ: 0,5

Бассейн глубиной (H=4) м заполнен водой, относительный показатель преломления на границе воздух-вода (n=4/3). Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?

Пусть (h) – кажущаяся высота.
По закону Снеллиуса [dfrac{sin beta}{sin alpha}= n] Рассмотрим ход лучей

Тогда [h=dfrac{tg alpha}{tg beta} H] Так как углы малые: [happrox dfrac{sin alpha}{sin beta} H approx dfrac{H}{n}=dfrac{4text{ м}}{4/3}approx 3 text{ м}]

Ответ: 3

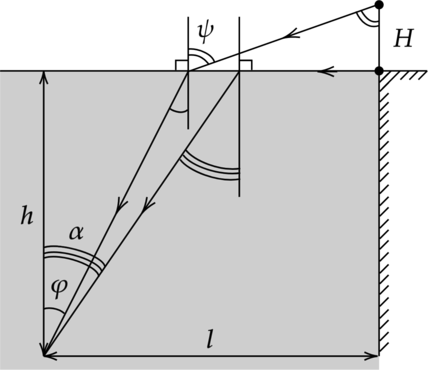
В горизонтальное дно водоема глубиной 3 м вертикально вбита свая, полностью скрытая под водой. При угле падения солнечных лучей на поверхность воды, равном 300, свая отбрасывает на дно водоёма тень длиной 0,8 м. Определите высоту сваи. Показатель преломления воды составляет (n = 4/3.) Ответ дайте в метрах и округлите до сотых.

Рассмотрим ход лучей

Из закона преломления, луч идущий горизонтально от ног тренера (угол падения равен 90(^circ)) следует по закону полного внутреннего отражения: [sin alpha = dfrac{1}{n} Rightarrow alpha = arcsin dfrac{3}{4}] Аналогично распишем закон преломления для луча идущего от головы тренера: [dfrac{sin psi}{sin varphi}= n Rightarrow sin psi = n sin varphi =dfrac{4}{3}cdot dfrac{1}{2}=dfrac{2}{3}] Из рисунка [H=(l-hcdot tg varphi)ctg psi =(l-h cdot tg varphi) dfrac{cos phi}{sin psi}= (l-h cdot tg varphi)=(l-h cdot tg varphi)dfrac{sqrt{1-sin^2 psi}}{sin psi}=dfrac{sqrt{1-n^2sin^2varphi^2}}{nsin varphi}] Подставляя числа из условий, получим [H= left(3-2,5cdot dfrac{sqrt{3}}{3}right)cdot dfrac{sqrt{5}}{2}approx 1,74text{ м}.]

Ответ: 1,74

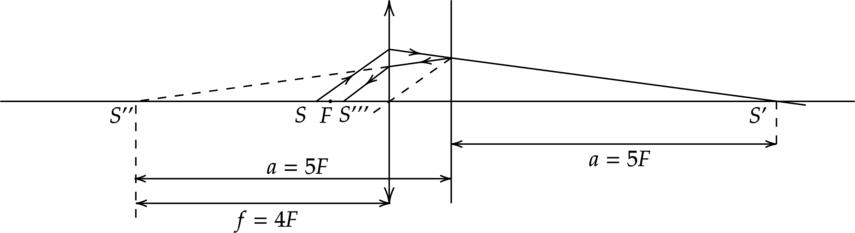
Точечный источник света находится на расстоянии 12 см от собирающей линзы с фокусным расстоянием 10 см. За линзой на расстоянии 10 см установлено плоское зеркало, перпендикулярное главной оптической оси линзы. На каком расстоянии (в см) от линзы находится изображение, образованное лучами, прошедшими через линзу после отражения от зеркала?

Формула тонкой линзы для собирающей линзы(без участия зеркала): [frac{1}{F}=frac{1}{d_1}+frac{1}{f_1}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f_1=frac{Fd_1}{d_1-F}=frac{10cdot12}{12-10}=60 text{ см}] Отразим лучи в зеркале после прохождения линзы один раз, получаем (S») – мнимый предмет, расстояние (d_2=40) см
Формула тонкой линзы для собирающей линзы (предмет S”, изображение S”’): [frac{1}{F}=-frac{1}{d_2}+frac{1}{f_2}] [f_2=frac{Fd_2}{F+d_2}=frac{10text{ см}cdot40text{ см}}{50text{ см}}=8 text{ см}]

Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

«Система подготовки учащихся к ЕГЭ.

Разбор проблемных задач

из КИМов ЕГЭ-2010»

(практикум)

1. При коротком замыкании выводов аккумулятора сила тока в цепи равна 12 А. При подключении к выводам аккумулятора электрической лампы электрическим сопротивлением 5 Ом сила тока в цепи равна 2 А. По результатам этих экспериментов определите внутреннее сопротивление аккумулятора.

Дано: Решение:

I к.з. = 12 А I к.з. = ε / r I = ε /( R+r)

R = 5 Ом ε = I к . з . ∙r ε = I ( R + r )

I = 2 А I к . з . ∙r = I ( R + r )

I к . з . ∙r = I∙R + I∙r

r — ? I к . з . ∙r — I∙r = I∙R

r ( I к . з . – I ) = I∙R

r = IR /( I к.з. — I )

r = 2 А∙5 Ом/(12А — 2А) =1 Ом

Ответ: 1 Ом

2. Найти внутреннее сопротивление и ЭДС источника тока, если при силе тока 30 А мощность во внешней цепи равна 180 Вт, а при силе тока 10 А эта мощность равна 100 Вт.

Дано: Решение:

Р 1 = 180 Вт Р 1 = I 1 2 R 1 Р 2 = I 2 2 R 2 R 1 ≠ R 2

I 1 = 30 А R 1 = Р 1 / I 1 2 R 2 = Р 2 / I 2 2

P 2 = 100 Вт ε = I 1 (R 1 + r) ε = I 2 (R 2 + r)

I 2 = 10 А ε = I 1 ( Р 1 / I 1 2 + r) ε = I 2 ( Р 2 / I 2 2 + r)

ε — ? r — ? I 1 ( Р 1 / I 1 2 + r) = I 2 ( Р 2 / I 2 2 + r )

Р 1 / I 1 + I 1 ∙ r = Р 2 / I 2 + I 2 ∙r

I 1 ∙ r – I 2 ∙ r = Р 2 / I 2 — Р 1 / I 1

r (I 1 – I 2 ) = Р 2 / I 2 — Р 1 / I 1

r (I 1 – I 2 ) = (I 1 P 2 -I 2 P 1 ) / I 1 I 2 r = (I 1 P 2 -I 2 P 1 ) / I 1 I 2 (I 1 – I 2 )

r = 0,2 Ом

ε = Р 1 / I 1 + I 1 ∙ r ε = 12 В

Ответ: 12 В; 0,2 Ом

3. Батарея состоит из 100 источников тока с ЭДС, равным 1 В и внутренним сопротивлением 0,1 Ом каждый. Источники соединили в группы по 5 штук последовательно, а эти группы соединили параллельно. Какая максимальная полезная мощность может выделяться в нагрузочном сопротивлении этой батареи?

Дано: Решение:

ε = 1 В ε – ЭДС 1 элемента, 5ε – ЭДС одной группы

r = 0,1 Ом и всей батареи

n = 5 r – внутреннее сопротивление элемента, 5 r – группы,

N = 100 5 r /20 = r /4 – внутреннее сопротивление батареи.

Р -? Максимальная мощность Р m будет при условии

равенства внутреннего и внешнего сопротивлений

R = r /4.

Через нагрузочное сопротивление идёт ток

I = 5 ε / (R + r /4) = 5 ε / (r /4 + r /4) = 5 ε∙ 4/2 r = 10 ε / r

P m = I 2 R = 100 ε 2 / r 2 ∙ r /4 = 25 ε 2 / r

P m = 250 Вт

Ответ : 250 Вт

Источник

32. Электродинамика. Квантовая физика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Геометрическая оптика

Рассмотрим ход лучей

Ответ: 3,4

“Демоверсия 2017”

1. Построение изображения (A’B’) предмета (AB) в линзе показано на рисунке.

Ответ: 25

Ответ: 12

Построим ход лучей:

Закон преломления:

[sin alpha=n sin beta] (n=4 / 3) (по условию), тогда: [tg=frac{sin beta}{cos beta}=frac{sin beta}{sqrt{1-sin ^{2} beta}}=frac{frac{sin alpha}{n}}{sqrt{1-frac{sin ^{2} alpha}{n^{2}}}}=frac{sin alpha}{sqrt{n^{2}-sin ^{2} alpha}}=frac{1 / 2}{sqrt{(4 / 3)^{2}-(1 / 2)^{2}}}=frac{1 / 2}{sqrt{55 / 36}}=frac{3}{sqrt{55}}] Пусть (x) – длина надводной части палки. Палка погружена наполовину, следовательно, длина подводной части – (x .) Тогда [begin{array}{c}
l=|A B|=|C D|=|P K|+|K M| tg alpha=|P N| tg alpha+x tg beta=x tg alpha+x tg beta \
x=frac{l}{tg alpha+tg beta}=frac{0,5}{frac{3}{sqrt{55}}+frac{1}{sqrt{3}}} approx 0,51 text{ м}
end{array}]

Ответ: 0,5

Пусть (h) – кажущаяся высота.
По закону Снеллиуса [dfrac{sin beta}{sin alpha}= n] Рассмотрим ход лучей

Тогда [h=dfrac{tg alpha}{tg beta} H] Так как углы малые: [happrox dfrac{sin alpha}{sin beta} H approx dfrac{H}{n}=dfrac{4text{ м}}{4/3}approx 3 text{ м}]

Ответ: 3

Рассмотрим ход лучей

Ответ: 1,74

Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Разделы сайта

Геометрическая оптика

Преломление — подготовка к олимпиадам — 2

Решаем задачи на закон Снелла. Будут призмы и неровная поверхность воды…
Задача 1.
Поверхности воды касается равнобедренная стеклянная призма АВС (см. рисунок). Луч света, падающий из воздуха под углом на грань АС, после прохождения призмы…

Преломление — подготовка к олимпиадам

Решаем задачи по геометрической оптике — готовимся к олимпиадам. Здесь снова зеркало и закон Снелла.
Задача 1.
По столу катится шарик со скоростью . В противоположном направлении со скоростью перемещают…

14.09.2022 08:30:15 | Автор: Анна

Зеркала — олимпиадная подготовка

Продолжаем готовиться к Всероссу и решаем с ребятами сложные задачки по оптике. В этой статье — зеркала.
Задача 1.
Машина удаляется с постоянной скоростью от большой зеркальной витрины, двигаясь по прямой. На машине установлена лампа Л, которая светит равномерно во все стороны с мощностью

12.09.2022 08:08:07 | Автор: Анна

Задачи с двумя линзами

Предлагаю вашему вниманию несколько задач, в которых обязательно присутствуют две линзы. Линзы могут быть – обе — собирающими, и собирающей в комбинации с рассеивающей.

Задача 1.
Две собирающие линзы с фокусными расстояниями см и

22.09.2020 05:59:10 | Автор: Анна

Использование графиков при решении задач с линзами — 2

Тема этой и предыдущей статей – использование графиков при решении задач на оптику, а именно – задач с линзами. Конспект занятий Пенкина М.А.
Сначала давайте построим график, использование которого сильно облегчит решение задач.
Собирающая линза. Для нее известно, что если расстояние от предмета до линзы меньше, чем фокусное,…

30.07.2019 06:05:08 | Автор: Анна

Тонкие линзы: решение задач с помощью графика

Тема этой и следующей статей – использование графиков при решении задач на оптику, а именно – задач с линзами. Конспект занятий Пенкина М.А.
Сначала давайте построим график, использование которого сильно облегчит решение задач.
Собирающая линза. Для нее известно, что если расстояние от предмета до линзы меньше, чем…

28.07.2019 11:59:10 | Автор: Анна

Камень, брошенный под углом к горизонту, и его тень

Откуда задача – сказать не могу. Решение свое отыскала в куче неразобранных бумаг, текст воспроизвожу по памяти.
Задача. Камень бросили со скоростью под углом

16.07.2019 06:02:30 | Автор: Анна

Линзы: мнимый предмет

Этой статьей продолжается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. В статье собраны задачи со сходящимися пучками лучей, когда предмет — мнимый. Начало здесь, здесь и здесь.
Задача 1.
Предмет…

16.08.2017 18:46:07 | Автор: Анна

Линзы -3

Этой статьей продолжается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. Начало здесь и здесь.
Задача 1.
Высота пламени свечи 5 см. Линза дает на экране изображение этого пламени высотой 15 см. Не…

14.08.2017 10:43:14 | Автор: Анна

Линзы 2: оптическая сила

Этой статьей продолжается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. Начало здесь, более сложные — в следующих статьях.
Задача 1.
Предмет расположен на расстоянии 40 см от линзы с оптической силой 2 дптр. Как…

12.08.2017 10:53:06 | Автор: Анна

Линзы 1

Этой статьей начинается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. Начнем с простых задач, более сложные — в следующих статьях.
Задача 1.
На рисунке даны положение главной оптической оси линзы, источник света

10.08.2017 10:30:55 | Автор: Анна

Геометрическая оптика: глаз и очки

В этой статье решаем задачи про очки – несложные. Глаз – это тоже линза, и если фокусное расстояние этой линзы избыточное или недостаточное, то очки могут поправить дело.
У хорошо видящего человека лучи света, попадающие в глаз, преломляются хрусталиком так, что попадают прямо на сетчатку –…

08.08.2017 20:23:43 | Автор: Анна

Геометрическая оптика: призмы

В этой статье решаем задачи с призмами. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача 1.
Монохроматический луч падает нормально на боковую поверхность призмы, преломляющий угол которой равен . Показатель преломления материала призмы для этого луча равен 1,5….

06.08.2017 20:17:29 | Автор: Анна

Геометрическая оптика: пластинки

В этой статье решаем задачи с пластинками – средние по сложности. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача 1. Прямоугольная стеклянная пластинка толщиной 4 см имеет показатель преломления 1,6. На ее поверхность падает луч света под углом . Определите,…

04.08.2017 18:45:18 | Автор: Анна

Закон преломления Снеллиуса — 3

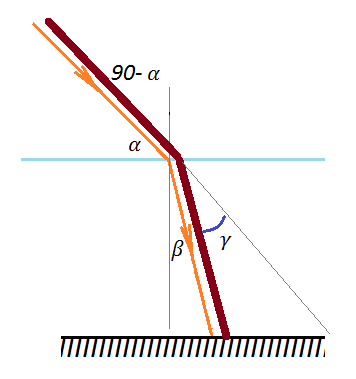
В этой статье будут представлены задачи на показатель преломления – средние по сложности. Здесь вы найдете простые задачи, здесь – задачи средние по сложности, но более простые, чем в этой статье. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача…

02.08.2017 18:21:55 | Автор: Анна

Геометрическая оптика: закон Снеллиуса — 2

В этой статье будут представлены задачи на показатель преломления – средние по сложности. Будем применять закон преломления Снеллиуса, а также геометрические знания. Начало здесь.
Задача 1.
Луч света падает на границу раздела двух сред под углом

30.07.2017 18:03:51 | Автор: Анна

Геометрическая оптика: закон Снеллиуса — 1

В этой статье я будут представлены задачи на показатель преломления – самые простые, стартовые задачи в одно действие. Будем применять закон преломления Снеллиуса.
Задача 1.
Определите показатель преломления скипидара и скорость распространения света в скипидаре, если известно, что при угле падения

28.07.2017 17:56:41 | Автор: Анна

Геометрическая оптика: зеркала

В этой статье собраны задачи на плоское зеркало. Угол падения равен углу отражения – это все, что нужно помнить для их решения.
Задача 1.
Почему мы не видим лица фехтовальщика, если оно закрыто частой сеткой, но она не мешает самому фехтовальщику хорошо видеть окружающие предметы?
Снаружи…

26.07.2017 17:50:43 | Автор: Анна

Геометрическая оптика: тень

Этой статьей я открываю серию статей по геометрической оптике. Все, что нам понадобится – это знания по элементарной тригонометрии: геометрические определения синуса, косинуса, тангенса угла и понятие о подобии треугольников.
Задача 1.
Ученик заметил, что палка длиной 1,2 м, поставленная вертикально, отбрасывает тень длиной 0,8…

24.07.2017 17:43:23 | Автор: Анна

Система из двух зеркал

В этой статье мы научимся строить изображения в системе из двух зеркал. Надо понимать, что предмет не обязательно должен находиться непосредственно перед зеркалом, чтобы можно было увидеть его изображение. Ведь часто мы видим, находясь в одной из комнат, что происходит в другой в зеркале, которое…

22.07.2017 17:34:21 | Автор: Анна

Задачи вступительного экзамена в Академическую гимназию СПбГУ по физике (прошлых лет)

В статье приведен типовой вариант задания вступительных испытаний по физике в Академическую гимназию СПбГУ, в класс физико-математического направления. Задачи разбиты по уровням сложности, есть очень непростые для среднего школьника.
Часть А.
Задача 1.
На рисунке приведен график зависимости скорости от времени для тела, движущегося прямолинейно. В…

06.06.2017 15:22:24 | Автор: Анна

Рыбак на льду

Задача о рыбаке на зимней рыбалке. Эх, оказаться бы на таком прозрачном льду, что сквозь него дно видно! И какими должны быть морозы, чтобы встал лед такой толщины, вы только представьте! Кстати, прозрачность льда зависит от наличия в нем пузырьков воздуха. Если лед замерзает медленно,…

10.05.2017 09:43:44 | Автор: Анна

Последние записи

Облако меток

Архивы

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 17 № 77

На тонкую собирающую линзу с главным фокусом F падает расходящийся пучок света, ограниченный лучами 1 и 2. Прошедший через линзу пучок света правильно изображен на рисунке, обозначенном цифрой:

Источник: Централизованное тестирование по физике, 2016

На рисунке изображены два зеркала, угол между плоскостями которых Если угол падения светового луча АО на первое зеркало то угол отражения ghama этого луча от второго зеркала равен:

Примечание. Падающий луч лежит в плоскости рисунка.

Источник: Централизованное тестирование по физике, 2015

На рисунке изображены два зеркала, угол между плоскостями которых = 75°. Если угол падения светового луча АО на первое зеркало = 55°, то угол отражения ghama этого луча от второго зеркала равен:

Примечание. Падающий луч лежит в плоскости рисунка.

Источник: Централизованное тестирование по физике, 2015

Источник: Централизованное тестирование по физике, 2016

На рисунке изображены два зеркала, угол между плоскостями которых = 85°. Если угол падения светового луча АО на первое зеркало = 50°, то угол отражения ghama этого луча от второго зеркала равен:

Примечание. Падающий луч лежит в плоскости рисунка.

Источник: Централизованное тестирование по физике, 2015

Пройти тестирование по этим заданиям

Источник

Геометрическая оптика

Геометрическая оптика

Разделы сайта

Рекомендую

Геометрическая оптика

Преломление — подготовка к олимпиадам — 2

Преломление — подготовка к олимпиадам

Зеркала — олимпиадная подготовка

Задачи с двумя линзами

Использование графиков при решении задач с линзами — 2

Тонкие линзы: решение задач с помощью графика

Камень, брошенный под углом к горизонту, и его тень

Линзы: мнимый предмет

Линзы -3

Линзы 2: оптическая сила

Линзы 1

Геометрическая оптика: глаз и очки

Геометрическая оптика: призмы

Геометрическая оптика: пластинки

Закон преломления Снеллиуса — 3

Геометрическая оптика: закон Снеллиуса — 2

Геометрическая оптика: закон Снеллиуса — 1

Геометрическая оптика: зеркала

Геометрическая оптика: тень

Система из двух зеркал

Задачи вступительного экзамена в Академическую гимназию СПбГУ по физике (прошлых лет)

Рыбак на льду

Последние записи

Облако меток

Архивы

Новое и интересное на сайте: