Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д9 B15 № 1702
При освещении дифракционной решетки монохроматическим светом на экране, установленном за ней, возникает дифракционная картина, состоящая из темных и светлых вертикальных полос. В первом опыте расстояние между светлыми полосами оказалось больше, чем во втором, а во втором больше, чем в третьем. В каком из ответов правильно указана последовательность цветов монохроматического света, которым освещалась решетка?
1) 1 — красный, 2 — зеленый, 3 — синий
2) 1 — красный, 2 — синий, 3 — зеленый
3) 1 — зеленый, 2 — синий, 3 — красный
4) 1 — синий, 2 — зеленый, 3 — красный
2
Задания Д9 B15 № 1705
В некотором спектральном диапазоне угол преломления лучей на границе воздух — стекло падает с увеличением частоты излучения. Ход лучей для трех основных цветов при падении белого света из воздуха на границу раздела показан на рисунке.
Цифрам соответствуют цвета
1) 1 — красный, 2 — зёленый, 3 — синий
2) 1 — красный, 2 — синий, 3 — зёленый
3) 1 — зёленый, 2 — синий, 3 — красный
4) 1 — синий, 2 — зёленый, 3 — красный
3
Задания Д9 B15 № 1715
Технология «просветления» объективов оптических систем основана на использовании явления
1) дифракция
2) интерференция
3) дисперсия
4) поляризация
4
Задания Д9 B15 № 1725
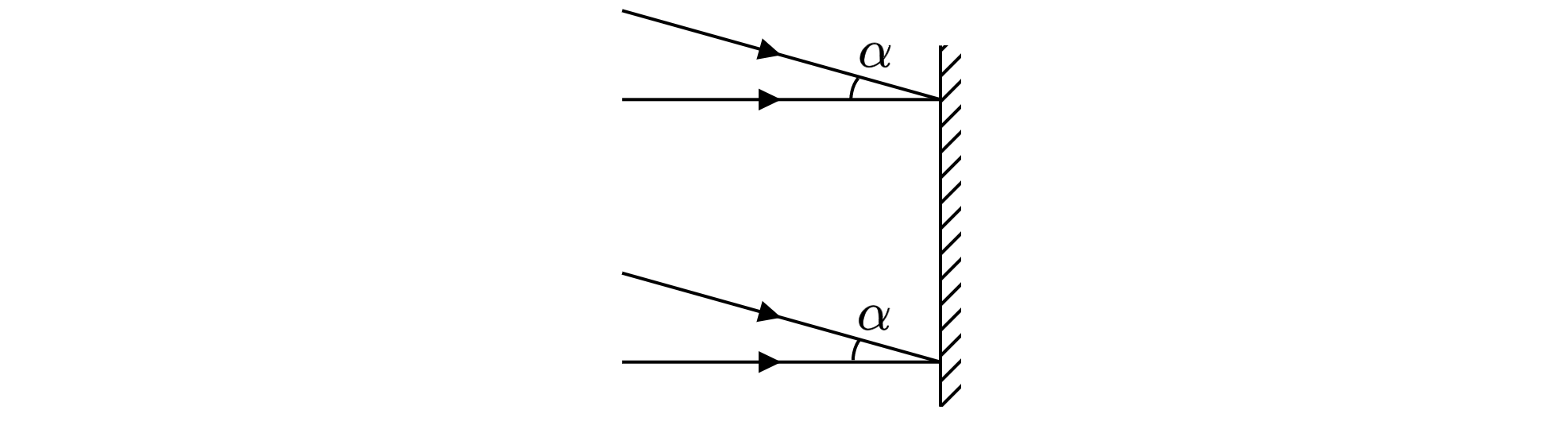
Луч от лазера направляется перпендикулярно плоскости дифракционной решетки (см. рис.) в первом случае с периодом d, а во втором — с периодом 2d.
Длина волны света такая, что первые дифракционные максимуму отклоняются на малые углы. Расстояние между нулевым и первым дифракционным максимумами на удаленном экране
1) в обоих случаях одинаково
2) во втором случае приблизительно в 2 раза меньше
3) во втором случае приблизительно в 2 раза больше
4) во втором случае приблизительно в 4 раза больше
5
Задания Д9 B15 № 1730
Лучи от двух лазеров, свет которых соответствует длинам волн и
поочередно направляются перпендикулярно плоскости дифракционной решетки (см. рис.).
Период дифракционной решетки такой, что первые дифракционные максимумы отклоняются на малые углы. Расстояние между первыми дифракционными максимумами на удаленном экране
1) в обоих случаях одинаково
2) во втором случае приблизительно в 1,5 раза больше
3) во втором случае приблизительно в 1,5 раза меньше
4) во втором случае приблизительно в 3 раза больше
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 42 1–20 | 21–40 | 41–42
Добавить в вариант
Задания Д9 B15 № 1715
Технология «просветления» объективов оптических систем основана на использовании явления
1) дифракция
2) интерференция
3) дисперсия
4) поляризация
Задания Д11 B20 № 2004
Явление интерференции электронов можно объяснить, используя представление об электронах как о потоке частиц, обладающих
1) электрическим зарядом
2) малой массой
3) малыми размерами
4) волновыми свойствами
Задания Д9 B15 № 1803
Два источника испускают электромагнитные волны частотой c одинаковыми начальными фазами. Максимум интерференции будет наблюдаться в точке пространства, для которой разность хода волн от источников равна
1) 0,9 мкм
2) 1,0 мкм
3) 0,3 мкм
4) 1,2 мкм
Задания Д9 B15 № 1806
Сложение в пространстве когерентных волн, при котором образуется постоянное во времени пространственное распределение амплитуд результирующих колебаний, называется
1) интерференцией
2) поляризацией
3) дисперсией
4) преломление
Задания Д9 B15 № 2328
При освещении мыльной пленки белым светом наблюдаются разноцветные полосы. Какое физическое явление обусловливает появление этих полос?
1) дифракция
2) интерференция
3) дисперсия
4) поляризация
Установите соответствие между физическими опытами и физическими явлениями, которые наблюдаются в этих опытах. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЙ ОПЫТ
А) Если направить красный свет лазера на две прорезанные в картоне узкие щели, близко расположенные друг к другу, то на расположенном позади картона экране будет видна система красных и тёмных полос.
Б) Если направить поток электронов на кристалл, поставив за кристаллом фотопластинку, то после проявления фотопластинки на ней будет видна картина, состоящая из симметрично расположенных светлых пятен.
ФИЗИЧЕСКОЕ ЯВЛЕНИЕ
1) дифракция
2) давление света
3) фотоэффект
4) интерференция
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Выберите все верные утверждения о физических явлениях, величинах и закономерностях.
Запишите в ответ их номера.
1) Вектор скорости материальной точки всегда направлен по касательной к её траектории.
2) В процессе кристаллизации постоянной массы вещества его внутренняя энергия увеличивается.
3) Разноимённые точечные электрические заряды отталкиваются друг от друга.
4) Явления интерференции и дифракции могут наблюдаться в любом диапазоне электромагнитных волн.
5) При переходе атома из одного стационарного состояния в другое стационарное состояние атом испускает или поглощает фотон.
Выберите все верные утверждения о физических явлениях, величинах и закономерностях.
Запишите в ответе их номера.
1) Плавание тел вследствие действия силы Архимеда возможно только в жидкостях.
2) Для конденсации жидкости ей необходимо сообщить некоторое количество теплоты.
3) В металлических проводниках электрический ток представляет собой упорядоченное движение электронов, происходящее на фоне их хаотического теплового движения.
4) Просветление линз и объективов базируется на явлении интерференции света.
5) Фотоны могут двигаться в вакууме со скоростями, равными 300 000 км/с.
Задания Д9 B15 № 1635
Одним из доказательств того, что электромагнитные волны поперечные, является существование у них свойства
1) поляризации
2) отражения
3) преломления
4) интерференции
Задания Д9 B15 № 1833
Какое явление служит доказательством поперечности световых волн?
1) интерференция света
2) дифракция света
3) поляризация света
4) дисперсия света
Задания Д11 B20 № 2041
Какое физическое явление служит доказательством квантовой природы света?
1) интерференция
2) дифракция
3) поляризация
4) фотоэффект
Задания Д9 B15 № 4879
Дифракцией света объясняется спектральное разложение
А. солнечного света призмой.
Б. белого света, прошедшего сначала малое отверстие, а затем — два близко расположенных отверстия.
Верно(-ы) утверждение(-я):
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 5., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 6.
Задания Д9 B15 № 1733
На плоскую непрозрачную пластину с двумя узкими параллельными щелями падает по нормали плоская монохроматическая волна из зеленой части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из фиолетовой части видимого спектра
1) расстояние между интерференционными полосами увеличится
2) расстояние между интерференционными полосами уменьшится
3) расстояние между интерференционными полосами не изменится
4) интерференционная картина станет невидимой для глаза
Задания Д9 B15 № 1809
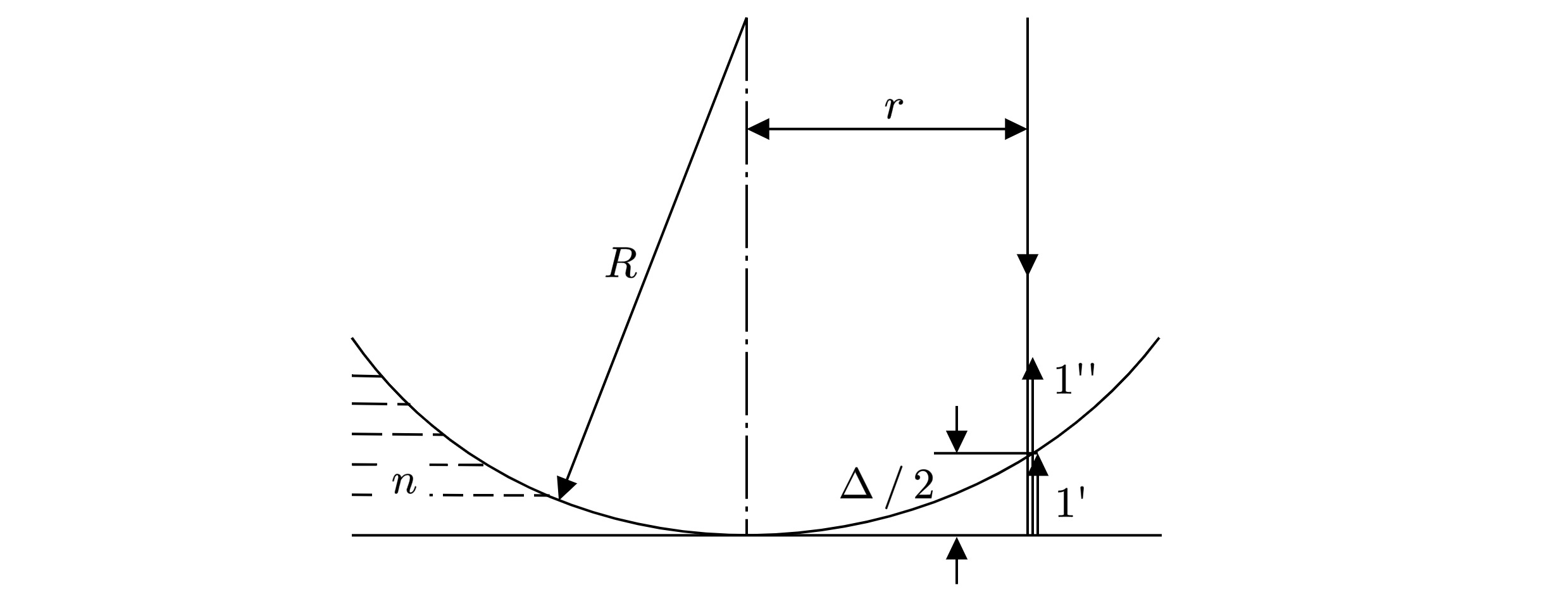
Одна сторона толстой стеклянной пластины имеет ступенчатую поверхность, как показано на рисунке. На пластину перпендикулярно ее поверхности падает световой пучок. Который после отражения от пластины собирается линзой. Длина падающей световой волны
При каком из указанных значений высоты ступеньки d интенсивность света в фокусе линзы будет минимальной?
Задания Д9 B15 № 3798
На поверхность тонкой прозрачной плёнки нормально падает пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с чуть бόльшим показателем преломления её окраска будет (дисперсией пренебречь)
1) полностью зелёной
2) ближе к красной области спектра
3) ближе к синей области спектра
4) полностью чёрной
Источник: Демонстрационная версия ЕГЭ—2013 по физике.
Задания Д9 B15 № 4949
В классическом опыте Юнга по дифракции пучок света, прошедший через узкое отверстие А, освещает отверстия В и С, за которыми на экране возникает интерференционная картина (см. рисунок).
Если уменьшить расстояние d вдвое, то
1) интерференционная картина сместится по экрану вправо, сохранив свой вид
2) интерференционная картина не изменится
3) расстояние между интерференционными полосами увеличится
4) расстояние между интерференционными полосами уменьшится
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 4.
Задания Д9 B15 № 5159
В классическом опыте Юнга по дифракции пучок света, прошедший через узкое отверстие А, освещает отверстия В и С, за которыми на экране возникает интерференционная картина (см. рисунок).
Если увеличить расстояние d вдвое, то
1) расстояние между интерференционными полосами увеличится
2) расстояние между интерференционными полосами уменьшится
3) интерференционная картина не изменится
4) интерференционная картина сместится по экрану влево, сохранив свой вид
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 2.
Задания Д9 B15 № 5194
В классическом опыте Юнга по дифракции пучок света, прошедший через узкое отверстие А, освещает отверстия В и С, за которыми на экране возникает интерференционная картина (см. рисунок).
Если уменьшить расстояние l вдвое, то
1) расстояние между интерференционными полосами уменьшится
2) расстояние между интерференционными полосами увеличится
3) интерференционная картина не изменится
4) интерференционная картина сместится по экрану вправо, сохранив свой вид
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 3., ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 5.
Задания Д9 B15 № 6346
Ученик наблюдал явление дифракции, глядя на источник света через дифракционную решётку. Затем он решил получить дифракционную картину на экране с помощью этой же дифракционной решётки, неподвижно установленной на оптической скамье, и тонкой собирающей линзы, направляя вдоль нормали к поверхности решётки монохроматический свет (см. рис.). Однако дифракционной картины на экране не получилось.
Для того чтобы наблюдать на экране картину, нужно
1) передвинуть экран влево, поместив его в фокус линзы
2) передвинуть экран вправо как можно дальше от линзы
3) передвинуть дифракционную решётку вправо, поместив её в фокус линзы
4) передвинуть дифракционную решётку влево, поместив её как можно дальше от линзы
Задания Д9 B15 № 6381
Ученик наблюдал явление дифракции, глядя на источник света через дифракционную решётку. Затем он решил получить дифракционную картину на экране с помощью этой же дифракционной решётки, неподвижно установленной на оптической скамье, и тонкой собирающей линзы, направляя вдоль нормали к поверхности решётки монохроматический свет (см. рис.). Однако дифракционной картины на экране не получилось.
Для того чтобы наблюдать на экране картину, нужно
1) переместить линзу вправо так, чтобы её фокус оказался в плоскости экрана
2) переместить линзу влево так, чтобы её фокус оказался в плоскости дифракционной решётки
3) переместить экран вправо, отодвинув его как можно дальше от линзы
4) переместить дифракционную решётку влево, отодвинув её как можно дальше от линзы
Всего: 42 1–20 | 21–40 | 41–42
Дифракционная решётка, имеющая 1000 штрихов на 1 мм своей длины, освещается параллельным пучком монохроматического света с длиной волны 420 нм. Свет падает перпендикулярно решётке. Вплотную к дифракционной решётке, сразу за ней, расположена тонкая собирающая линза. За решёткой на расстоянии, равном фокусному расстоянию линзы, параллельно решётке расположен экран, на котором наблюдается дифракционная картина. Выберите все верные утверждения.
1) Максимальный порядок наблюдаемых дифракционных максимумов равен 2.
2) Если увеличить длину волны падающего света, то максимальный порядок наблюдаемых дифракционных максимумов увеличится.
3) Если уменьшить длину волны падающего света, то расстояние на экране между нулевым и первым дифракционными максимумами уменьшится.
4) Если заменить линзу на другую, с бóльшим фокусным расстоянием, и расположить экран так, чтобы расстояние от линзы до экрана по-прежнему было равно фокусному расстоянию линзы, то расстояние на экране между нулевым и первым дифракционными максимумами уменьшится.
5) Если заменить дифракционную решётку на другую, с бóльшим периодом, то угол, под которым наблюдается первый дифракционный максимум, увеличится.
3.6.10 Интерференция света. Когерентные источники. Условия наблюдения максимумов и минимумов в интерференционной картине от двух синфазных когерентных источников
Взаимодействие световых волн
Для упрощения рассмотрения процессов взаимодействия нескольких световых волн, рассмотрим две волны. Рассматриваемые нами процессы могут происходить с любыми существующими волнами (светом, электромагнитными, механическими и др.).
Все превращения, которые происходят в результате наложения волн, наблюдаются в результате сложения их характеристик (амплитуды, фазы и др.).
Если накладываются две волны с одинаковыми фазами, то они соединяются в одну, с большей амплитудой.
Если же волны приходят в противофазе, то происходит постоянное гашение максимума минимумом, в результате чего волна выравнивается в ноль.
Когерентность
Когерентные волны — волны, имеющие одинаковую фазу и постоянную разность фаз (как на картинках выше)
Условия max и min
Кроме перечисленных выше физических величин, важна разность хода.
Для указанных когерентных волн, разностью хода будет разность между отрезками S1P и S2P.
Как можно заметить на рисунке, разность хода между волнами равна длине одной волны — одна имеет три полных длины волны, а вторая — четыре. В точке Р данные волны складываются вместе, а так как мы знаем, что подобное сложение приводит к увеличению амплитуды, то говорят, что наблюдается интерференционный максимум.
Условие максимума: Разность хода волн равна целому числу волн.
Теперь же рассмотрим иную ситуацию сложения двух когерентных волн:
В данном случае фазы отличаются на одинаковое значение, волны находятся в противофазе.
В таком случае наблюдается интерференционный минимум.
Условие минимума: Разность хода равна некоторому количеству полуцелых длин волн.
Интерференция
В результате того, что в некоторых местах наложения волн наблюдается максимум, а в некоторых минимум, появляется интерференционная картина. Однако стоит заметить, что данное явление справедливо только для когерентных волн.
На рисунке изображена интерференция от двух когерентных источников. Как можно заметить на рисунке. Нет конкретного разделения черных и белых полос, существуют промежуточные значения, которые рассматриваются серым цветом. То же можно наблюдать и в результате двух малых источников света — на экране мы будем видеть плавные переходы от черного до белого цвета. Белый — максимум, черный — минимум.
Интерференция в тонких пленках
Все мы наблюдали ситуацию, когда свет, преломляясь на мыльном пузыре, приобретает радужную окраску. Все это происходит в результате интерференции.
Представим себе тонкую прозрачную среду, на которую попадает луч. Как мы знаем, он отражается от нее и преломляется. Как можно заметить, в результате данного процесса выходят два луча. А так как они выпущены от одного источника, то они интерферентны, но с разностью хода. В результате данной разницы хода, белый цвет будет разделяться на цвета радуги, и в зависимости от толщины пленки, выходить будет какой-то один.
Ту же ситуацию можно наблюдать и при соприкосновении стеклышка и линзы.
Е
максимумы:
минимумы:
3.6.11 Дифракция света. Дифракционная решётка
Дифракция света
Волны могут огибать препятствия, имеющиеся на пути.
Дифракция — это процесс, при котором волна меняет свою траекторию движения, в результате появившегося на пути препятствия.
Аналогичная картина возможна, когда широкая река перетекает в некоторую часть через узкое отверстие. Волны от отверстия начнут распространяться во всех направлениях.
В центре имеется самое яркое пятно — оно, обычно, находится напротив отверстия, а вокруг наблюдаем волны, образованные источником света в результате огибания препятствия.
Дифракционная решётка — приспособление, имеющее большое количество преград, расположенных на небольшом расстоянии друг от друга. Получить её достаточно просто. Для этого необходимо взять тонкую ткань и взглянуть через нее на свет. Свет огибает небольшие преграды, и позволяют отчетливо наблюдать за происходящим.
Дифракционная решетка характеризуется шириной щелей, промежутков между ними, а также периодом решетки, равным сумме ширины щелей и промежутков:
Условие максимумов для дифракционной решетки:
Условие минимумом:
В данной формуле все величины Вам знакомы, кроме угла — это угол падения света.
Белый свет
До этого момента мы рассматривали, как ведет себя монохроматический свет. Но что же будет в случае, когда свет будет белым, то есть состоящий из всех цветов радуги? Данную картину мы наблюдаем с Вами постоянно, когда смотрим на каплю бензина, на компакт диск. В данном случае белый свет разделится на все цвета радуги.
Условие наблюдения главных максимумов при нормальном падении монохроматического света с длиной волны λ на решётку с периодом d:
3.6.12 Дисперсия света
Дисперсия — это процесс, при котором белый цвет разделяется в спектр, в случае специальных условий.
Тема 29.
Электродинамика. Квантовая физика (Расчетная задача высокого уровня сложности)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
электродинамика. квантовая физика (расчетная задача высокого уровня сложности)
29.01Отражение и преломление
29.02Формула тонкой линзы
29.03Оптические системы
29.04Скорость изображения в различных оптических системах
29.05Волновая оптика
29.06Фотоэффект
29.07Ядерные реакции. Энергия связи
29.08Энергетические уровни в атоме
29.09Квантовая физика
Решаем задачи
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: условие наблюдения
максимумов (или минимумов) в интерференционной картине от двух когерентных источников
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Пусть геометрическая разность хода лучей, идущих на расстоянии
от главной оптической оси
линзы (1’ и 1”). 1’ – отражен от верхней поверхности пластины, 1” – отражен от нижней поверхности
пластины (см. рис.).
По теореме Пифагора имеем
Так как разность ходу мала, то и приближенно получаем
Поскольку волны 1
и 1’ распространяются в бензоле, заполняющем зазор между линзой и пластинкой, оптическая разность
хода между волнами 1’ и 1” равна
Дополнительный фазовый набег, равный , волна 1’ приобретает при отражении волны 1 от
оптически более плотной среды. Таким образом, условие первого интерференционного минимума имеет
вид . Объединяя записанные выражения, получаем
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: условие наблюдения
максимумов (или минимумов) в интерференционной картине, расписана разность хода
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Запишем условие максимума:
где и
– расстояния от источников до данной точки на экране (см. рисунок),
– целое
число (порядок интерференционного максимума). Для волн первого максимума найдем из
рисунка:
Вычтем второе из первого
Разложим разность квадратов:
Учитывая, что ,
, можно приближенно положить
. Тогда
. Объединяя это равенство с записанным выше условием максимума первого порядка,
получаем
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: условие наблюдения
максимумов (или минимумов) в интерференционной картине от двух когерентных источников
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
НПокрытие в отраженном свете будет казаться зеленым, если в направлении, в котором проводится
наблюдение, в результате интерференции будут усиливаться волны с длиной , соответствующей
зеленому цвету. Ход двух интерферирующих лучей изображен на рисунке. Луч 1 преломляется в
верхней грани пластины, затем отражается от нижней и вновь, преломившись в верхней пластине
выходит на воздух. Луч 2, падая в точке выхода из пластины луча 1, сразу отражается от верхней части
пластины (см .рис.).
Найдём длину пути первого луча, она составляет . При этом из прямоугольного треугольника с
углом :
По закону Снеллиуса:
тогда
Откуда оптическая длина пути:
Разность хода первого и второго луча до падения на покрытие (см. рисунок) составляет
величину
определим из рисунка через
:
Отсюда
Разность хода между интерферирующими лучаи равна:
Амплитуды волн будут складываться, если наблюдается максимум , при этом минимальность
толщины соответствует минимальности , то есть
и
. Отсюда получаем, что минимальная
толщина покрытия
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: сказано в каком случае
наблюдается зеленый цвет, сделан поясняющий рисунок, записан закон Снеллиуса, расписана разность
хода )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
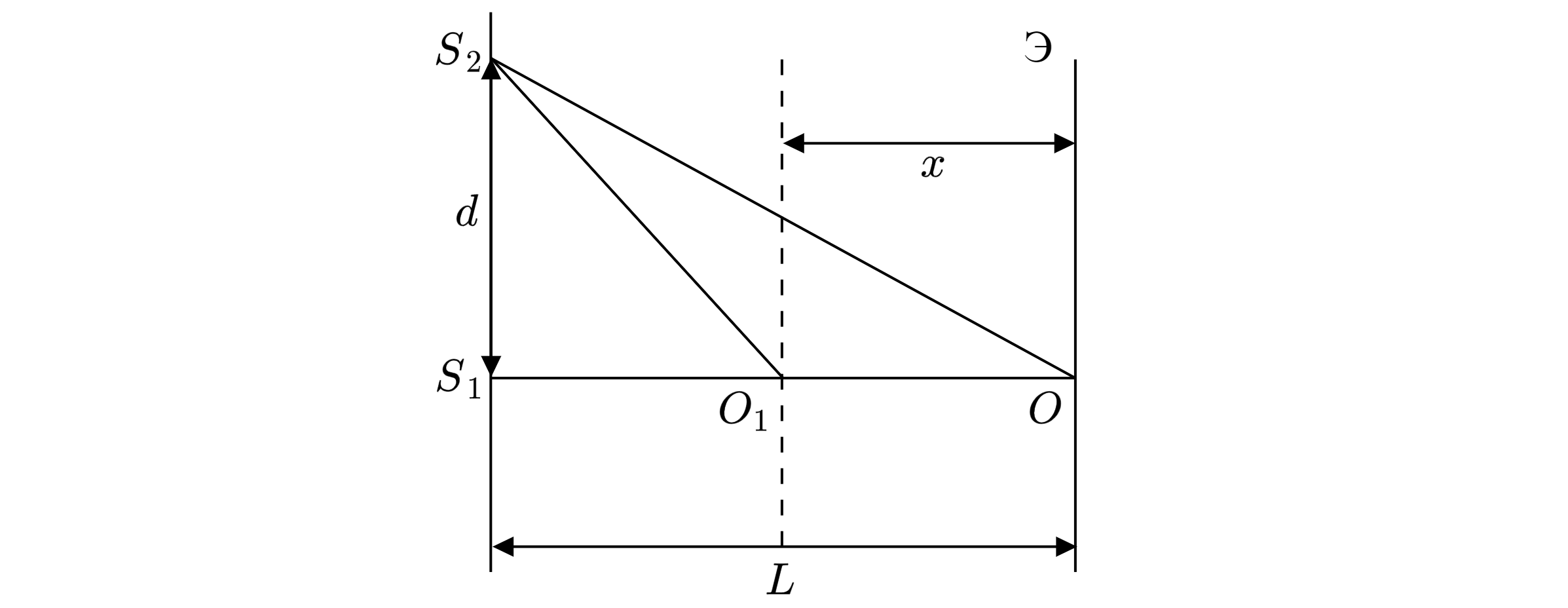
При удалении источника потемнение возникает в точке
при условии первого минимума, то
есть при условии:
где – длина волн.
Из прямоугольного треугольника:
Так как , то
можно считать малой величиной и
При приближении экрана на , то второй минимум в точке
будет соответствовать разности
хода
или
Аналогично
Приравнивая (1) и (2), получаем:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: условие наблюдения
максимумов (или минимумов) в интерференционной картине от двух когерентных источников
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
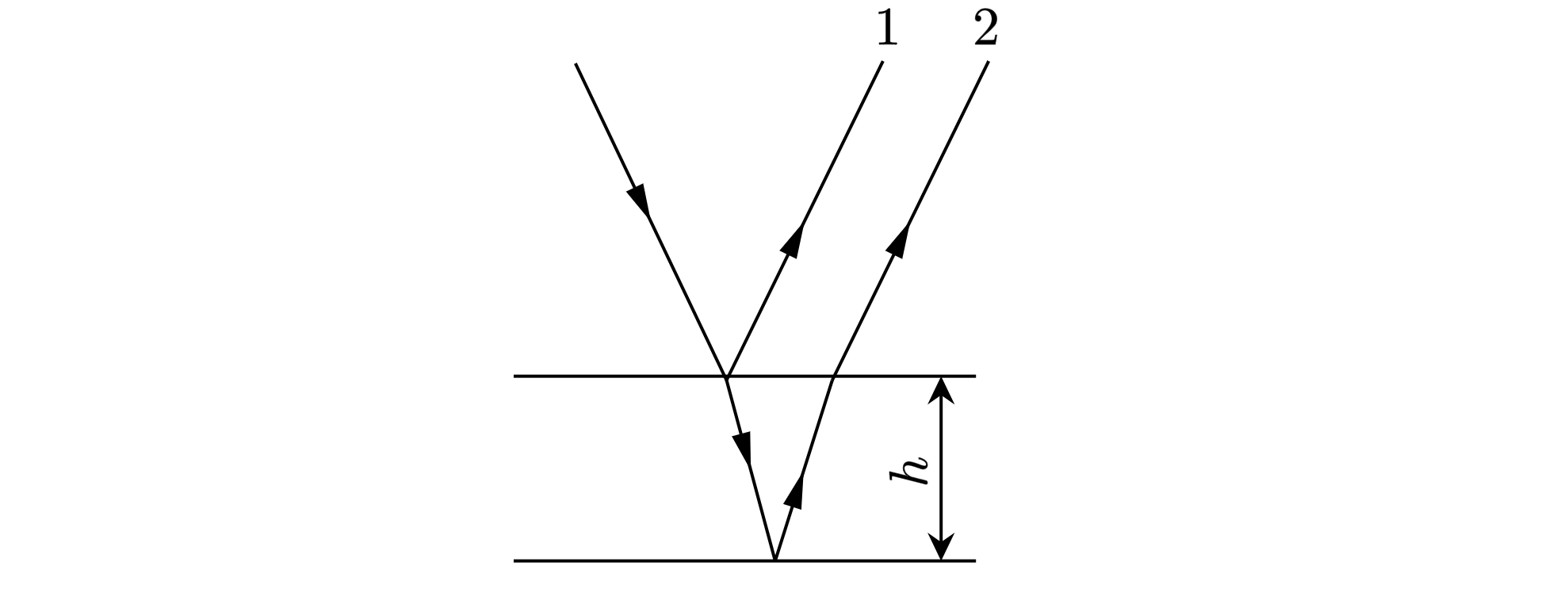
Ослабление отраженного света достигается за счет взаимного ослабления при интерференции двух
световых волн (см. рисунок): отраженной от внешней границы пленки и от границы пленка-стекло.
при отражении от более оптически плотной среды происходит потеря полуволны, а с
учетом того, что , где
– показатель преломления пленки,
– показатель
преломления стекла, то каждый луч при отражении теряет пол полны, и условие минимума не
меняется.
Запишем условие минимума для лучей, отраженный от поверхности плёнки и поверхности
стекла:
Отсюда:
Так как необходимо погасить обе волны, то
Отсюда
Для минимальности толщины плёнки необходима минимальность , найдем минимальные значения
и
Отсюда ,
и остается найти
:
Два когерентных световых пучка падают на экран: один пучок по нормали, а другой – под углом
рад. Найти период
интерференционной картины, т.е. расстояние между соседними
светлыми полосами на экране, если длина световой волны в обоих пучках равна
мкм.
ВМК МГУ
Показать ответ и решение
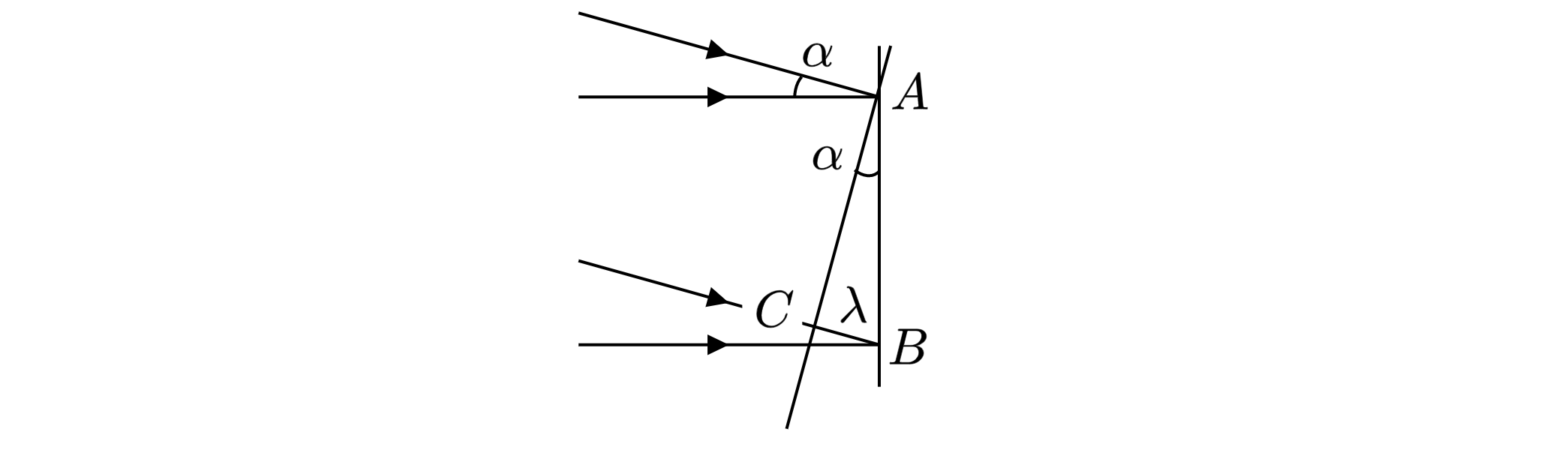
На рисунке изображены волновые фронты двух пучков – падающего на экран нормально (AB) и
падающего на экран наклонно (AC).
Пусть в некоторой точке A наблюдается один из максимумов интерференционной картины. Это
означает, что фазы обеих световых волн в этой точке совпадают. Соседний максимум интенсивности
находится в точке B, для которой также выполняется условие равенства фаз обеих волн. Это
имеет место, если расстояние между точками B и C равно длине световой волны . Из
треугольника ABC имеем Учитывая, что
(
) получаем
мкм
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: рассмотрен ход лучей и сказано
что расстояние между двумя точками равно длине волны )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
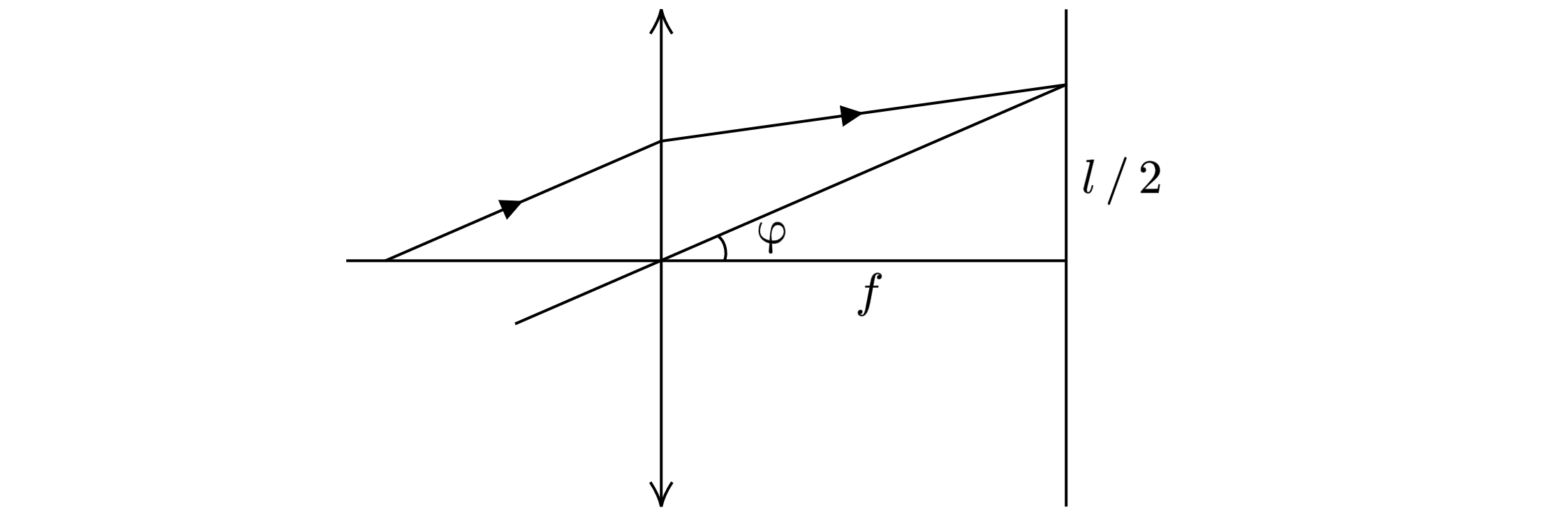
С помощью установки, схема которой показана на рисунке, наблюдают дифракцию параллельного пучка
белого света на дифракционной решетке Д, расположенной перпендикулярно оси пучка. При этом на
экране Э, установленном в фокальной плоскости тонкой собирающей линзы Л, видны две светлые
полосы, вызванные наложением спектральных компонент с длинами волн нм и
нм. Эти полосы расположены симметрично относительно главной оптической
оси линзы на расстоянии см друг от друга. Найдите минимальный период решетки
, при котором наблюдается эта картина, если фокусное расстояние линзы
см
ВМК МГУ
Показать ответ и решение
Введем величины: — период дифракционной решетки,
— длина волны лучей,
— угол
отклонения лучей, – порядок спектра. Запишем уравнение дифракционной решётки:
Чтобы волны наложились друг на друга должно выполняться условие:
Значит
Найдём минимальные значения и
. Это
,
. Следовательно,
Из рисунка видно, что
Используя формулу , получаем, что
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записано уравнение
дифркционной решётки )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
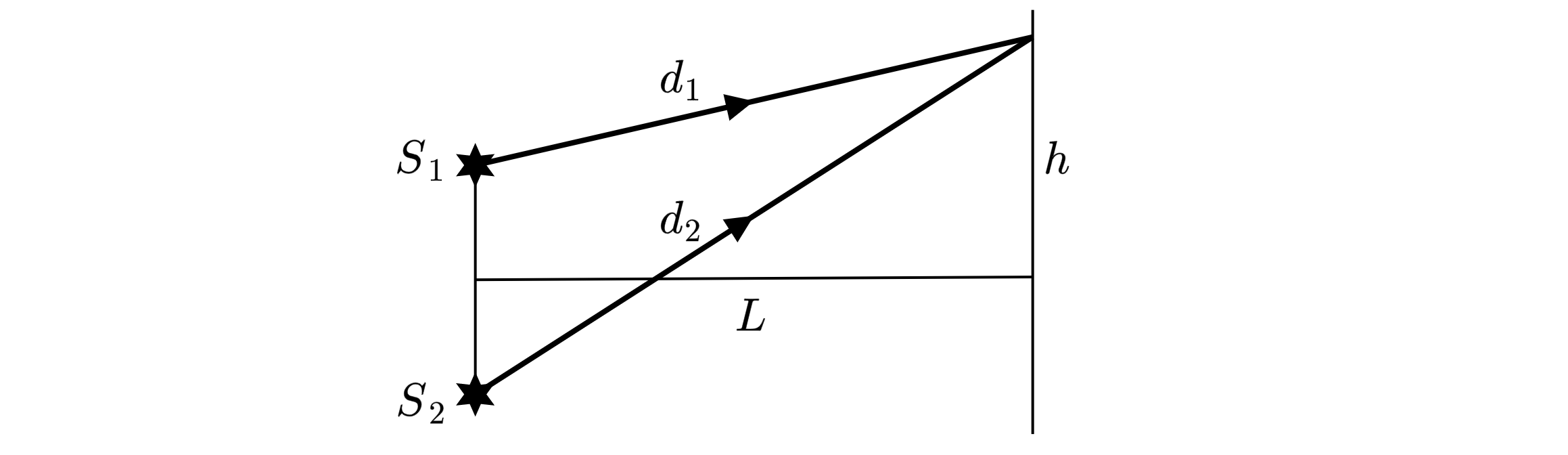
На рисунке представлена схема получения интерференции света с помощью плоского зеркала.
Центральный интерференционный максимум наблюдается в точке О экрана. Расстояние от источника S
до зеркала равно А, длина волны источника нм. Луч 1 идет параллельно зеркалу и попадает в
точку А экрана, где наблюдается второй интерференционный минимум. Чему равно расстояние А в этом
опыте?
Показать ответ и решение
Для наблюдения второго минимума необходима разность хода, равная
Первый луч проходит:
Второй луч проходит две гипотенузы прямоугольного треугольника:
При этом при отражении от более оптически плотной среды происходит потеря полуволны,
значит:
Отсюда:
Отсюда:
Возводим в квадрат
При этом , значит, при вычислении можем пренебречь
и окончательно
получим:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: сказано чему равна разность
хода, учтена потеря полуволны)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Углы, определяющие направления на дифракционные максимумы, при нормальном падении пучка на
решетку удовлетворяют условию где
— длина волны света,
.
Импульс фотона связан с его длиной волны соотношением
где
— постоянная Планка.
Из записанных соотношений находим:
Или
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула дифракционной
решётки, форула импульса фотона )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записано условие дифракции
первого максимума )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Волна красного света проходит через тонкую прозрачную пленку с показателем преломления 1,8.
Толщина пленки м. Определите, сколько раз длина волны света в пленке укладывается на ее
толщине, если длина волны в вакууме 720 нм. Волна падает на пленку перпендикулярно ее
плоскости.
Черноуцан
Показать ответ и решение
По закону преломления:
где – скорость света в среде,
– показатель преломления среды.
Частота волны при переходе из одной среды в другую не изменяется, следовательно
где – длина волны в вакууме,
– длина волны в среде.
Тогда
На толщине будет укладываться
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записан закон преломления
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
На дифракционную решетку перпендикулярно ее плоскости падает свет с длиной волны 500 нм. Сколько
штрихов на 1 мм должна иметь решетка, чтобы пятый главный максимум в дифракционной картине
находился под углом по отношению к падающему свету?
Черонуцан
Показать ответ и решение
По формуле дифракционной решетки:
где – порядок максимума,
– постоянная решетки,
– длина волны решётки,
–
направление на й максимум.
По условию ,
, откуда:
Тогда количество штрихов на мм:
Критерии оценки
Критерии проверки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение включающее следующие элементы: I) Записаны положения теории и
физические законы, закономерности, применение которых необходимо для решения задачи выбранным
способом (в данном случае: формула условия наблюдения главных максимумов при нормальном падении
света на дифракционную решетку, формула расчета числа штрихов, приходящихся на единицу длины
решетки)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены
необходимые преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Монохроматический свет с частотой Гц распространяется в пластинке,прозрачной для
этого света и имеющей показатель преломления 1,6. Чему равна длина волны этого света в
пластинке?
Черноуцан
Показать ответ и решение
Показатель преломления данной среды относительно вакуума называется абсолютным показателем
преломления данной среды , его можно определить как отношение скорости света в вакууме
, к
скорости света в данной среде
Откуда:
По формуле скорость света в среде равна
где – длина волны,
– частота света.
Приравняв (1) и (2), получим
Подставим числа из условий:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула
нахождения показателя преломления, записана формула нахождения скорости волны в среде
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Углы, определяющие направления на дифракционные максимумы, при нормальном падении пучка на
решетку удовлетворяют условию где
— длина волны света,
.
Импульс фотона связан с его длиной волны соотношением
где
— постоянная Планка.
Из записанных соотношений находим:
Следовательно,
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула
дифракционной решётки, записана формула импульса фотона )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Определите постоянную дифракционной решетки, если при нормальном падении света на решетку
зеленая линия спектра лампы (длина волны 550 нм) наблюдается в пятом порядке под углом
.
Показать ответ и решение
Формула для дифракционной решетки:
– постоянная дифракционной решетки,
– порядок дифракционного максимума,
–
длина волны, – угол наблюдения данного максимума. Максимальный синус равен 1,
следовательно:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула дифракционной
решётки )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
При исследовании спектра ртути с помощью дифракционной решётки и гониометра (прибора для
точного измерения углов дифракции света) было обнаружено, что в спектре 3-го порядка вблизи
двойной жёлтой линии ртути со средней длиной волны нм видна сине-фиолетовая линия 4-го
порядка. Оцените её длину волны .
Показать ответ и решение
Формула для дифракционной решетки:
– период дифракционной решетки,
– порядок дифракционного максимума,
–
длина волны, – угол наблюдения данного максимума. Максимальный синус равен 1,
следовательно:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана фомрула
дифракционной решётки )
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
При нормальном падении света с длиной волны = 455 нм на дифракционную решётку с периодом d = 3,64 мкм порядок m дифракционного максимума, наблюдаемого под углом
= 30° к нормали, равен:
Источник: Централизованное тестирование по физике, 2015
2
1) 540 нм
2) 520 нм
3) 500 нм
4) 480 нм
5) 460 нм
Источник: Централизованное тестирование по физике, 2015
3
При нормальном падении монохроматического света на дифракционную решётку дифракционный максимум четвёртого порядка наблюдается под углом = 30° к нормали. Если длина световой волны
= 430 нм, то период d дифракционной решётки равен:
1) 3,44 мкм
2) 3,26 мкм
3) 3,05 мкм
4) 2,81 мкм
5) 2,52 мкм
Источник: Централизованное тестирование по физике, 2015
4
При нормальном падении монохроматического света на дифракционную решётку дифракционный максимум второго порядка наблюдается под углом = 30° к нормали. Если длина световой волны
= 590 нм, то период d дифракционной решётки равен:
1) 1,84 мкм
2) 2,12 мкм
3) 2,36 мкм
4) 2,54 мкм
5) 2,72 мкм
Источник: Централизованное тестирование по физике, 2015
5
Если при нормальном падении монохроматического света на дифракционную решётку с периодом d = 1,83 мкм дифракционный максимум шестого порядка наблюдается под углом = 60° к нормали, то длина световой волны
равна:
1) 264 нм
2) 294 нм
3) 328 нм
4) 362 нм
5) 404 нм
Источник: Централизованное тестирование по физике, 2015
Пройти тестирование по этим заданиям
Задания по теме «Интерференция, дисперсия, дифракция»

диапазоне угол преломления лучей на границе воздух-стекло падает с
увеличением частоты излучения. Ход лучей для трех основных цветов
при падении белого света из воздуха на границу раздела показан на
рисунке.
Цифрам соответствуют цвета
1) 1 — красный, 2 —
зеленый, 3 — синий
2) 1 — красный,
2 — синий, 3 — зеленый
3) 1 — зеленый,
2 — синий, 3 — красный
4) 1 — синий,
2 — зеленый, 3 — красный
2. Технология «просветления»
объективов оптических систем основана на использовании явления:
1) дифракция 2)
интерференция 3) дисперсия 4) поляризация
3. На плоскую непрозрачную пластину с двумя узкими
параллельными щелями падает по нормали плоская монохроматическая
волна из зеленой части видимого спектра. За пластиной на параллельном
ей экране наблюдается интерференционная картина, содержащая
большое число полос. При переходе на монохроматический свет из фиолетовой
части видимого спектра
1) расстояние между интерференционными
полосами увеличится
2) расстояние между
интерференционными полосами уменьшится
3) расстояние между
интерференционными полосами не изменится
4) интерференционная
картина станет невидимой для глаза

и
находятся
близко друг от друга и создают на удаленном экране устойчивую интерференционную
картину (см. рисунок).
Это возможно, если и
— малые отверстия в непрозрачном экране, освещенные
1) каждое своим солнечным
зайчиком от разных зеркал
2) одно — лампочкой
накаливания, а второе — горящей свечой
3) одно синим светом,
а другое красным светом
4) светом от одного
и того же точечного источника монохроматического света
5. Два источника испускают электромагнитные
волны частотой c одинаковыми
начальными фазами. Максимум интерференции будет наблюдаться в
точке пространства, для которой разность хода волн от источников равна:
1) 0,9 мкм 2) 1,0 мкм 3) 0,3 мкм
4) 1,2 мкм

границе раздела двух сред уменьшается с увеличением длины волны излучения.
Ход лучей для трех цветов при падении белого света из воздуха на границу
раздела показан на рисунке. Цифрам соответствуют цвета
1) 1 — синий, 2 —
зелёный, 3 — красный
2) 1 — синий,
2 — красный, 3 — зелёный
3) 1 — красный,
2 — зелёный, 3 — синий
4) 1 — красный,
2 — синий, 3 — зелёный
7. Свет от двух точечных когерентных монохроматических
источников приходит в точку 1 экрана с разностью фаз , в точку 2 экрана с разностью фаз
. Одинакова ли в этих точках освещенность и
если не одинакова, то в какой точке она больше?
1) одинакова и отлична от нуля
2) одинакова и равна нулю 3) не одинакова, больше в точке 1
4) не одинакова, больше в точке 2
8. При освещении мыльной пленки белым светом наблюдаются
разноцветные полосы. Какое физическое явление обусловливает появление
этих полос?
1) дифракция 2) интерференция
3) дисперсия 4) поляризация
9. На плоскопараллельную стеклянную пластинку
и стеклянную призму падает луч белого света (см. рисунок).

света в виде радужных полос на экране
1) будет наблюдаться
только в случае А
2) будет наблюдаться
только в случае Б
3) будет наблюдаться
и в случае А, и в случае Б
4) не будет наблюдаться
ни в случае А, ни в случае Б
10. Дисперсией света объясняется:
А. возникновение окраски подвесок
люстры из бесцветного хрусталя в зависимости от точки наблюдения.
Б. цвет подвесок люстры,
изготовленных из окрашенного стекла.
Верно(-ы) утверждение(-я): 1)
только А 2) только Б 3) и А, и Б 4) ни А, ни Б

полученной от двух когерентных источников света. Какое(-ие) утвержден
ие(-я) являе(-ю)тся правильным(-и)?
А. Оптическая
разность хода лучей от источников до точки 1 равна чётному числу половин
длины волны.
Б. В точку
2 световые волны от источников приходят в одной фазе.
1) верно только А 2) верно
только Б 3) верно и А и Б
4) не верно ни А, ни Б
12. Если кольцо диаметром 3—4 см, согнутое из тонкой проволоки,
окунуть в раствор мыла или стирального порошка, то, вынув его из раствора,
можно обнаружить радужную пленку, затягивающую отверстие кольца.
Если держать кольцо так, чтобы его плоскость была вертикальна, и рассматривать
пленку в отраженном свете на темном фоне, то в верхней части пленки
через некоторое время будет видно растущее темное пятно, окольцованное
разноцветными полосами. Как чередуется цвет полос в направлении
от темного пятна к нижней части кольца? Ответ поясните, используя физические
закономерности.
Ответы к заданиям по теме
«Интерференция, дисперсия, дифракция» (тип задания 13 КИМов)
1.
Поскольку
угол преломления падает с увеличением частоты излучения, а красный
свет имеет самую маленькую частоту, получаем, что угол преломления
для него максимален, луч меньше всего преломляется (3 — красный).
Синий луч имеет самую большую частоту, а значит угол преломления для
него минимален (1 — синий). Остается 2 — зеленый. Правильный
ответ: 4.
2.
«Просветление»
объективов оптических систем заключается в нанесении на поверхность
линз тонких пленок для увеличения доли пропускаемого света. Технология
основана на использовании явления интерференции. Пленка наносится
таким образом, чтобы лучи, отраженные от ее внутренней и внешней сторон,
гасили друг друга вследствие интерференции, тем самым уменьшая долю отраженных
назад лучей. Ответ: 2.
3.
Две щели
играют роль когерентных источников света. Максимумы интерференции
наблюдаются в точках экрана, для которых оптическая разность хода
волн от источников кратна целому числу волн. Поскольку монохроматический
свет из фиолетовой части видимого спектра имеет меньшую длину волны,
чем свет из зеленой части, расстояние между интерференционными полосами
уменьшится.Правильный ответ: 2.
4.
Для формирования
устойчивой интерференционной картины необходимо наложение когерентных
световых волн. Когерентными называют монохроматические волны с
одинаковой частотой и постоянной разностью фаз. Источники света и
создают устойчивую интерференционную
картину, если и
—
малые отверстия в непрозрачном экране, освещенные светом от одного и
того же точечного источника монохроматического света. Правильный
ответ: 4.
5.
Длина
волны связана со скоростью света и частотой соотношением Отсюда
находим длину волны света, испускаемого источниками:
.
Так как источники испускают волны с одинаковыми начальными
фазами, максимум интерференции будет наблюдаться в точках пространства,
для которых оптическая разность хода волн от источников удовлетворяет
соотношению
Из предложенных
вариантов ответа подходит вариант 4 . Правильный ответ: 4.
6. Поскольку угол преломления
уменьшается с увеличением длины волны излучения, а синий свет имеет
самую маленькую длину волны, получаем, что угол преломления для него
максимален, луч меньше всего преломляется (3 — синий). Красный
луч имеет самую большую длину волны, а значит угол преломления для него минимален
(1 — красный). Остается 2 — зеленый. Правильный ответ: 3.
7.
Условие интерференционных минимумов имеет вид
то есть разность хода должна равняться полуцелому
числу длин волн.
Условие интерференционных максимумов:
(разность фаз равна целому числу волн). Следовательно,
в точке 1 экрана находится интерференционный минимум, освещенность
в этой точке равна нулю. А в точке 2 экрана находится интерференционный
максимум, и освещенность там отлична от нуля. Правильный
ответ: 4.
8.
Разноцветные
полосы на мыльной пленки при освещении белым светом обусловлены интерференцией
волн, отраженных от внешней и внутренней поверхностей пленки. Волны
когерентны, так как они испущены одним и тем же источником света. Усиление
света происходит, если разность хода равна целому числу длин волн. Волны
разного цвета в составе белого света имеют разную длину волны. Мыльная
пленка имеет неоднородную толщину, поэтому в разных местах происходит
усиление разных цветов. В итоге возникает такая переливчатая окраска.
Правильный ответ: 2.
9.
Дисперсией
называется зависимость фазовой скорости от длины волны, это приводит
к зависимости от длины волны показателя преломления. При нормальном
падении белого света на границу раздела двух сред разложения в спектр
не происходит, поскольку угол падения равен нулю. А вот при попадании
света под углом отличным от ,
волны разных длин волн преломляются по-разному, в результате чего
можно наблюдать радужные полосы. Таким образом, радужные полосы на
экране можно наблюдать и в опыте А, и в опыте Б. При этом в опыте Б получится
расходящийся пучок цветных лучей, а в опыте А получится пучок параллельных
цветных лучей, плоскопараллельная пластина сместит лучи разных длин
волн на разное расстояние.
Правильный ответ: 3
10.
Дисперсией
называется зависимость абсолютного показателя преломления вещества
от частоты (или длины волны) света.
Цветное стекло пропускает через себя
только свет соответствующего цвета, волны других частот поглощаются.
Утверждение Б ошибочно.
Возникновение окраски подвесок люстры
из бесцветного хрусталя в зависимости от точки наблюдения действительно
объясняется явлением дисперсии. Подвески представляют собой призмы.
Белый свет разлагается в спектр при прохождении через них из-за различия
в показателях преломления для разных частот. В зависимости от угла
наблюдения в глаз попадают лучи из разных участков спектра. Этим и
определяются радужные переливы. Таким образом, верно только утверждение
А. Правильный ответ: 1
11. Точка 1 лежит в центре тёмной полосы,
которая соответствует интерференционному минимуму. В этой точке
выполняется условие равенства оптической разности хода лучей полуцелому
числу длин волн, то есть нечетному числу полуволн: Δ = (2n+1)λ/2.
Утверждение А неверно.
Точка 2
лежит в центре светлой полосы, которая соответствует интерференционному
максимуму. В эту точку световые волны приходят в фазе, поэтому усиливают
друг друга. Утверждение Б верно. Правильный ответ 2.
12. 1. Окраска
пленки обусловлена интерференцией света, отраженного от передней
и задней поверхностей пленки.
2. Темное
пятно на пленке появляется, когда из-за стекания мыльного раствора
вниз толщина пленки становится слишком малой и не наблюдается интерференционный
максимум ни для одной из длин волн в видимом диапазоне.
3. По направлению
от темного пятна к нижней части кольца толщина пленки постепенно увеличивается,
поэтому условие наблюдения первого интерференционного максимума
при переходе от темного пятна к нижней части кольца выполняется сначала
для света с наименьшей длиной волны (фиолетового), а затем по очереди
для света всех цветов радуги, заканчивая светом с наибольшей длиной
волны (красным). Затем наблюдаются максимумы следующих порядков. В
результате под темным пятном пленка окрашена в фиолетовый цвет,
затем в синий и т. д. до красного. Затем чередование цветов повторяется,
но цвета начинают смешиваться, т. к. возможно наложение друг на
друга максимумов разных порядков для разных длин волн.