Решу егэ числовые последовательности - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Даны n различных натуральных чисел, составляющих арифметическую прогрессию

а)  Может ли сумма всех данных чисел быть равной 14?

б)  Каково наибольшее значение n, если сумма всех данных чисел меньше 900?

в)  Найдите все возможные значения n, если сумма всех данных чисел равна 123.

Источник: ЕГЭ 28.04.2014 по математике. Досрочная волна. Вариант 1., ЕГЭ по математике 23.04.2013. Досрочная волна. Вариант 902., Задания 19 (С7) ЕГЭ 2013

Каждое из чисел a₁, a₂, …, a₃₅₀ равно 1, 2, 3 или 4. Обозначим

Известно, что S₁ = 513.

а)  Найдите S₄, если еще известно, что S₂  =  1097 и S₃  =  3243.

б)  Может ли S₄  =  4547?

в)  Пусть S₄  =  4745. Найдите все значения, которые может принимать S₂.

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервная волна. Центр. Вариант 501, Задания 19 (С7) ЕГЭ 2013

В строку подряд написано 1000 чисел. Под каждым числом a первой строки напишем число, указывающее, сколько раз число a встречается в первой строке. Из полученной таким образом второй строки аналогично получаем третью: под каждым числом второй строки пишем, сколько раз оно встречается во второй строке. Затем из третьей строки так же получаем четвёртую, из четвёртой  — пятую, и так далее.

а)  Докажите, что некоторая строчка совпадает со следующей.

б)  Докажите, что 11‐я строка совпадает с 12‐й.

в)  Приведите пример такой первоначальной строчки, для которой 10‐я строка не совпадает с 11‐й.

Источник: А. Ларин: Тренировочный вариант № 51.

Можно ли из последовательности 1, 1/2, 1/3, 1/4,… выделить арифметическую прогрессию

а)  длиной 4

б)  длиной 5

в)  длиной k, где k  — любое натуральное число?

Источник: А. Ларин: Тренировочный вариант № 52.

Даны две последовательности: 2, 4, 8, 16, 14, 10, 2 и 3, 6, 12. В каждой из них каждое число получено из предыдущего по одному и тому же закону.

а)  Найдите этот закон.

б)  Найдите все натуральные числа, переходящие сами в себя (по этому закону).

в)  Докажите, что число 21991 после нескольких переходов станет однозначным.

Источник: А. Ларин: Тренировочный вариант № 61.

Пройти тестирование по этим заданиям

Источник

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Все члены геометрической прогрессии  — различные натуральные числа, заключенные между числами 510 и 740.

а)  может ли такая прогрессия состоять из четырех членов?

б)  может ли такая прогрессия состоять из пяти членов?

Натуральные числа a,b,c образуют возрастающую арифметическую прогрессию, причём все они больше 500 и являются квадратами натуральных чисел. Найдите наименьшее возможное, при указанных условиях, значение

Последние члены двух конечных арифметических прогрессий a₁ = 5, a₂ = 8, …, a_N и b₁ = 9, b₂ = 14, …, b_M совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих прогрессий равна 815. Найдите число членов в каждой прогрессии.

Дана последовательность из нескольких натуральных чисел, причём каждый следующий член отличается от предыдущего либо на 12, либо в 8 раз. Сумма всех членов последовательности равна 437.

а)  Какое наименьшее число членов может быть в этой последовательности?

б)  Какое наибольшее количество членов может быть в этой последовательности?

Перед каждым из чисел 14, 15, . . ., 20 и 4, 5, . . ., 8 прозвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 35 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Пройти тестирование по этим заданиям

Источник

Числовые последовательности в ОГЭ и ЕГЭ

Авторы
Руководители
Файлы работы
Наградные документы

Лебедева П.К. 1

1Частное общеобразовательное учреждение Школа –интернат № 1 среднего общего образования открытого акционерного общества «Российские железные дороги»

Рура Т.Н. 1

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ.

Задачи, связанные с последовательностями, в курсе алгебры рассматриваются фрагментарно. Немного больше времени уделяется частным видам последовательностей, а именно арифметической и геометрической прогрессиям. Однако для решения предлагаемых на Едином Государственном экзамене задач этих знаний недостаточно. В 2016 году задачу № 11 профильного уровня, согласно статистико-аналитическому отчёту о результатах ЕГЭ выполнили 32,2 % участников.

Цель исследования: изучить понятие числовой последовательности, виды числовых последовательностей и научиться решать задачи, связанные с числовыми последовательностями.

Для достижения цели поставлены следующие задачи:

1. изучение литературы по данной теме в печатном и электронном виде;

2. изучение видов последовательностей;

3. отработка полученных знаний в ходе решения задач;

4. ознакомление обучающихся 9 — 11 классов с решением задач из Единого Государственного экзамена, связанных с числовыми последовательностями.

Объект исследования: числовые последовательности

Предмет исследования: способы решения задач из ОГЭ и ЕГЭ, связанных с числовые последовательностями

Методы исследования:

изучение литературы;

2. выполнение практических заданий;

3. сравнение и обобщение полученных результатов.

Практическая значимость: использование материала при подготовке к Единому Государственному Экзамену.

Новизна проведённой исследовательской работы: изучение числовых последовательностей как темы, не входящей в школьную программу 7 класса. Задачи, связанные с числовыми последовательностями, также встречаются среди заданий под номером 19 Единого государственного экзамена, которые оцениваются максимальным количеством баллов.

Гипотеза:задачи, связанные с числовыми последовательностями, можно решить алгебраически, с помощью уравнений и преобразований выражений.

1. ОСНОВНАЯ ЧАСТЬ

1.1. Теоретическая часть

1.1.1.Определение числовой последовательности

Понятие числовой последовательности возникло задолго до создания учения о функциях. В нашей жизни многие события происходят последовательно: например, смена дня и ночи, смена дней недели, смена возраста живого существа с течением времени. Последовательно увеличивает свою скорость автомобиль, последовательно пронумерованы дома на улицах.

В математике мы впервые сталкиваемся с последовательностями в начальной школе, когда от нас требуется уловить закономерность и продолжить ряд чисел.

Определение. Если каждому натуральному числу 1, 2, 3….n,… поставлено в соответствие действительноечисло то множество действительных чисел , , ,….. , … называется числовой последовательностью.

Числа , , ,….. , … называются элементами (или членами) последовательности, а символ — общим членом последовательности.

Последовательность задают формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.

Элементами последовательности не обязательно должны быть различные числа. Так, если a_n = 1, то последовательность имеет вид 1, 1, …, 1, …

Общий член определяет знакочередующуюся последовательность вида 1, –1, 1, –1, …

Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения. В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому правилу. Например, известен первый член последовательности и известно, что , то есть ) и так далее до нужного члена.

Самым известным примером рекуррентно заданной последовательности является знаменитая последовательность чисел Фибоначчи 1, 1, 2, 3 ,5 8, 13, 21, 34…., в которой каждое последующее число является суммой двух предыдущих чисел. Данную последовательность можно задать следующим рекуррентным соотношением:

= +, где = 1

Числовые последовательности бывают конечными и бесконечными. К бесконечным последовательностям можно отнести ряд натуральных чисел, множество нечётных чисел, к конечным последовательностям можно отнести, например, последовательность чётных двузначных чисел.

1.1.2.Виды числовых последовательностей

1) Возрастающая последовательность – последовательность, каждый член которой больше предыдущего > , где n N

Примером возрастающей последовательности служит ряд натуральных чисел 1,2,3,4,…

2) Убывающая последовательность – последовательность, каждый член которой каждый меньше предыдущего < , где nN

Примером убывающей последовательности служит гармонический ряд — ряд чисел, обратных членам натурального ряда 1, , , ,….

Существуют следующие способы задания последовательности

— Словесный — правило составления последовательности выражается словесным описанием, например: последовательность простых двузначных чисел, меньших 100

11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,53,59,61,67,71,73,79,83,89,97;

— Графический

Числа последовательности можно отмечать на координатной плоскости, причем по оси абсцисс откладывается номер члена последовательности, а по оси ординат соответствующий этому номеру член последовательности

Рис.1

На левом рисунке изображена возрастающая последовательность,на правом убывающая последовательность

— Аналитический.

указывается формула n-го члена последовательности а_п= 5n+17 а_п= или рекуррентное соотношение.

1.1.3. Арифметическая и геометрическая прогрессии

В курсе алгебры 9 класса изучаются такие виды последовательностей, как арифметическая и геометрическая прогрессии.

Определение. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

(а_п) – арифметическая прогрессия, если для любого п N выполняется условие

а_п₊₁ = а_п + d, где d – некоторое число. Число d называется «разностью арифметической прогрессии», так как из определения следует, что а_п_{+ 1} – а_п = d. Если

d >0 , то прогрессия является возрастающей, в случае же, если d < 0,то прогрессия является убывающей.

Определение. Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число. Это число обозначается q и называется знаменателем геометрической прогрессии, поскольку q =b_п₊₁ : b_п.

В задании № 11 Основного Государственного экзамена и первой части Единого Государственного экзамена предложены задания, связанные с арифметической и геометрической прогрессиями. В задании № 19 ЕГЭ встречаются как арифметические и геометрические прогрессии, так и числовые последовательности.

Таблица 1. Основные формулы для арифметической и геометрической прогрессии

	Арифметическая прогрессия	Геометрическая прогрессия
Определение
Формула n-го члена	_a_n=a₁+(n-1)d,	b_n=b₁*qⁿ^-1,
Сумма n первых членов

Характеристическое свойство

1.2. ПРАКТИЧЕСКАЯ ЧАСТЬ

Решение задач, связанных с числовыми последовательностями.

Задача 1.(Открытый банк заданий ОГЭ, 1 часть, задача 11).

В первом ряду кинозала 20 мест, а в каждом следующем на 2 больше,чем в предыдущем. Сколько мест в 11 ряду?

Решение: в соответствии с условием последовательность мест в ряду 20, 22, 24,…- арифметическая прогрессия. Используем формулу для n-го члена арифметической прогрессии, получим 20 +2(11 — 1) =40.

Ответ:40 мест.

Задача 2(Открытый банк заданий ЕГЭ, задача 11)

Олегу надо решить 315 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Олег решил 11 задач. Определите, сколько задач решил Олег в последний день, если со всеми задачами он справился за 9 дней.

Решение: в данной задаче мы имеем дело с арифметической прогрессией, поскольку решает на одно и то же количество задач больше по сравнению с предыдущим днем.

Известно, =11 n = 9 =315. Согласно формуле суммы первых членов арифметической прогрессии = · n решим уравнение 315 = (11 + )·9 : 2,откуда =70 – 11 = 59. Ответ: 59

Задача 3 (ЕГЭ, № 19)

Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 10 раз больше, либо в 10 раз меньше предыдущего. Сумма всех членов последовательности равна 3024.
а) Может ли последовательность состоять из двух членов?
б) Может ли последовательность состоять из трёх членов?
в) Какое наибольшее количество членов может быть в последовательности?

Решение: а) Предположим, что последовательность состоит из двух членов, a и 10 a (в произвольном порядке).Тогда получим a+10a=3024

Поскольку корень уравнения 11a=3024 не является целым числом, как это требуется в условии, делаем вывод: последовательность не может состоять из двух членов.

б) Составим уравнение: a + 10a + a =3024,откудаa=252

10a + a+ 10a = 3024 , откуда a=144

(Пример). Последовательность может состоять из трёх членов. Например: 252, 2520, 252 или 1440,144,1440

в) Ближайшим к 3024 число, делящееся на 11 нацело, является 3014.

3014=11 174. Таким образом, в последовательности 174 пары вида (10; 1) и число 10.

Допустим, что в последовательности более чем 549 членов.

Разобьём первые 550 членов последовательности на 275 пар соседних членов: первый и второй, третий и четвертый, пятый и шестой и т.д.

Сумма двух членов в каждой паре делится на 11 и поэтому не меньше 11.

Значит, сумма всех членов последовательности не меньше, чем 275*11 = 3025 > 3024 ,следовательно, мы пришли к противоречию, а это значит, что наибольшее количество членов данной последовательности равно 549.

Ответ: а) нет; б) да; в) 549.

Задача 4 (№19, тренировочный вариант ЕГЭ №52)

Можно ли из последовательности 1, , , , …..

выделить арифметическую прогрессию, содержащую 5 членов?
Решение: Исходная последовательность (гармонический ряд) является убывающей. Значит, будем искать убывающую арифметическую прогрессию.

Пусть это будет последовательность вида ; ; ; .

Разность данной арифметической прогрессии равна

Нам осталось подобрать число n таким образом, чтоб все числители сократились, а это возможно в том случае, когда это число будет наименьшим общим кратным числителей. В нашем случае это будет число 60. Значит, выделенная из гармонического ряда последовательность будет такой:

; ; ; Ответ: можно.

Задача 5 (тренировочный вариант ЕГЭ 192, 2017г.).

Дана последовательность ( ): = (n-1)n(n+1)+133

Найти два соседних члена этой последовательности, разность которых равна 29700

=(n -1)n(n+1)+133 = n(n+1)(n+2)+133

Согласно условию вычтем и после приведения подобных слагаемых получим 3n(n+1)=29700 Тогда получим квадратное уравнение относительно n n(n+1)=9900=99▪100, откуда n=99.(второй корень уравнения не удовлетворяет условиям задачи, поскольку номер члена последовательности является натуральным числом)

Ответ : это 99 и 100 члены последовательности.

В приложении приведены задачи из открытого банка ОГЭ и ЕГЭ, связанные с числовыми последовательностями, первая из которых (№ 19 профильного ЕГЭ) — с решением.

ЗАКЛЮЧЕНИЕ

1.изучив литературу по теме, я ознакомилась с понятием числовой последовательности, с их видами, а также с их применением на практике.

2. рассмотрены основы ранее неизвестного мне раздела математики имеющего большую практическую пользу для решения задач из ЕГЭ и ОГЭ.

3. в ходе оформления работы я научилась работать с математическими формулами в редакторе Word.

Задания из ОГЭ и ЕГЭ 1 части, связанные с арифметической и геометрической прогрессиями, решаются достаточно быстро в соответствии с приведёнными формулами n-го члена последовательности, суммы первых n членов последовательности. Задания же № 19 требуют более деликатного подхода, однако алгебраический метод помогает справиться и с ними. Таким образом, выдвинутая гипотеза подтвердилась.

Можно сделать вывод, что изучение последовательностей полезно для каждого школьника, интересующегося математикой. Поскольку в будущем я собираюсь поступать в высшее учебное заведение и сдать Единый Государственный Экзамен на высокий балл, изучение данного материала было для меня очень полезным.

В будущем я планирую продолжить изучение последовательностей и их свойств.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1 М. М. Медынский. Полный курс элементарной математики в задачах и упражнениях. Книга 2: Числовые последовательности и прогрессии. М.: Эдитус, 2015.

2. Алгебра , 9 класс : учебник для общеобразовательных организаций (Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова) ; под редакцией С. А. Теляковского. М., «Просвещение»,2015.

3.Яковлев И.В. «Задача С6 на ЕГЭ по математике» (электронная версия книги на сайте http://mathus.ru/)

4. Ященко И.В. «ЕГЭ-2018. Типовые экзаменационные варианты». (М., «Экзамен», 2017)

5.Ященко И.В. « 3000 задач с ответами по математике. Все задания части 1 .- «Экзамен», МЦНМО,2014.

5. Сайт для подготовки к ЕГЭ по математике http://alexlarin.net/

6.Открытый банк заданий ОГЭ и ЕГЭ по математике

ПРИЛОЖЕНИЕ.

Задачи из открытого банка ОГЭ и ЕГЭ, связанные с числовыми последовательностями

Задача 6 (Единый Государственный Экзамен, № 19, 4 балла)

Дана последовательность натуральных чисел, причем каждый следующий ее член отличается от предыдущего либо на 10, либо в 6 раз. Сумма всех членов последовательности равна 257.

а) Какое наименьшее (минимальное) число членов может быть в данной последовательности?
б) Какое наибольшее (максимальное) количество членов может быть в этой последовательности?

Решение: а) Предположим, что последовательность состоит из двух чисел, одно из которых больше другого на 10. Если первое число нечетно, то второе число тоже нечетно. А сумма двух нечетных чисел есть число четное. Если же первое число четно, то второе число, которое больше первого на 10, тоже четно. А сумма двух четных чисел есть четное число. Получается, что нечетного числа 257 в сумме у нас не получится.

Предположим теперь, что второе число в 6 раз больше первого. То есть первое число есть x тогда второе число есть 6x. Их сумма равна 7x и равна 257. Однако 257 на 7 без остатка не делится. Значит, этот вариант также не удовлетворяет нашему условию. Исходя из вышеизложенного, делаем следующий вывод: двух чисел в этой последовательности быть не может.

Рассмотрим следующий вариант. Предположим, что последовательность состоит из 3 чисел. Пусть каждое из них на 10 больше предыдущего. Тогда первое равно х, второе равно х+10, а третье х+20. Тогда их сумма равна 3х+30 и равна 257. То есть

3х+30=257 ,откуда следует 3х=227. Но корень данного уравнения не является натуральным числом.

Рассмотрим такой вариант: пусть второе число в 6 раз больше первого, а третье на 10 больше второго. Тогда получим уравнение

х+6х+6х+10=257 , откуда 13х+10=257 , 13х=247, то есть х =19.

Значит, минимальное количество чисел в нашей последовательности равно трем. Меньше уже не получается. К примеру, это может быть вот такая последовательность: 19,114,124.

Б) Теперь нам нужно, чтобы в последовательности было как можно больше членов. Поэтому пара вида (1; 6) должна встречалась в ней как можно чаще.

Сумма чисел этой пары равна 7. Если разделить 257 на 7, то получится 36 и 5 в остатке. Но эту 5 не получится представить, используя члены нашей последовательности. Поэтому возьмём пар вида (1; 6) в последовательности 35 штук, а оставшееся число 12 будетпредставлено в ней парой (1;11). Теперь мы получили последовательность 1;11;1;6;1;6;1;.. (пар типа (1;6) всего 35 штук) с максимально возможным числом членов. В этой последовательности числа. То есть максимально возможное число членов последовательности равно 72.

Ответ: а)3 б) 72

ОГЭ по математике , № 11

1.Дана арифметическая прогрессия (a_n), разность которой равна −8,1, a₁ = 1,4. Найдите a₆.

2. В арифметической прогрессии известно, что . Найдите третий член этой прогрессии.

3. Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?

4.В геометрической прогрессии сумма первого и второго членов равна 48, а сумма второго и третьего членов равна 144. Найдите первые три члена этой прогрессии.

5. Дана арифметическая прогрессия (a_n), для которой a₅ = 71, a₁₁ = 149. Найдите разность прогрессии.

6. Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 465?

7. Выписаны первые несколько членов геометрической прогрессии: 5; −10; 20; … Найдите сумму первых пяти её членов.

8. В первом ряду кинозала 35 мест, а в каждом следующем на один больше, чем в предыдущем. Сколько мест в восьмом ряду?

ЕГЭ по математике, профильный уровень , № 11

1.Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.

2.Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за девятый день, если вся работа была выполнена за 14 дней.

3.Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?

4.Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.

ЕГЭ по математике ,профильный уровень , № 19

1. Даны n различных натуральных чисел, составляющих арифметическую прогрессию

а) Может ли сумма всех данных чисел быть равной 14?

б) Каково наибольшее значение n, если сумма всех данных чисел меньше 900?

в) Найдите все возможные значения n, если сумма всех данных чисел равна 123.

2.Возрастающие арифметические прогрессии и состоят из натуральных чисел.

а) Существуют ли такие прогрессии, для которых и — различные натуральные числа?

б) Существуют ли такие прогрессии, для которых и — различные натуральные числа?

в) Какое наименьшее значение может принимать дробь , если известно, что и — различные натуральные числа.

3.Возрастающие арифметические прогрессии и состоят из натуральных числе.

а) Приведите пример таких прогрессий, для которых

б) Существуют ли такие прогрессии, для которых ?

в) Какое наибольшее значение может принимать произведение если

4.Последовательность состоит из неотрицательных однозначных чисел. Пусть — среднее арифметическое всех членов этой последовательности, кроме k-го. Известно, что

а) Приведите пример такой последовательности, для которой

б) Существует ли такая последовательность, для которой

в) Найдите наименьшее возможное значение

5. Все члены конечной последовательности являются натуральными числами.
Каждый член этой последовательности, начиная со второго, либо в 5 раз больше, либо в 5 раз меньше предыдущего.

Сумма всех членов последовательности равна 2013.
а). может ли эта последовательность состоять из трёх членов?
б). может ли эта последовательность состоять из четырёх членов?
в). может ли эта последовательность состоять из пяти членов?
г). какое наибольшее число членов может быть в этой последовательности?

Просмотров работы: 1255

Источник

Характеристика задания

1. Тип ответа: два числовых ответа.

2. Структура содержания задания: дан текстовый файл, содержащий числовую информацию.

3. Уровень сложности задания: повышенный.

4. Примерное время выполнения: (1)(4) минут.

5. Количество баллов: (1).

6. Требуется специальное программное обеспечение: среда программирования.

7. Задание проверяет умение составить алгоритм обработки числовой последовательности и записать его в виде простой программы на языке программирования.

Пример задания (демоверсия (2022))

Рис. (1). Пример задания

Что нужно знать?

1. Как считать данные из файла в список.

Для работы с файлом удобно использовать конструкцию with:

with open (file) as f:
инструкции

Эта конструкция определяет для открытого файла переменную (f) и выполняет набор инструкций. После их выполнения файл автоматически закрывается. Метод readlines()прочитает и вернёт все строки в файле в виде списка.

Для работы с данными файла мы будем использовать следующий программный код:

with open ((’17.txt’)) as f:
(a=) [int((x)) for (x) in f.readlines()]

2. Основные операторы для работы со списками (массивами).

В Python для того, чтобы работать с большим количеством данных, используется структура данных под названием список. Список представляет собой последовательность (набор) элементов, пронумерованных от (0).

Чтобы объявить список, нужно в квадратных скобках перечислить его элементы через запятую:

Элементы списка могут быть разных типов в отличие от элементов массива, но, как правило, используются списки из элементов одного типа.

Методы списков

(a.append (x))	добавляет элемент (x) в конец списка (a)
(a.count (x))	возвращает количество элементов списка (a) со значением (x)
(а.sort ())	сортирует список (a) в порядке возрастания
(а.reverse ())	разворачивает список (a) в обратном порядке
(a.clear ())	очищает список (a)

Функции для работы со списками

(len(a))	возвращает длину списка (a) (количество элементов списка (a))
(min(a))	возвращает наименьший элемент списка (a)
(max(a))	возвращает наибольший элемент списка (a)
(sum(a))	возвращает сумму элементов списка (a)

Решение задачи можно разбить на этапы.

1. Считать данные из текстового файла в массив (список). Важно, чтобы программа решения и текстовый файл лежали в одной папке (или необходимо указать полный путь для считывания файла).

with open ((’17.txt’)) as(f):
(a=) [int((x)) for (x) in f.readlines()]

2. Необходимо в массиве найти максимальное число, кратное (3). Для этого инициализируем пустой массив (b). Затем с помощью цикла (for) переберём все элементы массива (a). Если элемент кратен (3), то запишем его в массив (b). После выполнения цикла в переменную (m) запишем максимальное значение массива (b).

(b=[])
for (i) in range ((0,len(a))):
if (a[i])%(3= =0):
b.append((a[i]))
(m=max(b))

3. Определим количество подходящих пар. Для этого очистим массив (b). Затем с помощью цикла (for) переберём все элементы массива (a). Если хотя бы один элемент пары делится на (3) и сумма элементов пары не больше (m), то запишем эту сумму в массив (b).

(b=[])
for (i) in range ((0),(len(a)-1)):
if ((a[i])%(3= =0) or (a[i+1])%(3= =0)) and ((a[i]+a[i+1]<=m)):
b.append ((a[i]+a[i+1]))

4. Выведем на экран количество элементов массива (b) — оно равно количеству подходящих пар — и максимальную сумму:

print ((len(b), max(b)))

Получилась программа:

with open ((’17.txt’)) as(f):
    (a=) [int((x)) for (x) in f.readlines()]
(b=[])
for (i) in range ((0,len(a))):
        if (a[i])%(3= =0):
            b.append ((a[i]))
(m=max(b))

(b=[])
for (i) in range ((0,len(a)-1)):
if ((a[i])%(3= =0) or (a[i+1])%(3= =0)) and ((a[i]+a[i+1]<=m)):
b.append ((a[i]+a[i+1]))

print ((len(b), max(b)))

Ответ: (2439) (998).

Источник

11. Числовые последовательности

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Числовые последовательности

Последовательность задана условиями (b_1=7), (b_{n+1}=-dfrac1{b_n}). Найдите (b_5).

Из данной в условии формулы следует, что [begin{aligned}
&b_2=-dfrac1{b_1}=-dfrac17 \[1ex]
&b_3=-dfrac1{b_2}=-dfrac1{-frac17}=7\[1ex]
&b_4=-dfrac1{b_3}=-dfrac17 \[1ex]
&b_5=-dfrac1{b_4}=7end{aligned}]

Ответ 7.

Ответ: 7

Последовательность задана условиями (b_1=-6), (b_{n+1}=-dfrac3{b_n}). Найдите (b_3).

Из данной в условии формулы следует, что [begin{aligned}
&b_2=-dfrac3{b_1}=-dfrac3{-6}=dfrac12 \[1ex]
&b_3=-dfrac3{b_2}=-dfrac3{frac12}=-6end{aligned}]

Ответ -6.

Ответ: -6

Последовательность задана формулой (c_n=-4n^2+7). Какое из указанных чисел является членом этой последовательности?
Укажите номер правильного ответа.

1) (-56)

2) (-58)

3) (-57)

4) (-55)

Способ 1.

Перепишем формулу как (4n^2=7-c_n). Из этой формулы видно, что левая часть делится на 4, следовательно, и правая часть должна делиться на 4. Отберем те числа (из данных четырех), которые подходят под условие ((7-c_n) vdots 4). Это единственное число (-57).
Проверим, действительно ли оно является членом последовательности:
(4n^2=7-(-57)=64), откуда (n^2=16), откуда (n=4) (так как (n) – натуральное число). Так как мы действительно получили натуральное (n), то (-57) является членом последовательности (причем четвертым).

Способ 2.

Данный способ – это та же самая проверка, как и во второй части решения первым способом, но для каждого из данных четырех чисел (без дополнительного отбора с помощью делимости). Этот способ менее предпочтителен тем, что является более долгим.

Ответ: 3

Последовательность задана формулой (c_n=-n^2+2). Какое из указанных чисел является членом этой последовательности?
Укажите номер правильного ответа.

1) (1)

2) (3)

3) (4)

4) (0)

Перепишем формулу как (n^2=2-c_n). Из этой формулы видно, что левая часть является полным квадратом, следовательно, и правая должна быть полным квадратом. Отберем те числа (из данных четырех), которые подходят под это условие. Это единственное число (1).
Проверим, действительно ли оно является членом последовательности:
(n^2=2-1=1), откуда (n^2=1), откуда (n=1) (так как (n) – натуральное число). Так как мы действительно получили натуральное (n), то (1) является членом последовательности (причем первым).

Ответ: 1

Последовательность задана формулой (x_n=19cdot dfrac{(-1)^n}n). Какое из указанных чисел не является членом этой последовательности?

1) (-dfrac{19}{21}qquad ) 2) (dfrac{19}{20}qquad ) 3) (-9,5qquad ) 4) (-dfrac{19}9)

Укажите номер правильного ответа.

Подставим:

1) (-frac{19}{21}=19cdot frac{(-1)^n}n), откуда (-frac1{21}=frac{(-1)^n}n). Подбором убеждаемся, что подходит (n=21).

2) (frac{19}{20}=19cdot frac{(-1)^n}n), откуда (frac1{20}=frac{(-1)^n}n). Тогда (n=20).

3) (-9,5=19cdot frac{(-1)^n}n). Так как (9,5=frac{19}{2}), то (-frac{19}{2}=19cdot frac{(-1)^n}n), откуда (-frac1{2}=frac{(-1)^n}n). Единственное (n), которое могло бы подойти – это (n=2). Но тогда ((-1)^{2}=1), а не (-1). Следовательно, это и есть число, которое не является членом данной последовательности.

(Для проверки можно также подставить и последнее, четвертое число.)

Ответ: 3

Последовательность задана формулой (x_n=-23cdot dfrac{(-1)^n}n). Какое из указанных чисел не является членом этой последовательности?

1) (dfrac{23}{19}qquad ) 2) (-dfrac{23}{24}qquad ) 3) (dfrac{23}{25}qquad ) 4) (11,5)

Укажите номер правильного ответа.

Подставим:

1) (frac{23}{19}=-23cdot frac{(-1)^n}n), откуда (frac1{19}=-frac{(-1)^n}n). Подбором убеждаемся, что подходит (n=19).

2) (-frac{23}{24}=-23cdot frac{(-1)^n}n), откуда (frac1{24}=frac{(-1)^n}n). Тогда (n=24).

3) (frac{23}{25}=-23cdot frac{(-1)^n}n), откуда (frac1{25}=-frac{(-1)^n}n). Тогда (n=25).

4) (11,5=frac{23}{2}), следовательно, (frac{23}{2}=-23cdot
frac{(-1)^n}n), откуда (frac1{2}=-frac{(-1)^n}n). Единственное (n), которое могло бы подойти – это (n=2). Но тогда ((-1)^{2}=1), а не (-1). Следовательно, это и есть число, которое не является членом данной последовательности.

Ответ: 4

Последовательность задана формулой (a_n=2n+4cdot dfrac{(-1)^n}n). Какое из указанных чисел не является членом этой последовательности?

1) (-3qquad ) 2) (9,dfrac15qquad ) 3) (6qquad ) 4) (-2)
Укажите номер правильного ответа.

Способ 1.

Заметим, что при (ngeqslant 2) все (a_n) будут положительными, так как (2ngeqslant 4), а (frac 4nleqslant 2). При (n=1) получим (a_1=2-4=-2). Следовательно, во-первых, число (-2) является членом последовательности, а во-вторых, больше отрицательных членов последовательности быть не может, то есть число (-3) не является членом последовательности. Ответ 1.

(Чтобы проверкой убедиться в этом, нужно решить (-3=2n+(-1)^ncdot frac 4n), откуда (2n^2+3n+4(-1)^n=0). Дискриминант этого уравнения (D=9-32(-1)^n). Следовательно, либо (D<0), либо (D=41). В первом случае корней нет, во втором случае корни есть, но иррациональные. А нам нужны натуральные корни (n).)

Способ 2.

Данный способ – это та же самая проверка, как и во второй части решения первым способом. Этот способ менее предпочтителен тем, что является более долгим.

Ответ: 1

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Опишите множество всех последовательностей из букв a и b таких, что в любом наборе подряд идущих символов (длины больше 1) букв a не меньше, чем букв b

Обратите внимание! В отличие от предыдущей задачи, рассматриваются не только начальные отрезки последовательности, а вообще любые!

Для описания используйте формулы, которые называются регулярными выражениями.

Так для повторения блока из нескольких букв используйте операцию «звездочка» (итерация), например, (abb)* задает множество слов {пустое слово, abb, abbabb, abbabbabb, …} Умножение множеств (эту операцию, как обычно в алгебре, изображают точкой или вообще опускают, что мы и будем делать), описывает склейку всех слов первого множества со словами второго (третьего и т. д.), например a*cb* обозначает множество слов: {с, ac, cb, acb, aac, …, aaa…acb.. b, …}. Обратите внимание что слова, в которых нет букв a или b, получаются за счет того, что результат итерации может не содержать символов, то есть быть пустым словом.

Последней операцией, которая используется в формулах, является сложение. Сложение соответствует объединению множеств. Так обозначение (a + b) c + d(ac*+) описывает множество всех последовательностей из букв a и b (обозначается (a +  b)*), к концу которых присоединена буква c, объединенного с множеством слов, начинающихся с буквы d, за которой следует буква a, а за ней любое число букв c и ещё одним однобуквенным словом (d умножить на пустое слово  — это d).

Слева приведены примеры слов, которые удовлетворяют нашему условию, справа примеры слов, которые не удовлетворяют ему. Благодаря подсветке вы можете видеть, какие из этих примеров и контрпримеров удовлетворяют построенному вами выражению, а какие  — нет.

Источник

В задание №17 добавлен файл. Он содержит последовательность целых чисел, которую необходимо будет использовать для обработки массива. Также в задании есть пример решения для другой последовательности. В ответ потребуется записать пару чисел, требуемую по условиям задачи.

Пара идущих подряд
Пара, последовательность не важна
Тройка идущих подряд
Тройка, последовательность не важна

Задание 17 проверяет умение написать простую переборную программу, на языке программирования, содержащую циклы и ветвление. Это задание проверяет только технические программистские умения, так как сам алгоритм решения описан в постановке задачи.

В отличии от 2021 года, в 2022 году к заданию 17 будет прилагаться файл данных. Отдельной технической задачей является чтение этого файла. Ответ будет зависеть от исходных данных.

Решением будет являться алгоритм последовательного просмотра пар.

Вариант 1. В данных задачах под парой подразумевается два идущих подряд элемента последовательности.

ДЕМО-вариант

В файле 17-demo1.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от −10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число делится на 3, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности. Например, для последовательности из пяти элементов: 6; 2; 9; –3; 6 — ответ: 4 11.

Решение:

Для выполнения этого задания необходимо:

Cкачать файл, создать папку и перенести его в эту папку;
Создать файл для программы и сохранить его тоже в эту папку;
Прочитать внимательно задание.

Описание программы:

Python может с относительной легкостью обрабатывать различные форматы файлов:

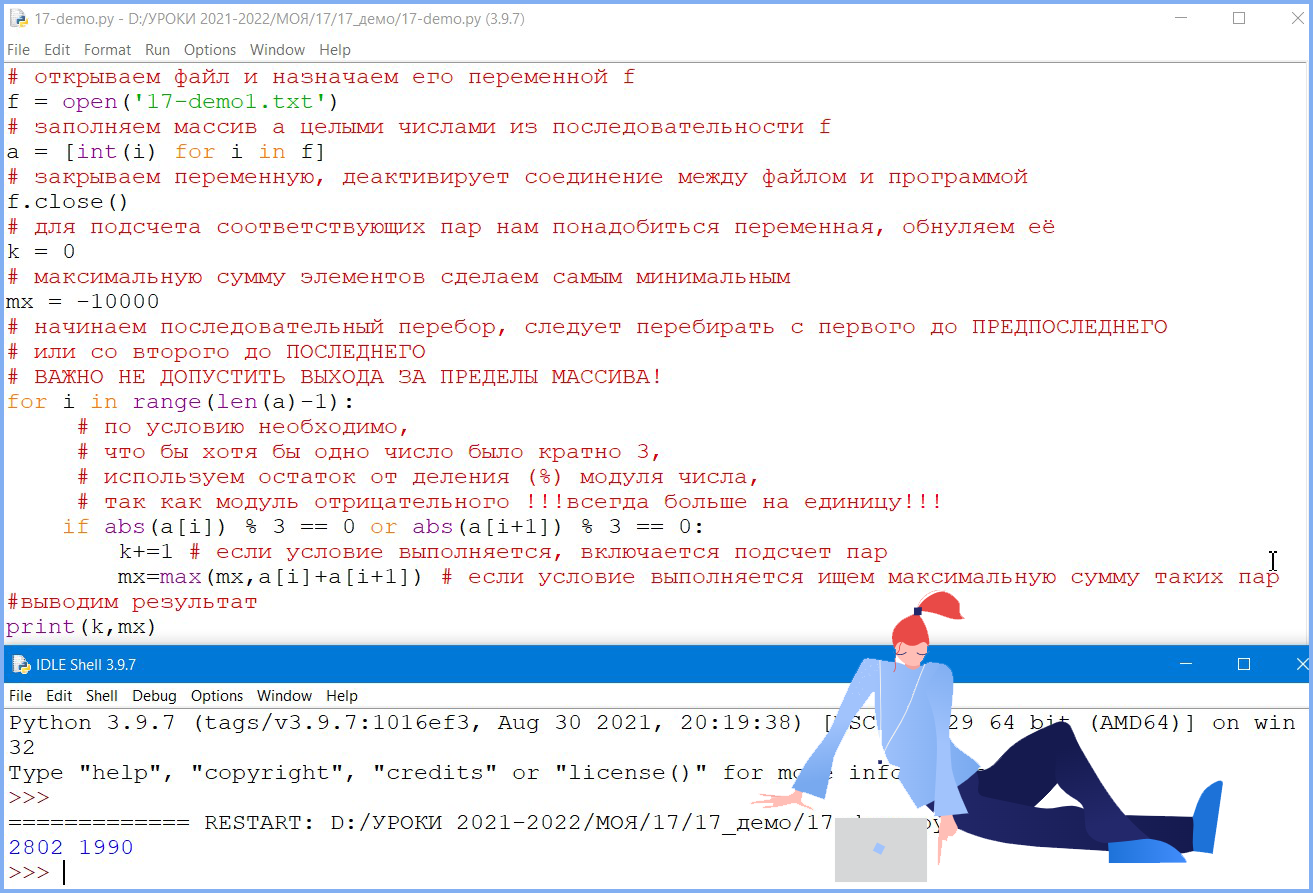
f = open('17-demo1.txt')
a = [int(i) for i in f]
f.close()
k = 0
mx = -10000
for i in range(len(a)-1):
    if abs(a[i]) % 3 == 0 or abs(a[i+1]) % 3 == 0:
    k+=1
    mx=max(mx,a[i]+a[i+1])
print(k,mx)

Ответ: 2802 1990

(№ 4352) (П. Волгин) В файле 17-P.txt содержится последовательность целых чисел. Элементы последовательности могут принимать значения от –100 до 100 включительно. Определите сначала количество пар элементов последовательности, в которых хотя бы одно число оканчивается на 7, а затем максимальную из сумм элементов таких пар. Под парой подразумевается два идущих подряд элемента последовательности. Например, для последовательности из 5 элементов: 7, 27, 17, 5, 57 ответ должен быть 4 62.

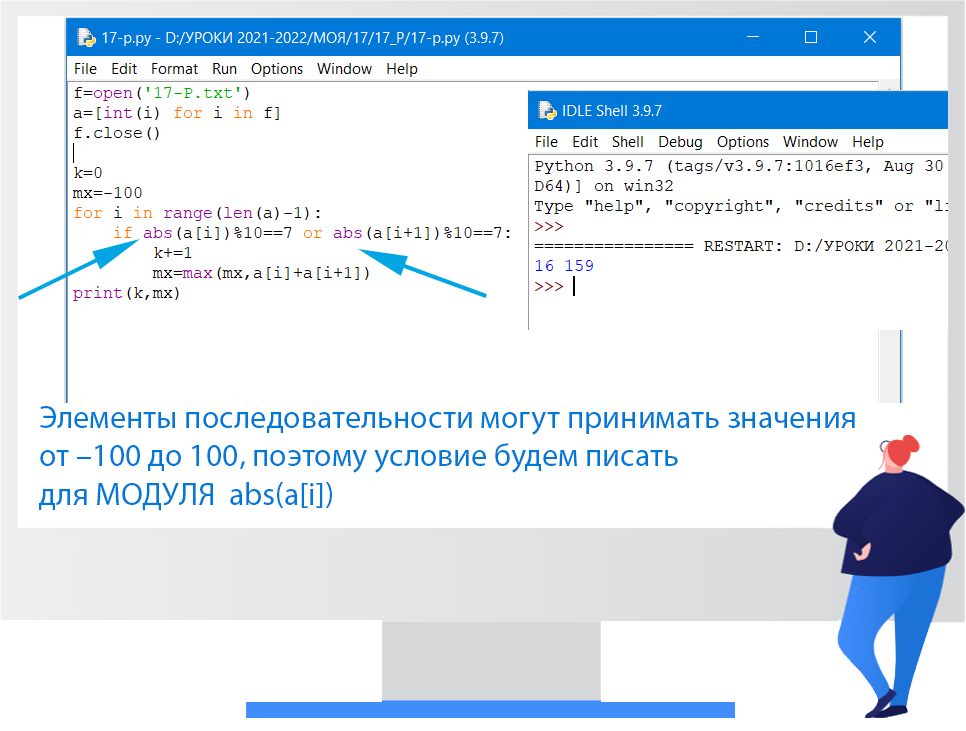
Ответ: 16 159

Проверим задачу в Excel

Импортируем данные в таблицу из текстового файла. Самый простой способ: открыть текстовый файл ➦ Ctrl+A ➦ Ctrl+C ➦ переходим в таблицу ➦ выделить ячейку А1 ➦ Ctrl+V.

Вот такую вложенную друг в друга формулу вставляем в ячейку В2:

=ЕСЛИ(ИЛИ(ОСТАТ(ABS(A1);10)=7;ОСТАТ(ABS(A2);10)=7);A1+A2;» «)

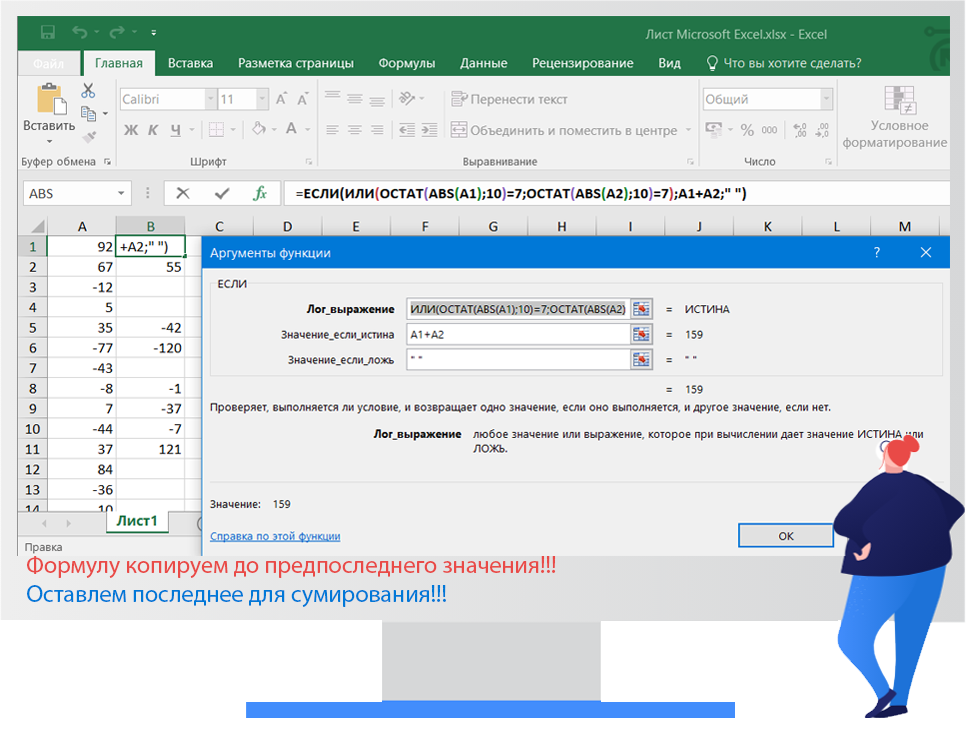
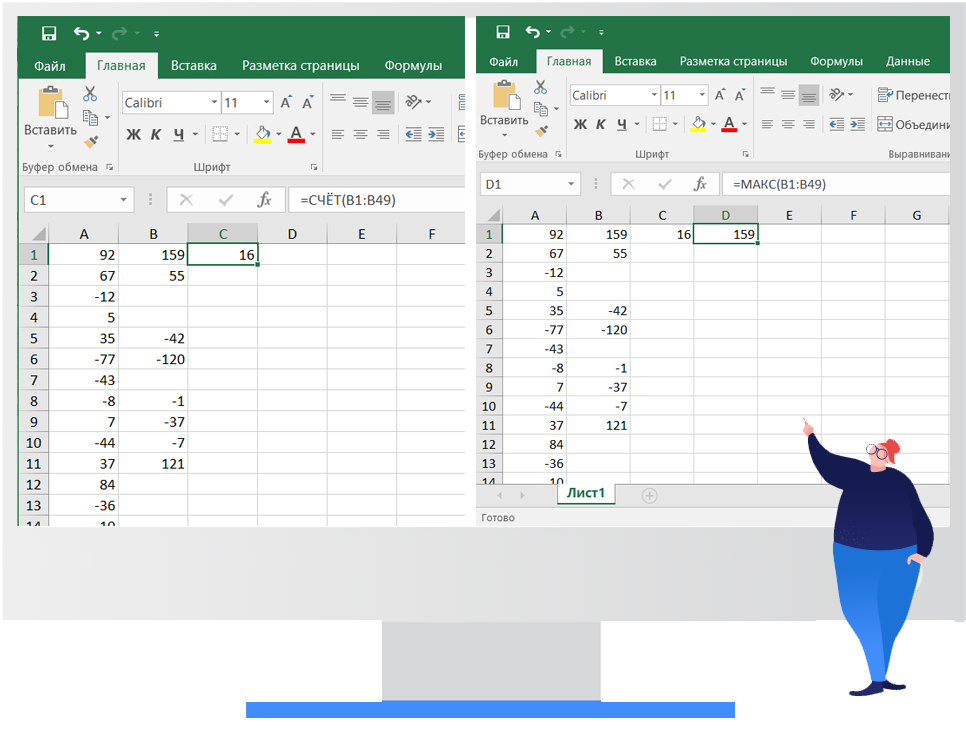
Ответ: 16 и 159

(№ 4707) (А. Кабанов) В файле 17-257.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые положительные значения до 10 000 включительно. Программа должна найти и вывести количество и наименьшую сумму пар элементов последовательности с чётной суммой, большей чем сумма максимального и минимального нечётного числа. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

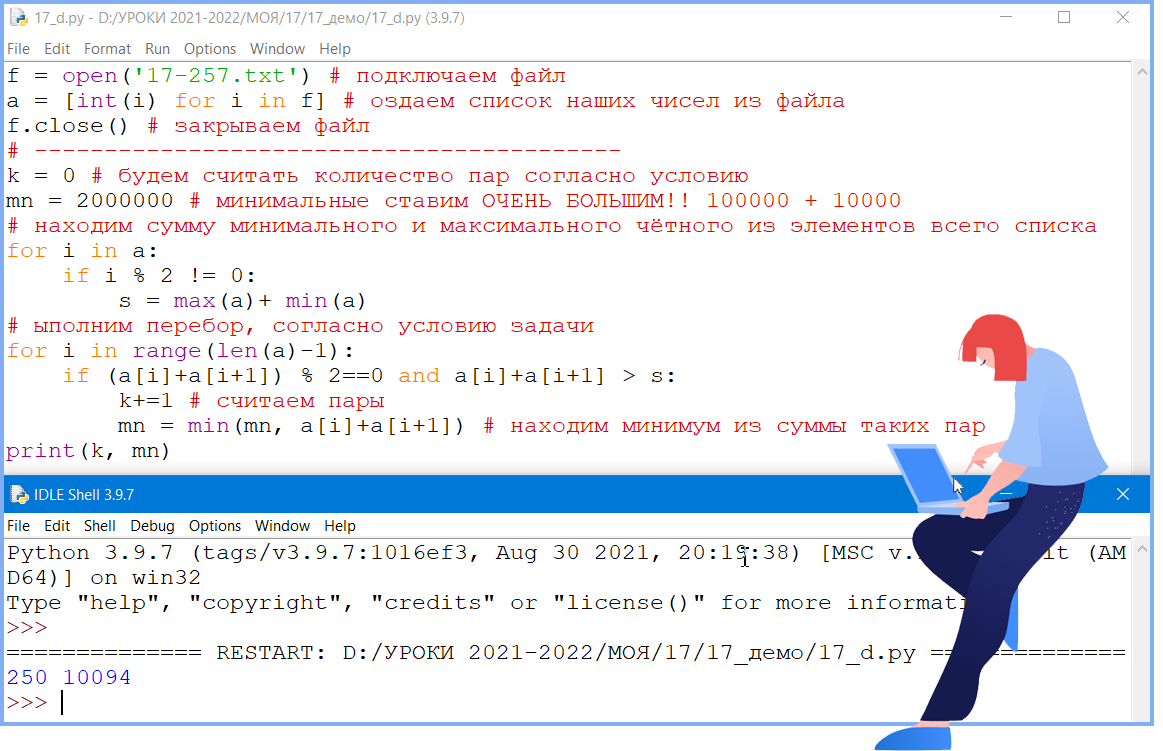
f = open('17-257.txt')
a = [int(i) for i in f]
f.close()
k = 0
mn = 2000000
for i in a:
    if i % 2 != 0:
        s = max(a)+ min(a)
for i in range(len(a)-1):
    if (a[i]+a[i+1]) % 2==0 and a[i]+a[i+1] > s:
        k+=1
        mn = min(mn, a[i]+a[i+1])
print(k, mn)

Ответ: 250 10094

(№ 4722) В файле 17-243.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 10 000 включительно. Определите количество пар чисел, в которых ровно один из двух элементов больше, чем сумма цифр всех чисел в файле, делящихся на 35, а шестнадцатеричная запись другого оканчивается на EF. В ответе запишите два числа: сначала количество найденных пар, а затем – минимальную сумму элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

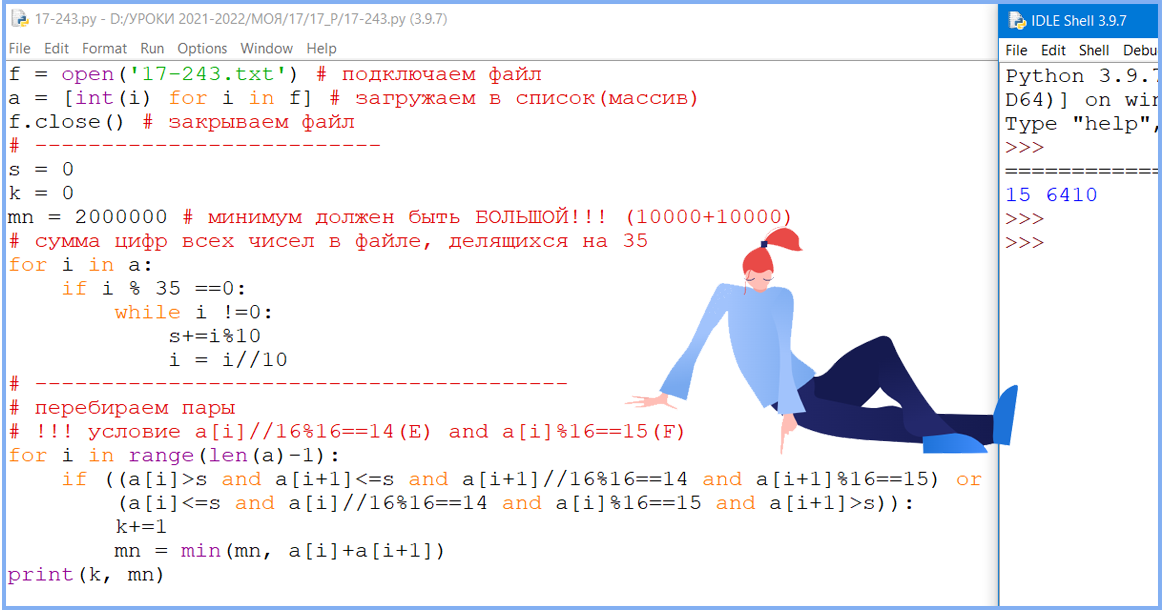
f = open('17-243.txt')
a = [int(i) for i in f]
f.close()
s = 0
k = 0
mn = 2000000
for i in a:
    if i % 35 ==0:
        while i !=0:
            s+=i%10
            i = i//10
for i in range(len(a)-1):
    if (a[i]>s and a[i+1]<=s and a[i+1]//16%16==14 and a[i+1]%16==15) or (a[i]<=s and a[i]//16%16==14 and a[i]%16==15 and a[i+1]>s)):
        k+=1
        mn = min(mn, a[i]+a[i+1])
print(k, mn)

Ответ: 15 6410

Вариант 2. В данных задачах под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.

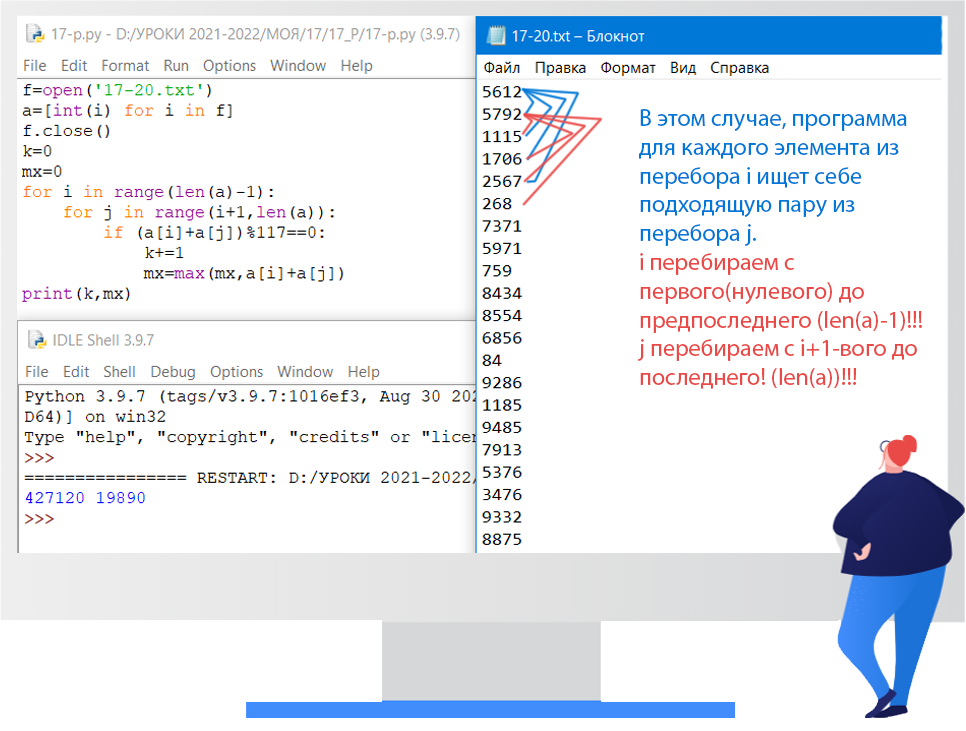
В файле 17-20.txt содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответ сначала количество пар элементов последовательности, у которых сумма элементов кратна 117, затем максимальную из сумм элементов таких пар. В данной задачи под парой подразумевают два различных элемента последовательности. Порядок элементов не важен.

f = open('17-20.txt')
a = [int(i) for i in f]
f.close()
k = 0
mx = 0
for i in range(len(a)-1):
    for j in range(i+1,len(a)):
        if (a[i] + a[j]) % 117 == 0:
            k+=1
            mx=max(mx,a[i]+a[j])
print(k, mx)

Ответ: 427120 и 19890

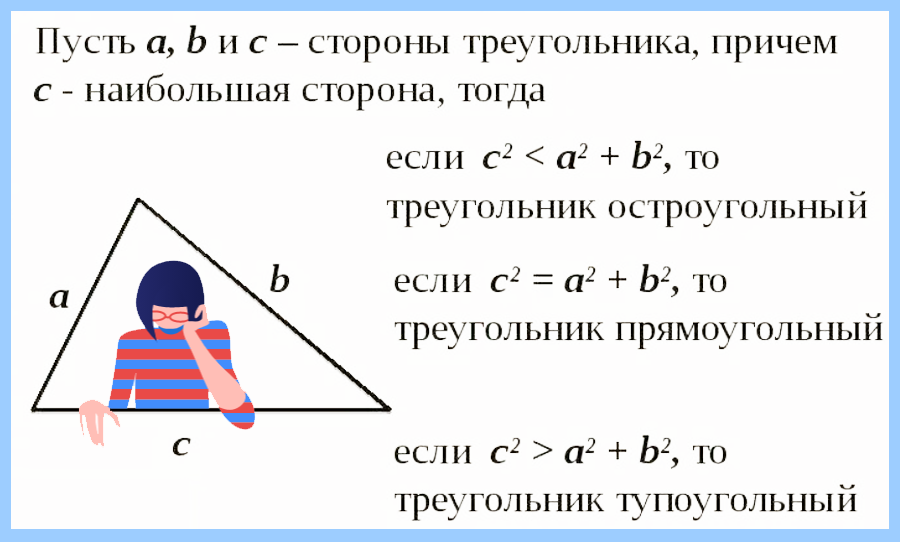
Вариант 3. В данных задачах считаем тройки элементов идущих подряд выполняя условие

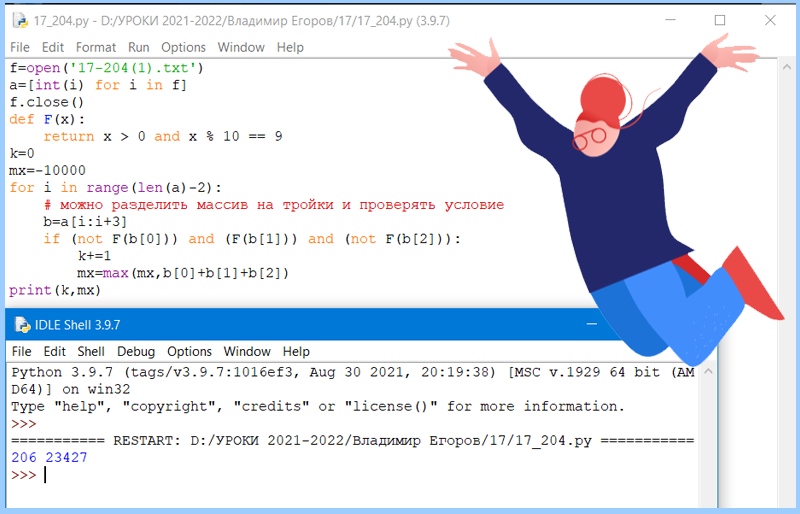
(П. Финкель) В файле 17-P2.txt содержится последовательность целых чисел, которые принимают значения от -10000 до 10000 включительно. Тройка идущих подряд чисел последовательности называется уникальной, если только второе из них является положительным числом, заканчивающимся на 9. Определите количество уникальных троек чисел, а затем – максимальную из всех сумм таких троек.

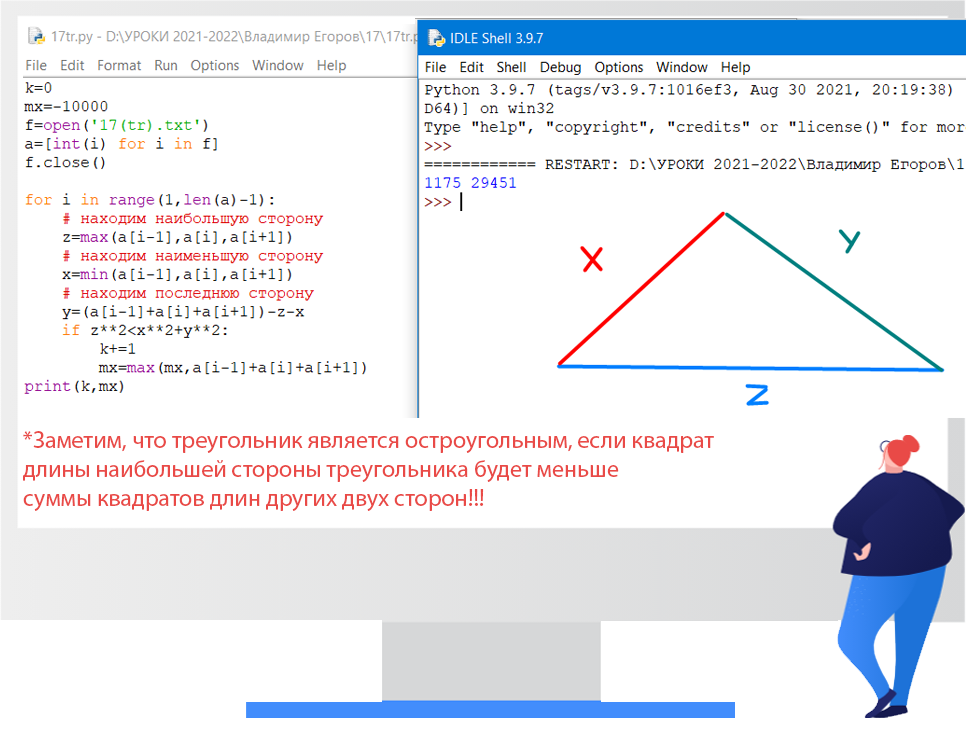
Файл 17tr.txt содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём тройкой три идущих подряд элемента последовательности. Определите количество троек чисел таких, которые могут являться сторонами остроугольного треугольника. В ответе запишите два числа: сначала количество найденных троек, а затем — максимальную сумму элементов таких троек. Если таких троек не найдётся — следует вывести 0 0.