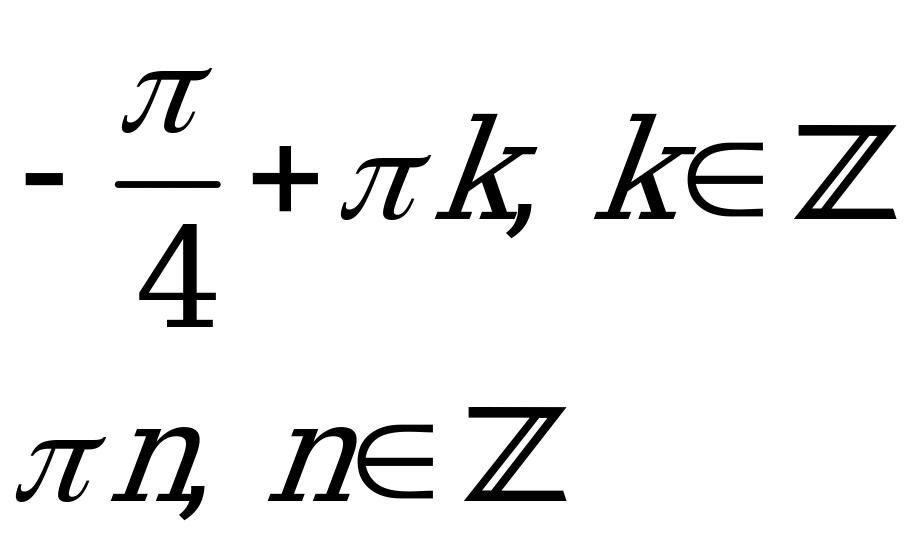Конференция молодых исследователей
«Шаг в будущее. Юниор»
Кафедра естественно-математических дисциплин.
Симпозиум 3. Математика и информационные технологии.
Секция 1. «Математика»
Направление работы секции : прикладная математика.
Проектная работа
Тригонометрия в ЕГЭ
Автор: Головачёва Валерия Алексеевна
Муниципальное бюджетное общеобразовательное учреждение «Гимназия» ,10 б класс
Руководитель: Перевозчикова Лилия Александровна,
высшая квалификационная категория,
учитель математики,
Муниципальное бюджетное общеобразовательное учреждение «Гимназия»
Подпись руководителя: ___________
Югорск, 2019 уч.г
Оглавление
Аннотация………………………………………………………………………………………
Введение……………………………………………………………………………………….
Из истории тригонометрии……………………………………………………………………
Основные тригонометрические формулы…………………………………………………….
Задачи группы В……………………………………………………………………………….
Из материалов ЕГЭ……………………………………………………………………………
Тригонометрия в ЕГЭ
Головачёва Валерия Алексеевна
Муниципальное бюджетное общеобразовательное учреждение «Гимназия», 10 класс
Аннотация
Цель работы: способствовать обобщению знаний по разделу «Тригонометрия».
Данный проект охватывает курс тригонометрии за 10 класс. Для успешной подготовки к ЕГЭ нужно усвоить основные тригонометрические формулы,знать определения обратных тригонометрических функций и их свойства, определять знаки тригонометрических функций и их свойства, работать с тригонометрической окружностью, уметь применять формулы приведения. А это поможет решать тригонометрические уравнения , неравенства, упрощать тригонометрические выражения.
Овладеть информацией о развитии тригонометрии; способствовать усвоению конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования.
Методы и приемы:
- поиск информации в источниках, справочниках
- работа с ресурсами Internet
- обработка и анализ информации
Полученные данные:были обобщены и систематизированы. Затем разработан целостный окончательный вариант информационного проекта, составлена брошюра по теме проекта.
Выводы:Выполняя работу
- не только рассмотрела все формулы, но и ликвидировала свои проблемы по данной теме. Для меня это очень важно при сдаче ЕГЭ по математике
- изучение столь важной и интересной темы дает положительную мотивацию для самообразования.
Тригонометрия в ЕГЭ
Головачёва Валерия Алексеевна
Муниципальное бюджетное общеобразовательное учреждение «Гимназия», 10 класс
Введение
На сегодняшний день одним из самых «проблемных» разделов школьного курса математики, выносимых на ЕГЭ, является тригонометрия.
Тригонометрия – важная и весомая составляющая контрольно-измерительных материалов единого экзамена, централизованного тестирования и заданий вступительных экзаменов; этот материал традиционно используется в математических олимпиадах.
Решение задач является важнейшим видом учебной деятельности, в процессе которой учащимися усваивается математическая теория и развиваются логическое мышление и творческие способности, а особенно при решении тригонометрических задач.
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд». Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции. В настоящее время изучению тригонометрических задач уделяется большое внимание в школьном курсе алгебры и начал анализа. Тригонометрические задачи из года в год встречаются среди заданий ЕГЭ, а именно базовый уровень: найти значение одной тригонометрической функции через другую; упростить тригонометрическое выражение, применяя формулы. Все выше сказанное и обуславливает актуальность выбора темы для данной проектной работы.
Цель :
Систематизировать, обобщить, расширить знания и умения, связанные с решением тригонометрических задач.
Задачи:
1. Найти и обобщить информацию о применении тригонометрии в задачах ЕГЭ.
2. Провести анализ и систематизацию собранной информации.
3. Составить учебное пособие по теме: «Тригонометрические задачи ЕГЭв части В».
Из истории тригонометрии.
История тригонометрии как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций, и поэтому понадобилось ввести особые тригонометрические функции, первоначально оформлявшиеся в виде числовых таблиц.
Историки полагают, что тригонометрию создали древние астрономы; немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, и в наши дни она включает практически все естественные науки, технику и ряд других областей деятельности[1].
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значениедля всей математики.
Тригонометрическая окружность для нахождения синуса, косинуса, тангенса и котангенса.
Синусом угла αназывается ордината точки единичной окружности, полученной при повороте точкиM(1;0) на угол α радиан вокруг начала координат.
sinα=
Например: sin 3

Косинусом угла αназывается абсцисса точки единичной окружности, полученной при повороте точки (1;0) на угол α радиан вокруг начала координат.
cosα=
Например: cos 3

Котангенсом угла αназывается отношение косинуса угла α к его синусу.
Например: ctg 3

Тангенсом угла aназывается отношение синуса угла a к его косинусу.
Например:tg 6

Задания из ЕГЭ на умение находить значения тригонометрических функций по окружности.
- Найдите значение выражения
Решение:
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
Основное тригонометрическое тождество и знаки тригонометрических функций.
- Найдите
, если
и
.
Решение:
Т.к. 
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
Чтобы найти тангенс нужно применить формулу: 
- Найдите
, если
и
.
- Найдите
, если
и
.
- Найдите
, если
и
.
Зависимость между тангенсом и котангенсом.
- Найдите значение выражения
Решение:
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
Формулы двойного угла:
- Найдите значение выражения
Решение: 
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найти значение выражения
Решение:
- Найти значение выражения
- Найти значение выражения
- Найти значение выражения
- Найдите
, если sin 3α=0,9
Решение:
- Найдите
, если sin 3α=-0,5
- Найдите
, если sin 3α=-0,6
- Найдите
, если sin 2α=0,2
- Найдите
, если sin 2α=0,8
Формулы приведения.
Формулы приведения – это такие формулы, которые позволяют сделать вычисления проще, а сложные аргументы тригонометрических функций привести к аргументам первой четверти.
|
|
|
|
|
|
|
|
|
|
|
|
sin |
— sinα |
cosα |
cosα |
sinα |
— sinα |
— cosα |
— cosα |
— sinα |
sinα |
|
cos |
cosα |
sinα |
— sinα |
— cosα |
— cosα |
— sinα |
sinα |
cosα |
cosα |
|
tg |
— tgα |
ctgα |
ctgα |
— tgα |
tgα |
ctgα |
-ctgα |
— tgα |
tgα |
|
ctg |
— ctgα |
tgα |
— tgα |
-ctgα |
ctgα |
tgα |
— tgα |
— tgα |
ctgα |
Мнемоническое правило для формул приведения («лошадиное правило»).
- Сначала нужно определить, меняется ли функция на кофункцию (например, синус на косинус, косинус на синус, тангенс на котангенс и котангенс на тангенс).
- Для этого надо подвигать головой вдоль той оси, на которой располагается ключевая точка. Если голова мотает вдоль горизонтальной прямой, мы как бы говорим, что «нет», функция остается неизменной.
- Если же, получается мотать головой вдоль вертикальной прямой, то мы как бы говорим «да», надо изменить функцию на кофункцию.
- Далее определяем, какой на выходе получается знак «-» или «+». Знак ставим тот, который несет в себе левая исходная часть.
- Найдите значение выражения
Решение: 
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
Решение:
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражение
- Найдите значение выражение
- Найдите значение выражение
- Найдите значение выражение
- Найдите значение выражение
- Найдите значение выражения
Решение: 26sin(360



- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
Решение: 8

- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
- Найдите значение выражения
Заключение.
Литература
- Глейзер Г.И. История математики в школе: IX-X кл. — М.: Просвещение, 1983.
- Маслова Т.Н. «Справочник школьника по математике»
- Рыбников К.А. История математики: Учебник. — М.: Изд-во МГУ, 1994.
- Сайт Ларина( Яндекс) « Готовим хорошистов и отличников к ЕГЭ»
- Открытый банк заданий по математике базовый и профильный уровень ур
МБОУ « Мордовско-Паёвская
СОШ» Инсарского района РМ

Выполнила: Пантилейкина Надежда,
ученица 11 класса
Руководитель: Кадышкина Н.В.,
учитель математики
Оглавление
Введение…………………………………………………………………………….
Глава I. О
тригонометрических уравнениях…………………………………..…5
1) Основные типы
тригонометрических уравнениях и методы их решения:
1. Уравнения,
сводящиеся к простейшим. …………………………………..5
2. Уравнения,
сводящиеся к квадратным…………………………………….5
3. Однородные
уравнения acosx + b sin x = 0…………………………………6
4.Уравнения
вида acosx + b sin x = c,
с≠ 0…………………………………7
5. Уравнения,
решаемые разложением на множители……………………….7
6. Нестандартные
уравнения………………………………………………….8
Глава II. Основные
понятия и формулы тригонометрии…………………….8-10
Глава III. Уравнения предлагавшиеся на ЕГЭ прошлых лет…………………10-14
Заключение………………………………………………………………………….14
Приложение……………………………………………..……………………….15-17
Литература…………………………………………………………………………..18
Введение
«Единственный путь, ведущий к знаниям — это деятельность…»
Бернард Шоу
Актуальность работы.
Через
несколько месяцев я заканчиваю школу.
Чтобы не
было проблем с дальнейшим выбором жизненного пути, необходимо получить школьный аттестат,
а для того чтобы получить школьный аттестат, необходимо сдать два обязательных
экзамена в форме ЕГЭ — и один из них математика. Что уж там
говорить, выпускные экзамены — ответственный период в жизни любого
школьника, от которого зависит не только итоговая оценка в аттестате, но и его
профессиональное будущее, доход и карьера.
Единый
Государственный Экзамен – это важный тест перед переходом в новую жизнь и
поступлением в университет или колледж. Особенно важно сдать его на хорошие
баллы. ЕГЭ по математике — серьезное испытание и без хорошей базы
ученик не сможет претендовать на приличный результат.
Как не допустить провала на
экзамене и получить хорошие баллы? Для этого необходимо хорошо решить задания.
Я не претендую на максимальный балл, тем не менее старательно готовлюсь. И
заметила, что даже на первом задании части С, а, именно, на решении
тригонометрических уравнениях и их системах допускаю ошибки. На первый
взгляд, задача С1 – это относительно несложное уравнение или система уравнений,
которое может содержать тригонометрические функции, одним
из основных подходов к решению которых состоит в их последовательном упрощении
с целью сведения к одному или нескольким простейшим. Так почему я
ошибаюсь?
Актуальность
темы определяется
тем, что учащиеся должны разбираться в тех или иных способах решения
тригонометрических уравнений.
Поэтому, перед собой я поставила следующую цель:
Систематизировать,
расширить знания и умения, связанные с применением методов решения
тригонометрических уравнений.
Объектом исследования является изучение тригонометрических уравнений в
заданиях ЕГЭ.
Предмет исследования — является решение тригонометрических уравнений
Таким
образом, основной целью написания данной курсовой работы является
изучение тригонометрических уравнений и их систем, способы их решения.
В
соответствии с целями, объектом и предметом исследования определены следующие задачи:
1). Изучить все
задания, связанные с решением тригонометрических уравнений, предлагавшиеся на
ЕГЭ работ предыдущих лет и при выполнении диагностических работ;
2)
Изучить методы решения тригонометрических уравнений.
3). Выявить
основные возможные ошибки при решении таких уравнений;
4). Выяснить
причину допущения таких ошибок.
5)Рассмотреть
рекомендации по решению тригонометрических уравнений;
6). Сделать
выводы.
В своей
работе я решу несколько тригонометрических уравнений, покажу возможные ошибки
при их решении и постараюсь ответить на следующие вопросы:
1).
Можно ли избежать ошибок при выполнении заданий типаС1
2)
Если я буду тренироваться в решении уравнений такого типа, то я смогу
ли безошибочно
выполнять такие задания?
Для
этой цели я изучила все демонстрационные и тренировочные задания, проводимые с
нами, материалы ЕГЭ предыдущих лет;
изучила
справочные источники;
самостоятельно
решала задания из Интернета;
консультировалась
со своим учителем в случае затруднения;
училась
анализировать и правильно оформлять результаты.
Глава I. О
тригонометрических уравнениях.
1) Определение 1. Тригонометрическим уравнением называется уравнение,
содержащее переменную под знаком тригонометрических функций.
Простейшие
тригонометрические уравнения — это уравнения вида sin x = a,
cos x=a,
tg x=a, ctg x = a.
В
таких уравнениях переменная находится под знаком тригонометрической функции, а
— данное число.
Решение
тригонометрического уравнения состоит из двух этапов: преобразование уравнения
для получения его простейшего вида и решение полученного простейшего
тригонометрического уравнения.
2)Основные типы тригонометрических уравнений.
1.
Уравнения, сводящиеся к простейшим.
Решить уравнение
Решение:
Ответ:
2. Уравнения,
сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Ответ:
3. Однородные
уравнения: asinx + bcosx = 0
a sin 2 x
+ b sinxcosx + c cos 2 x = 0.
Решить уравнение 2sinx – 3cosx = 0
Решение:
Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем,
что
sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно
поделить уравнение на cosx.
Получим
Ответ:
4.
Уравнения вида a sinx + b cosx = с,
с ≠ 0.
Пример: Решить уравнение
Решение:
Ответ:
5. Уравнения,
решаемые разложением на множители.
Припер: Решить уравнение sin2x – sinx = 0.
Решение: Используя формулу sin2x =
2sinxcosx, получим
2sinxcosx – sinx = 0,
sinx (2cosx – 1) = 0.
Произведение равно нулю, если хотя бы
один из множителей равен нулю.
Ответ:
6. Нестандартные
уравнения.
Решить уравнение cosx = х 2 + 1.
Решение:
Рассмотрим функции
Глава II. Основные понятия и формулы тригонометрии.
Тригонометрические
уравнения — обязательная тема любого экзамена по математике.
Ох,
сколько мучений доставляет ученикам изучение тригонометрии.
Определенные сложности возникают даже в
том случае, если рядом учитель по математике и
объясняет каждую мелочь. Это и понятно, одних только базовых формул существует
более двадцати. А уж если считать их производные … Ученик путается в
вычислениях и никак не может запомнить механизмы, при помощи которых эти
формулы позволяют найти, например, .
Вы
знаете формулы — вам легко решать. Не знаете — не поймете, даже если дадут
формулу.
Формулу нужно не просто тупо знать, а знать куда
ее можно применить, как раскрыть и в чем суть формулы, а для этого вам нужно
решать примеры именно для тех задач, которые даются с трудом.
Мне
поначалу казалось, тригонометрия — это скучный набор формул и
графиков. Однако, знакомясь с новыми понятиями тригонометрии и методами
решения тригонометрических уравнений, каждый раз убеждалась, насколько
интересен и увлекателен мир тригонометрии.
Во- первых, для успешного решения тригонометрических уравнений нужно хорошо
знать тригонометрические формулы, причем не только основные, но и
дополнительные (преобразование суммы тригонометрических функций в произведение
и произведения в сумму, формулы понижения степени и другие), так
как использование на ЕГЭ шпаргалок и мобильных телефонов запрещается
(Приложение1)
Во- вторых, мы должны четко знать стандартные
формулы корней простейших тригонометрических уравнений (полезно помнить или
уметь получать с помощью тригонометрической окружности упрощенные формулы для
корней уравнений)
Каждое
из таких уравнений решается по формулам, которые следует знать. Вот эти формулы:
а)
Функция y=sin x. Функция ограниченная:
находится в пределах [-1; 1]. Это значит, что при решении уравнений типа sinx=2 или sinx=-5 в ответе получается: нет
корней. Формулы для функции у= sinx
1) sinx =a, x= (-1)narcsin a +n,nZ
2) sinx = — a, x=
(-1)n+1arcsin
a +n,nZ
Также,
нужно знать частные случаи: 1) sinx =- 1,
2) sinx =0,
3) sinx =a,
Также нужно уметь решение в виде двух серий корней
.
2. Функция y= cos x. Функция ограниченная:
находится в пределах [-1; 1]. Это значит, что при решении уравнений типа cos x=2 или cos x=-5 в ответе получается: нет
корней. Формулы для функции у= cos x:
1. cosx =a,
X=± arccos a+2n,nZ
2. cos x=-a,
X=±( — arccos a)+2n,nZ
Частные
случаи: 1. cosx =-1, X= +2n,nZ
2. cosx =0,
3.
cosx =1, X= 2n,nZ
3. Функция y= tg x.
Тут
всего одна формула, без частных случаев: tg x =±a .
х=
± arctg a+n,nZ
В-третьих, надо знать значения тригонометрических функций;
(
Приложение 2)
В- четвёртых, Если в уравнении
тригонометрическая функция находится под знаком радикала, то такое
тригонометрическое уравнение будет иррациональным. В таких уравнениях следует
соблюдать все правила, которыми пользуются при решении обычных иррациональных
уравнений (учитывается область допустимых значений как самого уравнения, так и
при освобождении от корня четной степени).
V. Уравнения, предлагавшиеся на ЕГЭ
прошлых лет.
«Метод решения хорош, если с самого начала мы можем предвидеть – и
впоследствии подтвердить это, — что, следуя этому методу, мы достигнем
цели».
Лейбниц
1.
Уравнения, сводящиеся к квадратному.
С1. Решить уравнение:
Решение:
Воспользовавшись основным тригонометрическим тождеством, перепишем уравнение в виде
Заменой
cos=t уравнение
сводится к квадратному:2t2+ 9 t -5 =0,
которое имеет корни t 1= ½ и t2 = -5. Возвращаясь
к переменной х, получим ,
Второе
уравнение корней не имеет так как |cosx|≥1, а из первого x=±+6
k,k
Z
Ответ:
=±+6
k,k
Z
Вывод:
вводя новую переменную, нужно учитывать, что значения sin x
и cos x ограничены отрезком , а
иначе появятся посторонние
корни.
2.
Уравнения, решаемые разложением на множители
Задание С1 ( 2011 г.)
а)
Решить уравнение
б)
Указать корни уравнения, принадлежащие отрезку
Решение:
а) решаем разложением левой части на множители:
группируем
и выносим общий множитель за скобки, получим
 |
Уравнение 1) решений не имеет.
Второе уравнение однородное, решается
делением почленно на cosx ≠0, получим ,
откуда
б)
Ответ: а) б)
Вывод:
1.При
решении уравнения такого вида, во – первых, нужно знать, что |sinх|≤1
и |cosx|≤1, и уравнение sinx=-2
решений не имеет;
2.Во
– вторых, обосновать деление на cosx≠о (
так как , если cosx=0,то sinх=0
, а это невозможно;
в-
третьих, обоснованно произвести отбор корней, принадлежащие данному промежутку
3.Уравнение на применение
формул приведения
С1 (
2010 г.) Дано уравнение
а)
решить уравнение;
б) Указать корни,
принадлежащие отрезку
Решение:
Используя формулы приведения, получим :
sin
2 x – cos x =0,
2
sinx cosx- cosx =0,
сosx
(2 sinx -1 )=0, откуда cosx= 0 или
sinx =½,
б) Найдем значения к, при которых
корни будут принадлежать
указанному промежутку. Для того, чтобы
выбрать корни. принадлежащие заданному промежутку, решение представим в виде :

принадлежать указанному промежутку.
2)
Решая
это неравенство, целого

значения к не получим.
3)
Ответ: а)
б)
Вывод:
При
решении уравнения такого вида, необходимо знать формулы приведенного уравнения
и правильно её применить; уметь представлять решениена
две серии корней; правильно выбрать корни, принадлежащие заданному отрезку.
4.
Системы тригонометрических уравнений
С1 (2010). Решить систему уравнений
Решение: О.Д.З
Дробь
равна нулю, если числитель равен 0, а знаменатель не равен 0.
Из
уравнения 2sin2x
– 3 sinx +1 =0, решая методом введения новой
переменной, находим
или sin x=1.
1)Пусть
, тогда
и у = cos x =
›0 ( используя основное
тригонометрическое тождество)
либо
и
— нет
решения.
2)
Пусть sinx = 1, тогда у = cos x
= 0 – нет решения.
Ответ: и у =
Вывод:
1) нужно учитывать ограниченность тригонометрических
функций
2)
Записывать и учитывать О.Д.З.
5. С1 ( ЕГЭ 2011 г.)
Решить уравнение:
О.Д.З. – cos x ≥ 0, sin х ≤ 0.
4sin2 x + 12 sinx + 5 = 0
или cos x =0
sinx = t
4 t2 + 12 t + 5=0, откуда t1=-½ , t2 = —
sinx = -½ sinx =- — не имеет решения
х =
х =
с учётом О.Д.З. х =
Ответ:
х =
Вывод:
Ответ записать с учётом О.Д.З.
ЗАКЛЮЧЕНИЕ
В проделанной мною работе
были изучены решения тригонометрических уравнений, рассмотрены рекомендации по
решению тригонометрических уравнений, методы решения тригонометрических
уравнений и рассмотрены ошибки, которые возможны при их решении.
Я
пришла к следующим выводам:
1. Задания типа С1 проверяют умение
решать тригонометрические уравнения. Эти
задания являются, действительно, несложными, что придаёт лишнюю
самоуверенность и усыпляют внимательность. Единственной сложностью этих заданий
является то, что, решив уравнение или систему уравнений, отбросить посторонние
корни.
2. Задача С1 – это самая простая задача группы С. При ее решении не
должны возникать громоздкие преобразования и сложные вычисления. Если же они
появились – немедленно нужно остановиться, проверить решение и попробовать
понять, что же здесь не так.
3. В конечном итоге,
главное
требование — решение должно быть математически грамотным, из него
должен быть понятен ход рассуждений. Нужно постараться записать
свое решение кратко и понятно, но главное – правильно!
4. И самое
главное — чтобы научиться без ошибок решать уравнения , надо их решать! Ведь,
как говорил Пойа, « Если хотите научиться плавать,
то смело ныряйте в воду, а если хотите научиться решать задачи, надо их
решать!»
Приложение 1 ( основные формулы тригонометрии)
1)
основное тригонометрическое тождество sin2α +cos2 α= 1,
Деля
это уравнение на квадрат косинуса и синуса соответственно имеем
2)формулы
двойного аргумента sin2α =2 sinα cos α,
cos 2α = cos2 α — sin2α,
cos 2α = 1- 2sin2α,
3)формулы
понижения степени:
4)
формулы суммы и разности двух аргументов:
sin(α+β)=sinα cos β +cos α sin β
sin(α-β)=sinα cos β —cos α sin β
cos(α+β)=cosα cos β +sin α sin β
cos(α-β)=sinα cos β +sinα sin β
5)Формулы
приведения
Формулами приведения
называются формулы следующего вида:
Суммы
суммы и разности тригонометрических уравнений
Чётность
Косинус— чётная,
синус, тангенс и котангенс— нечётные,
то есть:
Непрерывность
Синус
и косинус — непрерывные функции.
Тангенс и имеет точки разрыва
,котангенс 0; ±π; ±2π;…
Периодичность
Функции y = cos x, y
= sin x — периодические с периодом 2π,
функции y = tg x и
y = ctg x — c периодом π.
Знаки тригонометрических функций по четвертям
Приложение
2(Таблица
значений тригонометрических функций некоторых углов)
|
Угол (a) |
Тригонометрическая функция |
||||||
|
Градусы |
Радианы |
sin a |
cos a |
tg a |
ctg a |
sec a |
cosec a |
|
0° |
0 |
0 |
1 |
0 |
∞ |
1 |
∞ |
|
30° |
|
|
|
|
|
|
2 |
|
45° |
|
|
|
1 |
1 |
|
|
|
60° |
|
|
|
|
|
2 |
|
|
90° |
|
1 |
0 |
∞ |
0 |
∞ |
1 |
|
120° |
|
|
|
|
|
-2 |
|
|
135° |
|
|
|
-1 |
-1 |
|
|
|
150° |
|
|
|
|
|
|
2 |
|
180° |
|
0 |
-1 |
0 |
∞ |
-1 |
∞ |
|
210° |
|
|
|
|
|
|
-2 |
|
225° |
|
|
|
1 |
1 |
|
|
|
240° |
|
|
|
|
|
-2 |
|
|
270° |
|
-1 |
0 |
∞ |
0 |
∞ |
-1 |
|
300° |
|
|
|
|
|
2 |
|
|
315° |
|
|
|
-1 |
-1 |
|
|
|
330° |
|
|
|
|
|
|
-2 |
|
360° |
|
0 |
1 |
0 |
∞ |
1 |
∞ |
ЛИТЕРАТУРА
1. Гилемханов Р.Г. О
преподавании тригонометрии в 10 классе по курсу В //Математика в школе. 2001-№ 6 —с. 26-28.
2. Глазков Ю. А. Математика. ЕГЭ:
сборник заданий и методических рекомендаций/ Ю. А. Глазков, И. К. Варшавский,
М. Я. Гаиашвили. – М.: Издательство «Экзамен», 2008-2010
3. Крамор В.С.
Тригонометрические функции. — М.: Просвещение, 1979.
4. Синакевич С.В.
Тригонометрические уравнения — М.: Учпедгиз, 1959.
5. Цукарь А.Я. Упражнения
практического характера по тригонометрии //Математика в школе. 1993-№3- с
12-15.
6. Выгодский М.Я.
Справочник по элементарной математике. — М.: Наука, 1978.
7. Крамор В.С. Повторяем
и систематизируем школьный курс алгебры и начал анализа. Москва, «Просвещение»,
1994.
8. Алимов Ш.А. Алгебра и
начала анализа 10-11. Учебник — М.: Просвещение, 2001.
9. ЕГЭ.
Контрольно-измерительные материалы. М: Просвещение, 2002-2011г.
10.http://www.ucheniki.hut2.ru/sprav/sprav_mathem/sprav_mathem_text/trigonom/sprav_mathem_znashen.php
11. http://www.webmath.ru/poleznoe/trig_formules.php
муниципальное бюджетное общеобразовательное учреждение
города Ульяновска
«Средняя школа №6 им. И.Н.Ульянова»
Защита проектов «Тригонометрия в заданиях ЕГЭ»
Открытый урок по математике
Макарова Татьяна Викторовна – учитель математики
Дата проведения – 16 марта 2016 года
2015-2016
Предмет – математика
Раздел – «Проект»
Тема – «Защита проектов «Тригонометрия в заданиях ЕГЭ»
Форма проведения – творческий монопроект с открытой координацией.
Цели:
Образовательный аспект: способствовать обобщению знаний по разделу «тригонометрия», расширить математические представления учащихся о тригонометрических функциях в системе подготовки к ЕГЭ; способствовать овладению конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования.
Развивающий аспект: развивать основные способы мыслительной деятельности учащихся (умение анализировать, ставить и разрешать проблемы), формировать и развивать познавательный интерес к предмету, развивать речь и способность убедительно излагать мысли, способствовать развитию самостоятельности учащихся.
Воспитательный аспект: воспитывать взаимопонимание и терпимость, самостоятельность, умение презентовать себя, оценивать себя и других, руководить коллективом.
Профориентационный аспект: способствовать созданию условий для формирования индивидуальной траектории развития профессиональных интересов учащихся, выработке профессионально значимых качеств личности (творческих, организаторских, ораторских).
Оборудование: компьютер, мультимедийный проектор, экран
Оформление: презентация, творческие работы учащихся.
«Меняется мир, непрерывно, неспешно,
Меняется все от концепций до слов.
И тот лишь сумеет остаться успешным,
Кто сам вместе с миром меняться готов!»
Петр Калита
Структура занятия
|
этапы занятия |
Содержание этапа |
Материально-техническая база |
|
1.организационно-подготовительный |
Приветствие. Проверка явки учащихся на занятие, их готовности. Активизация учащихся. Формулировка темы, целей занятия. Постановка перед учащимися учебной задачи. |
Оценочные листы |
|
2.Подготовка к активной учебно-познавательной деятельности |
Вступительное слово учителя |
Оформление занятия: -компьютер -мультимедийный проектор -экран |
|
3. Защита проектных работ |
Представление проектов, презентация окончательных результатов. Самооценка и взаимооценка выступлений. Оценивание качества выполнения работ членами оценочной комиссии |
Проектные работы учащихся: «Преобразование тригонометрических выражений» «Простейшие тригонометрические уравнения» «Решение тригонометрических уравнений» «Методы решения тригонометрических уравнений. Способы нахождения корней тригонометрических уравнений» «Тригонометрические неравенства» «Тригонометрия в физике» «Тригонометрия в геометрии» «Тригонометрия вокруг нас» |
|
4. Подведение итогов |
Демонстрация проектных работ. Сообщение итоговых оценок. |
Оценочные листы |
Ход урока.
-
Вступление.
Учитель:
Добрый день, дорогие друзья!
В этом учебном году нами изучен один из основных разделов математики «Тригонометрия». ЕГЭ содержит 28% задач по тригонометрии, при успешном решении которых можно заработать 30 баллов. В течение этого урока мы с вами повторим и обобщим все знания, полученные по данному разделу, совершив небольшое путешествие по всем заданиям ЕГЭ по математике, в которых необходимы знания по теме «Тригонометрия».
Дорогие ребята!
Прошел этап рутинной подготовки к нему. Вы много трудились. Задачи, которые необходимо было решить при выполнении проектной работы, были следующие:
-
проанализировать задания ЕГЭ,
-
найти информацию из ресурсов интернет, относящуюся к теме проекта,
-
выполнить практическую работу по данной теме, составив сборник заданий,
подготовить показ конечного продукта своей работы в форме презентации, продемонстрировав глубину практической работы в рамках проекта «Тригонометрия в заданиях ЕГЭ», сделать памятку для своих сверстников.
Основополагающим вопросом, направляющий проект есть вопрос «Для чего нужна тригонометрия? Чтобы ответить на данный вопрос, вам было дано задание систематизировать и расширить основные знания по разделу «Тригонометрия», рассмотреть и ответить на следующие проблемные вопросы учебной темы:
-Как тригонометрия помогает решать алгебраические задачи?
— Как тригонометрия помогает решать геометрические задачи?
— Как тригонометрия помогает решать физические задачи?
При подготовке необходимо было рассмотреть следующие учебные вопросы:
-Как возникла геометрия?
-Какие реальные явления она описывает?
-Как применяется в физике?
-Какие методы решения тригонометрических уравнений бывают?
-Как тригонометрия помогает решить неравенства?
— Как тригонометрия помогает решить геометрические задачи?
-Зачем нужно знать тригонометрию?
Оценивать ваши работы предстоит нашему компетентному, объективному, добродушному совету, в который входят учителя математики, а также и вам самим. Каждый член совета выставляет оценку в свой оценочный лист, при этом учитывается:
-актуальность темы
-значимость разработки
-объем и полнота разработки
-уровень творчества
-аргументированность предлагаемых решений
-качество доклада
-объем и глубина знаний по теме
-ответы на вопросы.
Выступающему могут быть заданы вопросы и членами совета, и вами. Затем подводится итог, который складывается из суммы оценок.
— Настало время продемонстрировать то, что у вас получилось. Желаю вам успехов!
2. Основная часть урока. Защита проектных работ. Презентация.
Проект, который мы представляем — наш первый шаг в подготовке к ЕГЭ.
Автор у проекта один – наш 10 класс.
Мы ответим на следующие вопросы:
-из каких компонентов складывается готовность к ЕГЭ?
-готовы ли мы к ЕГЭ?
-каков уровень готовности к ЕГЭ выпускников нашей школы в марте 2016года?
-изменится ли уровень готовности к декабрю 2016 года и повлияет ли на него выполнение проектных работ через составление и решение авторских ученических тестов по математике?
Поэтому главная цель проекта: саморазвитие всех участников проекта в процессе подготовки к ЕГЭ.
Мы предполагаем, что эта работа будет нам полезна, потому что поможет почувствовать структуру и сложность заданий каждой части ЕГЭ. Выполнение своих авторских задач и задач, составленных одноклассниками, станет для нас дополнительным тренингом и научит не бояться этой формы проверки наших знаний и умений.
Проект №1. «Преобразование тригонометрических выражений»
-Каковы основные формулы тригонометрии?
-Я предлагаю оценить результаты проекта по предложенным критериям.
Проект 2. «Простейшие тригонометрические уравнения»
-Какие из способов решения тригонометрических уравнений из рассмотренных оказались наиболее трудными?
-Я предлагаю оценить результаты проекта по предложенным критериям.
Проект 3. «Решение тригонометрических уравнений»
Проект 4. «Методы решения тригонометрических уравнений. Способы нахождения корней тригонометрических уравнений»
Проект 5. «Тригонометрические неравенства»
Проект 6. «Тригонометрия в физике»
Проект 7. «Тригонометрия в геометрии»
Проект 8. «Тригонометрия вокруг нас»
-Зачем нужно знать тригонометрию?
Участники выходят и представляют свой проект, после чего им могут быть заданы вопросы. Совет учителей оценивает работу.
3. Мастер – класс по теме: « Решение уравнений типа № 13 по материалам школьного сайта»
4. Задание на дом.
-Я предлагаю изучить способы решения остальных уравнений, после чего выполнить задания для самостоятельной работы.
5.Подведение итогов.
— Я думаю, что у вас сложилось более полное представление о заданиях тригонометрического содержания, которые предлагаются в ЕГЭ. И у меня появилась уверенность, что с решениями большинство из вас справится.
—Что нового узнали на уроке?
В процессе выполнения проекта мы узнали, что тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела, позволяют измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. А также узнали применение тригонометрии в таких областях, как техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография, конструирование и моделирование.
—Испытывали ли вы затруднения при выполнении проектной работы?
-Чему научились в процессе выполнения проектной работы?
В процессе реализации проекта мы приобрели следующие конкретные умения:
-
свободно ориентироваться в многообразных тригонометрических формулах;
-
решать геометрические задачи с помощью тригонометрии;
-
применять полученные знания на практике;
-
выдвигать гипотезы;
-
быстро и точно подбирать необходимые для работы ресурсы, вести поиск в Интернете;
-
работать в различных поисковых системах;
-
точно формулировать вопрос;
-
представлять результаты исследований в виде презентаций, публикаций и рефератов;
-
интерпретировать результаты исследования;
-
делать выводы;
-
обсуждать результаты исследования, участвовать в дискуссии.
Главная цель, которую мы определили, начиная работу над проектом, — саморазвитие в процессе подготовки к ЕГЭ считаю достигнутой. Мне кажется, нам удалось продвинуться в решении задач проекта. Мы теперь имеем представление о том, что подготовка к ЕГЭ – это не только изучение предмета. Умение решать складывается не только из выполнения действий по образцу, но и предполагает, что ты свободно ориентируешься в материале предмета. Мы знаем, несмотря на все трудности, успех на ЕГЭ возможен! Поэтому, подводя итог, я хочу сказать об огромной пользе проекта для меня и для большинства участников.
ЕГЭ на «5!» — это уже выполняемая программа, поэтому надо взять планку повыше и стремится к тому, чтобы сдать ЕГЭ на 100!
6. Рефлексивно – оценочная часть урока.
1) Совет учителей объявляет окончательные результаты.
2) Выбери портрет: «Мои эмоции».
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Тригонометрия в заданиях ЕГЭ
Содержание
-
1.
Презентация Тригонометрия в заданиях ЕГЭ -
2.
Тригонометрия в заданиях ЕГЭ РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ -
3.
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ЗАДАНИЕ В7 -
4.
Решим уравнение и в ответе напишем наибольший отрицательный корень: -
5.
Уравнение мы решили, но в ответ надо -
6.
Наибольший отрицательный корень: -1,5. -
7.
Решим уравнение и в ответе напишем наибольший -
8.
Слайд 8 -
9.
Наибольший отрицательный корень: -0,25 -
10.
Решим уравнение и найдем наименьший положительный корень: -
11.
Наименьший положительный корень: х=6. -
12.
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ ЗАДАНИЕ В11 -
13.
Найдите значение выражения -
14.
Найдите -
15.
ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ В ФИЗИКЕ ЗАДАНИЕ В12 -
16.
ЗадачаГруз массой 0,08 кг колеблется на пружине со -
17.
Слайд 17 -
18.
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ ЗАДАНИЕ В15 -
19.
Пример 1.Найдите точку минимума функции -
20.
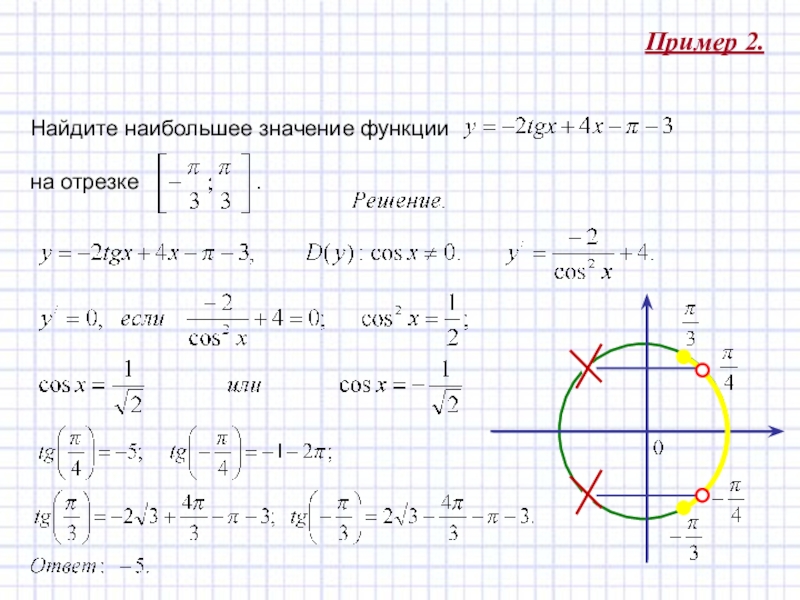
Пример 2.Найдите наибольшее значение функции на отрезке
Тригонометрия в заданиях ЕГЭ РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ЗАДАНИЕ В7 ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ ЗАДАНИЕ В11 ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ В ФИЗИКЕ ЗАДАНИЕ В12 ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
Слайд 1Андреева Зинаида Маркеловна,
учитель математики,
МАОУ СОШ № 41 с. Аксаково
МР Белебеевский район РБ
2017г.
Тригонометрия
в заданиях
ЕГЭ

Слайд 2Тригонометрия в заданиях ЕГЭ
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
ЗАДАНИЕ В7
ПРЕОБРАЗОВАНИЕ
ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
ЗАДАНИЕ В11
ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ В ФИЗИКЕ
ЗАДАНИЕ В12
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
ЗАДАНИЕ В15
Содержание

Слайд 3РЕШЕНИЕ
ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
ЗАДАНИЕ В7

Слайд 4Решим уравнение
и в ответе напишем наибольший отрицательный корень:

Слайд 5Уравнение мы решили, но в ответ надо записать наибольший отрицательный корень.
Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:

Слайд 6Наибольший отрицательный корень: -1,5.

Слайд 7Решим уравнение
и в ответе напишем наибольший отрицательный корень:
Уравнение мы
решили, но в ответ надо записать наибольший отрицательный корень.
Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:
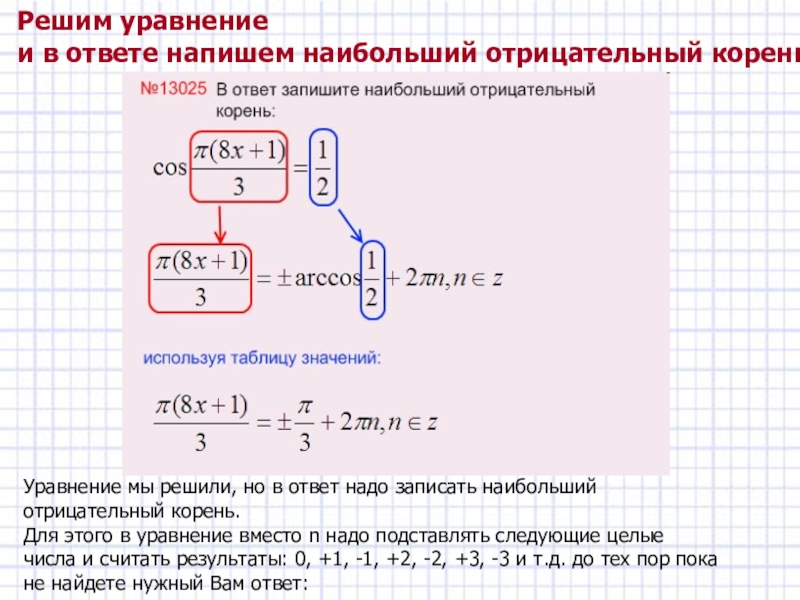
Слайд 9Наибольший отрицательный корень: -0,25

Слайд 10Решим уравнение
и найдем наименьший положительный корень:
Уравнение мы решили, но
в ответ надо записать наибольший отрицательный корень.
Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:

Слайд 11Наименьший положительный корень: х=6.

Слайд 12
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
ЗАДАНИЕ В11

Слайд 15
ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
В ФИЗИКЕ
ЗАДАНИЕ В12

Слайд 16Задача
Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по закону
, где t — время в секундах. Кинетическая энергия
груза, измеряемая в джоулях, вычисляется по формуле ,
где m — масса груза (в кг), v — скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая
энергия груза будет не менее Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Слайд 18
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
ЗАДАНИЕ В15

Слайд 19Пример 1.
Найдите точку минимума функции
,
принадлежащую промежутку .
у’
у
0,5
0
—
+

Слайд 20Пример 2.
Найдите наибольшее значение функции
на отрезке
Сложная тригонометрия в кимах ЕГЭ
1. Решение простейших тригонометрических уравнений
2. Решение тригонометрических уравнений разложением на множители
3. Решение тригонометрических уравнений с помощью замены неизвестного
4. Решение тригонометрических уравнений сводящихся к квадратным уравнениям
5. Решение тригонометрических уравнений преобразованием суммы тригонометрических функций в произведение
6. Решение тригонометрических уравнений преобразованием произведения тригонометрических функций в сумму
7. Решение тригонометрических уравнений с применением формул понижения степени
8. Решение тригонометрических уравнений как однородное
9. Решение тригонометрических уравнений с помощью введения вспомогательного аргумента
10. Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки
11. Решение тригонометрических уравнений содержащих тригонометрические функции под знаком радикала.
Исследовательская работа по теме «Тригонометрические уравнения. Способы выбора корней»
Школьный курс алгебры и начала анализа 10 — 11 классы . Исследовательская работа по теме «Тригонометрические уравнения. Способы выбора корней», выполненная ученицей 11 класса Толстых Владиславой под руководством учителя математики Исаковой Т.И. Работа может использована при подготовке к ЕГЭ
Скачать:
| Вложение | Размер |
|---|---|
| trigonometricheskie_uravneniya_sposoby_otbora_korney_22.03.17.doc | 630 КБ |
| trigonometricheskie_uravneniya_sposoby_otbora_korney.ppt | 799 КБ |
Предварительный просмотр:
Региональная научно-практическая конференция
для молодежи и школьников «Шаг в будущее, Сибирь!»
Способы выбора корней
Толстых Владислава, ученица 11класса
Муниципальное казённое обще – образовательное учреждение Средне –Муйская средняя общеобразовательная школа Усть — Удинского района Иркутской области
Исакова Тамара Ивановна, учитель математики, высшей квалификационной категории. МКОУ Средне – Муйская СОШ Усть Удинского района Иркутской области
с. Средняя Муя, 2017год
Из истории происхождения
Типы тригонометрических уравнений
Способы отбора корней в тригонометрических уравнениях
Практические применения тригонометрии
Актуальность темы: Почему я выбрала тему «Тригонометрические уравнения»?
- тригонометрические уравнения и неравенства встречаются в курсе алгебры и начала анализа, в разделе ЕГЭ по математике
- тригонометрия встречается в таких науках, как физика, биологии
- не последнюю роль играют и в медицине, и, что самое интересное, без них не обошлось даже в музыке и архитектуре.
Почему я выбрала тему «Тригонометрические уравнения»?
Тригонометрические уравнения – это одна из сложнейших тем математики, которая выходит на Единый Государственный Экзамен. Очень многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и выбирать корни, принадлежащие отрезку. Немаловажно знать, тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Следует отметить применение тригонометрии в следующих областях: техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ), компьютерная томография, фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография, геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Каждого изучающего математику, интересует как и где применяются полученные знания. Ответ на этот вопрос и дает данная работа.
- узнать как можно больше применений науки тригонометрия в повседневной практике
- изучить способы решения тригонометрических уравнений и способы выбора корней, принадлежащих промежутку
- расширить знания о применении тригонометрических уравнений в разных сферах жизни человека
- познакомиться с историей возникновения тригонометрических уравнений
- научиться решать тригонометрические уравнения
- уметь выбирать корни уравнения, принадлежащие промежутку
- сделать подборку задач из ЕГЭ
- поработать в Microsoft Word, Microsoft PowerPoint
- получить опыт публичного выступления
- ресурсы Интернет – сайтов, содержащих тригонометрические уравнения
- изучила материал энциклопедий и справочников
- просмотрела и выбрала задания из Демо — вариантов ЕГЭ разных лет по математике
- изучила способы решения тригонометрических уравнений и выбор корней уравнения принадлежащих отрезку
Методы и приемы :
- поиск информации в источниках, справочниках
- работа с ресурсами Internet
- обработка и анализ информации
- умение работать в Microsoft PowerPoint и Microsoft Word
Гипотеза : Существует две гипотезы:
- человек не сможет обойтись в жизни без тригонометрических уравнений
- тригонометрические уравнения не нужны человеку в жизни.
- я считаю, что в XXI веке все научные работы требующие исследования базируются на тригонометрических функциях, уравнениях. По этому знания о тригонометрических уравнениях нужны каждому. Решение тригонометрических уравнений встречается в ЕГЭ по математике
Выводы : Выполняя исследовательскую работу
- не только рассмотрела все способы выбора корней тригонометрического уравнения принадлежащего отрезку, но и ликвидировала свои проблемы по данной теме. Для меня это очень важно при сдаче ЕГЭ по математике
- выяснила какое значение имеют тригонометрические уравнения в жизни человека и как они работают в стране
- доказала, что в современном мире прожить без знаний тригонометрический уравнений невозможно. Чтобы быть хорошим специалистом, уметь разбираться в большом потоке информации, необходимо знать тригонометрические уравнения.
- изучение столь важной и интересной темы дает положительную мотивацию для самообразования.
1. Из истории происхождения
Слово тригонометрия составилось из двух греческих слов: τρίγονον (тригонон-треугольник) и и μετρειν (метрейн — измерять ) в буквальном переводе означает измерение треугольников .
Именно эта задача- измерение треугольников или, как принято теперь говорить, решение треугольников, т.е. определение всех сторон и углов треугольника по трем его известным элементам (стороне и двум углам, двум сторонам и углу или трем сторонам)- с древнейших времен составляла основу практических приложений тригонометрии.
Как и всякая другая наука, тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач. Первые этапы развития тригонометрии тесно связаны с развитием астрономии. Большое влияние на развитие астрономии и тесно связанной с ней тригонометрии оказали потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил. Значительную роль в развитии тригонометрии сыграла потребность в составлении географических карт и тесно связанная с этим необходимость правильного определения больших расстояний на земной поверхности.
Основополагающее значение для развития тригонометрии в эпоху ее зарождения имели работы древнегреческого астронома Гиппарха (середина II века до н.э.). Тригонометрия как наука, в современном смысле этого слова не было не только у Гиппарха, но и у других ученых древности, так как они еще не имели понятия о функциях углов и даже не ставили в общем виде вопроса о зависимости между углами и сторонами треугольника. Но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. При этом основным средством получения нужных результатов было умение вычислять длины круговых хорд на основании известных соотношений между сторонами правильных трех-, четырех-, пяти- и десятиугольника и радиусом описанного круга.
Гиппарх составил первые таблицы хорд, т.е. таблицы, выражающие длину хорды для различных центральных углов в круге постоянного радиуса. Это были, по существу, таблицы двойных синусов половины центрального угла. Впрочем, оригинальные таблицы Гиппарха (как и почти все им написанное) до нас не дошли, и мы можем составить себе о них представление главным образом по сочинению «Великое построение» или ( в арабском переводе) « Альмагест» знаменитого астронома Клавдия Птолемея , жившего в середине II века н.э.
Птолемей делил окружность на 360 градусов, а диаметр- на 120 частей. Он считал радиус равным 60 частям(60 ′′ ). Каждую из частей он делил на 60 ′ , каждую минуту на 60 ′′ , секунду на 60 терций (60 ′′′ ) и т.д., применяя указанное деление, Птолемей выражал сторону правильного вписанного шестиугольника или хорду, стягивающую дугу в 60 ° в виде 60 частей радиуса (60 ч ), а сторону вписанного квадрата или хорду в 90 ° приравнивал числу 84 ч 51 ′ 10 ″ .Хорду в 120 ° — сторону вписанного равностороннего треугольника- он выражал числом 103 ч 55 ′ 23 ″ и т.д. Для прямоугольного треугольника с гипотенузой, равной диаметру круга, он записывал на основании теоремы Пифагора: (хорда α ) 2 +(хорда | 180- α| ) 2 =(диаметру) 2 , что соответствует современной формуле sin 2 α +cos 2 α =1.
«Альмагест» содержит таблицу хорд через полградуса от 0 ° до 180 ° , которая с нашей современной точки зрения представляет таблицу синусов для углов от 0 ° до 90 ° через каждые четверть градуса.
В основе всех тригонометрических вычислений у греков лежала известная еще Гиппарху теорема Птолемея: «прямоугольник, построенный на диагоналях вписанного в круг четырехугольника, равен сумме прямоугольников, построенных на противолежащих сторонах» (произведение диагоналей равно сумме произведений противоположных сторон). Пользуясь этой теоремой, греки умели (с помощью теоремы Пифагора) по хордам двух углов вычислить хорду суммы (или хорду разности) этих углов или хорду половины данного угла, т.е. умели получать результаты, которые мы получаем теперь по формулам синуса суммы (или разности) двух углов или половины угла.
Новые шаги в развитии тригонометрии связаны с развитием математической культуры народов Индии, Средней Азии и Европы (V-XII) .
Важный шаг вперед в период с V по XII век был сделан индусами, которые в отличие от греков стали рассматривать и употреблять в вычислениях уже не целую хорду ММ ′ ( см. чертеж) соответствующего центрального угла, а только ее половину МР, т. е. то, что мы теперь называем линией синуса α — половины центрального угла.
Наряду с синусом индусы ввели в тригонометрию косинус, точнее говоря, стали употреблять в своих вычислениях линию косинуса. (термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в.из так называемого « синуса дополнения», т.е. синуса угла, дополняющего данный угол до 90 ° . «Синус дополнения» или ( по латыни) sinus complementi стали сокращенно записывать как sinus co или co-sinus).
Им были известны также соотношения cos α =sin(90 ° — α ) и sin 2 α +cos 2 α =r 2 , а также формулы для синуса суммы и разности двух углов.
Следующий этап в развитии тригонометрии связан со странами
Средней Азии, Ближнего Востока, Закавказья(VII-XV в.)
Развиваясь в тесной связи с астрономией и географией,- среднеазиатская математика имела ярко выраженный «вычислительный характер» и была направлена на разрешение прикладных задач измерительной геометрии и тригонометрии, причем тригонометрия сформировалась в особую математическую дисциплину в значительной мере именно в трудах среднеазиатских ученых. Из числа сделанных ими важнейших успехов следует в первую очередь отметить введение всех шести тригонометрических линий: синуса, косинуса, тангенса, котангенса, секанса и косеканса, из которых лишь первые две были известны грекам и индусам.
Решая задачу об определении высоты Солнца S по тени b вертикально стоящего шеста a (см чертеж), сирийский астроном ал-Баттани (Хв.)пришел к выводу, что острый угол ϕ в прямоугольном треугольнике определяется отношением одного катета к другому, и вычислил небольшую таблицу котангенсов через 1 ° . Точнее говоря, он вычислил длину тени b=a ⋅ =a ⋅ ctg ϕ шеста определенной длины (а=12) для ϕ =1 ° ,2 ° ,3 ° ……
Абу-ль-Вафа из Хоросана, живший в Х веке (940-998), составил аналогичную «таблицу тангенсов», т.е. вычислил длину тени b=a ⋅ =a ⋅ tg ϕ , отбрасываемой горизонтальным шестом определенной длины ( а=60) на вертикальную стену (см. чертеж).
Следует отметить, что сами термины «тангенс» (в буквальном переводе- «касающийся») и «котангенс» произошли из латинского языка и появились в Европе значительно позднее (XVI-XVIIвв.). Среднеазиатские же ученые называли соответствующие линии «тенями»: котангенс- «первой тенью», тангенс- «второй тенью».
Абу-ль-Вафа дал совершенно точное геометрическое определение линии тангенса в тригонометрическом круге и присоединил к линиям тангенса и котангенса линии секанса и косеканса. Он же выразил (словесно) алгебраические зависимости между всеми тригонометрическими функциями и, в частности, для случая, когда радиус круга равен единице. Этот чрезвычайно важный случай был рассмотрен европейскими учеными на 300 лет позднее. Наконец, Абу-ль-Вафа составил таблицу синусов через каждые 10 ′ .
В трудах среднеазиатских ученых тригонометрия превратилась из науки, обслуживающей астрономию, в особую математическую дисциплину, представляющую самостоятельный интерес.
Тригонометрия отделяется от астрономии и становится самостоятельной наукой. Это отделение обычно связывают с именем азербайджанского математика Насирэддина Туси (1201-1274).
Впервые в европейской науке стройное изложение тригонометрии дано в книге «О треугольниках разных родов», написанной Иоганном Мюллером , более известным в математике под именем Региомонтана(1436-1476). Он обобщает в ней методы решения прямоугольных треугольников и дает таблицы синусов с точностью до 0,0000001. При этом замечательно то, что он полагал радиус круга равным 10 000 000 или 10 000, т.е. выразил значения тригонометрических функций в десятичных дробях, перейдя фактически от шестидесятиричной системы счисления к десятичной.
Английский ученый XIV века Брадвардин (1290-1349) первый в Европе ввел в тригонометрические вычисления котангенс под названием «прямой тени» и тангенс под названием «обратной тени».
На пороге XVIIв. В развитии тригонометрии намечается новое направление- аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, вычисление элементов геометрических фигур и учение о тригонометрических функциях строилось на геометрической основе, то в XVII-XIX вв. тригонометрия постепенно становится одной из глав математического анализа. О свойствах периодичности тригонометрических функций знал еще Виет , первые математические исследования которого относились к тригонометрии.
Швейцарский математик Иоганн Бернулли (1642-1727) уже применял символы тригонометрических функций.
В первой половине XIXв. французский ученый Ж.Фурье доказал, что всякое периодическое движение может быть представлено в виде суммы простых гармонических колебаний.
Огромное значение в истории тригонометрии имело творчество знаменитого петербургского академика Леонарда Эйлера (1707-1783), он придал всей тригонометрии современный вид.
В своем труде «Введение в анализ» (1748 г.) Эйлер разработал тригонометрию как науку о тригонометрических функциях, дал ей аналитическое изложение, выведя всю совокупность тригонометрических формул из немногих основных формул.
Эйлеру принадлежит окончательное решение вопроса о знаках тригонометрических функций во всех четвертях круга, вывод формул приведения для общих случаев.
Введя в математику новые функции- тригонометрические, стало целесообразным поставить вопрос о разложении этих функций в бесконечный ряд. Оказывается, такие разложения возможны:
Эти ряды позволяют значительно облегчить составление таблиц тригонометрических величин и для нахождения их с любой степени точности.
Аналитическое построение теории тригонометрических функций, начатое Эйлером, было завершено в работах Н.И.Лобачевского, Гаусса, Коши, Фурье и других.
«Геометрические рассмотрения,- пишет Лобачевский,- необходимы до тех пор в начале тригонометрии, покуда они не послужат к открытию отличительного свойства тригонометрических функций…Отсюда делается тригонометрия совершенно независимой от геометрии и имеет все достоинства анализа».
В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть-учение о тригонометрических функциях -является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть- решение треугольников -рассматривается как глава геометрии.
II. Типы тригонометрических уравнений:
К определению тригонометрического уравнения различные авторы учебных пособий подходят по-разному. Мы назовем тригонометрическим уравнениям равенство тригонометрических выражений, содержащих неизвестное (переменную) только под знаком тригонометрических функций. Уравнения cos 3x=sin; tg(π/2 – 11x) – tg ((3/2)π-5x) = 0; sin 3x+sin 5x = sin 4x и т.д. суть тригонометрические уравнения. Уравнения sin x=(1/2)x; cos 2x = — (1/2)x + (1/3); tg x = x и т.д. не являются тригонометрическими, они относятся к типу трансцендентных уравнений и, как правило, решаются приближенно или графически. Может случиться так, что не является тригонометрическим согласно определению, однако оно может быть сведено к тригонометрическому. Например, 2(x-6) cos 2x=x-6. Мы видим, что x-6 не содержится под знаком тригонометрических функций, однако оно решается аналогически: (x-6) × (2 cos 2x -1)=0, откуда x=6 или cos 2x = (1/2), x=±(π/6)+nπ, nϵZ. Решить тригонометрическое уравнение – значит найти все его корни – все значения неизвестного, удовлетворяющие уравнению. При решении тригонометрических уравнений мы будем пользоваться известными тригонометрическими формулами. Простейшими тригонометрическими уравнениями являются: sin x=′a и cos x=a, где ׀а׀≤1, tg x=a и ctg x=a, где aϵR. Для решения различных видов тригонометрических уравнений необходимо уметь решать простейшие тригонометрические уравнения. Перейдем к рассмотрению решения тригонометрических уравнений различных видов.
1 тип — простейшие тригонометрические уравнения:
а) уравнения вида sin x=a
Уравнение вида sin x=a может иметь решении только при ׀а׀≤1. Известно, что решение этого уравнения находят по обобщенной формуле: x=(-1) n arcsin a+ nπ(1), где nϵZ и (-π/2)≤ arcsin a≤( π/2).
Решение. (2/3)x=(-1) n arcsin(1/2)+nπ, (2/3)x=(-1) n ( π/6) +nπ, x=(-1) n (π/4) +(3/2)nπ, nϵZ.
Ответ: x=(-1) n (π/4) +(3/2)nπ, nϵZ.
Решение. (3π/√x)= (-1) n+1 arcsin (√3/2) +nπ, (3π/√x)= (-1) n+1 (π/3) +nπ, (3/√x)= (-1) n+1 (1/3)+π, √x=(3/(-1) n+1 (1/3)+π) или √x=(9/3n+(-1) n+1 ), x=(81/((-1) n+1 (1/3)+π) 2 ), nϵN. Ответ: x=(81/((-1) n+1 (1/3)+π) 2 ), nϵN.
б) Уравнение вида cos x=a
Уравнение вида cos x=a может иметь решении только при ׀а׀≤1. Известно, что решение этого уравнения находят по обобщенной формуле: x= ±arccos a+ 2nπ, где nϵZ и 0≤ arccos a≤ π
Полезно знать, что arccos (-a) = π- arccos a.
Решение. (5/6)x= ±arccos(√3/2)+ 2nπ, (5/6)x=±( π/6) +2nπ, x=±( π/5) +(12/5)nπ, nϵZ.
Ответ: x=±(π/5) +(12/5)nπ, nϵZ.
Решение. cos(3x-2)=(√2/2), 3x-2 = = ±arccos(√2/2)+ 2nπ, 3x-2=±( π/4) +2nπ, x=(2/3)±(π/5)+ (2/3)nπ, nϵZ. Ответ: x=(2/3)±(π/5)+ (2/3)nπ, nϵZ.
в) Уравнение вида tg x=a, aϵR
Известно, что решение данного уравнения находят по обобщенной формуле: x=arctg a+ nπ, где nϵZ. Полезно помнить, что arctg (-a)= — arctg a.
Решение. 2x=arctg √3+nπ, 2x=( π/3)+ nπ, 2x=(3n+1)( π/3),x=(3n+1)( π/6), nϵZ.
Ответ: x=(3n+1)( π/6), nϵZ.
Решение. (2/3x)= arctg(-1)+ nπ, (2/3x)= -arctg1+ nπ, (2/3x)= (-π/4)+ nπ, (2/3x)= (-π/4)+ nπ, (2/3x)= (4π—1)(π/4), (1/x)= (4π—1)(3π/8), x=(8/(4π—1)3π), nϵZ.
Ответ: x=(8/(4π—1)3π), nϵZ.
г) уравнение вида ctg x=a, aϵ R
Известно, что решение данного уравнения находят по обобщенной формуле: x=arcctg a+ nπ,(5), где nϵZ и 0
При решении простейших уравнений можно использовать тригонометрический круг. Я считаю, что данный способ более рациональный, чем решение тригонометрических уравнений с помощью формулы.
2 тип-уравнения, сводимые к алгебраическим
Это уравнения, сводимые к одной и той же функции относительно одного и того же неизвестного выражения, выходящего только под знак функции.
Тригонометрические уравнение a sin 2 x+ b sin x+c=0, a cos 3 x+ b cos x+c=0; a tg 4 3x+ b tg 2 3x+c=0, a ctg 2 2x+ b ctg 2x+c=0 уже сведены к алгебраическим. Действительно, положив в них соответственно sin x=y, cos x=z, tg 3x=t, ctg 2x= u, получим алгебраические уравнения: ay 2 + by+c=0, az 2 + bz+c=0, at 4 + bt 2 +c=0; au 2 + bu+c=0. Решив каждое из них, найдем sin x, cos x, tg 3x, ctg 2x.
Уравнения a sin 2 x+ b cos x+c=0, a cos 2 x+ b sin x+c=0, a tg x+ b ctg x =0 не являются по виду алгебраическими, но их можно свести к алгебраическим: a cos 2 x- b cos x-(a+c)=0, a sin 2 x- b sin x-(a+c)=0 и a tg x +(b/tg x)=0.
При решении уравнений сводимых к алгебраическим необходимо знать формулы:
1) sin x+cos x=1; 2)tg a =(sin a/cos a); 3) ctg a=( cos a/ sin a); 4) ctg a=(1/tg a)
5)1+tg 2 a=(1/cos 2 a); 6)1+ctg 2 a=(1/sin 2 a); 7) 1+cos 2a=2cos 2 a; 
9)tg2a=(2 tga/1-tg 2 a); 10) sin2a=(2 tga/1+tg 2 a); 11)cos 2a=(1-tg 2 a/1+tg 2 a);
12)sin2a=2sin a cos a; 13) cos2a= cos 2 a-sin 2 a, или cos2a= 2cos 2 a-1, или cos2a= 1-2sin 2 a;
14) Формулы приведения;
- Ведём замену а.
- Находим корни квадратного уравнения.
- Возвращаемся к замене и решаем простейшее тригонометрическое уравнение.
- Записываем ответ.
Пример1: Решить уравнение2 sin 2 x + sin x – 1 = 0;
2 sin 2 x + sin x – 1 = 0;
sin x = а, ׀ а ׀ ≤ 1;
D = 9; а 1 = — 1; а 2 = 1 / 2 ;
sin x = -1; sin x = 1 / 2 ;
х 1 = — п / 2 + 2пn, n € N. x 2 = (- 1) k п / 6 + пk, k€ N.
Ответ: — п / 2 + 2пn; (- 1) k п / 6 + пk, n, k € N.
Приме 2: Решить уравнение
3 тип-однородные уравнения
Уравнения a sin x+ b cos x=0; a sin 2 x+b sin x cos x+c cos 2 x=0; a sin 3 x+b sin 2 x cos x+ c sin x cos 2 x+ d cos 3 x=0 и т.д. называют однородными относительно sin x и cos x. Сумма показателей степеней при sin x и cos x у всех членов такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Рассмотренные уравнения имеют соответственно первую, вторую и третью степень. Делением на cos k x, где k-степень однородного уравнения, уравнение приводится к алгебраическому относительно функции tg x.
Рассмотрим уравнение a sin 2 x+b sin x cos x+c cos 2 x=0(1). Разделим уравнение(1) на cos 2 x, получим: a tg 2 x+ b tg x+c=0(2).При a≠0 (1) и (2) равносильны, так как cos x≠0. Если же cos x=0, то из уравнения(1) видно, что и sin x =0, что невозможно, так как теряет смысл тождество .
При решении однородных уравнений применяем схему:
- Разделим обе части уравнения на cos 2 x ≠ 0.
- Ведём замену а.
- Находим корни квадратного уравнения.
- Возвращаемся к замене и решаем простейшее тригонометрическое уравнение.
- Записываем ответ.
Пример1. Решить уравнение: 3 sin2 x + sin x • cos x = 2 cos2 x;
3 sin 2 x + sin x · cos x = 2 cos 2 x;
3 tq 2 x + tq x = 2; х ≠ п / 2 + пn, n € N.
D = 25; а 1 = — 1; а 2 = 2 / 3 ;
tq x = — 1; tq x = 2 / 3 ;
х 1 = — п / 4 + пn, n € N. x 2 = arctq 2 / 3 + пn, n € N.
Ответ: — п / 4 + пn, arctq 2 / 3 + пn, n € N.
Пример 2. 5 sin x — 2 cos x = 0
Поделим обе части уравнения cos x (или на sin x). Предварительно докажем,
что cos x 0 (или sin x 0). (Пусть cos x = 0, тогда 5 sin x — 2 • 0 = 0, т.е. sin x = 0; но этого не может быть, так как sin 2 x + cos 2 x = 1).
Значит, можно делить на cos x:
5 sin x /cos x — 2 cos x / cos x = 0 / cos x. Получим уравнение
x = arctg 2/5 + n, n = Z.
Ответ: x = arctg 2/5 + n, n = Z.
Аналогично решаются однородные уравнения вида a sin 2 x + b sin x cos x + c cos 2 x = 0, их решение начинается с того, что обе части уравнения делятся на cos 2 x (или на sin 2 x).
Пример 3. 12 sin 2 x + 3 sin 2x — 2 cos 2 x = 2.
Данное уравнение не является однородным, но его можно преобразовать в однородное, заменив 3 sin 2x на 6 sin x cos x и число 2 на 2sin 2 x + 2cos 2 x.
Приведя подобные члены, получим уравнение
10sin 2 x + 6sin x cos x — 4 cos 2 x = 0.
(Пусть cos x = 0, тогда 10sin 2 x = 0, чего не может быть, т.к. sin 2 x + cos 2 x = 1, значит, cos x 0).
Разделим обе части уравнения на cos 2 x.
10 tg 2 x +6 tg x — 4 = 0,
tg x = -1 или tg x = 2/5,
x = — /4 + n, n = Z, x = arctg 2/5 + k, k = Z.
Ответ: x 1 = — /4 + n, n = Z, x 2 = arctg 2/5 + k, k = Z.
4 тип- уравнения, решаемые разложением на множители:
При решении уравнений методом разложения нужно пользоваться всеми известными способами разложения на множители алгебраических выражений. Это вынесение за скобки общего множителя, группировка, применение формул сокращенного умножения и деления и искусственные приемы. Необходимо так же знать формулы: 1) sin x+cos x=1; 2)tg a =(sin a/cos a); 3) ctg a=( cos a/ sin a); 4) ctg a=(1/tg a)
5)1+tg 2 a=(1/cos 2 a); 6)1+ctg 2 a=(1/sin 2 a); 7) 1+cos 2a=2cos 2 a; 
9)tg2a=(2 tga/1-tg 2 a); 10) sin2a=(2 tga/1+tg 2 a); 11)cos 2a=(1-tg 2 a/1+tg 2 a);
12)sin2a=2sin a cos a; 13) cos2a= cos 2 a-sin 2 a, или cos2a= 2cos 2 a-1, или cos2a= 1-2sin 2 a;
14)tg(a±b) = (tg a±tg b)/(1±tg a tg b); 15)sin 3a=3sin a – 4sin 3 a; 16)cos 3 a = 4 cos 3 a – 3 cos a;
Пример2. 2 sin 3 x — cos 2x — sin x = 0
Сгруппируем первый член с третьим, а cos 2x = cos 2 x — sin 2 x.
(2sin 3 x — sin x) – (cos 2 x — sin x) = 0,
Вынесем из выражения, стоящего в первой скобке sin x, а cos 2 x = 1 — sin x.
sin x (2sin 2 x – 1) – (1 — 2 sin 2 x) = 0,
sin x (2sin 2 x – 1) + (2 sin 2 x — 1) = 0,
(2 sin 2 x — 1) • ( sin x + 1) = 0.
2 sin 2 x – 1 = 0
Ответ: x 1 = ± /4 + n, n = Z, x 2 = — /2 +2 k, k = Z.
5 тип-уравнения, решаемые с помощью условия равенства одноименных тригонометрических функций
Многие тригонометрические уравнения могут быть приведены к равенству одноименных тригонометрических функций. Такие уравнения решаются на основании условий равенства одноименных тригонометрических функций, т.е. тех условий, которым должны удовлетворять два угла: a и b, если a) sin a =sin b, б) cos a= cos b, в) tg a = tg b.
Теорема I. Для того чтобы синусы двух углов были равны, необходимо и достаточно выполнения одного из следующих условий: разность этих углов должна равняться π, умноженному на четное число, или сумма этих углов должна равняться π, умноженная на нечетное число,
Теорема II . Для того чтобы косинусы двух углов были равны, необходимо и достаточно выполнения одного из следующих условий: разность(сумма) этих углов должна равняться произведению π на четное число.
Теорема II . Для того чтобы тангенсы двух углов были равны, необходимо и достаточно выполнения одного из следующих условий: тангенс каждого из данных углов существует и разность этих углов равна числу π, умноженному на целое число.
6 тип- уравнения, решаемые с помощью формул сложения тригонометрических функций:
Для решения данного типа применяются формулы преобразования суммы тригонометрических функций в произведение:
Sin a + sin b= 2 sin((a+b)/2) cos((a-b)/2);
Sin a — sin b= 2 sin((a-b)/2) cos((a+b)/2);
cos a + cos b= 2 cos ((a+b)/2) cos((a-b)/2);
cos a — cos b= 2 sin ((a+b)/2) sin ((b-a)/2) при b>a;
cos a — cos b= 2 sin ((a+b)/2) sin ((a-b)/2) при b
tg a ± tg b = (sin(a+b)/ cos a cos b);
ctg a + ctg b = (sin(a+b)/ sin a sin b);
ctg a — ctg b = (sin(b-a)/ sin a sin b);
В некоторых примерах прийдется применять формулы:
sin (a±b)= sin a cos b± cos a sin b;
cos (a±b)= cos a cos b± sin a sin b;
7 тип- уравнения, решаемые с помощью формул сложения углов и разложения произведения тригонометрических функций в сумму
Формулы сложения углов и разложения произведения тригонометрических функций в сумму:
sin (a±b)= sin a cos b± cos a sin b;
cos (a±b)= cos a cos b± sin a sin b;
tg(a±b) = (tg a±tg b)/(1±tg a tg b);
sin a cos b=(1/2)(sin(a+b)+ sin(a-b));
cos a cos b=(1/2)( cos (a+b)+ cos (a-b));
sin a sin b=(1/2)( cos (a-b)- cos (a+b));
8 тип-уравнения, решаемые с помощью формул понижения степени
Формулы понижения степени:
Sin 2 t=((1- cos 2t)/2)
Cos 2 t=((1+cos 2t)/2)
9 тип- уравнения вида a sin x+b cos x= c
В уравнении a sin x+b cos x= c a, b и c- любые действительные числа. Если а=b=0, а с≠0, то уравнение теряет слысл; если же а=b=с=0, то x- любое действительное число, т.е. уравнение обращается в тождество. Например, √3 sin x + cos x=1. Разделив обе части уравнения на 2, получим (√3/2) sin x + (1/2)cos x=(1/2), т.е. sin(x+(π/6))=1/2 или cos(x-(π/6))= 1/2. Уравнение sin x+ cos x=1 можно решать по крайней мере четырьмя способами. Например, разделив обе части уравнения на √2, получив: (1/√2) sin x+(1/√2) cos x= (1/√2), sin(x+(π/4))= (2/√2) и т.д.
Рассмотрим уравнение a sin x+b cos x= c, у которого произвольные коэффициенты. Такие уравнения решаются разными способами.
1-й способ решения уравнения a sin x+b cos x= c – введение вспомогательного угла.
Мы знаем, что если a 2 +b 2 =1, то существует такой угол как φ, а= cos φ, b= sin φ или наоборот. Для решения уравнения a sin x+b cos x= c вынесем за скобки множителем выражение √( a 2 +b 2 ). Получим: √( a 2 +b 2 )((a/√( a 2 +b 2 )) sin x+(b/√( a 2 +b 2 )) cos x)=c. Поскольку (((a/√( a 2 +b 2 )) sin x) 2 +((b/√( a 2 +b 2 )) cos x)) 2 =1, то первое число (a/√( a 2 +b 2 )) можно принять за косинус некоторого угла φ, а второе (b/√( a 2 +b 2 )) — за синус того же угла φ, т.е. (a/√( a 2 +b 2 ))= cos φ, (b/√( a 2 +b 2 )) = sin φ. В таком случае уравнение примет вид: √( a 2 +b 2 )( cos φ sin x+ sin φ cos x)= c или √( a 2 +b 2 ) sin(φ+x), откуда sin(φ+x)= (с/√( a 2 +b 2 )). Это уравнение имеет решение, если a 2 +b 2 =с 2 , тогда φ+x=(-1) n arcsin (с/√( a 2 +b 2 )) +nπ, x=(-1) n arcsin (с/√( a 2 +b 2 )) +nπ- φ, nϵZ. Угол φ находится из равенства tg φ =( sin φ/ cos φ) =(b/a), откуда φ=arctg(b/a). Ответ: x=(-1) n arcsin (с/√( a 2 +b 2 )) +nπ- arctg(b/a), nϵZ.
Пример: Решим уравнение 12cosx — 5sinx = -13
Решение: разделим обе части уравнения на , получим
Одним из решений системы cos = 12/13, sin = 5/13 является =arccos(12/13). Учитывая это, запишем уравнение в виде:
и, применив формулу для косинуса суммы аргументов, получим
2-й способ решения уравнения a sin x+b cos x= c – метод рационализации.
Известно, что если α≠π(2n+1), nϵZ, то sin α, cos α, tg α выражаются рационально через tg(α/2), т.е. sin α=( 2tg(α/2)/1+ tg 2 (α/2)), cos α=(1- tg 2 (α/2)/ 1+ tg 2 (α/2)), и tg α=( 2tg(α/2)/1- tg 2 (α/2)).
Метод рационализации заключается в следующем: вводится вспомогательное неизвестное так, чтобы после подстановки получилось рациональное уравнение относительно этого вспомогательного неизвестного. Рассмотрим уравнение a sin x+b cos x= c, которое можно переписать так: a( 2tg(α/2)/1+ tg 2 (α/2))+b(1- tg 2 (α/2)/ 1+ tg 2 (α/2))=c. Положим tg(x/2)=t, тогда получим: a( 2t/1+ t 2 )+b(1- t 2 / 1+ t 2 )=c. Это уравнение – рациональное относительно t. Умножим обе части уравнения на 1+ t 2 ≠0 при tϵR, получим: (b+c)t 2 -2at+(c-b)=0(2), (D/4)=a 2 -(c-b)(c+b)= a 2 +b 2 -с 2 . Полагаем, что a+b≠0 или с≠-b, тогда t 1.2 =((a±√( a 2 +b 2 -с 2 )/(b+c))(3). Значение t- действительные, если a 2 +b 2 ≥с 2 .
Если уравнение(2) с=-b, то оно обратится в уравнение первой степени: -2at-2b=0, t=-(b/a), т.е. tg(x/2)=- (b/a), x=-2 arctg(b/a)+2nπ. Выражение для вспомогательного неизвестного t= tg(x/2) теряет смысл при (x/2)= (π/2)+nπ, т.е. x=(2n+1)π. Решения уравнения(1) вида x=(2n+1)π (если такие решения существуют) могут быть потеряны. Подставив x=(2n+1)π в уравнение (1), получим a sin(2n+1)π +b cos(2n+1)π = c; a·0+b(-1)=c; с=-b. Том случае уравнение (1) имеет множество решений вида x=(2n+1)π, nϵZ.
- Если a 2 +b 2 2 , то уравнение (1) не имеет решений, так как уравнение (2) не имеет действительных корней.
- Если a 2 +b 2 ≥с 2 и с≠-b, то из уравнения(3) найдем: x=2arctg ((a±√( a 2 +b 2 -с 2 )/(b+c))+2nπ, nϵZ.
- Если с=-b, то уравнение (1) имеет два множества решений: x=(2n+1)π и x=-2 arctg++2nπ, nϵZ.
3-й способ решения уравнения a sin x+b cos x= c.
Можно возвести обе части уравнения в квадрат и привести его к однородному. Этот способ неприемлем, так как получаются посторонние корни.
4-й способ решения уравнения a sin x+b cos x= c.
- Запишем уравнение в виде: 2a sin(x/2) cos(x/2)+ b(cos 2 (x/2)- sin 2 (x/2))= c(cos 2 (x/2)+ sin 2 (x/2)), т.е. однородное уравнение:(с+b) sin 2 (x/2)- 2a sin(x/2) cos(x/2)+(c-b) cos 2 (x/2)=0 и т.
Универсальная тригонометрическая подстановка
Многие тригонометрические уравнения можно решить с помощью формул универсальной тригонометрической подстановки
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку не определен в точках , поэтому в таких случаях нужно проверять, являются ли углы , корнями исходного уравнения.
Пример. Решим уравнение
Решение:
Обращение к функции предполагает, что , то есть , .
По формулам универсальной тригонометрической подстановки исходное уравнение примет вид:
|: 2
, ;
IV. Способы отбора корней в тригонометрических уравнениях
1 способ: Арифметический(непосредственная подстановка корней в уравнение и имеющиеся ограничения)
2 способ. Геометрический способ(отбор корней тригонометрического уравнения на числовой прямой )
Отмечаю значения х при n,k,m=0 на числовой прямой и отрезок[-(3π/2); (π/2)]
Измеряю период 2 π с помощью линейки(период функции, входящей в уравнение) и откладываю период с помощью линейки вправо, влево.
Определяю значения углов, принадлежащих данному отрезку.
3 способ: Геометрический способ(отбор корней тригонометрического уравнения на числовой окружности)
Выбор корней уравнения 2 sin2x+ sinx-1=0, принадлежащих отрезку[π/2; 2π] покажу на тригонометрическом круге
4 способ: Функционально-графический способ
В одной системе координат строим графики функции у=sin x и у=-1; у=sin x и у=1/2. Показываем отрезок [-3п/2;п/2]. Находим точки пересечения графиков функций у=sin x и у=-1; у=sin x и у=1/2, входящих в промежутке [-3п/2;п/2].
х= -7п/6; х= -п/2; х=п/6 являются решением уравнения
5 способ: Алгебраический (решение неравенства относительно неизвестного целочисленного параметра и вычисления корней)
Считаю лучшим способом — это алгебраический (решение неравенства относительно неизвестного целочисленного параметра и вычисления корней)
- Практическое применение тригонометрии
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела.
Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Следует отметить применение тригонометрии в следующих областях: техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ), компьютерная томография, фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография, геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Приведу несколько примеров из практики, например: тригонометрия в медицине и биологии.
Модель биоритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.
Формула, получившая название тегеранской, была представлена широкой научной общественности на 14-й конференции географической медицины и затем — на 28-й конференции по вопросам применения компьютерной техники в кардиологии, состоявшейся в Нидерландах. Эта формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс Гибсон (James Gibson), строивший свои выводы на основе опыта работы с пилотами военной авиации. Однако после того о теории
Результаты нового исследования, как можно предположить, окажутся небезынтересны инженерам, конструирующим системы навигации для роботов, а также специалистам, которые работают над созданием максимально реалистичных виртуальных моделей. Возможны и приложения в области медицины, при реабилитации пациентов с повреждениями определенных областей мозга.
Выполняя исследовательскую работу, выяснила какое значение имеют тригонометрические уравнения в жизни человека и как они работают в стране. Рассмотрела способы выбора корней уравнения принадлежащих отрезку из раздела «ЕГЭ по математике» Доказала, что в современном мире прожить без знаний тригонометрический уравнений невозможно. Чтобы быть хорошими специалистами, уметь разбираться в большом потоке информации, необходимо знать тригонометрические уравнения. Изучение столь важной и интересной темы дает положительную мотивацию для самообразования
Исследовательская работа на тему» Тригонометрические уравнения в заданиях ЕГЭ»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
МБОУ « Мордовско-Паёвская СОШ» Инсарского района РМ
Выполнила: Пантилейкина Надежда,
ученица 11 класса
Руководитель: Кадышкина Н.В.,
Глава I. О тригонометрических уравнениях…………………………………..…5
1) Основные типы тригонометрических уравнениях и методы их решения:
1. Уравнения, сводящиеся к простейшим. …………………………………..5
2. Уравнения, сводящиеся к квадратным…………………………………….5
3. Однородные уравнения acosx + b sin x = 0………………………………. 6
4.Уравнения вида acosx + b sin x = c , с≠ 0…………………………………7
5. Уравнения, решаемые разложением на множители…………………. ….7
6. Нестандартные уравнения………………………………………………….8
Глава II. Основные понятия и формулы тригонометрии…………………….8-10
Глава II I . Уравнения предлагавшиеся на ЕГЭ прошлых лет…………. ……10-14
«Единственный путь, ведущий к знаниям — это деятельность. »
Бернард Шоу
Через несколько месяцев я заканчиваю школу.
Чтобы не было проблем с дальнейшим выбором жизненного пути, необходимо получить школьный аттестат, а для того чтобы получить школьный аттестат, необходимо сдать два обязательных экзамена в форме ЕГЭ — и один из них математика . Что уж там говорить, выпускные экзамены — ответственный период в жизни любого школьника, от которого зависит не только итоговая оценка в аттестате, но и его профессиональное будущее, доход и карьера.
Единый Государственный Экзамен – это важный тест перед переходом в новую жизнь и поступлением в университет или колледж. Особенно важно сдать его на хорошие баллы. ЕГЭ по математике — серьезное испытание и без хорошей базы ученик не сможет претендовать на приличный результат.
Как не допустить провала на экзамене и получить хорошие баллы? Для этого необходимо хорошо решить задания. Я не претендую на максимальный балл, тем не менее старательно готовлюсь. И заметила, что даже на первом задании части С, а, именно, на решении тригонометрических уравнениях и их системах допускаю ошибки. На первый взгляд, задача С1 – это относительно несложное уравнение или система уравнений, которое может содержать тригонометрические функции, одним из основных подходов к решению которых состоит в их последовательном упрощении с целью сведения к одному или нескольким простейшим. Так почему я ошибаюсь?
Актуальность темы определяется тем, что учащиеся должны разбираться в тех или иных способах решения тригонометрических уравнений.
Поэтому, перед собой я поставила следующую цель:
Систематизировать, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений.
Объектом исследования является изучение тригонометрических уравнений в заданиях ЕГЭ.
Предмет исследования — является решение тригонометрических уравнений
Таким образом, основной целью написания данной курсовой работы является изучение тригонометрических уравнений и их систем, способы их решения.
В соответствии с целями, объектом и предметом исследования определены следующие задачи:
1). Изучить все задания, связанные с решением тригонометрических уравнений, предлагавшиеся на ЕГЭ работ предыдущих лет и при выполнении диагностических работ;
2) Изучить методы решения тригонометрических уравнений.
3). Выявить основные возможные ошибки при решении таких уравнений;
4). Выяснить причину допущения таких ошибок.
5)Рассмотреть рекомендации по решению тригонометрических уравнений;
6). Сделать выводы.
В своей работе я решу несколько тригонометрических уравнений, покажу возможные ошибки при их решении и постараюсь ответить на следующие вопросы:
1). Можно ли избежать ошибок при выполнении заданий типаС1
2) Если я буду тренироваться в решении уравнений такого типа, то я смогу
ли безошибочно выполнять такие задания?
Для этой цели я изучила все демонстрационные и тренировочные задания, проводимые с нами, материалы ЕГЭ предыдущих лет;
изучила справочные источники;
самостоятельно решала задания из Интернета;
консультировалась со своим учителем в случае затруднения;
училась анализировать и правильно оформлять результаты.
Глава I . О тригонометрических уравнениях.
1) Определение 1. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Простейшие тригонометрические уравнения — это уравнения вида sin x = a ,
cos x=a, tg x=a, ctg x = a.
В таких уравнениях переменная находится под знаком тригонометрической функции, а — данное число.
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения.
2)Основные типы тригонометрических уравнений.
Уравнения, сводящиеся к простейшим.

Решение:
Ответ:
Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Ответ:
Однородные уравнения : asinx + bcosx = 0
a sin 2 x + b sinxcosx + c cos 2 x = 0.
Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем,
что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx.
Ответ:
Уравнения вида a sinx + b cosx = с, с ≠ 0.
Пример: Решить уравнение
Решение:
Ответ:
Уравнения, решаемые разложением на множители.
Припер: Решить уравнение sin2x – sinx = 0.
Решение: Используя формулу sin2x = 2sinxcosx, получим
2sinxcosx – sinx = 0,
sinx (2cosx – 1) = 0.
Произведение равно нулю, если хотя бы один из множителей равен нулю.
Ответ:
Решить уравнение cosx = х 2 + 1.
Глава II . Основные понятия и формулы тригонометрии.
Тригонометрические уравнения — обязательная тема любого экзамена по математике.
О х, сколько мучений доставляет ученикам изучение тригонометрии.
Определенные сложности возникают даже в том случае, если рядом учитель по математике и объясняет каждую мелочь. Это и понятно, одних только базовых формул существует более двадцати. А уж если считать их производные … Ученик путается в вычислениях и никак не может запомнить механизмы, при помощи которых эти формулы позволяют найти, например, 
Вы знаете формулы — вам легко решать. Не знаете — не поймете, даже если дадут формулу.
Формулу нужно не просто тупо знать, а знать куда ее можно применить, как раскрыть и в чем суть формулы, а для этого вам нужно решать примеры именно для тех задач, которые даются с трудом.
Мне поначалу казалось, тригонометрия — это скучный набор формул и графиков. Однако, знакомясь с новыми понятиями тригонометрии и методами решения тригонометрических уравнений, каждый раз убеждалась, насколько интересен и увлекателен мир тригонометрии.
Во- первых, для успешного решения тригонометрических уравнений нужно хорошо знать тригонометрические формулы, причем не только основные, но и дополнительные (преобразование суммы тригонометрических функций в произведение и произведения в сумму, формулы понижения степени и другие), так как использование на ЕГЭ шпаргалок и мобильных телефонов запрещается
Во- вторых , мы должны четко знать стандартные формулы корней простейших тригонометрических уравнений (полезно помнить или уметь получать с помощью тригонометрической окружности упрощенные формулы для корней уравнений)
Каждое из таких уравнений решается по формулам, которые следует знать. Вот эти формулы:
а) Функция y = sin x . Функция ограниченная: находится в пределах [-1; 1]. Это значит, что при решении уравнений типа sinx =2 или sinx =-5 в ответе получается: нет корней. Формулы для функции у= sinx
1) sinx =a, x= (-1) n arc sin a +n,n
2) sinx = — a, x= (-1) n+1 arc sin a +n,n
Также, нужно знать частные случаи: 1) sinx =- 1,
2) sinx =0,
3) sinx = a ,
Также нужно уметь решение 

2 . Функция y = cos x . Функция ограниченная: находится в пределах [-1; 1]. Это значит, что при решении уравнений типа cos x =2 или cos x =-5 в ответе получается: нет корней. Формулы для функции у= cos x :
1. cosx =a, X=± arccos a+2n,n
2. cos x=-a, X=±( — arccos a)+2n,n
Частные случаи: 1. cosx =-1, X = +2 n , n
2. cosx =0,
3. cosx =1, X= 2n,n
3. Функция y = tg x .
Тут всего одна формула, без частных случаев: tg x = ± a .
х = ± arctg a+n,n
В-третьих, надо знать значения тригонометрических функций;
В- четвёртых, Если в уравнении тригонометрическая функция находится под знаком радикала, то такое тригонометрическое уравнение будет иррациональным. В таких уравнениях следует соблюдать все правила, которыми пользуются при решении обычных иррациональных уравнений (учитывается область допустимых значений как самого уравнения, так и при освобождении от корня четной степени).
V . Уравнения, предлагавшиеся на ЕГЭ прошлых лет.
«Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, — что, следуя этому методу, мы достигнем цели».
1. Уравнения, сводящиеся к квадратному.
С1. Решить уравнение:
Решение: Воспользовавшись основным тригонометрическим тождеством, перепишем уравнение в виде
Заменой cos 

Второе уравнение корней не имеет так как | cosx |≥1, а из первого x =±


Ответ: =±


Вывод: вводя новую переменную, нужно учитывать, что значения sin x и cos x ограничены отрезком 
2. Уравнения, решаемые разложением на множители
Задание С1 ( 2011 г.)
а) Решить уравнение
б) Указать корни уравнения, принадлежащие отрезку
Решение: а) решаем разложением левой части на множители:
группируем и выносим общий множитель за скобки, получим
Уравнение 1) решений не имеет.
Второе уравнение однородное, решается делением почленно на cosx ≠0, получим 
б)
Ответ: а) 
1.При решении уравнения такого вида, во – первых, нужно знать, что | sin х|≤1 и | cosx |≤1, и уравнение sinx =-2 решений не имеет;
2.Во – вторых, обосновать деление на cosx ≠о ( так как , если cosx =0,то sin х=0 , а это невозможно;
в- третьих, обоснованно произвести отбор корней, принадлежащие данному промежутку
3
С1 ( 2010 г.) Дано уравнение
а) решить уравнение;
б
Решение: Используя формулы приведения, получим :
sin 2 x – cos x =0,
2 sinx cosx- cosx =0,
с osx (2 sinx -1 )=0, откуда cosx= 0 или sinx =½,
б) Найдем значения к, при которых корни будут принадлежать
указанному промежутку. Для того, чтобы выбрать корни. принадлежащие заданному промежутку, решение представим в виде :
б

Решая это неравенство, целого

Ответ: а) 
б)
При решении уравнения такого вида, необходимо знать формулы приведенного уравнения и правильно её применить; уметь представлять решение
4. Системы тригонометрических уравнений
С1 (2010). Решить систему уравнений
Решение: О.Д.З
Дробь равна нулю, если числитель равен 0, а знаменатель не равен 0.
Из уравнения 2 sin 2 x – 3 sinx +1 =0, решая методом введения новой переменной, находим

1)Пусть 


либо 

2) Пусть sinx = 1, тогда у = cos x = 0 – нет решения.
Ответ: 
Вывод: 1) нужно учитывать ограниченность тригонометрических
2) Записывать и учитывать О.Д.З.
5. С1 ( ЕГЭ 2011 г.) Решить уравнение:
О.Д.З. – cos x ≥ 0, sin х ≤ 0.
4sin 2 x + 12 sinx + 5 = 0 или cos x =0
sinx = t
4 t 2 + 12 t + 5=0, откуда t 1=-½ , t 2 = —
sinx = -½ sinx =- 
х =
х =
с учётом О.Д.З. х =
Ответ: х =
Вывод: Ответ записать с учётом О.Д.З.
В проделанной мною работе были изучены решения тригонометрических уравнений, рассмотрены рекомендации по решению тригонометрических уравнений, методы решения тригонометрических уравнений и рассмотрены ошибки, которые возможны при их решении.
Я пришла к следующим выводам:
1. Задания типа С1 проверяют умение решать тригонометрические уравнения. Эти задания являются, действительно, несложными, что придаёт лишнюю самоуверенность и усыпляют внимательность. Единственной сложностью этих заданий является то, что, решив уравнение или систему уравнений, отбросить посторонние корни.
2. Задача С1 – это самая простая задача группы С. При ее решении не должны возникать громоздкие преобразования и сложные вычисления. Если же они появились – немедленно нужно остановиться, проверить решение и попробовать понять, что же здесь не так.
3. В конечном итоге, главное требование — решение должно быть математически грамотным, из него должен быть понятен ход рассуждений. Нужно постараться записать свое решение кратко и понятно, но главное – правильно!
4. И самое главное — чтобы научиться без ошибок решать уравнения , надо их решать! Ведь, как говорил Пойа, « Если хотите научиться плавать, то смело ныряйте в воду, а если хотите научиться решать задачи, надо их решать!»
Приложение 1 ( основные формулы тригонометрии)
1) основное тригонометрическое тождество sin 2 α + cos 2 α= 1,
Деля это уравнение на квадрат косинуса и синуса соответственно имеем
2)формулы двойного аргумента sin 2α =2 sin α cos α,
cos 2 α = cos 2 α — sin 2 α ,
cos 2α = 1- 2 sin 2 α,
3)формулы понижения степени:
4) формулы суммы и разности двух аргументов:
sin (α+ β )= sin α cos β + cos α sin β
sin (α- β )= sin α cos β — cos α sin β
cos (α+ β )= cos α cos β + sin α sin β
cos (α- β )= sin α cos β + sin α sin β
Формулами приведения называются формулы следующего вида:
Суммы суммы и разности тригонометрических уравнений
Чётность
Косинус— чётная, синус, тангенс и котангенс— нечётные , то есть:
Непрерывность
Синус и косинус — непрерывные функции . Тангенс и имеет точки разрыва

Периодичность
Функции y = cos x , y = sin x — периодические с периодом 2π,
функции y = tg x и y = ctg x — c периодом π.
Знаки тригонометрических функций по четвертям
источники:
http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2017/11/28/issledovatelskaya-rabota-po-teme
http://infourok.ru/issledovatelskaya_rabota_na_temu_trigonometricheskie_uravneniya_v_zadaniyah_ege-282004.htm
0
Федеральное государственное казённое общеобразовательное учреждение
«Омский кадетский военный корпус
Министерства обороны Российской Федерации»

Проектная (исследовательская) работа
Тригонометрические уравнения:
виды и способы решения.
Автор: обучающийся 11-3 класса
Дускин Владислав
Руководитель:
преподаватель математики
Железная Н.О.
г. Омск
2022 год
Оглавление
Введение 3
1. Тригонометрические уравнения: виды, способы решения. 5
1. 1. Решение простейших тригонометрических уранений 5
1. 2. Основные способы решения тригонометрических уранений 6
1. 3. История понятия «тригонометрия» 15
2. Практикум «Решение тригонометрических уравнений» 18
2.1. Самостоятельные работы № 1, № 2 18
2.2. Обучающий тренажер и итоговый тест по теме
«Решение тригонометрических уравнений» 22
Заключение 27
Список литературы и использованных сайтов 28
ПРИЛОЖЕНИЕ 31
Введение
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает настойчивость
и упорство в достижении цели.
А. Маркушевич
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение данной темы в 4 четверти 10 класса. Сейчас я учусь в 11 классе и 1 июня 2023 года мне предстоит сдавать ЕГЭ по математике профильного уровня. Как часто тригонометрические уравнения встречаются на ЕГЭ? Тригонометрические уравнения могут встретиться до четырех раз в заданиях ЕГЭ. Это может быть:
Задача № 5 (простейшее тригонометрическое уравнение – встречается время от времени);
Задача № 8 (задача с прикладным содержанием, которая включает в себя решение тригонометрического уравнения – встречается изредка);
Задача № 11 (она на производную, но в конечном счёте сводится к решению простейшего тригонометрического уравнения – ЧАСТО ВСТРЕЧАЕТСЯ В ЕГЭ)
Задача № 12 – даёт 2 первичных балла – (решение тригонометрического уравнения средней или высокой сложности – ОЧЕНЬ ЧАСТО, ПРАКТИЧЕСКИ ВСЕГДА!)
Так что навык решения данного вида уравнений может добавить в мою копилку целых 5 первичных баллов из 31! Это наиболее актуально для меня сейчас, потому что каждый первичный балл важен, чем он больше — тем лучше для поступления.
В вариантах ЕГЭ задача 12, где нужно решить уравнение, состоит из двух пунктов. Первый пункт – решение самого уравнения. Второй – нахождение его корней на некотором отрезке. Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики. Другие являются специфическими именно для тригонометрии. Решение тригонометрических уравнений в большинстве случаев проводится либо с помощью замены переменной, либо разложения на множители, но и тот, и другой способ применяется в разных вариантах в зависимости от вида конкретного уравнения. Поэтому в данном проекте предлагается рассмотреть и изучить более подробно классификацию типов тригонометрических уравнений и методов их решения.
Были определены:
Объектная область исследования — учебный предмет «математика».
Объект исследования – решение тригонометрических уравнений.
Предмет исследования – математические задачи определённого типа.
Цель проекта:
— Повторение, обобщение и систематизация имеющихся знаний по теме «Тригонометрические уравнения»;
— Расширение и углубление знаний по теме «Решение тригонометрические уравнения», выработка навыка решения различных типов тригонометрических уравнений;
— Формирование устойчивого интереса к математике, умения и навыков исследовательской, проектной деятельности; развитие навыков самостоятельного поиска информации, формирование умения отбирать и структурировать материал.
Задачи:
-
Изучить литературу по теме проекта;
-
Систематизировать все собранные материалы;
-
Подготовить подборку задач по теме проекта и представить полученные результаты в виде обучающего тренажера;
Тип проекта:
по виду деятельности – практико-ориентированный;
по организационной форме – индивидуальный;
по времени выполнения — долговременный.
Этапы работы над проектом
Разработанный нами проект включает два этапа:
1-й этап аналитический
2-й этап обобщения
Основные виды работы над проектом:
-
Изучение дополнительной литературы (справочники, словари, энциклопедии, задачники по математике, Интернет-ресурсы)
— Анализ полученной информации (обобщение, сравнение, сопоставление с имеющимися знаниями по данной теме, решение задач).
Глава 1. Тригонометрические уравнения: виды, способы решения
Определение. Тригонометрическое уравнение — алгебраическое уравнение относительно тригонометрической функции неизвестного аргумента.
1.1. Простейшие тригонометрические уравнения
-
Частные случаи:
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
;
-
-
;
-
;
-
;
-
.
Пример 1. Решите уравнения
1) ;
2) ;
3)
4)
1.2. Основные способы решений тригонометрических уравнений
Основные способы:
-
разложение на множители;
-
введение новых переменных.
Пример 2. Ответ:
Пример 3.
Решение: 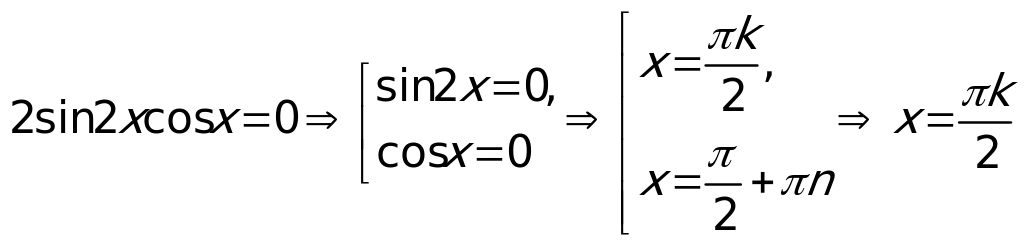
Пример 4. .
Решение: ОДЗ: . Так как
, получим:
или
, откуда
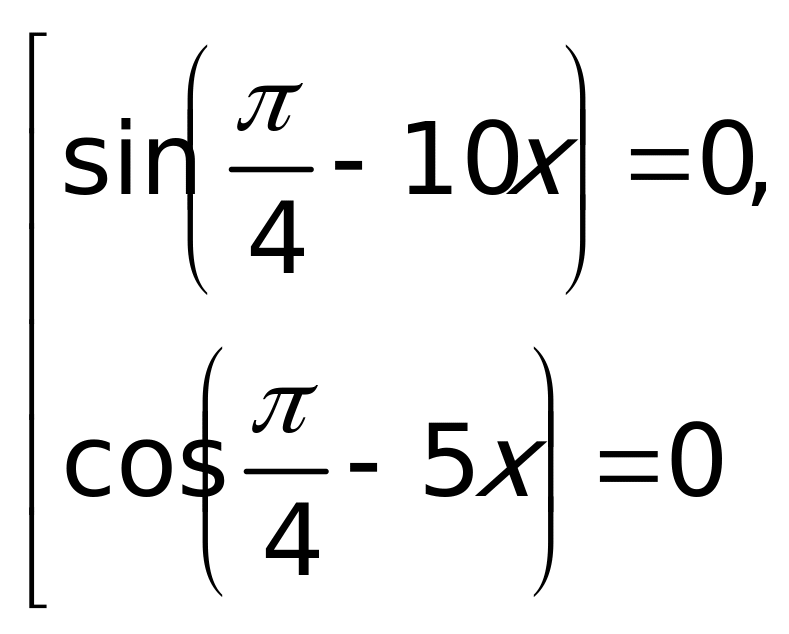
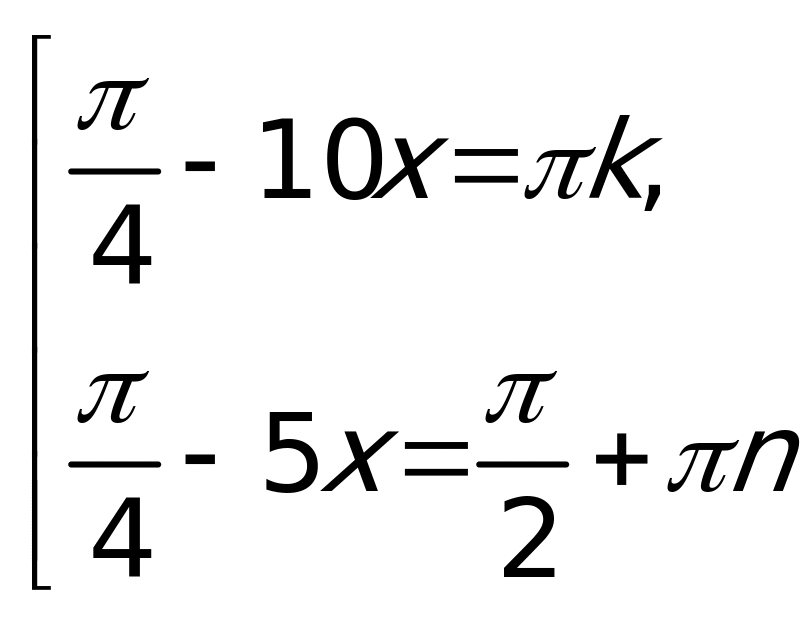
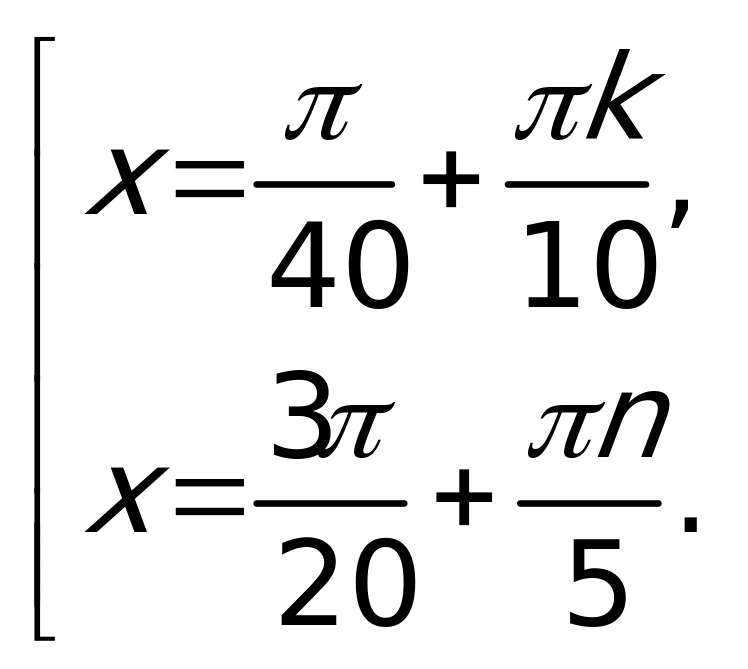
Ответ: .
Общая схема решения тригонометрических уравнений:
-
Указать ОДЗ уравнения.
-
С помощью тригонометрических формул и различных преобразований свести исходное уравнение к одному или нескольким простейшим.
-
Решить каждое из полученных простейших уравнений и записать ответ, объединяя полученные решения.
-
Проверить, входят ли найденные решения в ОДЗ.
Проверка найденных решений необходима, если в процессе решения:
-
произошло расширение области определения уравнения в результате некоторых преобразований (освобождение от знаменателей, сокращение дроби, приведение подобных членов);
-
использовалось возведение обеих частей уравнения в одну и ту же четную степень;
-
применялись тригонометрические тождества, левая и правая части которых имеют неодинаковые области определения (например:
через
,
,
и др.).
Чтобы не потерять корни в результате тождества преобразования, надо проверить все запрещаемые этим преобразованием значения переменной.
Пример 5.
Решение: ОДЗ: Пусть
, тогда
. Получим
или
, но
– тоже корни, которые мы потеряли, перейдя только к
.
Пример 6.
– выражение, получающееся из
и действительных констант с помощью четырех действий арифметики.
Пример 7.
Решение:
Ответ: .
-
– аналогично.
-
– однородное 1-й ст.
делим на
, получаем:
,
.
-
– однородное 2-й ст.
делим на
, получаем:
,
Пример 8.
Ответ:
Замечание: Любое уравнение с помощью замены через
сводится к уравнению, рациональному относительно
(не забыть проверить
). Поэтому такая подстановка называется универсальной.
Способ 1: Метод дополнительного угла.
Разделив обе части уравнения на величину , получим уравнение
. Введем дополнительный острый угол
, исходя из условий:
и
. К полученному после этих преобразований уравнению
применим формулу косинуса разности или суммы аргументов. Имеем:
. Последнее уравнение решается по стандартным формулам.
Способ 2: Так как ,
,
, то уравнение можно переписать в виде:
.
Это однородное уравнение 2-й степени, которое после приведения подобных членов решается соответствующим способом. Заметим, что этого же результата можно достичь сразу, используя универсальную подстановку.
Пример 9. .
Решение: 1 способ: разделив обе части уравнения на , получим
. Теперь уравнение можно переписать в виде:
или
, где
. Далее:
, или, выражая х,
.
Ответ: .
2 способ: ,
Ответ:
Решаются заменой .
Чтобы выразить произведение функций, возведем равенство в квадрат, получим или
, откуда
.
Пример 10.
Решение: Сделаем замену
, откуда
. Получаем уравнение
с корнями
. Делаем обратную замену:
.
Ответ: .
Пример 11. .
Решение: ОДЗ: . Так как
, имеем:
.Пусть
, тогда
,
.
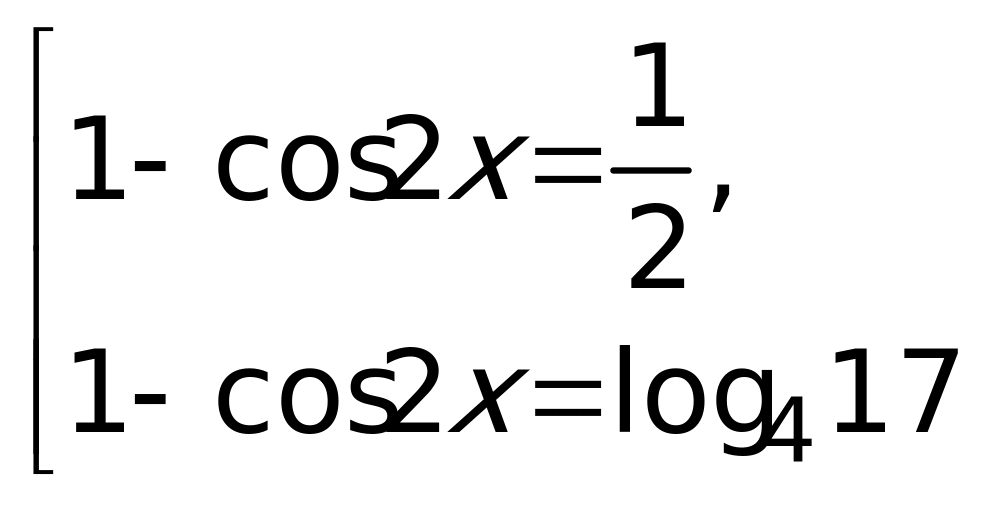
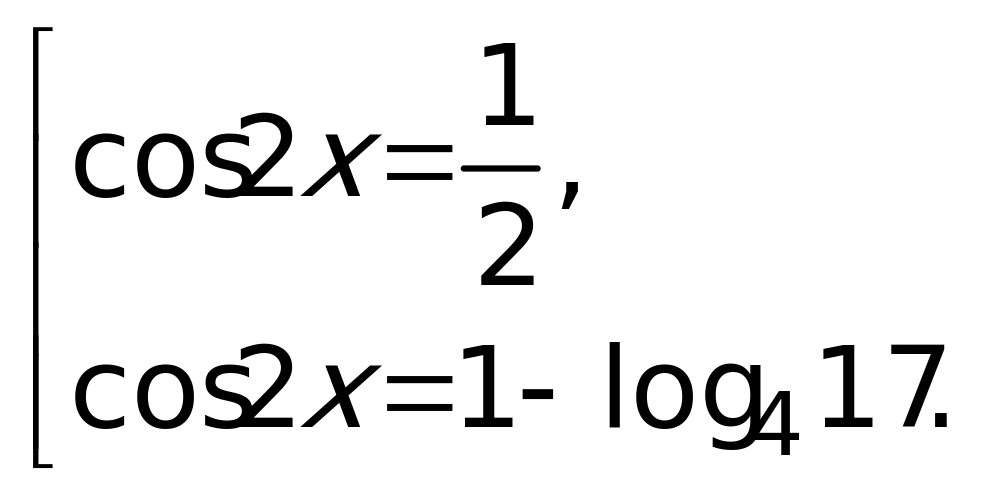
Второе уравнение полученной совокупности решений не имеет, так как , а, следовательно,
. Решая первое уравнение совокупности, получаем:
или
.
Ответ: .
Основные типы тригонометрических уравнений.
-
Уравнения
и
сводятся к квадратным относительно замены
и
.
-
Однородное уравнение
, где
, равносильно уравнению
.
-
Уравнение
удобно записать в виде
; здесь
— вспомогательный угол, такой что
,
.
-
Уравнения
и
сводятся к уравнениям вида
с помощью формул понижения степени:;
.
-
Уравнения
и
можно свести
либо к однородным, используя тождество ,
либо к уравнениям вида , используя формулы понижения степени.
-
Уравнения
сводятся к квадратным относительно замены
, т.к.
.
Пример 1. Найти число корней уравнения на интервале
.
Решение. Это уравнение решается методом введения вспомогательного аргумента. Разделив обе части уравнения на , получим
. Подсчитаем число корней, принадлежащих интервалу
: при
;
при
;
при
;
при
.
При и
корни не принадлежат интервалу
. Следовательно, число корней равно 4.
Ответ: 4.
Пример 2. Найти число корней уравнения , принадлежащих интервалу
.
Решение. Преобразуем уравнение к виду
. Введем новую переменную
, где
. Тогда получим квадратное уравнение
и
, где
не подходит по смыслу замены. Следовательно, исходное уравнение равносильно совокупности уравнений
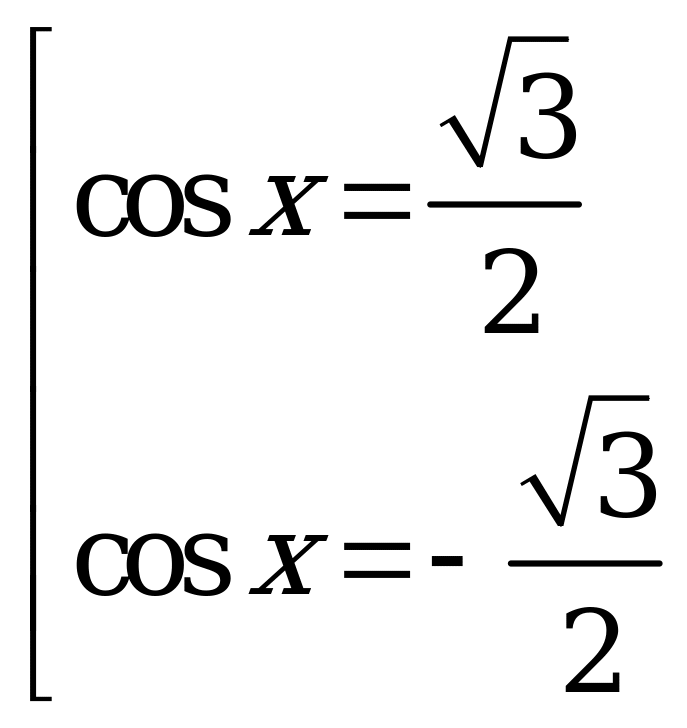
. Отбираем корни на интервале
:
при
; при
; при
. Других корней на этом интервале нет. Следовательно, число корней равно 4.
Ответ: 4.
Пример 3. Найти число корней уравнения на интервале
.
Решение. Введем новую переменную . Тогда получим иррациональное уравнение
,
– посторонний корень. Следовательно,
и
,
. Отбираем корни на интервале
: при
; при
; при
. Других корней на этом интервале нет. Следовательно, число корней равно 3.
Ответ: 3.
Пример 4. Найти число корней уравнения на интервале
.
Решение. Группируя слагаемые, получим . Преобразуя суммы в произведения, приводим уравнение к виду
. Отсюда
,
и
,
. Отбираем корни на интервале
: при
; при
; при
; при
; при
; при
; при
. Других корней на этом интервале нет. Следовательно, число корней равно 7.
Ответ: 7.
Пример 5. Найдите в градусах среднее арифметическое всех различных корней уравнения , принадлежащих промежутку
.
Решение. Данное уравнение равносильно системе
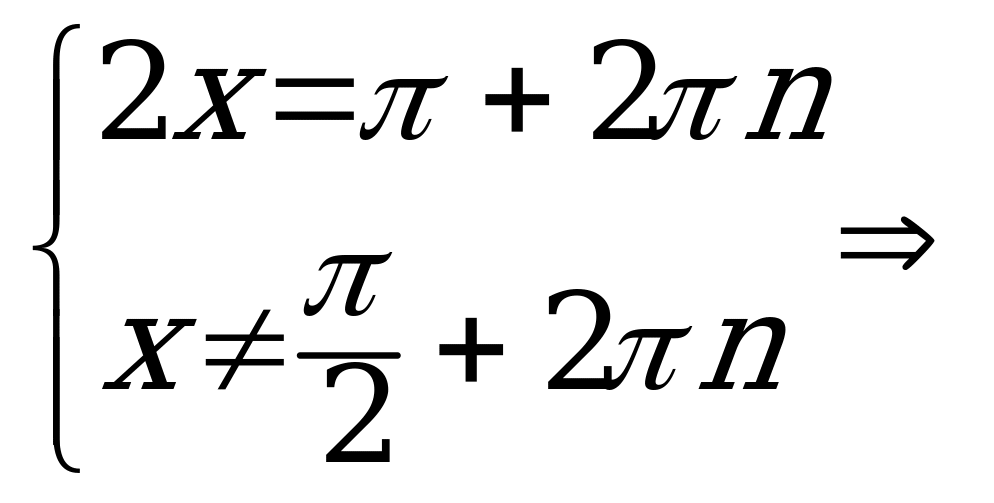
,
.
Среди корней этого уравнения промежутку принадлежат
и
. Среднее арифметическое этих корней равно
.
Ответ: .
1.3 История понятия “тригонометрия”
Слово “тригонометрия” (от греческих слов “тригон” — треугольник и “метрео” — измеряю) означает “измерение треугольников”. Возникновение тригонометрии связано с развитием астрономии и географии.
Начала тригонометрии обнаружены в сохранившихся документах Древнего Вавилона, сведения тригонометрического характера встречаются и в старинных памятниках других народов древности.
Древнегреческие учёные впервые поставили перед собой задачу решения прямоугольного треугольника, т.е. определения его элементов по трём данным элементам, среди которых хотя бы один – сторона треугольника. Для решения этой задачи Гиппарх и Птолемей (II в. до н. э.) составили таблицы длин хорд, соответствующих различным центральным углам кругам постоянного радиуса (через каждые полградуса до 180°).
Понятия синуса, косинуса и тангенса угла возникли в астрономии и геометрии. По существу, ими оперировали ещё древние математики, рассматривая отношения отрезков в треугольниках и окружностях. Древнегреческий учёный Клавдий Птолемей для своих астрономических исследований составил подробную, весьма точную таблицу синусов углов, в течение многих веков служившую средством для решения треугольников.
В XI-XIII вв. в трудах математиков Средней Азии, Закавказья, Ближнего Востока и Индии началось формирование тригонометрии как отдельной науки. У индийских учёных линия синусов именовалась “архаджива”, что буквально означало “половина тетивы лука”. Для угла a линия синусов – это хорда единичной окружности, соответствующая центральному углу 2а. Её длина равна 2 sina. В Индии были составлены таблицы значений синусов для всех углов от 0 до 90° через каждые 3°45′. Эти таблицы были точнее таблиц Птолемея. Об их высокой точности говорит тот факт, что для синуса и косинуса 3°45′ были вычислены значения 100/1529 и 466/467, отличающиеся от истинный менее чем на 0,00000001.
Косинус индийцы называли “котиджива”, т.е. синус остатка (до четвери окружности). В XV в. немецкий учёный Иоганн Мюллер (1436 — 1476), известный в науке под именем Региомонтам, как и другие математики, применял для понятия “косинус дуги x” латинский термин sinus complementi, т.е. синус дополнения, имея в виду sin(90° — x). От перестановки этих слов и сокращения одного из них (co-sinus) образовался термин “косинус”, встречающийся в 1620 г. у английского астронома Э. Гунтера, изобретателя счётной линейкой.
В IX-X вв. учёные стран Средней Азии (ал-Хабаш, ал-Баттани, Абу-л-Вефа и др.) ввели новые тригонометрические величины: тангенс и котангенс, секанс и косеканс. Понятия “тангенс” и “котангенс”, как и первые таблицы этих новых тригонометрических величин, родились не из рассмотрения тригонометрической окружности, а из учения о солнечный часах. Происхождение названия функции тангенс (термин введён в 1583 г. Немецким математиком Т. Финком), связана с геометрическим его представлением в виде отрезка прямой. Латинское слово tangens означает косающийся (отрезок касательной). Термин “котангенс” был образован в средние века по аналогии с термином “косинус”. Все три термина вырабатывались на протяжении веков и вышли во всеобщее употребление в первой половине XVII в.
В дальнейшем потребности географии, геодезии, военного дела способствовали развитию тригонометрии. Особенно усиленно шло её развитие в средневековое время, в первую очередь на юго-востоке: в Индии (Ариабхата, Брамагупта, Бхаскара), в Узбекистане, Азербайджане и Таджикистане (Насир ад-Дин ат-Тусси, ал-Каши, ал-Бируни), в Арибии (Ахмад Ибн-Абдаллах, ал-Баттани), а затем и в Европе (Пейрбах, Иоганн Мюллер, Коперник, Рети). Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому учёному Насир ад-Дину ат-Туси (1201-1274), написавшему “Трактат о полном четырёхстороннике”.
Творения учёных этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах ещё не была введена необходимая символика, и поэтому развитие тригонометрии происходило очень медленно.
Современный вид тригонометрии получила в трудах Леонарда Эйлера (1707-1783). Он, в частности, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных для него формул, ввёл единообразные знаки. Впервые в его трудах встречается запись sinx и др., доступно изложен вопрос о знаках тригонометрических функций в каждом квадрате, установлены формулы приведения.
Уже во “Введении в анализ бесконечных” (1748) Л. Эйлер впервые трактует синус, косинус и т.д. не как тригонометрические линии, обязательно связанные с окружностью, а как тригонометрические функции, которые он рассматривал как числовые величины.
До Эйлера совсем редко рассматривались тригонометрические функции дуг, превышающие π. Лишь в его трудах разрабатывается учение о тригонометрических функциях любого аргумента. На основании трудов Л. Эйлера были составлены учебники тригонометрии, излагавшие её в строгой научной последовательности.
Глава 2. Практикум по теме
«Решение тригонометрических уравнений».
Материал проекта представлен в виде практических заданий, которые позволят систематизировать и качественно улучшить уровень решения тригонометрических уравнений. В работе содержится достаточно большое количество взятых из различных источников заданий и упражнений, которые структурированы по методам решения уравнений — от самых элементарных до достаточно сложных.
Сводить тригонометрические уравнения к простейшим – задача творческая, тут нужно использовать и тригонометрические формулы, и особые методы решений уравнений:
— Метод введения новой переменной (самый популярный в ЕГЭ).
— Метод разложения на множители.
— Метод вспомогательных аргументов.
2.1 Самостоятельные работы № 1, № 2
Самостоятельная работа № 1 по теме
«Тригонометрические уравнения»
Вариант № 1 Решите уравнения:
1.
2.
3.
4.
5.
6.
7.
8. и найдите все его корни, принадлежащие промежутку
.
Вариант № 2 Решите уравнения:
1.
2.
3.
4.
5.
6.
7. .
8. и найдите все его корни, принадлежащие промежутку
.
Вариант № 3 Решите уравнения:
1.
2.
3.
4.
5.
6.
7.
8. и найдите все его корни, принадлежащие промежутку
.
Вариант № 4 Решите уравнения:
1.
2.
3.
4.
5.
6.
7.
8. и найдите все его корни, принадлежащие промежутку
.
Самостоятельная работа № 2
по теме «Тригонометрические уравнения»
Вариант № 1 Решите уравнения:
Вариант № 2 Решите уравнения:
Вариант № 3 Решите уравнения:
Вариант № 4 Решите уравнения:
Ответы к самостоятельной работе
|
№ вар. |
1 |
2 |
3 |
4 |
5 |
6 |
|
I |
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
III |
|
|
|
|
|
|
|
IV |
|
|
|
|
|
|
|
баллы |
1 |
2 |
2 |
2 |
2 |
2 |
|
номер |
7 |
8 |
9 |
|
I |
|
|
|
|
II |
|
|
|
|
III |
|
|
|
|
IV |
|
|
|
|
баллы |
3 |
3 |
3 |
-
Обучающий тренажер и итоговый тест по теме
«Решение тригонометрических уравнений»
Обучающий тренажер по теме «Тригонометрические уравнения»
-
Найдите решение уравнения на указанном промежутке:
,
(
)
,
(
)
,
(
)
II. Решите уравнение:
(
,
)
(
)
(
,
)
(
//
)
(
,
)
(
)
(
)
(
,
)
(
,
)
(
)
(
,
)
(
)
(
,
)
Найти число корней уравнения , принадлежащих интервалу
. (5)
Итоговый тест по теме
«Решение тригонометрических уравнений»
-
Найдите (в градусах) сумму корней уравнения
, принадлежащих интервалу
А) 280° B) 360° C) 540° D) 680° E) 900°
-
Сумма корней уравнения
, принадлежащих интервалу
А) 90° B) 150° C) 105° D) 180° E) 135°
-
Среднее арифметическое всех корней уравнения
, принадлежащих промежутку
, равно
А) B) 0 C)
D)
E)
-
Найдите количество решений уравнения
на интервале
А) 3 B) 4 C) 7 D) 8 E) 9
-
Найдите количество решений уравнения
, принадлежащих интервалу
А) 0 B) 7 C) 8 D) 9 E) 10
-
Сумма корней уравнения
, принадлежащих промежутку
, равна числу
А) B)
C)
D)
E)
-
Число корней уравнения
, лежащих в интервале
, равно
А) 3 B) 4 C) 5 D) 6 E) 7
-
Найдите в градусах среднее арифметическое всех различных корней уравнения
, принадлежащих промежутку
.
-
Найдите сумму (в градусах) двух самых больших корней уравнения
, принадлежащих промежутку
-
Укажите количество корней уравнения
, принадлежащих отрезку
.
-
Найдите число решений уравнения
, принадлежащих отрезку
-
Найдите сумму корней уравнения
, принадлежащих интервалу
-
Укажите количество корней уравнения
, принадлежащих отрезку
.
-
Укажите сумму корней (в градусах) уравнения
, принадлежащих отрезку
.
-
Найдите в градусах наименьший положительный корень уравнения
.
-
Укажите в градусах значение среднего арифметического всех корней уравнения
, принадлежащих промежутку
.
-
Найдите в градусах корень, если он единственный, или сумму корней уравнения
, принадлежащих промежутку
.
-
Решите уравнение
.
-
Решите уравнение
.
-
Решите уравнение
.
Ответы к обобщающему тесту
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
E |
E |
D |
C |
C |
C |
C |
114 |
570 |
2 |
6 |
60 |
2 |
360 |
45 |
80 |
|
17 |
18 |
19 |
20 |
|
– 270 |
|
|
|
Заключение
В данном проекте я изучил основные типы тригонометрических уравнений и методы их решения. Тригонометрические уравнения чаще всего встречаются в задаче 12 ЕГЭ. В большинстве случаев исходное уравнение в процессе решения сводится к простейшим тригонометрическим уравнениям. Однако для тригонометрических уравнений не существует единого метода решения. В каждом конкретном случае успех зависит от знания тригонометрических формул и от умения выбрать из них нужные. При этом обилие различных формул иногда делает этот выбор довольно трудным. В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Также потеря корней является распространенной грубой ошибкой. Другими такими ошибками являются неточное знание формул решений простейших тригонометрических уравнений, а также неумение правильно найти нужное значение аркфункции. Включение в ответ постороннего корня считается грубой ошибкой на ЕГЭ по математике.
В процессе работы над проектом мною составлены самостоятельные работы для подготовки к экзамену с ответами для самопроверки, собран материал о видах и способах тригонометрических задач. Разработан практикум по решению тригонометрических уравнений, содержащий задания различного уровня сложности, что позволит качественнее подготовиться к решению тригонометрических уравнений, встречающихся в контрольно-измерительных материалах ЕГЭ по математике профильного уровня.
Таким образом, в результате выполнения проекта поставленные цели достигнуты, задачи выполнены. Работая над проектом, я больше узнал об истории тригонометрии, типах и способах решения тригонометрических уравнений и, надеюсь, смогу успешно справиться с такими заданиями, которые могут встретиться мне на ЕГЭ.
СПИСОК ЛИТЕРАТУРЫ
-
Бородуля И.Т. Тригонометрические уравнения и неравенства: Книга для учителей/ Бородуля И.Т. – М.: Книга по требованию, 2013. [электронный вариант].
-
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Тригонометрия: Задачник к школьному курсу. – М.: АСТ-ПРЕСС: Магистр-S, 1998. [электронный вариант].
-
Шахмейстер А. Х. Тригонометрия. – 4-е издание. – М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс», 2017. [электронный вариант].
-
Райхмистр Р. Б. Задачник по математике для учащихся средней школы и поступающих в вузы (с решениями и ответами). – М.: Московский Лицей, 2000. [электронный вариант].
-
Система тренировочных задач и упражнений по математике/ А.Я. Симонов, Д.С. Бакаев, А.Г. Эпельман и др. – М: Просвещение, 1991. [электронный вариант].
-
Лурье М. В. Тригонометрия. Техника решения задач: Учеб. пособие. – М.: Издательство УНЦ ДО, 2004. [электронный вариант].
-
Шабунин М. И. Математика: пособие для поступающих в вузы/ М.И. Шабунин. – 7-е изд., исправ. и доп. – М.: Лаборатория знаний, 2016.
-
Колесникова С. И. Методы решений тригонометрических уравнений. ЕГЭ. Математика/ С.И. Колесникова. – М.: ООО «Азбука-2000», 2017.
-
Гущин Д. Д. Сборник заданий по алгебре. Для подготовки к ЕГЭ и конкурсным экзаменам. – 10-е изд., перераб. и доп. – Париж, СПб: Стетоскоп, ВВМ, 2007.
-
Куланин Е. Д., Федин С. Н. 5000 конкурсных задач по математике. – М.: ООО «Фирма «Издательство АСТ», 1999.
-
3000 конкурсных задач по математике. – 5-е изд., исПример. – М.: Айрис-пресс, 2003.
-
В.С. Крамор, К.Н. Лунгу. Повторяем и систематизируем школьный курс тригонометрии: Пособие для старшеклассников и абитуриентов. – М.: АРКТИ, 2001.
-
Шестаков С.А., Захаров П.И. ЕГЭ 2019. Математика. Уравнения и системы уравнений. Задача 13 (профильный уровень) / Под ред. И.В. Ященко. – М.: МЦНМО, 2019. [электронный вариант].
-
Азаров А. И. и др. Тригонометрия. Тождества, уравнения, неравенства, системы: Учеб. пособие/ А.И. Азаров, В.И. Булатов, В.С. Федосеенко, А.С. Шибут/ – Мн.: «Полымя», 1998.
-
Потапов М. К. Задачи по алгебре, тригонометрии и элементарным функциям / М.К. Потапов. – М.: Издательство «Экзамен», 2008.
-
Данилов А. М. Математика. Тригонометрия и геометрия: Учебное пособие / А.М. Данилов, Т.В. Куликова, Т.А. Мишанина; Под общ. ред. д-ра техн. наук, проф. А.М. Данилова. – Пенза: ПГАСА, 2003.
-
Прокофьев А. А., Корянов А. Г. Математика. Подготовка к ЕГЭ. Тригонометрические уравнения: методы решения и отбор корней (типовые задания С1). – Изд. 2-е, доп. – Ростов-на-Дону: Легион, 2014.
-
Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия. – 5-е изд., стереотип. — М.: МЦНМО, 2014. [электронный вариант].
-
Балаян Э. Н. Математика. ЕГЭ. Задачи типа С1 / Э.Н. Балаян. – Ростов н/Д: Феникс, 2013. [электронный вариант].
-
Крамор В.С., Михайлов П. А. Тригонометрические функции: (Система упражнений для самостоят. изучения). Пособие для учащихся. – 2-е изд., доп. – М: Просвещение, 1983.
-
А.И. Худобин, И.И. Худобин. Сборник задач по тригонометрии. Пособие для учителей. Изд. 2-е. – М.: Государственное учебно-педагогическое издательство Министерства просвещения РСФСР, 1955.
-
Просветов Г. И. Тригонометрия: задачи и решения: Учебно-практическое пособие. – М.: Издательство «Альфа-Пресс», 2010.
-
Севрюков П.Ф. Тригонометрические, показательные и логарифмические уравнения и неравенства: учебное пособие / П.Ф. Севрюков, А.Н. Смоляков. – М: Илекса; Народное образование; Ставрополь: Сервисшкола, 2008. [электронный вариант].
Использованные интернет-источники:
1. https://youclever.org/book/trigonometricheskie-uravneniya-1/
2. https://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskie-uravneniya/
3. http://cos-cos.ru/math/93/
4.https://www.yaklass.ru/p/algebra/10-klass/trigonometricheskie-uravneniia-9145/metody-ispolzuemye-dlia-resheniia-trigonometricheskikh-uravnenii-9134/re-995e0a3e-90bc-4e3a-b784-3f48ab285dde
5. https://www.resolventa.ru/index.php/trigonometricheskie-uravnenija
6. https://resh.edu.ru/subject/lesson/6320/conspect/200019/
7. https://dl.bsu.by/mod/book/view.php?id=10177&chapterid=1270
8. https://shkolkovo.net/catalog/reshenie_uravnenij_2/trigonometricheskie
9. https://mat.1sept.ru/view_article.php?ID=200301001
10. http://egesdam.ru/page310.php
11. http://egesdam.ru/page311.php
Приложение
Практикум по теме «Решение тригонометрических уравнений»




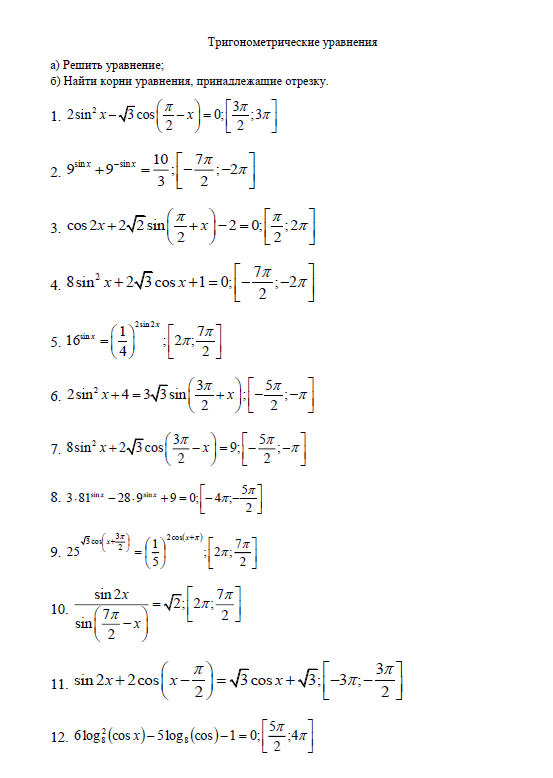
Тригонометрия в ЕГЭ
Задания открытого банка задач
1. Найдите значение выражения
Решение.
Использована формула: sin 2 t = 2sin t · cos t
2. Найдите значение выражения
Решение.
Использована формула: сos 2 t = cos 2 t – sin 2 t
Задания открытого банка задач
3. Найдите значение выражения
Решение.
Использована формула приведения: cos ( 90º – t) = sin t
4. Найдите значение выражения
Решение.
Использована таблица значений тригонометрических функций.
Задания открытого банка задач
5. Найдите значение выражения
Решение.
Использованы формулы приведения:
sin ( 90º + t) = cos t и sin ( 270º − t) = − cos t
6. Найдите значение выражения
Решение.
Использованы:
а) формулы приведения: tg ( 90º + t) = − ctg t и tg ( 180º + t) = tg t
б) тождество: tg t · ctg t = 1 .
Задания открытого банка задач
7. Найдите значение выражения
Решение.
Использованы:
а) формулы приведения:
sin ( 90º + t) = cos t и sin ( 180º + t) = − sin t
sin 2 ( 180º + t) = ( − sin t) 2 = sin 2 t
б) тождество: sin 2 t + cos 2 t = 1 .
Задания открытого банка задач
8. Найдите tg t, если
Решение.
sin t
Использованы тождества: sin 2 t + cos 2 t = 1 и tg t = .
cos t
Задания открытого банка задач
9. Найдите − 20cos 2t, если sin t = − 0,8
Решение.
Использована формула: сos 2 t = 1 – 2sin 2 t
10. Найдите , если sin 2t = − 0,7.
Решение.
Использована формула: sin 2 t = 2sin t cos t
Задания открытого банка задач
11. Найдите tg 2 t, если 5sin 2 t + 12cos 2 t = 6.
Решение.
1
Использовано тождество: tg 2 t + 1 = .
cos 2 t
Задания открытого банка задач
12. Найдите если tg t = 5.
Решение.
sin t
Использовано тождество: tg t = .
cos t
Задания открытого банка задач
13. Найдите tg t, если
Решение.
sin t
Использовано тождество: tg t = .
cos t
Задания открытого банка задач
14. Найдите значение выражения
Решение.
Использованы:
а) формула sin 2t = 2sin t · cos t
б) свойство периодичности функции sin t:
sin (2πn ± t) = ± sin t , где n ∈ Z
в) свойство нечетности функции sin t: sin ( − t) = − sin t
г) таблица значений тригонометрических функций .
Задания открытого банка задач
15. Найдите значение выражения
Решение.
Использованы:
а) формула cos 2t = cos 2 t – sin 2 t .
б) свойство периодичности функции cos t:
cos (2πn ± t) = cos t , где n ∈ Z
в) таблица значений тригонометрических функций .

























































































































































































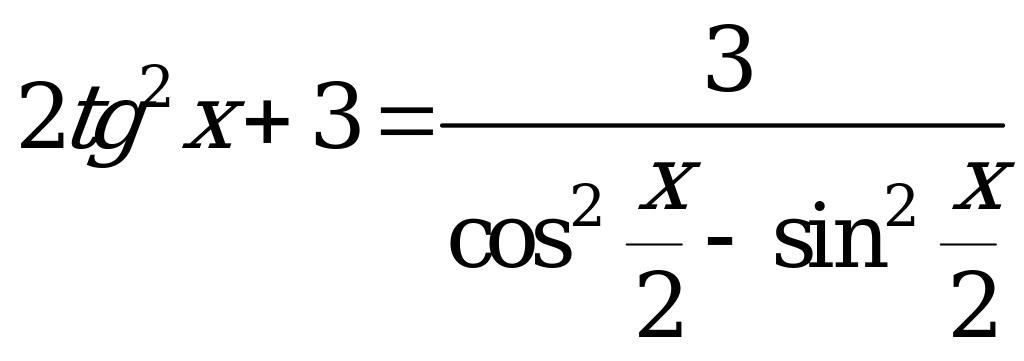 , принадлежащих отрезку
, принадлежащих отрезку