24
ПРОЕКТ
«Решение текстовых задач»
Исполнитель Манина Раиса Михайловна
Учитель МБОУ «Анциферовская ООШ»
Орехово-Зуевского района
Оглавление
страницы
1. Введение. 3
1) Актуальность проблемы. 3
2) Задачи проекта. 3
3) Цели решения текстовых задач. 3.
2. Основная часть. 4
1) Арифметический метод решения задач. 4
2) Алгебраический метод решения задач. 7
3) Комбинированный метод решения задач. 9
4) Текстовые задачи в учебниках алгебры 9 класса. 9
5) Алгоритм и приемы решения задач. 10
6) Примеры решения задач 11
7) Сложности при решении задач и пути их преодоления. 17
3. Заключение. 20
1) Советы по организации деятельности учащихся при решении задач.
2) Выводы. 21
4. Список литературы 22
Решение текстовых задач.
1. Введение.
Одним из важных вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.
Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности учащихся. Наблюдается активизация их мыслительной работы, формируется умение проводить исследование. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, абстрактное мышление, умение применять теорию к решению конкретных задач и закрепление на практике приобретённых умений и навыков.
Текстовые задачи входят в ГИА и ЕГЭ, являются традиционным разделом на вступительных экзаменах в Вузы. Таким образом, данная тема имеет важнейшее значение в обучении математике.
Задачи проекта:
-
Проведение теоретического анализа различных подходов к решению задач в современной науке.
-
Обобщение различных приемов решения текстовых задач.
-
Обобщение методики решения задач на движение, работу, проценты, смеси, сплавы и т.д.
-
Определение сложностей, которые испытывают учащиеся при решении текстовых задач, и пути их решения.
Основные цели решения текстовых задач в школьном курсе математики:
-
научить переводить реальные предметные ситуации в различные математические модели,
-
обеспечить действенное усвоение учащимися основных методов и приемов решения учебных математических задач.
2. Основная часть.
Текстовые задачи включены в учебники математики 5-11 классов, за период обучения школьники решают около 500 различных задач.
Для решения текстовых задач применяются три основных метода: арифметический, алгебраический и комбинированный. Рассмотрим каждый из этих методов.
I. Арифметический метод.
Первым этапом решения задач арифметическим методом является разбор условия задачи и составление плана её решения. Этот этап решения задачи сопровождается максимальной мыслительной деятельностью.
Вторым этапом является решение задачи по составленному плану. Этот этап решения проводится учащимися без особых затруднений и в большинстве случаев носит тренировочный характер.
Третьим важным этапом решения задачи является проверка решения задачи. Она проводится по условию задачи. Пренебрежение проверкой при решении задачи, замена её проверкой ответов снижает роль решения задачи в процессе развития логического мышления учащихся.
При решении текстовых задач арифметическим методом у учащихся вырабатываются определённые умения и навыки, которые в процессе дальнейшего обучения должны совершенствоваться и закрепляться.
При арифметическом методе решения задач формируются 56 основных умений и навыков. Из них 38 умений и навыков приобретаются при решении задач как арифметическим, так и алгебраическим методами.
К ним относятся следующие умения и навыки:
-
Краткая запись условия задачи.
-
Изображение условия задачи с помощью рисунка.
-
Логические приёмы мышления: наблюдение и сравнение, анализ и синтез, абстрагирование и конкретизация, обобщение и ограничение, умозаключения индуктивного и дедуктивного характера и умозаключения по аналогии.
-
Выполнение арифметических действий над величинами (числами).
-
Изменение (увеличение или уменьшение) величины (числа) в несколько раз.
-
Нахождение разностного сравнения величин (чисел).
-
Нахождение кратного сравнения величин (чисел).
-
Использование свойств изменения результатов действий в зависимости от изменения компонентов.
-
Изменение (увеличение или уменьшение) величины (числа) на несколько единиц величины (числа).
-
Нахождение дроби от величины (числа).
-
Нахождение величины (числа) по данной её (его) дроби.
-
Нахождение процентов данной величины (данного числа).
-
Нахождение величины (числа) по её (его) проценту.
-
Нахождение процентного отношения двух величин (чисел).
-
Составление пропорций.
-
Понятие прямой и обратной пропорциональной зависимости величин (чисел).
-
Понятие производительности труда.
-
Определение производительности труда при совместной работе.
-
Определение части работы, выполненной в течение некоторого промежутка времени.
-
Определение скорости движения.
-
Определение пути, пройденного телом.
-
Определение времени движения тела.
-
Понятие о собственной скорости (скорости в стоячей воде) движения тела по воде.
-
Нахождение пути, пройденного двумя телами при встречном движении.
-
Нахождение скорости движения тела по течению и против течения реки.
-
Нахождение времени прохождения телом единицы пути при заданной скорости движения.
-
Нахождение скорости сближения тел, движущихся в одном направлении, и скорости удаления.
-
Нахождение скорости сближения или скорости удаления тел, движущихся в противоположных направлениях или при встречном движении.
-
Нахождение части пути, пройденного телом за определённое время, когда известно время прохождения всего пути.
-
Нахождение количества вещества, содержащегося в растворе, смеси, сплаве.
-
Нахождение концентрации, процентного содержания.
-
Нахождение стоимости товара, акции.
-
Нахождение цены товара, акции.
-
Нахождение прибыли.
-
Нахождение количества вредных веществ в воде, воздухе.
-
Нахождение себестоимости продукции.
-
Расчёт начислений банка на вклады.
-
Проверка решения задачи по условию.
Умения и навыки, которые формируются в процессе решения задач только арифметическим методом, можно разбить на две группы. К первой группе относятся умения и навыки, которые необходимы для дальнейшего изучения математики.
К первой группе относятся следующие умения и навыки:
-
Перевод календарного времени в арифметическое число.
-
Перевод арифметического числа в календарное время.
-
Нахождение времени предыдущего события.
-
Нахождение времени последующего события.
-
Нахождение промежутка времени между двумя событиями.
Все умения и навыки этой группы формируются в процессе решения задач на вычисление времени, т.е. тех задач, которые нет смысла решать алгебраически.
Вторая группа – это те умения и навыки, без знания которых можно решить все текстовые задачи алгебраическим методом, и в дальнейшем их незнание не будет пробелом в математическом образовании учащихся.
Ко второй группе относятся следующие умения и навыки:
-
Введение понятия «часть».
-
Выполнение действий сложения и вычитания частей.
-
Выполнение умножения и деления части на число.
-
Приём уравнивания большего числа с меньшим и меньшего с большим.
-
Приём уравнивания прибавлением к меньшему числу и вычитанием из большего числа их полуразности.
-
Определение числа частей, составляющих данное число.
-
Введение понятий условной единицы.
-
Нахождение дроби условной единицы и её частей.
-
Сравнение частей величин.
-
Сложение и вычитание частей единицы.
-
Метод исключения неизвестного посредством замены одной величины другой.
-
Решение задач методом предположения.
-
Составление плана решения задачи.
Эти умения и навыки, несомненно, представляют интерес. Но почти все из них можно отнести к числу умений и навыков, формирующихся у учащихся при решении нестандартных задач. Решение таких задач следует проводить систематически наряду с решением стандартных текстовых задач.
II. Алгебраический метод.
Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или системы неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.
При решении задач алгебраическим методом основная мыслительная деятельность сосредотачивается на первом этапе решения задачи: на разборе условия задачи при составлении уравнений или неравенств по условию задачи.
Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств.
Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.
При алгебраическом методе решения формируются 55 основных умений и навыков.
Отличными от тех, которые формируются при арифметическом их решении, являются следующие:
-
Введение неизвестного.
-
Введение двух неизвестных.
-
Введение трёх и более неизвестных.
-
Выполнение действий сложения и вычитания неизвестных.
-
Выполнение действий умножения и деления неизвестных.
-
Запись зависимости между величинами с помощью букв и чисел.
-
Решение линейных уравнений.
-
Решение линейных неравенств.
-
Решение квадратных уравнений и неравенств.
-
Решение дробно-рациональных уравнений и неравенств.
-
Решение систем уравнений и систем неравенств.
-
Составление одного уравнения (неравенства) с двумя неизвестными.
-
Решение уравнения (неравенства) с двумя неизвестными.
-
Выбор значений неизвестных по условию задачи.
-
Составление уравнений с параметром по условию текстовой задачи.
-
Решение уравнений с параметром.
-
Исследовательская работа.
В связи с внедрением в школьную программу элементов высшей математики, с ускоренным развитием и внедрением во все сферы вычислительной математики большое значение имеет формирование у учащихся не отдельных специфических навыков, а тех умений и навыков, которые имеют дальнейшее приложение. К числу этих умений и навыков относятся умения и навыки, которые формируются в процессе решения задач алгебраическим методом.
III. Комбинированный метод.
Этот метод получается в результате включения в алгебраический метод решения задач решение, в котором часть неизвестных величин определяется с помощью решения уравнения или системы уравнений, неравенств или систем неравенств, а другая часть – арифметическим методом. В этом случае решение текстовых задач значительно упрощается.
Текстовые задачи в различных учебниках алгебры 9 класса
|
Учебники |
Текстовые задачи |
На работу |
Движение по окружности |
Смеси, сплавы |
Раздел «Для внекл. работы» |
|
Макарычев Ю.Н. |
65 |
15 |
— |
— |
|
|
Алимов Ш.А. |
55 |
7 |
— |
2 |
20 |
|
Мордкович А.Г. |
73 |
14 |
1 |
3 |
Этапы решения текстовых задач:
Анализ содержания задачи.
-
Поиск пути решения задачи и составление плана ее решения.
-
Осуществление плана решения задачи.
-
Проверка решения задач и исследование.
Алгоритм решения задач.
-
Обозначим неизвестную величину через х.
-
Выразим через нее другие величины.
-
Найдем зависимость между ними и на основании ее составим уравнение.
-
Решим уравнение.
-
Найдем ответ на вопрос задачи, выполнив отбор решений по смыслу задачи.
-
Проверим правильность решения задачи. Запишем ответ.
Приемы, используемые на этапе «Анализ задачи»
-
представление той жизненной ситуации, которая описана в задаче. Цель такого воспроизведения — выявление основных количественных и качественных характеристик ситуации, представленной в задаче.
-
постановка специальных вопросов и поиск ответов на них — включает следующий «стандартный» набор вопросов, ответы на которые позволяют детально разобраться в содержании задачи: О чем говорится в задаче? Что известно в задаче? Что требуется найти в задаче? Что в задаче неизвестно? и др.
-
переформулировка текста задачи — состоит в замене данного в задаче описания некоторой ситуации другим описанием, сохраняющим все отношения, связи, но более явно их выражающим. При необходимости строится вспомогательная модель задачи: краткая запись условия, таблица, рисунок, чертеж и т.п.
-
моделирование ситуации, описанной в задаче, с помощью реальных предметов, предметных моделей или графических моделей.
Приемы, используемые на этапе «Поиск пути решения задачи и составление плана ее решения».
-
анализ задачи по тексту или по ее вспомогательной модели;
-
от вопроса задачи к данным (аналитический путь) или от данных к вопросу (синтетический путь);
-
комбинированный (анализ и синтез), анализ часто производят «про себя»;
-
разбиение задачи на смысловые части; введение подходящих обозначений в том случае, когда данные (или искомые) в задаче не обозначены
Практическая часть.
Задача 1. Ваня, Петя и Сережа пошли на рыбалку и поймали вместе 51 рыбку. Ваня поймал рыбок в 2 раза больше, чем Петя, а Сережа на 3 рыбки больше, чем Петя. Сколько рыбок поймал каждый мальчик?
Ваня — ?, в 2 раза больше
Петя — ? р.
Сережа — ?, на 3 р. больше
Пусть
|
Ваня |
2х рыбок |
|
Петя |
Х рыбок |
|
Сережа |
(х + 3) рыбок |
|
Всего |
51 рыбка |
х + 2х + х +3 =51.
х = 12.
Следовательно,
Петя поймал 12 рыбок,
Ваня 24 рыбки,
Сережа 15 рыбок.
Задача 2. Пристани А и В расположены на реке, причем В – на 80 км ниже по течению, чем А. Катер прошел путь из А в В и обратно за 8 ч 20 мин. За какое время катер прошел расстояние от А до В и расстояние от В до А, если известно, что скорость в стоячей воде равна 20 км/ч?
Р е ш е н и е.
Первый этап.
Составление математической модели.
Пусть х км/ч – скорость течения реки.
Получим уравнение
80: (20+х )+ 80:(20-х) = 81/3 .
Второй этап. Работа с составленной моделью.
Решив уравнение, находим х = 4.
Третий этап. Ответ на вопрос задачи.
t = 3 ч, t = 5 ч.
Задача 3. Двое рабочих выполнили вместе некоторую работу за 12 ч. Если бы сначала первый рабочий сделал половину этой работы, а затем другой остальную часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить эту работу каждый рабочий в отдельности? Р е ш е н и е.
Р е ш е н и е.
Первый этап. Составление математической модели.
Примем всю работу за 1.
Производительность труда I рабочего x
, а II — y . За 12 ч, работая отдельно, I
рабочий выполнит 12/x всей работы, а II рабочий — 12/y
всей работы, т.е. 12/x+12/y = 1
12/x + 12/y = 1,
0,5x +0,5y = 25; находим решение: х = 20, у = 30 .
Третий этап. Ответ на вопрос задачи. 20 ч и 30 ч.
Задача 4. Сплав меди и цинка содержал 82 % меди. После добавления в сплав 18 кг цинка процентное содержание меди в сплаве понизилось до 70%. Сколько меди и сколько цинка было первоначально? Р е ш е н и е.
Первый этап. Составление математической модели.
Пусть первоначальная масса сплава х кг.
Расчет ведем по меди, масса меди в сплаве остается неизменной. Получим уравнение
0,82х= 0,7(х+18). Корень уравнения
х =105.
Тогда меди в первоначальном сплаве 86,1 кг,
цинка – 18,9 кг.
Задача5. Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого.
Решение (черновик).
Отвечаем на вопросы, поэтапно составляя таблицу.
1. Речь идёт о процессе движения, которое характеризуется тремя величинами: расстояние, скорость, время (3 столбца таблицы).
2. В задаче 3 процесса: движение скорого, пассажирского и товарного поездов (3 строчки таблицы).
Можно составить “скелет” таблицы.
|
Величины Процессы |
Расстояние (км) |
Скорость (км/ч) |
Время (ч) |
|
Скорый поезд |
с |
с |
с |
|
Пассажирский поезд |
с |
с |
с |
|
Товарный поезд |
с |
с |
с |
3. Заполняем таблицу в соответствии с условиями задачи
4. Вводим неизвестные величины: x, км/ч – скорость товарного поезда, y, ч – время движения скорого поезда.
5. Составим “модель”.
(x+50)y = 8/5 x(y+1)
8/5 x(y+1) = x(y+4)
6. Решаем эту систему. Из первого уравнения находим у. Из второго уравнения находим х.
Решение задачи (чистовик).
Пусть х, км/ч – скорость товарного поезда (х0), у, ч – время движения скорого поезда (у0).
Составляем таблицу.
|
Величины Процессы |
Расстояние (км) |
Скорость (км/ч) |
Время (ч) |
|
Скорый поезд |
(х+50)у |
х+50 ? |
у |
|
Пассажирский поезд |
8/5 х(у+1) |
8/5 х |
у+1 |
|
Товарный поезд |
х(у+4) |
х ? |
у+4 |
По условию задачи поезда прошли одно и то же расстояние. Получаем систему уравнений
8/5 х(у+1) = х(у+4)
(х+50)у = х(у+4).
По условию задачи х0, тогда
8(у+1) = 5(у+4)
(х+50)у = х(у+4),
3у = 12
(х+50)у = х(у+4),
у = 4
х+50 = 2х,
у = 4
х = 50.
Полученные значения неизвестных удовлетворяют условию х0, у0, значит удовлетворяют условию задачи.
50 км/ч – скорость товарного поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
Проверка по условию задачи.
50 км/ч – скорость товарного поезда,
4+4 = 8 (ч) – время движения товарного поезда.
50*8 = 400 (км) – расстояние, которое прошёл товарный поезд.
50*8/5 = 80 (км/ч) – скорость пассажирского поезда.
4+1 = 5 (ч) – время движения пассажирского поезда.
80*5 = 400 (км) – расстояние, которое прошёл пассажирский поезд.
4 ч – время движения скорого поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
100*4 = 400 (км) – расстояние, которое прошёл скорый поезд.
Каждый поезд прошёл одно и то же расстояние.
Задача решена верно.
Ответ: 50 км/ч, 100 км/ч.
Аналогично можно решать задачи “на работу”, “наполнение бассейна”.
В результате проведенной работы были выявлены проблемы и способы их решения для достижения практического эффекта.
Сложности при решении текстовых задач и
пути их решения.
|
|
|
непонимание физических, химических, экономических терминов, законов, |
Тщательно изучить и правильно истолковать содержание задачи, выразив искомые величины через известные величины и введенные переменные. Не зацикливаться на периодичности маршрута при движении по окружности, а мыслить только в категориях время, путь, скорость. |
|
непонимание связи между расстоянием, скоростью и временем при равномерном движении или между работой, производительностью труда и временем и т.п.зависимости |
|
|
затруднения в определении скорости сближения объектов при движении навстречу, в одном направлении или при движении по окружности |
|
|
2. Составление уравнений и неравенств, связывающих данные величины и переменные, которые вводят учащиеся |
|
|
неправильный выбор величин, относительно которых составляется уравнение |
Важно правильно выбрать величины, относительно которых будет составлено уравнение. Неправильный выбор делает процесс составления уравнения более сложным. |
|
усложнение процесса составления уравнения из-за неправильного выбора величин |
|
|
3. Нахождение соответствия между различными величинами, применительно к которым формулируется вопрос задачи. |
|
|
невозможность нахождения значения переменных, которые в уравнениях присутствуют и не являются необходимыми |
держать в поле зрения основную цель, не боясь вводить столько вспомогательных переменных, сколько их понадобится по ходу решения. Совсем необязательно ставить в качестве непременного условия сведение числа неизвестных к минимуму. |
|
большое количество неизвестных, нахождение значения которых не являются необходимыми |
|
|
4. Решение уравнений, системы уравнений или невозможность решения уравнения, неравенства. |
|
|
Невозможно решения уравнения, неравенства или их системы |
Решение полученной системы уравнений или неравенств желательно наиболее рациональным методом. |
|
решение уравнения, неравенства или их системы нерациональным способом или их системы |
3. Заключение.
При решении текстовых задач учащимся могут помочь несколько простых и общих советов.
Совет 1. Не просто прочитайте, а тщательно изучите условие задачи. Попытайтесь полученную информацию представить в другом виде – это может быть рисунок, таблица или просто краткая запись условия задачи.
Совет 2. Выбор неизвестных.
В задачах «на движение» – это обычно скорость, время, путь. В задачах “на работу” — производительность и т.д.
Не надо бояться большого количества неизвестных или уравнений. Главное, чтобы они соответствовали условию задачи и можно было составить соответствующую “математическую модель” (уравнение, неравенство, система уравнений или неравенств).
Совет 3. Составление и решение “математической модели”.
При составлении “математической модели” (уравнения, неравенства, системы уравнений или неравенств) ещё раз внимательно прочитайте условие задачи. Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый “знак” полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).
Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить составленное.
Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и полученную запись).
Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации. Например, не x и y, а x+y, x/y, 1/x и т.п.
Если кажется, что получилось правильное, но очень сложное выражение, то попробуйте ввести другие неизвестные, может быть, изменив их количество, чтобы получилась более простая модель.
Иногда неизвестные в задачах выражаются только целыми числами, тогда при решении задач нужно использовать свойства целых чисел.
Совет 4. Решение сложной текстовой задачи – процесс творческий. Иной раз требуется вернуться к самому началу задачи, учитывая и анализируя уже полученные результаты.
При решении задач короткую запись задачи можно сделать с помощью рисунка или таблицы.
Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.
Можно выделить семь вопросов, которые дают верное направление решению задач разных типов.
Вопросы к задаче с комментариями к ним:
-
О каком процессе идёт речь? Какими величинами характеризуется этот процесс? (Количество величин соответствует числу столбцов таблицы).
-
Сколько процессов в задаче? (Количество процессов соответствует числу строк в таблице).
-
Какие величины известны? Что надо найти? (Таблица заполняется данными задачи; ставится знак вопроса).
-
Как связаны величины в задаче? (Вписать основные формулы, выяснить связи и соотношения величин в таблице).
-
Какую величину (величины) удобно выбрать в качестве неизвестной или неизвестных? (Клетки в таблице заполняются в соответствии с выбранными неизвестными).
-
Какие условия используются для составления “модели”? (Выписать полученную “модель”)
-
Легко ли решить полученное? (Если решить сложно, ввести новые переменные, использовать другие соотношения).
Выводы:
-
Для того, чтобы научиться решать задачи, надо приобрести опыт их решения путем многократного повторения операций, действий, составляющих предмет изучения.
-
Редкие ученики самостоятельно приобретают такой опыт. Долг учителя — помочь учащимся приобрести опыт решения задач, научить их решать задачи.
-
Помощь учителя не должна быть чрезмерной, но и не быть слишком малой.
-
Навыки решения текстовых задач формируются на основе осмысленных знаний и умений.
-
Для формирования навыков нужна тщательно продуманная система упражнений и задач «от простого к сложному».
-
Знания учащихся по математике должны совершенствоваться с решением каждой новой задачи.
-
Следует добиваться, чтобы осознанные умения и навыки ученики получали при наименьших затратах времени.
-
Следует учитывать индивидуальные особенности и возможности учащихся.
Список литературы:
1. Алимов.- ,Алгебра 9класс , Москва, Просвещение, 2009
2. Ерина Т.М. Алгебра. Текстовые задачи — Москва, МГТУ «МАМИ»,2004
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.-,Алгебра 9класс ,Москва, Просвещение, 2009
4. Методика преподавания математики в средней школе: общая методика А.Я.Блох и другие, Москва, Просвещение, 1985.
5. Мордкович А.Г. -.Алгебра 9класс, Москва, Мнемозина, 2009
6. Примерные программы по учебным предметам. Математика .5 -9 классы проект- Москва, Просвещение, 2010 (Стандарты второго поколения)
7.Турецкий Е.Н., Фридман Л.М. -Как научиться решать задачи, Москва, Просвещение, 1989
8.Решение текстовых задач. http://school-collection.edu.ru/catalog/res/d92c7ae3-a9f1-4ff3-afb0-e1f1783fee48/?from=8f5d7210-86a6-11da-a72b-0800200c9a66&.
9. Презентационные подходы в решении текстовых задач. http://school-collection. edu.ru/.
Слайд 1
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА Решение типовых задач ЕГЭ по математике (В13) Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа№40» Подготовил: Сазонов Владимир, 10 «В» Старый Оскол, 2013 Решение типовых задач ЕГЭ по математике (В13) Решение типовых задач ЕГЭ по математике (В13)
Слайд 2
О работе; Способы решения задач; Разбор решённых задач: а) «3адачи на движение» б) «Задачи на сплавы» в) «Задачи на проценты» г) «Задачи на работу» Самостоятельная работа; Вывод; Источники материала. План работы
Слайд 3
В данной исследовательской работе мы будем рассматривать способы решения текстовых задач, которые встречаются в экзаменационных работах, в Едином Государственном Экзамене, а также в Государственной Итоговой Аттестации. В работе будут рассмотрены задачи на движение, задачи на сплавы, задачи на работу, задачи на проценты. О работе
Слайд 4
Рассмотрим методы решения задач на движение. Данные задачи решаются по формуле: S = v * t, где S – расстояние, v – скорость, а t – время. Решения задач на работу также сводятся к единственной формуле: А = p * t, где А – работа, p – производительность, а t – время. Если объём работы в задаче не важен, то его следует принять за 1. Если в работе участвуют несколько рабочих, то их производительности складываются . Способы решения задач
Слайд 5
Способы решения задач
Слайд 6
Способы решения задач В процессе решения задач на сплавы, встречаются такие понятия, как «абсолютное содержание веществ в смеси» и «относительное содержание веществ в смеси». Абсолютное содержание веществ в смеси – это количество вещества, выраженное в единицах измерения СИ. Относительное содержание веществ в смеси – это отношение абсолютного содержания к общей массе или объёму смеси. Абсолютное содержание веществ в смеси является равным относительному содержанию веществ в смеси.
Слайд 7
Задачи на движение
Слайд 8
№1 . Из пунктов A и B одновременно выехали навстречу друг другу два автомобиля. Первый автомобиль двигался в 2 раза быстрее второго и приехал в пункт B на 1 час раньше, чем второй приехал в пункт A. На сколько минут раньше встретились бы автомобили, если бы скорость второго автомобиля была равна скорости первого?
Слайд 9
Ход решения Для решения данной задачи нам потребуется составить таблицу. В неё мы, читая условие, будем записывать элементы уравнения. Скорость Время Расстояние Автомобиль №1 Автомобиль №2
Слайд 10
Ход решения Пусть х км/ч скорость второго автомобиля. По условию, скорость первого автомобиля в два раза больше скорости второго автомобиля, значит, скорость второго автомобиля равна 2х км/ч. Очевидно, что автомобили проехали одинаковое расстояние, значит его мы можем обозначить за 1. Занесём данные в таблицу: Скорость Время Расстояние Автомобиль №1 2х км/ч 1 Автомобиль №2 x км/ч 1
Слайд 11
Ход решения Скорость Время Расстояние Автомобиль №1 2х 1 Автомобиль №2 х 1
Слайд 12
Ход решения
Слайд 13
Ход решения
Слайд 14
№2. Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч.
Слайд 15
Составляем таблицу: Скорость Время движения Расстояние По течению Против течения Ход решения
Слайд 16
Пусть х км/ч скорость лодки в стоячей воде. Тогда скорость лодки по течению равна х+1 км/ч, а против течения равна х-1 км/ч. По условию задачи, расстояние в обе стороны равно 255 км. Также известно, что обратный путь на 2 часа меньше. Скорость Время движения Расстояние По течению х+1 км/ч 255 км Против течения х-1 км/ч 255 км Ход решения
Слайд 17
Ход решения
Слайд 18
Задачи на сплавы
Слайд 19
№1. Содержание меди в первом сплаве — 10%, содержание меди во втором сплаве — 40%. Второй сплав весит на 3 кг больше первого. Сплавив первые два сплава, получили третий сплав, содержание меди в котором оказалось 30%. Вычислите массу третьего сплава. Запишите ответ в килограммах.
Слайд 20
Итак, в задаче рассматриваются три вещества: первый сплав, второй сплав и третий сплав, состоящий из первых двух. Составляем таблицу: Концентрация Масса сплава Масса вещества 1-й сплав 2-й сплав 3-й сплав Ход решения
Слайд 21
Анализируя условие задачи, заполняем таблицу известными данными: Концентрация Масса сплава Масса вещества 1-й сплав 10%=0,1 2-й сплав 40%=0,4 На 3 кг больше 3-й сплав 30%=0,3 Ход решения
Слайд 22
Пусть х кг — масса первого сплава. Тогда масса второго сплава равна (х+3) кг. Чтобы найти массу меди, нужно массу сплава умножить на соответствующую концентрацию. Тогда масса меди в первом сплаве равна 0,1х кг, а во втором- (х+3)*0,4 кг. Масса общего сплава будет равна сумме масс первых двух сплавов, а именно: х+(х+3)=2х+3 кг. Масса меди в третьем сплаве будет равна: 0,1х+ +0,4(х+3)= 0,5х+12 кг. Занесём это в таблицу: Концентрация Масса сплава Масса вещества 1-й сплав 10%=0,1 x кг 0,1x кг 2-й сплав 40%=0,4 x+3 кг 0,4(x+3) кг 3-й сплав 30%=0,3 2x+3 кг 0,5x+12 кг Ход решения
Слайд 23
Ход решения
Слайд 24
№2. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора того же вещества. Сколько процентов составляет концентрация полученного раствора?
Слайд 25
Составим таблицу: Объём Объём чистого вещества Раствор №1 4 л 0,15 * 4 = 0,6 л Раствор №2 6 л 0,25 * 6 = 1,5 л Раствор №3 Ход решения
Слайд 26
Т.к. нам не известны масса раствора и масса чистого вещества в данном растворе, то примем за х общую массу, а массу основного вещества за у. Масса Масса чистого вещества Раствор №1 4 л 0,15 * 4 = 0,6 л Раствор №2 6 л 0,25 * 6 = 1,5 л Раствор №3 x л y л Ход решения
Слайд 27
Ход решения
Слайд 28
Задачи на проценты
Слайд 29
№1. В среду акции поднялись в цене на некоторое количество процентов, а в четверг — упали в цене не то же самое количество процентов. В результате они оказались на 4% дешевле изначальной стоимости. На сколько процентов подешевели акции в четверг?
Слайд 30
Как и в решении предыдущих задач, составим таблицу: Было Изменение Стало Среда Четверг Ход решения
Слайд 31
Было Изменение Стало Среда 1 +х % Четверг Ход решения
Слайд 32
Было Изменение Стало Среда 1 +х % Четверг -х% 0,96 Ход решения
Слайд 33
Ход решения
Слайд 34
№2. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рубля.
Слайд 35
Ход решения
Слайд 36
Задачи на «работу»
Слайд 37
№ 1. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Слайд 38
Составим таблицу: Производительность Время Работа Рабочий №1 Рабочий №2 Ход решения
Слайд 39
Пусть х деталей в час производительность второго рабочего, тогда производительность первого рабочего равна х+1 деталей в час. По условию задачи, по заказу всего 110 деталей. Также нам известно, что первый рабочий выполняет заказ на 1 час быстрее, чем второй рабочий. Производительность Время Работа Рабочий №1 х+1 деталей в час 110 деталей Рабочий №2 x деталей в час 110 деталей Ход решения
Слайд 40
Ход решения
Слайд 41
№4. Машинистка собралась напечатать на компьютере 300 страниц текста. Если бы она печатала на 5 страниц в день больше, чем запланировала, то смогла бы завершить работу на 3 дня раньше. Какое количество страниц в день запланировала печатать машинистка?
Слайд 42
Составим таблицу: Скорость работы Время работы Общая работа Планировала В реальности Ход решения
Слайд 43
По условию задачи, скорость работы машинистки в реальности на 5 страниц в день больше, чем она планировала. Если бы она соблюдала данную скорость, то она бы закончила работу на 3 дня раньше. Объём работы – 300 страниц. Скорость работы Время работы Общая работа Планировала 300 В реальности На 5 страниц больше На 3 дня меньше 300 Ход решения
Слайд 44
Скорость работы Время работы Общая работа Планировала x страниц в день 300 страниц В реальности х+5 страниц в день 300 страниц Ход решения
Слайд 45
Ход решения
Слайд 46
САМОСТОЯТЕЛЬНАЯ РАБОТА
Слайд 47
Задания для самостоятельной работы №1. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Ответ: 50. №2. В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 7%, а в 2010 году — на 8% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году? Ответ: 46224. №3. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня? Ответ: 20. №4. Баржа в 10:00 вышла из пункта А в пункт В , расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт А в 16:00. Определите скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч. Ответ: 2.
Слайд 48
Таким образом, мы выяснили, что при решении подобных текстовых задач гораздо удобнее использовать таблицы. Таблицы помогают более точно и быстро составить уравнение для решения задач. Вывод Источники материала www.uztest.ru – сайт для подготовки к ЕГЭ; www.ege-study.ru – сайт для подготовки к ЕГЭ; Сборник задач по математике с решениями для поступающих в вузы. Рывкин А.А., Ваховский Е.Б.; Сборник задач по математике для поступающих в вузы под редакцией М.И.Сканави.
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 9 с. НИНЫ
СОВЕТСКОГО РАЙОНА» СТАВРОПОЛЬСКОГО КРАЯ
ПРОЕКТ
РАЗРАБОТКА ФАКУЛЬТАТИВНЕГО ЗАНЯТИЯ В 11 КЛАССЕ :
« РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ
ПРИ ПОДГОТОВКЕ К ЕГЭ ПО МАТЕМАТИКЕ»
Учитель математики :
Чемодурова Е.В.
2016 г. Одним из вопросов методики преподавания математики является вопрос
формирования у учащихся умений и навыков решения текстовых задач.
Задачи являются материалом для развития логического мышления,
формирования умений анализировать, для осуществления межпредметных связей на
уроках математики и факультативных занятий. Задачи позволяют применять знания,
полученные при изучении математики, при решении вопросов, которые возникают в
жизни человека. Этапы решения задач являются формами развития мыслительной
деятельности
Образовательное значение математических задач
Решая математическую задачу, ученик познает много нового: знакомится с новой
ситуацией, описанной в задаче, с применением математической теории к ее решению,
познает новый метод решения или новые теоретические разделы математики,
необходимые для решения задачи, т. е. приобретает математические знания, повышает
свое математическое образование
Практическое значение математических задач
При решении математических задач ученик обучается применять
математические знания к практическим нуждам, готовится к практической
деятельности в будущем, к решению задач, выдвигаемых практикой, повседневной
жизнью. Почти во всех конструкторских расчетах приходится решать математические
задачи, исходя из запросов практики. Исследование и описание процессов и их свойств
невозможно без привлечения математического аппарата, т. е. без решения
математических задач. Математические задачи решаются в физике, химии, биологии,
сопротивлении материалов, электро и радиотехнике, особенно в их теоретических
основах, и др.
Это означает, что при обучении математике учащимся следует предлагать задачи,
связанные со смежными дисциплинами (физикой, химией, географией и др.), а также
задачи с техническим и практическим, жизненным содержанием.
Формирование умений и навыков по решению практикоориентированных
Цели проекта
текстовых задач В11.
Формирование интереса к предмету, развитие математических способностей,
подготовка к ЕГЭ.
Расширение математических представлений о приемах и методах решения задач.
Развитие логического мышления и навыков исследовательской деятельности.
1.
2.
3.
4. Основные задачи проекта
1.Обеспечить подготовку к экзамену по математике в форме ЕГЭ.
2.Способствовать усвоению фактических знаний и умений.
3.Показать практическую значимость задач в сфере прикладного исследования.
4.Научить способам решения стандартных и нестандартных задач.
5.Углубить знания по математике, предусматривающие формирование устойчивого
интереса к предмету.
Факультативное занятие по теме: «Решение текстовых задач при подготовке
учащихся 11 класса к ЕГЭ по математике» (2 часа)
обучающие:
Цели занятия:
обучение приёмам математизации текста задачи (перевод содержания задачи на
математический язык, т.е. выражение искомой величины через известные
величины и введенные переменные);
научить применять эти знания при решении задач;
развивающие:
работать над развитием понятийного аппарата;
развивать навыки самоконтроля и логического мышления;
развивать память, речь, умение анализировать, сопоставлять, формулировать
выводы;
совершенствовать навыки решения задач.
воспитательные:
прививать учащимся интерес к предмету через совместную творческую работу;
формировать умение аккуратно и грамотно выполнять математические записи.
Оборудование: раздаточный материал, компьютер, экран.
Ход занятия:
Учитель: На сегодняшнем уроке мы с вами рассмотрим текстовые задачи задания В11
трех типов : на движение, совместную работу и концентрацию.
Некоторые задачи мы будем решать с вами вместе, решение некоторых будет
предложено для самостоятельного выполнения.
I. Решение задачи на движение (вместе с учителем)
Задача 1. Из пункта А в пункт B, расстояние между которыми 30 км, одновременно
выехали автомобилист и велосипедист. За час автомобилист проезжает на 40 км
больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он
прибыл в пункт B на 1 час позже автомобилиста. Ответ дайте в км/ч [3].
Решение:
Выражение Анализ условия
x
скорость велосипедиста, км/ ч x + 40
30
30
x
30
x+40
30
x − 30
скорость автомобилиста, км/ ч
расстояние между пунктами, км
время, затрачиваемое велосипедистом на дорогу от пункта А
до пункта В, ч
время, затрачиваемое автомобилистом на дорогу от пункта А
до пункта В, ч
x+40=1Велосипедист приехал в пункт В на час позже автомобилиста.
Итоговое уравнение
30
x − 30
x+40=1;30∙(x+40)
x∙(x+40)
− 30∙x
x∙(x+40)
=1;
30x+1200−30x
x2+40x
=1;30x+1200−30x=x2+40x;
x2+40x−1200=0
D=(40)2−4∙1∙(−1200)=1600+4800=6400
D>0−уравнениеимеет2корня
x1=−40+80
2
=20×2=−40−80
2
=−60
x=20(км
ч)−скоростьвелосипелиста.
x2−постороннийкорень
ОТВЕТ: 20 км/ч.
За доски вызываются двое учащихся. Им предлагается самостоятельно сделать
краткий анализ условия предложенных учителем задач и составить к ним уравнения .
Класс в это время работает самостоятельно, потом проводится сверка правильности
составленных уравнений, корректировка по мере необходимости, самостоятельное
решение этих уравнений и проверка решения.
Текст задач для учащихся. 1. Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали
автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км
больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он
прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч
2. Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А.
Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в
18:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что
скорость течения реки 1 км/ч.
II. Решение задач на концентрацию (вместе с учителем)
Задача 2. Сколько килограммов воды нужно добавить в сосуд, содержащий 200г. 70%
го раствора уксусной кислоты, чтобы получить 8% раствор уксусной кислоты.
Решение:
Раствор уксусной кислоты = уксусная кислота + вода
Выражение
Анализ условия
x
200 + x
0.7∙200
0,7∙200
200+x
количество воды, которое нужно добавить к 200г. 70%
го раствора уксусной кислоты (в г.)
масса исходного раствора уксусной кислоты, к которому
добавили x граммов воды
количество уксусной кислоты в исходном растворе (в г.)
массовая доля уксусной кислоты, в исходном растворе к
которому добавили x граммов воды
0,7∙200
200+x =0.08 Итоговое уравнение
0,7∙200
200+x =0.08;16+0.08x−140=0;
x= 124
0.08=1550 (г.)=1,55(кг.)
ОТВЕТ: 1,55 кг. Классу предлагается самостоятельно сделать анализ условия задач на концентрацию,
и решить по одной задаче по вариантам. Затем учитель предлагает учащимся
обменяться вариантами и выполнить взаимопроверку. Затем открывает доски, где
заранее были подготовлены решения предложенных задач и представляет учащимся
для корректировки.
Текст задач для учащихся.
1. Морская вода содержит 5% соли. Сколько килограммов пресной воды нужно
добавить к 40 кг морской воды, чтобы содержание соли составляло 2%
2. В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого веще
ства, добавили 7 литров воды. Сколько процентов составляет концентрация получив
шегося раствора?
III. Решение задач на совместную работу (вместе с учителем)
Задача 3. Двое рабочих выполнили работу за 12 дней. За сколько дней может выполнить
работу каждый рабочий, если одному из них потребуется на 10 дней больше, чем
другому?
Решение:
Выражение
Анализ условия
x
x + 10
1
1
x
1
x+10
12∙1
x
12∙ 1
x+10
количество дней, за которое может выполнить работу
рабочий №1
количество дней, за которое может выполнить работу
рабочий №2
вся работа
часть работы, которую выполняет рабочий №1 за 1 день
часть работы, которую выполняет рабочий №2 за 1 день
часть работы, которую выполняет рабочий №1 за 12 дней
часть работы, которую выполняет рабочий №2 за 12 дней 12
x + 12
x+10=1
Итоговое уравнение
x + 12
12
x+10=1;12∙(x+10)
x∙(x+10)
+ 12∙x
x∙(x+10)
=1;
12x+120+12x
x2+10x
=1;x2+10x=24x+120;
x2−14x−120=0
D=(−14)2−4∙1∙(−120)=196+480=676
D>0−уравнениеимеет2корня
x1=14+√676
2
=20×2=14−√676
2
=−6−постороннийкорень.
x=20(дней)
ОТВЕТ: 20 дней.
Учащимся предлагаются тексты задач. Необходимо самостоятельно проанализировать
их условия и составить к ним уравнения. Текст задач для учащихся.
1. Заказ на изготовление 156 деталей первый рабочий выполняет на 1 час быстрее, чем
второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за
час изготавливает на 1 деталь больше второго?
2. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12
часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, рабо
тая втроем?
После обсуждения правильности полученных уравнений, двое учащихся идут к доске
решать составленные к предложенным задачам уравнения, учитель и класс следят за
правильностью их оформления и записывают в тетради.
Подведение итога урока, выставление оценок
Домашнее задание
Решить задачи: 1. Из пункта А в пункт B, расстояние между которыми 12 км, одновременно выехали 2
велосипедиста. За час первый велосипедист проезжает на 1 км больше, чем второй.
Определите скорость второго велосипедиста, если известно, что он прибыл в пункт B
на 1 час позже первого. Ответ дайте в км/ч.
2 . Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять
таких же рубашек дороже куртки?
3. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За
сколько минут пропалывает грядку одна Даша?
ЗАКЛЮЧЕНИЕ.
Как правило, с текстовыми задачами справляются 35 40% учащихся. Широко
известны серьёзные трудности, которые испытывают ребята при решении задач.
Первая трудность состоит в математизации предложенного текста задачи (в переводе
содержания задачи на математический язык, т.е. выражение искомой величины через
известные величины и введенные переменные). Проблемы, с которыми сталкиваются
дети, связаны с непониманием физических, химических, экономических терминов,
законов, зависимостей; с непониманием связи между расстоянием, скоростью и
временем при равномерном движении и движении по окружности; между работой,
временем и производительностью; с непониманием зависимости между целым, частью и
процентным содержанием.
Вторая трудность это составление уравнений или неравенств, связывающих данные
величины и переменные.
Третья трудность это решение полученного уравнения или системы уравнений
желательно наиболее рациональным способом (как минимум не методом подбора, хотя
в редких случаях он бывает рациональнее прочих методов) [5].
Разработанное занятие позволяет учителю помочь ученикам преодолеть все
вышеуказанные трудности.
Как правило, процесс решения каждой текстовой задачи можно разделить на этапы:
прочитать текст задачи;
определить все неизвестные величины;
сопоставить каждой неизвестной величине свою математическую
связать все неизвестные величины с данными задачи (т.е. составить
1.
2.
3.
переменную (неизвестную);
4.
уравнение);
5.
6.
решить полученное уравнение;
записать ответ задачи.
Каждая задача в данном уроке решается по этому алгоритму. Для того чтобы ученики легче восприняли новый материал первую задачу (типовую)
решает сам учитель. Таким образом, учащиеся овладевают базовыми навыками решения
подобного рода задач. Затем учащиеся вызываются к доске, где они вместе с учителем
решают аналогичные задачи. Таким образом, ученики закрепляют новые знания и
учатся правильно мыслить.
Домашнее задание, в которое входят несколько текстовых задач позволит учащимся
более полно осмыслить полученный в школе материал. В ходе его выполнения у
учащихся наверняка появятся вопросы, которые прежде (в ходе урока) не возникали,
поэтому на следующим после этого урока занятии стоит опросить класс, все ли им
было понятно при решении задач дома.
Одним из главных факторов успешного обучения является заинтересованность
личности в новых знаниях. Поскольку всем учащимся по окончанию обучения в школе
предстоит сдавать ЕГЭ, то в ходе урока не лишним будет проинформировать учащихся,
о том, что текстовые задачи встречаются в каждом работе.
Кроме того стоит отметить, что учебные математические задачи являются очень
эффективным и часто незаменимым средством усвоения учащимися понятий и методов
школьного курса математики, вообще математических теорий. Велика роль практико
ориентированных задач в развитии мышления и в математическом воспитании
учащихся, в формировании у них умений и навыков в практических применениях
математики. Решение задач хорошо служит достижению всех тех целей, которые
ставятся перед обучением математике. Именно поэтому для решения задач
используется половина учебного времени уроков математики. Правильная методика
обучения решению математических задач играет существенную роль в формировании
высокого уровня математических знаний, умений и навыков учащихся.
Решение текстовых задач приучает выделять посылки и заключения, данные и
искомые, находить общее, и особенно в данных, сопоставлять и противопоставлять
факты. При решении математических задач воспитывается правильное мышление, и,
прежде всего учащиеся приучаются к полноценной аргументации.
Ключ к успеху учащихся на экзамене лежит в планомерном и систематическом
изучении науки, а не в процессе натаскивания на различные типы задач.
ЛИТЕРАТУРА
1. Открытый банк задач ЕГЭ по математике 2012 [Электронный ресурс]. —
http://live.mephist.ru/show/mathege2010/solve/B13/solved/
2. Фестиваль педагогических идей «Открытый урок» [Электронный ресурс].:
http://festival.1september.ru/articles/531255/
3. Ф.Ф. Лысенко,, С.Ю.Кулабухова «Математика.Подготовка к ЕГЭ 40
тренировочных вариантов
4. «ЕГЭ. Математика 2016 .Сборник экзаменационных заданий» М. «Экзамен» ,
2016. 5. Обучающая система Д. Гущина «Решу ЕГЭ» 2016 https://ege.sdamgia.ru/problem?
id=28002
6. А. Ларин «ЕГЭ и ГИА по математике 2016» http://alexlarin.net/ege16.html
Слайд 1,
Решение
текстовых задач
при подготовке к ЕГЭ

Слайд 2 «Умение решать задачи – практически искусство, подобно плаванию, или
катанию на коньках, или игре на фортепиано: научиться этому можно,
лишь подражая избранным образцам и постоянно тренируясь»
Д. Пойа

Слайд 3Классификация текстовых задач
Задачи на движение.
Задачи на работу.
Задачи на смеси и сплавы.
Задачи на проценты.
Задачи на
прогрессии.

Слайд 4№26578. Из пункта A в пункт B одновременно выехали
два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй
проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
v
s
1
2
х
s
s
1) 24
2) х + 16
s = v · t
=

Слайд 5Решение. Пусть x км/ч – скорость первого автомобиля, где
х > 0, тогда скорость второго автомобиля на второй половине
пути равна x + 16 км/ч. Примем расстояние между пунктами за s. Автомобили были в пути одно и то же время, отсюда имеем:
Ответ: 32.
– не удовл-ет условию х > 0

Слайд 6№39369. Моторная лодка прошла против течения реки 224 км и
вернулась в пункт отправления, затратив на обратный путь на 2 часа
меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
v
s
224
224
х – 1
s = v · t
–
2 ч
х + 1

Слайд 7Решение. Пусть x км/ч – собственная скорость лодки, где
х > 0, тогда скорость лодки по течению реки
равна х + 1 км/ч, скорость лодки против течения – х – 1 км/ч. Зная, что на путь по течению реки она затратила на 2 часа меньше, чем на обратный путь, имеем:
Ответ: 15.
– не удов-ет условию х > 0

Слайд 8№39443. Теплоход проходит по течению реки до пункта назначения
247 км и после стоянки возвращается в пункт отправления. Найдите скорость
течения, если скорость теплохода в неподвижной воде равна 16 км/ч, стоянка длится 7 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него. Ответ дайте в км/ч.
v
s
247
247
16 + х
s = v · t
+
39 – 7 = 32 ч.
16 – х
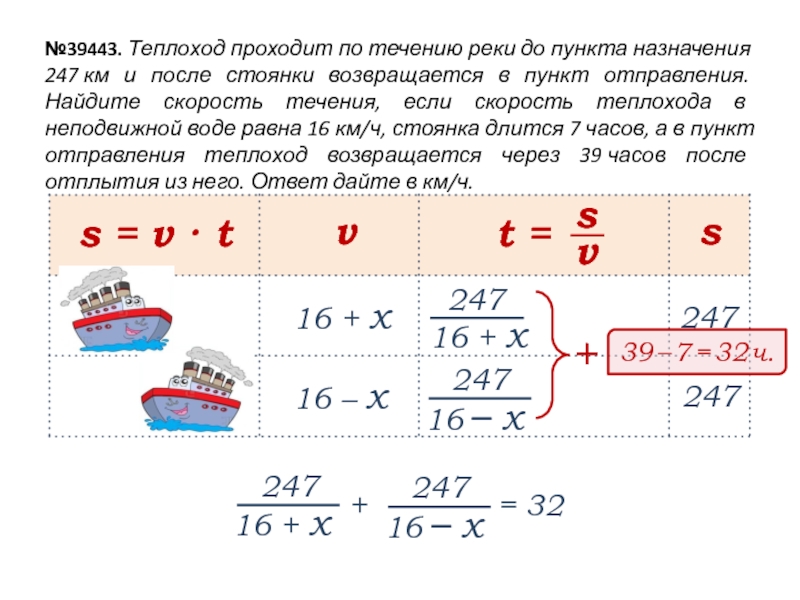
Слайд 9Решение. Пусть x км/ч – собственная скорость теплохода, где
х > 0, тогда скорость теплохода по течению равна 16
+ х км/ч, скорость теплохода против течения равна 16 – х км/ч. Зная, что теплоход был в пути 39 – 7 = 32 часа, имеем:
Ответ: 3.
– не удовл-ет условию х > 0

Слайд 10№113153. Товарный поезд каждую минуту проезжает на 300 метров
меньше, чем скорый, и на путь в 420 км тратит
времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Решение. Скорость товарного поезда меньше, чем скорого на 300 м/мин или на
Пусть х км/ч – скорость товарного поезда, тогда скорость скорого поезда х + 18 км/ч. На путь в 420 км товарный поезд тратит времени на 3 часа больше, чем скорый, отсюда имеем:

Слайд 11№113439. Два пешехода отправляются одновременно в одном направлении из
одного и того же места на прогулку по аллее парка.
Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 400 метрам?
v
t
s
1
2
х
(x + 0,5) · t
x · t
t
х + 0,5
s = v·t
0,8ч = 0,8 · 60 = 48 минут
Ответ: 48.
t
–
0,4км
Решение.

Слайд 12№113587. Два мотоциклиста стартуют одновременно в одном направлении из
двух диаметрально противоположных точек круговой трассы, длина которой равна 16
км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 10 км/ч больше скорости другого?
Слайд 13Решение. Пусть х км/ч – скорость первого мотоциклиста, тогда скорость
второго – х + 10 км/ч. Пусть через t часов мотоциклисты
поравняются в первый раз. Тогда расстояние, пройденное первым мотоциклистом:
Ответ: 48.
0,8ч = 0,8 · 60 = 48 минут

Слайд 14№114151. Из одной точки круговой трассы, длина которой равна
6 км, одновременно в одном направлении стартовали два автомобиля. Скорость
первого автомобиля равна 114 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Слайд 15Решение.
1 способ:
Пусть х км/ч – скорость второго автомобиля.
За 2/3 часа первый автомобиль прошел на 6 км больше,
чем второй, отсюда имеем:
Ответ: 105.
2 способ:
За 40 минут первый автомобиль обогнал второй на 6 км, значит за 60 минут обгонит на 9 км, т.е. скорость второго на 9 км/ч меньше скорости первого, значит,
х = 114 – 9 = 105 км/ч

Слайд 16№115195. Половину времени, затраченного на дорогу, автомобиль ехал со
скоростью 67 км/ч, а вторую половину времени – со скоростью 85
км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение.
Пусть t ч – время, затраченное на весь путь; 0,5·t·67 км – первая часть пути, 0,5·t·85 км – вторая часть пути. Тогда среднюю скорость находим по формуле:
Ответ: 76.

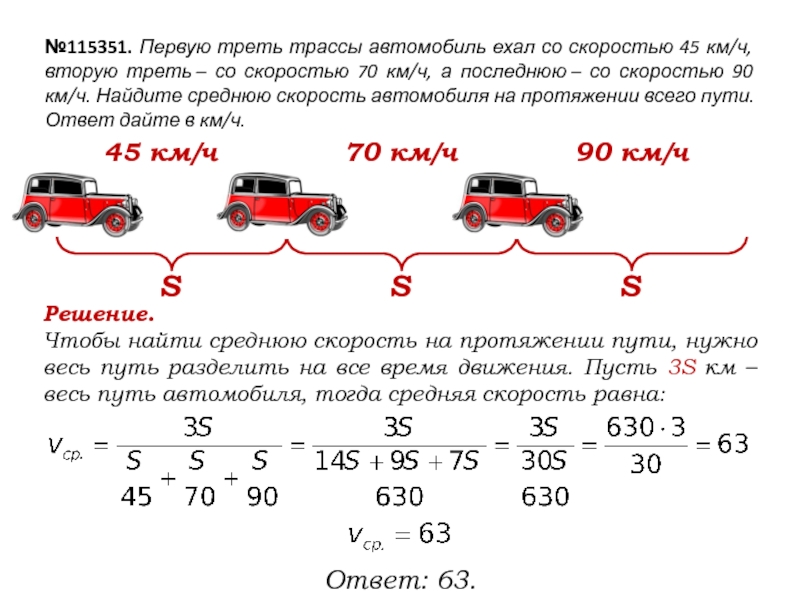
Слайд 17№115351. Первую треть трассы автомобиль ехал со скоростью 45
км/ч, вторую треть – со скоростью 70 км/ч, а последнюю – со
скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
45 км/ч
70 км/ч
90 км/ч
Решение.
Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть 3S км – весь путь автомобиля, тогда средняя скорость равна:
Ответ: 63.
Слайд 18№116385. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает
мимо придорожного столба за 45 секунд. Найдите длину поезда в
метрах.
Решение. Скорость поезда равна:
За 45 секунд поезд проходит мимо придорожного столба расстояние равное своей длине:
Ответ: 1000.
Слайд 19№116737. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает
мимо лесополосы, длина которой равна 300 метров, за 33 секунды.
Найдите длину поезда в метрах.
Слайд 20Решение.
Скорость поезда равна:
За 33 секунды поезд проходит
мимо лесополосы, то есть проходит расстояние, равное сумме длин лесополосы
и самого поезда, и это расстояние равно :
Ответ: 250.
Поэтому длина поезда равна 550 – 300 = 250 метров.

Слайд 21№117737. По двум параллельным железнодорожным путям в одном направлении
следуют пассажирский и товарный поезда, скорости которых равны соответственно 70
км/ч и 50 км/ч. Длина товарного поезда равна 900 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 3 минутам 9 секундам. Ответ дайте в метрах.

Слайд 22Решение.
Скорость опережения товарного поезда пассажирским равна:
За 3
мин 9 секунд или 189 секунд один поезд проходит мимо
другого, то есть преодолевает расстояние равное сумме их длин
Ответ: 150.
Поэтому длина пассажирского поезда равна
1050 – 900 = 150 метров.

Слайд 23№118237. По двум параллельным железнодорожным путям друг навстречу другу
следуют скорый и пассажирский поезда, скорости которых равны соответственно 85
км/ч и 50 км/ч. Длина пассажирского поезда равна 300 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 28 секундам. Ответ дайте в метрах.

Слайд 24Решение.
Скорость сближения поездов равна:
За 28 секунд один
поезд проходит мимо другого, то есть каждый из поездов преодолевает
расстояние равное сумме их длин
Ответ: 750.
Поэтому длина скорого поезда равна
1050 – 300 = 750 метров.

Слайд 25Использованы рисунки:
Коллекция картинок из галереи SMART Notebook 11
http://www.art-saloon.ru/ru/set.aspx?SetID=116 –
транспорт
http://www.art-saloon.ru/ru/comment.aspx?ItemID=5746 – гоночный автомобиль
http://www.fantasianew.ru/category/piraty-i-korsary-papo/ – плот
Использованы материалы:
http://mathege.ru/or/ege/Main.html
http://reshuege.ru/

- Долхонова Валентина Владимировна,
- учитель математики
- МБОУ «Еланцынская СОШ»
- 2016 г.
- Решение текстовых задач при
- подготовке к ОГЭ и ЕГЭ
- «Умение решать задачи – практически искусство, подобно плаванию, или катанию на коньках, или игре на фортепиано: научиться этому можно, лишь подражая избранным образцам и постоянно тренируясь»
- Д. Пойа
Одним из важных вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач. В процессе обучения математике задачи выполняют разнообразные функции. Задачи являются эффективным и незаменимым средством усвоения учащимися понятий и методов школьного курса математики.
- Одним из важных вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач. В процессе обучения математике задачи выполняют разнообразные функции. Задачи являются эффективным и незаменимым средством усвоения учащимися понятий и методов школьного курса математики.
- Правильная методика обучения решению математических задач играет существенную роль в формировании высокого уровня математических знаний, умений и навыков учащихся. С задачи учащиеся знакомятся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, для решения вопросов, которые возникают в жизни человека.
Этапы решения задач являются формами развития мыслительной деятельности учащихся. Наблюдается активизация их мыслительной работы, формируется умение проводить исследование. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, абстрактное мышление, умение применять теорию к решению конкретных задач и закрепление на практике приобретённых умений и навыков.
- Этапы решения задач являются формами развития мыслительной деятельности учащихся. Наблюдается активизация их мыслительной работы, формируется умение проводить исследование. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, абстрактное мышление, умение применять теорию к решению конкретных задач и закрепление на практике приобретённых умений и навыков.
- Текстовые задачи входят в ОГЭ и ЕГЭ, поэтому, данная тема имеет важнейшее значение в обучении математике.
- Для текстовых задач не существует единого алгоритма решения – в этом вся их сложность. Тем не менее существуют типовые задачи, которые вполне решаются стандартно.
- В обучении составлению уравнений оказывается весьма полезным такие упражнения:
- Записать в виде математического выражения:
- х на 5 больше у;
- х в 5 раз больше у;
- z на 8 меньше, чем х;
- частное от деления а на в в 1,5 раза больше в;
- п меньше х в 3,5 раза;
- квадрат суммы х и у равен 7;
- х составляет 60% от у;
- м больше п на 15%.
Классификация текстовых задач
- Задачи на движение.
- Задачи на работу.
- Задачи на смеси и сплавы.
- Задачи на проценты.
- Задачи на прогрессии.
- Подходы к решению текстовых задач
- Наиболее распространенный, довольно эффективный способ использования таблиц. В зависимости от типа решаемой задачи столбики в таблице будут иметь разные названия.
Задачи на движение
- Все задачи решаются по формуле S =Vt.
- В качестве переменной x удобно выбрать скорость,
- тогда задача точно решится.
- Уравнения составляются по одновременным событиям.
- Замечания:
- если время события задано, то удобнее составлять уравнение на путь;
- если уравнений меньше, чем неизвестных, то нужно ввести в систему искомую величину.
Задача
- Из А в В выехали одновременно два автомобиля. Первый проехал весь путь с постоянной скоростью. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 14 км/ч, а вторую половину пути – со скоростью 105 км/ч. Прибыли в В одновременно. Скорость первого — ? Если известно, что она больше 50 км/ч. Ответ в км/ч.
Решение
Задачи на работу
- А = рt, из этой формулы легко найти р (производительность) или t.
- Если объем работы не важен и нет никаких данных, позволяющих его найти – работу принимаем за единицу.
- Если трудятся два рабочих (два экскаватора и т.д.) – их производительности складываются.
- В качестве переменной удобно взять производительность.
Задача
- Заказ на деталей первый рабочий выполняет на час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на деталь больше?
Решение
Задачи на концентрацию
- PA% = CA 100%
- С1
- V1 — количество смеси из двух веществ
- С2
- + — соединение
- V2
- СA=
- кол-во вещества
- кол-во смеси
- концентр.
- |
- }
- C1
- V1
- C1V1
- C2
- V2
- C2V2
- C
- V
- CV
- C1V1 + C2V2 = CV – основное уравнение
- V1 + V2 = V – дополнительное уравнение
Задача
- При смешивании 10% раствора с 5% раствором получено 5 кг 6% раствора. Сколько каждого раствора было взято?
- 10х + 25х – 5х = 30
- 5х = 5
- Х = 1
- 5 – х = 5 – 1 = 4
- Ответ: х = 4
- }
- 6%
- 5 кг
- 5%
- 10%
- x
- (5-х)
- Решение
Задача
- Имеется два сплава. Первый сплав содержит никеля 10%, второй 30% — никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий никеля 25%. На сколько килограммов масса первого сплава меньше массы второго?
Решение
- Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой х+у=200.
- +
- =
- 10% от х
- 30% от у
- 25% от 200
- х+у = 200
- 0,1х + 0,3у = 0.25*200
- Ответ: 100
Задачи на проценты
- х%
- y%
- z%
- Если величина а изменяется на х%, то ее новое значение
Задача
- В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение
Задачи на прогрессии
- Арифметическая прогрессия:
- Геометрическая прогрессия:
- Бесконечно убывающая:
Задача
- Сумма первых трех членов возрастающей геометрической прогрессии равна 13, а их произведение 27. Вычислите сумму первых пяти членов этой прогрессии.
Решение
Выполнение вариантов единого государственного экзамена предполагает умение сконцентрироваться на полученном задании, внимательность к его выполнению, способность определять главное в большом потоке полученной информации, на быстрый переход от одного блока заданий к другому, и, конечно же, на владение приобретенными знаниями. На сегодняшнее время старшекласснику недостаточно просто «выучить некоторое количество данного в учебнике материала», необходимо приобрести широкий кругозор в процессе усвоения различных тем. Анализ содержания математических дисциплин определяет их главные отличительные признаки:
– преобразование выражений к конкретному правильному результату;
– владение формулами и теоремами для быстрого выполнения заданий;
– высокая степень самостоятельной работы.
ЕГЭ по математике позволяет максимально определить сформированность математических компетенций, которые закреплены требованиями Федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике. Школьный математический курс содержит изучение текстовых задач, являющихся неотъемлемыми при оценивании общей математической подготовки учащихся на ЕГЭ [2]. Данные задачи ориентированы на умение правильно составлять уравнения. Текстовые задачи подразделяются на несколько типов задач, которые для наглядности приводятся в таблице 1.
Таблица 1
|
Текстовые задачи |
ДВИЖЕНИЕ |
|
|
РАБОТА |
|
|
|
ПРОЦЕНТЫ |
|
|
|
КОНЦЕНТРАЦИЯ |
|
Анализ результатов выполнения заданий по математике приводит к выводу, что способность решать текстовые задачи является основополагающей в процессе подготовки к экзамену. В ходе решения различных задач практического характера были выделены основные этапы, представленные в таблице 2 [1].
Таблица 2
|
Э Т А П Ы |
Перевод исходных данных задачи на язык математики |
|
Решение полученной математической задачи |
|
|
Интерпретация найденного решения |
Последний этап позволяет выяснить практический смысл найденных результатов задачи. Текстовые задачи, как говорилось выше, вырабатывают умение составлять уравнения, для которого предлагается следующий алгоритм: составлять уравнение → решать → получать значение.
Но существует ряд проблем, с которыми сталкиваются учащиеся при решении данных заданий. Текстовые задачи содержат максимально возможное число учебных материалов сразу нескольких классов, из-за чего ученики во многих случаях не способны актуализировать необходимые знания для решения задач. А в действительности необходимо знать лишь несколько формул:
- формула взаимосвязи пройденного расстояния со скоростью и временем, потраченным на преодоление этого расстояния;
- формула связи совершенной работы с производительностью и временем, потраченным на выполнение данной работы;
- правила, используемые при решении задач на проценты, и умение составлять пропорции.
- Задачи на движение
Довольно часто в условии задачи не встречается дополнительных оговорок. В таком случае движение будем считать равномерным, тогда пройденный путь будем искать по следующей формуле: S=V*t, где S — расстояние, пройденное телом; V — скорость движения тела, t — время движения тела.
Все величины берутся положительными: S>0, V>0, t>0. Данные величины обязательно записываем в одной системе координат:
|
Расстояние |
Скорость |
Время |
|
километры |
километр/час |
час |
|
метры |
метр/секунд |
Секунда |
|
метры |
метр/минут |
минута |
- Движение по прямой
Задачи, в которых речь идет о равномерном движении, определяют вероятность возникновения следующих условий. Если первоначальный промежуток между предметами равен S, а скорость объектов V1 и V2, то:
а) при встречном движении тел время, через которое они встретятся, будет равно ;
б) при движении объектов в одну сторону (V1>V2) время, через которое первый объект догонит второй, находится как .
- Движение по замкнутой дороге
Если в условии задачи говорится, что дорога замкнута и ее длина определяется как S, а скорости объектов V1 и V2, то:
а) при совершении движения тел в одном и том же направлении время между их встречами находится по формуле (V1>V2);
б) при совершении движения тел в разных направлениях время между их встречами находится по формуле .
- Движение по реке
Если в условии говорится о движении по течению реки, то скорость, с которой плывет тело, находится по следующей формуле Vпо течению =Vсобств+Vтечен.
Если объект двигается против течения реки, то его скорость находится как Vпротив течения =Vсобств-Vтечен.
Скорость самого объекта в неподвижной реке определяется , а скорость течения реки равна
. Скорость, с которой совершает передвижение плот находится как скорость течения реки.
- Движение протяженных тел
При движении двух объектов навстречу друг другу скорость одного объекта относительно другого определяется как V1+V2. При движении двух объектов в одну сторону со скоростью V1, V2, скорость одного объекта относительно другого равна V1-V2(V1>V2).
- Средняя скорость
Чтобы определить среднюю скорость движения объекта, необходимо все пройденное расстояние разделить на общее время движения .
- Задачи на работу
В данных задачах обычно используются три величины: время t, в течение которого совершена работа; производительность N — работа, совершенная в единицу времени; работа A, произведенная в единицу времени.
Данные величины объединяются формулой A=N*t. Отсюда находим N=A/t, t=A/N. Все величины берутся положительные.
Задачи на работу делятся на два типа: с явным объемом работы (в условии указывается объем работы или необходимость его поиска) и неявным объемом работы (в условии объем работы не обозначается, в таких случаях он принимается за 1).
- Задачи на проценты
- Части и проценты
Чтобы найти проценты от данного числа, необходимо: а) записать с помощью дробей проценты; б) умножить данное число на эту дробь
(aсоставляет p % от b)
- Процентное сравнение величин
При выполнении сравнения заданных величин за 100 % берется та, с которой производится сравнение. В задачах на проценты первоначально необходимо выяснить, какую из данных величин взять за 100 %.
- Сложные проценты
Формула «сложных процентов» для двухкратного изменения находится A2=A0(1±0,01p1)(1±0,01p2), где A0 — первоначальное значение величины; A, A2 — новое значение величины A после ее двухкратного процентного изменения; ,
— проценты изменения величины A.
- Задачи на концентрацию
Массовой концентрацией вещества A в смеси называется отношение массы
этого вещества к общей массе M:
;
=
*M; M =
.
Массовым процентным содержанием вещества A в данной смеси называется величина
Если смесь массы M состоит из вещества A и B, то имеют место следующие равенства
;
;
;
.
Но бывают задачи, которые решаются не по данным формулам, а с помощью логических рассуждений.
Задача 1.
Поезд двигается со скоростью 65 км/ч, он проезжает мимо пешехода, двигающегося параллельно железнодорожным путям со скоростью 2 км/ч навстречу поезду за 18 секунд. Необходимо определить длину поезда в метрах, если учитывать, что движение поезда равномерно.
Такая задача относится к типу I — задач на движение. Покажем первый способ ее решения. Для наглядности продемонстрируем рисунок.
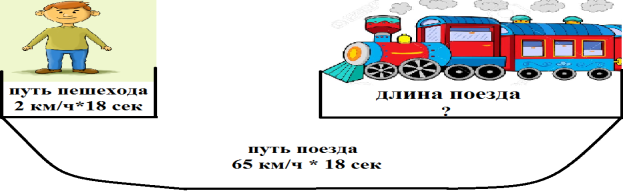
-
Из рисунка можно сделать вывод, что длина поезда находится следующим образом:
.
- Но условие задачи требует найти длину поезда в метрах, для этого выполняем следующую: 0,335*1000=335 м.
Ответ найден, однако, задача решается значительно быстрее, если воспользоваться определением скорости сближения. Скорость сближения — это расстояние, на которое сближаются объекты за единицу времени. Единицей измерения является км/ч, м/с. При равномерном движении объектов с разными скоростями расстояние между данными объектами либо увеличивается, либо уменьшается на одно и то же число единиц [3].
- Если в условии задачи сказано, что объекты совершают встречное движение со скоростью V1 и V2, то скорость сближения находится как Vсближ=V1+V2.
- Если объекты совершают движение в одном направлении со скоростью V1 и V2, то скорость сближения находится как Vсближ=V1-V2.
Тогда ответ в данной задаче может быть получен следующим способом.
- Определим, как быстро сближаются поезд и пешеход, двигаясь навстречу друг другу
65+2 = 67 км/ч.
- Необходимо по условию задачи длину поезда найти в метрах, следовательно совершаем следующее действие
67 км/ч = 67·1000/3600 = 670/36 = 335/18= (м/с).
- Для нахождения длины поезда необходимо скорость сближения пешехода и поезда умножить на затраченное время
(335/18)·18 = 335 (м) — длина поезда.
Данную задачу можно решить любым предложенным способом, однако, мониторинг решения задач ЕГЭ показывает, что большинство учащихся приходит к неправильному варианту ответа еще и по причине невыполнения требований условия задачи: нахождение длины поезда в метрах [2].
Ответ: 335 метров.
Большее затруднение у учащихся вызывает следующая задача.
Задача 2.
Поезд двигается со скоростью 90 км/ч, он проезжает мимо лесополосы, длина которойравна 500 метров. Поезд затрачивает время равное 1 минуте. Найдите длину поезда в метрах, если принимать его движение за равномерное.
Решение.
Чтобы решить такую задачу, нужно мысленно вообразить, как поезд совершает движение мимо леса. Если считать, что мы находимся в одном из вагонов поезда, то приближаясь к лесу, мы полностью проезжаем его (это расстояние равно 500 метров), но весь поезд еще не окончательно проезжает лес, так как с концом леса еще не поравнялся последний вагон, то есть поезду необходимо пройти расстояние, которое будет равно его длине.
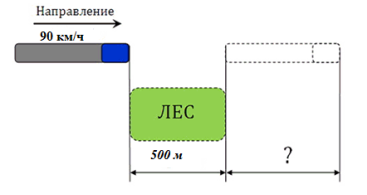
По условию задачи поезд затрачивает время равное 1 минуте для прохождения лесополосы. Следовательно можно найти расстояние, которое он преодолевает за указанное время:
Таким образом, длина поезда находится как 1,5–0,5 = 1 км. А так как по условию необходимо указать длину поезда в метрах, проделываем следующую операцию:
1*1000 =1000 метров.
Ответ: 1000 метров.
Задача 3.
9 рубашек дешевле одного костюма на 19 %, на сколько процентов 13 рубашек дороже одного костюма?
Решение.
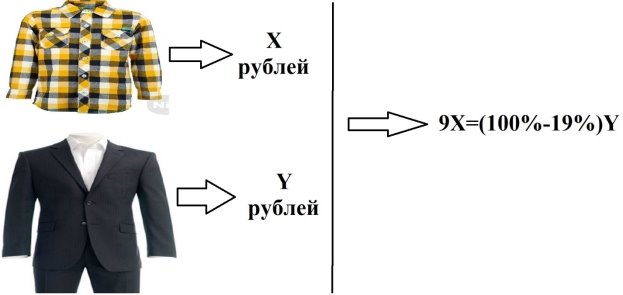
Рисунок говорит нам о том, что цену одной рубашки обозначили за x, а цену одного костюма — y. Условие задачи позволяет понять, что общая стоимость 9 рубашек дешевле стоимости одного костюма на 19 %, а значит, что стоимость 13 рубашек составляет 100 %-19 %=81 % стоимости одного костюма. Следовательно, можем составить уравнение:
9х=81/100y
9х=0,81y
x=0,09y
Записанное уравнение позволяет определить, что стоимость одной рубашки составляет некоторую часть стоимости одного костюма. Условие задачи требует найти процентное отношение 13 рубашек к стоимости одного костюма. Следовательно умножим обе части равенства на 13:
13x=1,17y.
Обозначим стоимость одного костюма за 100 %, тогда получается, что стоимость 13 рубашек больше стоимости одного костюма на 17 %.
Ответ: 17 %.
Рассмотрим еще одну задачу, которая на первый взгляд оказывается очень сложной для многих учащихся.
Василий Иванович плывет по океану на яхте, средняя скорость которой равна 27 км/ч. Доплыв до заданного пункта, он решил вернуться обратно, но только уже на самолете, скорость которого 513 км/ч. Необходимо найти среднюю скорость Василия Ивановича, с которой он путешествовал на всем пути. Ответ нужно дать в км/ч.
Задача решается очень быстро, если помнить формулу нахождения средней скорости . Данные задачи подставляем в формулу и находим
=51,3 км/ч.
Но довольно часто учащиеся испытывают затруднения на экзамене, так как из-за переживаний не способны вспомнить нужную формулу. Поэтому рассмотрим следующий способ нахождения ответа задачи по всем известной формуле. Для этого воспроизведем формулу скорости V, необходимо определить весь путь, который прошел Василий Иванович и общее время, которое потребовалось на прохождение всего участка. Данные задачи позволяют найти время, которое Василий Иванович прибывал в пути на яхте t1
часов, а время, за которое он долетел на самолете обратно, равно t2
часов. Таким образом, можно сделать вывод, что весь путь S=2S, а общее время в пути равно tобщ=t1+t2=
. Подставляем полученные значение пути и времени в формулу нахождения скорости:
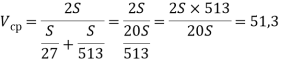
Ответ: 51,3 км/ч
Указанные выше особенности решения текстовых задач позволяют качественно и быстро решить задачи такого типа, повысить самооценку учащихся, создать благоприятный климат на экзамене.
Литература:
- Миронова С. В., Напалков С. В., Нестерова Л. Ю. О некоторых способах организации продуктивной математической деятельности учащихся в дополнительном образовании // Технологии продуктивного обучения математике: традиции и инновации: сборник статей участников Всероссийской научно-практической конференции с международным участием (посвящается памяти профессора М. И. Зайкина) / Научный редактор С. В. Миронова, ответственный редактор С. В. Напалков; Арзамасский филиал ННГУ. — Арзамас, 2016. — С. 70–75.
- Нестерова Л. Ю. Совокупности специализированных задач для подготовки учащихся к итоговой аттестации по математике // Задачные конструкции математического развития школьников: сборник статей участников научно-методического семинара / Под общей редакцией С. В. Арюткиной, С. В. Напалкова. — 2015. — С. 51–53.
- http://elhow.ru/ucheba/matematika/kak-najti-skorost-sblizhenija
Основные термины (генерируются автоматически): задача, длина поезда, условие задачи, скорость, время, движение, метр, скорость сближения, величина, единица времени.
Государственное образовательное учреждение
дополнительного профессионального образования (повышения
квалификации) специалистов Московской области Педагогическая
академия последипломного образования
(ГОУ ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ)
проект
«Решение текстовых задач»
Выполнила
Илюшина Галина Сергеевна,
учитель математики МБОУ
Петрово-Дальневской СОШ
Красногорского района
руководитель
к.п.н., доцент
Васильева М.В.
Красногоск
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3-8
1.1 Понятие тестовой задачи
1.2 Роль задачи в курсе математики
1.3 Виды текстовых задач
2. ОБУЧЕНИЕ ШКОЛЬНИКОВ ПРИЕМАМ РЕШЕНИЯ ТЕКСТОВЫХ
ЗАДАЧ 9-31
2.1 Решение задач на движение
2.2 Задачи на выполнение определенного объема работы
2.3 Задачи на на работу, на бассейны и трубы
2.4. Задачи на планирование
2.5 Задачи на проценты
2.6 Компетентностные задачи
2.7 Приложения
3. РАЗРАБОТКА УРОКА по теме: «Решение текстовых задач при
подготовке учащихся 11 класса к ЕГЭ по математике»
32-37
ЗАКЛЮЧЕНИЕ 37
СПИСОК ЛИТЕРАТУРЫ 38
ВВЕДЕНИЕ
ЦЕЛИ ПРОЕКТА:
1. Обобщение, углубление и систематизирование
знаний по решению текстовых задач.
2. Показать широту применения этой темы.
3. Приобретение практических навыков при решении
задач.
4. Развитие логического мышления учащихся.
ЗАДАЧИ ПРОЕКТА:
1. Вооружить учащихся системой знаний по решению
текстовых задач.
2. Сформировать умения и навыки при решении
разнообразных задач различной сложности.
3. Способствовать формированию познавательного
интереса к математике, развитию творческих способностей учащихся.
4. Повысить уровень математической подготовки
учащихся.
5. Подготовить учащихся к успешной сдаче ЕГЭ.
Актуальность темы
-
Решение текстовых задач — важная тема, касающаяся
математики. Еще в древности решали задачи с помощью составления
уравнений. -
В школьном курсе математики текстовые задачи решаются с 1 по
11 классы. -
Умение решать текстовые задачи с помощью уравнений важно для
физики и химии. -
Эти задачи присутствуют на экзамене 9 и 11 классов.
Умение решать задачи является одним из основных
показателей уровня математического развития, глубины освоения
учебного материала. Ребенок с первых дней занятий в школе
встречается с задачей. Сначала и до конца обучения в школе
математическая задача неизменно помогает ученику вырабатывать
правильные математические понятия, глубже выяснять различные
стороны взаимосвязей в окружающей его жизни, дает возможность
применять изучаемые теоретические положения. Текстовые задачи —
традиционно трудный для значительной части школьников материал.
Однако в школьном курсе математики ему придается большое значение,
так как такие задачи способствуют развитию логического мышления,
речи и других качеств продуктивной деятельности обучающихся.
Как обучать детей нахождению способа решения
текстовой задачи? Этот вопрос — центральный в методике обучению
решения задач. Для ответа на него в литературе предложено немало
практических приемов, облегчающих поиск способа решения задачи.
Однако теоретические положения относительного нахождения пути
решения задачи остаются мало разработанными.
Особенности текста задачи могут определить ход
мыслительного процесса при ее решении. Как сориентировать детей на
эти особенности? Знание ответов на них составляют
теоретико-методические положения, на основе которых можно строить
конкретную методику обучения; они помогут определить методические
приемы поиска способов решения задачи, в том числе решения
различными способами.
Текстовые задачи являются важным средством
обучения математике. С их помощью учащиеся получают опыт работы с
величинами, постигают взаимосвязи между ними, получают опыт
применения математики к решению практических (или правдоподобных)
задач.
Использование арифметических способов решения
задач развивает смекалку и сообразительность, умение ставить
вопросы, отвечать на них, то есть, развивает естественный язык,
готовит школьников к дальнейшему обучению.
Арифметические способы решения текстовых задач
позволяют развивать умение анализировать задачные ситуации, строить
план решения с учетом взаимосвязей между известными и неизвестными
величинами (с учетом типа задачи), истолковывать результат каждого
действия в рамках условия задачи, проверять правильность решения с
помощью составления и решения обратной задачи, то есть, формировать
и развивать важные общеучебные умения.
Арифметические способы решения текстовых задач
приучают детей к первым абстракциям, позволяют воспитывать
логическую культуру, могут способствовать созданию благоприятного
эмоционального фона обучения, развитию у школьников эстетического
чувства применительно к решению задачи (красивое решение) и
изучению математики, вызывая интерес сначала к процессу поиска
решения задачи, а потом и к изучаемому предмету.
Использование исторических задач и разнообразных
старинных (арифметических) способов их решения не только обогащают
опыт мыслительной деятельности учащихся, но и позволяют им
осваивать важное культурно-историческое наследие человечества,
связанный с поиском решения задач. Это важный внутренний (связанный
с предметом), а не внешний (связанный с отметками, поощрениями и
т.п.) стимул к поиску решений задач и изучению математики.
Первоначальные математические знания усваиваются
детьми в определенной, приспособленной к их пониманию системе, в
которой отдельные положения логически связаны одно с другим,
вытекают одно из другого. При сознательном усвоении математических
знаний учащиеся пользуются основными операциями мышления в
доступном для них виде: анализом и синтезом, сравнением,
абстрагированием и конкретизацией, обобщением; ученики делают
индуктивные выводы, проводят дедуктивные рассуждения. Сознательное
усвоение учащимися математических знаний развивает математическое
мышление учащихся. Овладение мыслительными операциями в свою
очередь помогает учащимся успешнее усваивать новые знания.
Решая задачи, учащиеся приобретают новые
математические знания, готовятся к практической деятельности.
Задачи способствуют развитию их логического мышления. Большое
значение имеет решение задач и в воспитании личности учащихся.
Поэтому важно, чтобы учитель имел глубокие представления о
текстовой задаче, о её структуре, умел решать такие задачи
различными способами.
Текстовая задача — есть описание некоторой
ситуации на естественном языке с требованием дать количественную
характеристику какого-либо компонента этой ситуации, установить
наличие или отсутствие некоторого отношения между её компонентами
или определить вид этого отношения.
Решение задач — это работа несколько необычная,
а именно умственная работа. А чтобы научиться какой-либо работе,
нужно предварительно хорошо изучить тот материал, над которым
придётся работать, те инструменты, с помощью которых выполняется
эта работа.
Значит, для того чтобы научиться решать задачи,
надо разобраться в том, что собой они представляют, как они
устроены, из каких составных частей они состоят, каковы
инструменты, с помощью которых производится решение задач.
Каждая задача — это единство условия и цели.
Если нет одного из этих компонентов, то нет и задачи. Это очень
важно иметь в виду, чтобы проводить анализ текста задачи с
соблюдением такого единства. Это означает, что анализ условия
задачи необходимо соотносить с вопросом задачи и, наоборот, вопрос
задачи анализировать направленно с условием. Их нельзя разрывать,
так как они составляют одно целое.
Математическая задача — это связанный
лаконический рассказ, в котором введены значения некоторых величин
и предлагается отыскать другие неизвестные значения величин,
зависимые от данных и связанные с ними определенными соотношениями,
указанными в условии.
Любая текстовая задача состоит из двух частей:
условия и требования (вопроса).
В условии соблюдаются сведения об объектах и
некоторых величинах, характеризующих данные объекта, об известных и
неизвестных значениях этих величин, об отношениях между ними.
Требования задачи — это указание того, что нужно
найти. Оно может быть выражено предложением в повелительной или
вопросительной форме («Найти площадь треугольника» или «Чему равна
площадь прямоугольника?»).
Иногда задачи формируются таким образом, что
часть условия или всё условие включено в одно предложение с
требованием задачи.
В реальной жизни довольно часто возникают самые
разнообразные задачные ситуации. Сформулированные на их основе
задачи могут содержать избыточную информацию, то есть, такую,
которая не нужна для выполнения требования задачи.
На основе возникающих в жизни задачных ситуаций
могут быть сформулированы и задачи, в которых недостаточно
информации для выполнения требований. Так в задаче: «Найти длину и
ширину участка прямоугольной формы, если известно, что длина больше
ширины на 3 метра» — недостаточно данных для ответа на её вопрос.
Чтобы выполнить эту задачу, необходимо её дополнить недостающими
данными.
Одна и та же задача может рассматриваться как
задача с достаточным числом данных в зависимости от имеющихся и
решающих значений.
Рассматривая задачу в узком смысле этого
понятия, в ней можно выделить следующие составные элементы:
-
Словесное изложение сюжета, в котором явно
или в завуалированной форме указана функциональная зависимость
между величинами, числовые значения которых входят в задачу. -
Числовые значения величин или числовые
данные, о которых говорится в тексте задачи. -
Задание, обычно сформулированное в виде
вопроса, в котором предлагается узнать неизвестные значения
одной или нескольких величин. Эти значения называют искомыми.
Задачи и решение их занимают в обучении
школьников весьма существенное место и по времени, и по их влиянию
на умственное развитие ребенка. Понимая роль задачи и её место в
обучении и воспитании ученика, учитель должен подходить к подбору
задачи и выбору способов решения обоснованно и чётко знать, что
должна дать ученику работа при решении данной им задачи.
Текстовые задачи условно можно разбить на следующие основные
группы:
Задачи на движение
по прямой (навстречу и вдогонку)
по замкнутой трассе
по воде
на среднюю скорость
протяженных тел
Задачи на производительность
задачи на работу
задачи на бассейны и трубы
Задачи на проценты, концентрацию, части и доли
Задачи на проценты и доли
Задачи на концентрацию, смеси и сплавы
Арифметическая прогрессия
Геометрическая прогрессия
Методы решения этих задач имеют много общего и одновременно
некоторые специфические особенности
Алгоритм решения текстовых задач
Ввод переменных, т.е. обозначение буквами x, y, z,… величины,
которые требуется найти по условию задачи.
Перевод условий задачи на язык математических соотношений, т.е.
составление уравнений, неравенств, введение ограничения.
Решение уравнений или неравенств.
Проверка полученных решений на выполнение условий задачи.
Указания к решению текстовых задач
Набор неизвестных должен быть достаточным для перевода условий
задачи на язык математических соотношений. Как правило, за
неизвестные следует принимать искомые величины.
Выбрав неизвестные, в процессе перевода условий задачи в
уравнения или неравенства необходимо использовать все данные и
условия задачи.
При составлении уравнений или неравенств необходимо исходить из
требования о решении задачи в общем виде.
В составленных уравнениях надо проверить размерность членов
уравнений
В процессе решения задачи, надо избегать результатов,
противоречащих физическому смыслу.
Задачи на движение
При решении задач на движение принимают такие допущения:
-
движение считается равномерным, если нет специальных
оговорок; -
изменение направления движения и переходы на новый режим
движения считаются происходящими мгновенно; -
если два тела начинают движение одновременно (если одно
тело догоняет другое), то в случае, если они встречаются,
каждое тело с момента выхода и до встречи затрачивает
одинаковое время; -
если тела выходят в разное время, то до момента встречи из
них затрачивает время больше то, которое выходит раньше. -
все величины, как правило, положительные (в природе
скорость расстояние и время положительны), поэтому можно смело
умножать, делить и возводить в квадрат получающиеся уравнения и
неравенства, не делая необходимых в таких случаях
оговорок; -
скорость перемещения лодки v по воде, при скорости течения
реки vр и собственной скорости движения
vс, выражается:
v по течению = vс + vр при
движении лодки по течению реки.
vпротив течения = vс− vр при
движении лодки против течения реки.
Основные соотношения
v= s/t- скорость движущегося объекта прямо пропорциональна пути
s и обратно пропорциональна времени t.
t=s0/(v1+v2) — время, за
которое два объекта движущиеся навстречу друг другу со скоростью
соответственно v1 и v2 преодолевают начальное
расстояние s0.
t=s0/(v1−v2) — время, за
которое два объекта движущиеся в одном направлении со скоростью
соответственно v1 и v2
(v1 v2)
v2)
преодолевают начальное расстояние между ними, равное s0
и первый объект догонит второго.
vпо течению− vпротив
течения=2vр — разность скоростей по течению и
против течения реки равна удвоенной скорости течения.
Задачи, связанные с движением двух тел удобно решать, если
занести исходные данные в таблицу:
Скорость v
Время t
Расстояние s
1 объект
v=s/t
t=s/v
s=v t
t
2 объект
После внесения данных, нужно составить уравнения, содержащие
искомую величину, исходя из условий задачи.
Задачи на движение по прямой (навстречу и вдогонку)
В задачах на движение есть две стандартные модели: движение
навстречу друг другу и движение вдогонку. В первой модели
рассматривается как бы совместная скорость сближения, как сумма
двух скоростей и поэтому время сближения считается
так:t=s/(v1+v2) . Во второй модели время, за
которое объект, идущий сзади с большей скоростью v1,
догонит другой объект, идущий с меньшей скоростью v2,
считается так: t=s/(v1−v2), где s —
расстояние между объектами в начальный момент времени.
Задача 1. Из городов А и
В, расстояние между которыми 480 км, навстречу
друг другу выехали два автомобиля. Из города А со
скоростью 55 км/ч, а из города В со скоростью 65
км/ч. Найдите расстояние от города А, где они встретятся.
Решение: Время до встречи считается по формуле
t=s/(v1+v2) и равно 4 часа. Расстояние от
города А до места встречи равно S=45• 5=220
км.
Задача 2. Два пешехода отправляются из аптеки
в одном направлении на прогулку по набережной. Скорость первого на
0,5 км/ч больше скорости второго. Найдите время в минутах, когда
расстояние между ними станет 200 м.
Решение: Время в часах, за которое расстояние
станет между ними 200 м, т.е. 0,2 км, считается по формуле t=0,2:
0,5=0,4 часа. Значит, через 24 минуты расстояние между ними будет
200 м.
Задачи на движение по замкнутой трассе
Движение по замкнутой трассе (допустим по стадиону) похоже на
движение
вдогонку: если два бегуна начинают двигаться по окружности
одновременно с разными скоростями соответственно v1 и
v2 (v1 v2), то
v2), то
первый бегун приближается ко второму бегуну со скоростью
v1−v2 и в момент, когда первый бегун догоняет
второго бегуна, то первый бегун как раз проходит на один круг
больше второго. И поэтому время считается так:
t=s/(v1−v2)
Задача. Из одной точки круговой трассы, длина
которой равна 16 км, в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 80 км/ч и через 40 минут после
старта, он опережает второй автомобиль ровно на один круг. Найдите
скорость второго автомобиля.
Решение: Примем скорость второго автомобиля за
x км/ч и учтем, что 40 минут составляют 32 часа, тогда
1680−x=32 160−2x=48
160−2x=48 x=56
x=56
Задачи на движение по воде
В задачах на движение по воде скорость реки считается
постоянной и неизменной. При движении по течению скорость реки
прибавляется к собственной скорости плывущего тела, так как
скорость реки помогает двигаться телу. При движении против течения
от собственной скорости вычитается скорость реки (реально
собственная скорость тела больше скорости реки), так как в этом
случае скорость реки мешает движущемуся телу. Скорость плота
считается равной скорости реки.
Скорость перемещения тела v по воде, при скорости течения реки
vр и собственной скорости движения vс,
выражается:
v по течению=vс+vр при
движении тела по течению реки.
v против течения=vс−vр при
движении тела против течения реки.
Замечание. v
потечению−vпротивтечения=2vр —
разность скоростей по течению и против течения реки равна удвоенной
скорости течения.
Замечание. vс=2vпо
течению+vпротив течения — формула нахождения
собственной скорости тела
Задача. Теплоход, скорость которого в
неподвижной воде равна 25 км/ч, проходит по течению реки и после
стоянки возвращается в исходный пункт. Скорость течения равна 3
км/ч, стоянка длилась 5 часов, а в исходный пункт теплоход
возвращается через 30 часов после отплытия из него. Определить
сколько километров теплоход прошел за весь рейс.
Решение: Заполним таблицу данными из условия
задачи: собственная скорость теплохода vс=25 , скорость
течения реки vр=3 , vпо
течению=vс+vр=28 при движении по
течению реки, vпротив
течения=vс−vр=22 при движении против
течения реки.
Скорость v
Время t: (t=s/v )
Расстояние s
по течению
v по течению=28
t по течению=x/28
x
против течения
v против течения=22
t против течения=x/22
x
Зная, что стоянка длилась 5 часов, а на весь путь затрачено 30
часов, составим уравнение: x/28+x/22+5=30 .
Решая его, получим x/28+x/22=25,
x/2•14+x/2•11=25,
(11x+14x)=25•2•14•11
x=308.
Ответ: искомый путь 616 км.
Задачи на определение средней скорости движения
Средняя скорость. Если S —
путь пройденный телом, а t — время за которое этот
путь пройден, то средняя скорость вычисляется по формуле:
v=s/t.
Если путь состоит из нескольких участков, то для нахождения
средней скорости на всем пути, надо весь пройденный путь разделить
на сумму времени, затраченного на каждый участок пути. Например,
если путь состоит из трех участков s1, s2,
s3, скорости на которых были соответственно равны
v1, v2, v3, то
s=s1+s2+s3 и
t=t1+t2+t3=s1/v1+s2/v2+s3/v3
, тогда средняя скорость на всем пути находится по формуле:
v=s/t=(s1+s2+s3)/(s1/v1+s2/v2+s3/v3).
Задача. Первую треть трассы велосипедист ехал
со скоростью 12 км/ч, вторую треть — со скоростью 16 км/ч, а
последнюю треть — со скоростью 24 км/ч. Найдите среднюю скорость
велосипедиста на протяжении всего пути.
Решение: Пусть весь путь равен
3S, тогда первую треть трассы велосипедист проехал
за время t1=s/12, вторую треть — за время
t2=s/16, последнюю треть — за время t3=s/24.
Значит, время, потраченное на весь путь находится так
t=t1+t2+t3=s/12+s/16+s/24=9s/48,и
поэтому средняя скорость вычисляется так v=3s:(9s/48)=16 км/ч
Задачи на движение протяженных тел
В задачах на движение протяжных тел требуется определить длину
одного из них. Наиболее типичные ситуации: определение длины поезда
проезжающего мимо придорожного столба, идущего параллельно путям
пешехода, лесополосы определенной длины, другого двигающегося
поезда.
Если поезд движется мимо столба, то он проходит расстояние
равное его длине. Если поезд движется мимо протяженной лесополосы,
то он проходит расстояние равное сумме длины самого поезда и
лесополосы.
Задача 1 Поезд, двигаясь равномерно со
скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд.
Найти длину поезда в метрах.
Решение: Зная скорость движения
v = 60 км/ч = 1000 м/мин и время, за которое он
проезжает мимо столба t = 30 сек. = 21мин, можно
найти длину поезда как пройденное расстояние
s=v•t=1000•21=500.
Задача 2 Поезд, двигаясь равномерно со
скоростью 90 км/ч, проезжает мимо лесополосы, длина которого 800
метрам, за 1 минуту. Найти длину поезда в метрах.
Решение: Зная скорость движения
v = 90 км/ч = 1500 м/мин и время, за которое он
проезжает мимо лесополосы длиной 800 метров за t =
1мин, можно найти длину поезда как пройденное расстояние
s=v t=1500•1=1500 плюс длина
t=1500•1=1500 плюс длина
лесополосы 800 метров и получим длину поезда, равную 2300
метра.
Задачи на выполнение определенного объема работы
Задачи на выполнение определенного объема работы по своему
решению очень схожи с задачами на движение: объем работы выполняет
роль расстояния, а производительность выполняет роль скорости. В
тех случаях, когда объем работы не задан, его принимают за единицу.
Большого разнообразия таких задач нет, во всех задачах идет речь о
выполнении определенного объема работы, без уточнения характера
самой работы.
Иногда в задачах на совместную работу можно обойтись без
решения уравнений.
Рассмотрим такой пример. Оформляя зал к школьному вечеру Антон,
Сергей и Максим готовы были работать парами. Антон и Сергей могут
оформить зал за 2 ч 20 мин, Антон и Максим — за 2 ч 48 мин и Максим
и Сергей — за 4 ч 40 мин. Найти, за сколько времени могут ребята
оформить зал, работая втроем. Заметим, что если сложить все
значения времени, то в этой сумме будет присутствовать удвоенное
время работы каждого в отдельности. Значит: 2 ч 20 мин + 2 ч 48 мин
+ 4 ч 40 мин = 9 ч 48 мин, разделив это значение на 2, получим
время 5 ч 28 мин, за которое могут ребята оформить зал, работая
втроем.
При решении задач, связанных с выполнением
определенного объема работ, используют следующие
соотношения: A=V•t, где A — количество
всей работы, t — время выполнения всего количества работы,
V — производительность труда, т.е. количество
работы, выполняемой в единицу времени.
Если весь объем работы, принятый за единицу, выполняется одним
работником за t1, а вторым- за t2 времени, то
производительность труда при их совместной работы равна
Vсовм=1/t1+1/t2 и
tсовм=1/Vсовм=t1•t2/(t1+t2).
Задачи, связанные с выполнением определенной работы удобно
решать, если занести исходные данные в таблицу:
Производительность v
Время t
Работа A
1 объект
v=A/t
t=A/v
A=v•t
2 объект
После внесения данных, нужно составить уравнения, содержащие
искомую величину, исходя из условий задачи.
Задачи на работу, на бассейны и трубы
Рассмотрим стандартную задача на работу: первый рабочий может
выполнить некоторую работу за a часов, а второй за b часов.
Определите время, за которое оба рабочих выполнят работу вместе.
Так как объем работы не задан, то его можно принять за единицу.
Тогда производительность первого рабочего будет 1/a,
производительность второго рабочего будет 1/b, а совместная
производительность равна 1/a+1/b. Значит, всю работу совместно два
рабочих выполнят за t=1/(1/a+1/b) времени.
Задачи на бассейны и трубы аналогичны задачам на совместную
работу. Математическая модель задачи сохраняется, только рабочим
будут соответствовать насосы разной производительности, а объем
работы будет представлять наполнение бассейна водой.
Задача. Две трубы наполняют бассейн за 4 часа, а одна первая
труба наполняет бассейн за 5 часов. Найдите время наполнения
бассейна одной второй трубой.
Решение: Заполним таблицу
Производительность
Время
Работа
две трубы
a+b=1/4
4
1
одна первая труба
a=1/5
5
1
одна вторая труба
b
1/b
1
Найдем b:
b=1/4−1/5=1/20, значит, время наполнения бассейна одной второй
трубой 20 часов.
На первом занятии сообщаются цели и задачи
курса, систематизируются знания учащихся об уравнениях и системах
уравнений, о способах их решений. Рассматривается классическая
задача о фазанах и кроликах, которую можно решить с помощью
уравнения, с помощью системы уравнений и рассуждая логически
(устно). Самостоятельное решение задач такого типа.
Задачи на планирование.
К задачам этого раздела относятся те задачи, в
которых выполняемый объём работы известен или его нужно определить
(в отличие от задач на совместную работу). При этом сравнивается
работа, которая должна быть выполнена по плану, и работа, которая
выполнена фактически. Так же как и в задачах на совместную работу,
основными компонентами задач на планирование являются работа
(выполненная фактически и запланированная), время выполнения работы
(фактическое и запланированное), производительность труда
(фактическая и запланированная). В некоторых задачах этого раздела
вместо времени выполнения работы дается количество участвующих в ее
выполнении рабочих.
Задачи на проценты.
Следует заметить, что задачи этого раздела
входят как составная часть в решение других типовых задач. Заменяя
проценты соответствующим количеством сотых долей числа, легко
свести данную задачу на проценты к задаче на части. При решении
задач данного типа необходимо считать устно. Для этого полезно
знать некоторые факты, например: чтобы увеличить величину на 50%,
достаточно прибавить ее половину; чтобы найти 20% величины, надо
найти ее пятую часть; что 40% некоторой величины в 4 раза больше,
чем ее 10%; что треть величины — это примерно 33% и т. д.
Сюжеты решаемых задач взяты из реальной жизни —
из газет, объявлений, документов. Часто задачи могут быть решены
разными способами. Важно, чтобы каждый ученик смог самостоятельно
выбрать свой способ решения, наиболее ему удобный и понятный.
Процент — это сотая часть. Наглядная иллюстрация
процента может быть продемонстрирована на метровой школьной линейке
с делениями по 1 см. В данном случае 1 см является сотой частью
линейки, т.е. 1%. Можно дать следующие задания:
-
показать на линейке 25%, 40% и т.д.
-
назвать число процентов, которые
показываются на линейке.
Затем работу можно продолжить на отрезках,
задавая вопросы, например:
Как показать 1% отрезка?
Ответ: отрезок нужно разделить на 100 равных
частей и взять одну часть.
Или: покажите 5% и т.д. (см. рис. 8).

Рис. 8. Метод отложения на отрезке
Условимся, что деление отрезка на 100 равных
частей делаем словно. Приступая к решению задач, их нужно сравнить
с задачами предыдущего пункта, что ускорит усвоение приемов
решения.
Пример №1. Ученик прочитал 138 страниц, что
составило 23% всех страниц книги. Сколько страниц в книге?

Рис. 9. Графическое изображение задачи из примера
№1
Объяснение: Число страниц в Кинге неизвестно.
Ставим знак вопроса. Но число страниц составляет 100%. Показываем
это на отрезке, выполняя деление на условные 100 равных частей (для
слабоуспевающих детей внизу отрезка можно ставить еще и число 100).
Затем отмечаем число 138 и показываем, что оно составляет 23%.
При решении задач предыдущего раздела и задач на
проценты следует объяснить учащимся, что прежде всего нужно
выяснить, сколько составляет 1 часть или 1%.
Так как 138 страниц составляют 23%, то находим,
сколько приходится на 1%.
138 / 23 = 6 (стр.) — составляет 1%.
Так как число страниц в книге составляет 100%,
то
6*100% = 600 (стр.) — в книге.
Ответ: В книге 600 страниц.
Пример №2. Мальчик истратил на покупку 40%
имевшихся у него денег, а на оставшиеся 30 копеек купил билет в
кино. Сколько денег было у мальчика?

Рис. 10. Графическое изображение задачи из
примера №2
Объяснение: Количество всех денег неизвестно,
ставим знак вопроса. Все деньги составляют 100%, поэтому разделим
отрезок условно на 100 равных частей. Найдем, сколько процентов
составляют 30 копеек.
100%-40% = 60% — составляют 30 копеек.
Обозначаем 60% на чертеже. Найдем, сколько
составляет 1% далее объяснение аналогичное.
Пример №3. В школе 700 учащихся. Среди них 357
мальчиков. Сколько процентов учащихся этой школы составляют
девочки?
Рис. 11. Графическое изображение задачи из
примера №3
Объяснение: Число учащихся 700 человек, что
составляет 100%. Отрезок условно делим на сто равных частей. (Само
выполнение чертежа подсказывает ученику первое действие).
700 / 100 = 7 (чел.) — составляют 1%.
Узнаем, сколько процентов составляют мальчики.
Для этого:
357 / 7 = 51%
(Можно сказать и так: «Сколько раз в 357
содержится по 7%?»)
Работаем с чертежом. Узнаем, сколько процентов
составляют девочки.
100%-51%=49%
Ответ 49%
При решении задачи чертеж должен быть постоянно
в поле зрения учащихся, так как является наглядной иллюстрацией
задачи.
Пример №4. По плану рабочий должен был сделать
35 деталей. Однако он сделал 14 деталей сверх плана. На сколько
процентов он перевыполнил план?
Рис.12. Графическое изображение задачи из примера
№4
Решая задачу, нужно объяснить, что план всегда
составляет 100% и поэтому 35 деталей составляют 100%. Чтобы узнать,
сколько составляет 1% нужно:
35 / 100 = 0,35 (дет.)
Узнаем, сколько процентов составляют 14 деталей
(сколько раз в 14 содержится по 0,35).
После изучения обыкновенных дробей и правил
нахождения части числа и числа по части большинство задач лучше
решать, переходя от процентов к дроби.
Пример №1. Ученик прочитал 138 страниц, что
составило 23% всех страниц книги. Сколько страниц в книге?
23% составляет 0,23. Так как известна часть
количества страниц, а нужно найти все количество, то выполняем
действие деления (по правилу, записанному выше):
138 / 0,23 = 13800 : 23=600 (стр.)
Пример №2. Покупатель израсходовал в первом
магазине 40% всех денег, а остальные — во втором. Сколько денег он
израсходовал во втором магазин, если у него было 160 рублей?
40% составляют 0,4. так как известно все
количество денег, а находим их часть, то выполняем действие
умножения.
160*0,4 = 64 (руб.) — израсходовал покупатель в
первом магазине.
Находим, сколько израсходовал покупатель во
втором магазине.
160 — 64=96 (руб.) Записываем ответ.
Практические советы:
1. В задачах на проценты — переходим от процентов к конкретным
величинам. Или, если надо — от конкретных величин к процентам.
Внимательно читаем задачу!
2. Очень тщательно изучаем, от чего нужно считать
проценты. Если об этом не сказано прямым текстом, то обязательно
подразумевается. При последовательном изменении величины, проценты
подразумеваются от последнего значения. Внимательно читаем
задачу!
3. Закончив решать задачу, читаем её ещё раз. Вполне возможно,
вы нашли промежуточный ответ, а не окончательный. Внимательно
читаем задачу!
Рассмотрим еще один важный момент:
В заданиях ЕГЭ обязательно встречаются задачи по математике. До
2010 года это были обычные задачи, которые мы решали в школе.
Задачи, как в учебниках, классические. А вот в 2010 году добавился
новый класс задач, которые в учебниках блистательно отсутствуют.
Итак, в ЕГЭ 2010 появились так называемые
компетентностные задачи. Суть их очень проста.
Нужно посчитать самый выгодный тарифный план для телефона. Или
выбрать самый короткий путь из нескольких вариантов. Или определить
самую низкую температуру за какой-то период. Или разобраться со
скидками на товары и выбрать самый дешёвый вариант. Короче, это
задачи на элементарные житейские навыки.
Задачи очень просты. В них, как правило, не нужно вводить икс,
составлять уравнения. Проблема только в том, что в школьных
учебниках такие задачи не рассматриваются. Поэтому кажутся
непривычными.
Как решать компетентностные задачи?
Всё, что надо для решения этих задачек, проходили в школе. И
проценты в математике, и формулы площадей, и среднюю скорость, и
графики. Причём в этих задачах и не требуются глубокие знания. Одно
— два действия на самые примитивные формулы. А вот житейская логика
необходима. Житейская логика, в этих задачах — самое главное.
Скажем, дана задачка, в которой нужно рассчитать количество
обоев для оклейки комнаты. Дана картинка комнаты с размерами. На
картинке нарисованы окно и дверь — тоже с размерами.
Из всех математических знаний здесь требуется всего одно
откровение — формула площади прямоугольника. Но этого мало. Нужна
ещё житейская логика. Допустим, вы никогда не клеили обои. И не
знаете всех тонкостей этого дела. Но сообразить, что заклеивать
окно обоями не следует, можно? Да и дверь тоже не надо. Собственно,
потолок и пол тоже обоями не принято оклеивать. Хотя в задаче все
эти условия не оговорены. Следовательно, считаем площадь стен (и
только их!) и вычитаем из этой величины площадь окна и двери. Всё.
В таких задачках математика обязательно должна дополняться
элементарными соображениями по жизни. Иначе задачки не решаются,
или решаются неправильно. Не нужно волноваться. Никто и не
предполагает, что ученики должны обладать знаниями
профессионального обойщика, пилота или доярки. Реально всё проще.
Главное — внимательно прочитать задачу! Там всё написано. А та
информация, которой как бы не хватает — берётся из житейской
логики.
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ УЧАЩИХСЯ
ПО ТЕМЕ «ЗАДАЧИ НА ДВИЖЕНИЕ»
1. Два пешехода выходят навстречу друг другу из
разных пунктов, расстояние между которыми 40 км. Если первый выйдет
на час раньше второго, то они встретятся через 3 часа после выхода
первого. Если второй выйдет на час раньше первого, то они
встретятся через 2 часа после выхода первого. С какой скоростью
идет каждый пешеход?
2. Два велосипедиста выезжают навстречу друг
другу из двух пунктов, расстояние между которыми 50 км. Если первый
выедет на час раньше второго, то они встретятся через 2 часа после
выезда второго. Если второй выедет на 2 часа раньше первого, то они
встретятся через час после выезда первого. С какой скоростью едет
каждый велосипедист?
3. Два пешехода выходят навстречу друг другу из
двух пунктов, расстояние между которыми 50 км. Если первый выйдет
на 3 часа раньше второго, то они встретятся через 4 часа после
выхода второго. Скорость первого пешехода на 1 км/ч больше скорости
второго. С какой скоростью идет каждый пешеход?
4. Два бегуна выбегают навстречу друг другу из
двух пунктов, расстояние между которыми равно 45 км. Сумма скорости
бегунов равна 16,5 км/ч. Если первый бегун выбежит на полчаса
раньше второго, то они встретятся через 2,5 часа после того, как
выбежит второй бегун. С какой скоростью бежит каждый бегун?
5. Два велосипедиста выезжают навстречу друг
другу из двух пунктов, расстояние между которыми 80 км. Скорость
первого на 3 км/ч меньше скорости второго. Если второй выедет на 1
час раньше первого, то они встретятся через 2 часа после выезда
первого. С какой скоростью едет каждый велосипедист?
6. Два пешехода выходят навстречу друг другу из
двух пунктов, расстояние между которыми 30 км. Если первый выйдет
на 2 часа раньше второго, то он встретит второго пешехода через 4,5
часа после своего выхода. Если второй выйдет на 2 часа раньше
первого, то он встретит первого пешехода через 5 часов после своего
выхода. С какой скоростью идет каждый пешеход?
Решение: пусть первый пешеход двигался со скоростью км/ч, а второй со
скоростью км/ч. В первом
случае один пешеход пройдет (4,5 х) км, а другой — (2,5 у) км. Во
втором случае первый пешеход пройдет (3 х) км, а второй — (5 у) км.
Зная, что расстояние между двумя пунктами равно 30 км, можем
составить систему уравнений:
Ответ: скорость первого пешехода 5 км/ч, а
второго 3 км/ч.
7. Турист, находящийся в спортивном лагере,
должен успеть к поезду на железнодорожную станцию. Если он поедет
на велосипеде со скоростью 15 км/ч, то опоздает на 30 минут. Если
же он поедет на автобусе, скорость которого 40 км/ч, то приедет за
2 часа раньше до отхода поезда. Чему равно расстояние от лагеря до
станции?
Решение: пусть расстояние от лагеря до станции равно (х) км.
Тогда на велосипеде турист проедет это расстояние за ч, а на
ч. Зная, что в первом
случае турист опоздает на 0,5 ч, а во втором приедет на 2 часа
раньше срока, составим уравнение:
2
Ответ: расстояние от лагеря до станции равно 60
км.
8. Николай и Владимир живут в одном доме.
Николай вышел из дома и направился к школе. Через 4 минуты после
него из дома вышел Владимир и догнал своего друга у школы. Найдите
расстояние от дома до школы, если Николай шел со скоростью 60
м/мин, а скорость Владимира 80 м/минуту.
9. Из пункта А в пункт В, расстояние между
которыми равно 8 км, одновременно вышли два лыжника. Скорость
одного из них на 4 км/ч меньше скорости другого. Лыжник, который
первым прибыл в пункт В, сразу же повернул обратно и встретил
другого лыжника через 45 мин. после выхода из пункта А. На каком
расстоянии от пункта В произошла встреча?
10. Из пункта А в пункт В, расстояние между
которыми 25 км, одновременно выехали автобус и автомобиль. Во время
пути автомобиль сделал остановку на 2 мин., но в пункт В приехал на
3 мин. раньше автобуса. Найдите скорости автомобиля и автобуса,
если известно, что скорость автобуса в 1,2 раза меньше скорости
автомобиля.
Решение: пусть скорость автобуса (х) км/ч, тогда скорость
автомобиля (1,2 х) км/ч. Таким образом, время движения автобуса
ч, а автомобиля
ч. Зная, что автомобиль
сделал остановку на 2 мин., но приехал на 3 мин. раньше автобуса,
составим уравнение:
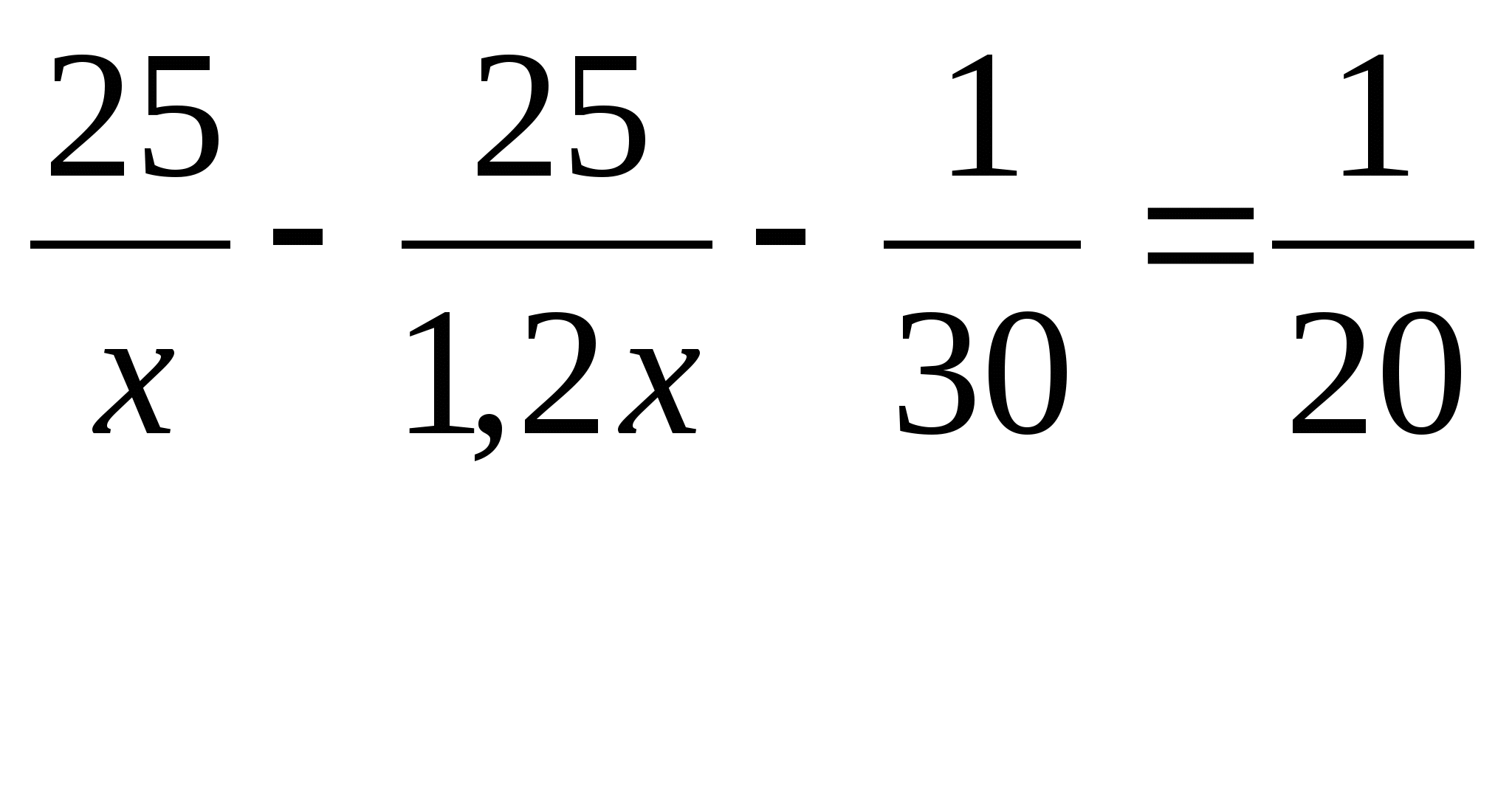
1. 1,2 = 60
(км/ч) — скорость автомобиля.
Ответ: 50 км/ч — скорость автобуса; 60 км/ч —
скорость автомобиля.
11. Катер, собственная скорость которого 8 км/ч,
прошел по реке расстояние, равное 15 км, по течению и такое же
расстояние против течения реки. Найдите скорость течения реки, если
время, затраченное на весь путь, равно 4 часа.
Решение: пусть скорость течения реки равна (х)
км/ч, тогда (8-х) км/ч — скорость катера против течения реки, а
(8+х) км/ч — скорость катера по течению реки. Запишем и решим
уравнение:
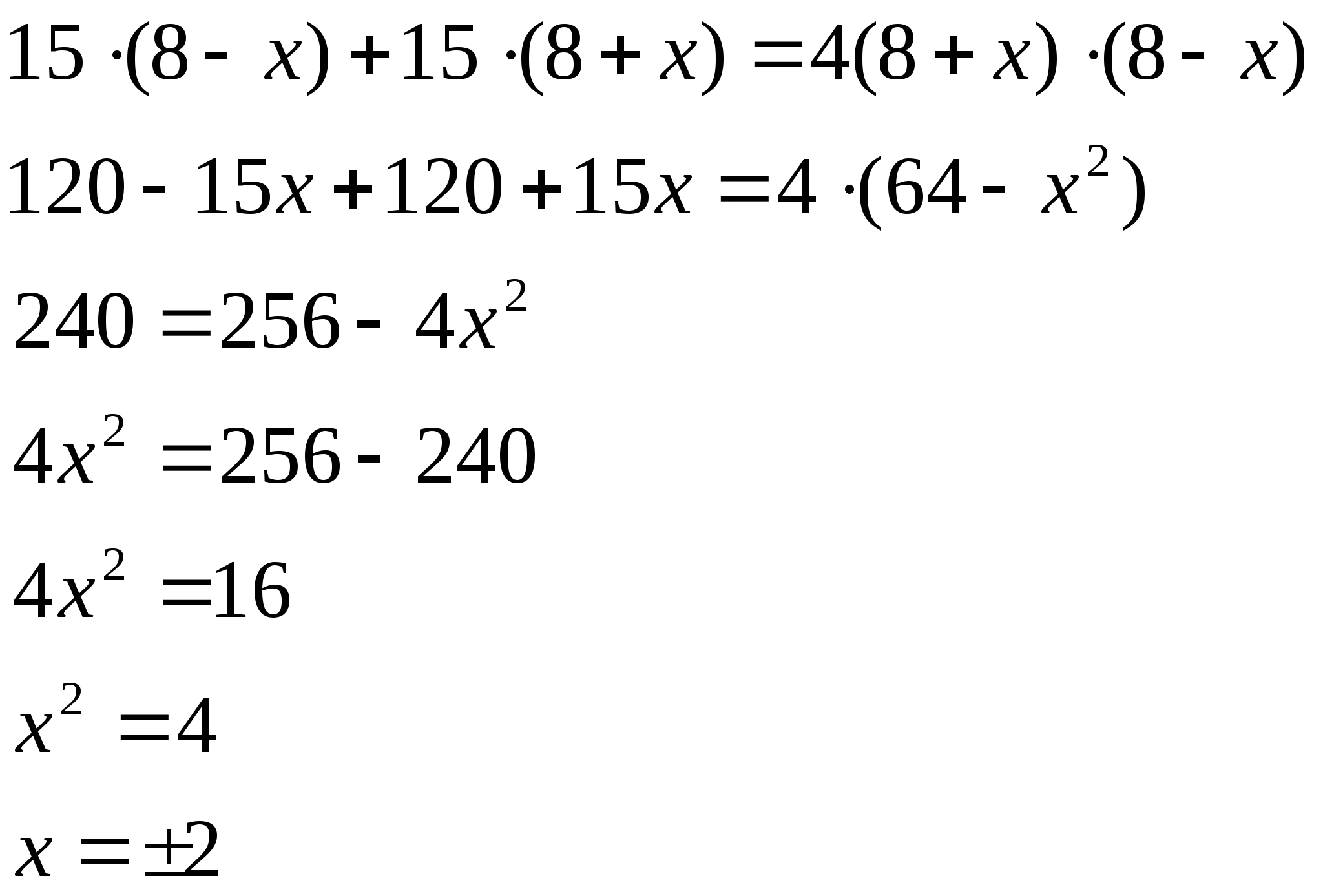
т.к. х = -2 не подходит по смыслу задачи, то
х=2.
Ответ: 2 км/ч — скорость течения реки.
12. Моторная лодка отправилась по реке от одной
пристани к другой и через 2,5 часа вернулась обратно, затратив на
стоянку 25 минут. Найдите скорость течения реки, если собственная
скорость лодки равна 20 км/ч, а расстояние между пристанями 20 км.
13. За 7 часов катер прошел 60 км по течению
реки и 64 км против течения. В другой раз катер за 7 часов прошел
80 км по течению реки и 48 км против течения. Определите
собственную скорость катера и скорость течения реки.
14. Катер проплывает 8 км против течения реки и
еще 30 км по течению за то же время, за которое плот может проплыть
по этой реке 4 км. Скорость катера в стоячей воде равна 18 км/ч.
Найдите скорость плота.
15. На соревнованиях по кольцевой трассе один
лыжник проходил круг на 2 мин. быстрее другого и через час обогнал
его ровно на круг. За сколько минут каждый лыжник проходил круг?
16. На соревнованиях по картингу по кольцевой
трассе один из картов проходил круг на 5 мин. медленнее другого и
через час отстал от него ровно на круг. За сколько минут каждый
карт проходил круг?
Решение: пусть первый карт проходит круг за (х)
мин., тогда второй карт проходит круг за (х+5) мин. Составим и
решим уравнение:
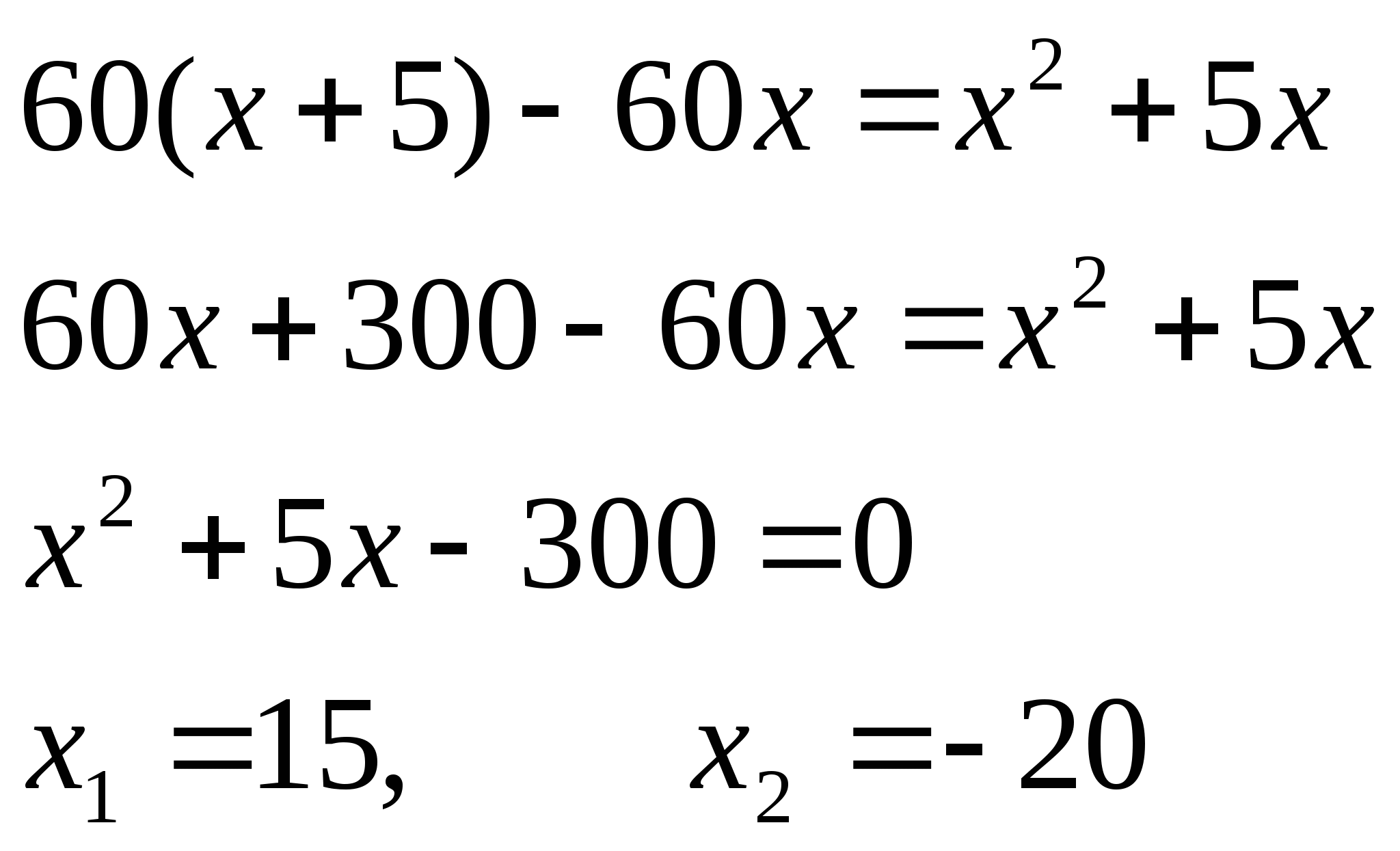
Т.к. по смыслу задачи 0, то х=15
1. 15 + 5 = 10 (мин.) время движения второго
карта.
Ответ: за 15 минут первый карт проходит круг, за
20 мин. второй карт проходит круг.
17. По окружности длиной 60 м равномерно в одном
направлении движутся две точки. Одна из них совершает полный оборот
на 5 с быстрее другой. При этом совпадение точек происходит каждый
раз через 1 минуту. Определите скорости движения точек.
18. Дорога от поселка до станции идет сначала в
гору, а потом под гору, при этом ее длина равна 9 км. Пешеход на
подъеме идет со скоростью, на 3 км/час меньшей, чем на спуске. Путь
от поселка до станции занимает у него 2 часа, а обратный путь — 2
ч. 30 мин. Определите длину подъема на пути к станции и скорость
пешехода на подъеме и на спуске.
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ УЧАЩИХСЯ
ПО ТЕМЕ «ЗАДАЧИ НА СОВМЕСТНУЮ РАБОТУ»
1. Две трубы при совместной работе могут
наполнить бассейн за 4 часа. Если бы сначала первая труба наполнила
половину бассейна, а затем ее перекрыли и открыли вторую, то
наполнение бассейна было бы закончено за 9 часов. За сколько часов
может наполнить этот бассейн каждая труба в отдельности?
Решение: вся работа равна 1. Пусть первая труба
заполнит бассейн за (х) час., а вторая — за (у) час. Составим и
решим систему уравнений:
Ответ одна труба может заполнить бассейн за 12
час., а вторая — за 6 час.
2. Одна из труб может наполнить водой бак на 10
мин. быстрее другой. За какое время может наполнить этот бак каждая
труба, если при совместном действии этих труб в течение 8 мин. было
заполнено бака?
Решение: пусть одна труба заполняет бак за (х)
мин., тогда вторая труба заполнит бак за (х + 10) мин. Составим и
решим уравнение:
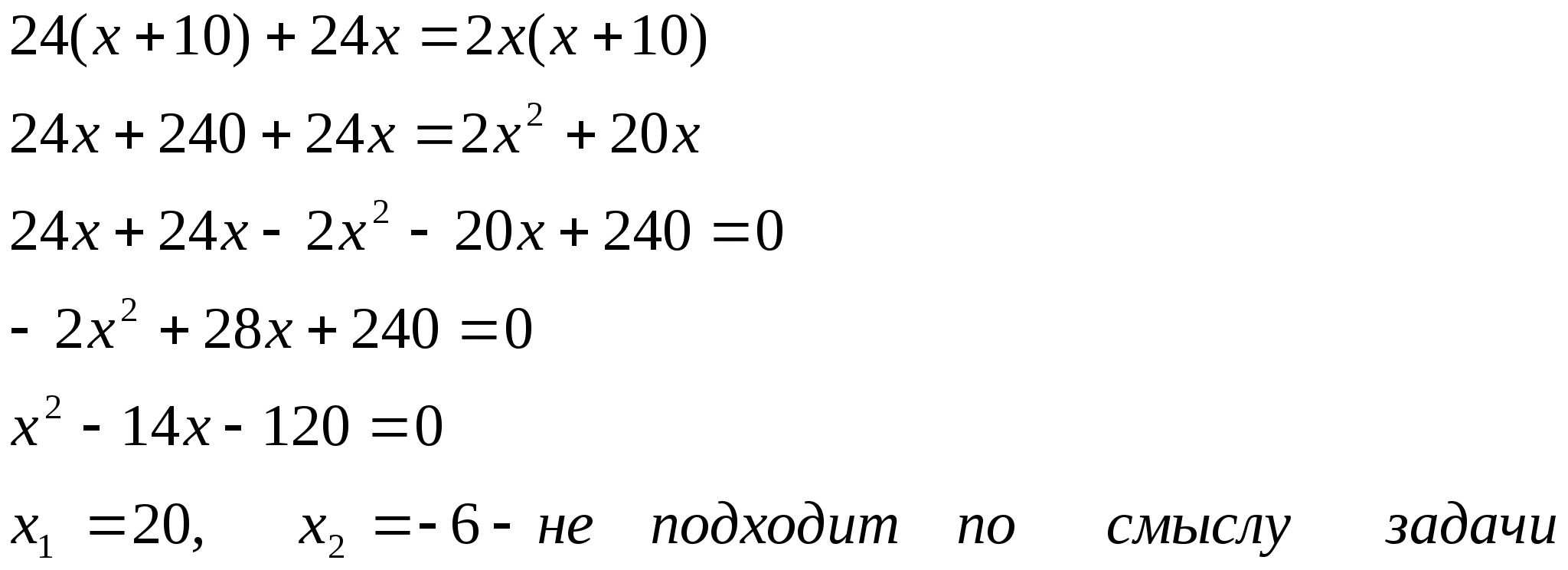
1) 20 + 10 = 30 мин.
Ответ: первая труба заполнит бак за 20 мин., а
вторая — за 30 мин.
3. В бассейн проведены две трубы разного
сечения. Одна равномерно подает, а вторая равномерно отводит воду,
причем через первую бассейн наполняется на 2 часа дольше, чем через
вторую опорожняется. При заполненном на бассейна были открыты
две трубы, и бассейн оказался пустым спустя 8 час. За сколько
часов, действуя отдельно, первая труба наполняет, а вторая
опорожняет бассейн.
4. Четыре бригады должны разгрузить вагон с
продуктами. Вторая, третья и четвертая бригады вместе могут
выполнить эту работу за 4 ч.; первая, третья и четвертая — за 3
часа. Если же будут работать только первая и вторая бригада, то
вагон будет загружен за 6 час. За какое время могут разгрузить
вагон все четыре бригады, работая вместе?
5. Две бригады, работая вместе, должны
отремонтировать участок дороги за 18 дней. В действительности же
получилось так, что сначала работала первая бригада, а заканчивала
ремонт участка дороги вторая бригада. В результате ремонт участка
дороги продолжался 40 дней, причем первая бригада в свое рабочее
время выполнила всей работы.
За сколько дней был бы отремонтирован участок дороги каждой
бригадой отдельно?
6. Одна мельница может смолоть 38 ц пшеницы за 6
часов, другая — 96 ц за 15 часов, третья — 35 ц за 7 часов. Как
распределить 133 т пшеницы между мельницами, чтобы они мололи зерно
в течение одного и того же времени.
7. Лесхоз планировал заготовить за несколько
дней 216 новогодних елей. Первые три дня лесхоз выполнял
установленную ежедневную норму, а потом стал заготавливать на 2 ели
в день больше. Поэтому уже за 1 день до срока было заготовлено 232
ели. Сколько елей ежедневно заготавливал лесхоз в первые три дня
работы.
8. Машинистка должна была напечатать за
определенное время 200 страниц. Печатая в день на 5 страниц больше,
чем планировала, она завершила работу на два дня раньше срока.
Сколько страниц в день печатала машинистка?
Решение: пусть машинистка фактически набирала
(х) страниц в день, тогда по плану она должна была набирать (х — 5)
страниц в день. Таким образом планировалось напечатать 200 страниц
за 200 : (х-5) дней, в то время как машинистка справилась с работой
на 2 дня раньше. Составим и решим уравнение:
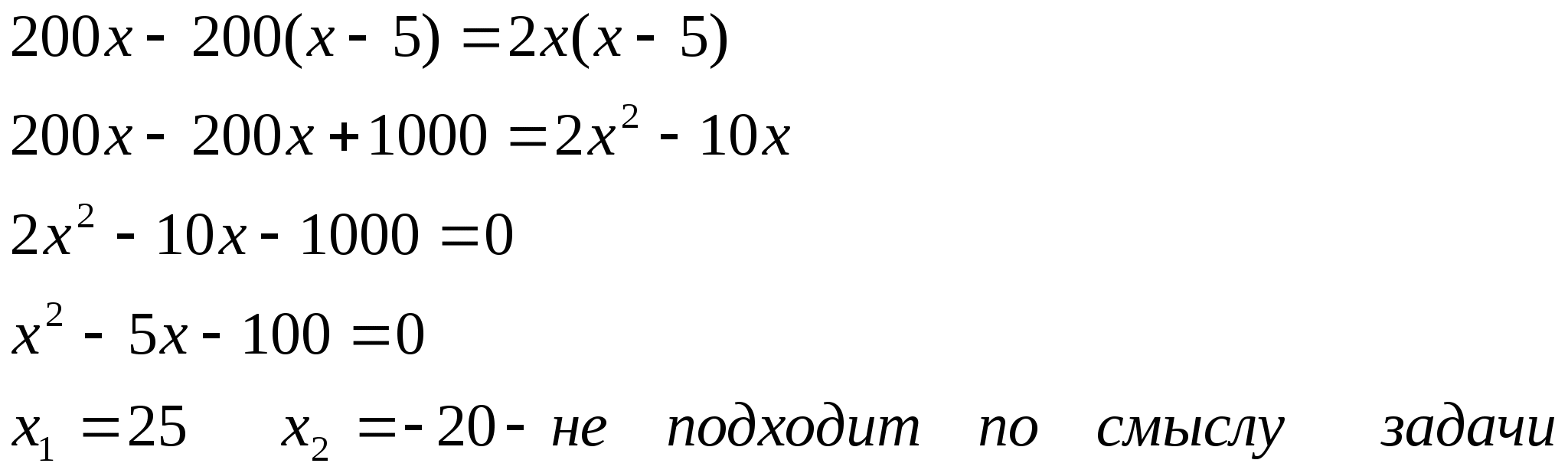
Ответ: машинистка печатала по 25 страниц в день.
9. Николай планировал, что сможет хорошо
подготовиться к экзамену, если будет решать по 12 задач в день.
Однако ежедневно он перевыполнял свою норму на 8 задач и уже за 5
дней до экзамена решил на 20 задач больше, чем планировал сначала.
Сколько задач решил Коля?
Урок в 11 классе по теме:
«Итоговое повторение. Решение текстовых задач.
Подготовка к ЕГЭ»
Цели урока:
1. Отработка практических навыков решения задач на совместную
работу;
2. Закрепление навыка решения дробно-рациональных уравнений;
3. Отработка практических навыков решения задач на части;
4. Повторение понятия процента и отработка навыка нахождения
процента от числа;
5. Отработка практических навыков решения задач на
арифметическую прогрессию;
6. Повторение и закрепление формулы n-го члена арифметической
прогрессии и формулу суммы n-первых членов арифметической
прогрессии;
7.Подготовка выпускников к ЕГЭ.
Оборудование: раздаточный материал, компьютер, экран
Ход урока
Учитель: На сегодняшнем уроке мы с вами
рассмотрим текстовые задачи, которые предлагались на ЕГЭ по
математике в прошлые годы.
Мы рассмотрим три типа задач: на совместную
работу, на части и на арифметическую прогрессию, отработаем решение
дробно-рациональных уравнений, вспомним понятие процента и правило
нахождения процента от числа. При решении задач на арифметическую
прогрессию мы повторим формулу суммы n-первых членов арифметической
прогрессии.
Некоторые задачи мы будем решать с вами вместе,
решение некоторых будет предложено для самостоятельного выполнения.
I.Решение задачи на совместную работу вместе с учителем.
Задача . Два мебельных мастера, работая вместе, могут за 1
неделю собрать 50 столов. Работая отдельно, первый мастер собирает
60 столов на одну неделю дольше, чем такое же число столов собирает
второй мастер. За
сколько недель первый мастер соберет 40 столов?
Решение.
Пусть первый мастер собирает за неделю x столов, тогда второй-
50-х столов. Тогда 60 столов первый мастер соберет за 60:х недель,
а второй за 60:(50-х) недель. Зная, что первый мастер собирает 60
столов на 1 неделю дольше, составим и решим уравнение:
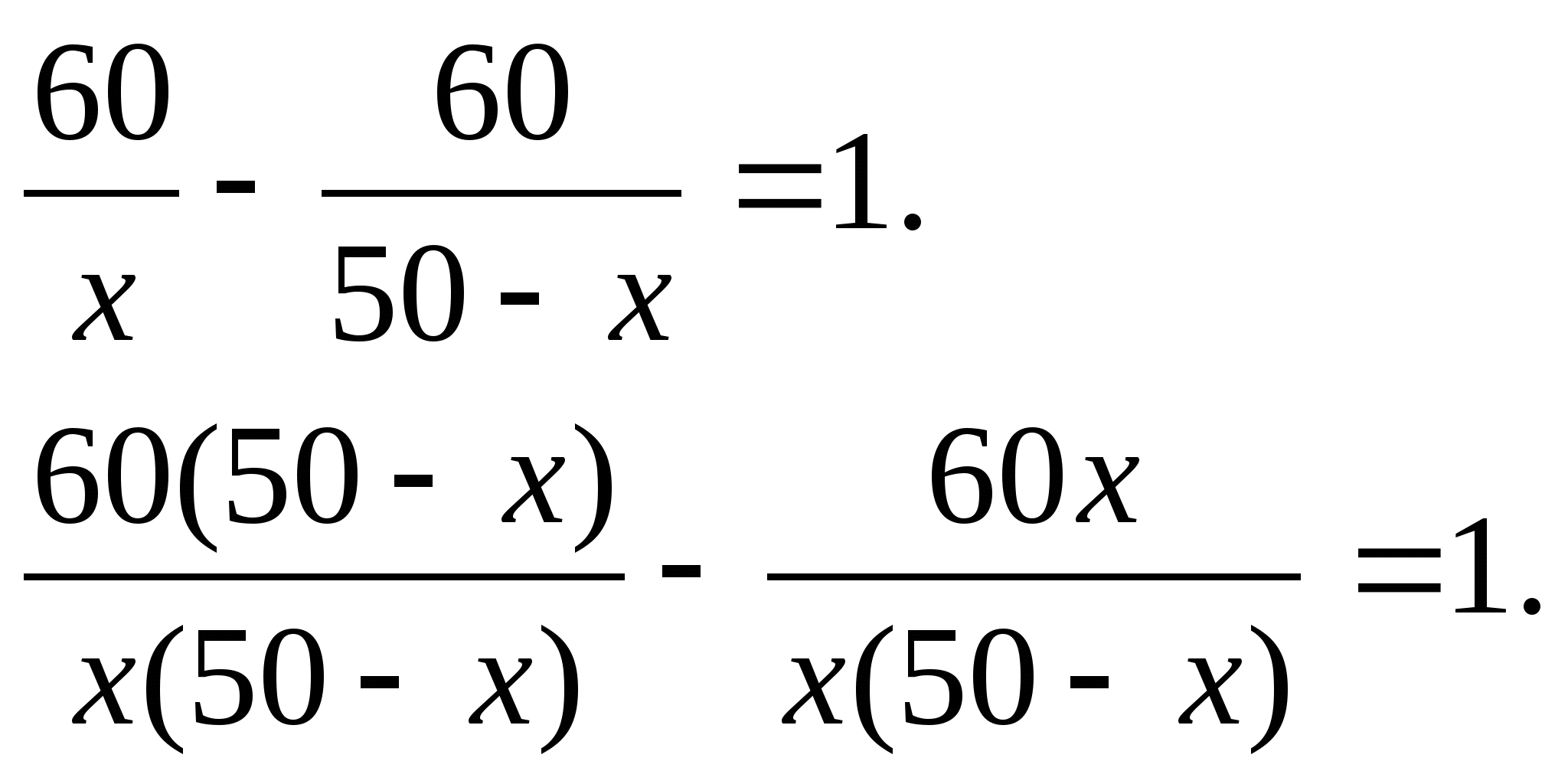
Получаем квадратное уравнение:
Решая его, находим корни х=20; х=150.
х=150 не удовлетворяет условию задачи, значит, для нашей задачи
х=20.
Таким образом, первый мастер за неделю собирает 20 столов.
Значит , 40 столов он соберет за 40:20=2(недели).
Ответ: первый мастер соберет 40 столов за 2 недели.
II. К доске вызываются двое учащихся. Им предлагается
самостоятельно решить по одной задаче на совместную работу. Класс в
это время работает самостоятельно, потом происходит проверка
решения.
Текст задач для учащихся.
-
Два маляра, работая вместе, могут за 1 ч покрасить стену
площадью
40 м2. Первый маляр, работая отдельно, может
покрасить 50 м2 стены
на 4 ч быстрее, чем второй покрасит 90 м2 такой же
стены. За сколько
часов первый маляр сможет покрасить 100 м2 стены?
2. Два оператора,
работая вместе, могут набрать 40 страниц текста за 1ч.
Работая отдельно, первый оператор на набор 90 страниц этого
текста
тратит на 5 ч больше, чем второй оператор на набор 25 страниц.
За
сколько часов второй оператор сможет набрать 275 страниц этого
текста?
III.Решение задачи на части вместе с учителем.
Задача. Первый сплав состоит из цинка и меди,
входящих в отношении 1:2, а другой сплав содержит те же металлов в
отношении 2:3. Из скольких частей обоих сплавов можно получить
третий сплав, содержащий те же металлы в отношении 17:27?
Решение.
Запишем условие задачи в виде таблицы.
Заметим, что =
, или 27x + 54y = 34x +
51y, откуда 3y = 7x.
Т.к. 3x = A, 5y = B, то =
=
=
.
Ответ: сплав следует взять в соотношении 9:35.
Задача . Объемы ежегодной добычи угля первой, второй и третьей
шахтами
относятся как 1: 2: 4. Первая шахта планирует уменьшить годовую
добычу угля на 8%, а вторая — на 2%. На сколько процентов должна
увеличить годовую добычу угля третья шахта, чтобы суммарный
объем
добываемого за год угля не изменился?
Решение: Пусть х- объем 1 части добываемого угля, а у-
планируемое увеличение годовой добычи угля третьей шахтой.
У нас 2 ситуации: первая — первоначальная добыча, вторая —
планируемая добыча. Составим таблицу:
-
Планируемая добыча
1 шахта
х
0,92х
2 шахта
2х
0,98∙2х
3 шахта
4х
4ху
Зная, что суммарный объем добываемого угля не должен измениться,
составим и решим уравнение:
Зная, что х не равен нулю, т.к. величина 1 части не может быть
нулевой, разделим данное уравнение на х.
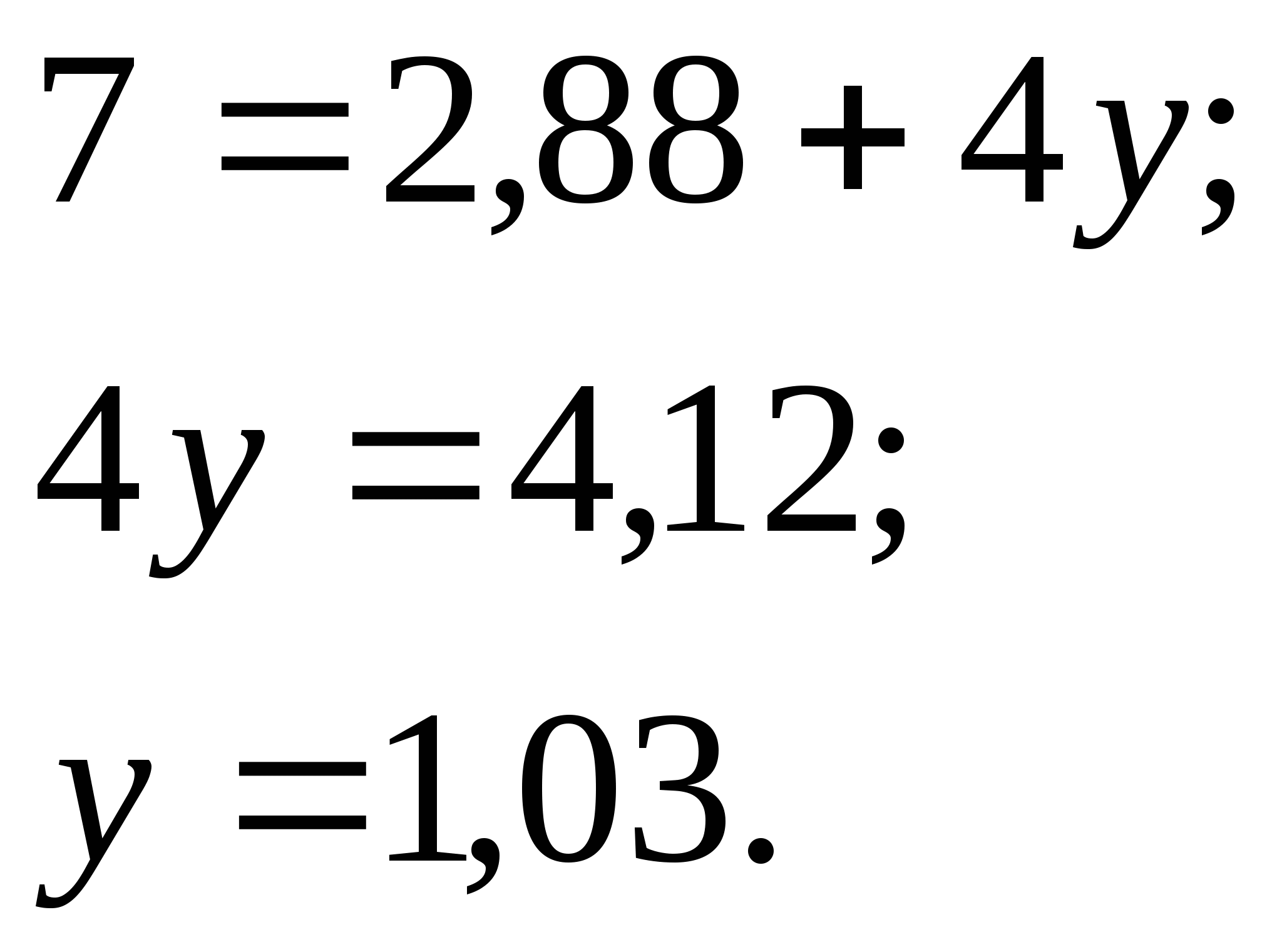
Вывод: добыча угля 3
шахтой должна увеличится на 3 %.
Ответ: третья шахта должна увеличить добычу на 3 процента.
IV.К доске вызываются двое учащихся. Им предлагается
самостоятельно решить по одной задаче на совместную работу. Класс в
это время работает самостоятельно, потом происходит проверка
решения.
1.Подарочный набор состоит из трех сортов конфет. Массы конфет
первого, второго и третьего сортов в этом наборе относятся как
3:8:17.
Массу конфет первого сорта увеличили на 10%, а второго — на 9%.
На
сколько процентов надо уменьшить массу конфет третьего сорта,
чтобы
масса всего набора не изменилась?
2.Набор химических реактивов состоит из трех веществ. Массы
первого,
второго и третьего веществ в этом наборе относятся как 5:8:12.
Массу
первого вещества увеличили на 8%, а второго — на 4%. На сколько
процентов надо уменьшить массу третьего вещества, чтобы масса
всего
набора не изменилась?
V. Решение задачи на арифметическую прогрессию (вместе с
учителем).
Задача 3. В первый день подготовки к экзамену школьник повторил
3 вопроса. В каждый следующий день он повторял на 2 вопроса больше,
чем в предыдущий, и успел вовремя подготовить все 48 вопросов
программы. Сколько дней заняла подготовка?
Решение. Количество вопросов, повторяемых школьником ежедневно
составляет арифметическую прогрессию, первый член которой равен 3,
а разность равна 2. Пусть n (натуральное число) — число дней,
потраченных на подготовку. Тогда количество повторенных вопросов
(48 вопросов) равно сумме n членов этой арифметической прогрессии,
т.е.
Получаем:
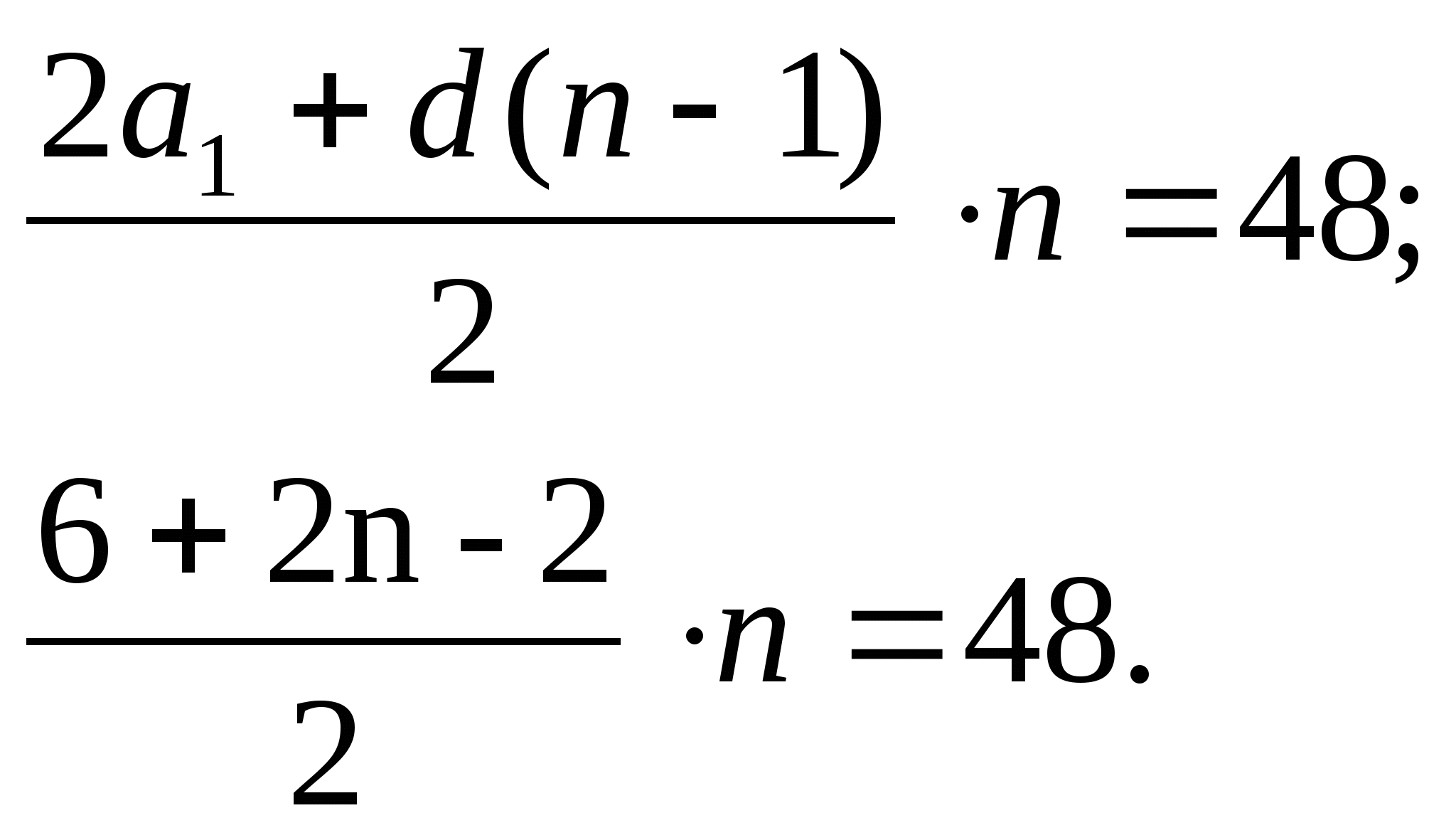
Необходимо решить квадратное уравнение:
Решая, находим корни: n=6, n= — 8. Берём положительный корень.
Таким образом, подготовка заняла 6 дней.
Ответ: подготовка заняла 6 дней.
VI. К доске вызывается 1 учащийся для решения аналогичной
задачи.
1.Группа туристов в первый день путешествия прошла 10 км. Далее
туристы решили ежедневно преодолевать на 5 км больше, чем в
предшествующий день, пользуясь при этом, если потребуется,
автостопом. В результате они преодолели расстояние 450 км. Сколько
дней туристы были на маршруте, если в течение этого времени 8 дней
они отдыхали?
Подведение итога урока.
Выставление оценок. Отмечаются учащиеся, работавшие у доски.
Домашнее задание: Решить задачи:
1. Один рабочий изготавливает 120 деталей на 1 ч дольше, чем
такие же 120
деталей изготавливает второй рабочий. Работая вместе, они за 1 ч
изготавливают 100 таких деталей. За сколько часов второй рабочий
может изготовить 300 деталей?
2. Объемы ежегодной добычи угля первой, второй и третьей шахтами
относятся как 13:14:8. Первая шахта планирует уменьшить годовую
добычу угля на 2%, а вторая — на 1%. На сколько процентов должна
увеличить годовую добычу угля третья шахта, чтобы суммарный
объем
добываемого за год угля не изменился?
3.Десятый член арифметической прогрессии равен 19, а сумма
первых пятидесяти членов равна 2500.Найти сумму третьего,
двенадцатого и двадцатого членов этой прогрессии.
ЗАКЛЮЧЕНИЕ
Математика в наши дни проникает во все сферы
жизни. Овладение практически любой профессией требует тех или иных
знаний по математике. Именно математическое мышление позволяет
адекватно воспринимать окружающий нас мир. Этому способствуют
многие темы по предмету, но особое место среди них занимает тема
«Решение текстовых задач». Текстовые задачи включены в материалы
итоговой аттестации за курс основной школы, в КИМы и ЕГЭ, в
конкурсные экзамены.
Этот проект позволяет сгладить противоречия,
которые возникают при изучении данной темы в школе и в предлагаемых
вариантах ЕГЭ. Он ориентирует учащихся на обучение по
естественно-научному и социально-экономическому профилю.
Познавательный материал проекта будет
способствовать не только выработке умений решать задачи, но будет
формировать устойчивый интерес учащихся к процессу и содержанию
деятельности, а также познавательной и социальной активности.
Он предназначен для предпрофильной подготовки
учащихся 9-х классов и для подготовки к ЕГЭ по математике.
СПИСОК ЛИТЕРАТУРЫ
-
Алгебра: Учеб. для 7 кл. сред шк./ Ю.Н.
Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред.
С.А. Теляковского. — М.: Просвещение, 1989. — 240 с.: ил. -
Алгебра: Учеб. для 8 кл. сред шк./ Ю.Н.
Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред.
С.А. Теляковского. — 2-е изд. — М.: Просвещение, 1991. — 239
с.: ил. -
Алгебра: Учеб. для 9 кл. общеобразоват.
учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.
Суворова; Под ред. С.А. Теляковского. — 4-е изд. — М.:
Просвещение, 1997. — 272 с.: ил. -
Обучение решению задач как средство развития
учащихся: из опыта работы. Методическое пособие для учителя. —
Киров, ИИУ. — 1999. — С.3-18. -
Фридман Л.М., Турецкий Е.Н. Как научится
решать задачи: Кн для учащихся ст. классов сред. шк. — 3-е
изд., дораб. — М.: Просвещение, 1989. — 192 с.: ил. -
Шевкин А.В. Материалы курса «Текстовые
задачи в школьном курсе математики»: Лекции 1-8 — М.:
Педагогический университет «Первое сентября», 2010 -
Дорофеев, Г.В., Седова, Е.А. Процентные
вычисления, 10-11 классы: учебно-методическое пособие. — М.
Дрофа, 2003. — 144с. -
Козина, М.Е. Сборник элективных курсов /
М.Е. Козина — Волгоград: Учитель, 2007. — 137с. -
Кузнецова, Л.В. Сборник заданий для
подготовки к итоговой аттестации в 9 кл. / В. Кузнецова, С.Б.
Суворова и др. М.: Просвещение, 2006 — 192с. -
Симонов, А.С. Сложные проценты. / Математика
в школе. — 1998. — № 5.