Задача 1
15 января планируется взять кредит в банке на 16 месяцев. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного погашения равнялась 2,34 млн рублей?
Дано:
S — кредит
n = 16 месяцев
r = 2%
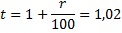
2,34 млн рублей — общая сумма выплат
Найти:
S — ?
Решение:
|
Долг |
Долг с % |
Выплаты |

|
St |
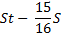
|
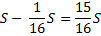
|

|
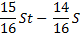
|
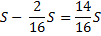
|

|
|
|
… |
… |
… |
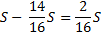
|

|

|
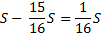
|
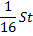
|

|
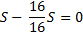
|
— |
— |
По условиям задачи, общая сумма выплат после полного погашения кредита равна 2,34 млн рублей.
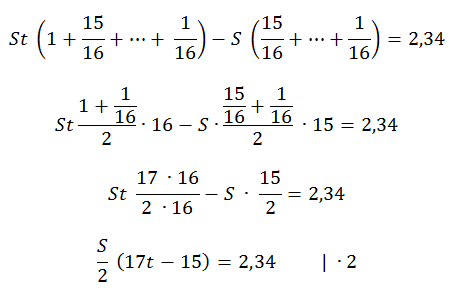
S (17t — 15) = 4,68
Подставим в полученное выражение известное значение t.
S (17 • 1,02 — 15) = 4,68
2,34 S = 4,68
S = 2 (млн рублей)
Ответ: 2 млн рублей
Задача 2
15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
Дано:
S = 2,4 млн рублей
n = 24 месяца
r = 3%
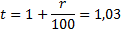
Найти:
Общую сумму выплат за первые 12 месяцев.
Решение:
|
Долг |
Долг с % |
Выплаты |

|
St |
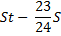
|
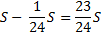
|

|
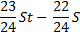
|

|
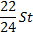
|
|
|
… |
… |
… |

|
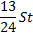
|

|

|
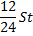
|
|
|
… |
… |
… |

|
— |
— |
Найдем общую сумму выплат за первые 12 месяцев.
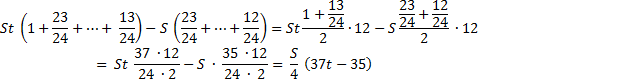
Подставим в полученное выражение значения известных переменных.
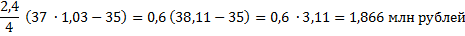
Ответ: 1,866 млн рублей
Задача 3
15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
- к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
Дано:
S тыс. рублей: кредит
n = 21 месяц
r = 3%
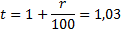
Общая сумма выплат равна 1604 тыс. руб.
Найти:
S — ?
Решение:
|
Долг |
Долг с % |
Выплаты |
|
S — 0 • 30 |
tS |
1) tS — (S — 1 • 30) |
|
S — 1 • 30 |
t (S — 1 • 30) |
2) t(S — 1 • 30) — (S — 2 • 30) |
|
S — 2 • 30 |
t (S — 2 • 30) |
3) t(S — 2 • 30) — (S — 3 • 30) |
|
S — 3 • 30 |
t (S — 3 • 30) |
4) t(S — 3 • 30) — (S — 4 • 30) |
|
… |
… |
… |
|
S — 18 • 30 |
t (S — 18 • 30) |
19) t(S — 18 • 30) — (S — 19 • 30) |
|
S — 19 • 30 |
t (S — 19 • 30) |
20) t(S — 19 • 30) — (S — 20 • 30) |
|
S — 20 • 30 |
t (S — 20 • 30) |
21) t(S — 20 • 30) — 0 |
|
0 |
По условию задачи известно, что общая сумма выплат равна 1604 тыс. рублей.
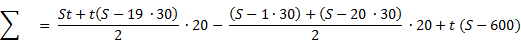
1) (St + St — 570t) • 10 — (2S — 630) • 10 + St — 600t = 20St — 5700t — 20S +6300 + St — 600t = 21St — 20S + 6300 — 5700t = 21 • 1,03S — 20S + 6300 — 5700 • 1,03 = 21,63S — 20S +6300 — 6489 = 1,63S — 189
2) Выплаты составили 1604 тыс. рублей:
1,63S — 189 = 1604
1,63S = 1793
S = 1100 тыс. рублей
Ответ: 1100 тыс. рублей.

ЕГЭ-2020. Математика. Сборник заданий: 500 заданий с ответами
Книга содержит задания разных типов и уровней сложности по темам, знание которых проверяется на ЕГЭ, а также комментарии к ним. Ко всем заданиям приводятся ответы. Поможет потренироваться в выполнении заданий, повторить пройденный материал и эффективно подготовиться к сдаче ЕГЭ.
Купить
Задача 4
15-го декабря планируется взять кредит в банке на 1200 тысяч рублей на (n + 1) месяц. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
- cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по n-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
- 15-го числа n-го месяца долг составит 400 тысяч рублей;
- к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1288 тысяч рублей.
Дано:
S = 1200 тыс. рублей (кредит)
n + 1 месяц — срок кредитования
r%
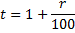
С 1-го по n-ный месяц долг уменьшается на 80 тыс. рублей.
15-го числа n-го месяца долг составит 400 тыс. рублей.
Общая сумма выплат составляет 1288 тыс. рублей (после полного погашения кредита).
Найти:
r — ?
Решение:
|
Долг |
Долг с % |
Выплаты |
|
S — 0 • 80 |
t • S |
1) tS — (S — 1 • 80) |
|
S — 1 • 80 |
t (S — 1 • 80) |
2) t(S — 1 • 80) — (S — 2 • 80) |
|
S — 2 • 80 |
t (S — 2 • 80) |
3) t(S — 2 • 80) — (S — 3 • 80) |
|
S — 3 • 80 |
t (S — 3 • 80) |
|
|
… |
… |
… |
|
S — (n — 1) • 80 |
t (S — (n — 1) • 80) |
n) t(S — (n — 1) • 80) — (S — n • 80) |
|
S — n • 80 |
t (S — n • 80) |
n + 1) t(S — n • 80) — 0 |
|
0 |
1) 15 числа n-го месяца долг составляет 400 тыс. рублей:
S — n • 80 = 400
1200 — n • 80 = 400
n • 80 = 800
n = 10
2) Общая сумма выплат составляет 1288 тыс. рублей.
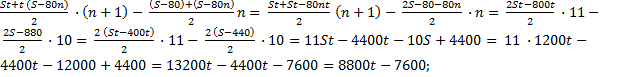
8800t — 7600 = 1288
8800t = 8888
t = 1,01
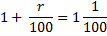
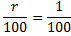
r = 1%
Ответ: 1%
Задача 5
В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
Дано:
S = 5 млн руб. (кредит)
r = 20%,
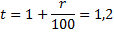
Общая сумма выплат после полного погашения кредита составит 7,5 млн. руб.
Найти:
n — ? (число лет)
Решение:
1)
|
Долг |
Долг с % |
Выплаты |
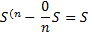
|
St |

|
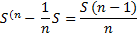
|

|
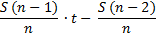
|
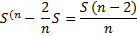
|
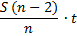
|
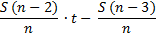
|
|
… |
… |
… |
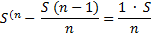
|
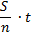
|
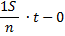
|
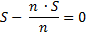
|
— |
— |
По формуле суммы арифметической прогрессии получим:
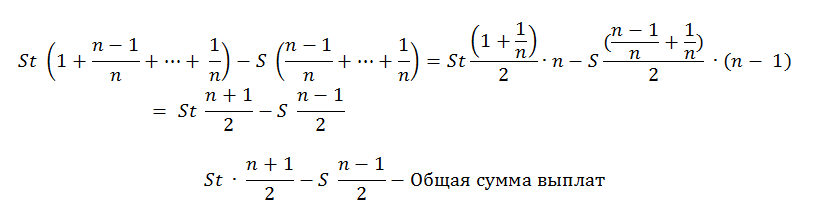
2) По условию задачи известно, что общая сумма выплат после полного погашения кредита составит 7,5 млн рублей, тогда:
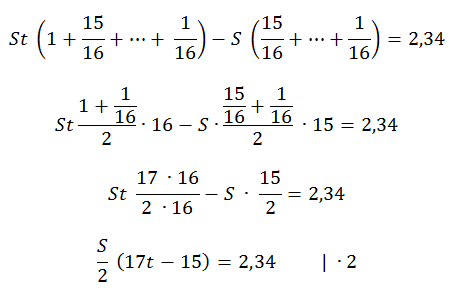
0,2n + 2,2 = 3
0,2n = 0,8
n = 4
4 года — на столько лет планируется взять кредит.
Ответ: 4
Задача 6
15-го января планируется взять кредит в банке на девять месяцев. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.
Дано:
S — кредит
n = 9 месяцев
r = r%
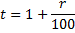
Со 2-го по 14-е число месяца необходимо выплатить часть долга.
15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Общая сумма выплат по кредиту на 25% больше суммы, взятой в кредит.
Найти:
r — ?
Решение:
|
Долг |
Долг с % |
Выплаты |
|
St |
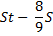
|
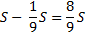
|
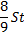
|
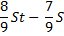
|
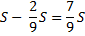
|

|

|
|
… |
… |
… |
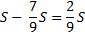
|

|
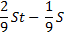
|

|

|
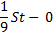
|
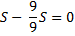
|
— |
— |
1) Найдем общую сумму выплат:
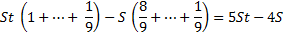
2) По условию задачи известно, что общая сумма выплат на 25% больше суммы, взятой в кредит:
S — 100%
(5St — 4S) — 125%
100 (5St — 4S) = 125S
500St — 400S = 125S
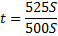
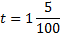
3) 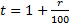
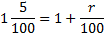
r = 5%
Ответ: 5%
Задача 7
15-го января планируется взять кредит в банке на 18 месяцев. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Дано:
S — кредит
n = 18 месяцев
r = 2%
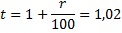
Долг уменьшается на одну и ту же сумму.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Решение:
|
Долг |
Долг с % |
Выплаты |
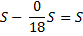
|
St |
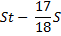
|
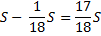
|
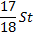
|

|

|
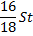
|

|
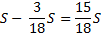
|

|
… |
|
… |
… |
… |
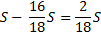
|

|
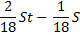
|
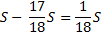
|
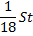
|

|
1) По формуле суммы арифметической прогрессии получим:
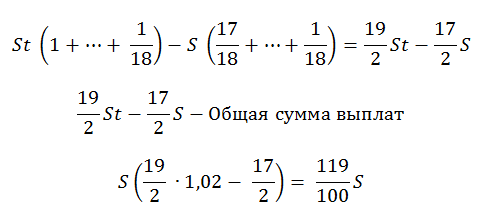
2) S — 100%
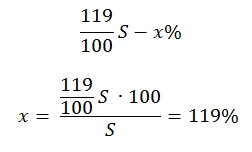
— столько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования.
Ответ: 119%
Задача 8
15-го декабря планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца, где r — целое число;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,7 млн рублей.
Дано:
S = 1 млн рублей (кредит)
n = 6 месяцев
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг |
1 |
0,7 |
0,6 |
0,4 |
0,2 |
0,1 |
0 |
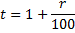
Найти:
Наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,7 млн рублей.
Решение:
1)
|
Долг |
Долг с % |
Выплаты |
|
1 |
1t |
1t — 0,7 |
|
0,7 |
0,7t |
0,7t — 0,6 |
|
0,6 |
0,6t |
0,6t — 0,4 |
|
0,4 |
0,4t |
0,4t — 0,2 |
|
0,2 |
0,2t |
0,2t — 0,1 |
|
0,1 |
0,1t |
0,1t — 0 |
|
0 |
— |
— |
Найдем общую сумму выплат:
t (1 + 0,7 + 0,6 + 0,4 + 0,2 + 0,1) — (0,7 + 0,6 + 0,4 + 0,2 + 0,1) = 3t — 2
3t — 2 — общая сумма выплат.
2) По условию задачи известно, что общая сумма выплат будет меньше 1,7 млн рублей:
3t — 2 < 1,7
3t < 3,7
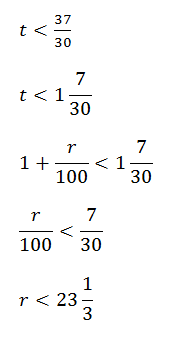
Наибольшее целое число этого неравенства r = 23%
Ответ: 23%
Задача 9
15 декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
- 15-го числа 20-го месяца долг составит 100 тысяч рублей;
- к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Дано:
S = 300 тыс. руб. (кредит)
n = 21 месяц
r = 2%
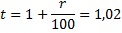
15-го числа 20-го месяца долг составит 100 тыс. рублей.
Найти:
Общую сумму выплат.
Решение:
Пусть х тыс. рублей — ежемесячный равный платеж.
|
Долг |
Долг с % |
Выплаты |
|
S — 0 • x |
t (S — 0 • x) |
1) t (S — 0 • x) — (S — 1x) |
|
S — 1 • x |
t (S — 1 • x) |
2) t (S — 1 • x) — (S — 2x) |
|
S — 2 • x |
t (S — 2 • x) |
3) t (S — 2 • x) — (S — 3x) |
|
S — 3 • x |
t (S — 3 • x) |
|
|
… |
… |
… |
|
18) S — 18x |
t (S — 18 • x) |
19) t (S — 18 • x) — (S — 19x) |
|
19) S — 19x |
t (S — 19 • x) |
20) t (S — 19 • x) — (S — 20x) |
|
20) S — 20x |
t (S — 20 • x) |
21) t (S — 20 • x) — 0 |
|
0 |
1) По условиям задачи известно, что 15-го числа 20-го месяца долг составит 100 тыс. рублей:
S — 20x = 100
300 — 20x = 100
20x = 200
X = 10 тыс. рублей
2) Найдем общую сумму выплат:
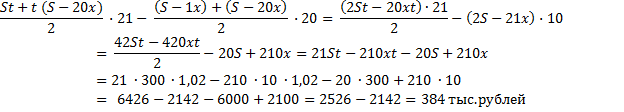
Ответ: 384 тыс. рублей.
#ADVERTISING_INSERT#
Всего: 71 1–20 | 21–40 | 41–60 | 61–71
Добавить в вариант
15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
− 1-го числа k-ого месяца долг возрастёт на 1% по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число k-того месяца необходимо выплатить часть долга;
− 15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 402 (C часть).
В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн рублей?
Источник: А. Ларин: Тренировочный вариант № 238.
Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект Х, а остальные 60% в проект Y. Проект Х может принести прибыль в размере от 19% до 24% годовых, а проект Y — от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможные уровни процентной ставки, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты Х и Y.
Источник: А. Ларин. Тренировочный вариант № 366.
15‐го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
Семья Ивановых ежемесячно вносит плату за коммунальные услуги, телефон и электричество. Если бы коммунальные услуги подорожали на 50%, то общая сумма платежа увеличилась бы на 35%. Если бы электричество подорожало на 50%, то общая сумма платежа увеличилась бы на 10%. Какой процент от общей суммы платежа приходится на телефон?
Источник: А. Ларин: Тренировочный вариант № 106.
В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 1,5 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
В июле планируется взять кредит в банке на сумму 17 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 3,4 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 10% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 8 млн.
В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017,2018 и 2019 долг остаётся равным S тыс. рублей;
− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;
− к июлю 2021 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 509 (C часть).
Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27% больше, чем сумма, взятая им в кредит. Найдите r.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С).
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С)., Задания 17 (С4) ЕГЭ 2015
15 января планируется взять кредит в банке на 6 месяцев в размере 1 млн руб. Условия его возврата таковы:
− Первого числа месяца долг увеличивается на r% по сравнению с концом предыдущего месяца, где r целое число.
− Со 2 по 14 число необходимо выплатить часть долга.
− 15 числа каждого месяца долг должен составлять некоторую сумму в соответствии с таблицей
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
| Долг | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее r, при котором сумма выплат будет меньше 1,25 млн руб.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 412. Запад (C часть).
В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 20%;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017-2019 долг остаётся S
− в 2020, 2021 выплаты по 360 тыс. руб.
− к июлю 2021 долг будет выплачен полностью
Найдите общую сумму выплат за 5 лет.
Источник: ЕГЭ по математике 06.06.2016. Основная волна.
В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 419 (C часть)., Задания 17 ЕГЭ–2020
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 2% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 327 тысяч рублей.
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 1% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 836 тысяч рублей.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S — натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 17,5% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в тыс. рублей) |
S | 0,9S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 703 (C часть).
По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика за два года станет больше 100 миллионов, а за четыре года станет больше 170 миллионов рублей.
Всего: 71 1–20 | 21–40 | 41–60 | 61–71
На чтение 12 мин Просмотров 33.5к. Опубликовано 7 февраля, 2019
Для решения таких задач необходимо понимать алгоритм решения экономических задач
За задание №17 по математике ЕГЭ профильный уровень можно получить 3 балла. Мы рассмотрим как решать экономические задачи ЕГЭ по математике, которые в каждом варианте профильного уровня по математике идут под номером 17.
Решение №17 включает в себя обязательное построение математической модели, то есть это обычная текстовая задача, но с экономическим (финансовым) уклоном и чаще всего с большим количеством вычислений.
Можно выделить несколько блоков заданий:
1. Вклады и кредиты
2. Акции и другие ценные бумаги
3. Методы оптимальных решений
Рассмотрим каждый из вышеперечисленных блоков.
Содержание
- Вклады и кредиты
- Акции и другие ценные бумаги
- Методы оптимальных решений
- Примеры решения задач
Вклады и кредиты
Вклады и кредиты – самый обширный блок. Здесь вы можете встретить различные схемы возврата кредита или увеличения суммы вклада, и ваша задача – упорядочить данные таким образом, чтобы большой массив текста превратился в удобную математическую схему.
Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов. Начисление по этой формуле предполагает, что каждый последующий год процент начисляется не на исходную сумму, а на исходную сумму, увеличенную предыдущим начислением процентов.
Формула выглядит следующим образом:
где FV – будущая сумма.
PV – текущая сумма.
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента.
Если начисления происходят не ежегодно, а чаще, например, ежеквартально, формула модифицируется в следующий вид:
,
где
FV – будущая сумма
PV – текущая сумма
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента
m – количество начислений в год (например, m=4, если начисления ежеквартальные).
Давайте отработаем эту формулу на подготовительной задаче.
Задача 1
Алексей положил 100 000 рублей в банк под 6% годовых на 3 года. Какая сумма будет у Алексея через год? Через 2 года? Через 3 года?
Решение:
Рассчитаем по формуле сложного процента сумму через год:
Теперь сумму через 2 года:
Теперь сумму через 3 года:
Более того, вам придётся работать со схемами кредитов/вкладов, поэтому решим более сложную задачу, в которой нужно будет переводить текст в таблицы и уравнения/неравенства.
Задача 2
Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 28 млн рублей.
Решение:
Пусть искомая сумма составит a млн рублей.
Составим таблицу, чтобы упорядочить данные и построить математическую модель.
По условию, нужно найти наименьшее целое x, для которого выполнено неравенство
14,641 + 2,31a ≥ 28
a ≥
Наименьшее целое число, при котором знак неравенства выполняется, это число 6.
Значит, искомая сумма — 6 млн рублей.
Ответ: 6 млн рублей.
Акции и другие ценные бумаги
Следующий блок, который мы рассмотрим, затрагивает относительно новое понятие ценной бумаги. Что вам нужно знать о ценной бумаге, чтобы решать подобные задания, не вдаваясь в экономические особенности, это то, как она может приносить доход.
Тип 1: когда вы получаете доход от того, что ценная бумага, которую вы купили ранее, растет в цене. Например, сначала ценная бумага стоила 3 000, а через год стала стоить 4 000. Непосредственно этих 4 000 у вас нет, но вы можете продать ценную бумагу за 4 000 и получите больше, чем потратили за год до этого.
Тип 2: когда вы получаете некий процент от прибыли компании за то, что ранее приобрели ценную бумагу этой компании. Если вы являетесь владельцем акции, то доход данного типа вы получаете в форме дивидендов.
Помимо этого дохода вы также можете продать эту ценную бумагу и, если она теперь стоит больше, чем когда вы ее покупали, вы также получите прибыль. Это не все пути получения дохода от ценных бумаг, но других особенностей вам знать не нужно. При необходимости все дополнительные условия будут описаны в самой задаче.
Рассмотрим следующую задачу, в которой как раз фигурирует понятие ценной бумаги.
Задача 3.
Григорий приобрёл ценную бумагу компании за 9000 рублей в начале 2016 года. Компания находится на стадии активного роста, поэтому цена данной бумаги каждый год возрастает на 2000 рублей. В любой момент Григорий может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 12 %. В начале какого года Григорий должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Решение:
Продать бумагу нужно тогда, когда прирост стоимости ценной бумаги станет меньше, чем банковский процент. Пусть это случится в год n.
К этому моменту n к изначальной цене акции 9000 прибавится n раз по 2000, тогда на текущий момент её цена составит:
9000 + 2000n
Чтобы получить прирост, который Григорий получит, если хранить деньги в форме акции, необходимо ежегодный прирост (в данной задаче – 2000 рублей) поделить на накопленную к данному моменту сумму.
Прирост денежной суммы в банке всегда одинаков и равен предложенному проценту, то есть 0,12.
Либо можем составить уравнение, которое объединит все строчки нашей таблицы:
По прошествии четырёх лет Григорий должен продать бумагу, то есть в начале 2020 года.
Ответ: 2020
Методы оптимальных решений
Это особый блок, позволяющий максимизировать одну целевую функцию при учёте данных в условии ограничений.
Основные типы заданий в этом блоке:
1. Оптимизация работы на производстве с учётом цен на рынке товара и факторов производства;
2. Многозаводское производство (включая разные заводы/ отели/ другие рабочие пространства);
3. Транспортная задача.
Разберём несколько задач с основными методами решения.
Задача.
У фермера есть 2 поля, площадь каждого из которых составляет 10 гектаров. На каждом поле можно выращивать пшеницу и ячмень. Урожайность пшеницы на первом поле составляет 500 ц/га, а на втором поле – 300 ц/га. Урожайность ячменя, наоборот, на первом поле составляет 300 ц/га, а на втором поле – 500 ц/га. При этом известно, что между данными злаками поля можно делить в любом соотношении.
Если известно, что на рынке установилась цена на пшеницу 7000 рублей за центнер, а цена на ячмень 9000 рублей за центнер, то какой наибольший доход фермер может получить?
Решение:
Имеем 2 поля с различными характеристиками.
В целом, продавать ячмень выгоднее, чем продавать пшеницу, так как 9000 > 7000 рублей.
Более того, известно, что на втором поле урожайность ячменя выше, чем урожайность пшеницы (500 ц/га против 300 ц/га). Тогда очевидно, что второе поле полностью фермер займёт ячменём, откуда получит:
10·500· 9000= 45000000 рублей
Ситуация с первым полем не так очевидна.
Продавать ячмень, как и прежде, выгоднее, чем продавать пшеницу. Однако на первом поле урожайность ячменя ниже, чем урожайность пшеницы (300 ц/га против 500 ц/га).
Поэтому необходимо сравнить соотношения этих величин:
Тогда получается, что засеять первое поле пшеницей выгоднее, так как низкая цена компенсируется высокой урожайностью.
Доход с первого поля:
10 · 500 ·7000 = 35000000 рублей
Суммарный доход составит:
35000000 рублей + 45000000 рублей = 80000000 рублей
Ответ: 80000000 рублей
Есть и другие типы заданий, в которых необходимо будет применить не житейские знания, а навыки составления уравнений и нахождения наименьшего/ наибольшего значений функций.
Задача.
На двух заводах есть по 360 рабочих, каждый из которых готов трудиться по 5 часов в сутки для обработки чёрных или цветных металлов. На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов. На втором заводе для обработки x кг чёрных металлов в день требуется x2 человеко-часов труда, а для обработки у кг цветных металлов в день требуется у2 человеко-часов труда.
Владельцу заводов поступил заказ на обработку металлов, причём 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов. Какую наибольшую массу обработанных металлов может за сутки суммарно получить заказчик?
Решение:
Как и дано в условии, 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов, что означает, что металлы взаимозаменяемы в пропорции 1:1.
Пусть на втором заводе t рабочих обрабатывают чёрные металлы, тогда (360-t) рабочих обрабатывают цветные металлы.
Знаем, что x2 человеко-часов труда требуется обработки x кг чёрных металлов, а у2 человеко-часов труда требуется в день для обработки у кг цветных металлов.
На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов, однако чёрные и цветные металлы для заказчика равнозначны, из чего сделаем вывод, что все 360 рабочих обрабатывают чёрные металлы, то есть 108*5 = 540 кг в день.
Имея соотношение на втором заводе и производительность рабочих на первом заводе, составим функцию возможного количества обработанных металлов:
Необходимо найти наибольшее значение этой функций. Последовательность действий мы уже знаем из темы «Анализ функций». Необходимо:
1. Найти производную функции;
2. Приравнять производную к 0, получить точки, подозрительные на экстремум;
3. Определить знаки производной на полученных промежутках и проверить, какие точки являются точкой максимума, а какие – точкой минимума.
Проведём такую последовательность действий с нашей производственной функцией.
Приведём к общему знаменателю.
Приравняем числитель к 0.
Возведём в квадрат.
Получили единственную точку экстремума.
- Проверим, является ли она точкой максимума.
Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.
Ответ: 600 кг
Видим, что экономическая задача достаточно разнообразна, но и решать вы её можете абсолютно разными способами – через производные, составление таблиц, схем, выведение формул и простой перебор вариантов.
Самое главное – внимательно прочитать и понять условие.
Примеры решения задач
Задача 1. В 2019 году клиент планирует открыть вклад в банке 1 ноября сроком на 1 месяц под 11% годовых. Какая сумма денег окажется на счёте вклада 1 декабря того же года, если планируемая сумма вклада равна 100 000 рублей? Ответ округлите до двух знаков после запятой.
Решение: При однократном начислении процентов через дней на вклад под годовых в невисокосный год получим сумму
Воспользуемся этой формулой, считаяS0= 100 000, r = 11 , m = 30 (так как в ноябре 30 дней).
Получим:
Число в скобках с точностью до 7 знаков после запятой равно 1,0090411, значит, S=100 904,11Таким образом, на счёте вклада будет 100 904 рубля 11 копеек.
Задача 2. Через сколько полных лет у клиента на счету будет не менее 950 000 рублей, если он намерен открыть вклад 31 декабря и планирует каждый год класть на счет 260 000 рублей при условии, что банк раз в год (начиная со следующего года) 31 декабря будет начислять 10% на имеющуюся сумму?
Решение:
Будем последовательно вычислять сумму на счете и упорядочивать данные с помощью таблицы.
Задача 3. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» увеличивает эту сумму на 11% в течение каждого из первых двух лет, а на третий год начисляемые проценты изменяются. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором по истечении трёх лет этот вклад всё ещё будет выгоднее вклада «А».
Решение:
Пусть на каждый тип вклада была внесена сумма По вкладу «А» сумма каждый год увеличивается на
умножается на коэффициент 1,1.
Тогда по вкладу «А» после первого года сумма станет равна ;
после второго года: 1,21S;
после третьего года: 1,331S.
По вкладу «Б» после первого года сумма станет равна1,11S;
после второго года 1,2321S.
Пусть на третий год по вкладу «Б» банк увеличивает сумму на r%. Тогда после третьего года по вкладу «Б» сумма станет равна
, где r— натуральное число,
коэффициент повышения в третий год.
По условию требуется найти наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А», то есть сумма через три года на вкладе «Б» должна быть больше суммы на вкладе «А». Составим неравенство:
Так как r— натуральное число, то наименьший процент равен 9%.
Задача 4. Сергей планирует приобрести ценную бумагу за 7 тысяч рублей. Цена бумаги каждый год будет возрастать на 2 тысячи рублей. В любой момент Сергей сможет продать ценную бумагу и вырученные деньги положить на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В течение какого года после покупки Сергей должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на счете стала наибольшей?
Решение.
Во второй год цена ценной бумаги составит: (7+2) тысячи рублей
В третий год (7+2)+2= 7+2∙2 тысячи рублей
В четвертый год (7+2)+2)+2= 7+2∙3 тысячи рублей
.
Сопоставим 10% банковский рост цены бумаги ее ежегодному росту на 2000 рублей.
10% от цены бумаги на
Ценную бумагу стоит продать тогда, когда 10% от цены бумаги станут больше, чем 2 тысячи рублей.
Получаем неравенство:
Наименьшее натуральное n, удовлетворяющее этому неравенству, равно 8.
Задача 5.
Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 20%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце тридцатого года сумма на его счёте была наибольшей?
Решение:
2 декабря 2021
В закладки
Обсудить
Жалоба
В данной работе рассмотрены основные методы решения задач на кредит, вклады и оптимизацию.
Разобраны 8 типов заданий
→ 1 тип: Нахождение количества лет (месяцев) выплаты кредита. (Аннуитетные платежи) — 3 задачи.
→ 2 тип: Вычисление процентной ставки по кредиту. (Фиксированные платежи) – 3 задачи.
→ 3 тип: Нахождение суммы кредита. (Аннуитетные платежи)- 3 задачи.
→ 4 тип: Нахождение ежегодного (ежемесячного) транша. (Аннуитетные платежи)- 3 задачи.
→ 5 тип: Нахождение разницы. (Аннуитетные платежи) – 3 задачи.
→ 6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)- 3 задачи.
→ 7 тип: Задачи, связанные с дифференцированными платежами.- 3 задачи.
→ 8 тип: Нестандартные задачи, связанные с кредитом.- 4 задачи.
50ek.docx
Муниципальное казенное общеобразовательное учреждение гимназия
г. Вятские Поляны Кировской области, ул. Гагарина, д.17, факс/телефон
(83334) 6-29-29 e-mail: vpschool3@mail.ru, сайт: гимназия-вп.рф
Решение экономических задач с помощью таблицы в ЕГЭ
Составила: Гатауллина Гульфия Анасовна
учитель математики
МКОУ гимназии г. Вятские Поляны
Кировской области
2019
Оглавление
Введение 3
Примеры решения задач 4
Задачи для самостоятельного решения 11
Заключение 12
Список литературы 13
Введение
В условиях современных требований к выпускникам средней школы при поступлении в ВУЗы, профилирующие предметы которых связаны с математической наукой, ЕГЭ по математике профильного уровня расширен.
С 2015 года в него добавлено экономическая (банковская) задача. Эта задача ориентирована на реальную жизнь. В этих заданиях рассматриваются идеализированные жизненные ситуации, которые являются некоторыми текстовыми упрощениями, моделями, реально возникающих, например, при обращении в банк, покупке или продаже ценных бумаг, выпуск производственной продукции и получение прибыли.
За правильное решение задания № 17 на ЕГЭ можно получить три балла.
В своей работе я решила обратиться к рассмотрению решения таких задач, потому, что с одной стороны по ним представлено не много материала в открытых источниках, а с другой – было большое желание разобраться в их решении на собственном опыте.
Рассмотрим один из подходов к решению задач с «экономическим содержанием» с помощью таблицы на примере следующих задач.
Примеры решения задач
1) В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
-каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Решение:
Пусть 𝑛− срок кредита
Составим таблицу:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
28 |
|
|
|
… |
|||
|
𝑛 |
|
|
|
Очевидно, что наибольший годовой платёж будет в первом году (потому что платежи равномерно уменьшаются в течение 𝑛 лет)
Наибольший годовой платёж = 9 млн
𝑛 = 14
В таблице все значения становятся известными:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
28 |
|
7 |
|
… |
|||
|
14 |
2 |
2 |
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
80,5
Ответ: 80,5 млн
2) В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн рублей?
Решение:
Пусть 𝑛− срок кредита
Составим таблицу:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
9 |
|
|
|
… |
|||
|
𝑛 |
|
|
|
Очевидно, что наименьший годовой платёж будет в последнем году (потому что платежи равномерно уменьшаются в течение 𝑛 лет)
Наибольший годовой платёж = 1.25 млн
𝑛 = 9
В таблице все значения становятся известными:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
9 |
|
2.25 |
|
… |
|||
|
9 |
1 |
1 |
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
20.25
Ответ: 20.25 млн
3) В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
Решение:
Пусть 𝑛− срок кредита
Составим таблицу:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
16 |
|
|
|
… |
|||
|
𝑛 |
|
|
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
Ответ: 10
4) 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 𝑟% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на
30% больше суммы, взятой в кредит. Найдите 𝑟.
Решение:
Пусть 𝑥 − сумма кредита
Тогда 1,3𝑥 − общая сумма выплат, превышающая сумму кредита на 30%
Составим таблицу:
|
Месяц |
Долг на начало месяца |
Основной платёж |
Дополнительный платёж |
|
1 |
𝑥 |
|
|
|
2 |
|
|
|
|
… |
|||
|
19 |
|
|
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
Ответ: 3
5) К 15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тыс. рублей меньше долга на 15-ечисло предыдущего месяца;
— к 15 –му числу 21 месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного погашения составит 1604 тыс. рублей.
S тыс.руб – сумма, которую планируют взять в кредит.
3%=0,03
|
№ |
Долг по кредиту на начало месяца |
Сумма, на которую возрастает долг на 1-е число каждого месяца |
Выплата |
|
1. |
s |
s∙0,03=0,03 s |
30+0,03 s |
|
2. |
s-30 |
0,03 (s-30) |
30+0,03 (s-30) |
|
3. |
s-2∙30 |
0,03(s-2∙30) |
30+0,03(s-2∙30) |
|
4. |
s-3∙30 |
0,03(s-3∙30) |
30+0,03(s-3∙30) |
|
5. |
s-4∙30 |
0,03(s-4∙30) |
30+0,03(s-4∙30) |
|
… |
…. |
…. |
… |
|
20 |
s-19∙30 |
0,03(s-19∙30) |
30+0,03(s-19∙30) |
|
21 |
s-20∙30 |
0,03(s-20∙30) |
s-20∙30+0,03(s-20∙30) |
|
Итого: |
1604 тыс. рублей |
Составим и решим уравнение:
Общая сумма выплат представляет собой сумму суммы, которую планируют взять в кредит, и сумму сумм, на которые возрастает долг на 1-е число каждого месяца.
s +0,03 s +0,03 (s-30)+ 0,03(s-2∙30)+….+ 0,03(s-20∙30)=1604
s +0,03∙(s+( s-30)+(s-2∙30)+… (s-20∙30))=1604
s+0,03∙( 21s- (30+2∙30+…20∙30)+=1604
30;2∙30;…;20∙30-арифметическая прогрессия, а1 =30, а21 =20∙30
S=*20=6300
s+0,03∙( 21s-6300)=1604
1,63 s-189=1604
1,63s=1793
s=1793:1,63
s=1100
Ответ: 1100 тыс. Рублей
Задачи для самостоятельного решения
- Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
- Александр взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Александром. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Александром банку (сверх кредита)?
3) 15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
— 1-го числа каждого месяца долго возрастёт на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?
Заключение
Я считаю введение таких задач чрезвычайно полезным так как, работая над моделями, сформулированными в условиях, они заставляют задумываться о реальной жизни. О том, что кредиты, отношения с банками, игра на бирже, колебания курсов ценных бумаг, начисление процентов дело сложное и требует больших знаний. К этому нельзя относиться легкомысленно. С чего начинать решать экономические задачи – очень внимательно читать условия задачи и по шагам распределить действия, затем постараться математически выразить их и постараться прийти к ответу.
Список литературы
1. Ященко И. В. и др. Подготовка к ЕГЭ по математике в 2018 году. Базовый и профильный уровни. Методические указания / И. В. Ященко, С. А. Шестаков, А. С. Трепалин. – М.: МЦНМО, 2015. – 288 с.
2. Демонстрационный вариант контрольно-измерительных материалов единого государственного экзамена 2018 года по математике. Профильный уровень. Сайт http://www.ege.edu.ru/
3. Спецификация контрольно-измерительных материалов для проведения в 2018 году единого государственного экзамена по математике. Профильный уровень. Сайт http://www.ege.edu.ru/
