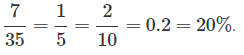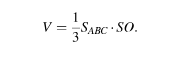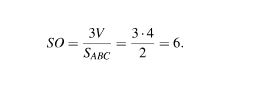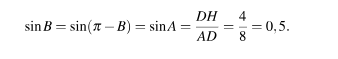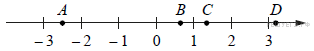В данном разделе мы занимаемся подготовкой к ЕГЭ по математике как базового, профильного уровня — у нас представлены разборы задач, тесты, описание экзамена и полезные рекомендации. Пользуясь нашим ресурсом, вы как минимум разберетесь в решении задач и сможете успешно сдать ЕГЭ по математике в 2020 году. Начинаем!
ЕГЭ по математике является обязательным экзаменом любого школьника в 11 классе, поэтому информация, представленная в данном разделе актуальна для всех. Экзамен по математике делится на два вида — базовый и профильный. В данном разделе я приведен разбор каждого вида заданий с подробным объяснением для двух вариантов. Задания ЕГЭ строго тематические, поэтому для каждого номера можно дать точные рекомендации и привести теорию, необходимую именно для решения данного вида задания. Ниже вы найдете ссылки на задания, перейдя по которым можно изучить теорию и разобрать примеры. Примеры постоянно пополняются и актуализируются.
Структура базового уровня ЕГЭ по математике
Экзаменационная работа по математике базового уровня состоит из одной части, включающей 20 заданий с кратким ответом. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Ответом к каждому из заданий 1–20 является целое число, конечная десятичная дробь, или последовательность цифр.
Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов №1 в той форме, которая предусмотрена инструкцией по выполнению задания.
Разбор заданий ЕГЭ по математике (база)
ЕГЭ математика — База 2022. Открытый банк заданий с ответами.
Незнайка → ЕГЭ → Математика → Базовая
Рейтинг: 475
Рейтинг: 471
Рейтинг: 466
Рейтинг: 434
Рейтинг: 422
Математика Базовый уровень
Об экзамене
Базовая математика – для слабаков, скажут одни, другие – для тупых гуманитариев, а третьи (те, что не снобы) просто используют ее в качестве разминки перед математикой профильной. Пусть гуманитарии не обижаются и не принимают все так близко к сердцу, самоирония должна быть. Просто, чтобы сдать базу, надо лишь ходить на уроки по математике и хотя бы немного слушать учителя. Никаких проблем не возникнет.
Структура
Экзаменационная работа состоит из одной части, включающей 20 заданий с кратким ответом базового уровня сложности. Ответом к каждому из заданий 1–20 является целое число или конечная десятичная дробь, или последовательность цифр.
На выполнение экзаменационной работы отводится 3 часа (180 минут).
Пояснения к оцениванию заданий
Правильное решение каждого из заданий 1–20 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби, или последовательности цифр. Максимальный первичный балл за всю работу – 20.
Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу.
Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Ознакомьтесь с подробной видеоинструкцией по использованию модуля.
Решение и ответы заданий демонстрационного варианта ЕГЭ 2022 по математике (базовый уровень). Демоверсия ФИПИ для 11 класса. Демовариант.
Задание 1.
Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?
ИЛИ
Килограмм моркови стоит 40 рублей. Олег купил 1 кг 600 г моркови. Сколько рублей сдачи он должен получить со 100 рублей?
ИЛИ
Для ремонта требуется 63 рулона обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 6 рулонов?
Задание 2.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) рост ребёнка | 1) 32 км |
| Б) толщина листа бумаги | 2) 30 м |
| В) протяжённость автобусного маршрута | 3) 0,2 мм |
| Г) высота жилого дома | 4) 110 см |
ИЛИ
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) масса взрослого человека | 1) 8 т |
| Б) масса грузового автомобиля | 2) 5 г |
| В) масса книги | 3) 65 кг |
| Г) масса пуговицы | 4) 300 г |
Задание 3.
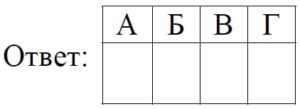
На диаграмме приведены данные о длине восьми крупнейших рек России (в тысячах километров). Первое место по длине занимает река Лена.
На каком месте по длине находится река Амур?
ИЛИ
В таблице представлены данные о стоимости некоторой модели смартфона в различных магазинах.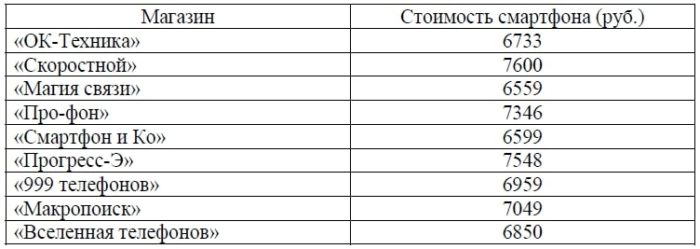
ИЛИ
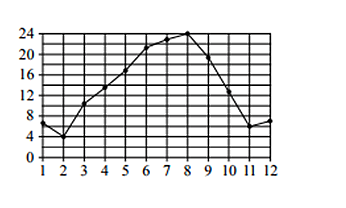
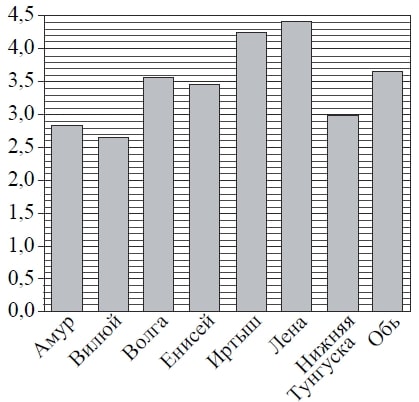
На графике показано изменение температуры воздуха на протяжении трёх суток. На горизонтальной оси отмечены число, месяц, время суток в часах; на вертикальной оси — значение температуры в градусах Цельсия.
Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
Задание 4.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2·R, где I – сила тока (в амперах), R – сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R = 5 Ом и I = 7 А.
ИЛИ
Среднее геометрическое трёх чисел: a, b и c – вычисляется по формуле g=sqrt[3]{abc}. Вычислите среднее геометрическое чисел 5, 25, 27.
Задание 5.
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.
ИЛИ
Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной?
Задание 6.
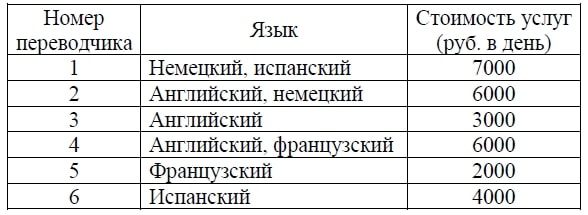
Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.
Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день.
В ответе укажите какой-нибудь один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.
ИЛИ
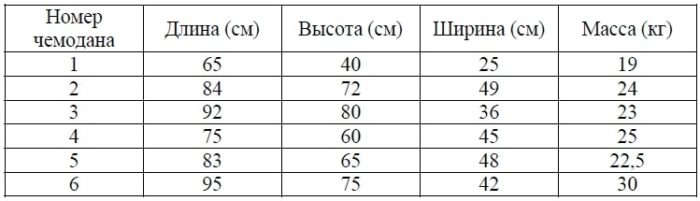
В таблице приведены данные о шести чемоданах.
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера всех выбранных чемоданов без пробелов, запятых и других дополнительных символов.
ИЛИ
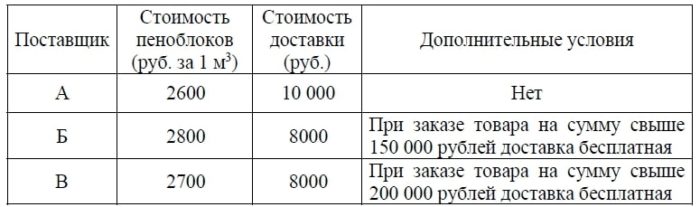
Строительная фирма планирует купить 70 м3 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.
Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
Задание 7.
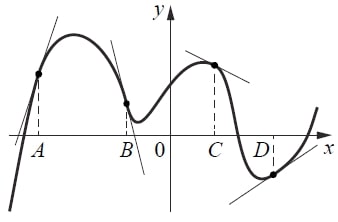
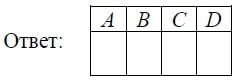
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1) –4 |
| B | 2) 3 |
| C | 3) frac{2}{3} |
| D | 4) –0,5 |
В таблице под каждой буквой укажите соответствующий номер.
ИЛИ
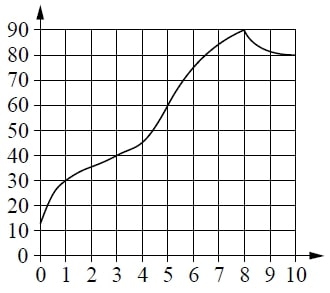
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 0–1 мин. | 1) Самый медленный рост температуры. |
| Б) 1–3 мин. | 2) Температура падала. |
| В) 3–6 мин. | 3) Температура находилась в пределах от 40°C до 80°C. |
| Г) 8–10 мин. | 4) Температура не превышала 30°C. |
В таблице под каждой буквой укажите соответствующий номер.
ИЛИ
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1].
ХАРАКТЕРИСТИКИ
1) Функция имеет точку максимума на отрезке [−1; 1].
2) Функция имеет точку минимума на отрезке [−1; 1].
3) Функция возрастает на отрезке [−1; 1].
4) Функция убывает на отрезке [−1; 1].
В таблице под каждой буквой укажите соответствующий номер.
Задание 8.
В классе учится 20 человек, из них 13 человек посещают кружок по истории, а 10 – кружок по математике. Выберите утверждения, которые верны при указанных условиях.
1) Каждый ученик этого класса посещает оба кружка.
2) Найдётся хотя бы двое из этого класса, кто посещает оба кружка.
3) Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике.
4) Не найдётся 11 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ИЛИ
Во дворе школы растут всего три дерева: ясень, рябина и осина. Ясень выше рябины на 1 метр, но ниже осины на 2 метра. Выберите все утверждения, которые верны при указанных условиях.
1) Среди указанных деревьев не найдётся двух одной высоты.
2) Ясень, растущий во дворе школы, выше осины, растущей там же.
3) Любое дерево, помимо указанных, которое ниже ясеня, растущего во дворе школы, также ниже рябины, растущей там же.
4) Любое дерево, помимо указанных, которое ниже рябины, растущей во дворе школы, также ниже ясеня, растущего там же.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Задание 9.
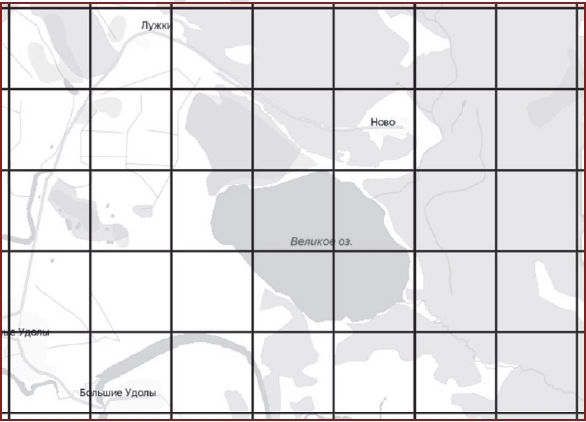
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
ИЛИ
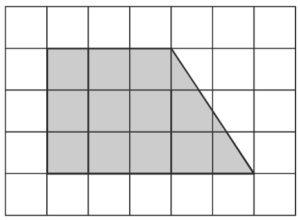
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Задание 10.
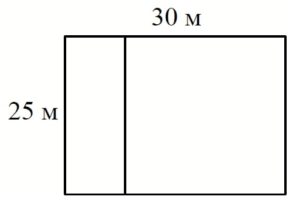
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
ИЛИ
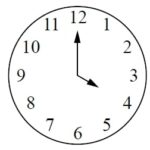
Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
Задание 11.
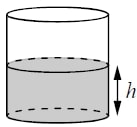
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
ИЛИ
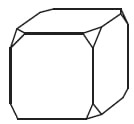
От деревянного кубика отпилили все его вершины (см. рисунок). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Задание 12.
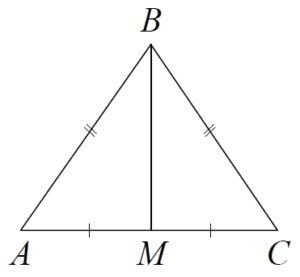
В треугольнике ABC известно, что AB = BC = 13, AC =10. Найдите длину медианы BM.
Задание 13.
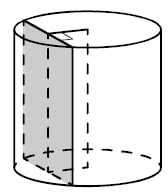
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
ИЛИ
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
ИЛИ
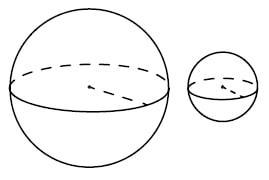
Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?
Задание 14.
Найдите значение выражения (6,7 − 3,2)·2,4.
ИЛИ
Найдите значение выражения (frac{8}{33}+frac{13}{22}):frac{5}{18}.
Задание 15.
Ивану Кузьмичу начислена заработная плата 20 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13%. Сколько рублей он получит после уплаты подоходного налога?
ИЛИ
ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?
ИЛИ
Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 24 гектара и распределена между зерновыми и овощными культурами в отношении 5:3 соответственно. Сколько гектаров занимают овощные культуры?
Задание 16.
Найдите значение выражения frac{14^{9}}{2^{7}cdot 7^{8}}.
ИЛИ
Найдите cosα, если sinα = 0,8 и 90° < α <180°.
ИЛИ
Найдите значение выражения (2sqrt{13} – 1)(2sqrt{13} + 1).
ИЛИ
Найдите значение выражения log31,8 + log35.
Задание 17.
Найдите корень уравнения 3x−3 = 81.
ИЛИ
Найдите корень уравнения log2(x − 3) = 6.
ИЛИ
Решите уравнение x2 − x − 6 = 0.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Задание 18.
На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| А | 1) log210 |
| В | 2) frac{7}{3} |
| С | 3) sqrt{26} |
| D | 4) (frac{3}{5})^{–1} |
В таблице под каждой буквой укажите соответствующий номер.
ИЛИ
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
В таблице под каждой буквой укажите соответствующий номер.
Задание 19.
Найдите трёхзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
ИЛИ
На шести карточках написаны цифры 2, 3, 5, 6, 7, 7 (по одной цифре на каждой карточке). В выражении
вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20. В ответе укажите какую-нибудь одну такую сумму.
ИЛИ
Вычеркните в числе 75157613 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно получившееся число.
Задание 20.
Расстояние между городами А и В равно 470 км. Из города А в город В выехал первый автомобиль, а через 3 часа после этого навстречу ему из города В выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города А. Ответ дайте в км/ч.
ИЛИ
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Задание 21.
Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в 3 раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?
ИЛИ
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
ИЛИ
В доме всего 14 квартир с номерами от 1 до 14. В каждой квартире живёт не менее одного и не более четырёх человек. В квартирах с 1-й по 12-ю включительно живёт суммарно 14 человек, а в квартирах с 11-й по 14-ю включительно живёт суммарно 12 человек. Сколько всего человек живут в этом доме?
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
ЕГЭ по математике (базовый уровень)
Рассмотрим задания из ЕГЭ по математике базового уровня. С подробным объяснением и примерами решения задач.
Маша и Медведь едят варенье и печенье –
Покажем возможный вариант задания, которое в ЕГЭ по
Базовая математика — обязательный предмет ЕГЭ, который ежегодно сдают все российские школьники. Для того, чтобы получить школьный аттестат, вполне достаточно минимального балла по базовой математике, а вот для поступления в вуз может потребоваться экзамен по профильной математике. Минимальный балл, который необходимо набрать для получения аттестата — 23. Чтобы поступить в вуз, понадобится не менее 27 баллов. Рассмотрим демовариант ЕГЭ по математике 2019 и разберем некоторые из этих заданий.
Задание №1
Это задание основано на проверке простейших математических навыков: сложение, вычитание, деление, умножение, а также действия десятичными дробями и перевод одних единиц измерения в другие.
Пример задачи
В 23.50 минут по московскому времени из Санкт-Петербурга в Москву выехал поезд. В Москву он приехал на следующие сутки в 7 часов 50 минут. Необходимо вычислить, какое количество времени поезд был в пути.
Решение
Зная о том, что в сутках всего 24 часа, и их начало приходится на 00:00, а конец — на 24 часа, вычисляем: в первые сутки поезд находился в пути десять минут, во вторые — 7 часов и 50 минут.
7 ч. 50 мин. + 0 ч. 10 мин. = 7 ч. 60 мин. или 8 часов
Задание №2
Задание проверяет, насколько хорошо выпускники умеют интерпретировать различные таблицы, графики и диаграммы, а также совершать с их помощью простейшие вычисления. Как правило, речь идет об анализе графика функции и поиске наибольших и наименьших значений.
Пример задачи
В задаче представлен график, отображающий среднюю температуру Сочи за каждый месяц 1920 года. Необходимо определить, сколько месяцев в году температура была выше 18 градусов Цельсия.
Решение
Для того, чтобы найти правильное решение, необходимо провести горизонтальную линию от точки с цифрой 18 (указана температура в градусах Цельсия). Таким образом станет очевидно, что такая температура держалась 4 месяца подряд: в июне, июле, августе и сентябре.
Задание №3
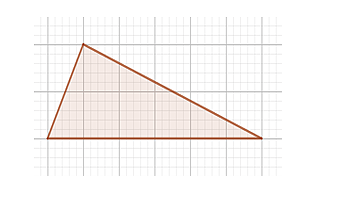
Школьники должны продемонстрировать знание основ планиметрии, а именно: уметь вычислять площадь фигур, рассчитывать градусные меры углов, диаметры и находить другие значения. Например, найти площадь треугольника, начерченного на бумаге с размером клеток 1х1. В этом задании важно продемонстрировать знание формул и умение пользоваться различными способами решения задачи.
Задание №4
Задача из курса “Теория вероятностей и статистика”. Выпускникам предлагается высчитать вероятность того или иного события, произошедшего в повседневной ситуации.
Пример задачи
Ученикам предложено выучить 25 билетов по биологии. Лишь два из них содержат вопрос о грибах. Каждому школьнику предстоит ответить лишь на один билет. Вычислите вероятность того, что вопрос о грибах будет содержаться именно в этом билете.
Решение
Вероятность события можно рассчитать по формуле Р(А) = m/n, где m — количество благоприятных исходов, а n — общее их количество. 25 билетов означают 25 исходов, 2 из которых — благоприятные. Значит, вероятность равна 2/25, то есть 0,08.
Задача №5
Здесь проверяется умение решать уравнения, находить неизвестные, извлекать корни и т. д.
Пример задачи
Найти корень уравнения 3x-5 = 81
Решение
3х-5 = 34
х-5 = 4
х = 9
Задание №6
Здесь необходимо продемонстрировать умение моделировать различные ситуации при помощи геометрических понятий. Важно знание теорем, умение определять длину, градус угла и другие величины.
Пример задачи
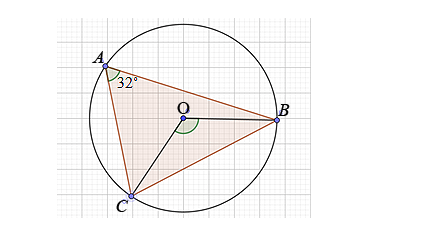
Треугольник с углами А, B и С вписан в окружность с центром О. Угол BAC — 32 градуса. необходимо найти угол BOC.
Решение
COB — центральный угол, равный дуге CB
САВ — вписанный угол, равный ½ дуги СВ
Значит, САВ = ½ СОВ. Так как ½ угла СОВ равна 32 градусам, то угол СОВ равен 64о
Ответ: 64о
Задача №7
Выпускник должен продемонстрировать знание понятия “функция” и умение выполнять с ним различные действия: руководствуясь графиком, описывать свойства и поведение функции; находить наибольшие и наименьшие значения; самостоятельно строить графики.
Пример задачи
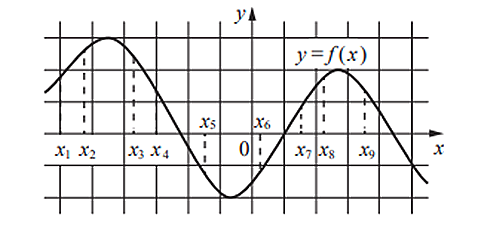
На графике дифференцируемой функции y = f(x) на оси абсцисс отмечены девять точек. Необходимо найти все точки, в которых производная функции f(х) отрицательна.
Решение
Необходимо проследить, в каких местах графика убывает функция: именно там ее производная будет отрицательна. Всего на этом графике 4 таких точки.
Задача №8
Задачи на знание основ стереометрии, простейших геометрических понятий и умение использовать при решении стереометрических задач планиметрические методы.
Пример задачи
В условии даны два цилиндрических сосуда. Уровень жидкости в первом достигает 16 сантиметров. Всю жидкость перелили во второй сосуд, диаметр которого дважды превышает диаметр основания первого. Необходимо определить уровень жидкости во втором сосуде.
Решение
Для вычисления объема цилиндра следует воспользоваться этой формулой: V = πR2H, где R — это радиус цилиндра, а Н — его высота. Так как уровень жидкости поднимается до 16 см, значит, высота также равна 16.
V = πR2H = πR216
Зная о том, что диаметр второго сосуда в два раза больше первого, мы можем сделать вывод, что радиус второго сосуда в два раза больше первого (2R). Вычисляем объем жидкости во втором сосуде: V = π(2R)2h или V = 4R2h
При переливании жидкости из одного сосуда в другой ее объем не изменился.
πR216 = π4R2h
4h = 16
Задача №9
В этом разборе задания очень важно уметь выполнять простейшие вычисления и преобразования, поэтому знание формул просто необходимо.
Пример задачи
Необходимо найти sin2α, если учесть, что cosα = 6, а π < α < 2π
Решение
sin2α = 2sinα х cosα
(sinα)2 + (cosα)2 = 1
(sinα)2 + (0,6)2 = 1
(sinα)2 = 1 — 0,36
(sinα)2 = ±0,8
sinα = –0,8
sin2α = 2 х (–0,8) х (0,6)
sin2α = –0,96
Задача №10
Здесь выпускники демонстрируют умение решать прикладные задачи социально-экономической и физической направленности. Необходимо знать и уметь пользоваться формулами, быть точным в расчетах и внимательным при записи ответа.
Пример задачи
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий̆ первым, окажется из России.
Решение
Вероятность определяется, как количество положительных вариантов к количеству всех вариантов. Например, у вас есть 10 монеток и только 2 из них — десятирублёвые, то если вы возьмёте одну монетку, вероятность того, что она будет десятирублёвой, составит
В нашей задаче 35 спортсменов, из которых 7 — из России.
Значит, вероятность того, что первый спортсмен будет из России, составляет:
Ответ: 0.2.
Задача №11
Текстовые задачи с чуть более сложными условиями нужны для того, чтобы экзаменуемый продемонстрировал не только свои знания, но также аналитические способности и умение мыслить логически.
Пример задачи
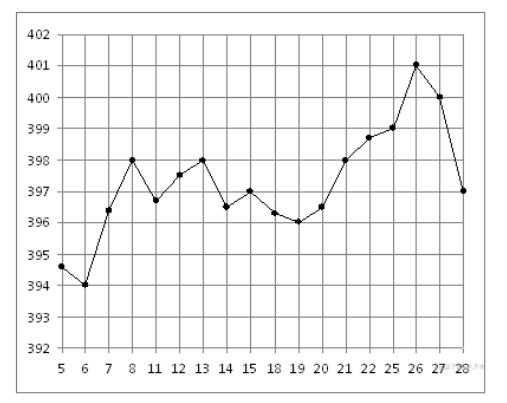
На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.
Решение
Из графика видно, что наименьшей цена была 6 марта.
Ответ: 6.
Задача №12
12 задача из демоверсии ЕГЭ по математике базового уровня посвящена теме “экстремум”. Здесь необходимо найти производную функции и ее критические точки.
Пример задачи
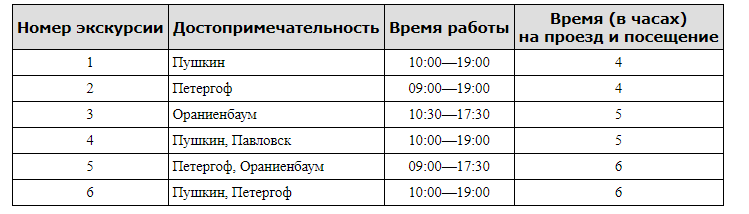
Турист подбирает себе экскурсионную программу. Сведения о некоторых музеях и парках, подготовленные туристическим бюро, представлены в таблице.
Пользуясь таблицей, подберите экскурсионную программу так, чтобы турист посетил не ме-нее трёх достопримечательностей за один день.
В ответе для подобранной программы укажите номера экскурсий без пробелов, запятых и других дополнительных символов.
Решение
У туриста всего 10 часов. Если он выберет шестую экскурсию, то на третью экскурсию времени уже не хватит, а вот если выберет пятую, то вполне успевает и на первую. Та-ким образом, 5 и 1.
При выборе четвертой успевает только на вторую. Таким образом, 4 и 2. При выборе третьей посмотреть три достопримечательности никак не успеет.
Ответ: 1 и 5 или 2 и 4.
Задача №13
Задания из этого раздела демо-варианта ЕГЭ проверяют знание стереометрии. Необходимо знать формулы нахождения площадей разных фигур: прямоугольного параллелепипеда, призмы, пирамиды, куба, цилиндра и т. д.
Пример задачи
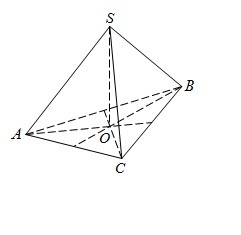
В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 4. Найдите длину отрезка OS.
Решение
Отрезок OS высотой треугольной пирамиды SABC, ее объем выражается формулой
Значит,
Ответ: 6.
Задача №14
Для решения этого задания стоит повторить свойства функций. Необходимо знать, что такое область определения и область значений, экстремальные значения, убывание и возрастание.
Пример задачи
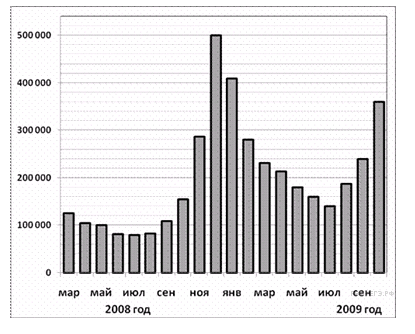
На диаграмме показано количество запросов со словом СНЕГ, сделанных на поисковом сайте Yandex.ru во все месяцы с марта 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество запросов за данный месяц.
Пользуясь диаграммой, установите связь между промежутками времени и характером изме-нения количества запросов.
|
ПРОМЕЖУТКИ ВРЕМЕНИ |
ХАРАКТЕР ИЗМЕНЕНИЯ КОЛИЧЕСТВА ЗАПРОСОВ |
|
А) Весна 2008 года |
1) Количество запросов резко снижалось |
|
Б) Лето 2008 года |
2) Количество запросов заметно увеличивалось |
|
В) Осень 2008 года |
3) Количество запросов практически не менялось |
|
Г) Зима 2008-2009 года |
4) Количество запросов плавно снижалось |
Решение
Весной 2008 года количество запросов падало примерно со 120 000 до 100 000.
Летом 2008 года количество запросов изменялось примерно с 82 000 до 80 000.
Осенью 2008 года количество запросов возрастало примерно со 115 000 до 283 000.
Зимой 2008 года количество запросов падало с 500 000 до 280 000.
Таким образом, получаем следующее: A — 4, Б — 3, В — 2, Г — 1.
Ответ: 4321.
Задача №15
Еще одна задача по планиметрии, для решения которой необходимо повторить формулы нахождения площади фигур на плоскости. и основные теоремы.
Пример задачи
В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, AD=8. Найдите синус угла B.
Решение
Ответ: 0,5.
Задача №16
Задача на знание стереометрии. Для ее решения необходимо разбираться в типах пространственных фигур, знать их элементы, а также основные формулы: объем, площадь поверхности и т. д.
Пример задачи
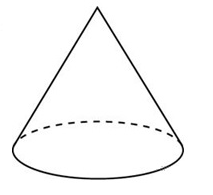
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение
Площадь основания конуса равна Sосн = πr2, а площадь боковой поверхности Sбок = πrl. Из условия имеем:
Значит, в прямоугольном треугольнике, образованном высотой, образующей и ра-диусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Значит, угол между образующей конуса и плоскостью осно-вания равен 60°.
Задача №17
Решение простейших неравенств. В этом задании необходимо составить математическую модель и прописать, что является здесь переменной x, p и переменной z. Даже если само уравнение решить не получится, за правильно составленную задачу вы сможете получить один балл.
Пример задачи
На координатной прямой отмечены точки A, B, C, и D.
Число m равно log54.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответ-ствие между указанными точками и числами.
ТОЧКИ ЧИСЛА
А) A
Б) B
В) C
Г) D
В таблице под каждой буквой укажите соответствующий номер.
Решение
Ответ: 2431.
Задача №18
Выпускникам предлагается решить задачу с параметром, в которой необходимо будет проявить аналитические способности и владение логикой.
Пример задачи
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение
Согласно условию, если кошка идёт по забору, то Шарик лает. Рассмотрим предложенные утверждения:
- Если Шарик не лает, значит, по забору идёт кошка — неверно, так как, если кошка идёт, то Шарик обязательно лает.
- Если Шарик молчит, значит, кошка по забору не идёт — верно, так как, если молчит — значит, никакая кошка не идет.
- Если по забору идёт чёрная кошка, Шарик не лает — неверно, так как, если любая кошка идет по забору — Шарик лает.
- Если по забору пойдет белая кошка, Шарик будет лаять — верно, согласно условию.
Задача №19
Чтобы решить задание под номером 19 по математике базового уровня, необходимо владеть следующими понятиями: числа и их свойства, числовые последовательности и прогрессии, признаки делимости чисел. В самом задании выпускникам для разбора будет предложена задача.
Пример задачи
Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что его квадрат делится на 16.
Решение
Разложим число 25 на слагаемые: 25 = 9 + 9 + 7 = 9 + 8 + 8.
Квадрат числа делится на 16, значит, само число делится на 4. Это значит, что оно заканчивается на чётную цифру. То есть первый набор отпадает, так как в нём нет четных чисел. Из второго мы можем составить числа 988 и 898. Первое число походит по условия задачи.
Ответ: 988.
Задача №20
Одно из самых интересных заданий заставляет задействовать не только логику, но и смекалку: правильный ответ необходимо найти при помощи рассуждений и внимательного отношения к каждой детали.
Пример задачи
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение
Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14 + 4 + 6 = 24 линии, следовательно, кусков будет 25.
Ответ: 25.
Таким образом видим, что разбор заданий для подготовки к ЕГЭ не представляет особых трудностей: при желании к экзамену можно как следует подготовиться и сдать его на максимально высокие баллы.
Найдите корень уравнения (displaystyle log_{frac{1}{2}} (7-2x)+log_{frac{1}{2}} frac{1}{8}=log_{frac{1}{2}} 15).
Найдите корень уравнения (displaystyle log_{frac{1}{2}} (2x+5)-log_{frac{1}{2}} 13=log_{frac{1}{2}} 5).
Найдите корень уравнения (log_5 (2x-3)-log_5 7=log_5 28).
Найдите корень уравнения (log_4 (5x+10)-log_4 5=log_4 3).
Найдите корень уравнения (log_{13} (-4x+23)=2).
Найдите корень уравнения (log_5 (-2x+9)=2).
Найдите корень уравнения (log_3 (2x-3)=2).
Найдите корень уравнения (log_7 (2x+3)=1).
Найдите корень уравнения (log_{17} (6x+29)=log_{17} 5).
Найдите корень уравнения (log_6 (4x+21)=log_6 9).







![Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1]. Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1].](https://ege314.ru/wp-content/uploads/2020/08/Ustanovite-sootvetstvie-mezhdu-grafikami-funktsij-i-harakteristikami-etih-funktsij-na-otrezke-1-1..jpg)