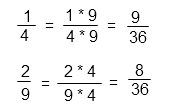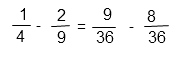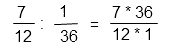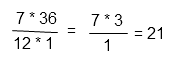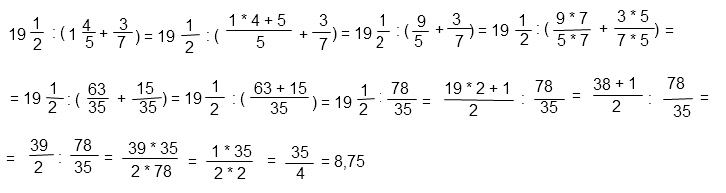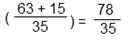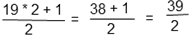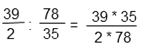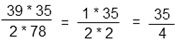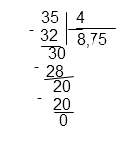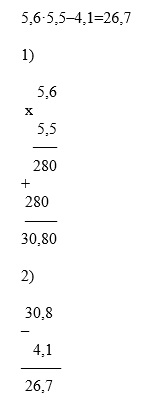Практика по заданию №1 ЕГЭ по математике базового уровня — вычисления (действия с дробями).
Для выполнения задания №1 необходимо уметь выполнять вычисления и преобразования
Практика
| time4math.ru | Скачать задания |
| math100.ru | Действия с дробями |
| vk.com/math.studying | Задания + ответы |
Коды проверяемых элементов содержания (по кодификатору) — 1.1.1, 1.1.3, 1.4.1
Уровень сложности задания — базовый
Максимальный балл за выполнение задания — 1
Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 5
Связанные страницы:
Задание 14 ЕГЭ по математике профильный уровень — неравенства
Решение 17 задания ЕГЭ по профильной математике
Задание 5 ЕГЭ по математике профильный уровень — стереометрия
Задание 4 ЕГЭ по математике (профиль) — вычисления и преобразования
Задание 11 ЕГЭ 2022 по математике: «Наибольшее и наименьшее значения функции»
Вариант 1 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значения выражения:
8. Найдите значение выражения
9. Найдите значение выражения
10. Найдите значение выражения .
Вариант 2 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения .
3. Найдите значение выражения
4. Найдите значение выражения .
5. Найдите значение выражения
6. Найдите значение выражения
7. Найдите значение выражения .
8. Найдите значение выражения .
9. Найдите значение выражения .
10. Найдите значение выражения:
Вариант 3 1. Вычисления. Действия с дробями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения .
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения 10.Найдите значение выражения .
Вариант 4 1. Вычисления. Действия с дробями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения .
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения 10. Найдите значение выражения .
Вариант 5 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения
10. Найдите значение выражения
Вариант 6 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения .
10. Вычислите
Вариант 7 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения .
7. Найдите значение выражения .
8. Найдите значение выражения (3,9 − 2,4) · 8,2.
9. Найдите значение выражения
10. Найдите значение выражения .
Вариант 8 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения .
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения .
9. Найдите значение выражения 1000 − 35 · 20 − 43.
10. Найдите значение выражения
Вариант 9 1. Вычисления. Действия с дробями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения:
5. Найдите значение выражения .
6. Вычислите:
7. Найдите значение выражения .
8. Найдите значение выражения
9. Найдите значение выражения 1000 − 35 · 20 − 43.
10. Найдите значение выражения
Вариант 10 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Вычислите
6. Найдите значение выражения
7. Найдите значение выражения (3,9 − 2,4) · 8,2.
8. Найдите значение выражения
9. Найдите значение выражения .
10. Найдите значение выражения
|
Вычисления. Действия с дробями. |
||||
|
Вариант 1 1. 0,5 2. 14,49 3. -0,43 4. 20,4 5. 1 6. 26,25 7. 0,4 8. -3 9. 3,5 10. -0,1 |
Вариант 2 1. -4,375 2. 31 3. 27,75 4. 56 5. 2,65 6. 4 7. -1,05 8. 10 9. 80,625 10. -500 |
Вариант 3 1.-2,5 2. 1,25 3. -4,9 4. 1 5. 49 6. 56 7. 27,75 8. 45 9. 1,8 10.1 |
Вариант 4 1. -2,5 2. 1,25 3. -4,9 4. 1 5. 49 6. 56 7. 27,75 8. 45 9. 1,8 10. 1 |
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
Найдите значения выражений
| 1 | frac{7}{2} cdot frac{5}{4} — frac{3}{8} | Смотреть видеоразбор >> |
| 2 | frac{22}{3}:frac{2}{15} cdot frac{6}{5} | Смотреть видеоразбор >> |
| 3 | (frac{9}{14}-frac{10}{21}) cdot 42 | Смотреть видеоразбор >> |
| 4 | (frac{11}{10}+frac{11}{13}):frac{22}{39} | Смотреть видеоразбор >> |
| 5 | (frac{11}{10}-frac{13}{15}):frac{7}{60} | Смотреть видеоразбор >> |
| 6 | frac{19}{6}:(frac{5}{6}+frac{3}{4}) | Смотреть видеоразбор >> |
| 7 | frac{0,9+0,7}{3,2} | Смотреть видеоразбор >> |
| 8 | frac{3,2-5,7}{2,5} | Смотреть видеоразбор >> |
| 9 | frac{4,7-1,4}{7,5} | Смотреть видеоразбор >> |
| 10 | frac{2,4}{1,2-0,4} | Смотреть видеоразбор >> |
| 11 | frac{5,6}{1,9-7,5} | Смотреть видеоразбор >> |
| 12 | (1,7+2,8) cdot 4,8 | Смотреть видеоразбор >> |
| 13 | 4,1 cdot 7,7 + 0,86 | Смотреть видеоразбор >> |
| 14 | 1,2 : 0,6 cdot 1,5 | Смотреть видеоразбор >> |
| 15 | 1 + frac{1}{7} cdot 0,77 | Смотреть видеоразбор >> |
| 16 | frac{5}{3}:frac{2}{7}-frac{11}{6} | Смотреть видеоразбор >> |
| 17 | frac{5}{6}+frac{5}{2} cdot frac{2}{3} | Смотреть видеоразбор >> |
| 18 | (frac{5}{12}-frac{3}{20}) cdot frac{45}{2} | Смотреть видеоразбор >> |
| 19 | (frac{17}{35}+frac{3}{8}):frac{5}{28} | Смотреть видеоразбор >> |
| 20 | (frac{11}{5}-frac{13}{6}):frac{1}{90} | Смотреть видеоразбор >> |
| 21 | frac{12}{7}:(frac{6}{7}-frac{3}{4}) | Смотреть видеоразбор >> |
| 22 | frac{7,9+3,4}{0,2} | Смотреть видеоразбор >> |
| 23 | frac{2,6-8,4}{2,5} | Смотреть видеоразбор >> |
| 24 | frac{2,6-2,6}{7,8} | Смотреть видеоразбор >> |
| 25 | frac{5,6}{1,7-1,6} | Смотреть видеоразбор >> |
| 26 | frac{9,2}{0,5-2,8} | Смотреть видеоразбор >> |
| 27 | (1,7+2,8) cdot 24 | Смотреть видеоразбор >> |
| 28 | 5,6 cdot 5,5 — 4,1 | Смотреть видеоразбор >> |
| 29 | frac{1}{4} cdot 0,48 + 1 | Смотреть видеоразбор >> |
| 30 | frac{1}{frac{1}{5}-frac{1}{30}} | Смотреть видеоразбор >> |
| 31 | frac{14}{9} cdot frac{3}{2}:frac{7}{6} | Смотреть видеоразбор >> |
| 32 | frac{5}{4}+frac{7}{6}:frac{2}{3} | Смотреть видеоразбор >> |
| 33 | (frac{11}{9}+frac{4}{9}):frac{5}{36} | Смотреть видеоразбор >> |
| 34 | (frac{5}{7}-frac{3}{7}):frac{2}{21} | Смотреть видеоразбор >> |
| 35 | (frac{8}{25}-frac{13}{38}):frac{6}{19} | Смотреть видеоразбор >> |
| 36 | 3:(frac{6}{7}-frac{3}{4}) | Смотреть видеоразбор >> |
| 37 | frac{6,9+4,1}{0,2} | Смотреть видеоразбор >> |
| 38 | frac{0,5-1,5}{0,8} | Смотреть видеоразбор >> |
| 39 | frac{3,8}{2,6+1,2} | Смотреть видеоразбор >> |
| 40 | frac{2,6}{3,1-0,6} | Смотреть видеоразбор >> |
| 41 | frac{6,9}{3,2-5,7} | Смотреть видеоразбор >> |
| 42 | (6,9-3,4) cdot 8,4 | Смотреть видеоразбор >> |
| 43 | 5,4 cdot 1,9 — 2,15 | Смотреть видеоразбор >> |
| 44 | frac{1}{6} cdot 9,6 — 1 | Смотреть видеоразбор >> |
| 45 | frac{1}{frac{1}{2}+frac{1}{3}} | Смотреть видеоразбор >> |
| 46 | frac{18}{7} cdot frac{14}{3} : frac{4}{5} | Смотреть видеоразбор >> |
| 47 | (frac{5}{6}+frac{7}{15}) cdot frac{30}{13} | Смотреть видеоразбор >> |
| 48 | (frac{3}{22}+frac{2}{11}):frac{5}{33} | Смотреть видеоразбор >> |
| 49 | (frac{13}{6}-frac{11}{6}):frac{1}{90} | Смотреть видеоразбор >> |
| 50 | frac{13}{7}:(frac{1}{3}+frac{2}{7}) | Смотреть видеоразбор >> |
| 51 | frac{1,8+1,9}{3,7} | Смотреть видеоразбор >> |
| 52 | frac{7,5+3,5}{2,5} | Смотреть видеоразбор >> |
| 53 | frac{7,3-2,5}{1,2} | Смотреть видеоразбор >> |
| 54 | frac{9,4}{2,1+2,6} | Смотреть видеоразбор >> |
| 55 | frac{4,4}{5,8-5,3} | Смотреть видеоразбор >> |
| 56 | frac{0,6}{1,7-2,9} | Смотреть видеоразбор >> |
| 57 | (5,3-2,8)cdot38 | Смотреть видеоразбор >> |
| 58 | 1,32:1,2-0,8 | Смотреть видеоразбор >> |
| 59 | 3-frac{1}{4}cdot5,6 | Смотреть видеоразбор >> |
| 60 | frac{1}{frac{1}{4}-frac{1}{5}} | Смотреть видеоразбор >> |
| 61 | frac{15}{2}:frac{5}{21}cdotfrac{4}{3} | Смотреть видеоразбор >> |
| 62 | (frac{4}{15}+frac{1}{20})cdot60 | Смотреть видеоразбор >> |
| 63 | (frac{13}{21}+frac{3}{14}):frac{10}{27} | Смотреть видеоразбор >> |
| 64 | (frac{17}{8}-frac{1}{16}):frac{11}{48} | Смотреть видеоразбор >> |
| 65 | 13:(frac{1}{3}+frac{2}{7}) | Смотреть видеоразбор >> |
| 66 | frac{4,2+3,3}{0,3} | Смотреть видеоразбор >> |
| 67 | frac{2,7+5,8}{6,8} | Смотреть видеоразбор >> |
| 68 | (frac{6,8-4,7}{1,4}) | Смотреть видеоразбор >> |
| 69 | frac{5,6}{8,5-2,9} | Смотреть видеоразбор >> |
| 70 | frac{2,1}{6,6-2,4} | Смотреть видеоразбор >> |
| 71 | frac{7,7}{3,7-8,7} | Смотреть видеоразбор >> |
| 72 | 3,5cdot6,6+1,6 | Смотреть видеоразбор >> |
| 73 | 2,7+1,32:1,2 | Смотреть видеоразбор >> |
| 74 | 0,15:frac{3}{7}+1 | Смотреть видеоразбор >> |
| 75 | frac{1}{frac{1}{10}-frac{1}{15}} | Смотреть видеоразбор >> |
Найдите значение выражения (dfrac{7{,}6}{2{,}6+1{,}2}).
Найдите значение выражения (2:0{,}04+34)
Найдите значение выражения (5dfrac{5}{6} — 0{,}5 cdot dfrac{5}{3}).
Вычислите (1{,}7+1{,}56:1{,}2)
Найдите значение выражения (3dfrac{8}{15}-0{,}2cdot 2dfrac{2}{3}).
Найдите значение выражения (left(dfrac{2}{3} — dfrac{1}{5}right)cdot 12).
Найдите значение выражения (left(dfrac{1}{3}+dfrac{1}{5}right)cdot6).
Найдите значение выражения (dfrac{2}{5}+dfrac{1}{4}+2).
Найдите значение выражения (3cdotleft(dfrac{3}{4}+dfrac{1}{12}-dfrac{5}{6}right)).
Вычислите (left(2dfrac{4}{5} – 2dfrac{3}{8}right)⋅16)
В задании №1 ЕГЭ по математике базового уровня необходимо провести элементарные вычисления — сложение, вычитание, деление и умножение дробей. Ответом в первом задании является целое число или конечная десятичная дробь.
Примерное время выполнения: 3 мин.
Разбор типовых вариантов заданий №1 ЕГЭ по математике базового уровня
Во всех заданиях необходимо найти значение выражения.
Вариант 1МБ1
Алгоритм решения:
- Определить порядок действий.
- Выполнить действия в скобках.
- Преобразовать смешанное число в неправильную дробь.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Произвести действия в числителе.
- Знаменатель оставить наименьший общий.
- Умножить числитель получившейся дроби на 9.
- Полученный результат сократить и преобразовать в десятичную дробь.
Решение в общем виде:
Пояснения к решению:
Первым всегда выполняется действие в скобках, в данном случае вычитание.
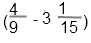
в неправильную дробь. Для этого умножим целую часть на знаменатель, и прибавим числитель
3 • 15 + 1 = 46
Запишем результат в числитель, знаменатель оставим без изменения.
Действие в скобках примет вид:
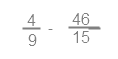
Приводим дроби к общему знаменателю – 45. Для этого по основному свойству дроби необходимо и числитель и знаменатель дроби умножить на одно и то же число, чтобы дробь не изменилась. Это число называется дополнительным множителем. Дополнительный множитель к первой дроби — 5 (9*5=45). Чтобы получить в знаменателе первой дроби 45 необходимо умножить на 5 и числитель и знаменатель.
Вторую дробь умножим на 3 (15 • 3=45)
Действие в скобках после преобразования будет выглядеть так:
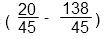
Выполним действие за скобками, в данном случае умножение на целое число. Для этого умножим числитель дроби на 9, а знаменатель оставим без изменений. Числитель и знаменатель полученной дроби сократим на 9, то есть разделим и числитель и знаменатель дроби на 9. По основному свойству дроби дробь не изменится.
Минус в числителе выносится за дробную черту.
Полученную дробь преобразуем в десятичную, поделив в столбик.
Не забудьте о знаке «минус» в ответе.
Ответ: 23,6
Вариант 1МБ2
Алгоритм решения:
- Определить порядок действий.
- Выполнить действие в скобках.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Выполнить вычитание числителей, знаменатель оставить без изменений.
- Выполнить деление. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Решение в общем виде:
 Пояснения к решению:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае вычитание.
Для того чтобы выполнить вычитание дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 4, и на 9. 9 на 4 не делится. Удвоим больший знаменатель: 18 не делится на 4. Утроим больший знаменатель: 27 не делится на 4. Увеличим больший знаменатель в 4 раза: 36 делится и на 9, и на 4 одновременно. Следовательно, 36 – наименьший общий знаменатель для дробей 1/4 и 2/9.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 1/4 и 2/9. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 1/4 нужно умножить на 9(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36. Дробь 2/9 нужно умножить на 4 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36.
В результате получим:
Действие в скобках примет вид:
Выполним вычитание дробей с одинаковыми знаменателями. Для этого вычтем из числителя первой дроби числитель второй, результат запишем в числитель. Знаменатель оставим прежним.

Сократим (разделим и числитель и знаменатель) полученную дробь на 12.
Ответ: 21
Вариант 1МБ3
Алгоритм решения:
- Определить порядок действий.
- Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
- Перевести смешанное число в неправильную дробь.
- Привести полученные дроби к наименьшему общему знаменателю.
- Выполните сложение дробей с одинаковыми знаменателями. Для этого сложить числители, результат записать в числитель, знаменатель оставить без изменений.
- Выполнить деление.
- Перевести смешанное число в неправильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
- Числитель первой дроби умножить на знаменатель второй – записать в числитель. Знаменатель первой дроби умножить на числитель второй результат записать в знаменатель.
- Сократить получившуюся дробь.
- Привести результат к десятичному виду.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
Нужно сложить смешанное число и правильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним. Переведем смешанное число в неправильную дробь:
Действие в скобках примет вид:
Для того, чтобы выполнить сложение дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 5, и на 7. 7 на 5 не делится. Удвоим больший знаменатель: 14 не делится на 5. Утроим больший знаменатель: 21 не делится на 5. Увеличим больший знаменатель в 4 раза: 28 не делится 5. Увеличим больший знаменатель в 5 раз: 35 делится одновременно и на 5, и на 7. Следовательно, 35 – наименьший общий знаменатель для дробей 9/5 и 3/7.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 9/5 и 3/7. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 9/5 нужно умножить на 7(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35. Дробь 3/7 нужно умножить на 5 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35.
В результате получим:
Действие в скобках примет вид:
Выполним сложение дробей с одинаковыми знаменателями. Для этого сложим числители, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Переведем смешанное число в неправильную дробь, для этого целую часть нужно умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
Выполнить деление дробей. Числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель, и знаменатель на одно и то же число) полученную дробь на 39.
Переведем полученную дробь в десятинную.
Ответ: 8,75
Вариант 1МБ4
(6,7 − 3,2) ⋅ 2,4
В данном случае первым действием мы выполняем вычитание в скобках, а затем производим умножение:
6,7 − 3,2 = 3,5
3,5⋅ 2,4 = 8,4
Отдельно остановлюсь на последнем действии. Его можно вычислить умножением в столбик, либо посчитать устно, воспользовавшись следующими логическими операциями:
2,4 ⋅ 3 + 2,4 ⋅ 0,5 = 2 ⋅ 3 + 0,4 ⋅ 3 + 2,4/2 = 6 + 1,2 +1,2 = 8,4
Ответ: 8,4
Вариант 1МБ5
В данном случае необходимо выполнить сложение обыкновенных дробей. Общий знаменатель для дробей в скобках — 15 (если вы забыли как определять общий знаменатель, смотрите здесь). Первую дробь домножаем на 5, вторую на 3. Получаем:
(5 + 3)/15
После сложения:
8/15
Теперь выполняем умножение:
8•6/15 = 48/15
В таком варианте дробь в ответ записать мы не можем, выделяем сначала целую часть, это 3 (45/15=3), в остатке получим:
3/15
После сокращения на 3:
1/5
и перевода в десятичный вид:
1/5 = 20/100 = 2/10 = 0,2
Не забываем про целую часть и получаем ответ:
3,2
Ответ: 3,2
Вариант 1МБ6
- Если представить черту дроби в виде знака деления, то получим выражение: (2,7+5,8):6,8. Отсюда получаем приоритет действий: 1) сложение в скобках; 2) деление. Поэтому сначала выполняем действие в числителе.
- Избавляемся от десятичных запятых в числителе и знаменателе. Для этого применяем основное свойство дроби и умножаем числитель и знаменатель на 10.
- Делим 85 на 68 в столбик.
Решение
Ответ: 1,25
Вариант 1МБ7
- Учитываем приоритетность операций. Здесь 1-м действием выполняется умножение, а затем вычитание.
- При умножении числа записываем друг под другом, выровняв их по последней цифре. В результирующем числе отделяем столько знаков после запятой, сколько имеется суммарно в обоих множителях. В данном случае нужно отделить 2 знака.
- При выполнении вычитания в столбик числа располагают так, чтобы десят.запятые располагались на друг под другом.
Решение
Ответ: 26,7
Вариант 1МБ8
- Умножаем 1/5 на 5,5. При этом 5,5 переходит в числитель дроби.
- Выполняем сокращение полученной дроби на 5. Получаем десят.дробь
- Находим конечную разность.
Решение
Ответ:0,1
Вариант 1МБ9
- Находим разность в скобках. Для этого находим НОК (25, 38) и приводим дроби к общему знаменателю.
- Делим результат в скобках на дробь 6/19. Для этого переходим к умножению дробей, перевернув 9/16 и получив 16/9. Далее сокращаем множители в числителе и знаменателе и находим результирующую дробь.
- Полученную дробь записываем в десят.виде.

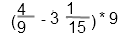
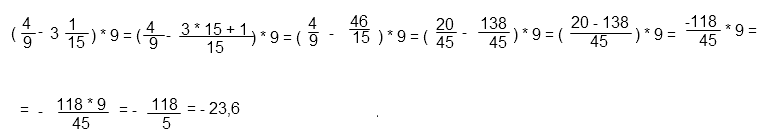
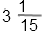
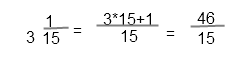
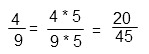
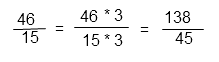
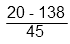
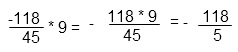
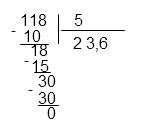
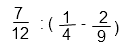
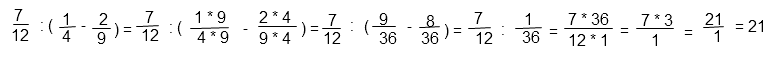 Пояснения к решению:
Пояснения к решению: