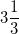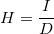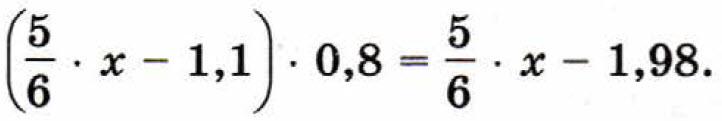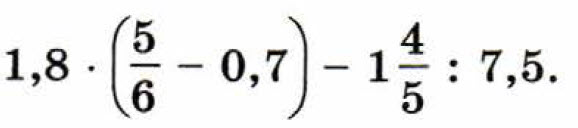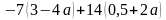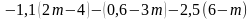Переводной экзамен по математике 6 класс мерзляк

По теме: методические разработки, презентации и конспекты

Промежуточная аттестация по математике

 6 класс

1.    Назначение
КИМ —
оценить уровень общеобразовательной подготовки по математике учащихся 6 классов:
итоговый контроль

2. Документы,
определяющие содержание КИМ

 Федеральный государственный образовательный стандарт основного общего
образования (приказ министерства образования и науки РФ от 7.12.2010 №1987 «Об
утверждении федерального государственного образовательного стандарта основного
общего образования»)

Примерные
программы основного общего образования. Математика. «Просвещение» 2015г.

УМК – «Математика
6» А.Г.Мерзляк, В.Б.Полонский, М.С.Якир, Е.В. Буцко (М.: Вентана-Граф,2015)

3. Подходы к
отбору содержания, разработке структуры КИМ

Структура Ким отвечает
системе дифференцированного обучения математике в современной школе.

Кодификатор
данного КИМ — это кодификатор государственной итоговой аттестации по образовательным
программам общего образования в форме ОГЭ.

4. Содержания КИМ

 Работа
состоит из двух частей и содержит 14 заданий. В первую часть включены 6 заданий
с выбором одного верного ответа из четырех предложенных и 5 задания с кратким
ответом. Задания 1 части соответствуют уровню базовой подготовки обучающихся.

Вторая
часть работа состоит из 3 заданий : 1 –базового уровня,2- повышенного уровня
сложности. На выполнение работы отводится — 40 минут.

5. Обобщенный план
КИМ

6. Система
оценивания

Для оценивания результатов выполнения работы
используется общий балл.  Максимальный балл за работу в целом – 19.

Задания, оцениваемые 1 баллом, считаются выполненными
верно, если указан номер верного ответа (в заданиях с выбором ответа), или
вписан верный ответ (в заданиях с кратким ответом). Задания,
оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал
правильный путь решения, из письменной записи решения понятен ход его
рассуждений, получен верный ответ. В этом случае ему выставляется полный балл,
соответствующий данному заданию. Если в решении допущена ошибка, не имеющая
принципиального характера и не влияющая на общую правильность хода решения, то
выставляется 1 балл

Критерии оценивания заданий 12
задания 2 части

Критерии оценивания заданий 13,14 
задания 2 части

Итоговая
аттестационная работа по математике  за 20___-___ учебный год

ученика
(цы)____ класса    МАОУ «СОШ №4»

Ф.И.
_________________________________________________________

1
вариант

1. Какое из чисел
делится на 5?

1) 121333           2) 133050         3) 411148     
4) 555554

2.Найдите сумму чисел:  и ?

1)   
2)          3)           4)

3.
Вычислите : 4−

1)             2)
     3)           4)

4.Выполните деление  :

 Ответ________________

5.       
Вычислите: 
−12−18

1) −6           2) 30         3)
−30          4)  6

6.  Вычислите:  0,8* (−0,3)

1) 0,24           2) 2,4         3)
-2,4          4) −0,24

7.     
В
классе 20 учеников, 75% из них изучают английский язык. Сколько учеников
изучают английский язык?

Ответ:
_________________

8.      Найдите
неизвестный член пропорции:  6 : х = 3,6 : 0,12

Ответ:__________________

9.      Упростите
выражение:  3(2х−1) − 2(2−4х)

Ответ:__________________

10.  На рисунке
определите координаты точки пересечения прямых АВ и СК

1)     
(3;2)    
2) (−3;0)     3) (2;3)     4) (0; −2)

11. 
На
диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте
на вопрос. Какое озеро занимает третье место по величине площади среди
представленных на диаграмме?

 Ответ____________________________

2 часть

Запишите полное решение

12. 
На первой полке стояло в 3 раза меньше книг, чем на второй. После того как со
второй полки переставили 10 книг на первую, книг на полках стало поровну.
Сколько книг на первой полке?

    13.Периметр треугольника равен 48,8
см. Длина первой стороны составляет 84% от длины второй стороны, а длина
третьей стороны составляет длины
первой стороны. Найдите длину каждой  стороны треугольника.

14.Решите уравнение (14х+21)(1,8-0,3х)=0

Итоговая
аттестационная работа по математике  за 20___-___ учебный год

ученика
(цы)____ класса    МАОУ «СОШ №4»

Ф.И.
_________________________________________________________

2
вариант

1. Какое из чисел
делится на 3?

1)452312       2) 233050         3)
23652         4) 55559

2.Найдите сумму чисел:  и ?

1)             2)                 3)              4)

3.
Вычислите:  7−

1)             2)
                  3)            4)

4.Выполните деление:  :

 Ответ________________

6.       
Вычислите: 
−1,5−2,6

1) −1,1          2) 4,1         3) -3,1         
4)  -4,1

6.  Вычислите:  — 0,9* (−0,4)

1) 0,36           2) 3,6         3) -0,36         
4) −3,6

12.            
В
классе 32 ученика.  25% из них умеют играть в шахматы. Сколько учеников в
классе умеют играть в шахматы ?

Ответ:
_________________

13.  Найдите
неизвестный член пропорции:  6 : 5 = х : 75

Ответ:__________________

14.  Упростите
выражение: 4(-2х+1) − 3(7−5х)

Ответ:__________________

15.  На рисунке
определите координаты точки пересечения прямых EF и PQ

2)     
(6;3)    
2) (−6;3)     3) (3;-6)     4) (-6; −3)

16. 
На
диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте
на вопрос. Какое озеро занимает четвертое место по величине площади среди
представленных на диаграмме?

 Ответ____________________________

2 часть

Запишите полное решение

17.    В двух сараях
сложено сено, причем в первом сарае сена в 3раза больше, чем во втором. После
того как из первого сарая увезли 20т сена, а во второй привезли 10т, в обоих
сараях сена стало поровну. Сколько тонн сена было в каждом сарае?

18.  Садоводы собрали
85 тонн трёх сортов. Масса яблок первого сорта составляет 45% массы яблок
второго сорта, а масса яблок третьего сорта составляет массы яблок первого сорта. Сколько тонн
яблок каждого сорта собрали садоводы?

19.  Решите уравнение
(12х — 6)(2,8 + 0,4х) = 0

Итоговая
аттестационная работа по математике  за 20___-___ учебный год

ученика
(цы)____ класса    МАОУ «СОШ №4»

Ф.И.
_________________________________________________________

3
вариант

1. Какое из чисел
делится на 3?

1) 452312        2) 233051          3)
23653            4) 55551

2.Найдите разность чисел:  и ?

1)               2)  2                 3) 
               4)

3.
Вычислите:  8−

1)             2)
                  3)            4)

4.Выполните деление:  :

 Ответ________________

7.       
Вычислите: 
−23− 28

1) −51          2)   51         3) -5         
4)  5,1

6.  Вычислите:  — 0,7* (−0,6)

1) 0,42          2) 4,2         3) -0,42         
4) −41

20.                      
В
классе 30 учеников 60% из них учатся на «4» и «5».Сколько человек в классе
учатся на «4» и «5»?

Ответ:
_________________

21.  Найдите
неизвестный член пропорции:  х: 5 = 21:15

Ответ:__________________

22.  Упростите
выражение: -2(3х-5) − 3(7+5х)

Ответ:__________________

23.  На рисунке
определите координаты точки пересечения прямых PQ и EF

3)     
(3;-6)    
2) (-6; −3)     3) (6;3)     4) (−6;3)    

24. 
На
диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте
на вопрос. Какое озеро занимает второе место по величине площади среди
представленных на диаграмме?

 Ответ____________________________

2 часть

Запишите полное решение

25.    В первом ящике
было в 5 раз больше апельсинов, чем во втором. Когда из первого ящика взяли 16
апельсинов, а во второй положили 12, то в обоих ящиках апельсинов стало
поровну. Сколько апельсинов было в каждом ящике первоначально?

26.  Садоводы собрали 54
тонны груш трёх сортов. Масса груш первого сорта составляет 55% массы груш
второго сорта, а масса груш третьего сорта составляет массы груш первого сорта. Сколько тонн груш
каждого сорта собрали садоводы?

27.  Решите уравнение
(8х — 24)(4,8 + 0,6х) = 0

Итоговая
аттестационная работа по математике  за 20___-___ учебный год

ученика
(цы)____ класса    МАОУ «СОШ №4»

Ф.И.
(в Р.п.)_________________________________________________________

4
вариант

1. Какое из чисел
делится на 9?

1) 452313        2) 233051          3)
23653            4) 55551

2.Найдите сумму чисел:  и ?

1)               2)  2                 3) 
               4)

3.
Вычислите:  10−

1)             2)
                  3)            4)

4.Выполните деление:  :

 Ответ________________

8.       
Вычислите: 
−15− 36

1) −21          2)   51         3) — 51         
4)  — 41

6.  Вычислите:  — 0,9* (−0,3)

1) 0,27        2) 2,7         3) -0,27        
4) −2,7

28. 
В
классе 25 учеников 96% из них прошли успешно промежуточную аттестацию. Сколько
человек в классе прошли успешно промежуточную аттестацию?

Ответ:
_________________

29.  Найдите
неизвестный член пропорции:  7 :8 = х : 96

Ответ:__________________

30.  Упростите
выражение:  5(- 3х +  5) − 4(7 — 5х)

Ответ:__________________

31.  На рисунке
определите координаты точки пересечения прямых PQ и EF

4)     
(3;-6)    
2) (-6; −3)     3) (−6;3)     4) (6;3)    

32. 
На
диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте
на вопрос. Какое озеро имеет наименьшую площадь среди представленных озер на
диаграмме?

 Ответ____________________________

2 часть

Запишите полное решение

33.        
  На
первом складе было в 3 раза больше телевизоров, чем на втором. Когда с первого
склада увезли 20 телевизоров, а на второй привезли 14, то на обоих складах
телевизоров стало поровну. Сколько телевизоров было на каждом складе первоначально?

34.        
Садоводы
собрали 80 тонны винограда трёх сортов. Масса винограда первого сорта
составляет 35% массы винограда второго сорта, а масса винограда третьего сорта
составляет массы винограда первого сорта. Сколько
тонн винограда каждого сорта собрали садоводы?

35. 
Решите
уравнение (8х — 40)(4,8 + 0,8 х) = 0

Пояснительная записка

Аттестационная работа
(тестирование) составлена
в соответствии с действующей программой по математике на основании
государственного образовательного стандарта общего образования и предназначена
для проведения промежуточной аттестации по математике в 6 -ом классе.

Цель: установление
фактического уровня теоретических знаний обучающихся по математике
обязательного компонента учебного плана, их практических умений и навыков;
установление соответствия уровня ЗУН обучающихся требованиям государственного
образовательного стандарта общего образования.

Задачи: проверить уровень
усвоения учащимися основных тем курса математики 6 класса:

·  обыкновенные
дроби;

·  рациональные числа
и действия над ними;

·  отношения и
пропорции, модуль числа;

·  нахождение дроби
от числа или числа по его дроби;

·  решение текстовых
задач алгебраическим способом;

·  вычислительные
навыки.

Аттестационная работа
(тестирование) содержит
2 варианта. Каждый вари­ант состоит из 10 заданий, которые отличаются уровнем
сложности и формой заданий.

В заданиях
1–7, 9 необходимо записать только
ответ, направлены на проверку достижения уровня базовой подготовки. Она
содержит задания, предусматривающие три формы ответа:

· задания с выбором ответа из четырех
предложенных;

· задания с кратким ответом;

· задания на соотнесения.

С
помощью этих заданий, проверяется знание и понимание важных элементов
содержания. Владение основными алгоритмами, умение применить знания к решению
математических задач, не сводящихся к прямому применению алгоритма, а также
применение знаний в простейших практических ситуациях.

Задания 8, 10
с развернутым ответом и направлены на дифференцированную проверку повышенного
уровня владения материалом. Все задания этой части носят комплексный характер.
Они позволяют проверить владение формально-оперативным алгебраическим
аппаратом, способность к интеграции знаний из различных тем школьного курса,
владение исследовательскими навыками, а также умение найти и применить
нестандартные приемы рассуждений. При выполнении заданий 8, 10 учащиеся должны
продемонстрировать умение математически грамотно записать решение, приводя при
этом необходимые пояснения и обоснования.

В заданиях
1–2 проверяется владение
понятиями отрицательные числа,
обыкновенная дробь.

В задании
3 проверяется умение
находить часть числа и число по его части.

В задании 4 проверяется владение понятием
десятичная дробь.

В
задании 5 проверяется умение находить информацию,               представленную
в таблицах, на диаграммах.

В задании 6 проверяется умение оперировать понятием
модуль числа.

В задании
7 проверяется умение
сравнивать обыкновенные дроби, десятичные дроби и смешанные
числа.

В
задании 8 проверяется умение находить значение арифметического выражения
с обыкновенными дробями и смешанными числами.

Задание 9 направлено на проверку умения решать несложные
логические задачи, а также на проверку умения находить пересечение, объединение, подмножество в простейших
ситуациях.

В задании 10 проверяются умения решать текстовые
задачи на проценты, задачи практического содержания.

На
выполнение аттестационной работы отводится 40 минут.

При выполнении работы нельзя пользоваться учебниками,
рабочими тетрадями, справочниками, калькулятором. При необходимости можно
пользоваться черновиком. Записи в черновике проверяться и оцениваться не будут.

По
результатам работы каждому учащемуся выставляется оценка по матема­тике,
которую учитель заносит в классный журнал на соответствующую страницу. Итоговая
оценка по мате­матике выставляется с учетом оценки за аттестационную работу.

Критерии оценивания

Для
оценивания результатов выполнения работ учащимися применяются два
количественных показателя: традиционная отметка и рейтинг (от 0 до 12 баллов).

Рейтинг
формируется путем подсчета общего количества баллов, полученных учащимися за
выполнение заданий работы.

Правильное решение каждого
из заданий 1–7, 9 оценивается 1 баллом. Задание считается выполненным верно, если ученик дал
верный ответ: записал правильное число, правильную величину. Выполнение заданий 8, 10
оценивается от 0 до 2 баллов.  Максимальный первичный балл – 12.

Учащиеся
выполняют задания на полученных бланках. Исправления и зачеркивания, ес­ли они
сделаны аккуратно, не являются основанием для снижений оценки.

М
– 6                       Аттестационная работа (тестирование)

Вариант 1

1. Вычислите: -31 + 32 : 4.

2. Вычислите:     

3. Число уменьшили в три раза, и получилось 81. Найдите исходное
число.

4. Вычислите: (- 9,7 +2,8) : 2,3

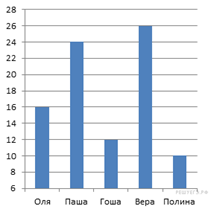
5. На диаграмме показано время, которые ребята тратят на дорогу от
дома до школы. По вертикали указано время в минутах. Сколько в среднем тратят
ребята на дорогу от дома до школы?

6. Найдите значение
выражения   6х -│8х — 13│при х = -5

7. На координатной прямой отмечены точки A, B и C.

Установите соответствие между точками и их координатами.

 В таблице под каждой буквой укажите номер
соответствующей координаты.

Ответ:

8. Вычислите:  Запишите
решение и ответ.

9. В семье Скрипкиных семеро детей: три мальчика и четыре девочки.

Выберете верные утверждения и запишите в ответе их номера.

1) У каждой девочки в семье Скрипкиных сестер больше, чем
братьев.

2) У каждой девочки в семье Скрипкиных 3 сестры.

3) Большинство детей в семье Скрипкиных — девочки.

4) У каждого мальчика в семье Скрипкиных братьев больше,
чем сестер.

10.  Сумма трёх чисел равна 160.
Первое число составляет 14% от этой суммы. Второе число в четыре раза больше
первого. Найдите третье число.  Запишите решение и ответ.

Вариант 2

1. Вычислите: -24 + 72 : 4.

2. Вычислите:      

3. Число уменьшили в семь раз, и получилось 15. Найдите исходное
число.

4. Вычислите: (-7,5 + 1,7) : 2,9

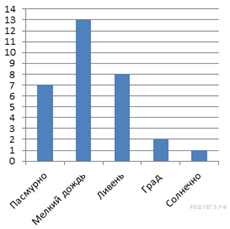
5. На диаграмме представлены данные по погоде в Санкт-Петербурге в
июле. По вертикальной оси указано количество дней. Сколько июльских дней в
Санкт-Петербурге не было осадков?

6. Найдите значение выражения│7
— 4х│- 5х при х = 7

7. На координатной прямой отмечены точки A, B и C.

Установите соответствие между точками и их координатами.

В таблице под каждой буквой укажите номер соответствующей
координаты.

Ответ: 

8. Вычислите:  Запишите
полностью решение и ответ.

9. В ящике стола лежит 7 синих и 6 чёрных ручек.  Выберете верные
утверждения и запишите в ответе их номера.

1) Среди любых 9 ручек обязательно найдётся 3 синих ручки.

2) Если достать 5 ручек, то все они могут оказаться одного
цвета.

3) Среди любых 6 ручек обязательно будет хотя бы одна
чёрная.

4) Среди любых 8 ручек, обязательно найдётся 2 чёрных
ручки.

10. Контрольную работу писало 20 учеников. За выполнение контрольной
работы выставляется одна из отметок: «5», «4», «3» или «2». Отметку «4»
получили 60% учеников, писавших контрольную, а тех, кто получил «2» или «3»
было на 7 человек меньше, чем тех, кто получил «4». Сколько учеников получили
отметку «5»? Запишите решение и ответ.

Ответы для поверки

аттестационной работы
по математике

(тестирования)

Промежуточная аттестационная работа по математике.

Контрольная работа.

Демонстрационный вариант.

Часть 1. В заданиях 1–4 выберите один правильный, по вашему мнению, ответ.

1. Укажите наибольший общий делитель чисел 60 и 24.

а) 24 б) 12 в) 6 г) 4

2. Найдите неизвестный член пропорции







х



а) 24 б) 30 в) 20 г) 15

3. Укажите верное неравенство:

а) -3,7 < -3,6 б) -5 < -5,1 в) 0 < -7 г) —2,8 ˃ -2,6

4. Вычислите значение выражения (4,6 – 7,4) : (–0,4).

а) 0,7 б) – 0,7 в) 7 г) – 7

Часть 2. В заданиях 5–10 выполните решение.

5. Выполните действия: (











 





6. В доме 16 трехкомнатных квартир, что составляет





количества всех квартир в доме. Сколько в

этом доме квартир?

7. Упростите выражение –3(x – 5y) + 5(x + 3y) =

8. Решите задачу с помощью уравнения. В первом бидоне было в 5 раз больше молока, чем во

втором. После того как из первого бидона отлили 2 л, а во второй долили 6 л, в обоих бидонах

молока стало поровну. Сколько литров молока было во втором бидоне первоначально?

9. Отметьте на координатной плоскости точки M(2; 3) и N(–2; –1). Проведите отрезок MN. Найдите

координаты точки пересечения отрезка MN с осью абсцисс.

Вопросы к промежуточной аттестации

по математике

в 6 классе

(по учебнику А.Г. Мерзляка)

Вопросы для устного экзамена по математике в 6 классе.

Каждый билет состоит из двух вопросов, первый – теория по курсу математики 5-6 классов, второй – практическое задание.

1. Определение натурального числа. Законы сложения и умножения: переместительный, сочетательный, распределительный (формулы и правила).

2. Обыкновенные дроби. Правильные и неправильные дроби. Сложение и вычитание дробей с одинаковым знаменателем. Смешанные числа. Перевод из неправильной дроби в смешанное число (выделить целую часть) и из смешанного числа в неправильную дробь.

3. Десятичные дроби. Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной. Сложение и вычитание десятичных дробей.

4. Умножение и деление десятичных дробей на 10, 100, 1000 и т.д. Умножение и деление десятичной дроби на десятичную дробь.

5. Делители и кратные. Признаки делимости на 2, 3, 5, 9, 10, 4, 8.

6. Простые и составные числа, взаимно простые числа. Разложение на простые множители. Нахождение НОД и НОК чисел.

7. Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю.

8. Правила сложения, вычитания, умножения и деления обыкновенных дробей.

9. Взаимно обратные числа. Правила нахождения дроби (процентов) от числа и числа по значению его дроби (процентов).

10. Преобразование обыкновенной дроби в десятичную дробь. Бесконечные периодические десятичные дроби (примеры). Рациональные числа.

11. Отношения и пропорция. Основное свойство пропорции.

12. Прямая и обратная пропорциональные зависимости. Случайные события и вероятность случайного события.

13. Окружность и круг (понятия радиуса, диаметра, хорды). Длина окружности и площадь круга (формулы). Площадь квадрата и прямоугольника (формулы). Объем куба и прямоугольного параллелепипеда (формулы).

14. Целые числа. Противоположные числа. Понятие модуля числа. Сравнение положительных и отрицательных чисел.

15. Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

16. Переместительное, сочетательное и распределительное свойства умножения рациональных чисел. Коэффициент. Правила раскрытия скобок, перед которыми стоит знак «плюс» или знак «минус».

17. Решение уравнений. Что значит «решить уравнение». Что такое «корень уравнения».

18. Прямая, отрезок, луч. Перпендикулярные и параллельные прямые. Свойство параллельных прямых.

19. Центральная и осевая симметрии (примеры).

20. Представление о координатной плоскости. Координаты точки на плоскости. График.

Практические задания к экзамену.

1. Задачи на проценты.

1. За контрольную работу по математике было поставлено 15% пятёрок. Сколько учеников писало контрольную работу, если пятёрки получили 6 человек?

(Ответ. 40 учеников)

1. Из 76 м² площади квартиры кухня занимает 12%. Найдите площадь кухни.

(Ответ. 9,12 м²)

1. Примеры на действия с положительными и отрицательными числами.

1. Задание на нахождение длины окружности и площади круга.

Найдите длину окружности и площадь круга, если диаметр круга равен 15 см. (Число 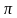округлите до сотых).

(Ответ. C = 47,1 см, S = 176,625 см²)

1. Задачи на масштаб.

а) На чертеже изображен прямоугольник, площадь которого 216 см². Найдите площадь этого прямоугольника в действительности, если чертеж выполнен в масштабе 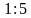. (Ответ. 1080 см²)

б) Расстояние между двумя городами равно 615 км. Каким будет это расстояние на карте, если масштаб карты 1:1500000? (Ответ. 41 см)

1. Координатная плоскость: построение точек с указанными координатами и нахождение координат указанных точек.

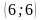
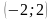
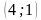
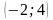
Отметьте на координатной плоскости точки M , N , K и P . Укажите в какой четверти лежит каждая точка. Проведите прямые MN и KP. Найдите координаты точки пересечения:

а) прямых MN и KP;

б) прямой MN с осью абсцисс;

в) прямой KP с осью ординат.

(Ответ. Точки K, M – 1 ч. и точки N, P – 2 ч.; а) (0;3); б) (-6;0); в) (0;3))

1. Задача на формулу объёма прямоугольного параллелепипеда.

Ширина прямоугольного параллелепипеда 12 дм, длина в 3 раза больше, а высота на 3 дм больше ширины. Найдите объем прямоугольного параллелепипеда. (Ответ. 6480 дм³).

1. Задание на понятие модуля числа.

Найдите значение выражения:

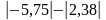
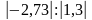
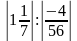
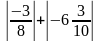
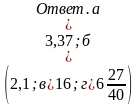
а) б) в) г)

1. Упростить выражения.

1. Текстовая задача на движение.

Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.

(Ответ. 3,2 км/ч и 12,8 км/ч)

1. Текстовая задача на составление уравнения.

На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свёклы, а капусты – на 80 кг больше, чем свёклы. Сколько кг каждой культуры было собрано?

(Ответ. 40 кг свёклы, 200 кг картофеля, 120 кг капусты)

1. Задание на нахождение НОД и НОК чисел.

Найдите наименьшее общее кратное и наибольший общий делитель чисел:

а) 68 и 170;

б) 792 и 1188.

(Ответ. а) НОД = 34, НОК = 340; б) НОД = 396, НОК = 2376)

1. Примеры на действия с обыкновенными дробями.

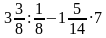
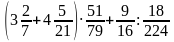
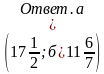
а) б)

1. Решение уравнений.

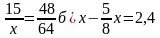
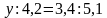
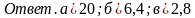
а) в)

( )

1. Задачи на пропорции.

1. 24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью? (Ответ. 4 дня)

2. Для изготовления 14 деталей требуется 16,8 кг металла. Сколько металла пойдет на изготовление 27 таких деталей? (Ответ. 32,4 кг металла)

1. Примеры на действия с десятичными дробями.

а) ;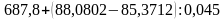

б)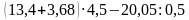

(Ответ. а) 748; б) 36,76)

1. Задания на сравнение чисел.

Сравните числа:

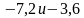
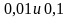
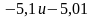
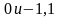
а) ; б) ; в) ; г) ;

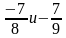
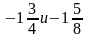
д) ; е) .

1. Примеры на действия с обыкновенными, десятичными дробями и квадрат, куб числа.

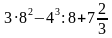
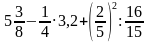
а) 1 ; б)

1. Задание на раскрытие скобок.

Раскройте скобки и найдите значение выражения:

а) ;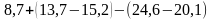

б) .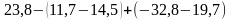

(Ответ. )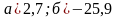

1. Решение уравнений.

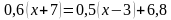
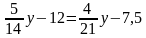
а) ; б)

(Ответ. )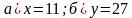

1. Задачи на нахождение дроби от числа и числа по его дроби.

1) Рабочие засадили пшеницей 0,6 часть участка, что составляет 132 га. Какова площадь всего участка, который нужно засадить? (Ответ. 220 га)

2) В магазине 1 кг конфет стоит 318 рублей. Сколько стоят 0,4 кг этих конфет? (Ответ. 127,2 р.)

1. Определение натурального числа. Законы арифметических действий: переместительный, сочетательный, распределительный.

1. Обыкновенные дроби. Правильные и неправильные дроби. Смешанные числа.

1. Определение десятичной дроби. Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной.

1. Арифметические действия с десятичными дробями (правила сложения, вычитания, умножения, деления).

1. Определения уравнения и корня уравнения. Перенос слагаемых из одной части уравнения в другую.

1. Проценты. Нахождение процента от величины, величины по её проценту.

1. Определение целого числа. Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

1. Определение простого и составного числа, взаимно простых чисел. НОД и НОК чисел.

2. Признаки делимости на 2, 3, 5, 9,10, 4, 8.

1. Правила сложения, вычитания, умножения и деления обыкновенных дробей.

1. Правила нахождения части от целого и целого по его части.

1. Представление об отношении и о пропорции. Основное свойство пропорции.

1. Понятие модуля числа. Противоположные числа.

1. Представление о координатной плоскости. Координаты точки.

1. Прямая, отрезок, луч как геометрические понятия. Перпендикулярные и параллельные прямые.

1. Определение угла. Виды углов. Биссектриса угла.

1. Треугольник. Виды треугольников. Сумма углов треугольника.

1. Окружность, круг как геометрические фигуры. Длина окружности и площадь круга.

1. Правила раскрытия скобок, перед которыми стоит знак «плюс» или знак «минус». Подобные слагаемые.

1. Прямоугольный параллелепипед и куб. Формулы объёма.

1. Задачи на проценты.

1) За контрольную работу по математике было поставлено 15% пятёрок. Сколько учеников писало контрольную работу, если пятёрки получили 6 человек?

2) Из 76 м² площади квартиры кухня занимает 12%. Найдите площадь кухни.

1. Примеры на действия с положительными и отрицательными числами.

1. Задание на нахождение длины окружности и площади круга.

Найдите длину окружности и площадь круга, если диаметр круга равен 15 см. (Число 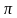округлите до сотых).

1. Задачи на масштаб.

а) На чертеже изображен прямоугольник, площадь которого 216 см². Найдите площадь этого прямоугольника в действительности, если чертеж выполнен в масштабе .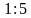

б) Расстояние между двумя городами равно 615 км. Каким будет это расстояние на карте, если масштаб карты 1:1500000?

1. Координатная плоскость: построение точек с указанными координатами и нахождение координат указанных точек.

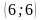
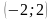
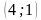
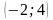
Отметьте на координатной плоскости точки M , N , K и P . Укажите в какой четверти лежит каждая точка. Проведите прямые MN и KP. Найдите координаты точки пересечения: а) прямых MN и KP; б) прямой MN с осью абсцисс; в) прямой KP с осью ординат.

1. Задача на формулу объёма прямоугольного параллелепипеда.

Ширина прямоугольного параллелепипеда 12 дм, длина в 3 раза больше, а высота на 3 дм больше ширины. Найдите объем прямоугольного параллелепипеда.

1. Задание на понятие модуля числа.

Найдите значение выражения:

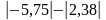
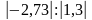
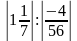
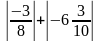
а) б) в) г)

1. Упростить выражения.

1. Текстовая задача на движение.

Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.

1. Текстовая задача на составление уравнения.

На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свёклы, а капусты – на 80 кг больше, чем свёклы. Сколько кг каждой культуры было собрано?

1. Задание на нахождение НОД и НОК чисел.

Найдите наименьшее общее кратное и наибольший общий делитель чисел:

а) 68 и 170;

б) 792 и 1188.

1. Примеры на действия с обыкновенными дробями.

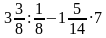
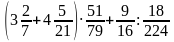
а) б)

1. Решение уравнений.

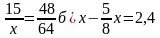
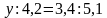
а) в)

1. Задачи на пропорцию.

1) 24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?

2) Для изготовления 14 деталей требуется 16,8 кг металла. Сколько металла пойдет на изготовление 27 таких деталей?

1. Примеры на действия с десятичными дробями.

а) ;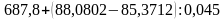

б)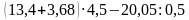

1. Задание на сравнение чисел.

Сравните числа:

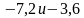
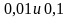
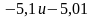
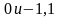
а) ; б) ; в) ; г) ;

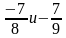
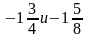
д) ; е) .

1. Примеры на действия с обыкновенными, десятичными дробями и квадрат, куб числа.

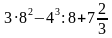
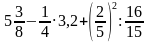
а) 1 ; б)

1. Задание на раскрытие скобок.

а) ;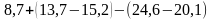

б) .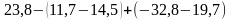

1. Решение уравнений.

а) ;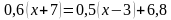

б)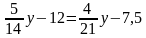

1. Задачи на нахождение части от целого и целого по его части.

1) Рабочие засадили пшеницей 0,6 часть участка, это составляет 132 га. Какова площадь всего участка, который нужно засадить?

2) В магазине килограмм конфет стоит 318 рублей. Сколько стоят 400 грамм этих конфет?